Rapid branching

Abstract

We propose rapid branching (RB) as a general branch-and-bound heuristic for solving large scale optimization problems in traffic and transport. The key idea is to combine a special branching rule and a greedy node selection strategy in order to produce solutions of controlled quality rapidly and efficiently. We report on three successful applications of the method for integrated vehicle and crew scheduling, railway track allocation, and railway vehicle rotation planning.

1 Introduction

Traffic and transport is one of the classical application areas of combinatorial optimization and integer programming. Network-based models, which give rise to integer programming formulations, which in turn can be solved by column generation algorithms, have proved particularly effective. Successful applications of this approach include network design, line planning, timetabling, track allocation, platforming, fleet, vehicle, and tail assignment, crew scheduling, rostering, and assignment, and many others, see Lusby et al. (2011) and Borndörfer et al. (2010a) for overviews.

Network models for transportation problems involve a large scheduling graph, in which some cost-minimal structure such as a collection of paths or cycles has to be determined. The size of this structure, measured in numbers of arcs, is in general (sub)linear in the number of nodes |V|, while the number of network arcs is quadratic (or larger for multi-commodity type problems), i.e., the relative size of the solution structure in the network model is O(|V|⁻¹), which goes to zero as |V| goes to infinity. This obvious observation has an unavoidable algorithmic consequence: In fact, branching on individual arcs makes little difference in large models, and the zero branch is infinitely worse in this respect than the one branch. This “empty space” phenomenon is unavoidable. On the positive side, however, many of these models produce amazingly strong linear programming (LP) relaxations.

Rapid branching is a partial branch-and-bound method that is built on these two observations. The main ideas are to drive the LP relaxations towards integrality by slight perturbations (perturbation branching), and to branch on large sets of variables simultaneously to one, controlled by a “target” estimation of the expected objective value, and backtracking in a binary search manner if necessary (binary search branching). The method fits perfectly with approximate large-scale LP solution methods, in particular, the bundle method.

Rapid branching was initially developed for the solution of integrated vehicle and duty scheduling problems in public transport, see Weider (2007) and Borndörfer et al. (2008). Recently, it has also been successfully applied to railway track allocation problems (Schlechte 2012), and railway vehicle rotation planning (Borndörfer et al. 2011). We are convinced that rapid branching works for other problems of this type as well. We document in this article the rapid branching method and our three successful applications, providing computational results for real-world large-scale problems.

Search methods using branching on sets of variables, rather than individual variables, are well known in the literature and have their origin in the works of Beale and Tomlin (1970) and Beale and Forrest (1976). They introduced the notion of special ordered sets (SOS) of 0/1 variables, of which one (SOS1 constraints) or two consecutives ones (SOS2) can have a value of one. This structure can be exploited to produce a balanced branch-and-bound tree by recursively subdiving the SOS, fixing entire subsets of variables to zero. Different ways to choose the these subsets have been suggested, some exploiting a modelling background (e.g., using SOS2 constraints to construct piecewise linear approximations of nonlinear functions), some using general LP information. When applied to models involving SOS constraints (as most combinatorial optimization problems do and as we do in this paper), rapid branching can be seen as a heuristic branching method of this kind, which places specific emphasis on mastering a column generation context. In fact, all our applications lead to very large-scale models that can not be written down explicitely and for which rapid branching is the only way we know to produce high quality integer solutions.

The organization of the paper is as follows. Section 2 describes the rapid branching method in a general problem setting. Section 3 provides details and computational results for an application to integrated vehicle and duty scheduling in public transit. Rapid branching for railway track allocation problems is discussed in Sect. 4. We finally report results on railway vehicle rotation planning in Sect. 5.

2 Rapid branching

Branch-and-bound is a basic method to solve combinatorial optimization problems. The idea is to partition the finite and discrete solution space of a problem into subsets (“branch”) and to prune subsets which can be excluded from containing the optimum by using lower bounds (“bound”). This is done recursively until an optimal solution is found. Rapid branching tries to branch in order to construct solutions rapidly. The branching is done in a heuristic manner, i.e., subsets are not only pruned because of their bounds.

We introduce the following notation in order to describe the method.

Definition 1

(integer program (IP))

Given a matrix $A \in \mathbb {R}^{m \times n}$, vectors $b \in \mathbb {R}^{m}$, and c∈R ⁿ, the binary integer program IP=(A,b,c) is to solve

The vectors contained in the set X _IP ={x∈{0,1}ⁿ : Ax=b} are called feasible solutions of IP. A feasible solution x ^⋆∈X _IP of IP is called optimal if its objective value satisfies c ^T x ^⋆=c ^⋆(IP).

We consider problems (IP) with the following characteristics. The number of constraints is rather small in comparison to the number variables, i.e., n≫m; we will therefore use a column generation procedure to solve (IP). Furthermore, the linear relaxation (LP) of problem (IP) is reasonably strong, i.e., (1+ϵ)c ^⋆(LP)=c ^⋆(IP) with some small ϵ≥0. In addition, we assume that the problems are feasible (which is a rather strong assumption). However, in most cases it is possible to find a problem formulation that guarantees feasibility by adding appropriate slack variables.

Let l,u∈{0,1}ⁿ, l≤u, be vectors of bounds that model fixings of variables to 0 and 1. Denote by L:={j∈{1,2,…,n}:u _j =0} and U:={j∈{1,2,…,n}:l _j =1} the set of variables fixed to 0 and 1, respectively, and by

the problem derived from IP by such fixings. Denote further by N⊆1,2,…,n some set of variables which have, at some point in time, already been generated by a column generation algorithm for the solution of IP. Let RIP and RIP(l,u) be the restrictions of the respective IPs to the variables in N (we assume that L,U⊆N holds at any time when such a program is considered, i.e., variables that have not yet been generated are not fixed). Finally, denote by MLP, MLP(c,l,u), RMLP, and RMLP(c,l,u) the LP relaxations of the integer programs under consideration; MLP and MLP(c,l,u) are called master LPs, RMLP and RMLP(c,l,u) restricted master LPs. We included the objective c in the notation for MLP(c,l,u) and RMLP(c,l,u) because the tree construction of rapid branching is guided by perturbations of the original cost vector c. More details will be given in Sect. 2.1.

The main idea of the rapid branching heuristic is that fixing a single variable to zero or one has most of the time almost no effect on the value of the LP relaxation of the (IP), see Lübbecke and Desrosiers (2005). The authors of Borndörfer et al. (2008), see also the thesis (Weider 2007), proposed in the context of integrated vehicle and duty scheduling a heuristic that tries to overcome this problem by a combination of cost perturbation to “make the LP more integer”, partial pricing to generate variables that are needed to complete integer solutions down in the tree, a selective branching scheme to fix large sets of variables, and an associated backtracking mechanism to correct wrong decisions. Rapid branching belongs to the class of branch-and-generate (BANG) methods for the construction of high-quality integer solutions for very large scale integer programs. Branch-and-generate is an adaption of a branch-and-price algorithm with partial pricing and branching, see Subramanian et al. (1994).

Rapid branching tries to compute a solution of IP by means of a search tree with nodes IP(l,u). Starting from the root (IP)=(IP)(0,1), nodes are spawned by additional variable fixings using a strategy that we call perturbation branching. The tree is depth-first searched, i.e., rapid branching is a plunging (or diving) heuristic. The nodes are analyzed heuristically using restricted master LPs RMLP(c,l,u). The generation of additional columns and node pruning are guided by so-called target values as in the branch-and-generate method. To escape unfavorable branches, a special backtracking mechanism is used that performs a kind of partial binary search on variable fixings. The idea of the method is as follows: we try to make rapid progress towards a feasible integer solution by fixing large numbers of variables by perturbation branching in each iteration, repairing infeasibilities or deteriorations of the objective by regeneration of columns if possible, and exploring the tree in a binary search manner with controlled backtracking.

We give a generic variant of rapid branching in Algorithm 1. The sets S ₀,S ₁,… of Algorithm 1 are sets of subsets of the solution space X _IP of IP. At every iteration i we select one element of S _i denoted by N _i (line 3). This step will be explained in detail in Sect. 2.2. Solving a relaxation, e.g., a linear relaxation or Lagrangian relaxation of problem IP restricted to set N _i (line 4) provides a lower bound of the corresponding subproblem. In addition, we use advanced solution techniques like column generation for large scale problem instances in that step. If we found a feasible solution for IP (line 5), which can happen if the relaxation is integral or some heuristic provides a solution, we update our best incumbent solution for problem IP in case of an improvement. Then we either delete it (line 13) because of a larger lower bound in comparison to our best incumbent solution or we subdivide it into disjoint sets (line 20). In our implementations of rapid branching we also use a target objective value, which will be used additionally to ignore subproblems with an unfavourable lower bound. Note that in that case we accept to cut off heuristically potential solutions (line 13).

Algorithm 1

Rapid branching (for minimization problems)

In a complete search like full branch and bound, a partition $N_{i} = \bigcup_{j=1}^{k^{i}} Q^{j}_{i}$ is used for the decomposition. Rapid branching concentrates only on some promising subsets Q _i ⊂N _i of the solution space. In Sect. 2.1 we will explain the perturbation branching method which determines the remaining subproblems to evaluate.

Figure 1 shows a rapid branching run for a track allocation problem, namely, scenario r_48 of the TTPlib, see also Sect. 4. On the left hand side the objective value of the primal solution, the upper bound, and the objective of the fixation evaluated by the rapid branching heuristic is plotted. In the initial LP stage (dark gray/blue), a global upper bound is computed by solving the Lagrangian dual using the bundle method after approximately 15 seconds. In that scenario the upper bound is only slightly below the trivial upper bound, i.e., the sum of all maximum profits. In the succeeding IP stage (light gray/blue) an integer solution is constructed by a simple greedy heuristic and improved by the rapid branching heuristic. It can be seen that the final integer solution has virtually the same objective value as the LP relaxation and the method is able to close the gap between the greedy solution and the proven upper bound. On the right hand side of the figure, one can see that indeed often large numbers of variables are fixed to one and several backtracks are performed throughout the course of the rapid branching heuristic until the final solution was found. In addition, we plotted the development of the integer infeasibilities, i.e., the number of integer variables that still have a fractional value.

Fig. 1

Solving track allocation problem r_48 with rapid branching

2.1 Perturbation branching

The idea of perturbation branching is to solve a series of MLPs with objectives c ⁱ,i=0,1,2,… that are perturbed in such a way that the associated LP solutions x ⁱ are likely to become more and more integral. In this way, we hope to construct an almost integer solution at little cost. The perturbation is done by decreasing the cost of variables with LP values close to one according to the formula:

$$\begin{array}{l@{\quad }l} c^0_j := c_j, & j\in N \\ c^{i+1}_j := c^i_j - c_j\alpha x_j^2, & j\in N, \ i=0,1,2, \ldots. \end{array} $$

The idea behind this quadratic perturbation is that variables with values close to 1 are driven towards 1. The perturbation factor α>0 controls the rate of decreasing the costs. The progress of this procedure is measured in terms of the potential function

$$v\bigl(x^i\bigr) := c{^{\textsf {T}}}x - \delta \bigl|B\bigl(x^i\bigr)\bigr|, \quad B\bigl(x^i\bigr) := \bigl\{ j\in N: x^i_j > 1 - \epsilon \bigr\}, $$

where ϵ and δ are parameters for measuring near-integrality and the relative importance of near-integrality (we use ϵ=0.1 and δ=1), and B(x ⁱ) is the set of variables that are one or almost one. The perturbation is continued as long as the potential function decreases; if the potential does not decrease for some time, a spacer step is taken in an attempt to continue, i.e., we use as simple backup strategy to perturbate the objective of the most fractional variable and add this variable to the candidate set. On termination, the variables in the set B(x ⁱ) associated with the minimal potential are fixed to one. If no variables at all are fixed, we choose a single candidate by strong branching, see Applegate et al. (1995). Objective perturbation has also been used in Wedelin (1995) for the solution of large-scale set partitioning problems, and, e.g., in Eckstein and Nediak (2007) in the context of general mixed integer programming.

Algorithm 2 gives a pseudocode listing of the complete perturbation branching procedure. The main work is in solving the perturbed reduced master LP (line 3), generating new variables if necessary. Fixing candidates are determined (line 4) and the potential is evaluated (line 5). If the potential decreases (in case of minimization the approximate costs) (lines 15–17), the perturbation is continued (line 18). If no progress was made for k _s  steps (line 10), the objective is heavily perturbed by a spacer step in an attempt to continue (lines 10–13). However, this perturbation does not guarantee that any variable will get a value above 1−ϵ, for arbitrary ϵ>0. If this happens and the iteration limit is reached, a single variable is fixed by strong branching (line 24).

Algorithm 2

Perturbation branching (in case of a minimization problem)

2.2 Binary search branching

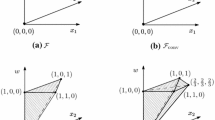
The fixing candidate sets B ^∗ produced by the perturbation branching algorithm are used to define nodes in a branch-and-generate search tree by imposing bounds x _i =1 for all i∈B ^∗. This typically fixings many variables to one, which is what we wanted to achieve. However, sometimes too much is fixed and some of the fixings turn out to be disadvantageous. In such a case we must backtrack. We propose to do this in a binary search manner by successively undoing half of the fixings until either the fixings work well or only a single fix is left as shown in Fig. 2. We call this incomplete search procedure binary search branching.

Fig. 2

The considered and ignored branch and bound nodes for candidates B ^∗

Let B ^∗ be a set of potential variable fixings proposed by perturbation branching, see Algorithm 2, and K=|B ^∗|. Assume the variables in B ^∗ are sorted by some reasonable criterion as i ₁,i ₂,…,i _K and define sets

$$B^\ast_{k} := \{i_1, \ldots,i_k\}, \quad k=1, \ldots,K. $$

We denote the associated subproblems by

$$P_k = \min\limits _{l\leq x \leq u} \bigl\{ c {^{\textsf {T}}}x \, : \,Ax = b, x \in [0,1]^n \mid x_{j} = 1, j \in B^\ast_k \bigr\} $$

or short . The complement of problem P _K is the set of solutions where at least one of the variables in $B^{\ast}_{K}$ is zero. This could be formulated by adding a constraint of the type

$$\sum_{i\in B^\ast_K} x_i \leq \bigl|B^\ast_K\bigr|-1 $$

to the current solution set, but this may destroy the structure of the pricing problem. Therefore, we split this solution set into |K| subsets as if we had fixed the variables in B ^∗ subsequently. Consider the problems

with 1≤k≤K. Then holds.

We focus on the search tree nodes defined by fixing

$$x_j=l_j=1,\quad j\in B^\ast_k, \ k=K, \lceil K/2\rceil, \lceil K/4\rceil, \ldots,2,1. $$

These nodes are examined in the above order. Namely, we first try to fix all variables in $B^{\ast}_{K}$ to one, since this raises hopes for maximal progress. If this branch comes out worse than expected, it is pruned, and we backtrack to examine $B^{\ast}_{\lceil K/2\rceil}$ and so on until possibly $B^{\ast}_{1}$ is reached. In this situation, the single fix is applied imperatively. The resulting search tree is a path with some pruned branches, i.e., binary search branching is a plunging heuristic. Figure 2 shows the ignored nodes and the potentially evaluated ones (P _k ,P ₄,P ₂, and P ₁).

In our implementation, we order the variables by increasing reduced cost of the restricted root LP, i.e., we unfix half of the variables of smallest reduced cost. This sorting is inspired by the scoring technique of Caprara et al. (2000). The decision whether a branch is pruned or not is done by means of a target value as introduced in Subramanian et al. (1994). Such a target value is a guess about the development of the LP bound if a set of fixings is applied. Furthermore, we use a linear function of the integer infeasibility. If the LP bound stays below the target value, the branch develops according to our expectations, if not, the branch “looks worse than expected” and we backtrack, see line 13 of Algorithm 1. In terms of Algorithm 1 we choose

$$S_{i+1} = \bigl(S_i \setminus \{N_i\}\bigr) \cup \bigl\{B^\ast_{\lceil K\rceil}\bigr\} \cup \bigl\{B^\ast_{\lceil K/2\rceil} \bigr\} \cup \bigl\{B^\ast_{\lceil K/4\rceil}\bigr\} \cdots \bigl \{B^\ast_{\lceil 2\rceil}\bigr\} \cup \bigl\{B^\ast_{\lceil 1\rceil} \bigr\} $$

in Step 20 and evaluate it recursively in chronological order in Step 3.

3 Integrated duty and vehicle scheduling

In this section we apply the rapid branching heuristic to the integrated duty and vehicle scheduling problem in public transit (ISP). Vehicle and duty scheduling are two of the most important planning steps in public transit, because vehicles and drivers are the two most important cost factors of public transit companies. Often at first vehicles and then drivers are scheduled. But, in particular, for regional public transit vehicles and drivers have to be scheduled in one planning step, because there are few relief points for drivers and thus the interdependencies between drivers and vehicles are stronger than in an urban context.

The resulting integrated problems are quite large, because on the one hand the number of potential deadhead trips grows quadratically in the number of timetabled trips, on the other hand, the number of potential vehicle changes of drivers is also quite large, resulting in a complex graph model and a potentially huge integer programming model. To tackle this complexity, we use column generation in the duty scheduling subproblem, and the rapid branching heuristic to find high quality integer solutions.

3.1 Model and algorithm

Let $\mathcal {D}$ be the set of all feasible duties, $\mathcal {F}$ the set of all potential deadhead trips, and $\mathcal {T}$ the set of timetabled trips. The set of duties which contain deadhead trip $f\in \mathcal {F}$ and the set of duties which contain timetabled trip $t\in \mathcal {T}$ are denoted by $\mathcal {D}_{f}$ and $\mathcal {D}_{t}$, respectively. We consider the vehicle scheduling graph with nodes associated with set $\mathcal {T}$ and arcs associated with $\mathcal {F}$ or pull-in or pull-out trips. In addition, we distinguish between different commodities $g\in \mathcal {G}$, which result from different depots or vehicle types. The set of all ingoing deadheads or pull-in trips of $t\in \mathcal {T}$ is defined as $\delta _{}^{\mathrm {in}} (t)$ and accordingly $\delta _{g}^{\mathrm {out}} (t)$ denotes the set of all outgoing arcs of t associated with either with deadheads of commodity g or a pull-out trip. Furthermore, c _d and c _f are cost values associated to duty d and deadhead f, respectively. Then the model (ISP) reads:

$$\begin{aligned} &\min \sum_{d\in \mathcal {D}} c_{d}x_{d} + \sum_{f\in \mathcal {F}}c_{f} y_{f}, \end{aligned}$$

(3.1)

$$\begin{aligned} &\mbox{such that} \\ &\phantom{\mbox{such that}}\quad \sum_{d\in \mathcal {D}_{t}} x_{d} = 1, \quad \forall t\in \mathcal {T} , \end{aligned}$$

(3.2)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum_{f\in \delta _{g}^{\mathrm {in}} (t) } {y_{f}} - \sum_{f\in \delta _{g}^{\mathrm {out}} (t) } {y_{f}} = 0, \quad \forall t\in \mathcal {T}, g\in \mathcal {G}, \end{aligned}$$

(3.3)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum_{f\in \delta _{}^{\mathrm {in}} (t) } {y_{f}} = 1, \quad \forall t\in \mathcal {T}, \end{aligned}$$

(3.4)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum_{d\in \mathcal {D}_{f}} x_{d} -y_{f} = 0, \quad \forall f\in \mathcal {F}, \end{aligned}$$

(3.5)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad x_{d}, y_{f} \in\{0,1\}, \quad \forall d\in \mathcal {D},\; f\in \mathcal {F}. \end{aligned}$$

(3.6)

The variables x _d , $d\in \mathcal {D}$ are 1 if duty d is in the solution and 0 otherwise. Analogously, y _f , $f\in \mathcal {F}$ is 1 if the respecting deadhead is used and zero otherwise. The objective (3.1) minimizes the total cost of the duty and vehicle schedule. Equations (3.2) of (ISP) are set-partitioning constraints that model, that every obligatory task from the timetable is serviced by exactly one duty. Equations (3.3) ensure that every block uses only trips of the same commodity. Equations (3.4) can be interpreted as set partitioning constraints, because they take care that every timetabled trip is covered by exactly one arc ending at it. Thus, Eqs. (3.3) and (3.4) are forming a multi-commodity min-cost-flow-problem guaranteeing that every timetabled trip is serviced by exactly one vehicle. Finally, the coupling constraints (3.5) are ensuring that every deadhead trip used in a duty is also serviced by a vehicle.

Our algorithm IsOptsolves (ISP) in a two stage approach. In the first stage the vehicle variables y are fixed by rapid branching, in the second stage the duty variables x are also fixed by rapid branching. The LP-relaxation of (ISP) as well as the LP-relaxation of the duty scheduling subproblem is solved by the proximal bundle method (see Kiwiel 1995). Further details on the model and on the solver IsOpt can be found in Weider (2007) or Borndörfer et al. (2008).

3.2 Scenarios

We present in this section rapid branching results for four scenarios.

Scenario 1 is a mainly urban one stemming from a southeast-European public transit carrier. Scenario 2 is mixed regional and urban, from an east-Baltic company, scenario 3 is a German regional scenario, and scenario 4 is a small German urban scenario with many relieve points and deadheads. Column 2 of Table 1 contains the number of tasks that has to be covered by duties, this number is equal to the number of rows of constraints (3.2) of (ISP). Column 3 contains the number of timetabled trips, they may differ from the number of tasks, because a trip may contain a relief point for drivers, where drivers can enter or leave the vehicle. The number of trips is equal to the number of constraints (3.4). The next column contains the number of potential deadheads which is equal to the number of coupling constraints of (ISP). Column “depots” is the number of valid combinations of vehicle types and depots of the vehicle scheduling subproblem of (ISP). This is equal to the number of commodities of the multi-commodity-flow problem formed by constraints (3.3). The column “max columns” is the largest number of x-variables used at once throughout our algorithm.

Table 1 Characteristics of the ISP-scenarios

The last two columns contain the number of duties and vehicles in the best known solutions of the scenarios. Scenario 3 uses fewer duties than vehicles, because some of vehicles are not driven by drivers of the planning company, but by subcontractors. Therefore these duties are not planned in the problem but by the subcontractors, which may include own tasks in their duty schedules.

3.3 Computational results

The following computations use version 4.030 of our SCHED-OPT optimization suite for public transit which is integrated in the commercial software suite ivu.plan. All computations were done on an Intel(R) Xeon(R) CPU E31280 with 3.50 GHz. We used only one core. Our code was compiled as 32 bit code, that is, the memory consumption of our code is below 4 GB.

Table 2 shows some characteristics of rapid branching for the scenarios of Sect. 3.2. The first four columns are for the first phase of IsOpt, i.e., the fixing of deadhead-variables, the next four columns are for the second phase, i.e., the fixing of duty-variables, and the last four columns are the sums of the two phases.

Table 2 Results of rapid branching for ISP

The columns “iter” are the number of examined branch-and-bound nodes, columns “b.” are the number of backtracks, “gap” is the increase of the objective value after the respective phase, and “time” is the time in seconds of each phase.

In Table 2, one can see that the remaining problem of the second phase is easy if only few relieve points exist. The largest gap between the first objective value and the solution found is for scenario 3 with 2.2 %. However, we are not able to find a “real” lower bound on the optimal objective value of (ISP), because the column generation is heuristical, so the gap stated here is only an estimation of the quality of our solution. Nevertheless, the solutions found by rapid branching are of high quality and used by planners in public transit companies in their daily operations, see IVU Plattform (2008).

4 Railway track allocation

Railway track allocation is one of the most challenging planning problems for every railway infrastructure provider. Due to the ongoing deregulation of the transportation market in Europe, new railway undertakings are entering the market. This leads to an increase in train path requests and thus to a higher number of conflicts among them. The goal of track allocation is to resolve these problems as much as possible by producing a feasible, i.e., conflict free, timetable that achieves a maximal utilization of the railway infrastructure.

4.1 Path coupling problem formulation

We briefly recall in this section a formal description of the track allocation problem. Further details can be found in the survey article (Lusby et al. 2011). Consider an acyclic digraph D=(V,A) that represents a time-expanded railway network. Its nodes represent arrival and departure events of trains at a set S of stations at discrete times $T\subseteq \mathbb {Z}$, its arcs model activities of running a train over a track, parking, or turning around. Let I be a set of requests to route trains through D. More precisely, train i∈I can be routed on a path through some suitably defined subdigraph D _i =(V _i ,A _i )⊆D from a starting point s _i ∈V _i to a terminal point t _i ∈V _i . Denote by P _i the set of all routes for train i∈I, and by P=⋃ _i∈I P _i the set of all train routes (taking the disjoint union).

Let s(v)∈S be the station associated with departure or arrival event v∈V, t(v) the time, and J={s(u)s(v):(u,v)∈A} the set of all railway tracks. An arc (u,v)∈A blocks the underlying track s(u)s(v) for the time interval [t(u),t(v)[, and two arcs a,b∈A are in conflict if their respective blocking time intervals overlap. Two train routes p,q∈P are in conflict if any of their arcs are in conflict. A track allocation or timetable is a set of conflict-free train routes, at most one for each request set. Given arc weights w _a , a∈A, the weight of route p∈P is w _p =∑ _a∈p w _a , and the weight of a track allocation X⊆P is w(X)=∑ _p∈X w _p . The track allocation problem is to find a conflict-free track allocation of maximum weight.

The track allocation problem can be modeled as a multi-commodity flow problem with additional packing constraints, see, e.g., Caprara et al. (2006), Borndörfer et al. (2006), Fischer et al. (2008). We focus on an alternative formulation as a path coupling problem based on ‘track configurations’, see, e.g., Borndörfer and Schlechte (2007), Fischer and Helmberg (2010), Schlechte (2012). A valid configuration is a set of arcs on some track j∈J that are mutually not in conflict. Denote by Q _j the set of configurations for track j∈J, and by Q=⋃ _j∈J Q _j the set of all configurations. In addition, the set of paths and the set of configurations which contain arc a∈A is denoted by P _a and Q _a , respectively. Introducing 0/1-variables x _p , p∈P, and y _q , q∈Q, for train paths and track configurations, the track allocation problem can be stated as the following integer program (PCP):

$$\begin{aligned} &\max \sum \limits _{p\in P} w_p x_p, \end{aligned}$$

(4.1)

$$\begin{aligned} &\mbox{such that} \\ &\phantom{\mbox{such that}}\quad \sum \limits _{p\in P_i} x_p = 1, \quad \forall i\in I , \end{aligned}$$

(4.2)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum \limits _{q\in Q_j} y_q = 1, \quad \forall j\in J , \end{aligned}$$

(4.3)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum \limits _{p\in P_a} x_p - \sum \limits _{q\in Q_a} y_q = 0, \quad \forall a\in A , \end{aligned}$$

(4.4)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad x_p, y_q \in\{0,1\}, \quad \forall p\in P,\; q\in Q. \end{aligned}$$

(4.5)

The objective PCP (4.1) maximizes the weight of the track allocation. Constraints (4.2) state that a train can run on at most one route, constraints (4.3) allow at most one configuration for each track. Inequalities (4.4) link train routes and track configurations to guarantee a conflict-free allocation. Finally, (4.5) are the integrality constraints. This type of problem formulation fits perfectly in the setting presented in Sect. 2.

4.2 Computational results

We tackle large scale instances of PCPwith slight modifications of the general approach presented in Sect. 2, i.e., we consider maximization instead of minimization and perform only partial rapid branching on the y-variables. The concrete details on the algorithmic part can be found in Borndörfer et al. (2010b) and Schlechte (2012). All computations in the following were performed on computers with an Intel Core i7 870 with 3 GHz, 8 MB cache, and 16 GB of RAM.

In our experiments, we consider the Hanover-Kassel-Fulda area of the German long-distance railway network. It includes data for 37 stations, 120 tracks and 6 different train types (ICE, IC, RE, RB, S, ICG). Because of various possible turn around and running times for each train type, this produces a macroscopic railway model with 146 nodes, 1480 arcs, and 4320 headway constraints. All instances related to hakafu_simple are freely available at our benchmark library TTPlib, see Erol et al. (2008).

Table 3 shows results for solving the test instances by our code TS-OPT. We choose ϵ=0.25 in Algorithm 2. The table lists the number of scheduled paths in the best solution found, the number of requested trains, the size of the model in terms of number of rows and columns, the upper bound produced by the bundle method (v(LP)), the solution value of the rapid branching heuristic (v ^∗), the optimality gap,¹ the total running time in CPU seconds, and the number of rapid branching nodes (iter).

Table 3 Results of rapid branching for TTPlib-scenarios

The benefit of our algorithmic approach is apparent for very large scale instances, i.e., r_506 to r_906 with more than 500 train requests. In addition, these instances have much more coupling rows than the standard instances of the TTPlib. This demonstrates that rapid branching is a powerful heuristic to solve large scale track allocation problems and is able to produce high quality solution with a small optimality gap.

5 Vehicle rotation planning in inter city railway transportation

In this section we give a brief and rudimentary description of the cyclic vehicle rotation planning problem (VRPP). For the sake of simplicity, we focus on the train composition part of the problem in case of Inter City railway transportation. The integration of other major technical aspects like maintenance requirements and capacities, and regularity can be found in Maróti (2006), Borndörfer et al. (2011), and Giacco et al. (2011).

5.1 Hypergraph based integer programming model

We consider a set of trains $\mathfrak {T}$. Each train consists of at least one timetabled trip. The set of timetabled trips is denoted by T. A vehicle group is the most basic type of the physical vehicle resources. In other contexts this is called vehicle type, fleet, or abstractly commodity. A vehicle configuration (or short configuration) is a non-empty multiset of vehicle groups. It represents a temporary coupling of its vehicle groups. A trivial configuration is a configuration of cardinality one. The set of vehicle configurations is denoted by C. For each trip t∈T there exists a set of feasible vehicle configurations C(t)⊆C which can be used to operate t. A vehicle configuration can be changed at the departure and at the arrival of a trip but not inside a trip. A change of a vehicle configuration is called coupling. We consider only coupling activities that can be made on the fly, i.e., without the need of special machines and crews. For t∈T and c∈C(t) we have a special technical time—called turn time for cleaning and maintaining the involved vehicle resources after the trip t is done. Note, that operational cost per kilometer depends on the used vehicle configuration.

A vehicle rotation is a cyclic concatenation of trips which are operated by a vehicle group. The number of physical vehicle groups needed to operate a vehicle rotation is the number of times the cycle passes the whole standard week. It is not decidable whether a single vehicle rotation is feasible or not without knowing the complete vehicle configurations of the involved trips. A vehicle rotation plan is an assignment of vehicle configurations, timetabled trips, and a set of feasible connections between these configurations, such that each used vehicle group rotates in a vehicle rotation. The vehicle rotation problem is to find a cost optimal vehicle rotation plan.

We model the considered vehicle rotation planning problem by using a hypergraph based integer programming formulation. Since a vehicle configuration c∈C is a multiset, we denote the number of elements—called multiplicity—in c of a vehicle group f∈F by m(f,c). In order to clearly identify the elements of a vehicle configuration c∈C we index all elements of vehicle group f∈F in c by natural numbers $\{1,\ldots, m ( f , c )\}\subset \mathbb {N}$.

We define a directed hypergraph $G =( V , \mathcal { V } , A )$ with node set V, hypernode set $\mathcal { V }$ and hyperarc set A. Our definition of a directed hypergraph is slightly different to standard definitions from the literature, e.g. (Cambini et al. 1997), and therefore we define the sets V, $\mathcal { V }$, and A as follows:

A node v∈V is a four-tuple $v = ( t , c , f , m ) \in T \times C \times F \times \mathbb {N}$ and represents a trip t∈T operated with a vehicle configuration c∈C(t) and with vehicle group f∈c of multiplicity m∈{1,…,m(f,c)}. The set $V (\mathfrak{ t },\mathfrak{ c }) = \{ ( t , c , f , m ) \,|\, t = \mathfrak{ t },\, c =\mathfrak{ c }\}$ denotes all nodes belonging to a trip $\mathfrak{ t }\in T$ operated with a vehicle configuration $\mathfrak{ c }\in C (\mathfrak{ t })$. Each V(t,c) with t∈T and c∈C(t) is a hypernode $v \in \mathcal { V }$. A hypernode can be seen as a feasible assignment of a vehicle configuration to a trip.

A link is a tuple (v,w)∈V×V. A hyperarc a∈A—or short arc—is a non-empty set of links, thus a⊆V×V. For a∈A we define the tail component of a by tail(a)={v∈V | ∃ w∈V : (v,w)∈a} and the head component by head(a)={v∈V | ∃ u∈V : (u,v)∈a}.

We assume that the tail set and head set of a hyperarc must be not empty and of equal cardinality, because hyperarcs model the transition of individual vehicles. In addition we do not assume that the tail set and head set have to be disjoint due to the cyclicity. There is an hyperarc a∈A if the operational rules, e.g. the turn times of the involved configuration, are fulfilled. The objective function $c : A \mapsto \mathbb {Q}^{+}$ includes vehicle cost, deadhead cost, coupling cost, and regularity aspects.

Let $G =( V , \mathcal { V } , A )$ be a hypergraph modeling the VRPP as described above. We introduce binary decision variables x _a ∈{0,1} and y _v ∈{0,1} for each hyperarc a∈A and each hypernode $v \in \mathcal { V }$ of G. Those variables take value one if the corresponding nodes and hyperarcs are used in the vehicle rotation plan and otherwise zero. The set of all hypernodes $v \in \mathcal { V }$ for trip t∈T is denoted by $\mathcal { V } ( t )$ and $\mathcal { V } ( v )$ denotes the set of all hypernodes of G containing v. By definition, the set $\mathcal { V } ( v )$ for v∈V has cardinality one. The set of all ingoing hyperarcs of v∈V is defined as $\delta _{}^{\mathrm {in}} ( v ) :=\{ a \in A \,|\,\exists (u,w)\in a \,:\,w= v \}\subseteq A$, in the same way $\delta _{}^{\mathrm {out}} ( v ) :=\{ a \in A \,|\,,\exists(u,w)\in a \,:\,u= v \} \subseteq A$ denotes the set of all outgoing hyperarcs of v.

Our hyperflow based Integer Programming formulation (HFIP) states:

$$\begin{aligned} &\min \sum_{ a \in A } {c_{ a } x _{ a }} \end{aligned}$$

(5.1)

$$\begin{aligned} &\mbox{such that} \\ &\phantom{\mbox{such that}}\quad \sum_{ v \in \mathcal { V } ( t )} { y _ v } = 1, \quad \forall t \in T , \end{aligned}$$

(5.2)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum_{ a \in \delta _{}^{\mathrm {in}} ( v ) } { x _{ a }} - \sum _{ v \in \mathcal { V } (v)}{ y _ v } = 0, \quad \forall v \in V , \end{aligned}$$

(5.3)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad \sum_{ a \in \delta _{}^{\mathrm {out}} ( v ) } { x _{ a }} - \sum _{ v \in \mathcal { V } (v)} { y _ v } = 0, \quad \forall v \in V , \end{aligned}$$

(5.4)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad x _ a \in\{0,1\}, \quad \forall a \in A , \end{aligned}$$

(5.5)

$$\begin{aligned} &\phantom{\mbox{such that}}\quad y _ v \in\{0,1\}, \quad \forall v \in \mathcal { V } . \end{aligned}$$

(5.6)

Our objective function (5.1) minimizes the total cost. Constraints (5.2) assign one hypernode of graph G to each trip of the VRPP. This models the configuration assignment of vehicle configurations to trips. Constraints (5.3) and (5.4) can be seen as flow conservation constraints for each node v∈V. If one interprets an (5.3) equation as a departure and the (5.4) equation as an arrival node, a hypernode $v \in \mathcal { V }$ can be even seen as a hyperarc between these departure and arrival nodes. With this interpretation the (5.3) and (5.4) constraints become constraints conserving hyperflow on the trips and connections between trips. Finally, (5.5) and (5.6) states that all variables are binary.

5.2 Solution approach

In this section we present our rapid branching approach for the VRPP. In case of only trivial configurations the hypergraph is a standard graph. In this case our problem reduces to the Integer Multi-Commodity-Flow problem, which is known to be NP-hard, see Löbel (1997). Furthermore, if all trip configurations are fixed, problem VRPP is a simple assignment problem and hence an optimal solution of the LP relaxation of our model is already integral.

Due to the NP-hardness of problem VRPP, we propose a heuristic Integer Programming approach to solve model HFIP. We are mainly utilizing two general techniques. First we use a column generation approach to solve the LP-relaxation of model HFIP. Note, that the number of variables is very large, i.e., one for each hyperarc and hypernode. Second, we adapt the rapid branching heuristic of Sect. 2 and consider only a subset of the variables—in our case the y-variables for the hypernodes assigning the vehicle configurations to the trips. The reason is the observation that the model is almost integral and rather easy to solve if the configurations for the trips are fixed. After the arc generation and rapid branching we use CPLEX 12.2 to solve the generated model so far, i.e., a restricted variant of model HFIP, as a static IP.

5.3 Results

We tested the hypergraph based model HFIP and our algorithmic approach on a large set of real world instances that are provided by our project partner DB Fernverkehr. The problem set contains small and rather easy instances, e.g., instance vrp015 and vrp016 with only 19 trains, as well as very large scale ones, e.g., instance vrp011 and vrp014 with more than 24 million hyperarcs. We consider instances for the currently operated high speed intercity vehicles (ICE) of DB Fernverkehr as well as instances of conceptional studies for future rolling stock fleets. Today, there are some fleets in operation that can not be coupled on the fly and some of the conceptional studies also consider only scenarios with trivial configurations. Therefore, most of the instances contain only trivial configurations.

Table 4 gives some statistics on the number of trains, the number of vehicle groups, and the number of vehicle configurations. In addition, the number of nodes, number of hypernodes, and the total number of hyperarcs of the hypergraphs associated with model HFIPare listed. In case of only trivial configurations the number of hypernodes equals the number of nodes, otherwise it has to be smaller because the set V is a subset of $\mathcal { V }$, e.g., instance vrp015.

Table 4 Characteristics of the VRP test instances

All our computations were performed on computers with an Intel Core 2 Extreme CPU X9650 with 3 GHz, 6 MB cache, and 16 GB of RAM. CPLEX Barrier was running with 4 threads as well as the CPLEX MIP solver. We were able to solve all 31 instances to nearly optimality by the solution approach presented in Sect. 5.2. Table 5 shows the detailed results, i.e., the number of vehicles $\mathfrak {v}$ to operate the $| \mathfrak {T} |$ trains, the total objective value of the solutions, the optimality gap, and the total running time in seconds. We marked 5 instances which are solved to proven optimality. Except for instance vrp005 the gap is considerably below 1 %. This demonstrates that our solution approach can be used to produce high quality solutions for large-scale vehicle rotation planning problems.

Table 5 Results for all 30 instances

6 Conclusion

We provide a computational study for rapid branching applied to several real world transportation problems. By different variants of rapid branching we were able to compute high-quality integer solutions for the mentioned large-scale problems in practice. The core idea of all presented solution approaches is the same, namely, rapid branching. This documents that rapid branching is a general solution approach and a successful method for large scale optimization problems in public transport.

Applications of the rapid branching heuristic are not limited to optimization problems in transportation. There are several other areas for which also very large scale and similar linear programming models are used. A prominent example is the steel mill slab problem or other production planning problems, e.g., the integrated sequencing and scheduling problem of coils presented in König (2009). These problems are typically tackled by a large scale set partitioning formulation.