1 Introduction

Fluids (gas, water, aggressive agents, ...) may penetrate through concrete due to its porous structure and to micro/macro cracks. Strictly related to the concrete heterogeneous nature, their presence is inevitable even in the presence of small loading levels or at early-age [10, 64, 76]. This aspect is of crucial importance, because cracks represent preferential flow paths for the transport of fluid species, and strongly contributes to the deterioration of structural durability [3, 40, 41] and safety [18, 27, 66].

Many numerical models aiming to model strain localisation and cracking in porous solids (e.g. concrete) have been proposed in the literature. Mainly developed in the framework of the finite element method (FEM), from a conceptual point of view these formulations can be classified in relation to their modelling scale. In multiscale models [4, 11, 12, 34, 35, 51, 62, 63], transport processes in porous material, the localised flow through the discontinuity and their mutual exchanges are explicitly modelled. In macroscopic formulations [6, 17, 25, 26, 44, 46] these phenomena are treated as a whole in the framework of the Theory of Porous Media [14, 37]. Each cracked volume element is then represented through an equivalent porous medium, with effective hydro-mechanical (HM) properties (i.e. Biot’s coefficients, permeabilities, diffusivities, etc.) depending on the local mechanical fields (i.e. stress, strain, damage, crack opening, etc.).

Although multi-scale approaches allow for a more physical description of transport process in cracked domains [8], in particular when dealing with localised cracking, macroscopic formulations have been often preferred for engineering oriented applications. This is due to different reasons, and among others: they generally require lower computational ressources, their numerical implementation is quite simple, well established and validated thermodynamic frameworks are available, different physics can be coupled into a unified formulation in a natural way.

Whatever the finalities of the coupled modelling (e.g. prediction of fluid leakage through fluid containment structures, durability analysis of concrete structures) the model capabilities in predicting concrete cracking represent a key aspect.

Among the different mechanical models available in the literature, probabilistic formulations have proven to deal to a proper description of concrete. In these formulations, concrete heterogeneity and the related scale effects are taken into account by defining the material properties through random fields [13, 30, 38, 57, 69, 70].

In particular, if the equivalence between a FE and a volume of heterogeneous material is postulated [57], the use of spatially uncorrelated random fields allows for a relevant modelling of scale effects and cracking. Based on this original idea different numerical formulations have been developed in recent years [60, 71–73].

Drawing from these theoretical and numerical frameworks, a three-dimensional (3D) macroscopic modelling approach of fluid transfers in cracking concrete and concrete structures is presented in the paper.

The article is structured in three parts as follows:

  1. 1.

    a probabilistic mechanical model, developed in the FEM context, is first presented. In the present formulation, it is assumed that the cracking process (i.e. the creation and propagation of a crack within the element itself) induces some local energy dissipation. This dissipative process is mathematically represented through a probabilistic isotropic damage model. According to the aforementioned modelling assumption, material properties (strength and fracture energy) are defined element-by-element according to spatially uncorrelated random fields. Their statistical parameters are defined for each element depending on its own elementary volume according to experimentally validated laws;

  2. 2.

    the second part of the paper presents the coupled HM cracking-transfer modelling procedure. In this simplified formulation, the sole considered source of HM coupling is the influence of elementary cracking on the local variation of the transfer properties of the cracked volume. At the FE scale, this leads to consider that the localised flow through the crack induces a loss of isotropy in the elementary permeability tensor. The “apparent” elementary permeability is then computed through the experimentally adapted parallel plates model [50, 78];

  3. 3.

    in the final part of the article the self-consistency of the proposed approach is explored. For this purpose, the experimental HM test proposed by [50] to monitor the real-time evolution of the water permeability of a concrete sample under Brazilian loading is numerically modelled. Purely mechanical experimental results are used as reference data to calibrate the mechanical model parameters first. Then the HM response of cylindrical sample under mechanical and hydraulic loading is simulated.

2 Probabilistic cracking model

2.1 Problem setting

A macroscopic formulation for modelling pure tension (mode I) concrete cracking is presented. The probabilistic aspects of the model are based on the following fundamental modelling and physical assumptions [59, 71]:

  1. 1.

    each FE is assumed to be representative of a volume of heterogeneous material, whose degree of heterogeneity \(\xi _e\) is defined as the ratio of its volume \(V_e\) to the volume of the coarsest aggregate \(V_g\):

    $$\begin{aligned} \xi _e = \frac{V_e}{V_g}\, ; \end{aligned}$$
    (1)
  2. 2.

    the physical mechanisms controlling the cracking process are independent on the scale of modelling. Consequently, it is assumed that it is possible to define macroscopic quantities regardless of the size of the FE, whether a representative elementary volume (REV) or not;

  3. 3.

    the mechanical behaviour of each FE depends on its own volume and is prone to random variations. This aspect is represented by considering the elementary mechanical properties as randomly distributed over the computational mesh according to spatially uncorrelated random fields. Their statistical parameters thus vary element-by-element depending on the local heterogeneity ratio \(\xi _e\);

  4. 4.

    crack propagation is not explicitly addressed, at least in the sense of the Fracture Mechanics. A propagation criterion is not introduced, but cracking is modelled element-by-element. The occurrence of a macro-crack (i.e. strain localisation) then results from the coalescence of some randomly created elementary cracks. In other words, at a macroscopic level, the progressive cracking of consecutive FEs is considered as representative of a macro-crack propagation.

According to these aspects, the presented approach is denoted in the following as “semi-explicit” instead of macroscopic. This term is here used to specify that, a discrete vision of cracking is preserved (the material’s properties are discretely distributed in the mesh, the crack is treated element-by-element) but elementary cracking is taken into account through its local energetic effect.

2.2 Model formulation

Standard FEM procedures are used to solve quasi-static equilibrium equations. At the FE scale, the energetic effect associated to the elementary cracking process is represented through a simple isotropic damage law with a single scalar parameter [36]. A probabilistic energetic regularisation is also retained.

Without going into details of numerical implementation of the model, its main features can be summarised as follows:

  1. 1.

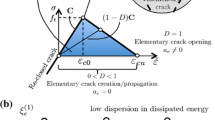
    a bilinear stress–strain (\(\varvec{\sigma },\varvec{\varepsilon }\)) relationship is used to represent elementary cracking (Fig. 1). The elementary dissipative process (i.e. crack propagation inside the FE itself) starts when the major principal stress \(\sigma _{\max }^{prin}\) at a given Gauss point equals the material tensile strength \(f_t\). Dissipation is then driven by the positive part, denoted by \(\langle \bullet \rangle ^+\), of the projection of \(\varvec{\varepsilon }\) along the direction \({{\mathbf {n}}}_\sigma\) of the major principal stress: \(\tilde{\varepsilon } = \tilde{\varepsilon }(\varvec{\varepsilon }) = \langle {{\mathbf {n}}}_\sigma \cdot \varvec{\varepsilon } \rangle ^+\). When the total energy available for the FE is dissipated (i.e. \(D=1, D\) being the damage variable), it is declared cracked and its elementary stiffness matrix is set to zero [71]. This allows to avoid stress-locking phenomena;

  2. 2.

    The model is numerically implemented using a rotating crack approach [33, 61]. During the dissipative phase (i.e. \(D < 1\)), the normal \({{\mathbf {n}}}_\sigma\) is allowed to evolve according to any changes in the stress state \(\varvec{\sigma }\) in the material. Only when the element is declared as cracked, the normal to the crack plane fixed: \({{\mathbf {n}}}^c = {{\mathbf {n}}}_{\sigma }\);

  3. 3.

    Differently from smeared-cracking approaches [20, 32, 39], no additive decomposition is introduced in the constitutive law to distinguish between elastic deformation and crack contributions. A elementary crack is supposed to exist only after the condition \(D=1\) is achieved [56]. The elementary crack opening \(a_e\) is then computed from the projection of the elementary displacements along the direction of \({{\mathbf {n}}}^c\);

  4. 4.

    For sake of simplicity, crack re-closure is not explicitly treated. The model assumes that the dissipative process does not influence the elementary stiffness in compression. So, for reclosed cracks, the elementary stiffness matrix in compression is completely recovered while the elementary tensile strength \(f_t\) is set to zero.

Fig. 1
figure 1

Illustration of the main aspects of the proposed “semi-explicit” probabilistic cracking model

Full size image

2.3 Statistical model parameters

The constitutive law (\({\varvec{\sigma }},{\varvec{\varepsilon }}\)) is completely defined by two parameters: the tensile strength \(f_t\) and the volumetric density of dissipated energy \(g_c\). An energetic regularisation technique allows to compute \(g_c\) from the surface cracking energy \({{\mathcal {G}}}_c\): \(g_c = {{{\mathcal {G}}}_c}/l_e\) [7]. The quantity \(l_e\) denotes the elementary characteristic length and is here computed from elementary volume as \({l}_e = V_e^{1/3}\). More complex definitions are possible, depending on the FE shape and the order of interpolation of the displacement field. This choice can influence the predicted crack paths, however due to the probabilistic aspects of the model this effect is strongly reduced.

Mechanical properties \(f_t\) and \({{\mathcal {G}}}_c\) are defined element-by-element according to spatially uncorrelated Weibull and lognormal statistical laws respectively [23].

Due to the aforementioned modelling assumptions (Sect. 2.1), their statistical parameters depend on the elementary volume through the local heterogeneity ratio \(\xi _e\). The only exception is the mean value of the energy distribution, which is assumed independent of \(\xi _e\). Its value is estimated as \(\mu _G = {{\mathcal {G}}}_c\), where \({{\mathcal {G}}}_c\) is the critical strain energy release rate as defined in the context of the linear fracture mechanics (LFM) by [31]. For the concrete formulation used herein (Table 1) its value has been experimentally obtained by [55]: \({{\mathcal {G}}}_c = 1.31410 \times 10^{-4}\,{{\rm MN}}/{{\rm m}}\).

Using \({{\mathcal {G}}}_c\) as model parameter instead of the fracture energy \({{\mathcal {G}}}_f\) [29], as stated by non linear fracture mechanics (NLFM) for quasi-brittle materials, is based on two strong physical assumptions [56, 73]:

  1. 1.

    the Griffith’s theory for brittle fracture is assumed valid at the FE level. According to this theory, \({{\mathcal {G}}}_c\) is proportional to the specific fracture energy per unit area \(\gamma\), which is an intrinsic material parameter (e.g. in plane strain conditions: \({{\mathcal {G}}}_c = 2\gamma\)). Therefore \({{\mathcal {G}}}_c\) can also be considered as such, at least in average value. This assumption is reasonable, in light of the experimental results obtained by [55, 58];

  2. 2.

    due to the material heterogeneity, the dissipated energy can undergo variations (dispersion in statistical terms) around the average value. This dispersion is considered as directly influenced by the size of the stressed volume (i.e. of the finite element), as this volume may (or may not) be concerned by the propagation of a crack. In particular, as qualitatively illustrated in Fig. 2, it should increase as \(\xi _e\) decreases and vice-versa.

The laws \(b_{s} = b_{s}(\xi _e)\) and \(c_{s} = c_{s}(\xi _e)\) defining shape and scale factors of the Weibull distribution for the tensile strength, as well as the variance \(\eta _{G} = \eta _{G}(\xi _e)\) of the cracking energy distribution, have to be identified through an inverse analysis approach.

This calibration phase generally requires a large number of computations and is rather computationally expensive. However, once the statistical laws have been obtained for a given material, they can be directly used in other computations without any ajustements.

Table 1 Ordinary concrete mix design
Full size table
Fig. 2
figure 2

Influence of the local heterogeneity \(\xi _e\) on the crack propagation on a heterogeneous volume element and influence on the cracking energy dispersion

Full size image

3 Fluid transfer in cracking concrete

To study the feasibility of the coupling between probabilistic cracking and fluid transfers in concrete, a simplified transfer model is considered. Concrete is treated as a saturated and initially isotropic porous medium, and the flow is assumed to be incompressible. Furthermore, the sole considered source of HM coupling is the influence of cracking on the local transfer properties.

Under these assumptions, transport problem is governed by the sole continuity equation of the fluid phase, and can be separately solved from the mechanical one. The numerical solution is obtained through a standard FEM formulation [18, 37, 38], using the same computational grid adopted in mechanical computations. The treatment of more complex thermo-hydraulic problems can be easily integrated using fully coupled staggered solution procedures [38].

3.1 Apparent permeability of the cracked element

Darcy-like fluid flows are assumed both in cracked and undamaged volume elements. In the absence of body forces and assuming a steady-stated, single-phase and laminar flow, the fluid specific mass flow rate \({{\mathbf {q}}}\) depends on the local pressure gradient \(\nabla p\) according to the linear relation [19]:

$$\begin{aligned} {{\mathbf {q}}} = \rho \, {{\mathbf {v}}} = - \rho \, \mu ^{-1} {{\mathbf {k}}} \nabla p \end{aligned}$$
(2)

where \({{\mathbf {v}}}\) is the mean fluid velocity, \(\rho\) is the fluid density, \(\mu\) is its cinematic viscosity and \({{\mathbf {k}}}\) denotes the elementary permeability tensor.

For undamaged FEs, \({{\mathbf {k}}}\) coincides with the so-called intrinsic permeability tensor of the porous medium:

$$\begin{aligned} {{\mathbf {k}}} = {{\mathbf {k}}}^0 = k^0 {{\mathbf {I}}} \end{aligned}$$
(3)

where \(k^0\) is the intrinsic permeability of the porous medium and \({{\mathbf {I}}}\) denotes the second order identity tensor.

Once a FE is cracked, the macro-crack represents a preferential pathway for the penetration of fluids. At the FE scale, this can be taken into account [21, 39, 65] by introducing the non-isotropic “apparent” elementary permeability tensor:

$$\begin{aligned} {{{\mathbf {k}}}} = {{\mathbf {k}}}^0 + {{\mathbf {T}}}^t{{{\mathbf {k}}}}^{c}{{\mathbf {T}}} \end{aligned}$$
(4)

where \({{{\mathbf {k}}}}^{c}\) is the cracking induced anisotropic contribution to the apparent permeability (written in the local reference system of the crack), and \({{\mathbf {T}}}\) is the rotation tensor. The term “apparent” is here used to remark that in presence of a localised/discrete cracks the rigorous definition of homogenised quantities (e.g. permeabilities) is not possible, as the assumption of statistical homogeneity [22, 24, 28, 43, 68] underlying the existence of a REV is not verified [8, 38].

The crack contribution \({{\mathbf {k}}}^c\) figuring in Eq. (4) have to be properly defined, to take into account the loss of isotropy of the flow within a cracked area and to ensure the mesh objectivity of the simulated response. If one assumes that the crack does not modify the flow along the direction of \({{\mathbf {n}}}^c\) [21, 47], the apparent permeability tensor \({{\mathbf {k}}}^c\) can be written as follows:

$$\begin{aligned} {{{\mathbf {k}}}}^c(a_e,{{\mathbf {n}}}^c) = k^c(a_e) \frac{a_e}{l_e} \left( {{\mathbf {I}}} - {{\mathbf {n}}}^c \otimes {{\mathbf {n}}}^c \right) \end{aligned}$$
(5)

where \(k^c = k^c(a_e)\) is the intrinsic crack permeability and \(l_e\) denotes the the elementary characteristic length for the hydraulic problem (estimated as in mechanical computations). From Eqs. (4) and (5) stems directly that when \(a_e=0\), the crack contribution vanishes. Therefore, no irreversible effects on local fluid flow due to residual cracks can be taken into account.

3.2 Crack permeability: experimental constitutive law

The intrinsic permeability of the crack \(k^c\) is conventionally estimated according to the so-called parallel plates model [67]. This conductivity model stems directly from the resolution of Navier-Stokes equations [74] assuming that the fracture walls are two smooth and parallel plates, separated by an aperture \(a_e\) [78]. Real cracks in concrete, however, have rough walls and variable apertures. In numerical modelling, some authors [62, 63] suggest to correct the standard cubic law by introducing a phenomenological factor \(\alpha > 1\) such that:

$$\begin{aligned} k^c = k^c(a_e) = \frac{a_e^2}{12 \, \alpha } \end{aligned}$$
(6)

The factor \(\alpha\) is typically assumed constant, with values ranging between 10 and 1000 [1, 45, 77] depending on concrete formulations and adopted experimental procedures. However, as experimentally shown by [50], the parameter \(\alpha\) could not be considered as a constant as it should decrease during the crack opening process. In particular, the following power-law relation can be used:

$$\begin{aligned} \alpha = \alpha (a_e) = \beta a_e ^\gamma \end{aligned}$$
(7)

where \(\beta >0\) and \(\gamma <0\) are two parameters depending on the crack geometry and, indirectly, on the concrete formulation. For the ordinary concrete formulation herein used (Table 1), the following values hold: \(\beta = 5.625 \times 10^{-5}\) and \(\gamma = -1.19\) (if a e is expressed in metres).

Finally, combining Eqs. (6) and (7), the following constitutive law can be used in numerical computations:

$$\begin{aligned} k^c = {\left\{ \begin{array}{ll} \frac{a_e^{2-\gamma }}{12\beta } &\quad a_e < a_{e,t}\\ \frac{a_e^{2}}{12} &\quad \text {otherwise} \end{array}\right. } \end{aligned}$$
(8)

where \(a_{e,t}\) is the the crack opening such that the parallel plates model is recovered (\(\alpha = 1\)) (Fig. 3).

Fig. 3
figure 3

Experimentally adapted parallel plates model (Eq. 8)

Full size image

4 Coupling procedure

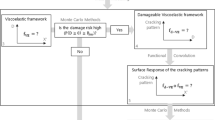
A Monte-Carlo like procedure is used to obtain a statistical description of the HM response of the analysed system. Under the aforementioned weak HM coupling assumption, the mechanical and hydraulic problems are sequentially solved (using two specialised and ad-hoc developed FE codes) as follows:

  1. 1.

    a series of mechanical simulations is performed to induce cracking and to estimate the structural mechanical response;

  2. 2.

    the local cracking informations (elementary openings \(a_e\), cracks orientations \({{\mathbf {n}}}^c\)) obtained in mechanical computations are used, in hydraulic computations, to define elementary apparent permeability tensors \({\mathbf {k}}\);

  3. 3.

    the transfer properties of the cracking structure are then statistically analysed and put into relation with mechanical fields.

In the following sections, the feasibility of the proposed modelling strategy is explored by simulating the HM splitting tests by [50], for estimating the real-time evolution of the transfer properties of a concrete sample under Brazilian loading. This study in performed in two phases:

  1. 1.

    purely mechanical experimental results are first used (Sect. 5) in order to identify the statistical parameters \(b_s, c_s\) and \(\eta _G\) (defined in Sect. 2.3) for two values of the elementary heterogeneity ratio:

    $$\begin{aligned} \xi _e = 0.01 \quad \text {and} \quad \xi _e = 0.001 \, ; \end{aligned}$$
    (9)
  2. 2.

    in the second phase (Sect. 6), the calibrated parameters are used as input data in HM computations. These latter are performed using a FE mesh which is different from those used in previous phase. This allows to obtain a first validation of calibrated statistical parameters and, at the same time, an estimation of the model capabilities in predicting fluid transfers in cracking media.

5 Mechanical model parameters identification

Purely mechanical experimental results obtained by [50] on samples d s  = 110 mm in diameter and t s  = 50 mm in thickness are considered as reference data to perform a preliminary inverse analysis on the statistical parameters of the mechanical model. The choice of the optimal set of parameters is performed using a semi-automatic procedure, based on the comparison between the experimental and numerical global sample responses.

5.1 Numerical modelling of the Brazilian test

The mechanical response of a cylindrical sample under Brazilian loading is numerically simulated according to the proposed “semi-explict” cracking model.

Numerical computations are performed using two FE mesh (Fig. 4). They are composed respectively of 4250 and 13,037 four-noded tetrahedral FEs with linear interpolation in the the displacement field. For both mesh, the central zones of the sample are discretised through structured grids composed by FEs with quasi-constant \(\xi _e\) values (i.e. elementary volumes).

The upper and lower steel bearing plates are represented through two linear elastic parallelepipeds \(b\) in width. Their presence allows to distribute external load over a finite width bearing strip and ensure to limit damage concentrations near the bearing surfaces (i.e. constrained nodes). It is well-known that, in Brazilian tests, the \(b/d_s\) ratio sensibly influences the sample mechanical response and can induce scale effects [53, 54]. However, the chosen width (b = 1 cm) is small enough to neglect its influence on the simulated response [49] and, at the same time, it is completely representative of the experimentally observed contact areas between the bearing plates and the sample surfaces [9, 50].

Diametrical loading is simulated by imposing vertical displacements of the upper bearing strip. In analogy with the experiments, a indirectly controlled loading technique is used to avoid mechanical instabilities (snap-backs/through phenomena) in the phase post-peak of force. The vertical displacement increment at each loading step is then adjusted to ensure monotonically growing mean sample diameter variations \(\varDelta d_s\). These latter are computed as linear combination of the horizontal displacements of the four nodes representative of the real measurement points (Fig. 8). Numerically, this is obtained through the arc-length type algorithm [15, 48, 52] presented by [49].

In the following, in analogy with experiments, the mechanical response of the sample is represented through the average diameter variation of the sample \(\varDelta d_s\) and the diametrical load \(F\).

Fig. 4
figure 4

a Finite element mesh used to calibrate the statistical parameters of the mechanical model (inverse analysis), b imposed boundary conditions, c definition of the loading control variable

Full size image

5.2 Parameters identification: global sample responses

Ten simulations for each set of parameters are performed. One can show that this represent a good compromise between CPU time and accuracy of the solution. Further increases in the number of simulations do not induce sensible variations in terms of mean sample response.

Based on the statistical interpretation of about 4000 computations, the following parameters have been finally chosen:

$$\begin{aligned} b_s&= {\left\{ \begin{array}{ll} 6.6 , &{} \xi _e = 0.01 \\ 7.0 , &{} \xi _e = 0.001 \end{array}\right. } \quad c_s = {\left\{ \begin{array}{ll} 1.0, &{} \xi _e = 0.01 \\ 1.0 , &{} \xi _e = 0.001 \end{array}\right. }\end{aligned}$$
(10)
$$\begin{aligned} \mu _g&= {{\mathcal {G}}}_c \quad \forall \, \xi _e \quad \eta _G = {\left\{ \begin{array}{ll} 7 \times {{\mathcal {G}}}_c , &{} \xi _e = 0.01 \\ 10 \times {{\mathcal {G}}}_c , &{} \xi _e = 0.001 \end{array}\right. } \end{aligned}$$
(11)

to obtain the tensile strength in MN and the cracking energy in MN/m. From parameters \(b_s\) and \(c_s\) is easy to compute, the mean values and the variance of the strength distribution [23]:

$$\begin{aligned} \mu _s = b_s \, {\Gamma }( 1 + c_s^{-1}) \quad \eta _s^2 = b_s^2 \, {\Gamma }( 1 + 2 c_s^{-1}) - \mu _s^2 \end{aligned}$$
(12)

where \({\Gamma }\) is the so-called gamma function.

The \((F,\varDelta d_s)\) responses corresponding to the calibrated parameters are depicted in Fig. 5. A good agreement with experimental results can be put in evidence both in terms of mean values and dispersion. However, it is worth observing that numerical simulations cannot continue after \(\varDelta d_s\) reaches the maximum value of 80 μm (i.e. <300 μm experimentally analysed). For larger \(\varDelta d_s\) levels, the iterative resolution algorithm fails to converge, due to the poor conditioning of the stiffness matrix, resulting from the presence of many cracked elements in the central zone of the specimen and/or to uncontrolled oscillations in elementary opening process.

Fig. 5
figure 5

Global (\(F,\varDelta d_s\)) responses obtained through the two FE mesh using the chosen statistical parameters, with approximative identification of the loading levels corresponding to the crack distributions and displacement fields depicted in Fig. 6

Full size image

It is worth observing that the unity value assigned to the shape factor of the Weibull law, for both \(\xi _e\) values, corresponds to the transition between lognormal and exponential distributions. This result is consistent with the results of the inverse analysis performed by [71] using a probabilistic elastic-brittle constitutive law. Furthermore, consistently with the main modelling assumptions, the variance of the energy distribution increases with the elementary heterogeneity \(\xi _e\).

5.3 Local informations: crack openings

Figure 6 represents the horizontal displacement fields and elementary cracks distributions for three phases of a representative test. Numerical results put in evidence that: (1) in the pre-peak load phase, the deformation process between the two faces of the sample remains symmetric and the stress/strain fields are well approximated by standard elastic solutions [75]; (2) once the peak of load is attained, the crack opening process become strongly un-symmetric. Crack localisation starts on one face of the sample and rapidly propagates to the other one. The deformation field then localises in a band of width approximately equal to the size of one element. As experimentally observed by [50], in this phase the sample is split into two undamaged quasi-elastic blocks. From a qualitative point of view the computed displacement fields are very similar to those obtained by [50] using a digital imaging correlation technique.

A good agreement between numerical and experimental results can be observed also in quantitative terms. In Fig. 7 the comparison is established in terms of mean crack opening \(a_{{\rm m}}\) at mid-height of the plane faces of the sample. For both sides of the sample, crack apertures are numerically computed as follows. In a first step, the position of the “crack” is obtained from the displacement field corresponding to the last loading step. In a second step the crack aperture \(a_{{{\rm m,f(r)}}}\) at mid-height of the sample is computed as the relative displacement of the two nodes disposed on the opposite sides of the crack. As these nodes share two FEs, a crack is considered as present (i.e. \(a_{{{\rm m,f(r)}}} \ne 0\)) only if both the elements are cracked. Otherwise \(a_{{{\rm m,f(r)}}} = 0\). Finally, the mean crack opening is computed as \(a_{{{\rm m}}} = (a_{{{\rm m,f}}}+a_{{{\rm m,r}}})/2\).

For both mesh, once a macro-crack develops into the sample, the relation \((a_{{\rm m}},\varDelta d_s)\) is pseudo-linear as in experiments.

Fig. 6
figure 6

Crack distributions and horizontal displacement fields inside the sample for three phases of a representative numerically simulated Brazilian test

Full size image
Fig. 7
figure 7

Procedure to compute crack opening displacement at mid-height of the sample \(a_m\) from displacement field and comparison between numerically computed and experimentally obtained (\(a_{{\rm m}},\varDelta d_s\)) relationships

Full size image

6 Hydro-mechanical computations

The complete HM splitting test is modelled in this section. The statistical parameters calibrated in Sect. 5, are used as input data of the mechanical model. However, due to the variable dimensions of the FEs ensuring the spatial discretisation of the sample, linear functions of \(\xi _e\) are used to define \(b_s = b_s(\xi _e), c_s = c_s(\xi _e)\) and \(\eta _G = \eta _G(\xi _e)\) (Sect. 2.3).

6.1 Numerical modelling of the HM test

The real-time evolution of the transfer properties of a cylindrical sample under loading is numerically simulated. The FE mesh adopted in computations is depicted in Fig. 8. It is composed of approximately 44,000 tetrahedral finite elements with linear interpolations of nodal displacements and pressures.

The mechanical loading is performed according the numerical procedure presented in previous section. Concerning the hydraulic boundary conditions, two constant fluid pressure distributions \(p^{in(out)}\) are applied on two circular plane surfaces \(S^{in(out)}\) of the sample in real-time with the mechanical load. Their diameter \(d = 0.077\,{{\rm m}}\) is equal to those of the silicone joints experimentally adopted in order to ensure the absence of leaks at the contact between the experimental equipment and the sides of the sample. More details are given in [50].

Fig. 8
figure 8

a Finite element mesh used in HM computations and b hydraulic boundary conditions

Full size image

6.2 Representative transfer variables

The hydraulic response of the sample is represented through the sample transmissivity \({T}_{num}\).

Under the assumption of unidirectional flow between the two plane faces of the sample, it is obtained at each calculation step as:

$$\begin{aligned} T_{num} = - Q_{num} \frac{\mu }{\rho } \left[ \frac{\varDelta p}{t_s} \right] ^{-1} \end{aligned}$$
(13)

where \(Q_{num}\) is the mass flow rate (computed at the outlet/inlet section) and \(\varDelta p\) is the differential pressure.

The comparison of \(T_{num}\) with the homologous experimentally obtained quantity call for some considerations. Due to the saturated and laminar flow conditions, the total transmissivity \(T_{num}\) can be additively decomposed as follows:

$$\begin{aligned} T_{num} = T^{0}_{num} + T_{num}^{c} \end{aligned}$$
(14)

where \(T^{0}_{num}\) is the contribution of the flow through the porous medium and \(T^{c}_{num}\) is those corresponding to the crack flow. In all rigour, this quantity is not directly comparable to experimental one, as in this case only the crack contribution \(T^{c}_{exp}\) is known. The comparison is however possible if one observes that due to the low permeability of the material (\(k^0 \approx 10^{-21} {{\rm m}}^2\) [5]), the crack contribution to the mass flow rate is several times greater than those associated to the porous medium (\(T_{num}^{0} \approx 10^{-24} {{\rm m}}^4\)), already for very small crack openings. Therefore: \(T_{exp} \approx T_{exp}^{c}\).

6.3 Numerical results

The mean (\(F,\varDelta d_s\)) and (\(T_{num},\varDelta d_s\)) responses, computed over ten mechanical and hydraulic simulations, are represented in Fig. 9. The crack distributions and the fluid flow fields for three phases of a representative test are depicted in Fig. 10.

During the test, sample transmissivity \(T_{num}\) evolves according two main phases: (1) For low \(\varDelta d_s\) levels (<15 μm), approximately up to the the peak force, the sample transmissivity \(T_{num}\) remains almost constant (\(T_{num} = T_{num}^{0}\)). This condition does not correspond to the absence of cracks in the sample, as isolated elementary cracks may be present already for moderate loading levels. However, their contribution to \(T_{num}\) remains negligible (\(T_{num}^{c} < T_{num}^{0}\)). It is worth observing that this behaviour should not be interpreted as a numerical evidence of the existence of threshold crack opening beyond which the water flux is not influenced by the crack [2, 77], as a a unique macro-crack (i.e. continuous flowing path) is not yet present in the specimen and a crack opening can not be defined; (2) Once the peak load is attained, a macro-crack propagates through the specimen. Due to the creation of this preferential flow path, \(T_{num}\) rapidly increases by several orders of magnitude. Numerical results tends to overestimate the experimental transmissivity values (\(T_{num} > T_{exp}\)). This is partly due to the fact that the experimentally adapted parallel plates model (Eq. (7)) is strictly valid only in the range of experimentally explored crack apertures (20 μm < a < 160 μm). Therefore, the extrapolation of these results to thinner cracks (a < 20 μm) calls for further confirmations. From the numerical point of view, a further cause for over-estimation may be associated with the possible presence of adjacent cracked FEs. In this case, each FE contributes to the \(T_{num}\) in proportion to the third power of its own crack opening.

A good agreement between numerical and experimental results can be put in evidence both in terms of mechanical and hydraulic responses. The comparison among the mechanical responses obtained in this series of analysis and those previously obtained using different FE mesh, provides a further confirmation of the independence of the global simulated response with respect to the computational grid. Due to the aforementioned difficulties in simulating Brazilian tests, a complete validation of the proposed modelling approach can not be obtained. One can however show that the simulated responses are completely comparable to the experimental ones, at least in terms of tendency, over the whole range of experimentally explored \(\varDelta d_s\).

Fig. 9
figure 9

(\(F,\varDelta d_s\)) and (\(T_{num},\varDelta d_s\)) responses for the whole hydro-mechanical series of computations and approximative identification of the simulation steps corresponding to the crack distributions and fluid flow fields depicted in Fig. 10

Full size image
Fig. 10
figure 10

Distribution of cracked FEs and fluid flow field computed for three phases of a representative hydro-mechanical Brazilian test

Full size image

7 Conclusions

A numerical finite element study on fluid leakage in cracking concrete has been presented. Concrete cracking is modelled through a macroscopic (“semi-explicit”) probabilistic model. Material heterogeneity is taken into account through the use of statistical distributions of mechanical properties (tensile strength and cracking energy) [57, 60, 71–73]. Cracking is treated element-by-element without an explicit definition of a propagation criterion. In this approach, macro-cracks results from the progressive and random creation of elementary cracks. The main physical assumption is that each FE represents a volume of heterogeneous material [57, 71], whose mechanical behaviour is controlled by its own heterogeneity degree \(\xi _e=V_e/V_g\) (i.e. the ratio of the elementary volume \(V_e\) to a volume representative of the heterogeneity of the material \(V_g\)). In the present formulation, it is assumed that the cracking process (i.e. the creation and propagation of a crack within the element itself) induces some local energy dissipation. This dissipative process is mathematically represented through a probabilistic isotropic damage model [36]. According to the aforementioned modelling assumption, material properties (strength and fracture energy) are defined element-by-element according to spatially uncorrelated random fields. Their statistical parameters are defined for each element depending on its own elementary volume (\(V_e\)) according to experimentally validated laws.

The cracking-transfer coupling is treated as weak. It is assumed that the cracking of the FE, of mechanical origin, induces a loss of isotropy of its own apparent permeability tensor. The use of an experimentally modified parallel plates model [50] allows to compute the crack permeability, macroscopically taking into account the main causes of the deviation between the idealised Pouiselle-like flow and the flow in real cracks [78].

A probabilistic Monte-Carlo type approach allows to statistically validate the numerical results.

The feasibility of the proposed modelling strategy is explored by simulating the HM splitting tests developed by [50], for mass flow rate measurements through concrete samples under Brazilian loading. Experimental results have been first used to identify the statistical parameters of the mechanical model for two \(\xi _e\) values. Then, the calibrated parameters have been used as input data in HM computations. Numerical results provided two kinds of informations. The first-one concerns the relevance of the mechanical model in predicting cracking. The second-one, concerns a verification of the validity of the coupling strategy in estimating fluid leakage in cracking concrete (at least at the sample scale). This second aspect represents a further indirect verification of the adequacy of the mechanical model in a “fine” description of cracking. According to the theoretical predictions, the laminar flow through a crack is indeed completely determined by the geometry of the crack itself. Therefore, an accurate prediction of the fluid flow rate through the cracking sample can be interpreted as an indicator of the level of accuracy (at least in statistical terms) of the model in predicting local cracks informations (i.e. openings, spatial distribution of the local apertures).

Further research are needed to validate the model at a structural scale. Furthermore, the complexity of the transfer model should be increased by taking into account compressible flows (e.g. air), partially saturated conditions and stronger HM couplings. These aspects are important in modelling of cracking at a early-age [10, 64, 76], concrete behaviour at high temperatures [16, 25, 38], hydraulic fracturing [12, 42, 62].