Minimizing the weighted sum of maximum earliness and maximum tardiness in a single-agent and two-agent form of a two-machine flow shop scheduling problem

Abstract

In the past decade, multi-agent scheduling studies have become more widespread. However, the evaluation of these issues in the flow shop scheduling environment has received almost no attention. In this article, we investigate two problems. One problem is a common due date problem of constrained two-agent scheduling of jobs in a two-machine flow shop environment to minimize the weighted sum of maximum earliness and maximum tardiness of first-agent jobs and restrictions of non-eligibility on the tardiness of second-agent jobs. Another problem is a single-agent form of the two-agent problem when the number of second-agent jobs is zero. So, an optimal algorithm with polynomial time complexity is presented for the single-agent problem. For the two-agent problem, after it was shown to have minimum complexity of ordinary NP-hardness, a branch and bound algorithm, based on efficient lower and upper bounds and dominance rules, was developed. The computational results show that the algorithm can solve the large-size instances optimally.

1 Introduction

In most production and assembly systems, production scheduling is used widely and has great functional importance. In this situation, more than one operation is often performed on every job. Because most operations for all jobs must be done in a certain way, workshop scheduling is like a flow shop environment. Because of the importance of the flow shop scheduling problem, many researchers studied it under various assumptions (e.g. Hamdi and Loukil 2015; Li et al. 2019; Rakrouki et al. 2020). Multi-agent scheduling problems in which several agents are competing for the use of shared resources have received growing attention in recent years. Unlike general multi-criterion scheduling problems, in which all jobs have to be evaluated by each criterion, in the multi-agent problems, each agent has its own set of jobs and follows only the desired criterion. Baker and Cole Smith (2003) and Agnetis et al. (2004) presented scheduling problems with two agents for the first time. Since then, more focus has been given to the multi-agent scheduling problems. In these problems, each agent has a criterion different from those of the other agents, and limited resources are used jointly. For more detailed discussion of multi-agent problems, interested readers are referred to Agnetis et al. (2014) and Perez-Gonzalez and Framinan (2014).

To date, few studies have been conducted on multi-agent flow shop scheduling problems. Suppose $C_{j}^{k}$ and $T_{j}^{k}$ denote completion time and tardiness of job $j$ of agent k, respectively, and $U_{j}^{k}$ has a zero–one value that indicates if the job j of agent k is tardy. Besides, $C_{max}^{k}$, $T_{max}^{k}$ indicate maximum completion time and maximum tardiness of the agent k jobs, respectively. Agnetis et al. (2004) examined the complexity of two-agent scheduling problems and showed that the problem $F2||C_{max}^{1} :C_{max}^{2} \le Q$ is NP-hard in the ordinary sense. Kim et al. (2017) studied this problem considering three special structures for processing times of each job of agents and investigated the complexity of these cases. Lee et al. (2010) studied the two-agent scheduling problem $F2||\sum T_{j}^{1} :\sum U_{j}^{2} \le 0$ and proposed a branch and bound algorithm and a simulated annealing algorithm. Lee et al. (2011) investigated the problem $F2||\sum C_{j}^{1} :\sum U_{j}^{2} \le 0$, and after examining the complexity, provided a branch and bound algorithm and a simulated annealing algorithm to solve it. Luo et al. (2012) investigated the ordinary NP-hard problems $F2||C_{max}^{1} + \theta C_{max}^{2}$ and $F2||C_{max}^{1} :C_{max}^{2} \le Q$. For the first problem, they provided a pseudo-polynomial dynamic programming algorithm and then a simple approximation algorithm and a fully polynomial-time approximation scheme. For the second problem, a pseudo-polynomial dynamic programming algorithm was also proposed, showing that if constraint $C_{max}^{2} \le Q$ is relaxed in the form of $C_{max}^{2} \le \left( {1 + \varepsilon } \right)Q$ for $\varepsilon > 0$, the approximation algorithm shows a worst-case ratio of $\left( {1 + \varepsilon } \right)$. They applied a fully polynomial-time approximation scheme to the relaxed problem. Shiau et al. (2015) investigated the problem $F2\left| {LE} \right|\sum C_{j}^{1} :T_{max}^{2} \le Q$ in which LE refers to the learning effect. They proposed a branch and bound algorithm and a genetic algorithm to solve the problem. The branch and bound algorithm and the genetic algorithm with a uniform crossover operator and a one-point mutation operator showed acceptable performance for problems with up to 20 jobs and larger ones.

Fan and Cheng (2016) studied the problems $F2||C_{max}^{1} + \alpha C_{max}^{2}$ and $F2||\sum C_{j}^{1} + \alpha C_{max}^{2}$ in which $\alpha$ is the importance weight of the second agent objective function relative to the first one. They proved the ordinary NP-hardness of the first problem and proposed a pseudo-polynomial-time algorithm for it. For the second problem, they proposed an approximation algorithm based on linear programming relaxation. Yin et al. (2017) investigated a two-machine flow shop scheduling problem with two competing agents such that each agent has a criterion which is a function of the weighted number of just-in-time (JIT) jobs. They focused on finding the Pareto frontier and presented a bicriteria analysis of the problem. Jeong et al. (2018) studied the same problem in which the first agent jobs are urgent, and the second agent ones are normal. The problem is minimizing the weighted sum of the total tardiness of the first agent and makespan of the second one. They proposed a branch and bound algorithm to solve the problem. The problem $F2||\sum T_{j}^{1} :C_{max}^{2} \le Q$ was studied by Ahmadi-Darani et al. (2018). They proposed some optimal properties and a tabu search algorithm. Chen et al. (2018) investigated a multi-agent scheduling problem in a no-wait flow shop environment considering the weighted number of just-in-time jobs as agents’ objective function. They studied two variants of the problem: Constrained optimization and Pareto optimization. They proved the complexity of these two variants and proposed approximation algorithms to solve them.

Meeting job due dates is a widely used criterion in scheduling problems, that is highly valued from the perspective of customers. Development and adoption of management methodologies such as the just-in-time (JIT) strategy have added value to this criterion. Not paying attention to due dates and delivering orders after due dates, in addition to penalties for tardiness, causes customer dissatisfaction and a desire to do business with rival companies. Finishing the jobs earlier than their due dates increases the storage costs or increase the probability of job deterioration. Most earliness/tardiness scheduling studies have considered min-sum criteria. However, there may be large values of earliness or tardiness for some jobs that cause difficulties in the production system. In assembly lines, jobs must be delivered by specified due dates. If a job is significantly early or tardy, then other jobs will not be completed, resulting in an imbalance in the assembly line. In the food industry, where companies must deliver fresh food to customers on time, earliness and tardiness are both highly undesirable, especially when the product is perishable. This problem is solved by establishing a balance among job costs through the minimization of the maximum scheduling cost of each job (min–max criteria). One of these criteria is the sum of maximum earliness and tardiness. This criterion seeks to minimize the gap between maximum earliness and maximum tardiness; in the best-case scenario, this value will be zero.

The sum of the maximum earliness and maximum tardiness criterion ($ET_{max}$) was first studied by Amin-Nayeri and Moslehi (2000). They proposed a branch and bound algorithm for the single-machine scheduling problem. Moslehi et al. (2010) improved the presented branch and bound algorithm using an efficient dominance rule and a heuristic procedure as an upper bound. Since $ET_{max}$ is a non-regular criterion, better solutions can be achieved by adding forced idle time. Some researchers investigated the $ET_{max}$ criterion in different environments and with different assumptions, and provided numerous optimal and heuristic methods (Tavakkoli-Moghaddam et al. 2005; Mahnam and Moslehi 2009; Moslehi et al. 2009; Yazdani et al. 2017).

Benmansour et al. (2014) considered the single-machine scheduling problem with restricted common due dates, aiming to minimize the weighted sum of maximum earliness and tardiness penalties for the jobs, with and without periodic maintenance activity. They provided a polynomial-time algorithm to solve the problem without the periodic maintenance activity constraint. They then showed that the second problem is a combination of the first one and the bin-packing problem.

In this article, we investigate the two-agent scheduling problem in a two-machine flow shop environment. The objective function is minimizing the weighted sum of maximum earliness and tardiness penalties and constraints on ineligible tardiness of second-agent jobs. Also, the single-agent form of this problem, when the number of second-agent jobs is zero, is studied. Hence, this article is an extension form of Benmansour et al. (2014) research from two points of view. First, we consider the two-machine flow shop scheduling problem, and second, we extend the defined two-machine flow shop scheduling problem to a two-agent form.

The studied problem is interesting for production environments with periodic production and delivery. In these environments, manufacturers are faced with some orders that must be processed and delivered at the end of each period (e.g., weekly). The orders belong to the different types of customers (agents). For the first type of customers, a just-in-time objective of the weighted sum of maximum earliness and tardiness is essential, and early production or late one has imposed a penalty. For the second agent, which is more important than the other agent, no tardy delivery is allowed. So, the common due date of both agents is justified based on the defined period of the manufacturer.

The article is organized as follows: In the next section, the problem and notations are defined. In Sect. 3, the optimal properties of the single-agent problem are checked, and an optimal polynomial-time algorithm is provided. In Sect. 4, the two-agent constrained scheduling problem in a two-machine flow shop environment is assessed. After investigating the complexity of the problem and developing a mathematical model, a branch and bound algorithm is provided to solve the problem. Computational experiments and results are reported in Sect. 5. Finally, conclusions and suggestions for future research are discussed in Sect. 6.

2 Problem definition

The objective of the studied two-agent scheduling problem is minimizing the weighted sum of maximum earliness and tardiness penalties for the first-agent and restrictions on ineligible tardiness for the second-agent. The problem is defined in a two-machine flow shop environment. Also, the due dates of jobs are common. If $n$ represents the total number of jobs, the problem is described as follows:

There are n jobs including $J_{1} , J_{2} , \ldots , J_{n}$. Each job belongs to the first or second agent and should be processed on two machines, $M_{1}$ and $M_{2}$. The set of first-agent jobs has $n_{1}$ members, including jobs $J_{1} , J_{2} , \ldots , J_{{n_{1} }}$, and the set of second-agent jobs has $n_{2}$ members, including jobs $J_{{n_{1} + 1}} , J_{{n_{1} + 2}} , \ldots , J_{n}$. Processing time on machine $i$ of job $j$ is defined as $p_{ij}$. All jobs of the agents has a common due date value equal to $d$. The assumptions of this problem are:

• The machines are always available.

• All jobs are available at zero time

• Machines cannot process more than one job at a time, and jobs cannot be processed simultaneously on two machines.

• Preempting the job processing on each machine is not allowed.

• Machines can also have forced idle time. This kind of idle time can be added before each job processing.

• Unforced idle time is a kind of idle time that cannot be removed by shifting the scheduled jobs to the left-hand side because of existing the previous jobs.

By defining the completion time of job $j$ belonging to agent $k$ on machine $i$ as $C_{ij}^{k}$, earliness and tardiness values of job $j$ belonging to agent $k$ are obtained by Eqs. (1) and (2).

$$E_{j}^{k} = max\left\{ {d - C_{2j}^{k} ,0} \right\}$$

(1)

$$T_{j}^{k} = max\left\{ {C_{2j}^{k} - d ,0} \right\}$$

(2)

The objective function of the problem is shown as $WET_{max}^{1}$, which is equal to $\alpha E_{max}^{1} + \beta T_{max}^{1}$. In this notation, $E_{max}^{1}$ is the maximum earliness and $T_{max}^{1}$ is the maximum tardiness of first-agent jobs. The objective is to obtain optimal job scheduling such that the amount of $\alpha E_{max}^{1} + \beta T_{max}^{1}$ for first-agent jobs is minimized, provided that none of the second-agent jobs are tardy. Suppose that $\alpha$ and $\beta$ are the weight of earliness and tardiness, respectively. Using the standard three-field notation scheme of Graham et al. (1979), this problem is denoted by $F2\left| {d_{j} = d} \right|\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$. Since the objective function is not regular, it is possible to improve the objective function value by inserting idle time to increase the completion time of jobs. As mentioned before, we call this kind of idle time as forced idle time. Hence, the optimal solution may not exist in the set of semi-active schedules.

Some necessary notations are as follows:

$n_{k}$:

Number of jobs of agent $k$ where $n_{1} + n_{2} = n$. $k = 1,2$

$N_{k}$:

Set of jobs of agent $k$ where $\mathop {\bigcup }\nolimits_{k = 1}^{2} N_{k} = N$. $k = 1,2$

$J_{\left[ j \right]}^{k}$:

The job of agent $k$ in the jth position of the sequence $j = 1,2, \ldots ,n$, $k = 1,2$

$p_{i\left[ j \right]}$:

Processing time of the job in the jth position of the sequence on machine i $i = 1,2$, $j = 1,2, \ldots ,n$

$C_{i\left[ j \right]}^{k}$:

Completion time of the job of agent $k$ in the jth position of the sequence on machine $i$ $i = 1,2$, $k = 1,2$, $j = 1,2, \ldots ,n$

$C_{max\left( S \right)}^{k}$:

Makespan of agent k jobs in a given set/sequence S $k = 1,2$

$E_{max\left( S \right)}^{k}$:

Maximum earliness of agent k jobs in a given set/sequence S $k = 1,2$

$T_{max\left( S \right)}^{k}$:

Maximum tardiness of agent k jobs in a given set/sequence S $k = 1,2$

$C_{max\left( S \right)}$:

Makespan of jobs in a given set/sequence S

$U_{j}^{2}$:

If $T_{j}^{2} > 0,$ it is equal to 1; otherwise, it is equal to 0. $j = 1,2, \ldots ,n_{2}$

$FIT$:

Sum of forced idle time on the second machine for a given sequence

UIT:

Sum of unforced idle time on the second machine for a given sequence

$\mathop \sum \nolimits_{j} U_{j}^{2}$:

Number of tardy jobs of the second agent $j = 1,2, \ldots ,n_{2}$

3 The single-agent scheduling problem in a two-machine flow shop

If in the problem $F2\left| {d_{j} = d} \right|WET_{max}^{1} :\sum U_{j}^{2} \le 0$, the number of second-agent jobs is zero; the problem of minimizing the weighted sum of earliness and tardiness is obtained. Using the notation scheme of Graham et al. (1979), this problem is denoted as $F2\left| {d_{j} = d} \right|WET_{max}$. In this section, some optimal properties of this problem are provided and proved, and then an optimal polynomial time algorithm is developed to solve it.

3.1 Optimal properties

In this section, some of the optimal properties of the problem $F2\left| {d_{j} = d } \right|WET_{max}$ are presented.

Theorem 1

In the problem $F2\left| {d_{j} = d} \right|WET_{max}$, there is an optimal sequence with a permutation schedule.

Proof

Consider a schedule in which the sequences of jobs on machines 1 and 2 are different. In such a schedule, we can find a pair of jobs, $j$ and $k$, such that job $j$ operation precedes job $k$ operation on machine 1, but on machine 2, job $k$ operation precedes job $j$ operation. If the operation of job $j$ on machine 1 is interchanged by operation of job $k$, considering the common due date for all the jobs, and also the possibility of entering forced idle time, this change will not have a negative effect on the objective function. In other words, as a result of this change, the completion time of any operation on the second machine will not increase, and the possible reduction of completion time of any job on the second machine is repairable by adding forced idle time to the beginning of the schedule of machine 2. Therefore, no increase in the maximum earliness and tardiness, and accordingly in the objective function value, will result from this change. Since the same argument applies to any schedule in which job sequences differ on machines 1 and 2, the property must hold in general.$\square$

According to Theorem 1, to solve the problem $F2\left| {d_{j} = d } \right|WET_{max}$, it is sufficient to consider permutation schedules.

Theorem 2

In the problem $F2\left| {d_{j} = d} \right|WET_{max}$, there is an optimal sequence where there is not any type of idle time between two adjacent jobs on each machine.

Proof

Suppose in schedule $S$, we have an idle time of duration $l$ between two adjacent jobs $j$ and $k$. If the idle time is transferred to before the first job of the sequence, the completion time of job $k$ and jobs after that will not change on the second machine. As a result, the maximum tardiness will not change. Also, the completion time of job $j$ and previous jobs will be increased by $l$. As a result, the maximum earliness will not increase. Therefore, the proof is complete.$\square$

Theorem 3

In the problem $F2\left| {d_{j} = d} \right|WET_{max}$, there is an optimal sequence where jobs on machine 1 start at time zero.

Proof

Suppose that, in an optimal schedule, there is an idle time of duration $l$ before processing the jobs on the first machine. By eliminating idle time on machine 1 and starting the jobs from time zero, no change in the amount of completion time on machine 2 will be created. So, the objective function value does not increase.$\square$

Considering the possibility of tardiness of the first job of a certain sequence, without adding unforced or forced idle times, we define $Y$ as the processing amount of the first job completed before $d$ on the second machine. The maximum value of $Y$ is calculated by Eq. (3).

$$Y_{max} = \hbox{min} \left\{ {p_{2\left[ 1 \right]} ,d - p_{1\left[ 1 \right]} } \right\}$$

(3)

Theorem 4

In the problem $F2\left| {d_{j} = d} \right|WET_{max}$, the objective function value for any given sequence is a function of $FIT$, $UIT$ and $p_{2\left[ 1 \right]}$.

Proof

Considering a given sequence $S$. If $C_{2\left[ 1 \right]}$ and $C_{2\left[ n \right]}$ are completion time of the first and last job on the second machine, respectively, the objective function value can be calculated as Eq. (4).

$$WET_{max} = \alpha max\left\{ {d - C_{2\left[ 1 \right]} , 0} \right\} + \beta max\left\{ {C_{2\left[ n \right]} - d , 0} \right\}$$

(4)

As a result of Theorem 2 and given adding forced idle time is allowed, the values of $C_{2\left[ 1 \right]}$ and $C_{2\left[ n \right]}$ can be calculated from Eqs. (5) and (6).

$$C_{2\left[ 1 \right]} = UIT + FIT + p_{2\left[ 1 \right]}$$

(5)

$$C_{2\left[ n \right]} = UIT + FIT + \mathop \sum \nolimits_{j} p_{2j}$$

(6)

By substituting Eqs. (5) and (6) in Eqs. (4), (7) is obtained.

$$WET_{max} = \alpha max\left\{ {d - \left( {UIT + FIT + p_{2\left[ 1 \right]} } \right) , 0} \right\} + \beta max\{ (UIT + FIT + \mathop \sum \nolimits_{j} p_{2j} ) - d , 0\}$$

(7)

To simplify Eq. (7), we investigated two cases of the problem, including the completion time of the first job in the sequence that is less or greater than the common due date, without considering unforced or forced idle times.

• Case 1. If $p_{2\left[ 1 \right]} < d - p_{1\left[ 1 \right]}$, then $Y_{max} = p_{2\left[ 1 \right]}$. Possible cases of the problem are as follows, by adding forced or unforced idle times:

• Case 1.1. If $UIT + p_{2\left[ 1 \right]} \ge d$, because all the jobs are non-early, in both cases $\alpha \le \beta$ and $\alpha > \beta$, forced idle time is not added ($FIT = 0$). As a result, $C_{2\left[ 1 \right]} \ge d$ and the maximum tardiness will be associated with the last job in the sequence. Therefore, the objective function using Eq. (7) will be as Eq. (8).

  $$WET_{max} = \beta \left( {UIT + \mathop \sum \nolimits_{j \in N } p_{2j} - d} \right)$$

  (8)

  Since the amount of $\mathop \sum \nolimits_{j} p_{2j}$ and $d$ is always constant; the objective function value is a function of $UIT$. As noted above, $FIT$ in this case is zero.

• Case 1.2. Suppose $UIT + p_{2\left[ 1 \right]} < d < UIT + \mathop \sum \nolimits_{j \in N } p_{2j}$. In this case, given the lack of idle time, the amount of earliness and tardiness is non-zero. So, the problem is investigated in both cases $\alpha \le \beta$ and $\alpha > \beta$.

  • If $\alpha \le \beta$, because tardiness is more important than earliness, forced idle time is not added ($FIT = 0$). The objective function is written as Eq. (9) using Eq. (7).

    $$WET_{max} = \left( {\alpha - \beta } \right)d + \left( {\beta - \alpha } \right)UIT - \alpha p_{2\left[ 1 \right]} + \beta \mathop \sum \nolimits_{j \in N } p_{2j}$$

    (9)

    Since the amount of $\mathop \sum \nolimits_{j \in N} p_{2j}$ and $d$ is always constant; the objective function value is a function of $UIT$ and $p_{2\left[ 1 \right]}$. As noted above, $FIT$ in this case is zero.

  • If $\alpha > \beta$, given the lack of idle time, the earliness and tardiness are non-zero. Therefore, the objective function is written as Eq. (10) using Eq. (7).

    $$WET_{max} = \left( {\alpha - \beta } \right)\left( {d - UIT - FIT} \right) - \alpha p_{2\left[ 1 \right]} + \beta \mathop \sum \nolimits_{j \in N } p_{2j}$$

    (10)

    Given that $UIT + p_{2\left[ 1 \right]} < d$, and earliness is more important than tardiness, before starting the first job on the second machine, forced idle time is added by $d - UIT - p_{2\left[ 1 \right]} .$ So, the first job will be completed in the time of $d$ ($C_{2\left[ 1 \right]} = d$). By substituting $FIT = d - UIT - p_{2\left[ 1 \right]}$, Eq. (11) will be obtained from Eq. (10).

    $$WET_{max} = \beta (\mathop \sum \nolimits_{j \in N } p_{2j} - p_{2\left[ 1 \right]} )$$

    (11)

    Since $\mathop \sum \nolimits_{j \in N} p_{2j}$ is always constant, the objective function value is a function of $p_{2\left[ 1 \right]}$. As mentioned before, $FIT$ in this case is equal to $d - UIT - p_{2\left[ 1 \right]}$.

• Case 1.3. If $UIT + \mathop \sum \nolimits_{j \in N } p_{2j} \le d$, then all the jobs are non-tardy. The problem is investigated in two cases, $\alpha \le \beta$ and $\alpha > \beta$.

  • If $\alpha \le \beta$, the objective function using Eq. (7) is written as Eq. (12).

    $$WET_{max} = \alpha \left( {d - UIT - FIT - p_{2\left[ 1 \right]} } \right)$$

    (12)

    By adding a forced idle time of $d - UIT - \mathop \sum \nolimits_{j \in N } p_{2j}$ before the first job on the second machine and finishing the last job in the time of $d$ ($C_{2\left[ n \right]} = d$), the last job has zero earliness and tardiness, the remained jobs are early, and the maximum earliness will be associated with the first job. The objective function of the problem, by substituting $FIT = d - UIT - \mathop \sum \nolimits_{j \in N } p_{2j}$ in Eq. (12), is written as Eq. (13).

    $$WET_{max} = \alpha \left (\mathop \sum \nolimits_{j \in N } p_{2j} - p_{2\left[ 1 \right]} \right )$$

    (13)

    According to Eq. (13), since $\mathop \sum \nolimits_{j \in N } p_{2j}$ is always constant, the objective function value is a function of $p_{2\left[ 1 \right]}$. As mentioned earlier, $FIT$ in this case is equal to $d - UIT - \mathop \sum \nolimits_{j \in N } p_{2j}$.

  • If $\alpha > \beta$, similar to the second part of case 1.2., the objective function of the problem is written as Eq. (14).

    $$WET_{max} = \beta \left (\mathop \sum \nolimits_{j \in N } p_{2j} - p_{2\left[ 1 \right]} \right )$$

    (14)

    Since $\mathop \sum \nolimits_{j \in N } p_{2j}$ is always constant, the objective function value is a function of $p_{2\left[ 1 \right]}$. As mentioned above, $FIT$ in this case is equal to $d - UIT - p_{2\left[ 1 \right]}$.

• Case 2. If $p_{2\left[ 1 \right]} \ge d - p_{1\left[ 1 \right]}$, then $Y_{max} = d - p_{1\left[ 1 \right]}$. In this case, similar to case 1.1, in both cases, $\alpha \le \beta$ and $\alpha > \beta$, the objective function of the problem will be as Eq. (15).

  $$WET_{max} = \beta \left( {UIT + \mathop \sum \nolimits_{j \in N } p_{2j} - d} \right)$$

  (15)

  Since the amount of $\mathop \sum \nolimits_{j \in N } p_{2j}$ and $d$ is always constant; the objective function value is a function of $UIT$. As noted above, $FIT$ in this case is zero.$\square$

Corollary 1

In the problem $F2\left| {d_{j} = d} \right|WET_{max}$, for any given sequence, following Table 1, we can calculate the amount of forced idle time and the objective function.

Table 1 Amount of forced idle time and the objective function in the problem $F2 | {d_{j} = d} |WET_{max}$

It is notable to mention that Table 1 contents are a summary of the proof cases in Theorem 4.

Emmons and Vairaktarakis (2013) demonstrated that, in the two-machine flow shop scheduling problem of minimizing the maximum completion time of jobs considering non-simultaneous machine available times, the Johnson (1954) order is the optimal sequence. Thus, according to Theorem 4, Corollary 1, and Emmons and Vairaktarakis (2013), Theorem 5 can be drawn.

Theorem 5

To obtain the optimal schedule of problem $F2\left| {d_{j} = d} \right|WET_{max}$, it is sufficient to consider $n$ sequences where each job is placed in the first position of the sequence, and the other jobs are scheduled according to the Johnson order. Forced idle time is also determined, according to Corollary 1.

Proof

According to Theorem 4 the objective function value for any given sequence is a function of $FIT$, $UIT$ and $p_{2\left[ 1 \right]}$. Therefore, to find an optimal sequence, it is sufficient to determine the total amount of forced idle time and the first-position job in the sequence on the second machine. The value of forced idle time is also calculated by Corollary 1. So, to find an optimal solution, n sequences are considered that each job is placed in the first position, and the other jobs are sequenced to minimize unforced idle time on the second machine. Emmons and Vairaktarakis (2013), proved that the Johnson order minimizes makespan (or total unforced idle time) in a two-machine flow shop scheduling problem considering ready time for each machine. Hence, the other jobs are sequenced based on the Johnson order. Therefore, the proof is complete.$\square$

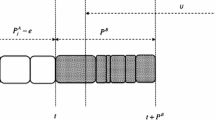
According to Corollary 1, the maximum earliness and tardiness of jobs in a sequence can be determined by specifying the start time of the first job on the second machine. If $t_{0}$ is the start time of the first job of the sequence on the second machine, the maximum earliness and tardiness are calculated by Eqs. (16) and (17), respectively. In Eqs. (16) and (17), the interval $\left[ {0 - t_{0} } \right]$ includes forced and unforced idle time on the second machine.

$$E_{max} = {max} \left\{ {0, d - t_{0} - p_{2\left[ 1 \right] } } \right\}$$

(16)

$$T_{max} = t_{0} + \mathop \sum \nolimits_{j} p_{2j} - d$$

(17)

Considering the mentioned properties, the general structure of the optimal solution of jobs with the objective function $\alpha E_{max} + \beta T_{max}$ is shown in Fig. 1. In this figure, $I_{2}$ is equal to $UIT + FIT$.

Fig. 1

The general structure of the optimal solution of the problem $F2\left| {d_{j} = d} \right|WET_{max}$

3.2 Solution algorithm

In this section, we proposed an algorithm that determines the optimal sequence of jobs and the start time of the first job of the sequence on the second machine. According to Corollary 1, the algorithm tries to obtain the optimal schedule, determining unforced idle time, the processing time of the first job on the second machine, and forced idle time.

The proposed algorithm performs as follows: First, the jobs are ordered according to the Johnson rule in order to minimize the maximum completion time on the second machine ($C_{max}$). Then, $n$ different sequences of jobs are generated, transferring job $j$ to the beginning of the sequence. The aim of generating $n$ sequences is to find a schedule that has a minimum value of $WET_{max}$. In the case of $\alpha \le \beta$, for each sequence, the jobs on the first machine are started from time zero and placed on the second machine without forced idle time. Unforced idle time on the second machine is transferred to the start of the sequence. The objective function for each $n$ sequence is calculated, and a sequence with the minimum cost is selected. In the $\alpha > \beta$ case, for each sequence, jobs are started on the first machine from time zero and placed on the second machine in such a way that the first job is completed in $d$ or later (if there is no possibility of completion in time $d$). Unforced idle time on the second machine is transferred to the start of the sequence. The objective function value for each $n$ sequence is calculated, and a sequence with the minimum cost is selected. The pseudo-code of this algorithm is shown in Fig. 2.

Fig. 2

Pseudo-code of solution algorithm for $F2\left| {d_{j} = d} \right|WET_{max}$

The above presented exact algorithm includes jobs sorting according to the Johnson rule, with the time complexity of $O\left( {nlogn} \right),$ and then a loop to transfer each job to the start of the sequence. Since each time a job is transferred to the start of the sequence, the Johnson order remains constant; the provided algorithm has a time complexity of $O\left( {nlogn} \right)$. This algorithm determines the optimal values of three decision variables: idle time on the second machine, maximum earliness, and maximum tardiness.

4 The two-agent scheduling problem in a two-machine flow shop

In this section, the constrained two-agent scheduling problem in a two-machine flow shop environment is investigated. The objective is minimizing the weighted sum of earliness and tardiness penalties considering the constraint of non-eligibility of tardiness for the second-agent. First, the complexity and some of the optimal properties of the problem are studied. Then, the mathematical programming model of the problem is developed. Finally, a branch and bound algorithm is presented to find the optimal solution.

4.1 Complexity, theorems and optimal properties

To the best of our knowledge, no studies in the literature have examined the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$. So, before using and providing any solution procedure, the problem complexity is examined in Theorem 6.

Theorem 6

The problem $F2 | {d_{j} = d} | \alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$ has a minimum complexity of ordinary NP-hardness.

Proof

Consider the problem $F2 | {d_{j} = d} |\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$ with the assumptions $\alpha = 0$, $\beta = 1,$ and $d = Q$. So, the problem converts to $F2 | {d_{j} = Q} |T_{max}^{1} :\sum U_{j}^{2} \le 0$. Because the due date is common for all jobs, the constraint of ineligibility of tardiness for the second-agent is equivalent to requiring that the completion time of any second-agent job does not exceed the common due date $Q$. Therefore, the constraint $\sum U_{j}^{2} \le 0$ can be written as $C_{j}^{2} \le Q$ for all second-agent jobs. Given that constraint $C_{j}^{2} \le Q$ is equivalent to requiring that the maximum completion time of the second-agent jobs does not exceed $Q$ i.e. $C_{max}^{2} \le Q$, the investigated problem can be written as $F2||max\left\{ {C_{max}^{1} - Q,0} \right\}:C_{max}^{2} \le Q$.$\square$

In the term $max\left\{ {C_{max}^{1} - Q,0} \right\}$, because $Q$ is constant, it is sufficient just to minimize the maximum completion time of the first-agent jobs. Therefore, the problem $F2\left| {d_{j} = d} \right|\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$, with the assumptions $\alpha = 0$, $\beta = 1$ and $d = Q$, converts to the problem $F2||C_{max}^{1} :C_{max}^{2} \le Q$. Since the problem $F2||C_{max}^{1} :C_{max}^{2} \le Q$ is NP-hard in the ordinary sense (Agnetis et al. (2004)), the problem $F2 | {d_{j} = d} |\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$ has a minimum complexity of ordinary NP-hardness.

In the third section, the problem $F2 | {d_{j} = d} |WET_{max}$ was investigated, and some optimal properties were presented. For some of the presented single-agent theorems, adding second-agent jobs and the constraint of not having tardiness does not change the optimality conditions of the single-agent properties, and therefore, they are extended for the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$. It is notable to mention that proofs of these theorems are very similar to the single-agent ones. These properties are presented in the form of three theorems, as follows:

• 1. In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, there is an optimal sequence with a permutation schedule.

• 2. In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, there is an optimal sequence where there is no idle time between two consecutive jobs on each machine.

• 3. In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, there is an optimal sequence where jobs on the first machine are started at time zero.

Because there is no possibility of completing the second-agent jobs after the due date, any feasible sequence of the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$ can be classified as four sets $A$, $B$, $C$ and $D$, according to Fig. 3.

Fig. 3

The general structure of jobs sequence on the second machine in a feasible solution of problem $F2\left| {d_{j} = d} \right|WET_{max}^{1} :\sum U_{j}^{2} \le 0$

According to Fig. 3, the sets $A$, $B$, $C$ and $D$ are defined as follows:

Set $A$: A set of second-agent jobs that are completed at the beginning of the sequence and before the first scheduled job of the first agent (Eq. (18)).

$$A = \{ j|C_{2j}^{2} < C_{2\left[ 1 \right]}^{1} \}$$

(18)

Set $B$: Single-member set that includes the first scheduled job of the first agent.

Set $C$: A set of first- and second-agent jobs that are completed after the first scheduled job of the first agent and before the due date (Eq. (19)).

$$C = \left\{ {j\left| {C_{2j} } \right\rangle C_{2\left[ 1 \right]}^{1} \& C_{2j} \le d} \right\}$$

(19)

Set $D$: A set of first-agent jobs that are completed after the due date (Eq. (20)).

$$D = \left\{ {j\left| {C_{2j}^{1} } \right\rangle d} \right\}$$

(20)

Each set $A$, $C$ and $D$ can be empty. The set of all jobs is equal to $A \cup B \cup C \cup D$.

Theorem 7

In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, there is an optimal schedule in which the jobs order of the sets $A$, $C$ and $D$ is the Johnson order.

Proof

The proof is clear.$\square$

4.2 The mixed-integer linear programming model

In this section, a mixed-integer linear programming model is developed for $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$ based on the permutation property of the optimal solution and Theorem 7. This model is developed based on assigning the jobs to the sets $A$, $B$, $C$ and $D$. In this model, $C_{ij}$, $E_{j}$, $T_{j}$, $E_{max}$ and $T_{max}$ are continuous and non-negative decision variables, and $AS_{j}$, $BS_{j}$, $CS_{j}$ and $DS_{j}$ are binary decision variables having a value of one if job $j$ is placed in the specified set; otherwise, they will be zero. It is assumed that all jobs, including first- and second-agent jobs, are sorted based on the Johnson rule, and have been indexed accordingly. It should be noted that the agent index has not been used in the symbols. Also, the objective function of each agent is determined in the constraints.

$$\hbox{min} WET_{max} = \alpha E_{max} + \beta T_{max}$$

(21)

Subject to

$$AS_{j} + CS_{j} = 1 \; \forall j \in N_{2}$$

(22)

$$BS_{j} + CS_{j} + DS_{j} = 1\; \forall j \in N_{1}$$

(23)

$$\mathop \sum \nolimits_{j} BS_{j} = 1\; \forall j \in N_{1}$$

(24)

$$C_{ij} \le C_{il} - p_{il} + BigM_{1} \left( {2 - AS_{j} - AS_{l} } \right)\; \forall j,l \in N_{2} ,\; \forall i \in M ,\;j < l$$

(25)

$$C_{ij} \le C_{il} - p_{il} + BigM_{1} \left( {2 - CS_{j} - CS_{l} } \right)\; \forall j,l \in N,\; \forall i \in M ,\;j < l$$

(26)

$$C_{ij} \le C_{il} - p_{il} + BigM_{2} \left( {2 - DS_{j} - DS_{l} } \right)\; \forall j,l \in N_{1} ,\; \forall i \in M ,\;j < l$$

(27)

$$C_{ij} \le C_{il} - p_{il} + BigM_{1} \left( {2 - AS_{j} - BS_{l} } \right)\; \forall j \in N_{2} , \; \forall l \in N_{1} , \; \forall i \in M$$

(28)

$$C_{ij} \le C_{il} - p_{il} + BigM_{1} \left( {2 - BS_{j} - CS_{l} } \right)\; \forall j \in N_{1} , \; \forall l \in N , \; \forall i \in M$$

(29)

$$C_{ij} \le C_{il} - p_{il} + BigM_{2} \left( {2 - BS_{j} - DS_{l} } \right)\; \forall j \in N_{1} , \; \forall l \in N , \; \forall i \in M$$

(30)

$$C_{ij} \le C_{il} - p_{il} + BigM_{2} \left( {2 - CS_{j} - DS_{l} } \right)\; \forall j \in N , \; \forall l \in N_{1} , \; \forall i \in M$$

(31)

$$C_{2j} - BigM_{2} \left( {1 - CS_{j} } \right) \le d\; \forall j \in N$$

(32)

$$C_{2j} - BigM_{2} \left( {1 - DS_{j} } \right) \ge d + 1\; \forall j \in N_{1}$$

(33)

$$C_{1j} \ge p_{1j} \; \forall j \in N$$

(34)

$$C_{2j} \ge C_{1j} + p_{2j} \; \forall j \in N$$

(35)

$$T_{j} - E_{j} = C_{2j} - d\; \forall j \in N_{1}$$

(36)

$$E_{max} \ge E_{j} \; \forall j \in N_{1}$$

(37)

$$T_{max} \ge T_{j} \; \forall j \in N_{1}$$

(38)

$$AS_{j} \in \left\{ {0,1} \right\}\; \forall j \in N_{2}$$

(39)

$$CS_{j} \in \left\{ {0,1} \right\}\; \forall j \in N$$

(40)

$$DS_{j} ,BS_{j} \in \left\{ {0,1} \right\}\; \forall j \in N_{1}$$

(41)

$$T_{j} ,E_{j} \ge 0\; \forall j \in N$$

(42)

In this model, Eq. (21) represents the objective function. Equation (22) assigns each second agent job to just one of the sets $A$ and $C$. Also, Eq. (23) assigns each first agent job to just one of the sets $B$, $C$ and $D$. Equation (24) ensures that among the first agent jobs, only one job can be placed in the position of the first job of the first agent.

Constraints (25) (26) and (27) indicate that no two jobs of one of the sets $A$, $C$ and $D$ can overlap in a time. Also, given that these three constraints are defined for jobs $j < l$, in the sets $A$, $C$ and $D$, the jobs are ordered according to the Johnson rule. In constraints (28), (29), (30) and (31), the time overlap between the jobs of the sets ($B$ and $A$), ($C$ and $B$), ($D$ and $B$) and ($D$ and $C$) is controlled. It is notable to mention that by considering constraints (32) and (33), constraint (31) is redundant. However, adding constraint (31) to the model reduces the solution time.

Constraint (32) controls the condition of completing jobs in the set $C$ at or before the time $d$. Constraint (33) specifies that the jobs of the set $D$ should be completed after the time $d$. Constraint (34) ensures that the completion time of each job on the first machine is not less than its processing time. In other words, the start time of any job will not have a negative value on the first machine. Constraint (35) ensures that the completion time of each job on the second machine will not be less than the sum of the completion time of that job on the first machine and its processing time on the second machine. In other words, no job can be started on the second machine before completing its operation on the first machine. $BigM_{1}$ and $BigM_{2}$ are sufficiently large positive scalars with minimum values of $d$ and $C_{{{max} \left( {\overline{jo} } \right)}} + d$, respectively. $C_{{{max} \left( {\overline{jo} } \right)}}$ is equal to the maximum completion time of the reverse Johnson order of all jobs.

Since any solution satisfying $E_{j} \ge 0$ and $T_{j} \ge 0$ is dominated by Eq. (43) or Eq. (44), then Eq. (36) is always applied.

$$T_{j} = C_{2j} - d\;{\text{and}}\;E_{j} = 0 \; {\text{if}}\;C_{2j} > d$$

(43)

$$E_{j} = d - C_{2j} \;{\text{and}}\;T_{j} = 0 \; {\text{if}}\;C_{2j} \le d$$

(44)

Constraints (37) and (38) determine the maximum earliness and tardiness. Constraints (39), (40) and (41) define the binary variables $AS_{j}$, $BS_{j}$, $CS_{j}$ and $DS_{j}$. Constraints (42) defines the non-negative variables $E_{j}$ and $T_{j}$.

4.3 Heuristic procedure (METRSA)

According to the presented optimal properties, a heuristic algorithm called METRSA (Minimizing ET_max Regardless of the Second Agent jobs) is provided for $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$. In this algorithm, the second-agent jobs are placed at the beginning of the sequence based on the Johnson order. Then $n_{1}$ sequences are considered such that in each one, a first-agent job is placed after the second-agent jobs, and the remainder of the first-agent jobs are sorted based on the Johnson order. The objective function values of these $n_{1}$ sequences are calculated, and a sequence with the minimum cost is selected. The steps of METRSA are as follows:

• Step 1. Arrange and index the first-agent jobs according to the Johnson order. Name the set of the arranged jobs $I^{AG1}$ and consider its $k$th job as $J_{\left[ k \right]}$. Set $k = 1$.

• Step 2. Arrange the second-agent jobs according to the Johnson order and place them at the beginning of the sequence.

• Step 3. Place job $J_{\left[ k \right]}$ immediately after the second-agent scheduled jobs and schedule the remained jobs of set $I^{AG1}$ after that, based on the indexed order. Name the resulting sequence $s_{\left[ k \right]}$.

• Step 4. Move unforced idle time to the beginning of the sequence and calculate the optimal value of forced idle time for machines.

• Step 5. Calculate the maximum value of earliness and tardiness of sequence $s_{\left[ k \right]}$ and set $F_{\left[ k \right]} = \alpha E_{max}^{1} + \beta T_{max}^{1}$. If $k = n_{1}$, go to Step 6; otherwise, set $k = k + 1$ and go to Step 3.

• Step 6. Calculate the minimum value of $F_{\left[ k \right]}$ for $1 \le k \le n_{1}$ and put it in $F^{*}$. $F^{*}$ is the objective value of the algorithm solution.

• Step 7. Stop.

The METRSA algorithm includes sorting of jobs based on the Johnson rule, with time complexity of $O\left( {nlogn} \right),$ and then a loop to transfer each first-agent job to the beginning of the sequence of first-agent jobs. Since every time a first-agent job is transferred to the beginning of the first-agent sequence, the Johnson order remains constant. So, the proposed algorithm has a time complexity of $O\left( {nlogn} \right)$.

4.4 Branch and bound algorithm

According to Theorem 7, we designed a branch and bound algorithm to solve the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$. In this algorithm, the branching strategy is based on assigning each job to each of the sets A, B, C, and D, and the jobs of sets A, C and D, are arranged according to the Johnson rule. Components of the proposed branch and bound algorithm are described below.

Branching scheme The basis of branching is assigning each job to any of the sets $A$, $B$, $C$ and $D$. It is assumed that all first- and second-agent jobs are sorted based on the Johnson order and indexed accordingly. The order of entering the jobs to the tree is the same. In the first level of the tree, the first job of the first agent is determined among the indexed jobs of the first agent and assigned to the set $B$. At the next levels, two branches should be generated for any job entering the search tree. If the entering job belongs to the first agent, a branch is associated with the job assigned to the set $C,$ and the other branch is related to the assignment of the job to the set $D$. If the entering job belongs to the second agent, two branches are associated with assigning the job to the set $A$ and $C$. Because the entering order of jobs to the tree is based on the Johnson order, in each node of the tree, the order of scheduled jobs in each set is based on the Johnson order. Figure 4 shows the tree search of the proposed branch and bound for an example with four jobs. In this example, the jobs were indexed based on the Johnson order. The jobs J₁ and J₃ belong to the first agent, and the jobs J₂ and J₄ belong to the second agent. For each node, the number in the square reflects the generating order of that node.

Fig. 4

Tree search of the proposed branch and bound for an example with four jobs

Search strategy A depth-first strategy is used to select the node for branching. In each step having a partial sequence of jobs ($\sigma$), new branches are generated by adding unscheduled jobs to the set $\sigma$ such that they satisfy feasibility conditions and dominance rules. During the search procedure, the objective function of a found schedule is compared with the upper bound, and the upper bound is updated if required. It should be noted that the optimal duration of forced idle time cannot be calculated until a complete sequence is achieved. So, a partial sequence of $\sigma$ is not a final schedule, and there is a possibility of changes in forced idle time calculated in each node and completion times in the complete sequence.

Whenever a complete sequence of $S$ is achieved, after transferring the unforced idle time of the second machine to the beginning of the sequence, the conditions of forced idle time are investigated. The UIT value for the complete sequence $S$ is calculated according to Eqs. (45) and (46).

$${\text{if}}\;C_{{max\left( S \right)}} < d\;{\text{and}}\;\alpha \le \beta \Rightarrow ~~~~UIT = d - C_{{max\left( S \right)}}$$

(45)

$${\text{if}}\;\alpha > \beta \Rightarrow UIT = min\left\{ {max\left\{ {d - C_{{2\left[ 1 \right]}}^{1} ~,0~} \right\}~,~d - C_{{max\left( S \right)}}^{2} } \right\}$$

(46)

According to Eq. (45), if $C_{max\left( S \right)} < d$ and $\alpha \le \beta$, all jobs are non-tardy. As a result, the maximum tardiness value will be zero, and the maximum earliness value will be positive. By adding forced idle time with a value of $d - C_{max\left( S \right)}$ before starting the first job on the second machine and finishing the last job in the time $d$ ($C_{2\left[ n \right]} = d$), the last job of sequence $S$ has an earliness and a tardiness value of zero. The remaining jobs will be early, and the maximum earliness will be calculated from the first job of the first agent. Also, according to Eq. (46), if $\alpha > \beta$, forced idle time is added before the start of the first job on the second machine such that the first-agent job is completed at $d$ and none of the second-agent jobs will be tardy. So, if the first job of the first agent is scheduled between the second-agent jobs, idle time will be $- C_{max\left( S \right)}^{2}$; and if it is scheduled after the all second-agent jobs, idle time will be $max \left\{ {d - c_{{2\left[ 1 \right]}}^{1} ,0} \right\} .$

After calculating the optimal forced idle time for a complete sequence, it will be accepted as a feasible sequence. Then, the objective function of this sequence is calculated and compared with the upper bound. If the objective function value is less than the upper bound, the upper bound will be updated.

Lower bound In each node, the lower bound of the partial sequence, indicated as $LB_{WETmax}$, is calculated based on Theorem 8 (named $LB1_{WETmax}$), Theorem 9 (named $LB2_{WETmax}$) and Corollary 2. In the following, one algorithm for calculating each lower bound and the related theorems are given.

Calculation algorithm for $\vec{ LB}1_{{\vec{WETmax}}}$:

• Step 1 Consider $\sigma$ as the sequence of scheduled jobs in the sets $A$, $B$, $C$ and $D$.

• Step 2 Add forced idle time of duration $d - C_{max \left( C \right)}$ before the first job of the first agent such that the last job of set $C$ is completed at time $d$.

• Step 3 Calculate the maximum earliness value of the first-agent jobs and set it to $E_{max\left( \sigma \right)}^{1}$.

• Step 4 Set the completion time of the first job of the set $D$ to $d + 1$.

• Step 5 Calculate the maximum tardiness of jobs of the set $D$ and set it to $T_{max\left( \sigma \right)}^{1}$.

• Step 6 Set $LB1_{WETmax} = \alpha E_{{max} \left( \sigma \right)}^{1} + \beta T_{max\left( \sigma \right)}^{1}$.

• Step 7 Stop.

Theorem 8

The value obtained from the calculation algorithm for $LB1_{WETmax}$ is a lower bound for a partial sequence in the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$.

Proof

Since due dates have a common value, after transferring the unforced idle time of the second machine to the beginning of the sequence and considering forced idle time, the maximum earliness of a partial sequence $\sigma$ is calculated by Eq. (47).

$$E_{max\left( \sigma \right)}^{1} = max\left\{ {d - C_{2\left[ 1 \right]}^{1} ,0} \right\}$$

(47)

According to the algorithm for calculating $LB1_{WETmax}$, in Eq. (47), the amount of forced idle time before the first-agent job is added by $UIT = d - C_{max \left( C \right)}$ such that the last job of the set $C$ is completed at time $d$. Therefore, Eq. (47) can be written as Eq. (48). In Eq. (48), $C_{max \left( C \right)}$ is the maximum completion time belonging to the set $C$.

$$E_{max\left( \sigma \right)}^{1} = max\left\{ {C_{max \left( C \right)} - C_{2\left[ 1 \right]}^{1} ,0} \right\}$$

(48)

Since $C_{max \left( C \right)}$ is not decreased by completing the partial sequence $\sigma$, the maximum earliness of the complete sequence will not be less than $E_{max\left( \sigma \right)}^{1}$. In other words, inequality (49) is established. In this equation, $E_{max}^{*}$ represents the maximum earliness of the optimal sequence.

$$E_{max}^{*} \ge E_{max\left( \sigma \right)}^{1}$$

(49)

It is clear that in a partial sequence $\sigma$, among the jobs of the sets $A$, $C$ and $D$, only the jobs of the set $D$ have positive tardiness value. Given the existing condition of a job in set $D$ (completing after $d$), to calculate the maximum tardiness of a partial sequence $\sigma$, it is assumed in Eq. (50) that the first job of the set $D$ is completed at the earliest possible time of $d + 1$. In this equation, $C_{max \left( D \right)}$ and $C_{2\left[ 1 \right]\left( D \right)}$ show, respectively, the maximum completion time of the jobs that belong to the set $D$, and the completion time of the first job in the schedule of the jobs belonging to the set $D.$

$$T_{max\left( \sigma \right)}^{1} = C_{max\left( D \right)} - C_{2\left[ 1 \right]\left( D \right)} + 1$$

(50)

Given that in a complete sequence, the completion time of the first job of the set $D$ will not be less than $d + 1$, the maximum tardiness of the set $D$ jobs in a complete sequence will not be less than $T_{max\left( \sigma \right)}^{1}$. In other words, inequality (51) is established. In this constraint, $T_{max}^{*}$ represents the maximum earliness of the optimal sequence.

$$T_{max}^{*} \ge T_{max\left( \sigma \right)}^{1}$$

(51)

By comparing inequalities (49) and (51), inequality (52) is obtained.

$$\alpha E_{max}^{*} + \beta T_{max}^{*} \ge \alpha E_{{max} \left( \sigma \right)}^{1} + \beta T_{max\left( \sigma \right)}^{1}$$

(52)

So, we can say that the value obtained from the algorithm for calculating $LB1_{WETmax}$ is a lower bound for $\alpha E_{max}^{*} + \beta T_{max}^{*}$ in the problem $F2 | {d_{j} = d} |\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$.$\square$

Calculation algorithm for $\vec{ LB}2_{{\vec{WETmax}}}$:

• Step 1 Consider $\sigma$ as the sequence of scheduled jobs in the sets $A$, $B$, $C$ and $D$. Define the set of unscheduled jobs as $\sigma^{\prime}$.

• Step 2 If $\alpha > \beta$, go to Step 3; otherwise, go to Step 5.

• Step 3 Set ${{\varOmega }} = \sigma \cup \sigma^{\prime}$ and calculate $E_{{max\left( {{\varOmega }} \right)}}^{1}$ similarly to the calculation procedure for $LB1_{WETmax}$.

• Step 4 Schedule the first-agent jobs of $\sigma^{\prime}$ in the set $D$ and after the set $\sigma$ jobs according to the Johnson order. Go to Step 11.

• Step 5 Schedule the second-agent jobs of the set $\sigma^{\prime}$ in the set $A$ after the set $\sigma$ jobs according to the Johnson order. In the case of infeasibility, schedule the remained jobs in the set $C$ after the set $\sigma$ jobs.

• Step 6 Add the first-agent jobs of the set $\sigma^{\prime}$ to the set $C$ according to the Johnson order until the completion time of jobs of the set $C$ does not exceed $d$.

• Step 7 Add forced idle time of duration $d - C_{max \left( C \right)}$ before the first job of the first agent, such that the last job of the set $C$ is completed at $d$.

• Step 8 Calculate the maximum earliness of the first-agent jobs and put it in $E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$.

• Step 9 In order to calculate the maximum tardiness, reconsider the sequence $\sigma$ and the set $\sigma^{\prime}$. Schedule the scheduled jobs, including the first job of the first agent and jobs of the set $C$ along with all the second-agent jobs of the set $\sigma^{\prime}$ immediately after the jobs of the set $A$, according to the Johnson order. Do this procedure until the completion time of the last job is greater than or equal to $d$ for the first time.

• Step 10 Assign the unscheduled first-agent jobs to the set $D$.

• Step 11 Set the completion time of the first job of the set $D$ to $d + 1$.

• Step 12 Calculate the maximum tardiness of the set $D$ jobs and put it in $T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$.

• Step 13 Set $LB2_{WETmax} = \alpha E_{{{max} \left( {\sigma \cup \sigma^{\prime}} \right)}}^{1} + \beta T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$.

• Step 14 Stop.

Theorem 9

The value obtained from the calculation algorithm for $LB2_{WETmax}$ is a lower bound for a partial sequence in the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$.

Proof

In the algorithm for calculating $LB2_{WETmax}$, the values of $E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$ and $T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$ are calculated separately. Calculation of these two values in the two cases of $\alpha > \beta$ and $\alpha \le \beta$ is different. These two cases are examined below.

• Case $\alpha > \beta$:

In the case of $\alpha > \beta$, the $E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$ is calculated similarly to the calculation algorithm for $LB1_{WETmax}$. In other words, according to inequality (49), inequality (53) is established.

$$E_{max}^{*} \ge E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$$

(53)

Since $\alpha > \beta$ is established, in the complete sequence, efforts are made to complete the first job of the first agent at $d$ or later (if there is no possibility of completing in $d$), and the remained jobs of the first-agent after $d$. This action improves the objective function of the problem. According to the calculation algorithm of $LB2_{WETmax}$, in the complete sequence, the number of tardy first-agent jobs cannot be less than the number of the set $D$ jobs. Also, the completion time of the first job of the set $D$ is not less than $d + 1$. Therefore, the tardiness of the set $D$ jobs in the complete sequence will not be less than $T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$. In other words, inequality (54) is established.

$$T_{max}^{*} \ge T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$$

(54)

• Case $\alpha \le \beta$:

Since $\alpha \le \beta$ is established, in the complete sequence, efforts are made to complete the first-agent jobs before the due date $d$ as far as possible. These efforts lead to improving the objective function of the problem. So, in the calculation algorithm for $LB2_{WETmax}$, to calculate $E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$, efforts are made to schedule all second-agent jobs and the largest possible number of first-agent jobs before the due date $d$. The remaining space will be filled by adding forced idle time before the first job of the first agent. Therefore, the maximum earliness of the complete sequence will not be less than $E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$. In other words, inequality (55) is established.

$$E_{max}^{*} \ge E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$$

(55)

In the algorithm for calculating $LB2_{WETmax}$, efforts are made to complete the largest possible number of jobs before the due date $d$. These jobs have no tardiness. Next, the remained first-agent jobs are assigned to the set $D$. In the complete sequence, the number of the set $D$ jobs will not be less than this number. In the calculation algorithm for $LB2_{WETmax}$, the first job of the set $D$ is completed at the earliest possible time of $d + 1$, and in the complete sequence, the completion time of the first job of the set $D$ will not be less than $d + 1$. Therefore, the maximum tardiness of the set $D$ in the complete sequence will not be less than $T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$. In other words, inequality (56) is established.

$$T_{max}^{*} \ge T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$$

(56)

According to inequalities (53) and (54) for the case $\alpha > \beta$, and inequalities (55) and (56) for the case $\alpha \le \beta$, inequality (57) is obtained.

$$\alpha E_{max}^{*} + \beta T_{max}^{*} \ge \alpha E_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1} + \beta T_{{max\left( {\sigma \cup \sigma^{\prime}} \right)}}^{1}$$

(57)

So, we can say that the value obtained from the calculation algorithm for $LB2_{WETmax}$ is a lower bound for $\alpha E_{max}^{*} + \beta T_{max}^{*}$ in the problem $F2 | {d_{j} = d} |\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$.

By comparing Eqs. (52) and (57), Eq. (58) is obtained.

$$\alpha E_{max}^{*} + \beta T_{max}^{*} \ge max\left\{ {\alpha E_{{max} \left( \sigma \right)}^{1} + \beta T_{{max} \left( \sigma \right)}^{1} , \alpha E_{{{max} \left( {\sigma \cup \sigma^{\prime}} \right)}}^{1} + \beta T_{{{max} \left( {\sigma \cup \sigma^{\prime}} \right)}}^{1} } \right\}$$

(58)

According to inequality (58), Corollary 2 can be drawn.

Corollary 2

The value of $LB_{WETmax}$ obtained from Eq. (59) is a lower bound for a partial sequence $\sigma$ in the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$.

$$LB_{WETmax} = max \left\{ {LB1_{WETmax} , LB2_{WETmax} } \right\}$$

(59)

Upper bound To get a feasible solution for $F2 | {d_{j} = d} |\alpha E_{max}^{1} + \beta T_{max}^{1} :\sum U_{j}^{2} \le 0$ as an upper bound, before entering the branching and in the root node, the METRSA algorithm is executed. The objective function obtained from the METRSA algorithm is considered as the upper bound $UB_{WETmax}$.

Dominance rules The following three dominance rules are presented. They are used for fathoming the nodes and branches in the branch and bound algorithm.

Consider schedule $s^{DR1}$ in which the second-agent jobs are scheduled at the beginning of the sequence based on the Johnson order, and the first-agent jobs are scheduled after them based on the reverse Johnson order. Maximum completion time of all the jobs of schedule $s^{DR1}$ is denoted by $C_{{max\left( {s^{DR1} } \right)}}$.

Theorem 10

(Dominance rule 1) In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, assuming $\alpha \le \beta$, if inequality (60) is established, the sequence obtained from the METRSA algorithm is optimal.

$$C_{{max \left( {s^{DR1} } \right)}} \le d$$

(60)

Proof

According to inequality (60), due date $d$ is greater than the maximum completion time in the schedule $s^{DR1}$. The METRSA algorithm acquires the best scheduling of the first-agent jobs with the assumption that the second-agent jobs are scheduled at the beginning of the sequence. Also, the reverse Johnson order will result in the maximum value of maximum completion time. Therefore, if due date $d$ is greater than the maximum completion time for all the jobs in the schedule $s^{DR1}$, considering the assumption of $\alpha \le \beta$, forced idle time is added to the beginning of the sequence of the second machine such that the last job of the second machine in the sequence obtained from the METRSA algorithm is completed at time $d$. The duration of this forced idle time is more than or equal to the makespan resulting from the sequence of the Johnson order of the second-agent jobs. Consequently, scheduling the second-agent jobs at the beginning of the sequence and during idle time, according to the Johnson order, is possible, and the sequence derived from the METRSA algorithm is optimal.$\square$

Theorem 11

(Dominance rule 2) In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0,$ assuming $\alpha > \beta$, if inequality (61) is established, the sequence obtained from the METRSA algorithm is optimal.

$$C_{{2\left[ 1 \right] \left( {METRSA} \right)}}^{1} \le d$$

(61)

Proof

According to inequality (61), due date $d$ is greater than the completion time of the first job of the first agent in the sequence obtained from the METRSA algorithm with the notation of $C_{{2\left[ 1 \right] \left( {METRSA} \right)}}^{1}$. In the optimal schedule of the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0,$ assuming $\alpha > \beta$, concerning the legality of forced idle time, jobs on the second machine are arranged in such a way that the first job will be completed at or later than time $d$ (if there is no possibility of completion at time $d$). If due date $d$ is greater than or equal to the makespan derived from scheduling the second-agent jobs at the beginning of the sequence and after the first job of the first agent according to the Johnson order, which is obtained from the METRSA algorithm, the amount of space required to place the second-agent jobs based on the Johnson order exists at the beginning of the sequence. Hence, the sequence obtained from the METRSA algorithm is optimal.$\square$

Theorem 12

(Dominance rule 3) In the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, if in a partial sequence $\sigma$, the maximum completion time of the sequence obtained from the Johnson order of the jobs of the sets $A$, $B$ and $C$, along with all the second-agent jobs of the set $\sigma^{\prime}$, is greater than the common due date $d$, this sequence is not feasible.

Proof

It is not allowed to complete the second-agent jobs after the due date based on the problem definition. Also, having a job in the sets $A$, $B$ or $C$ requires completing it before $d$. If the maximum completion time obtained by the Johnson order of the sets $A$, $B$ and $C$, along with all the second-agent jobs of the set $\sigma^{\prime}$, and as a result, the minimum possible makespan for these operations exceeds $d$, at least one of the above two conditions are violated. Thus, by completing the partial sequence $\sigma$, an infeasible sequence is obtained.$\square$

5 Computational results

In order to investigate the performance of the proposed branch and bound algorithm in the problem $F2 | {d_{j} = d} |WET_{max}^{1} :\sum U_{j}^{2} \le 0$, two sets of instances for both cases $\alpha = 1 \le \beta = 5$ and $\alpha = 5 > \beta = 1$ were generated. Because the processing time of jobs does not affect the performance of the algorithm, it was generated from a discrete uniform distribution in the range of [1, 10]. The common due date value in the case $\alpha \le \beta$ is determined by Eq. (62), according to the literature on the scheduling problem (Gelders and Sambandam 1978; Armentano and Ronconi 1999; Hasija and Rajendran 2004; Perez-Gonzalez and Framinan 2010) and adapting for the two-agent problem. Also, since the due dates calculated by Eq. (62), for the instances with the assumption $\alpha > \beta$ have large values, and due to dominance rule 2, these instances were solved polynomially before entering the branch and bound. Therefore, to determine more difficult instances in the case $\alpha > \beta$, the common due date was generated by Eq. (63). Because of the desirability of generating instances with different difficulty levels, two equations were used to generate the common due date. In order to evaluate the effect of the due date on algorithm performance, in Eq. (62), the value of $\rho_{1}$ was selected from the set of {0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1.0 and 1.2}, and in Eq. (63), the value of $\rho_{2}$ was selected from the set of {0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1.0}. In this equation, $C_{{{max} \left( {jo} \right)}}^{1}$ and $C_{{{max} \left( {jo} \right)}}^{2}$ indicate maximum completion time of the first- and second-agent jobs based on the Johnson order, respectively.

$$d = C_{{{max} \left( {jo} \right)}}^{2} + \rho_{1} C_{{{max} \left( {jo} \right)}}^{1}$$

(62)

$$d = C_{{{max} \left( {jo} \right)}}^{2} + \rho_{2} \mathop {{max} }\limits_{{j \in N_{1} }} \left\{ {p_{2j} } \right\}$$

(63)

To investigate the effects of the number of first- and second-agent jobs on the algorithm performance, three combinations $2n_{1} = n_{2}$, $n_{1} = n_{2}$ and $n_{1} = 2n_{2}$ were considered. Based on the number of these combinations and the values of $\rho_{1}$ and $\rho_{2}$, 24 (3 × 8) problem groups named $GA01$ to $GA24$ for the case of $\alpha \le \beta$ and 21 (3 × 7) groups named $GB01$ to $GB21$ for the case $\alpha > \beta$ were formed. In each group, in the case $\le \beta$, 20 instances were generated for each size 45, 50, 100, 150, 200, 300, 500, 1000 and 2000 jobs. Also, in the case $\alpha > \beta$, 20 instances were generated for each size 100, 150, 200, 300, 500 and 700 jobs.

The branch and bound algorithm was coded in ${\text{Visual C }}\# 2013$, and problem instances were solved on a computer system with Intel® Core™ i7-2600 CPU 3.4 GHz and $4.00 {\text{GB RAM}}$ in a $32 - {\text{bit Windows }}7$ operating system environment. A time constraint of 3600 s was applied to solve instances by the branch and bound algorithm optimally. Tables 2 and 3 show the computational results for $F2\left| {d_{j} = d} \right|WET_{max}^{1} :\sum U_{j}^{2} \le 0$ in cases $\alpha \le \beta$ and $\alpha > \beta$, respectively.

Table 2 Computational results for the branch-and-bound algorithm in the case $\alpha \le \beta$

Table 3 Computational results for the branch-and-bound algorithm in the case $\alpha > \beta$

The proposed mixed-integer linear programming model was able to solve instances up to 25 jobs in size. Since the branch and bound algorithm showed better performance than the model, the results of the model are not presented.

According to Table 2, 93.54% of the instances studied in the case $\alpha \le \beta$, were solved optimally, that 96.1% of these optimally solved instances were solved by the branch and bound algorithm and 3.9% of them were solved by dominance rule 1.

Figure 5 shows the percentages of optimally solved instances concerning problem size. Increasing the number of jobs decreases the number of instances solved by the branch and bound. This trend is logical due to increased solution time and the increase in the number of schedules examined to find the optimal solution. The vertical dotted line on the graph represents a threshold for disability to solve all groups. Therefore, instances that are placed before this line were solved in all groups optimally. However, instances that are placed after the line belong to only the groups that the branch and bound algorithm were capable of solving them. So, in groups $GA07$, $GA08$, $GA15$, $GA16$, $GA23$, $GA24$, i.e., the groups with $\rho_{1}$ of 1.0 and 1.2, the instances were solved up to 200 jobs in size and their results are reported. Also, the percentage of optimally solved instances increased in the instances with more than 200 jobs in size.

Fig. 5

Diagram of the percentage of optimally solved instances concerning problem size in the case $\alpha \le \beta$

As is evident in Fig. 5, the percentage of optimally solved instances by dominance rule 1 is decreased by increasing the problem size, and for instances with 300 jobs or more becomes zero. The reason for this decline is that by increasing the number of jobs and therefore increasing unforced idle time, conditions for the establishment of dominance rule 1 require a greater due date. Therefore, a lower number of instances satisfies the dominance rule 1 condition, and the instances are solved before entering the branch and bound.

Figure 6 shows the diagram of the percentages of optimally solved instances concerning $\rho_{1}$. This diagram shows that by increasing $\rho_{1}$, the number of instances solved optimally by dominance rule 1 in groups with $\rho_{1}$ values higher than 0.8 increases. Therefore, the number of optimally solved instances entered into the branch and bound algorithm decreases. Since by increasing $\rho_{1}$, due dates increase, more instances satisfy the conditions of dominance rule 1, and the percentage of optimally solved instances by dominance rule 1 increases.

Fig. 6

Diagram of the percentage of optimally solved instances concerning $\rho_{1}$ in the case $\alpha \le \beta$

Given the results in Table 3, among all instances examined in the case $\alpha > \beta$, 96.11% were solved optimally, that 73.9% of them were solved by the branch and bound algorithm, and 26.1% of them were solved by dominance rule 2.

Figure 7 shows the diagram of the percentages of optimally solved instances concerning problem size in the case $\alpha > \beta$. In all groups, all instances were solved up to 500 jobs optimally. Also, the percentage of instances solved optimally by dominance rule 2 shows a constant trend for all sizes. Also, the percentage of instances solved optimally by the branch and bound algorithm up to 500 jobs shows a constant trend. This percentage is reduced for larger sizes because of increasing in solution time and increasing in the number of schedules to be checked to find the optimal solution.

Fig. 7

Diagram of the percentage of optimally solved instances concerning problem size in the case $\alpha > \beta$

Figure 8 shows the diagram of the percentages of optimally solved instances concerning $\rho_{2}$. By increasing $\rho_{2}$, the number of optimal instances solved by dominance rule 2 increases. Also, due dates are increased, and more instances satisfy the dominance rule 2 conditions. So, the number of optimally solved instances by this dominance rule increases. As a result of the increasing number of instances solved by dominance rule 2, the number of instances entered into the branch and bound algorithm decreases.

Fig. 8

Diagram of the percentage of optimally solved instances concerning $\rho_{2}$ in the case $\alpha > \beta$

Previously, the branch and bound performance was investigated in both cases $\alpha \le \beta$ and $\alpha > \beta$ and effective factors were introduced and analyzed. Table 4 summarizes the branch and bound performance.

Table 4 A summary of the branch-and-bound performance in two cases $\alpha \le \beta$ and $\alpha > \beta$

Based on Table 4, the percentage of instances solved optimally by dominance rules 1 and 2 before entering the branch and bound is higher in $\alpha > \beta$. This is because of greater due date in the case $\alpha > \beta$ which causes more instances to be satisfied in the condition of dominance rule 1. Also, a meaningful difference exists between the sizes that all the instances were solved in both cases $\alpha \le \beta$ and $\alpha > \beta$. This difference arises because, in the case $\alpha > \beta$, to obtain an optimal solution, it has to be decided whether the assignment of the second-agent jobs to the set $C$ can improve the objective function. However, in the case $\alpha \le \beta$, to obtain an optimal solution, the position of all first- and second-agent jobs must be examined on the eligible sets. As a result, the two-agent problem in the case $\alpha \le \beta$ is more difficult than in the case $\alpha > \beta$. That is why the sizes in which all the instances were solved in the time constraint of 3600 s are greater in the case $\alpha > \beta$ than in the case $\alpha \le \beta$.

In the case $\alpha \le \beta$, the branch and bound algorithm was able to solve most of the large instances. This ability is due to the excellent performance of $LB2_{WETmax}$ in fathoming the nodes in the first level of the branch and bound tree. So, in the case $\alpha \le \beta$, the branch and bound algorithm can solve instances up to 2000 jobs in the time constraint of 3600 s, while in the case $\alpha > \beta$, the maximum size of solved instances is 700.

Since the basis for calculating the lower bounds is the objective function of the first-agent jobs, by increasing the number of first-agent jobs, the efficiency of these lower bounds increases. So, the most difficult groups in both cases $\alpha \le \beta$ and $\alpha > \beta$ are the groups with greater numbers of second-agent jobs than first-agent jobs. According to Eqs. (62) and (63), the due date in the case $\alpha > \beta$ gets smaller values than in the case $\alpha \le \beta$. So, dominance rule 3 performs better in fathoming the nodes. Because this dominance rule investigates the completion possibility of the second-agent jobs before the due date according to a partial sequence at each node before calculating the lower bound $LB2_{WETmax}$. The lower bound $LB2_{WETmax}$, which determines the position of all jobs, including scheduled and unscheduled jobs in each set, gets a greater maximum tardiness value in the case $\alpha \le \beta$ and this lower bound fathoms more nodes than $LB1_{WETmax}$ and $DR3$.

6 Conclusions and suggestions for future researches

In this article, the constrained two-agent scheduling problem in a two-machine flow shop environment was investigated. The objective is minimizing the weighted sum of maximum earliness and maximum tardiness of the first-agent jobs considering that the second agent jobs are not allowed to be tardy. Also, a single-agent form of this problem when the number of second-agent jobs is zero was studied. To solve the single-agent problem, we investigated the optimal scheduling properties. Based on these properties, an exact algorithm with polynomial time complexity was presented. To solve the two-agent problem, we show that it had a minimum complexity of ordinary NP-hard. Then, the optimal scheduling properties of this problem were studied, and a mathematical programming model based on the optimal properties was proposed. Also, a branch and bound algorithm based on efficient lower and upper bounds and dominance rules were developed for the two-agent problem. To investigate the performance of the proposed branch and bound algorithm, we generated and solved several instances. The computational results showed the ability of the algorithm to solve 93.54% of the total generated instances up to 2000 jobs in the case $\alpha \le \beta$ and 96.11% of the total generated instances up to 700 jobs in the case $\alpha > \beta$.

Considering different weights for the job or different specifications of them can be carried out as an extension of the investigated problems. Another suggestion for further research is the development of the two-agent problem, which can be presented by considering a common due date for the jobs of each agent separately. Also, considering a different due date for each job can be an exciting issue.