1 Introduction

In order to create positional advantages in today’s marketplaces and gain better performances, perspective of companies has transformed from the traditional business principles to the modern concepts such as the supply chain. During recent years, integration of supply chain activities and processes has improved the total performance of supply chains (Chang et al. 2016). The supply chain integration requires coordinating the flows of materials and information among its entities and their collaboration. In fact, collaboration and coordination could have great role in reducing costs and creating superior value for customers (Arkan et al. 2011; Ivanov et al. 2016).

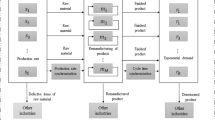
One of the most important problems in companies and organizations is to decide on the planning of production and inventory problems. Till now, different models in the field of production and inventory control systems have been developed and discussed in order to solve these interrelated problems in various approaches and scenarios. Among traditional supply chain models, there is a dominant approach in which each supply chain echelon (e.g., suppliers, manufacturers, distributers or even retailers) is sole responsible for his inventory and production control activities (Sadeghi et al. 2014a, b). As a result of such a circumstance, each echelon has just information on inventory or demand of his own downstream and upstream neighbor echelons. Particularly, the downstream echelon has the role of leader in this way of managing of supply chain system, and the upstream echelon just gets the production order quantity and should supply the necessary delivery to downstream as requested. The upstream perceives market demand indirectly just via the downstream ordering activities. Indeed, the supplier does not have any responsibility for the decision of production order quantities made by buyer and its consequences. Figure 1 shows a schematic illustration of a traditional supply chain. The triangle icon indicates the storage at buyer’s site.

Fig. 1
figure 1

The traditional structure of supply chain

Full size image

This traditional type of relationship among supply chain echelons caused some problems in traditional supply chain management. Hence, many industries were decided to share more information inside supply chain so as to improve their supply chain performances (Lin et al. 2010). The vendor managed inventory (VMI) is one of the mechanisms which are recently used as an integration and coordination system of SCM. Under VMI, the downstream no longer manages its production and inventory control system and leaves his responsibilities to the upstream. Moreover, by implementing the VMI policy, SCM permits the upstream to have access into the demand and inventory information, and receives market data directly. In contrast to traditional way of managing the supply chain systems, the upstream and the downstream operates as a single unit under VMI agreement. They act based on an admitted policy whose main idea is that the upstream receives demand data directly from market, and in turn he should manage the production and inventory policies for both upstream and downstream, appropriately. As one of the main characteristics of VMI is that, in such agreement, the upstream pays the costs of inventory system on behalf of the downstream echelon, and it is also assumed that the downstream pays no cost (Mateen and Chatterjee 2015). The upstream determines the quantity of production in terms of his own inventory cost, which is the total cost of the supply chain. Figure 2 depicts the structure of supply chain under such VMI system.

Fig. 2
figure 2

The VMI structure of supply chain

Full size image

In this research, a single-supplier multi-buyer multi-product economic production quantity (EPQ) model is presented and discussed. The majority of researches on VMI in literature were presented on economic order quantity (EOQ) models where the rate of replenishment is assumed infinite, while it is not necessarily confirmed in real supply chains. It is also considered that shortage is allowed in each inventory cycle with a mixed type of backorders and lost sales. The traditional researches consider either no shortage in the model or shortage with full backordering, while in real-world situations, a number of customers wait for backorders and remaining leaves the store encountering with shortage. Thus, in this paper, it is assumed that a percentage of backorders becomes lost and we have hence a partial backordering. A supplier is responsible to manage the production quantities of all of the products for a set of multiple buyers under VMI agreement. Furthermore, in order to take into account the concern about environmental impact of SCM activities, the total green house gas (GHG) emission factor is considered to design a green EPQ model. In addition, in order to improve the applicability of suggested model to the real-world inventory control systems the total GHG emission level are limited in the problem formulation as a model constraint. The aim is to find the appropriate values of production quantities and the maximum shortage levels in such a way that the total cost of supply chain is minimized. Under above conditions and VMI policy, the problem is formulated as a non-linear programming model and then a decomposition based solution approach is proposed to solve it optimally. At the end, a numerical example is discussed to investigate the proposed approach.

The rest of this paper is structured as follows. Section 2 reviews the related literature. Then, Sect. 3 discusses the problem definition and modeling. A solution approach is presented in Sect. 4, and a numerical example is described in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Literature review

The concept of VMI was first introduced by Magee (1958) via describing about the authority on the control of inventory. He discussed on who is responsible for managing the inventory decisions in business activities. Afterwards, in real-world, the interest in the VMI concept has been extended during the 1990s. Although the VMI has been primarily popular in grocery sector, however its applications were extended into other sectors like steel, book and petrochemicals (Disney and Towill 2003). The companies and organizations have employed VMI as a way of creating the competitive advantage in marketplaces. Many successful businesses have benefited from the implications of VMI, like Wal-Mart, and Proctor and Gamble (Dong and Xu 2002). In research presented by Waller et al. (1999), it was discussed that VMI can enhance performance of inventory management systems as well as the customer services in a supply chain. Disney and Towill (2002) showed that sharing demand and inventory information inside a supply chain leads to (1) minimizing the chain cost, and (2) satisfying a pre-determined customer service levels. In another work presented by Lee et al. (2005) and Vergin and Barr (1999), it was reported that that VMI is effective in improving the entire financial performance of supply chain. The VMI can be applied to different inventory control models. Among them, the most well known model is the classical economic order quantity (EOQ) which is using in many real-world applications. During recent years, numerous researchers tried to extend EOQ with practical conditions (Pentico and Drake 2011).

A great number of VMI literatures have used EOQ formula in modeling of the inventory system (Hill and Omar 2006). In an in-depth analysis, Yao et al. (2007) discussed the VMI problem for a single-supplier and single-buyer and reported the advantages of VMI agreement in such structure of supply chain. In addition, Van der Vlist et al. (2007) extended the work of Yao et al. (2007) by considering the cost of shipments between supplier and buyer. In another work, Darwish and Odah (2010) introduced a single-supplier multi-buyer supply chain with VMI model and a penalty cost for supplier, and then developed a computationally efficient solution algorithm. Besides, Marque‘s et al. (2010) presented a review study on the VMI implementations. Pasandideh et al. (2011) considered a VMI model in a two-echelon supply chain with constraints and full backordered shortages, and devised a genetic algorithm to solve their suggested model. Moreover, Cárdenas-Barrón et al. (2012) extended the model presented by Pasandideh et al. (2011) by adding a constraint that the maximum backorder level should be less or equal than the order quantity at each inventory cycle. Sadeghi et al. (2011) proposed a VMI model with the replenishment frequency. They suggested a genetic algorithm to solve the problem. As another research in VMI field, Yu et al. (2012) introduced an EOQ model for perishable inventories, and solved it through a golden search algorithm. Besides, in order to reduce the Bullwhip effect within supply chain, Kristianto et al. (2012) analyzed a VMI model via an adaptive fuzzy based approach. Hariga et al. (2013) designed a heuristic procedure to solve a modified VMI model on the basis of Darwish and Odah (2010) using unequal replenishment intervals. Recently, Park et al. (2016) formulated an inventory-routing problem in a single-manufacturer and multiple-retailer supply chain with lost sales under VMI strategy.

The economic production quantity (EPQ) model is another classical inventory model which can be implemented through VMI policy. In contrast to the number of researches devoted to EOQ models, the VMI research on EPQ models is very limited in literature. Based on EPQ model with a finite production rate, Hill (1999) developed a one-supplier multi-buyer VMI model with different shipment sizes. In another work presented by Hill and Omar (2006), they suggested the unit holding cost between the supplier and the buyer with different shipment sizes. As an extension, Braglia and Zavanella (2003) modified the work of Hill (1999) for a single-vendor single-buyer case through EPQ environment. Zavanella and Zanoni (2009) studied a model with multiple buyers, and performed a sensitivity analysis for model parameters. Besides, Pasandideh et al. (2014) and Sadeghi et al. (2014a, b) considered EPQ cases of VMI with one supplier and one buyer with several constraints. Mateen and Chatterjee (2015) investigated the analytical models for various approaches of single vendor–multiple retailer system to coordinate via VMI.

Table 1 represents the characteristics of literature in terms of number of suppliers, number of buyers, number of products and model structure (EOQ or EPQ). The last row shows the characteristics of present work. As can be seen, the case of VMI supply chain with single supplier, multi-buyer, multi-product via EPQ structure is not studied till now.

Table 1 The characteristics of previous researches in literature
Full size table

Moreover, in real-world situations, the consumer behavior does not necessarily coincide with full backorders or full lost sales. It often follows a mixed type of backorders and lost sales. In other words, the needs of some customers are not critical exactly at the time of order, and hence, they can wait for the next production cycle. Indeed, a fraction of customers who are faced with a shortage are willing to wait for next replenishment. While, other customers are not willing to wait, and hence decide to leave the buyer’s store and then purchase from another source. By considering a finite production rate in EPQ, Abad (2000) discussed some inventory models combined with additional characteristics. San José et al. (2005), studied some models with a variable backordering rate, and Taleizadeh et al. (2010) investigated production and repair of products with partial backordering on a single machine. Pentico and Drake (2011) reviewed the structure of all of the models with mixed backorders and lost sales. Moreover, Pentico and Drake (2009), and San José et al. (2014) have evaluated the partial backordering in EPQ model.

The design of business activities with less green house gas (GHG) emissions is now a concern of governments, social organizations and NGOs. This concern has motivated the researchers to consider green supply chain as an interesting area of academic research (Zhu and Sarkis 2004; Linton et al. 2007). A decision methodology was done by Nagurney et al. (2006) to find optimal strategy on carbon taxes in electric supply chains. In order to determine the supply chain decisions, Ramudhin et al. (2008) formulated a mathematical optimization model for carbon trading. Moreover, Guillen-Gosalbez and Grossmann (2009) have designed a supply chain model so as to maximize the financial performance and simultaneously minimize environmental impact. Besides, a strategic planning with carbon market considerations was proposed by Ramudhin et al. (2008) for a supply chain design problem. Roozbeh Nia et al. (2015) described a green EOQ model under VMI with multiple items and shortage. More recently, Govindan and Sivakumar (2016) analyzed a supply chain design problem to optimize both the GHG emissions and supply chain costs.

In this paper, we propose a green single-supplier multi-buyer multi-product economic production quantity (EPQ) model with partial backordering under VMI among supplier and buyers. In subsequent section, the mathematical formulation is presented.

3 Problem definition and modeling

There is a production-inventory system with one supplier and multiple buyers \( \left( {i = 1, 2, \ldots , I} \right) \) that work under VMI policy for managing multiple products \( \left( {j = 1, 2, \ldots , J} \right) \). The buyers face with external demand from customers, where demands are assumed to be deterministic. The supplier manufactures products to meet the orders received from buyers. The production-inventory system follows an EPQ model where the procurement is carried out via a finite rate of production, and the shortage is allowed with a mixed type of backorders and lost sales. Figure 3 shows the inventory level corresponding to a single buyer \( i \) for a specific product \(j .\) At every inventory cycle \( T_{ij} \), the production is processed until the inventory reaches to maximum level \( I_{ij}^{ \hbox{max} } \), and then the stored inventory is consumed with the demand rate \( D_{ij} \). until shortage occurres and reaches to maximum level \( b_{ij} \). during shortage period \( t_{ij} \). The maximum shortage in each cycle \( b_{ij} \) includes both tackorders \( \beta_{ij} b_{ij} \) and the lost sales \( \left( {1 - \beta_{ij} } \right)b_{ij} \). As a green constraint, a legal limitation on total G emissions \( T_{e} \) should be satisfied. The aim is to find the appropriate values of production quantities \( Q_{ij} \) and the maximum shortage levels \( b_{ij} \) in such a way that the total cost of supply chain is minimized.

Fig. 3
figure 3

The inventory level for product \( j \) of a single buyer \( i \)

Full size image

The problem assumptions, parameters and variables are given in sequel.

3.1 Assumptions

  • There are single supplier and multiple buyers.

  • The supplier manages the quantities of production in each cycle under VMI policy.

  • The shortages are allowed.

  • There is mixed backorders and lost sales (partial backordering).

  • The production rate is finite (EPQ).

  • The production rate is greater than the demand rate.

  • The lead time is assumed zero.

  • There is no quantity discount.

  • The price is fixed over the planning period.

  • The demand is deterministic and constant.

  • The total GHG emission level is limited.

3.2 Notations

Problem parameters

i :

Buyer index \( i = 1, \ldots , I \)

j :

Product index \( j = 1, \ldots , J \)

Iij(t):

The inventory level for product \( j \) of buyer \( i \) at time \( t \)

A Bij :

The fixed ordering cost of buyer i per order of product j

A Sij :

The fixed ordering cost of supplier per order of product j from buyer i

h ij :

The holding cost of product j per unit for buyer i in each period

ω ij :

The backorder cost of product j for buyer i per unit per time unit

τ ij :

The lost sale cost of product j for buyer i per unit

D ij :

The demand rate of buyer i for product j in each period

P ij :

The production rate of buyer i for product j in each period

β ij :

The proportion of shortage that is backordered in each perd (0 ≤ βij ≤ 1)

\( I_{ij}^{ \hbox{max} } \) :

The maximum inventory level of product j for buyer i

SC A :

The inventory cost of supplier with VMI policy

SC B :

The inventory cost of supplier without VMI policy

BC i A :

The inventory cost of buyer i with VMI policy

BC i B :

The inventory cost of buyer i without VMI policy

TC A :

Total inventory cost of chain with VMI policy

TC B :

Total inventory cost of chain without VMI policy

ζ :

The emissions cost per order

q :

The amount of GHG emission per order

T e :

The legal threshold on total GHG emissions

Problem variables

Q ij :

The order quantity for product \( j \) of buyer \( i \) per cycle

T ij :

The inventory cycle interval of product j for buyer i

b ij :

The maximum shortage level for product \( j \) of buyer \( i \) per cycle, including both backorders and lost sales

t ij :

The shortage period for product \( j \) of buyer \( i \)

3.3 The case of traditional non-VMI policy

In the case of non-VMI policy, the buyers determine their quantity level, usually from economic production quantity model in terms of their specific inventory cost parameters, and order the products to vendor. In such cases, the buyers act at their economic points, whereas, the vendor should supply the requested amount of products by buyers which is not necessarily at his economic point. In this section, we aim to model the inventory cost functions for buyers and vendor separately, and then formulate the total inventory cost of chain under non-VMI policy. To this end, we borrow from basic EPQ model presented by Mak (1987) and customize it next.

Under non-VMI policy, each buyer \( i \) has his specific ordering cost as follows.

$$ \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Bij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]\quad \quad \forall i \in I $$
(1)

Moreover, the inventory holding cost for all of the products requested by each buyer \( i \) is calculated as follows.

$$ \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \quad \quad \forall i \in I $$
(2)

in which \( \rho_{ij} \) is utilization factor in the form of \( D_{ij} /P_{ij} \). The inventory backordering cost for possible shortage of products at each buyer \( i \) can be formulated as follows.

$$ \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right]\quad \quad \forall i \in I $$
(3)

Additionally, the inventory lost sales cost for each buyer \( i \) can be formulated as follows.

$$ \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]\quad \quad \forall i \in I $$
(4)

In order to preserve the environmental and social issues, a green inventory system should be designed. In general, one of the key cost factors in a green inventory system includes the emission cost of green house gas incurred by transportation of orders from supplier to buyer. To this end the emission cost of green house gas (GHG) for each buyer \( i \) is calculated in terms of number of orders sent out during inventory horizon. It can be modeled as follows.

$$ \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\zeta D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]\quad \quad \forall i \in I $$
(5)

By using above inventory costs consisting of (1) ordering cost, (2) holding cost, (3) backordering cost, (4) lost sales cost and (5) green considerations cost, we can calculate the total inventory cost for each buyer \( i \) as follows.

$$ \begin{aligned} BC_{B}^{i} = & \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Bij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\ + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\ + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\zeta D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]\quad \quad \forall i \in I \\ \end{aligned} $$
(6)

Furthermore, the production-inventory system of each buyer has a cycle interval \( T_{ij} = \left( {Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} } \right)/D_{ij} \) and a shortage period \( t_{ij} = b_{ij} /D_{ij} \).

On other hand, the supplier has an ordering cost according to sent orders to the buyer \( i \) as follows.

$$ \mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]\quad \quad \forall i \in I $$
(7)

Hence, the total cost of supplier considering all of the buyers’ orders is given as follows.

$$ SSC_{B} = \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] $$
(8)

3.4 The case of integrated VMI policy

As mentioned before, in traditional inventory policy of a supply chain, the buyer derives his optimal replenishment policy in terms of his total cost function, and send an order with the size of optimal order quantity to supplier. In such situation there is no role for the supplier where supplier receives the buyer’s order and prepares the order to be send to the buyer. In other word, buyer acts at his optimal point, whereas supplier acts at a point not necessarily near to his optimal point. However under VMI policy, the supplier is decision maker of system. In such system, the inventory costs of both buyers and suppliers, and hence the total inventory costs of the supply chain, are formulated as follows:

$$ BC_{A}^{i} = 0\quad \quad \forall i \in I $$
(9)
$$ \begin{aligned} SC_{A} &= \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{i = 1}^{I} \left( {\mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right. \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \left. { \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\zeta qD_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right) \end{aligned} $$
(10)

Hence, we have:

$$ \begin{aligned} TC_{A} &= SC_{A} + \mathop \sum \limits_{i = 1}^{I} BC_{A}^{i} \\ &= \mathop \sum \limits_{i = 1}^{I} \left( {\mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right. + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Bij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left. {\left[ {\frac{{\zeta qD_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right) \end{aligned} $$
(11)

In addition, the total GHG emission level of each buyer should not exceed a legal threshold \( T_{e} \), which is.

$$ \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{qD_{i} }}{{Q_{i} + \left( {1 - \beta_{i} } \right)b_{i} }}} \right] \le T_{e} $$
(12)

By incorporating the above green constraint into total cost \( TC_{A} \), the final optimization problem becomes a non-linear programming model as follows:

$$ \begin{aligned} {\text{min }} TC_{A} &= \mathop \sum \limits_{i = 1}^{I} \left( {\mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right. + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Bij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left. {\left[ {\frac{{\zeta D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right) \end{aligned} $$
(13)

subject to

$$ \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{qD_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \le T_{e} $$
$$ \rho_{ij} = D_{ij} /P_{ij} \quad \quad \forall i \in I $$
$$ Q_{ij} , b_{ij} \ge 0 , \quad \quad \forall i \in I $$

The aim is to delineate the values of both the order quantity and the backorder level of buyers such that the total cost of the supply chain under VMI policy is minimized. We discuss a solution approach in subsequent section.

4 A solution approach

In this section, we are going to design an analytic solution algorithm for the problem formulated in previous section. A deep investigation reveals that this problem is comprised of similar subsystems, represented by \( I \) buyers and \( J \) products. We can exploit this observation, and apply a Lagrangian relaxation (LR) approach to decompose the problem and into smaller easier sub-problems and solve the problem via LR. In standard LR approach, a hard problem is usually decomposed to smaller and easier problems. However, a problem to perform this decomposition is that there may be a set of coupling constraints. There are some independent blocks linked by a coupling constraint in the technological coefficient matrix. In such situations, decomposing the coupling constraints generates a Lagrangian problem which is easier to solve. Generally, the Lagrangian optimization method can be incorporated with the Kuhn-Tucker conditions to solve minimization problems subject to a single inequality constraint. Let us consider a general minimization function \( f\left( {X_{1} , X_{2} , \ldots , X_{n} } \right) \) subject to an inequality constraint \( g\left( {X_{1} , X_{2} , \ldots , X_{n} } \right) \le b \) where both are continuous and differentiable. For this case, the Lagrangian method simply minimizes the unconstrained function:

$$ L\left( {X_{1} , X_{2} , \ldots , X_{n} ,\lambda } \right) = f\left( {X_{1} , X_{2} , \ldots , X_{n} } \right) + \lambda \left[ {g\left( {X_{1} , X_{2} , \ldots , X_{n} } \right) - b} \right] $$
(14)

where \( \lambda \) is a nonnegative Lagrangian multiplier.

To minimize the function \( L\left( {X_{1} , X_{2} , \ldots , X_{n} ,\lambda } \right) \) the Kuhn–Tucker conditions for are as presented below.

$$ \frac{{\partial L\left( {X_{1} , X_{2} , \ldots , X_{n} ,\lambda } \right)}}{{\partial X_{j} }} = \frac{{\partial f\left( {X_{1} , X_{2} , \ldots , X_{n} } \right)}}{{\partial X_{j} }} + \lambda \frac{{\partial g\left( {X_{1} , X_{2} , \ldots , X_{n} } \right)}}{{\partial X_{j} }} = 0 , $$
(15)
$$ \frac{{\partial L\left( {X_{1} , X_{2} , \ldots , X_{n} ,\lambda } \right)}}{\partial \lambda } = g\left( {X_{1} , X_{2} , \ldots , X_{n} } \right) - b = 0 $$
(16)

By simultaneously solving the above equations for variables \( X_{j} \) and Lagrangian multiplier \( \lambda \), the minimum solution is obtained.

In sequel, we aim at adapting Lagrangian method for our problem (13). In this problem, the green constraint couples different buyers and hence make the decomposition procedure to be complicated. To overcome this difficulty, we consider Lagrangian relaxation of the original problem (13) by decomposing green constraint. By utilizing multiplier \( \lambda \) corresponding to green constraint, the LR problem is formulated as follows.

(LR)

$$ L\left( \lambda \right) = \hbox{min} TC_{LR} $$
(17)

subject to

$$ \begin{aligned} TC_{LR} &= \mathop \sum \limits_{i = 1}^{I} \left( {\mathop \sum \limits_{J = 1}^{J} \left[ {\frac{{A_{Sij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right. + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{A_{Bij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\& \quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\ &\quad + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] \\ &\quad + \mathop \sum \limits_{j = 1}^{J} \left. {\left[ {\frac{{\zeta D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right) + \lambda \left( {\mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \left[ {\frac{{qD_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] - T_{e} } \right) \end{aligned} $$
$$ \rho_{ij} = D_{ij} /P_{ij} \quad \quad \forall i \in I $$
$$ Q_{ij} , b_{ij} \ge 0 ,\quad \quad \forall i \in I .$$

The LR objective function \( TC_{LR} \) can be summarized as follows.

$$ \begin{aligned} TC_{LR} &= \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \left( {\left[ {\frac{{\left( {A_{Sij} + A_{Bij} + \zeta q + \lambda q} \right)D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right. + \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \left. {\left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right]} \right) - \lambda T_{e} \end{aligned} $$
(18)

where \( \rho_{ij} = D_{ij} /P_{ij} \). The last term in \( TC_{LR} \) is a constant, and can be rewrite as \( \mathop \sum \nolimits_{i = 1}^{I} \mathop \sum \nolimits_{j = 1}^{J} \left( {\frac{{\lambda T_{e} }}{IJ}} \right) \). Therefore, the LR problem can be decomposed into \( I \times J \) single sub-problems (one for each product of each buyer) as follows.

$$ ({\text{LR}}^{{\left( {i,j} \right)}}) \qquad L^{{\left( {i,j} \right)}} \left( \lambda \right) = \hbox{min} TC_{LR}^{{\left( {i,j} \right)}} $$
(19)

subject to

$$ \begin{aligned} TC_{LR}^{{\left( {i,j} \right)}} &= \left[ {\frac{{\left( {A_{Sij} + A_{Bij} + \zeta q + \lambda q} \right)D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] + \left[ {\frac{{h_{ij} \left[ {Q_{ij} \left( {1 - \rho_{ij} } \right) - \beta_{ij} b_{ij} } \right]^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] \\& \quad + \left[ {\frac{{\omega_{ij} \beta_{ij} b_{ij}^{2} }}{{2(Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} )\left( {1 - \rho_{ij} } \right)}}} \right] + \left[ {\frac{{\tau_{ij} (1 - \beta_{ij} )b_{ij} D_{ij} }}{{Q_{ij} + \left( {1 - \beta_{ij} } \right)b_{ij} }}} \right] - \frac{{\lambda T_{e} }}{IJ} \end{aligned} $$
$$ \rho_{ij} = D_{ij} /P_{ij} \quad \quad \forall i \in I $$
$$ Q_{ij} , b_{ij} \ge 0 ,\quad \quad \forall i \in I,\quad \quad j \in J \quad{\text{and}}\quad \lambda \ge 0 .$$

By setting \( A_{ij} = A_{Sij} + A_{Bij} + \zeta q + \lambda q \), we can rewrite objective function \( TC_{LR}^{{\left( {i,j} \right)}} \) in a more simple form. Therefore, the resultant sub-problems can be solved independently by using classical EPQ model with partial backordering (Mak 1987). For applicability of Mak’s results, we transform the decision variables \( Q_{ij} \) and \( b_{ij} \) to inventory cycle \( T_{ij} \) and shortage period \( t_{ij} \) in \( TC_{LR}^{{\left( {i,j} \right)}} \) by equation \( Q_{i,j} = D_{ij} \left( {T_{ij} - \left( {1 - \beta_{ij} } \right)t_{ij} } \right) \) and \( b_{ij} = D_{ij} t_{ij} \) without loss of generality. Therefore, by adapting Mak’s results, we can infer that the objective functions \( TC_{LR}^{{\left( {i,j} \right)}} \) are convex. Then we can get partial derivative from \( TC_{LR}^{{\left( {i,j} \right)}} \) to obtain optimal solutions for sub-problems \( \left( {T_{ij} , t_{ij} } \right) \) as follows:

$$ \frac{{\partial TC_{LR}^{{\left( {i,j} \right)}} }}{{\partial T_{ij} }} = 0 ,\quad \quad \frac{{\partial TC_{LR}^{{\left( {i,j} \right)}} }}{{\partial t_{ij} }} = 0 .$$
(20)

By doing so, the shortage period \( t_{ij} \) is attained as:

$$ \begin{aligned} t_{ij} &= \left\{ {\tau_{ij} \left( {1 - \beta_{ij} } \right)D_{ij} + \left( {\frac{{h_{ij} \left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)}}{{\omega_{ij} \beta_{ij} }}\left( {2A_{ij} \omega_{ij} \beta_{ij} D_{ij} \frac{{\left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)}}{{1 - \rho_{ij} }}} \right.} \right.} \right. \\& \left. {\left. {\left. {\quad + 2A_{ij} h_{ij} D_{ij} \frac{{\left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)^{2} }}{{1 - \rho_{ij} }} - \left( {\tau_{ij} \left( {1 - \beta_{ij} } \right)D_{ij} } \right)^{2} } \right)} \right)^{1/2} } \right\} \\ &\quad /\left\{ {\frac{{D_{ij} \left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)}}{{1 - \rho_{ij} }}\left( {\beta_{ij} \omega_{ij} + h_{ij} \left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)} \right)} \right\} \end{aligned} $$
(21)

and then the inventory cycle \( T_{ij} \) can be obtained by substituting \( t_{ij} \) into formula:

$$ T_{ij} = \frac{{\left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)t_{ij} }}{{\left( {1 - \rho_{ij} } \right)}} + \left( {\frac{{\beta_{ij} \omega_{ij} t_{ij} }}{{h_{ij} \left( {1 - \rho_{ij} } \right)}}} \right) + \frac{{\tau_{ij} \left( {1 - \beta_{ij} } \right)}}{{h_{ij} \left( {1 - \left( {1 - \beta_{ij} } \right)\rho_{ij} } \right)}} $$
(22)

The condition for the partial backordering to be feasible is that \( t_{ij} \ge 0 \), otherwise no shortage is allowed and \( t_{ij} = 0 \). In such case \( \left( {t_{ij} = 0} \right) \), the classical EPQ formula is employed to determine the optimal inventory cycle as follows.

$$ T_{ij} = \left[ {\frac{{2A_{ij} }}{{h_{ij} D_{ij} \left( {1 - \rho_{ij} } \right)}}} \right]^{{\frac{1}{2}}} $$
(23)

where the optimal cost function is determined by classical EPQ optimal function:

$$ TC_{LR}^{{\left( {i,j} \right)}} = \left[ {2A_{ij} h_{ij} D_{ij} \left( {1 - \rho_{ij} } \right)} \right]^{{\frac{1}{2}}} $$
(24)

Moreover, the Lagrange multiplier can be obtained by solving partial derivative:

$$ \frac{{\partial TC_{LR}^{{\left( {i,j} \right)}} }}{\partial \lambda } = 0 .$$
(25)

It yields:

$$ \frac{q}{{T_{ij} }} = \frac{{T_{e} }}{IJ} $$
(26)

By substituting \( T_{ij} \) and \( t_{ij} \) into above equation, we can simply find the optimal value of Lagrange multiplier \( \lambda \). An interesting fact is that the above optimality condition enforces all of the \( I \times J \) sub-problems to have identical inventory cycle \( T_{ij} = \frac{IJq}{{T_{e} }} \). The optimal multiplier is then substituted into Eqs. (21) and (22) to obtain the value of variables \( T_{ij} \) and \( t_{ij} \). Using these values, we can obtain the optimal order quantity and shortage level for each sub-problem by \( Q_{i,j} = D_{ij} \left( {T_{ij} - \left( {1 - \beta_{ij} } \right)t_{ij} } \right) \) and \( b_{ij} = D_{ij} t_{ij} \). Substituting \( Q_{i,j} \), \( b_{ij} \) and \( \lambda \) into \( TC_{LR}^{{\left( {i,j} \right)}} \) yields the optimal cost function for sub-problem \( {\text{LR}}^{{\left( {i,j} \right)}} \). Then the value of these cost functions are employed to gain the solution of Lagrangian problem LR whose objective function is computed by \( TC_{LR} = \mathop \sum \nolimits_{i \in I} \mathop \sum \nolimits_{j \in J} TC_{LR}^{{\left( {i,j} \right)}} \). Moreover, the optimal value of total cost function is attained by substituting \( Q_{i,j} \) and \( b_{ij} \) into \( TC_{A} \) in Eq. (13). The proposed approach is shown below.

The proposed Lagrangian relaxation procedure

 

01: Initialize the problem parameters

02: Construct the main problem

03: Construct the LR problem by penalizing the constraint into objective function

04: Construct the sub-problems \( {\text{LR}}^{{\left( {{\text{i}},{\text{j}}} \right)}} \) by decomposing the LR problem

05: Calculate the optimal value for Lagrange multiplier \( \uplambda \) by solving \( \frac{\text{q}}{{{\text{T}}_{\text{ij}} }} = \frac{{{\text{T}}_{\text{e}} }}{\text{IJ}} \)

06: By using \( \uplambda \), calculate the optimal solution for sub-problems \( {\text{LR}}^{{\left( {{\text{i}},{\text{j}}} \right)}} \) in terms of \( {\text{t}}_{\text{ij}} \) and \( {\text{T}}_{\text{ij}} \)

07: Transform the optimal value of variables \( {\text{t}}_{\text{ij}} \) and \( {\text{T}}_{\text{ij}} \) to \( {\text{Q}}_{{{\text{i}},{\text{j}}}} \) and \( {\text{b}}_{{{\text{i}},{\text{j}}}} \)

08: Calculate the optimal value of cost function for sub-problems \( {\text{TC}}_{\text{LR}}^{{\left( {{\text{i}},{\text{j}}} \right)}} \)

09: Calculate the optimal value of cost function for LR problem by \( TC_{LR} = \mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} TC_{LR}^{{\left( {i,j} \right)}} \) and total cost of main problem by \( {\text{TC}}_{\text{A}} \)

 

5 A numerical example

In order to illustrate the applicability of the suggested approach, we design a numerical example, in this section, by setting values for the parameters with two buyers \( I = 2 \) and three products \( J = 3 \). Then, we carry out a sensitivity analysis by changing the value of input parameter \( \beta \) in sub-problem model, to illustrate the model under various settings. To this end, all the suggested procedure is coded in MATLAB software. The characteristics of the example are presented in Table 2. Furthermore, for green considerations, we set the amount of GHG emission per order q = 3.75 kg, the emission cost per order \( \zeta = 15 \$ \) and the legal threshold on total GHG emissions Te = 30 kg.

Table 2 Example characteristics
Full size table

The problem is formulated as non-linear programming model, and then is relaxed by decomposing the green constraint to form LR problem. The objective function \( TC_{LR} \) is separable and hence can be simply decomposed into 6 sub-problems, each one for each product of each buyer \( {\text{LR}}^{{\left( {i,j} \right)}} , \forall i = 1, 2, j = 1, 2, 3 \). By using Mak’s results, the sub-problems \( {\text{LR}}^{{\left( {i,j} \right)}} \) can be optimally solved independently. It is achievable when the partial backordering is feasible \( t_{ij} \ge 0 \left( {{\text{or}} b_{ij} \ge 0} \right) \). After checking the condition, the solutions are obtained for all sub-problems and presented in terms of \( T_{ij} , t_{ij} , Q_{ij} , b_{ij} \) and \( TC_{LR}^{{\left( {i,j} \right)}} \) as follows.

Sub-problem \( {\text{LR}}^{{\left( {1,1} \right)}} \) (buyer \( i = 1 \), product \( j = 1) \):

\( Q_{1,1} = 522.67 \)

\( b_{1,1} = 255.18 \)

\( T_{1,1} = 0.75 \)

\( t_{1,1} = 0.3002 \)

\( TC_{LR}^{{\left( {1,1} \right)}} = 1632.87 \)

 

Sub-problem \( {\text{LR}}^{{\left( {1,2} \right)}} \) (buyer \( i = 1 \), product \( j = 2) \):

\( Q_{1,2} = 185.54 \)

\( b_{1,2} = 2.30 \)

\( T_{1,2} = 0.75 \)

\( t_{1,2} = 0.0092 \)

\( TC_{LR}^{{\left( {1,2} \right)}} = 153.17 \)

 

Sub-problem \( {\text{LR}}^{{\left( {1,3} \right)}} \) (buyer \( i = 1 \), product \( j = 3) \):

\( Q_{1,3} = 334.27 \)

\( b_{1,3} = 9.22 \)

\( T_{1,3} = 0.75 \)

\( t_{1,3} = 0.0205 \)

\( TC_{LR}^{{\left( {1,3} \right)}} = 557.57 \)

 

Sub-problem \( {\text{LR}}^{{\left( {2,1} \right)}} \) (buyer \( i = 2 \), product \( j = 1) \):

\( Q_{2,1} = 178.24 \)

\( b_{2,1} = 11.57 \)

\( T_{2,1} = 0.75 \)

\( t_{2,1} = 0.4630 \)

\( TC_{LR}^{{\left( {2,1} \right)}} = 885.76 \)

 

Sub-problem \( {\text{LR}}^{{\left( {2,2} \right)}} \) (buyer \( i = 2 \), product

\( j = 2) \):

\( Q_{2,2} = 555.18 \)

\( b_{2,2} = 6.1664 \)

\( T_{2,2} = 0.75 \)

\( t_{2,2} = 0.0082 \)

\( TC_{LR}^{{\left( {2,2} \right)}} = 522.85 \)

 

Sub-problem \( {\text{LR}}^{{\left( {2,3} \right)}} \) (buyer \( i = 2 \), product \( j = 3) \):

\( Q_{2,3} = 377.57 \)

\( b_{2,3} = 206.95 \)

\( T_{2,3} = 0.75 \)

\( t_{2,3} = 0.3450 \)

\( TC_{LR}^{{\left( {2,3} \right)}} = 1214.35 \)

 

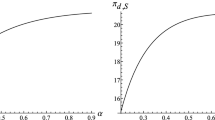
Thus the optimal value of Lagrangian cost functions \( TC_{LR}^{{\left( {i,j} \right)}} \) are employed to gain the solution of Lagrangian problem LR whose objective function is computed \( TC_{LR} = \mathop \sum \nolimits_{i \in I} \mathop \sum \nolimits_{j \in J} TC_{LR}^{{\left( {i,j} \right)}} = 4966.57 \). Moreover the optimal \( Q_{i,j} \) and \( b_{ij} \) are employed to obtain the optimal cost function \( TC_{A} \). Since the green constraint is satisfied, the optimal cost function \( TC_{A} \) equals to optimal LR objective function \( TC_{LR} \). For further analysis, we carry out a sensitivity analysis by changing the value of important parameter \( \beta \) (shortage proportion) in sub-problem \( {\text{LR}}^{{\left( {1,1} \right)}} \) as an example. The results are presented in Table 3 and depicted in Fig. 4. It can be seen that as the value of \( \beta \) increases, the value of order quantity increases, the value of maximum shortage level decreases, and the optimal total cost decreases. Thus, we can infer that the optimal production-inventory policies are sensitive to the type of demand (proportion of backorder and lost sale) during the shortage period.

Table 3 Sensitivity analysis results on \( \beta \) (for buyer \( i = 1 \), product \( j = 1 \))
Full size table
Fig. 4
figure 4

Effect of \( \beta \) on the optimal total cost

Full size image

6 Conclusion

In this paper, we extended a model of production-inventory problem with mixed backorders and lost sales to a green supply chain consisting of a single supplier, multi-buyer and multi-product that operates under vendor management inventory (VMI) policy. To the best of our knowledge, this problem has not been treated in literature yet. To address this problem, a non-linear programming model was constructed. To solve it optimally, we exploited a special structure of problem and applied a Lagrangian relaxation (LR) approach to decompose the problem into smaller and easier sub-problems and solve the problem via LR. In this approach, the structure of LR is similar to the standard LR approach. However, in addition, we recognize a structural property of our production-inventory planning problem. A deep investigation reveals that this problem is comprised of similar subsystems, represented by \( I \) buyers and \( J \) products, and there are some independent blocks linked by a coupling constraint (green constraint in model) in the technological coefficient matrix. Exploiting this interesting property of problem we could decompose the problem, after relaxation, into.

\( I \times J \) single sub-problems which make us hopeful for optimal solving of the main problem. Moreover, as another key characteristic of our solution approach is that the resulted sub-problems can be optimally solved by an analytical closed-form formula. This is applicable by transforming our decision variables \( Q_{ij} \) and \( b_{ij} \), into inventory cycle \( T_{ij} \) and shortage period \( t_{ij} \). At the end, we investigated a numerical example to demonstrate the application of the proposed approach. A sensitivity analysis was also carried out to assess trade-off between lost sale and backorder types of demand.

This paper can be extended via various aspects. An appropriate suggestion for future research is to extend the model for a multi-supplier, multi-buyer and multi-products case where each supplier has its own characteristics in purchasing the products to the buyers like time, cost, geographical zones, and contract options. Other constraints such as total available budget and storage capacity can be taken into account. Moreover demand correlation between products can be considered.