1 Introduction

In supply chain management, the vendor managed inventory (VMI), sometimes called vendor-managed replenishment, is one of the popular policies to minimize the total costs in warehouse management. Successful suppliers such as JC Penney and Walmart show that this policy significantly mitigates the bullwhip effect (Simchi-Levi et al. 2007). Supply chains are trying to find effective solutions, which are the responsiveness of facilities and distribution networks to best serve a market. The VMI helps supply chains to make better decisions than the past in such a way that it shares inventory levels and sale information of retailers with vendors to control retailer inventory and minimize associated costs (Hudnurkar and Rathod 2012). The significant reduction in the total inventory costs by using VMI policy shows the importance of information sharing in operational levels of supply chains.

The last decade shows significant attention to the integrating supply chains using VMI policy. Darwish and Odah (2010) developed a VMI model for a two-echelon supply chain including retailers and vendors. They used a heuristic to solve the proposed mathematical model. The prior studies have a large focus on the VMI mathematical models such multiple vendors (Sadeghi et al. 2013), a hybrid with redundancy allocation (Sadeghi, Sadeghi, et al. 2014a, b), a three-echelon supply chain (Sadeghi, Mousavi et al., 2014a, b), and fixed shipping cost allocation (Son and Ghosh 2019), and stochastic demand (Pramudyo and Luong 2019). There is scant research on the effect of upper limits of inventory levels on the total inventory cost. Thus, the research questions are How does the tradeoff between ordering and holding look like? How does a vendor behave when there is an upper limit on the inventory?

High inventory costs motivate to focus on supplier–buyer relationships to optimize the total cost from both perspectives. Due to possible limitations on the warehouse capacity, vendors are limited to keep a large quantity of inventory. Moreover, just in time approach encourages vendors to reduce the inventory. Thus, it is important to have a focus on the vendors’ behavior when the inventory is limited.

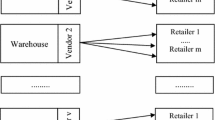
To answer the aforementioned research questions, this research develops the work presented by Darwish and Odah (2010) to consider upper inventory limits as decision variables. The goal of this research is to present a mathematical model for a single-vendor multi-retailer supply chain based on VMI policy in which a vendor has to determine an upper limit for the inventories while there is a constraint on the orders. The objective of the proposed mathematical model is to determine order size, upper limits on the inventory level of retailers, and replenishment frequencies of retailers by a vendor. To solve the proposed mathematical model, we use the imperialist competitive algorithm (ICA) (Sadeghi, Mousavi, et al., 2016a, b) in meta-heuristic optimization.

We organize the paper as follows. Next section presents a short background of VMI. Section 3 presents the proposed mathematical model. The solution algorithm, imperialist competitive algorithm, and results are given in Sects. 4 and 5, respectively. Finally, Sect. 6 shows the conclusion and future research.

2 Prior research

Prior studies conducted a review of VMI from different aspects such as process perspective (Marque`s et al., 2010), based on dimensions (Govindan, 2013), and theoretical developments (Zhao, 2019). To name a few, Bazan et al. (2015) proposed a VMI with consignment stock (VMI-CS) agreement policy in which transportation and production followed a multi-level emission-taxing scheme. Using a neighborhood search algorithm, Hemmati et al. (2015) modeled a VMI policy for a tramp shipping. Following risk preference, Huynh and Pan (2015) formulated a VMI in a two-echelon supply chain. In a case including perishable products, Shaabani and Kamalabadi (2016) developed a multi-period inventory model and then employed a simulated annealing algorithm to obtain the near-optimal solutions. In a case in which the vendor uses the retailer's warehouse to store products, Khan et al. (2016) presented a VMI in which a known fraction of lots is defective. Cai et al. (2017) developed a VMI problem for a two-echelon supply chain with uncertain demand in which there are two substitutable brands in different scenarios. In a single-supplier multi-retailer supply chain, Verma and Chatterjee (2017) presented a nonlinear mixed-integer programming model based on VMI policy to minimize the total costs by finding the optimal values for replenishment frequency and order quantity. Lee et al. (2017) showed that the amount of stock displayed has an effect on demand in VMI systems, and then developed a mathematical model based on consignment stock agreement in which the vendor's stocking policy is assumed to be either forward or backward. Although VMI policy in most cases assumes products are stored in retailers’ warehouse, sometimes it is impossible to follow it. Following this assumption violation, Akbari Kaasgari et al. (2017) presented a mathematical model based on VMI policy in which there were perishable products. They used the particle swarm optimization algorithm to obtain the near-optimal solutions.

Stellingwerf et al. (2019) considered the effect of VMI decision on the environment. Their results show that demand and location are two main factors impacting environment in such a way that these two factor significantly increases the carbon emission and total costs. Sainathan and Groenevelt (2019) considered contracts in vendor managed inventory policy in which a few types of contracts do not follow under vendor-managed inventory.

Inflation plays an important role in inventory models. Esmaeili and Nasrabadi (2021) proposed an inventory model to include effects of inflation on the outcomes in which results indicated that both vendor and retailer can take advantage of proposed decision tool in terms of the total profits. With the advent of technologies, big data is a growing topic in supply chain and operations management. Maheshwari et al. (2021) provided a systematic review of the role of big data in supply chain management. Along with their findings, Talwar et al. (2021) proposed a theoretical framework to use big data in supply chain management. When it comes to disruptions, the ripple effect is inevitable in the supplier–buyer relationships (Hosseini et al. 2020; Li et al. 2021). Hosseini et al. (2020) developed a stochastic model to address the uncertainty in the suppliers’ performance regarding the ripple effect. Their findings showed that high-risk paths can be addressed using the proposed methodology when it comes to disruptions. Maintenance techniques are a vital part of manufacturing processes. Khanna et al. (2016) addressed imperfect production in vendor’s activities which can be resulted in a shortage. Their results showed that the proposed decision tool enables managers to have an optimized decision in buyer-vendor relationships. Moreover, Khanna et al. (2020) developed a vendor managed inventory in which production activities are controlled based on warranty and maintenance policy. Their results showed that inventory managers can handle the uncertainty in VMI models when it comes to maintenance activities. Sustainability development is becoming one of the parts of inventory decisions (Gautam et al. 2019). Kamna et al. (2021) developed a sustainable production inventory model in which agility was addressed in the manufacturing process. Their findings showed that the model has a better outcome when volume agility is included than is not.

3 A mathematical model based on Vendor Managed Inventory

We used the following notations to develop the mathematical model.

Parameters

\(r\) Number of retailers.

\({A}_{V}\) The vendor's ordering cost.

\({A}_{j}\) Ordering cost for retailer \(j\)

\(D\) The vendor's annual demand that is \(D={\sum }_{j=1}^{r}{D}_{j}\)

\({D}_{j}\) Annual demand for \({j}^{th}\) retailer.

\({h}_{V}\) The vendor's holding cost per year.

\({h}_{j}\) Holding cost for retailer \(j\) per year.

\({\pi }_{j}\) Overstock penalty cost for retailer \(j\) per year.

\(S\) Set of all retailers whose upper limits of inventory are exceeded.

\(X\) Maximum number of orders for vendor per year.

Variables

\({q}_{j}\) Order quantity for retailer \(j\) per cycle (decision variable).

\({Q}_{V}\) Total vendor's order quantity per cycle that is \({Q}_{V}=nq\)

\(q\) Order quantity for all retailers per cycle that is \(q = \sum\nolimits_{j = 1}^{r} {q_{j} }\).

\({q}_{1}\) Order quantity for 1th retailer per cycle (decision variable).

\({U}_{j}\) Upper limit on the inventory level of retailer \(j,\) (integer decision variable).

\(n\) Annual replenishment frequency of retailers per cycle (integer decision variable).

To develop the model, there are some assumptions in the proposed supply chain:

  1. a)

    Retailer’s inventory levels are defined by vendors.

  2. b)

    Retailers have to share information about inventory levels and sells.

  3. c)

    There are no stochastic or fuzzy parameters.

  4. d)

    The model follows the economic order quantity (EOQ) policy.

  5. e)

    There are two levels of echelons in the proposed supply chain.

Darwish and Odah (2010) developed Eq. (1) based on the VMI policy. For more details, we recommend Darwish and Odah (2010) to the interested readers. We contribute to this model by considering the upper limits of inventory levels (\({U}_{j}\)) as decision variables. Moreover, the number of a vendor’s orders faces a restriction in Eq. (2). Thus, the total cost function is as follows.

$$\begin{aligned} {\text{Min}}\,TC_{VMI} = & \frac{{q_{1} }}{{2D_{1} }}\sum\nolimits_{j = 1}^{r} {h_{j} D_{j} } + \left( {A_{v} + n\sum\nolimits_{j = 1}^{r} {A_{j} } } \right){{D_{1} } \mathord{\left/ {\vphantom {{D_{1} } {nq_{1} }}} \right. \kern-\nulldelimiterspace} {nq_{1} }} + {{0.5\left( {n - 1} \right)Dh_{v} q_{1} } \mathord{\left/ {\vphantom {{0.5\left( {n - 1} \right)Dh_{v} q_{1} } {D_{1} }}} \right. \kern-\nulldelimiterspace} {D_{1} }} \\ + & \frac{{D_{1} }}{{2q_{1} }}\sum\limits_{j \in S} {\left( {\frac{{\pi_{j} }}{{D_{j} }}\left( {\frac{{D_{j} }}{{D_{1} }}q_{1} - U_{j} } \right)^{2} } \right)} \\ \end{aligned}$$
(1)

s.t,

$$\frac{{D_{1} }}{{nq_{1} }} \le X\quad \left( {\text{Order Constraint}} \right)$$
(2)
$$q_{1} ,n,U_{j} \ge 0\,\quad \left( {\text{Decision Variables}} \right)$$
(3)

where the first term is the retailers’ holding cost in Eq. (1). The second term indicates the total order cost for both the vendor and the retailers. The third term presents the vendor’s holding cost. Finally, the penalty cost is shown in the last term for those orders that exceed the upper limit.

Section 3 provides a metaheuristic approach in the optimization to obtain a near-optimal solution including \({q}_{1},n,\) and \({U}_{j}\) for Eq. (1).

4 The proposed solution algorithm: the imperialist competitive algorithm (ICA)

In order to solve integer linear programming models, metaheuristic methods are a powerful and fast approach (Sadeghi and Haapala, 2019). Other approaches such as DNA computing (Molaei et al. 2014) also solve nonlinear problems. Single solution-based search and population-based search such as swarm (Roozbeh Nia et al. 2015; Sadeghi, Niaki, et al. 2016a, b) are two classes in metaheuristic optimization. As a population-based search algorithm, Atashpaz-Gargari and Lucas (2007) developed the imperialist competitive algorithm (ICA) to solve integer linear programming models, which is powerful. ICA shows an accurate and fast solution compared with swarm algorithm and genetic algorithm (Sadeghi 2015). Since the proposed model is an integer linear programming model, it is impossible to find points satisfying Karush–Kuhn–Tucker (KKT) conditions as the solution algorithm suggested by Darwish and Odah (2010) due to integer conditions. Prior studies used the genetic algorithm and the particle swarm optimization to solve the VMI models (Sadeghi et al. 2015). Thus, we employed ICA to solve the proposed mathematical model for two reasons. First, ICA is more accurate and faster than the genetic algorithm and the particle swarm optimization in the VMI models. Second, ICA is a new algorithm used in VMI model optimization.

The following steps show the ICA to solve a mathematical model (Atashpaz-Gargari and Lucas 2007).

4.1 The power of the empires

In order to calculate the power of each imperialist, all imperialists costs (\(c_{i}\)) are normalized; thus, the normalized cost of the \(n^{th}\) imperialist (\(C_{n}\)) is:

$$C_{n} = c_{n} - \mathop {\max }\limits_{i} \left\{ {c_{i} } \right\}$$
(4)

Considering Eq. (4), the normalized power of each imperialist (\(p_{n}\)) is as follows.

$$p_{n} = \left| {\left. {C_{n} /\sum\nolimits_{i = 1}^{{N_{imp} }} {C_{i} } } \right|} \right.$$
(5)

The empires (e.g., 10) seize the initial colonies based on their power. Therefore, the initial number of colonies (e.g., 100) of the \(n^{th}\) empire (\(N.C._{n}\)) can be calculated as,

$$N.C._{n} = round\{ p_{n} .N_{col} \}$$
(6)

4.2 Changing the colonies

In this stage of ICA, the colonies can be improved with assimilation and revolution. It may be that an empire is eliminated, or the positions of the colony and the imperialist exchange together. To consider these conditions, changing the colonies is described as follows.

4.2.1 Assimilation

The imperialist tries to assimilate their colonies with respect to the specification of imperialism. For instance, the colonies, which some of their socio-political characteristics like culture and language are changed by the imperialist, will liken their imperialist. All the colonies completely liken the imperialist if there is continual assimilation. Therefore, to control this condition, a constant coefficient (\(\beta\)), which is greater than one, impresses the process of assimilation. Consequently, the amount of movement of the colony (\(x\)) is,

$$x \sim U(0,\beta \times d)$$
(7)

where \(x\) follows a uniform distribution and \(d\) is the distance between the imperialist and the colony. Since this method of assimilation is restricted to the direct movement, a random amount of deviation (\(\theta\)) impresses the direct movement (see Fig. 1). Thus

$$\theta \sim U( - \gamma ,\gamma )$$
(8)

where \(\theta\) follows a uniform distribution and \(\gamma\) is an arbitrary number to search around the imperialist. It has been suggested that the values of \(\beta\) and \(\gamma\) be set about 2 and \({\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}\) (Rad), respectively (Atashpaz-Gargari and Lucas 2007).

Fig. 1
figure 1

New direction for the colony (Atashpaz-Gargari and Lucas 2007)

Full size image

4.2.2 Revolution

In ICA, a revolution which is similar to a mutation in the genetic algorithm can prevent presenting a suboptimal solution as the optimal solution. In other words, revolution reduces the convergence speed. The power of colonialism will be increased by incurring less revolution in the colonies. The revolution changes randomly 20 percent of the positions of colonies with a 0.2 revolutions rate (\(P_{r}\)).

4.3 Total power of the empire

After changing colonies in regard to assimilation and revolution, it is probable that an empire is deleted or the positions of the imperialist and the colony replace one another. Therefore, it is reasonable to recalculate the total power for all the empires (\(T.C._{n}\)), which can be modeled by utilizing the total cost (Eq. 9).

$$T.C._{n} = Cost(imperialist_{n} ) + \xi mean\{ Cost(colonies \, of \, empire_{n} )\}$$
(9)

where, \(T.C._{n}\) is the total cost for \(n^{th}\) empire and \(\xi\) is an arbitrary number that is less than one. \(\xi\) controls balance between the effect of the colonies and the imperialist on the power of the empire, where the value of ξ is set at about 0.1 (Atashpaz-Gargari and Lucas 2007).

4.4 Imperialistic competition

In the imperialistic competition, an empire seizes the weakest colony from the empire; afterward, the empires must compete for possessing the colonies to stay a powerful empire. Notice that the power of the empires is modeled based on the costs. It is necessary to compute the possession probability of empires to determine the empire that seizes the weakest colony. Thus, the possession probability for each empire is:

$$P_{{p_{n} }} = \left| {N.T.C._{n} /\sum\nolimits_{i = 1}^{{N_{imp} }} {N.T.C._{i} } } \right|$$
(10)

where, \(N.T.C._{n}\) is the normalized total cost of the \(n^{th}\) empire, which is calculated as follows.

$$N.T.C._{n} = T.C._{n} - \mathop {\max }\limits_{i} \{ T.C._{i} \}$$
(11)

In order to select an empire to possess a colony, Atashpaz-Gargaria and Lucas (2007) proposed the following method:

First, form the vector \(P\) (see Eq. 12).

$$P_{{p_{n} }} = \left[ {p_{{p_{1} }} ,p_{{p_{2} }} ,p_{{p_{3} }} ,...,p_{{p_{{N_{imp} }} }} } \right]$$
(12)

Second, according to a uniform distribution (U (0,1)), create a vector with the size of \(P\).

$$R = \left[ {r_{1} ,r_{2} ,r_{3} ,...,r_{{N_{imp} }} } \right]$$
(13)

Then, obtain the vector \(D\) that is the difference of \(R\) from \(P\).

$$D = \left[ {p_{{p_{1} }} - r_{1} ,p_{{p_{2} }} - r_{2} ,p_{{p_{3} }} - r_{3} ,...,p_{{p_{{N_{imp} }} }} - r_{{N_{imp} }} } \right]$$
(14)

Finally, the empire with its index having the highest value in the \(D\) vector, possesses the weakest colony. Considering imperialistic competition, strong empires will eliminate powerless empires as well as divide its colonies between other empires.

4.5 Convergence

There are several termination criteria. First, collapsing all empires to one empire; in other words, the world has only one empire. Second, to determine maximum decades, which means a fixed number of iterations (\(It\)) (Shahvari and Logendran 2016). Third, there is an unchanging best solution for a determined number of iterations. Another method is a combination of the above methods. This paper uses the second method of stopping the ICA that is a fixed number of iterations (i.e., 1000).

5 Results

In this section, we validate both the proposed algorithm, the ICA, and the mathematical model using a global optimal solution in the VMI literature. Table 1 shows a comparsion between the proposed methodology and an exact method. The results show that the solution obtained by the ICA and the exact method (Darwish and Odah 2010) are the same. Note that in Table 1, we used the same examples for ICA optimization and the exact method.

Table 1 Comparing the ICA with Darwish and Odah (2010) method
Full size table

The results presented in Table 1 show the validation of the proposed methodology. In order to solve the mathematical model and consider the behavior of \({U}_{j},\) we solve the mode in 14 different scenario using numerical examples shown in Table 2. We use example data from the work presented by Darwish and Odah (2010). Based on results shown in Table 3, the optimized values for order quantity for the retailer (\({q}_{j}\)) is always lower than upper limits on the inventory level of retailers (\({U}_{j}\)). Therefore, the optimized solutions have a tendency to the situation in which there is not any overstock penalty for the vendor (that is \({U}_{j}>{q}_{j}\)). Note that Fig. 2 shows the convergence of the best costs in ICA in which decade represents iterations in ICA terminologies.

Table 2 Example data (Darwish and Odah 2010)
Full size table
Table 3 Results of examples
Full size table
Fig. 2
figure 2

The convergence of the best costs

Full size image

6 Discussion and managerial implications

This paper contributed to the prior studies in VMI models by including overstock penalty for the vendor. The results were based on an algorithm, verified by the exact method. The results indicated that the vendor avoids shortage due to overstock penalty. The findings had a focus on the vendor’s behavior in terms of keeping inventory in which the vendor was likely to keep as much as inventory to satisfy retailers. From managerial perspectives, the vendor’s behavior can be controlled by imposing an overstock penalty if the management has a plan to follow just in time approach. When it comes to lean implementation, inventory plays an important role in reducing extra inventory. Thus, the proposed decision tool herein can be used to manage vendor’s behavior to reduce the inventory levels.

7 Conclusion and future research

The vendor managed inventory is a well-known business policy to facilitate the relationship between buyer and suppliers (vendor and retailer). We continued the work presented by Darwish and Odah (2010) which is an inventory model in supply chains including a single-vendor and multiple retailers to incorporate their suggestion, which is consideration of upper limits on the inventory level of retailers as decision variables. The contribution of this paper was twofold. First, we developed a non-linear programming model by considering upper limits on the inventory levels as decision variables. Second, we contributed to the VMI literature by developing a meta-heuristic algorithm called imperialist competitive algorithm (ICA) to solve the mathematical model. To close the real-world situation, the number of orders was assumed to be limited. The aim of this paper was to develop a mathematical model to consider a vendor's behavior under a situation in which the upper limits of inventories are relaxed and considered as a decision variable. Does a vendor violate inventory limits and pay penalty to make more profits or follows the penalty policy? To answer this question, we developed a mathematical model. The objective of the model was to determine the order size, the replenishment frequency, and upper limits on the inventory levels to optimize the total cost function. Since the proposed model was an integer nonlinear programming problem, a meta-heuristic optimization called the imperialist competitive algorithm (ICA) was employed to obtain a near-optimal solution. We validate the proposed methodology with an exact method. Based on results, the proposed model provides solutions that follow the condition in which there is not any overstock penalty for the vendor (which means upper limits are higher than orders, that is \({U}_{j}>{q}_{j}\)), which is similar to backorder inventory models in inventory management.

There are some gaps to fill as future studies. For example, here we used a trial-and-error method to tune parameters of the algorithm. Statistical methods, such as Taguchi method, are able to improve the quality of the algorithm. Other views that can be developed in future research are consideration of economic production policy in mathematical modeling and the consideration of inflation rate in prices.