1 Introduction

In 1922 Hamel [9] used the variational method to obtain the existence of \(2\pi \)-periodic solutions of forced pendulum equations

$$\begin{aligned} y''+a \sin y=b \sin t, \end{aligned}$$
(1.1)

where a, b are constants. It is worth noting that this is the first result of the existence of periodic solutions for the forced pendulum equation. Similar research methods can be extended to study the existence of T-periodic solutions of general forced pendulum equations \(y''+a \sin y=f(t),\) where \(f:{\mathbb {R}} \rightarrow {\mathbb {R}}\) is a continuous T-periodic function with \(\int _{0}^{T} f(t)\textrm{d}t=0\), see [17, 18].

If there is friction, then the forced pendulum Eq. (1.1) becomes the equations

$$\begin{aligned} x''+kx'+A \sin x=e(t), \end{aligned}$$
(1.2)

where k, A are constants, external force e(t) is a continuous T-periodic function with \(\int _{0}^{T}e(t)\textrm{d}t=0\). When \(k \ne 0\), then variational methods are not applicable to establish the existence of periodic solutions of Eq. (1.2). Therefore, many scholars used some classical tools such as fixed point theorems in cones, topological degree theory and the upper and lower solutions methods to study the existence, multiplicity and stability of the periodic solution for the forced pendulum equations. For instance, Amster and Mariani in [1, 2] investigated the existence of periodic solutions for the forced pendulum equations in the presence of friction by shooting type argument and Lyapunov-Schmidt reduction; Cid in [4] studied the existence of periodic solutions for the \(\phi \)-laplacian pendulum equation by using continuation theorem; Mawhin and Fournier in [6] considered the existence and multiplicity of periodic solutions for the forced pendulum equation by using topological degree theory and the upper and lower solutions methods; Lomtatidze and S̆remr in [15] studied the existence and uniqueness of positive periodic solution to the forced pendulum equation by using method of lower-upper functions; Torres in [24] proved the existence of periodic solution for the forced pendulum equation with friction and a singular \(\phi \)-Laplacian operator of relativistic type by using Schauder’s fixed point theorem; Yu in [27] studied the existence or nonexistence of periodic solutions with prescribed minimal periods to the classical forced pendulum equation by using critical point theory. Some scholars have also studied the conclusion that the nonexistence of periodic solution to the forced pendulum Eq. (1.2), see [3, 21]. To know more about the forced pendulum equations, we recommend to readers Mawhin’s survey papers [19, 20]. At the same time, many scholars also pay attention to the periodic solutions of second order differential equations, see [8, 12, 16, 25].

Most of the early studies on the forced pendulum equation considered the case where the pendulum length is constant. In recent years, some scholars began to pay attention to the forced pendulum equation with periodic change of pendulum length, see [5, 22, 23, 26, 28], because this kind of equations can describe many physical phenomena, for instance, the pendulum equation of the pendulum length variation can describe particle motion on a pulsating circle under the action of gravity and motion of satellites in orbit around the earth, see [11, 13, 29]. In particular, it can describe a swing model we played as children, the authors in [21, 28] discussed the adequacy of the pendulum with periodically varying length as a swing model. Therefore, the issue concerning existence of periodic solutions for the forced pendulum equations with periodically varying of pendulum length should be interesting and be of considerable significance.

The motivation of the current article is to investigate the existence of periodic solutions of forced pendulum equations with friction and periodically varying of pendulum length

$$\begin{aligned} x''+k x'+a(t) \sin x = e(t), \end{aligned}$$
(1.3)

where \(k \in {\mathbb {R}}\) is a constant, a(t), e(t) are continuous T-periodic functions. It is worth noting that in Eq. (1.3), when periodic function a(t) is constant, then Eq. (1.3) reduces to Eq. (1.2), and in the study of periodic solutions of forced pendulum equations, most literatures consider the case of \(\int _0^T e(t)\textrm{d}t=0\), in this paper, we only need \(e(t)\not \equiv 0\) (see assumption (H1) in Sect. 2). Obviously, the situation we consider is more general. At the end of this paper, we give some specific examples and numerical simulations to illustrate the applicability of the conclusions obtained in this paper.

The remainder part of this paper is organized as follows. In Sect. 2, for the convenience of the readers we collect some general results, given some notations and assumptions. In Sect. 3, under suitable hypotheses, we apply the Mawhin’s continuation theorem to obtain the existence of periodic solutions for the Eq. (1.3). In Sect. 4, we apply the previous results to some examples to demonstrate the applicability of our main results.

2 Preliminaries

In this section, we first introduce some mathematical settings where we settle the problem. Then, we given some assumptions and recall some known results.

Throughout this paper, let Banach spaces \( C_{T}=\{x \in C({\mathbb {R}},{\mathbb {R}}):x(t+T)=x(t) \ for\ all\ t \in {\mathbb {R}}\} \) with the norm \(\Vert {x}\Vert ={\max \nolimits _{t\in [0,T]}}\vert {x(t)}\vert .\) For a given continuous function \(g: [0,T] \rightarrow {\mathbb {R}}\), when g(t) does not change the sign on [0, T], we denote

$$\begin{aligned} g^+=\max _{t \in [0,T]}|g(t)|,\ g^-=\min _{t \in [0,T]}|g(t)|, \end{aligned}$$

we clearly have \(g^->0\) and \(g^+>0\). When g(t) changes sign on [0, T], we represent

$$\begin{aligned} g^*=\max \{g(t):t \in [0,T]\},\ g_*=\min \{g(t):t \in [0,T]\}, \end{aligned}$$

then we have \(g_*\leqslant 0\), \(g^*\geqslant 0\) and \(g_{*},g^{*}\) are not zero at the same time.

Now we give expressions of constants \(C_1\) and \(C_2\). Let

$$\begin{aligned} C_{1}:=\left( \frac{R_1}{a^{+}\sin R_1+e^{+}}\right) ^{\frac{1}{2}}, \end{aligned}$$

where \(R_{1}=2\arcsin (\frac{e^{+}}{a^{-}}+\epsilon )\) is a constant, here \(\epsilon >0\) is small enough such that \(\frac{e^{+}}{a^{-}}+\epsilon \leqslant \frac{\sqrt{2}}{2}\). Let

$$\begin{aligned} C_2:=\min \left\{ \left( \frac{R_{2}}{a^{+}\sin R_{2}+e^{*}}\right) ^{\frac{1}{2}}, \left( \frac{R_{2}}{a^{+}\sin R_{2}-e_{*}}\right) ^{\frac{1}{2}}\right\} , \end{aligned}$$

where \( R_2=\max \big \{2\arcsin (\frac{e^{*}}{a^{-}}+\epsilon ),2\arcsin (\frac{-e_*}{a^{-}}+\epsilon )\big \}\) is a constant and \(\epsilon >0\) is small enough such that \(\max \{\frac{e^{*}}{a^{-}}+\epsilon ,\frac{-e_{*}}{a^{-}}+\epsilon \}\leqslant \frac{\sqrt{2}}{2}\).

In order to study the existence of T-periodic solutions of Eq. (1.3), we list the following assumptions.

(H1):

Suppose a(t) is a continuous T-periodic function and does not change the sign on [0, T], e(t) is a continuous T-periodic function with \(e(t) \not \equiv 0\).

(H2):

When both functions a(t) and e(t) does not change the sign on [0, T],assume that functions a(t), e(t) satisfy \(\frac{e^{+}}{a^{-}}<\frac{\sqrt{2}}{2}\);when functions a(t) does not change the sign on [0, T] and e(t) changes sign on [0, T], assume that functions a(t), e(t)satisfy \(\max \{\frac{e^{*}}{a^{-}},\frac{-e_{*}}{a^{-}}\}<\frac{\sqrt{2}}{2}\).

(H3):

Suppose period T satisfy \(0<T < C\), where \(C=\min \{C_1,C_2\}\).

For convenience, we introduce some notations and an abstract existence theorem about coincidence degree theory. For more details see [7].

Let X, Y be two Banach spaces, \(L:{\text {Dom}}L \subset X \rightarrow Y\) be a linear mapping and \(N:X \rightarrow Y\) be a continuous mapping. The mapping L is said to be a Fredholm mapping of index zero if \({\text {Im}}L\) is closed in Y and \(\dim \textrm{Ker} L={\text {codim}}{\text {Im}}L<+\infty \). If L is a Fredholm mapping of index zero, then there exist continuous projectors \( P:X \rightarrow X\) and \(Q:Y \rightarrow Y\) such that \({\text {Im}} P=\textrm{Ker} L\) and \(\textrm{Ker} Q={\text {Im}} L={\text {Im}} (I-Q)\). It follows that the restriction \(L_P\) of L to \( {\text {Dom}}L \cap \textrm{Ker} P:(I-P)X \rightarrow {\text {Im}}L\) is invertible, then we denote the inverse of \( L_P\) by \(K_P\). If \(\Omega \) is a bounded open subset of X, N is called L-compact on \({\overline{\Omega }}\) if \(QN({\overline{\Omega }})\) is bounded and \(K_P(I-Q)N:\Omega \rightarrow X\) is compact.

Lemma 2.1

(Mawhin’s Continuation Theorem) Let X and Y be two Banach spaces, L be a Fredholm mapping of index zero, \(\Omega \subset X\) is an open bounded set and N is L-compact on \({\overline{\Omega }}\). If all the following conditions hold:

(1):

\(Lx \ne \lambda Nx\) for all \(x \in \partial \Omega \cap {\text {Dom}}L\), and all \(\lambda \in (0,1)\);

(2):

\(QNx \ne 0\), for all \(x \in \partial {\Omega } \cap {\text {Ker}} L\);

(3):

\(\deg \{{JQN,{\Omega }\cap {{\text {Ker}} L},0}\}\ne 0\), where \( J:{\text {Im}}Q \rightarrow {\text {Ker}} L\) is an isomorphism.

Then the equation \(Lx = Nx\) has at least one solution in \({\text {Dom}}L \cap {\overline{\Omega }}\).

Lemma 2.2

([10, Lemma 5.2]) Let \(x: [0,T]\rightarrow {\mathbb {R}}\) be an arbitrary absolutely continuous function with \(x(0)=x(T)\). Then the inequality

$$\begin{aligned} \left( \max _{t \in [0,T]}x(t)-\min _{t \in [0,T]}x(t)\right) ^{2} \leqslant \frac{T}{4}\int _{0}^{T}|x'(t)|^{2}\textrm{d}t \end{aligned}$$

holds.

3 Main Results

In this section, we can state and prove the main results of this article.

Theorem 3.1

Suppose that assumptions (H1)–(H3) hold. Then Eq. (1.3) has at least one T-periodic solution.

Remark 3.1

Conditions (H2) and (H3) are all related to the signs of e(t) and a(t), for instance, if \(a(t)>0\), \(e(t)>0\), we suppose functions a(t), e(t) satisfy \(\frac{e^{+}}{a^{-}}<\frac{\sqrt{2}}{2}\) and take \(C=C_1\); if \(a(t)>0\), e(t) changes sign, we suppose functions a(t), e(t) satisfy \(\max \{\frac{e^{*}}{a^{-}},\frac{-e_{*}}{a^{-}}\}<\frac{\sqrt{2}}{2}\) and take \(C=C_2\), we will give the reasons in the proof of Theorem 3.1.

Proof

Let \(X=Y=C_{T}\). Define linear operator \(L:{\text {Dom}}L \subset X \rightarrow Y\) by setting

$$\begin{aligned} Lx=x''+k x',\quad x \in {\text {Dom}}L, \end{aligned}$$

where \( {\text {Dom}}L=\{x|x \in X, x'' \in C({\mathbb {R}},{\mathbb {R}})\}. \) It is immediate to prove that \({\text {Ker}} L={\mathbb {R}}\) and \({\text {Im}}L=\{y\mid {y\in {Y},~\int _{0}^{T}y(s)\textrm{d}s=0}\}\), hence we have \( \dim {\text {Ker}} L={\text {codim}}{\text {Im}}L=1. \) It is not difficult to see that \({\text {Im}}L\) is a closed set in Y. Thus the operator L is a Fredholm operator with index zero.

Define nonlinear operator \(N:X \rightarrow Y \)

$$\begin{aligned} Nx= e(t)- a(t) \sin x. \end{aligned}$$

Further, we define the projectors \(P:X\rightarrow {\text {Ker}} L\) and \( Q:Y \rightarrow Y\)

$$\begin{aligned} Px(t) =&{\frac{1}{T}}\int _{0}^{T}x(s)\textrm{d}s, \nonumber \\ Qx(t) =&{\frac{1}{T}}\int _{0}^{T}x(s)\textrm{d}s. \end{aligned}$$

Clearly, \({\text {Im}}P= {\text {Ker}} L\), \( {\text {Ker}} Q={\text {Im}}L\). Then \(K_P:{\text {Im}}L \rightarrow {\text {Dom}}L \cap {\text {Ker}} P\) can be given by

$$\begin{aligned} K_{P}y(t)=\int _{0}^{T}G(s,t)y(s)\textrm{d}s, \end{aligned}$$

where G(t, s) is the Green’s function of

$$\begin{aligned} \left\{ \begin{array}{ll} x''(t)+k x'(t) = 0,\,\, t \in [0,T], &{} \hbox {} \\ \int _{0}^{T}x(t)\textrm{d}t = 0,\,\, x^{(i)}(0)=x^{(i)}(T),\,\, i=0,1. &{} \hbox {} \end{array} \right. \end{aligned}$$

It is immediate to prove that \(K_P:{\text {Im}}L \rightarrow {\text {Dom}}L \cap {\text {Ker}} P\) is a linear completely continuous operator and \(N:X \rightarrow Y \) is continuous bounded operator, therefore N is L-compact on \({\overline{\Omega }}\) with any open bounded subset \(\Omega \subset X\).

From the assumption (H1), we know that function a(t) has two cases: \(a(t)>0\) or \(a(t)<0\), and function e(t) has three cases: \(e(t)>0\), \(e(t)<0\) or e(t) changes sign. Without loss of generality, for the function a(t), we only discuss the case of \(a(t)>0\), \(a(t)<0\) is similar. Next, we classify and discuss the three cases of function e(t).

Case 1: If \(e(t)>0\), in this case, Eq. (1.3) is equivalent to equation

$$\begin{aligned} x''+k x' + a(t)\sin x -e(t)=0, \end{aligned}$$
(3.1)

where \(0<a^{-} \leqslant a(t) \leqslant a^{+} \), \(0<e^{-} \leqslant e(t) \leqslant e^{+} \).

Let

$$\begin{aligned} {\Omega }_{1}:=\{x \in X \mid \Vert {x}\Vert <R_{1}\}, \end{aligned}$$
(3.2)

where \( R_1=2\arcsin \big (\frac{e^{+}}{a^{-}}+\epsilon \big )\) is a constant, here \(\epsilon >0\) is small enough such that \(\frac{e^{+}}{a^{-}}+\epsilon \leqslant \frac{\sqrt{2}}{2}\).

Now we prove that condition (1) of Lemma 2.1 hold. Suppose the converse: there exist \(0<\lambda <1\) and \(\forall x\in {{\partial {\Omega }_{1}}} \cap {\text {Dom}}L\) such that condition (1) of Lemma 2.1 hold, that is

$$\begin{aligned} x''+k x' +\lambda a(t)\sin x -\lambda e(t)=0. \end{aligned}$$
(3.3)

Multiplying (3.3) by x and integrating from 0 to T

$$\begin{aligned} \int _{0}^{T}[{(x')}^{2}-\lambda xa(t) \sin x +\lambda e(t)x]\textrm{d}t=0. \end{aligned}$$
(3.4)

From (3.2) we know that for \(\forall x\in {\partial \Omega }_{1}\), there is \(\Vert {x}\Vert = R_{1}\). For \(\Vert {x}\Vert = R_{1}\), we have \(|x_{\max }-x_{\min }|\geqslant \frac{R_{1}}{2}\) or \(|x_{\max }-x_{\min }| <\frac{R_{1}}{2}\). Further, when \(\Vert {x}\Vert = R_{1}\) and \(|x_{\max }-x_{\min }|<\frac{R_{1}}{2}\), by \(\Vert {x}\Vert ={\max \limits _{t\in [0,T]}}\vert {x(t)}\vert \), we also have \(\frac{R_{1}}{2}<x\leqslant R_{1}\) or \(-R_{1}\leqslant x <-\frac{R_{1}}{2}\). Next, we will discuss these situations in categories.

When \(\frac{R_{1}}{2}<x\leqslant R_{1}\), according to \(\frac{e^{+}}{a^{-}}+\epsilon \leqslant \frac{\sqrt{2}}{2}\) we know that \(\sin R_1\geqslant \sin x>\sin \frac{R_1}{2}>0\), then integrating (3.3) from 0 to T

$$\begin{aligned} 0&=\int _{0}^{T}[\lambda a(t)\sin x -\lambda e(t)]\textrm{d}t \nonumber \\&>\int _{0}^{T}\left( a_-\sin \frac{R_{1}}{2}-e^+\right) \textrm{d}t \nonumber \\&>0. \end{aligned}$$

When \(-R_1\leqslant x <-\frac{R_1}{2}\), by \(\frac{e^+}{a^-}+\epsilon \leqslant \frac{\sqrt{2}}{2}\) we know that \(\sin (-R_1)\leqslant \sin x<\sin (-\frac{R_1}{2})<0\), integrating (3.3) from 0 to T

$$\begin{aligned} 0=\int _{0}^{T}[\lambda a(t)\sin x -\lambda e(t)]\textrm{d}t<0. \end{aligned}$$

If \(|x_{\max }-x_{\min }|\geqslant \frac{R_{1}}{2}\), from (3.4), \(\sin R_1\geqslant \sin x\) and Lemma 2.2, we obtain

$$\begin{aligned} 0&=\int _{0}^{T}[{(x')}^{2}-\lambda xa(t) \sin x +\lambda e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{4}{T}|x_{\max }-x_{\min }|^2-\int _{0}^{T}[ xa(t) \sin x - e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{R_{1}^{2}}{T}-T(a^{+} R_{1}\sin R_{1}+ e^{+}R_{1}) \nonumber \\&=R_{1}T\left( \frac{R_{1}}{T^{2}}-(a^{+}\sin R_{1}+ e^{+})\right) \nonumber \\&>0. \end{aligned}$$

All of the above situations are contradictory to the facts, so the condition (1) of Lemma 2.1 hold.

Next we prove that condition (2) of Lemma 2.1 hold. By simple calculation, we have

$$\begin{aligned}&e(t)- a(t) \sin (-R_1) =e(t)+ a(t) \sin R_1>0,\nonumber \\&e(t)- a(t) \sin R_1 \leqslant e^{+} - a^{-} \sin R_1<0. \end{aligned}$$

That is, for \(\forall t \in [0,T]\), we get

$$\begin{aligned}&e(t)- a(t) \sin (-R_1)>0, \end{aligned}$$
(3.5)
$$\begin{aligned}&\quad e(t)- a(t) \sin R_1<0. \end{aligned}$$
(3.6)

Take \(x \in \partial {\Omega }_{1} \cap {\text {Ker}} L\), we have \(x=-R_1\) or \(x=R_1\). From (3.5) and (3.6), for \(\forall x\in \partial {\Omega }_{1} \cap {\text {Ker}} L\), we obtain

$$\begin{aligned} QNx={\frac{1}{T}}\int _{0}^{T}( e(t)- a(t) \sin x)\textrm{d}t \ne 0. \end{aligned}$$

Hence condition (2) of Lemma 2.1 hold.

Now, we prove that condition (3) of Lemma 2.1 hold. We define a continuous function

$$\begin{aligned} H(x,\mu )=-(1-\mu )x+\mu {\frac{1}{T}}\int _{0}^{T}( e(t)- a(t) \sin x)\textrm{d}t,\quad \mu \in [0,1]. \end{aligned}$$

Obviously, we have

$$\begin{aligned} H(x,\mu )\ne 0,\quad \forall x\in {\partial \Omega }_{1} \cap {\text {Ker}} L. \end{aligned}$$

By using the homotopy invariance theorem

$$\begin{aligned} \deg (QN,\Omega _{1} \cap {\text {Ker}} L,0) =&\deg \left( H(x,1), \Omega _{1} \cap {\text {Ker}} L,0\right) \nonumber \\ =&\deg \left( H(x,0), \Omega _{1} \cap {\text {Ker}} L, 0\right) \nonumber \\ =&-1 \ne 0. \end{aligned}$$

Therefore condition (3) of Lemma 2.1 hold.

So we conclude from Lemma 2.1 that Eq. (3.1) has at least one T-periodic solution in \({{\overline{\Omega }}}_{1}.\)

Case 2: If e(t) changes sign, in this case, Eq. (1.3) is equivalent to equation

$$\begin{aligned} x''+k x' + a(t) \sin x - e(t)=0, \end{aligned}$$
(3.7)

where \(0<a^{-} \leqslant a(t) \leqslant a^{+} \), \(e_{*} \leqslant e(t) \leqslant e^{*} \). Obviously, \(e_{*}\leqslant 0,e^{*}\geqslant 0\) and \(e_{*},e^{*}\) are not zero at the same time.

Let

$$\begin{aligned} {\Omega }_{2}:=\{x \in X \mid \Vert X\Vert <R_{2}\}, \end{aligned}$$
(3.8)

where \(R_2=\max \big \{2\arcsin (\frac{e^{*}}{a^{-}}+\epsilon ),2\arcsin (\frac{-e_*}{a^{-}}+\epsilon )\big \}\) is a constant and \(\epsilon >0\) is small enough such that \(\max \{\frac{e^{*}}{a^{-}}+\epsilon ,\frac{-e_{*}}{a^{-}}+\epsilon \}\leqslant \frac{\sqrt{2}}{2}\).

Now we prove that condition (1) of Lemma 2.1 hold. Suppose there exist \(0<\lambda <1\) and \(\forall x\in {{\partial {\Omega }_{2}}} \cap {\text {Dom}}L\) such that condition (1) of Lemma 2.1 hold, that is

$$\begin{aligned} x''+k x' +\lambda a(t)\sin x -\lambda e(t)=0. \end{aligned}$$
(3.9)

Multiplying (3.9) by x and integrating from 0 to T

$$\begin{aligned} \int _{0}^{T}[{(x')}^{2}-\lambda xa(t) \sin x +\lambda e(t)x]\textrm{d}t=0. \end{aligned}$$
(3.10)

By (3.8) we know that for \(\forall x\in \partial \Omega _ 2\), we have \(\Vert {x}\Vert = R_2\), at this time we have \(|x_{\max }-x_{\min }|\geqslant \frac{R_{2}}{2}\) or \(|x_{\max }-x_{\min }| <\frac{R_{2}}{2}\). If \(\Vert {x}\Vert = R_2\) and \(|x_{\max }-x_{\min }|<\frac{R_{2}}{2}\), by \(\Vert {x}\Vert ={\max \limits _{t\in [0,T]}}\vert {x(t)}\vert \), we also have \(\frac{R_{2}}{2}<x\leqslant R_{2}\) or \(-R_{2}\leqslant x <-\frac{R_{2}}{2}\). Next, we will discuss these situations in categories.

When \(\frac{R_{2}}{2}<x\leqslant R_{2}\), by \(0<\max \{\frac{e^{*}}{a^{-}}+\epsilon ,\frac{-e_*}{a^-}+\epsilon \}\leqslant \frac{\sqrt{2}}{2}\) we know that \(\sin R_2\geqslant \sin x>\sin \frac{R_2}{2}>0\), then integrating (3.9) from 0 to T

$$\begin{aligned} 0&=\int _{0}^{T}\left[ \lambda a(t)\sin x -\lambda e(t)\right] \textrm{d}t\\&>\int _{0}^{T}\left( a_{-}\sin \frac{R_2}{2}-e^{*}\right) \textrm{d}t\\&>0. \end{aligned}$$

When \(-R_{2}\leqslant x <-\frac{R_{2}}{2}\), by \(0<\max \{\frac{e^{*}}{a^{-}}+\epsilon , \frac{-e_{*}}{a^{-}}+\epsilon \}\leqslant \frac{\sqrt{2}}{2}\) we know that \(\sin (-R_2)\leqslant \sin x< \sin (-\frac{R_2}{2})<0\), then integrating (3.9) from 0 to T

$$\begin{aligned} 0 =&\int _{0}^{T}[\lambda a(t)\sin x -\lambda e(t)]\textrm{d}t\\ \leqslant&\int _{0}^{T} \left[ a^{-}\sin \left( -\frac{R_{2}}{2}\right) -e_*\right] \textrm{d}t < 0. \end{aligned}$$

If \(|x_{\max }-x_{\min }|\geqslant \frac{R_{2}}{2}\) and \(e^*\geqslant |e_*|\), from (3.10), \(\sin R_2\geqslant \sin x\) and Lemma 2.2, we obtain

$$\begin{aligned} 0&=\int _{0}^{T}[{(x')}^{2}-\lambda xa(t) \sin x +\lambda e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{4}{T}|x_{\max }-x_{\min }|^2-\int _{0}^{T}[ xa(t) \sin x - e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{R_{2}^{2}}{T}-T(a^{+} R_{2}\sin R_{2}+ e^{*}R_{2}) \nonumber \\&=R_{2}T\left( \frac{R_{2}}{T^{2}}-(a^{+}\sin R_{2}+ e^{*})\right) >0. \end{aligned}$$

If \(|x_{\max }-x_{\min }|\geqslant \frac{R_{2}}{2}\) and \(e^*< |e_*|\), from (3.10), \(\sin R_2\geqslant \sin x\) and Lemma 2.2, we have

$$\begin{aligned} 0&=\int _{0}^{T}[{(x')}^{2}-\lambda xa(t) \sin x +\lambda e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{4}{T}|x_{\max }-x_{\min }|^2-\int _{0}^{T}[ xa(t) \sin x - e(t)x]\textrm{d}t \nonumber \\&\geqslant \frac{R_{2}^{2}}{T}-T(a^{+} R_{2}\sin R_{2}- e_{*}R_{2}) \nonumber \\&=R_{2}T\left( \frac{R_{2}}{T^{2}}-(a^{+}\sin R_{2}- e_{*})\right) >0. \end{aligned}$$

Through some simple calculations, for \(\forall t \in [0,T]\), we get

$$\begin{aligned}&e(t)- a(t) \sin (-R_2)>0,\nonumber \\&e(t)- a(t) \sin R_2<0. \end{aligned}$$

The following proof is similar to the proof of case 1, and so we omit it.

So we conclude from Lemma 2.1 that Eq. (3.7) has at least one T-periodic solution in \({{\overline{\Omega }}}_{2}\).

Case 3: If \(e(t)<0\), in this case, let \({\widetilde{e}}(t)=-e(t)\), then Eq. (1.3) is equivalent to equation

$$\begin{aligned} x''+k x' +a(t)\sin x +{\widetilde{e}}(t)=0, \end{aligned}$$
(3.11)

where \(0<a^{-} \leqslant a(t) \leqslant a^{+} \), \(e^{-} \leqslant {\widetilde{e}}(t) \leqslant e^{+} \).

Let

$$\begin{aligned} \Omega _3:=\{x \in X \mid \Vert x\Vert <R_3 \}, \end{aligned}$$

where \(R_3=R_1=2\arcsin (\frac{e^{+}}{a^{-}}+\epsilon )\) are constants, here \(\epsilon >0\) is small enough such that \(\frac{e^{+}}{a^{-}}+\epsilon \leqslant \frac{\sqrt{2}}{2}\).

The following proof is similar to the proof of case 1, and so we omit it.

So we conclude from Lemma 2.1 that Eq. (3.11) has at least one T-periodic solution in \({{\overline{\Omega }}}_{3}\).

When \(a(t)<0\) and \(e(t)>0\) the proof is the same as when \(a(t)>0\) and \(e(t)<0\); when \(a(t)<0\) and \(e(t)<0\) the proof is the same as when \(a(t)>0,\, e(t)>0\); when e(t) changes sign and \(a(t)<0\) the proof is the same as case 2.

In view of all the above discussion, we know that Eq. (1.3) has at least one T-periodic solution. This completes the proof. \(\square \)

Similar to the proof of Theorem 3.1, we can prove the existence of periodic solutions to equation

$$\begin{aligned} x''+k x'+a(t) \tan x = e(t), \end{aligned}$$
(3.12)

where \(k \in {\mathbb {R}}\) is a constant, a(t), e(t) are continuous T-periodic functions. Next, we give expressions of constants \(K_1\) and \(K_2\).

Let

$$\begin{aligned} K_1:= \left( \frac{F_1}{a^{+}\tan F_1+e^{+}}\right) ^{\frac{1}{2}}, \end{aligned}$$

where \(F_{1}>2\arctan \frac{e^{+}}{a^{-}}\) is a constant. Let

$$\begin{aligned} K_2:=\min \left\{ \left( \frac{F_{2}}{a^{+}\tan F_{2}+e^{*}}\right) ^{\frac{1}{2}}, \left( \frac{F_{2}}{a^{+}\tan F_{2}-e_{*}}\right) ^{\frac{1}{2}}\right\} , \end{aligned}$$

where \( F_{2}>\max \big \{2\arctan \frac{e^{*}}{a^{-}},2\arctan \frac{-e_*}{a^{-}}\big \}\) is a constant.

Similarly, we list the following assumption.

(H4):

Suppose period T satisfy \(0<T \leqslant K\), where \(K=\min \{K_1,K_2\}\).

Corollary 3.1

Suppose that assumptions (H1) and (H4) hold. Then Eq. (3.12) has at least one T-periodic solution.

Remark 3.2

In Corollary 3.1, the interpretation of the constant K is similar to the interpretation of the constant C in Theorem 3.1.

Fig. 1
figure 1

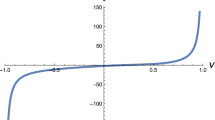
Periodic solution of Eq. (4.1)

Full size image
Fig. 2
figure 2

Periodic solution of Eq. (4.2)

Full size image

4 Examples

In this section, we apply the main results of this paper to several specific examples to obtain existence of periodic solutions of the equations, and verify the correctness of the conclusions of this article through numerical simulations.

Example 4.1

Consider the following forced pendulum equation

$$\begin{aligned} x''+6x'+ \big (\cos (20 \pi t)+6\big ) \sin x= \cos (20 \pi t)+2. \end{aligned}$$
(4.1)

It is clear that Eq. (4.1) is the case of Eq. (1.3) when \(k=6,\,a(t)=\cos (20 \pi t)+6,\,e(t)=\cos (20 \pi t)+2\). It is easily seen that functions \(a(t)>0,\ e(t)>0\) and \(a^-=5,\,a^+=7,\,e^-=1,\,e^+=3\), then functions a(t), e(t) satisfy assumption (H1) and by simple calculation we know that functions a(t), e(t) satisfy assumption (H2). Let \(\epsilon =\frac{1}{100}\), then we have \(\frac{e^+}{a^-}+\epsilon =0.601\leqslant \frac{\sqrt{2}}{2}\). By some simple calculations, we get \(R_1^\prime =1.2976\). It is easy to verify that \(T=0.1\) satisfy assumption (H3).

Then Theorem 3.1 guarantees that Eq. (4.1) has at least one periodic solutions in \(\overline{\Omega _1^\prime }\), where \(\Omega _1^\prime :=\{x \in X \mid \Vert x\Vert <R_1^\prime \}\). At the same time, we use numerical simulation to show the existence of periodic solution of Eq. (4.1), which further illustrates the correctness of the conclusions obtained in this paper. For the convenience of observation, we draw the image of three periods (Fig. ).

Example 4.2

Consider Eq. (1.3) with \(k=2,\,a(t)=\cos 5\pi t+3,\,e(t)=\sin 5 \pi t\), that is

$$\begin{aligned} x''+2x'+ (\cos 5\pi t+3) \sin x= \sin 5 \pi t. \end{aligned}$$
(4.2)

Obviously, function e(t) changes sign and function \(a(t)>0\), and they are all continuous T-periodic functions, we have \(a^-=2,\,a^+=4,\,e_*=-1,\,e^*=1\). It is not difficult to see that functions a(t), e(t) satisfy assumptions (H1) and (H2). Let \(\epsilon =\frac{1}{100}\), by simple calculation, we get \(R_2^\prime =1.0704\). Further, we can take the period \(T=0.4\), which is easy to verify that the period T satisfy assumption (H3).

From Theorem 3.1 we conclude that Eq. (4.2) has at least one periodic solutions in \(\overline{\Omega _2^\prime }\), where \(\Omega _2^\prime :=\{x \in X \mid \Vert x\Vert <R_2^\prime \}\). Next, we obtain the existence of periodic solutions of Eq. (4.2) by numerical simulation. For the convenience of observation, we draw the image of two periods (Fig. ).