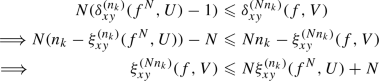Distributional Chaos on Uniform Spaces

Abstract

We introduce and study here the notion of distributional chaos on uniform spaces. We prove that if a uniformly continuous self-map of a uniform locally compact Hausdorff space has topological weak specification property then it admits a topologically distributionally scrambled set of type 3. This extends result due to Sklar and Smítal (J Math Anal Appl 241:181–188, 2000). We also justify through examples necessity of the conditions in the hypothesis of the main result.

1 Introduction

The term chaos in connection with a map was first used by Li and Yorke [15]. Since then various definitions of chaos have been introduced and extensively studied. A common idea of all of them is to show the complexity and unpredictability of behavior of the orbits of a system. Study of implications among various definitions of chaos has attracted a lot of researchers in recent times. For recent development in chaos theory one can refer to [14].

In [1], authors have studied the notion of topological entropy for a continuous self-map of a compact topological space. A dynamical system is called deterministic if its topological entropy vanishes [11]. In a similar way positive topological entropy can be related to randomness and chaos. Schweizer and Smítal introduced the concept of distributionally chaotic pair based on the asymptotic measure of the distance between the trajectories of the points [17]. In the case of continuous maps defined on a unit interval, class of distributionally chaotic maps coincide with the class of functions with positive topological entropy [16]. Distributional chaos implies Li–Yorke chaos for maps on intervals.

Distributional chaos was later divided into three types, DC1, DC2 and DC3 [4, 21] It is obvious that DC1 implies DC2 and DC2 implies DC3. It is well known that these three notions are equivalent for continuous maps defined on an interval [17]. However, in general this is not true. Another notion of chaos (much stronger than Devaney’s definition or positive topological entropy) is the specification property which was introduced by Bowen in [6]. In [20], Sklar and Smítal has related weakened versions of the specification property with the existence of a two point scrambled set consisting of DC3 chaotic pair.

The metric notions of chaos were extended to uniform spaces and to general topological spaces in [3, 22]. In [10], second author and others have extended the metric notions of expansivity and shadowing to the general topological spaces. We have extended the notion of specification to uniform spaces in [18] and we could relate it with the notions of expansivity and shadowing on uniform spaces. We have also obtained relation of topological specification property with topological entropy in [19]. Recently, T. Arai gave a definition of chaos in the sense of Li–Yorke for an action of a group on a uniform space [2].

As discussed above, there is a natural relation between specification and distributional chaos, distributional chaos and Li–Yorke chaos, distributional chaos and entropy. With this motivation we try to extend the definition of distributional chaos for uniform spaces. Our aim in this paper is to extend Sklar and Smítal’s result [20] in case of uniformly continuous maps defined on a uniformly locally compact space.

Let $(X, \mathcal {U})$ be a uniform Hausdorff space and let $f:X \rightarrow X$ be a uniformly continuous map. In this paper we extend the notion of distributional chaos to uniform spaces that are not necessarily compact metrizable. In this paper there are four sections. In Sect. 2, we introduce the basic definitions and terminologies required for the development of the paper. In Sect. 3, for a map f, we define the notions of topologically distributionally chaotic of type k (abbreviated as TDCk), where $k \in \{1, 2, 3\}$. We prove that if f is TDC1 or TDC2 then it is Li–Yorke chaotic. Moreover we show that these notions are preserved under topological conjugacy and f is TDC1 if and only if $f^{N}$ is TDC1. In Sect. 4, we obtain that a uniformly continuous map with topological weak specification property defined on a uniformly locally compact space having a distal pair admits a topologically distributionally scrambled set of type 3. In the end, we give an example to support our main theorem and we also give examples to justify the necessity of conditions in the hypothesis of the main result.

2 Preliminaries

For completion we give the metric definitions of Li–Yorke chaos and distributional chaos.

2.1 Li–Yorke Chaos

Let $f: X \rightarrow X$ be a continuous map of a compact metric space (X, d). A set $D\subset X$ containing at least two points is called a Li–Yorke scrambled set if for any two distinct points $x, y \in D$, we have

$$\begin{aligned} \liminf \limits _{n \rightarrow \infty } d(f^n(x), f^n(y))= 0\, \mathrm{and} \limsup \limits _{n \rightarrow \infty } d(f^n(x), f^n(y))> 0. \end{aligned}$$

The function f is said to be chaotic in the sense of Li–Yorke if there exists an uncountable Li–Yorke scrambled set [5].

2.2 Distributional Chaos

The notion of distributional chaos was initially defined for interval maps and then extended for compact metric spaces. Define distribution function $F_{xy}^{(n)}(t)$ by

$$\begin{aligned} F_{xy}^{(n)} (t)= \frac{1}{n} \# \{0 \le i< n | d(f^i(x), f^i(y))<t\}, \end{aligned}$$

where $\#A$ denotes the cardinality of the set A. Clearly, $F_{xy}^{(n)}(t)$ is a non-decreasing function, $F_{xy}^{(n)}(t)=0$, for $t\le 0$ and $F_{xy}^{(n)}(t)=1$, for t greater than the diameter of X. Using these functions we can rewrite the lower and upper distribution functions as

$$\begin{aligned} F_{xy}(t)=\liminf \limits _{n \rightarrow \infty }F^{(n)}_{xy}(t),\\ F_{xy}^*(t)=\limsup \limits _{n \rightarrow \infty }F^{(n)}_{xy}(t). \end{aligned}$$

Definition 1

If there exists a pair of points $x, y \in X$ such that

• (i) $F_{xy}^{*}\equiv 1$ and $F_{xy}(t)=0$, for some $t>0$, then f is said to be distributionally chaotic in the strict sense (or distributionally chaotic of type 1, abbreviated as DC1) [17].

• (ii) $F_{xy}^{*}\equiv 1$ and $F_{xy}< F_{xy}^{*}$, then f is said to be distributionally chaotic in the wider sense (or distributionally chaotic of type 2, abbreviated as DC2) [21].

• (iii) $F_{xy}< F_{xy}^{*}$, then f is said to be distributionally chaotic of type 3 (abbreviated as DC3) [4].

2.3 Uniform Spaces

Let X be a non-empty set and let $\bigtriangleup _{X} = \{(x, x) | x \in X\}$, called as the diagonal of $X\times X$. A subset M of $X\times X$ is said to be symmetric if $M=M^T$, where $M^{T}=\{(y, x) | (x, y) \in M\}$. The composite$U\circ V$ of two subsets U and V of $X\times X$ is defined to be the set $\{(x,y) \in X \times X |$ there exists $z \in X$ satisfying $(x, z) \in U$ and $(z, y) \in V \}$. We denote $U\circ U$ by $U^{2}$.

Definition 2

[13] Let X be a non-empty set. A uniform structure on X is a non-empty set $\mathcal {U}$ of subsets of $X \times X$ satisfying the following conditions:

• (i) if $U\in \mathcal {U}$ then $\bigtriangleup _X \subset U$,

• (ii) if $U\in \mathcal {U}$ and $U \subset V \subset X\times X$ then $V \in \mathcal {U}$,

• (iii) if $U\in \mathcal {U}$ and $V\in \mathcal {U}$ then $U \cap V \in \mathcal {U}$,

• (iv) if $U\in \mathcal {U}$ then $U^{T}\in \mathcal {U}$,

• (v) if $U\in \mathcal {U}$ then there exists $V\in \mathcal {U}$ such that $V\circ V \subset U$.

The elements of $\mathcal {U}$ are then called the entourages of the uniform structure and the pair $(X, \mathcal {U})$ is called a uniform space.

By a space $(X, \mathcal {U})$ we mean a uniform Hausdorff space without isolated points with uniformity $\mathcal {U}$ and by a map f we mean a uniformly continuous map $f: X \rightarrow X$. If U is a neighborhood of $\bigtriangleup _{X}$, then $U\cap U^{T}$ is a symmetric neighborhood of $\bigtriangleup _{X}$, thus we can often work with symmetric neighborhoods without loss of generality. Note that the fact that points x and y are close (in terms of distance) in a metric space X is equivalent to the fact that point (x, y) is close to the diagonal $\bigtriangleup _{X}$ of $X\times X$ in a uniform space $(X, \mathcal {U})$. If $(X, \mathcal {U})$ is a uniform space, then there is an induced topology on X characterized by the fact that the neighborhoods of an arbitrary point $x \in X$ consists of the sets U[x], where U varies over all entourages of X. The set $U[x] = \{y \in X | (x, y) \in U\}$ is called the cross section of U at $x \in X$. A space X with uniformity $\mathcal {U}$ is said to be uniformly locally compact if there exists $U \in \mathcal {U}$ such that U[x] is compact for each $x \in X$ [12].

3 Topological Distributional Chaos: Definitions and Basic Properties

In this section we extend the definition of distributional chaos for uniform spaces and study its basic properties. Let $(X, \mathcal {U})$ be a Hausdorff uniform space and let $f: X \rightarrow X$ be a uniformly continuous map. We denote the map $f \times f$ by F.

For any positive integer n, points $x, y \in X$ and $E \in \mathcal {U}$, define

$$\begin{aligned} F_{xy}^{(n)}(E)= & {} \frac{1}{n}\#\{i | F^{i}(x, y)\in E, 0 \leqslant i < n\},\\ F_{xy}(E)= & {} \liminf \limits _{n\rightarrow \infty } F_{xy}^{(n)}(E),\\ F_{xy}^{*}(E)= & {} \limsup \limits _{n\rightarrow \infty }F_{xy}^{(n)}(E). \end{aligned}$$

Note that the function $F_{xy}$ and $F_{xy}^{*}$ are non-decreasing and $F_{xy}(E)=1=F_{xy}^{*}(E)$, if $E=X$. Clearly, $F_{xy}\leqslant F_{xy}^{*}$, for all $E \in \mathcal {U}$.

In particular for $y=x$, we have

$$\begin{aligned} F_{xx}(E)=F_{xx}^{*}(E)=1, \end{aligned}$$

for all $E \in \mathcal {U}$.

Definition 3

A pair of points x, y in X is called topologically distributionally chaotic of type 1 if

• (i) $F_{xy}(E)=0$, for some $E \in \mathcal {U}$, and

• (ii) $F_{xy}^{*}(E)=1$, for all $E \in \mathcal {U}$.

Definition 4

A pair of points x, y in X is called topologically distributionally chaotic of type 2 if

• (i) $F_{xy}(E)<F_{xy}^{*}(E)$, for some $E \in \mathcal {U}$, and

• (ii) $F_{xy}^{*}(E)=1$, for all $E \in \mathcal {U}$.

Definition 5

A pair of points x, y in X is called topologically distributionally chaotic of type 3 if $F_{xy}(E)<F_{xy}^{*}(E)$, for some $E \in \mathcal {U}$.

Definition 6

A set containing at least two points is called a topologically distributionally scrambled set of typek for f if any pair of its distinct points is topologically distributionally chaotic of type k, where $k\in \{1, 2, 3\}$.

Definition 7

Let $f:X \rightarrow X$ be a uniformly continuous map of a uniform space X. Then we say that f is topologically distributionally chaotic of typek (TDCk) if there exists an uncountable topologically distributionally scrambled set of type k for f, where $k \in \{1, 2, 3\}$.

Remark 1

If we consider the uniform space $(X, \mathcal {U})$, where (X, d) is a metric space and $\mathcal {U}$ is the natural uniformity generated by the family $\{d^{-1}[0, \epsilon ]| \epsilon >0\}$, then every entourage E contains $E_{\epsilon }=d^{-1}[0, \epsilon ]$, for some $\epsilon >0$ and any $E_{\epsilon }$ is an entourage. Therefore, in this case, the above topological notions of TDC1, TDC2 and TDC3 coincide with the corresponding metric notions of DC1, DC2 and DC3, respectively. By definition, we have the following implications

$$\begin{aligned} TDC1 \Longrightarrow TDC2 \Longrightarrow TDC3 \end{aligned}$$

In [2], author has introduced the notion of Li–Yorke chaos for an action of a group on a uniform space. In view of that we define the following terms necessary for the definition of Li–Yorke chaos for a uniformly continuous map $f:X \rightarrow X$ on a uniform space X. A pair of points $x, y \in X$ is said to be asymptotic with respect tof, if for any $U\in \mathcal {U}$ there exists $k \in \mathbb {N}$ such that $F^{i}(x, y)\in U$, for each $i \ge k$. We denote by AR the collection of all pairs of asymptotic points with respect to f. A pair of points $x, y \in X$ is said to be proximal with respect tof, if for any $U\in \mathcal {U}$, there exists $j \in \mathbb {N}$ such that $F^{j}(x, y)\in U$. We denote by PR the collection of all pairs of proximal pairs with respect to f. If points are not proximal, then we say they are distal. A uniform space $(X, \mathcal {U})$ is said to be distal if for every pair of distinct points x, y there exists $U\in \mathcal {U}$, such that $F^{i}(x, y)\not \in U$, for all $i\in \mathbb {N}$. A subset S of a uniform space X is a scrambled set forf if $(x, y)\in PR {\setminus } AR$, for any distinct elements x and y of S. A map $f:X \rightarrow X$ is called Li–Yorke chaotic if there exists an uncountable scrambled set for f. We denote by LYR the set $PR {\setminus } AR$.

Proposition 1

Let $(X, \mathcal {U})$ be a uniform Hausdorff space and let $f : X \rightarrow X$ be a uniformly continuous map. If f is TDCk, $k \in \{1, 2\}$, then f is Li–Yorke chaotic.

Proof

Let S be an uncountable scrambled set of type k, $k \in \{1, 2\}$. Then for every $x, y \in S$, $x \not = y$, we have $F_{xy}^{*}(U)=1$, for all $U\in \mathcal {U}$. This implies that for each $U\in \mathcal {U}$, there exists some $j \in \mathbb {N}$ such that $F^{j}(x, y)\in U$. Thus $(x, y)\in PR$. Note that $(x, y)\not \in AR$. For if $(x, y)\in AR$, then for any $U\in \mathcal {U}$, there exists $l\in \mathbb {N}$ such that $F^{i}(x, y)\in U$, for all $i \ge l$. Let $j_{l}=i-l\ge 0$. Then $F^{j_l}(x, y)=F^{i-l}(x, y)\in U$, for each $j_l\ge 0$. This implies that for each $U\in \mathcal {U}$, $F_{xy}(U)=1=F_{xy}^{*}(U)$, which contradicts that f is TDCk, $k \in \{1, 2\}$. This proves that $(x, y)\in LYR$ and uncountability of the set S implies LYR is also uncountable. Thus f is Li–Yorke chaotic. $\square$

Let $\delta _{xy}^{(n)}(f, U) = \#\{i | F^{i}(x, y)\not \in U, 0\leqslant i <n\}$ and let $\xi _{xy}^{(n)}(f, U) = \#\{i | F^{i}(x, y) \in U, 0\leqslant i <n\}$. In the following two results, for $N>0$, we denote $F^{N}=f^{N}\times f^{N}$ by G. Proof for the following two propositions is similar to that given in [23] for a compact metric space. We present the proofs here for completion.

Proposition 2

Let $(X, \mathcal {U})$ be a uniform Hausdorff space and let $f : X \rightarrow X$ be a uniformly continuous map. For $x, y \in X$, $N>0$ and $U \in \mathcal {U}$,

• (i) if $F_{xy}(U)=0$ then $G_{xy}(U)=0$.

• (ii) if $F_{xy}^{*}(U)=1$ then $G_{xy}^{*}(U)=1$.

Thus, if f is TDC1 then so is $f^{N}$.

Proof

• (i) If $F_{xy}(U)=0$ then there is an increasing sequence $\{n_{k}\}$ of positive integers such that $F_{xy}^{(n_{k})}(U) \rightarrow 0$ as $k\rightarrow \infty$. Put $m_{k}=[\frac{n_{k}}{N}]$, where [x] denotes the integral part of the real number x. For each k, $\xi _{xy}^{(m_{k})}(f^{N}, U)\leqslant \xi _{xy}^{(n_{k})}(f, U)$. Then using this inequality and the fact that $F_{xy}^{(n_{k})} \rightarrow 0$ as $k\rightarrow \infty$, we get that $G_{xy}^{(m_{k})}(U) \rightarrow 0$ as $k \rightarrow \infty$. Hence $G_{xy}(U)=0$.

• (ii) If $F_{xy}^{*}(U)=1$ then there is an increasing sequence $\{n_{k}\}$ of positive integers such that $F_{xy}^{(n_{k})} (U)\rightarrow 1$ as $k\rightarrow \infty$. Then $\frac{1}{n_{k}} \delta _{xy}^{(n_{k})}(f, U)\rightarrow 0$ as $k \rightarrow \infty$. Put $m_{k}=[\frac{n_{k}}{N}]$. Then as argued earlier, $\frac{1}{m_{k}}\delta _{xy}^{(m_{k})}(f^{N}, U) \rightarrow 0$ as $k \rightarrow \infty$. Using $\frac{1}{m_{k}}\xi _{xy}^{(m_{k})}(f^{N}, U) + \frac{1}{m_{k}}\delta _{xy}^{(m_{k})}(f^{N}, U) =1$, we get that $\frac{1}{m_{k}}\xi _{xy}^{(m_{k})}(f^{N}, U)\rightarrow 1$ as $k \rightarrow \infty$. Hence $G_{xy}^{*}(U)=1$.

$\square$

Proposition 3

Let $(X, \mathcal {U})$ be a uniform Hausdorff space and let $f : X \rightarrow X$ be a uniformly continuous map. For $x, y \in X$ and $N>0$, we have the following:

• (i) If for $U\in \mathcal {U}$, $G_{xy}(U)=0$, then there exists $V\in \mathcal {U}$ such that $F_{xy}(V)=0$.

• (ii) If $G_{xy}^{*}(U)=1$, for all $U\in \mathcal {U}$, then $F_{xy}^{*}(V)=1$, for all $V\in \mathcal {U}$.

Thus, if $f^{N}$ is TDC1 then so is f.

Proof

• (i) If for $U\in \mathcal {U}$, $G_{xy}(U)=0$ then there exists an increasing sequence $\{n_{k}\}$ of positive integers such that $\frac{1}{n_{k}}\xi _{xy}^{(n_{k})}(f^{N}, U) \rightarrow 0$ as $k \rightarrow \infty$. For each $i = 1, 2, \ldots , N$ by uniform continuity of F, there exists $V_{i}$ such that $F^{i}(V_{i})\subset U$. Let $V = \cap _{i=1}^{N}V_{i}$. Then for each $i = 1, 2, \ldots , N$, $V\subset V_{i}$ and $F^{i}(V)\subset U$. Hence $(x, y)\in V$ implies that $F^{i}(x, y)\in U$, for each $i = 1, 2, \ldots , N$ implying that if $G(x, y)=F^{N}(x, y)\not \in U$ then $F^{i}(x, y)\not \in V$, for all $i = 0, 1, 2, \ldots , N-1$. Thus,

  

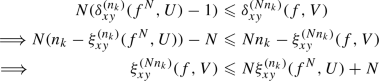
  Taking $Nn_{k}=m_{k}$ we get

  $$\begin{aligned} \frac{1}{m_{k}} \xi _{xy}^{(m_{k})}(f, V) \leqslant \frac{1}{n_{k}} \xi _{xy}^{(n_{k})}(f^{N}, U)) + \frac{1}{n_{k}}. \end{aligned}$$

  Since $\frac{1}{n_{k}}\xi _{xy}^{(n_{k})}(f^{N}, U) \rightarrow 0$ as $k \rightarrow \infty$, we have $\frac{1}{m_{k}} \xi _{xy}^{(m_{k})}(f, V) \rightarrow 0$ as $k \rightarrow \infty$. Thus $F_{xy}(V)=0$.

• (ii) Suppose $G^{*}_{xy}(U)=1$, for all $U \in \mathcal {U}$. Fix $V \in \mathcal {U}$. For each $i=0, 1, \ldots , N-1$, by uniform continuity of $F^{i}$, there exists $U_{i}$ such that $F^{i}(U_{i})\subset V$. Let $U=\cap _{i=0}^{N-1}U_{i}$. Then for each $i=0, 1, \ldots , N-1$, $U\subset U_{i}$ and $F^{i}(U)\subset V$. Thus $(x, y) \in U$ implies $F^{i}(x, y) \in V$, for each $i=0, 1, \ldots , N-1$. For this U, by assumption we have $G^{*}_{xy}(U)=1$. Therefore there exists an increasing sequence $\{n_{k}\}$ of positive integers such that $G_{xy}^{(n_{k})}(U)\rightarrow 1$ as $k\rightarrow \infty$. Hence

  $$\begin{aligned} N(\xi _{xy}^{(n_{k})}(f^{N}, U)-1) \leqslant \xi _{xy}^{(Nn_{k})}(f, V) \end{aligned}$$

  Taking $Nn_{k}=m_{k}$ we get

  $$\begin{aligned} G_{xy}^{(n_{k})}(U)=\frac{1}{n_{k}} \xi _{xy}^{(n_{k})}(f^{N}, U) \leqslant \frac{1}{m_{k}} \xi _{xy}^{(m_{k})}(f, V) + \frac{1}{n_{k}}. \end{aligned}$$

  Since $G_{xy}^{(n_{k})}(U)\rightarrow 1$ as $k\rightarrow \infty$, we have $F_{xy}^{(m_{k})}(U)\rightarrow 1$ as $k\rightarrow \infty$. Since V is arbitrary, it follows $F_{xy}^{*}(V)=1$, for all $V\in \mathcal {U}$.

$\square$

Definition 8

A set $S \subseteq \mathbb {N}$ is syndetic if there exists a positive integer a such that $\{i, i+1, \ldots , i+a\}\cap S\not = \phi$, for any $i \in \mathbb {N}$. A pair of points $x, y\in X$ is syndetically proximal if for every entourage $U\in \mathcal {U}$, the set $A_{xy}^{U}=\{j\in \mathbb {N} | F^{j}(x, y)\in U\}$ is syndetic.

Proposition 4

Let $(X, \mathcal {U})$ be a uniform Hausdorff space and let (x, y) be a syndetically proximal pair with respect to f then such a pair cannot be a topologically distributionally chaotic of type 1.

Proof

Let $U\in \mathcal {U}$. Then (x, y) is a syndetically proximal pair implies that the set $A_{xy}^{U}$ is syndetic. Therefore there exists a positive integer m such that $\{i, i+1, \ldots , i+m\}\cap A_{xy}^{U}\not =\phi$, for every $i \in \mathbb {N}$. Now, $m\cdot [\frac{n}{m}]\leqslant n\leqslant (m+1)[\frac{n}{m}]$, for every $n \in \mathbb {N}$. We have

$$\begin{aligned} F_{xy}^{(n)}(U)&=\frac{1}{n} \# \{i | F^{i}(x, y) \in U, 0\leqslant i < n \}\\&\ge \frac{1}{n} [\frac{n}{m}]\\&\ge \frac{1}{m+1}>0, \end{aligned}$$

which implies $F_{xy}^{(n)}(U)>0$, for any $U\in \mathcal {U}$. $\square$

Proposition 5

Let $(X, \mathcal {U})$ and $(Y, \mathcal {V})$ be uniform Hausdorff spaces. Suppose $f:X \rightarrow X$ and $g:Y \rightarrow Y$ are topologically conjugate. Then f is TDCk implies g is TDCk, $k \in \{1, 2, 3\}$.

Proof

Maps f and g are topologically conjugate implies that there exists a uniform homeomorphism $h: X \rightarrow Y$ such that $hf=gh$ and suppose f is TDCk, $k \in \{1, 2, 3\}$. Then f is TDCk implies that f has an uncountable scrambled set S of type k, $k \in \{1, 2, 3\}$. Let $x_{1}, x_{2}\in S$, $y_{1}=h(x_{1}), y_{2}=h(x_2)$. Let $U \in \mathcal {U}$. Then h is a uniform homeomorphism implies that $V=h(U)\in \mathcal {V}$. Now

$$\begin{aligned} G_{y_{1}y_{2}}^{(n)}(V)= & {} \frac{1}{n} \# \{i | G^{i}(y_{1}, y_{2}) \in V, \quad 0\leqslant i< n \}\\= & {} \frac{1}{n} \# \{i | (g^{i}h(x_{1}), g^{i}h(x_{2})) \in V, \quad 0\leqslant i< n \}\\= & {} \frac{1}{n} \# \{i | (hf^{i}(x_{1}), hf^{i}(x_{2})) \in h(U), \quad 0\leqslant i< n \}\\= & {} \frac{1}{n} \# \{i | (hF^{i}(x_{1}, x_{2}) \in h(U), \quad 0\leqslant i< n \}\\= & {} \frac{1}{n} \# \{i | (F^{i}(x_{1}, x_{2}) \in U, \quad 0\leqslant i < n \}\\= & {} F_{x_{1}x_{2}}^{(n)}(U)(*) \end{aligned}$$

Thus, h being a uniform homeomorphism, using $(*)$ we have f is TDCk implies g is TDCk, $k \in \{1, 2, 3\}$. $\square$

4 Topological Weak Specification Property and Topological Distributional Chaos

The specification property for homeomorphisms on a compact metric space has turned out to be an important notion in the study of dynamical systems. It was first introduced by Bowen to give the distribution of periodic points for Axiom A diffeomorphisms [6]. Informally the specification property means that it is possible to shadow two distinct pieces of orbits which are sufficiently apart in time by a single orbit.

A continuous self-map f on a uniform space X is said to have topological specification property if for every symmetric neighborhood U of the diagonal $\bigtriangleup _X$ there exists a positive integer M such that for any finite sequence of points $x_{1}, x_{2}, \ldots , x_{k}$ in X, any integers $0= a_{1} \le b_{1}< a_{2}\le b_{2}< \cdots <a_{k}\le b_{k}$ with $a_{j} - b_{j-1} \ge M$$(2 \le j \le k)$ and any $p>M+(b_{k} - a_{1})$, there exists $x \in X$ such that $f^p(x)=x$ and $F^i(x,x_{j}) \in U$, $a_{j}\le i \le b_{j}$, $1\le j \le k$ [19]. If we drop the periodicity condition in the definition of topological specification property then such a map is said to satisfy topological weak specification property [8]. We now prove our main result.

Theorem 1

Let $(X, \mathcal {U})$ consisting of closed entourages be a uniformly locally compact Hausdorff space without isolated points having a distal pair and let f be a uniformly continuous map of X onto itself having topological weak specification property then f admits a topologically distributionally scrambled set of type 3.

Proof

Let $y, z \in X$ be a distal pair. Then there exists $U_{1} \in \mathcal {U}$ such that $F^{i}(y, z)\not \in U_{1}$, for all $i \in \mathbb {N}\cup \{0\}$. Also, X is uniformly locally compact space implies that there exists $U_{2}\in \mathcal {U}$ such that $U_{2}[t]$ is compact for each $t\in X$.

Step 1 Let $U=U_{1}\cap U_{2}\in \mathcal {U}$ and let $U_{0}$ be such that $U_{0}^{4}\subset U$. For $V_{0}=U_{0}\in \mathcal {U}$, choose a positive integer $M(V_{0})$ as in the definition of topological weak specification property. For $x_{1}=y$, $x_{2}=z$, choose integers $a_{1}=0$, $b_{1}$, $a_{2}=b_{1}+M(V_{0})$, $b_{2}=qa_{2}=l_{1}$, where $q\ge 2$. By definition of topological weak specification property there exists $y_{1}\in X$ such that

$$\begin{aligned} F^{i}(y_{1}, x_{j})\in V_{0}, \quad a_{j}\leqslant i \leqslant b_{j}, \quad j\in \{1, 2 \}. \end{aligned}$$

Note that $(y_{1}, x_{1})=(y_{1}, y)\in V_0$, which implies that $y\in V_{0}[y_{1}]$. By uniform continuity of f, we get that $V_{1} = \cap _{j=1, 2} \cap _{a_{j}\leqslant i \leqslant b_{j}} F^{-i}(V_{0})\in \mathcal {U}$. Then $V_{1}\subset V_{0}$ and hence $V_{1}[y_{1}]\subset V_{0}[y_{1}]=U_{0}[y_{1}]\subset U_{2}[y_{1}]$. Since $U_{2}[y_1]$ is compact, it follows that $V_{1}[y_1]$ and $V_{0}[y_1]$ are compact sets.

Let $w\in V_{1}[y_{1}]$. Then $(y_{1}, w)\in V_{1}$ implies that $F^{i}(y_{1}, w)\in V_{0}$, for $a_{1}\leqslant i \leqslant b_{1}$ and $a_{2}\leqslant i \leqslant b_{2}$. This further implies

$$\begin{aligned} F^{i}(w, x_{j})\in V_{0}^{2}, \quad a_{j}\leqslant i \leqslant b_{j}, \quad j\in \{1, 2 \} \end{aligned}$$

(1)

Thus, each point $w\in V_{1}[y_{1}]$ satisfies (1). This completes step 1.

Step 2 For $V_{1}\in \mathcal {U}$, choose a positive integer $M(V_{1})$ as in the definition of topological weak specification property. For $x_{1}=y_{1}$, $x_{2}=y$, integers $a_{1}=0$, $b_{1}=l_{1}$, $a_{2}=b_{1}+M(V_{1})$, $b_{2}=q^{2}a_{2}=l_{2}$, by definition of topological weak specification property there exists $y_{2}\in X$ such that

$$\begin{aligned} F^{i}(y_{2}, x_{j})\in V_{1}, \quad a_{j}\leqslant i \leqslant b_{j},\quad j\in \{1, 2 \}. \end{aligned}$$

Now $(y_{2}, y_{1})\in V_{1}$, which implies $y_{2}\in V_{1}[y_{1}]$. As argued earlier, let $V_{2}^{'} = \cap _{j=1, 2} \cap _{a_{j}\leqslant i \leqslant b_{j}}F^{-i}(V_{1})$ and let $V_{2}^{''}\in \mathcal {U}$ be such that $V_{2}^{''}[y_{2}]\subset V_{1}[y_{1}]$. Let $V_{2}= V_{2}^{'}\cap V_{2}^{''}$. Note that each $w \in V_{2}[y_2]$ satisfies

$$\begin{aligned} F^{i}(w, x_{j})\in V_{1}^{2}, \quad a_{j}\leqslant i \leqslant b_{j}, \quad j\in \{1, 2 \} \end{aligned}$$

(2)

Continuing like this, after $(n-1)$-steps we have $V_{n-1}\in \mathcal {U}$, a point $y_{n-1}$ and a positive integer $l_{n-1}$.

Step n For $V_{n-1}\in \mathcal {U}$, choose a positive integer $M(V_{n-1})$ as in the definition of topological weak specification property. For $x_{1}=y_{n-1}$, $x_{2}=y$, if n is even otherwise choose $x_2=z$, integers $a_{1}=0$, $b_{1}=l_{n-1}$, $a_{2}=b_{1}+M(V_{n-1})$, $b_{2}=q^{n}a_{2}=l_{n}$, by definition of topological weak specification property there exists $y_{n}\in X$ such that

$$\begin{aligned} F^{i}(y_{n}, x_{j})\in V_{n-1}, \quad a_{j}\leqslant i \leqslant b_{j},\quad j\in \{1, 2 \}. \end{aligned}$$

Now $(y_{n}, y_{n-1})\in V_{n-1}$, which implies $y_{n}\in V_{n-1}[y_{n-1}]$. Let

$$\begin{aligned} V_{n}^{'} = \cap _{j=1, 2} \cap _{a_{j}\leqslant i \leqslant b_{j}}F^{-i}(V_{n-1}) \end{aligned}$$

and let $V_{n}^{''}\in \mathcal {U}$ be such that $V_{n}^{''}[y_{n}]\subset V_{n-1}[y_{n-1}]$. Let $V_{n}= V_{n}^{'}\cap V_{n}^{''}$. Note that each $w \in V_{n}[y_n]$ satisfies

$$\begin{aligned} F^{i}(w, x_{j})\in V_{n-1}^{2}, \quad a_{j}\leqslant i \leqslant b_{j}, \quad j\in \{1, 2 \} \end{aligned}$$

(3)

So we get a nested sequence of non-empty compact sets $\{V_{n}[y_{n}]\}$ of X with $\cap _{n\in \mathbb {N}}V_{n}[y_{n}]\not =\phi$. Let $x \in \cap _{n\in \mathbb {N}}V_{n}[y_{n}]$. Then $x\in V_{n}[y_n]$, for each $n \in \mathbb {N}$. Therefore, if n is even then by (3),

$$\begin{aligned} F^{i}(x, y)\in V_{n-1}^{2}, \quad (l_{n-1}+M(V_{n-1}))\leqslant i \leqslant l_{n}. \end{aligned}$$

(4)

Hence for n even,

$$\begin{aligned} F^{j+l_{n-1}+M(V_{n-1})}(x, y)\in V_{n-1}^{2}, \quad 0 \leqslant j \leqslant (l_{n}-l_{n-1}-M(V_{n-1})). \end{aligned}$$

(5)

It follows that for n even,

$$\begin{aligned} F_{xy}^{(l_{n}-l_{n-1}-M(V_{n-1}))}(V_{n-1}^{2})=1. \end{aligned}$$

(6)

Note that for $n=2k+1$,

$$\begin{aligned} F^{i}(x, z)\in V_{2k}^{2}, \quad (l_{2k}+M(V_{2k}))\leqslant i \leqslant l_{2k+1}. \end{aligned}$$

For if,

$$\begin{aligned} F^{i}(x, y)\in V_{2k}^{2}, \quad (l_{2k}+M(V_{2k}))\leqslant i \leqslant l_{2k+1}, \end{aligned}$$

then we have

$$\begin{aligned} F^{i}(z, y)\in V_{2k}^{4}, \quad (l_{2k}+M(V_{2k}))\leqslant i \leqslant l_{2k+1}, \end{aligned}$$

which implies that

$$\begin{aligned} F^{i}(z, y)\in V_{2k}^{4}\subset U_{0}^{4}\subset U_{1}, \quad (l_{2k}+M(V_{2k}))\leqslant i \leqslant l_{2k+1}, \end{aligned}$$

a contradiction.

Hence for odd n,

$$\begin{aligned} F_{xy}^{(l_{n}-l_{n-1}-M(V_{n-1}))}(V_{n-1}^{2})\rightarrow 0. \end{aligned}$$

(7)

Thus, $F_{xy}\not =F_{xy}^{*}$. Hence f has a topologically distributionally scrambled set of type 3. $\square$

Corollary 1

Let $(X, \mathcal {U})$ be a uniformly locally compact, totally bounded Hausdorff space and let $f: X \rightarrow X$ be a uniformly continuous map having topological specification property then f admits a topologically distributionally scrambled set of type 3.

In [10], the second author and others have extended Smale’s spectral decomposition theorem [7] to those spaces which are not necessarily metrizable and not necessarily compact. They have obtained the following result.

Theorem 2

[10] Let X be a first countable, locally compact, paracompact, Hausdorff space and $f:X \rightarrow X$ an expansive homeomorphism with the shadowing property. Then the non-wandering set $\Omega (f)$ can be written as a union of disjoint closed invariant sets (called as basic sets for f) on which f is topologically transitive. If X is compact then this decomposition is finite.

We have proved the following result in [9].

Theorem 3

[9] Let X be a first countable, locally compact, paracompact, Hausdorff space and $f:X\rightarrow X$ be an expansive homeomorphism with the shadowing property. Then there exists a subset S of a basic set R and $k>0$ such that $f^k(S)=S$, $S\cap f^j(S)=\phi$$(0<j<k)$, $f^k|_S$ is topologically mixing and $R=\cup _{j=0}^{k-1}f^j(S)$.

We present here an interesting corollary of the above theorem, which will provide us of an example to support our main theorem.

Corollary 2

Let X be a first countable, locally compact, paracompact, Hausdorff space and $f:X\rightarrow X$ be an expansive homeomorphism with the shadowing property. Suppose $(\Omega (f), f)$ is topologically transitive and has a fixed point. Then $(\Omega (f), f)$ is mixing.

Remark 2

If in addition X is totally bounded and $f|_{\Omega (f)}$ has shadowing property then $f|_{\Omega (f)}$ has topological specification property [18]. Hence $f|_{\Omega (f)}$ admits a topologically distributionally scrambled set of type 3.

The following example justifies that the condition of topological weak specification property is necessary in Theorem 1.

Example 1

Let $f: \mathbb {R} \rightarrow \mathbb {R}$ be defined by $f(x)=2x$, where $\mathbb {R}$ equipped with the usual uniformity is a uniformly locally compact space. The map f does not have the topological weak specification property [8]. Note that for any two distinct points $x, y \in \mathbb {R}$, $F_{xy}= F_{xy}^{*}$. Thus f does not admit any TDC1 pair.

Remark 3

Note that the entropy of the map f in the above example is $h(f)=log 2$ [19] but f is not TDCk for any $k=1, 2, 3$. Thus positive topological entropy need not imply TDCk.

The following example justifies that Theorem 1 need not be true if the underlying space is not Hausdorff.

Example 2

Let $f: S^1 \rightarrow S^1$ be defined by $f(e^{i\theta })=e^{2i\theta }$, where $S^1$ is equipped with the cofinite topology. Then $S^1$ is uniformly locally compact but not Hausdorff. Note that f has topological specification property and hence topological weak specification property but f does not have any TDC1 pair. In fact, for any two distinct points $x, y \in S^1$, $F_{xy}= F_{xy}^{*}$.