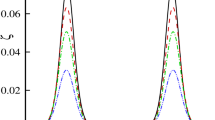Head-on Collision Between Two Hydroelastic Solitary Waves in Shallow Water

Abstract

A comprehensive theoretical study on the head-on collision between two solitary waves in a thin elastic plate floating on an inviscid fluid of finite depth is investigated analytically by means of a singular perturbation method. The effects of plate compression are also taken into account. The Poincaré–Lighthill–Kuo method has been used to derive the solution up to the fourth order of the resulting nonlinear differential equation, which in principle gives the asymptotic series solution. It is found that after collision, both the hydroelastic solitary waves preserves their original shape and positions. However a collision does have imprints on colliding waves with non-uniform phase shift up to the third order which creates tilting in the wave profile. Maximum run-up amplitude, wave speed, phase shift and distortion profile have also been calculated and plotted for two colliding solitary waves.

1 Introduction

The hydroelastic problems are very important in different fields of sciences such as biology, polar engineering, offshore engineering and also many other industrial applications. Hydroelasticity is related to the deformations of elastic bodies that corresponds to excitations of hydrodynamics and together with the refinement of these excitation owing to the deformation of the body. Many of the problems in hydroelasticity are coupled which state that deformations of the elastic bodies depend on the hydrodynamic forces. It is very difficult to study numerically and theoretically for both coupled fluid motion and the deformation of the elastic bodies. These difficulties are in fact due to hydrodynaimc forces that are acting on the surface of the elastic body which strongly depends on the surface displacements.

A number of applications are dedicated to nonlinear hydroelastic waves in polar areas where ice sheets are treated as roads and aircraft runways in winters and air-cushioned automobiles are used to break the ice. Forbes [1] investigated the periodic waves under an elastic sheet which is placed on the surface of infinitely deep water. Forbes [1] obtained the series solution for the periodic waves with the help of higher-order series expansion technique and also found that the waves of maximum height move with infinite speed for at least a single value of the flexural rigidity. Later, Forbes [2] also examined solution for surface waves of large amplitude beneath an elastic sheet with the help of the Galerkin method. Recently, Părău and Vanden-Broeck [3] studied three-dimensional nonlinear hydroelastic (flexural-gravity) waves under an ice sheet due to a steadily moving pressure by using the boundary integral method. Deike et al. [4] investigated experimentally linear and nonlinear waves beneath an elastic sheet where flexural waves and tension waves occur. Deike et al. [4] used the optical method to attain the full time and space field wave, and found that when the forcing is increased, a momentous nonlinear shift has been observed in the dispersion relation. Chen et al. [5] studied numerically the nonlinear hydroelastic waves of a moored floating body and established the governing equation of motion in a frequency domain. Chen et al. [5] found that the coupling resonance and the rigid resonance of a moored floating body can be originated in a low frequency domain whereas the flexible resonance happens in a higher frequency domain. Plotnikov and Toland [6] described the special Cosserat theory of hyperelastic shells that satisfy Kirchoff’s theory and the irrotational flow theory. This theory describes the modeling of interaction between a thin heavy elastic sheet under the ocean. Blyth et al. [7] investigated the two-dimensional nonlinear traveling waves that are bounded above and below by two elastic plates.

In the framework of the potential flow theory, Vanden-Broeck and Părău [8] investigated numerically weakly nonlinear and fully nonlinear generalized two-dimensional solitary waves and periodic waves under an ice sheet. Milewski et al. [9] studied asymptotically and numerically the nonlinear hydroelastic solitary waves in an infinite depth which are bounded below and above by an elastic sheet. Milewski et al. [9] found that for the unforced problems that the wave packets of solitary waves bifurcate from nonlinear periodic waves and when there is a moving load for small amplitude, steady responses can be obtained easily at all critical speeds, but for higher loads there are no steady solutions for transcritical range. Later, Guyenne and Părău [10] described the forced and unforced flexural-gravity solitary waves by means of Hamiltonian formulation. Alam [11] asymptotically found the series solution for the dromions of nonlinear hydroelastic waves.

It is very well known that during the past few years solitary waves and their interaction received an enormous attention among many distinct researchers [12,13,14,15,16,17,18,19,20]. When two solitary waves become closer they collide, their energies and their positions have been transferred with one another. After collision both the solitary waves regain their initial forms. The only important and unique influence of collision is their phase shifts, and it is notable that solitary waves can only be kept in an integrable system during striking and colliding. During this process of collision solitary waves can maintain their identities. Many authors have presented the solution for solitary waves. Laitone [21] extended Friedrich’s technique and included the terms upto the fourth order with the help of shallow water theory for a flat bottom, and then obtained the second order solutions for both the canodial and solitary waves. Grimshaw [22] analyzed the deformation of solitary waves which generates due to slow variation in the bottom topography.

As we are very much familiar that asymptotic behavior between two uni-directional nonlinear gravity waves in shallow water is presented by the Korteweg–de Vries (KdV) equation. To analyze the solution of KdV equation we can easily find it with the help of the inverse scattering transform method [23]. For two overtaking solitary waves, the inverse scattering transform method can also be used to see the effects of colliding. For the head-on collision between two waves, we employ the Poincaré–Lighthill–Kuo (PLK) method. Basically, it is the method of strained coordinates which was first presented by Poincaré in 1892 for ordinary differential equations. Later, Lighthill [24] and Lin [25] used this methodology for hyperbolic partial differential equations [26]. Kuo [27] performed a perfect combination of the Lighthill technique with the boundary layer method for the flow along a flat plate [28]. Detailed discussion has been described by Van Dyke [29] and Dai [28]. Zhu and Dai [30] analyzed the head-on collision between two generalized KdV (gKdV) solitary waves in a stratified fluid by the reductive perturbation method with a combination of the PLK method and two parameter expansions, and found that gKdV solitary waves keep their original shapes and during colliding of both the waves. Further, Zhu [31] also found the solution for two modified KdV solitary waves using the PLK technique and the reductive perturbation technique. Zhu [31] examined that the waves do not preserve their original shape after collision due to non-uniform in the phase shift.

The purpose of this study is to analyze the effects of hydroelasticity on the head-on collisions between two solitary waves in a thin elastic plate floating on a fluid of shallow depth. In Sect. 2 we describe the statement of problem mathematically. For the mathematical model of the plate, we follow the formulation proposed by Xia and Shen [32] who used linear Euler–Bernoulli beam theory, in which the gravity, elastic, inertial and lateral forces are taking into consideration. We assume here that the gravity force is the predominant one. The incompressible and homogenous fluid is assumed to be inviscid and the motion be irrotational. A thin elastic plate of infinite extension is floating on the surface of the fluid. To study the head-on collision in shallow water, we assume that both the solitary waves are small in amplitude $( a/H \ll 1 )$ and long in wavelength $( \lambda / H \gg 1)$, where a is amplitude, $\lambda$ is the wavelength and H the depth of the fluid. The parameters and the wavelength are associated with Ursell’s ordinary theory of shallow water i.e $H^3 \approx a \lambda ^2$. In Sects. 3 and 4 we will apply the PLK method to our resulting non-linear partial differential equations and obtain the series solution upto the third order approximation. A preliminary study on this problem was presented by Bhatti and Lu [33] while detailed mathematical method and results are elucidated here.

It is well known that different asymptotic regimes will lead to different approximate results. In above-mentioned assumptions, we shall find the 3rd-order KdV equation, with the combined effects of inertial and lateral forces, is the leading contribution to the wave motion considered here, and the effect of elastic force appears in a higher order. This approximation scheme is similar to that of Guyenne and Părău [34] for the case with $H^3 \approx a \lambda ^2$. Guyenne and Părău [34] also showed that the 3rd-order KdV equation can be the leading order while the 5th-order term appears for higher-order asymptotic expansion. Xia and Shen [32], however, assumed that the effects of the gravity force and the elastic force are in the same order so that the 3rd-order and the 5th-order terms are of the leading contribution in the 5th-order KdV equation they derived. It is noted that the mathematical models for the ice sheet in Xia and Shen [32] and Guyenne and Părău [34] are different. Xia and Shen [32] considered a linear Euler–Bernoulli model, taking the elastic force, inertial force and lateral force into account while Guyenne and Părău [34] used a nonlinear Kirchhoffs–Love plate with Plotnikov and Toland’s formulation [6]. However, the linear part of the elastic force in Plotnikov and Toland’s model [6] is the same as that of the Euler–Bernoulli model. The discrepancy in the structure models is not responsible to the difference in the KdV equations for the leading-order approximation.

2 Mathematical Formulation

Let us consider the nonlinear hydroelastic waves in a two-dimensional channel of finite depth. We have selected the Cartesian coordinate system with the x-axis is taken along the horizontal direction of the channel and the z-axis is taken along the vertical direction of the channel. The horizontal plane bottom is situated at $z=0$ where the normal velocity of the fluid is considered to be zero, since the fluid particles do not involve in any motion. The deflection of the plate is presented at $z=H(x,t)$. Under the approximation that fluid having constant density is incompressible and inviscid, and the motion is irrotational, with the help of potential flow theory the velocity field for the governing flow is described by the potential function $\phi (x,z,t)$ statifying

$$\begin{aligned} \nabla ^2\phi =0,\quad (0<z<H). \end{aligned}$$

(1)

The bottom boundary condition can be described as

$$\begin{aligned} \frac{\partial \phi }{\partial z}=0, \quad (z=0). \end{aligned}$$

(2)

The kinematic boundary condition at the free surface can be written as

$$\begin{aligned} \frac{\partial H}{\partial t} + \nabla \phi \cdot \nabla H - \frac{\partial \phi }{\partial z}=0. \end{aligned}$$

(3)

With the help of Euler–Bernoulli’s beam theory, the kinematic boundary condition for the floating elastic plate at the free surface is described by

$$\begin{aligned} \frac{\partial \phi }{\partial t} + gH +\frac{1}{2}|\nabla \phi |^2 + \frac{1}{\rho } \left( D \nabla ^4 H + M \frac{\partial ^2H}{\partial t^2} + Q\frac{\partial ^2H}{\partial x^2} \right) = B(t), \end{aligned}$$

(4)

where $D=Ed^3/[12(1-\nu ^2)]$ is the flexural rigidity of the plate, $M=\rho _{\text {e}} d$ is a mass per unit area of the plate, Q is associated to the lateral stress of the plate (with compression at $Q > 0$), B(t) is the Bernoulli constant, E, d, $\nu$, and $\rho _{\text {e}}$ are Young’s modulus, the thickness of plate, Poisson’s ratio, and the density of the plate, respectively.

For long waves in shallow water, we can easily describe the potential function $\phi (x,z,t)$ can be presented as the Taylor series at $z=0$. With the help of Eqs. (1) and (2), we get

$$\begin{aligned} \phi (x,z,t)=\sum _{n=0}^{\infty } (-1)^n \frac{z^{2n}}{(2n)!} \nabla ^{2n}\Phi , \end{aligned}$$

(5)

where

$$\begin{aligned} \Phi (x,t)=\phi (x,0,t). \end{aligned}$$

(6)

Rewriting Eqs. (3) and (4) in terms of $\Phi$, we obtain

$$\begin{aligned}&\frac{\partial H}{\partial t} + \nabla \cdot \left[ \sum _{n=0}^{\infty } (-1)^n \frac{H^{2n+1}}{(2n+1)!} \nabla ^{2n} (\nabla \Phi )\right] =0, \end{aligned}$$

(7)

$$\begin{aligned}&\frac{\partial \Phi }{\partial t} + gH + \frac{1}{2}|\nabla \Phi |^2 + \frac{1}{\rho } \left( D \nabla ^4 H + M \frac{\partial ^2H}{\partial t^2} + Q\frac{\partial ^2H}{\partial x^2} \right) \nonumber \\&\quad +\, \sum _{n=1}^{\infty } (-1)^n\frac{H^{2n}}{(2n)!}\left[ \nabla ^{2n} \Phi _t + \frac{1}{2}\sum _{m=0}^{2n} (-1)^m \mathbb {C}_m^{2n} \nabla ^{m+1} \Phi * \nabla ^{2m-n+1} \Phi \right] , \end{aligned}$$

(8)

where

$$\begin{aligned} \mathbb {C}_m^{2n}=\begin{pmatrix} 2n \\ m \end{pmatrix} = \frac{2n}{m!(2n-m)!} \end{aligned}$$

(9)

is the binomial coefficients and $U=\partial \Phi /\partial x$ is the tangential velocity at the bottom of the channel. In Eq. (8) the asterisk represents the vector inner product for usual multiplication of even m and odd n.

3 Method of Solution

In this section, we apply the PLK method to obtain the solution of Eqs. (7) and (8). We define the following transformations of wave frame coordinates with phase functions

$$\begin{aligned} \xi = \varepsilon ^{\frac{1}{2}}k(x-C_+ t) +\varepsilon k \theta (\xi ,\eta ), \qquad \eta = \varepsilon ^{\frac{1}{2}}\bar{k}(x+C_- t) +\varepsilon \bar{k} \varphi (\xi ,\eta ). \end{aligned}$$

(10)

In Eq. (10) k and $\bar{k}$ are the wave numbers of left- and right-going waves of order unity whereas $\varepsilon$ is the dimensionless parameters which defines the amplitude of the wave and order of the magnitude where $0<\varepsilon \ll 1$, $C_+$ and $C_-$ the corresponding wave speed for the right- and left going wave, $\theta$ and $\varphi$ are the phase functions. According to Ursell’s relationship, the scaling of the horizontal wavelength is taken as $\varepsilon ^{1/2}$. We derive the following transformation between the derivatives as

$$\begin{aligned}&\frac{\partial }{\partial t} +C_+ \frac{\partial }{\partial x} = \frac{\varepsilon ^\frac{1}{2}}{\mathbb {D}}(C_+ + C_-) \left[ \bar{k} \frac{\partial }{\partial \eta } + \varepsilon k\bar{k} \left( \frac{\partial \theta }{\partial \eta } \frac{\partial }{\partial \xi } - \frac{\partial \theta }{\partial \xi } \frac{\partial }{\partial \eta } \right) \right] , \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial }{\partial t} -C_-\frac{\partial }{\partial x} = - \frac{\varepsilon ^\frac{1}{2}}{\mathbb {D}}(C_+ +C_-) \left[ k\frac{\partial }{\partial \xi } +\varepsilon k\bar{k} \left( \frac{\partial \varphi }{\partial \xi } \frac{\partial }{\partial \eta } -\frac{\partial \varphi }{\partial \eta } \frac{\partial }{\partial \xi } \right) \right] , \end{aligned}$$

(12)

where

$$\begin{aligned} \mathbb {D} = \left( 1-\varepsilon k \frac{\partial \varphi }{\partial \eta } \right) \left( 1-\varepsilon \bar{k} \frac{\partial \theta }{\partial \xi } \right) - \varepsilon ^2 k\bar{k}\frac{\partial \varphi }{\partial \xi } \frac{\partial \theta }{\partial \eta }. \end{aligned}$$

(13)

Let

$$\begin{aligned} H=H_0 \left( 1+\zeta \right) , \end{aligned}$$

(14)

where $H_0$ is a undisturbed depth of a fluid and $\zeta$ is a nondimensional elevation of plate-fluid interface. Let $C=\sqrt{gH_0}$ is a phase speed of linear waves in the shallow water of a constant depth. Rewriting Eqs. (7) and (8) yields

$$\begin{aligned} \left( \frac{\partial }{\partial t} + C_{\pm } \frac{\partial }{\partial x} \right) \left( U\pm C\zeta \right) + \frac{\partial F_{\pm }}{\partial x} =0, \end{aligned}$$

(15)

where

$$\begin{aligned}&F_{\pm } =\pm (C-C_{\pm })(U \pm C\zeta ) + \frac{1}{2}U^2 \pm C \zeta U + \frac{1}{\rho } \left( D \frac{\partial ^4 \zeta }{\partial x^4 } + M \frac{\partial ^2 \zeta }{\partial t^2} + Q \frac{\partial ^2 \zeta }{\partial x^2} \right) \nonumber \\&\qquad \quad +\,\sum _{n=1}^{\infty } \frac{(-1)^n H_0^{2n} (1+\zeta )^{2n}}{2n!} \left( \frac{\partial ^{2n} U }{\partial t \partial x^{2n-1}} \pm \frac{C(1+\zeta )}{(2n+1)} \frac{\partial ^{2n} U }{\partial x^{2n}} +\frac{1}{2} \sum _{m=0}^{2n} \mathbb {C}_m^{2n}(-1)^m \frac{\partial ^m U}{\partial x^m} \frac{\partial ^{2n-m} U}{\partial x^{2n-m}} \right) . \end{aligned}$$

(16)

Let us make the following changes in the dependent variables

$$\begin{aligned} U+C\zeta = 2\varepsilon C \alpha , \qquad U-C\zeta = -2\varepsilon C\beta . \end{aligned}$$

(17)

With the help of Eqs. (10) and (17), Eq. (15) can be written as

$$\begin{aligned}&2 \varepsilon C (C_+ +C_-) \left[ \bar{k} \frac{\partial \alpha }{\partial \eta } +\varepsilon k\bar{k} \left( \frac{\partial \theta }{\partial \eta } \frac{\partial \alpha }{\partial \xi } -\frac{\partial \theta }{\partial \xi } \frac{\partial \alpha }{\partial \eta } \right) \right] \nonumber \\&\quad +\, \left[ \bar{k}\frac{\partial }{\partial \eta } +k\frac{\partial }{\partial \xi } +\varepsilon k\bar{k} \left( \frac{\partial }{\partial \eta } (\theta -\varphi ) \frac{\partial }{\partial \xi } - \frac{\partial }{\partial \xi } (\theta - \varphi )\frac{\partial }{\partial \eta } \right) \right] F_+=0. \end{aligned}$$

(18)

We can get similar equation for $\beta$ if we replace $\alpha$ by $\beta$, $\xi$ by $\eta$, k by $\bar{k}$, $F_+$ by $F_-$ and $\theta$ by $\varphi$. According to the PLK method, we define the following expansions:

$$\begin{aligned}&\alpha (\xi , \eta )=\alpha _0 + \varepsilon \alpha _1 +\varepsilon ^2 \alpha _2 +\ldots , \end{aligned}$$

(19)

$$\begin{aligned}&\beta (\xi , \eta ) =\beta _0 + \varepsilon \beta _1 +\varepsilon ^2 \beta _2 +\ldots , \end{aligned}$$

(20)

$$\begin{aligned}&\theta (\xi , \eta )=\theta _0(\eta ) + \varepsilon \theta _1(\xi , \eta ) +\varepsilon ^2 \theta _2 (\xi , \eta )+\ldots , \end{aligned}$$

(21)

$$\begin{aligned}&\varphi (\xi , \eta )=\varphi _0 (\xi )+ \varepsilon \varphi _1 (\xi , \eta )+\varepsilon ^2 \varphi _2 (\xi , \eta )+\ldots , \end{aligned}$$

(22)

$$\begin{aligned}&C_+=C\left( 1+\varepsilon a R_1 +\varepsilon ^2 a^2 R_2+\ldots \right) , \end{aligned}$$

(23)

$$\begin{aligned}&C_- = C\left( 1+\varepsilon b L_1 +\varepsilon ^2 b^2 L_2+\ldots \right) , \end{aligned}$$

(24)

where $R_1, R_2, R_3, \ldots$ and $L_1, L_2, L_3 \ldots$ are the parameters for removing secular terms in the perturbation solution.

4 Perturbation Analysis

Substituting Eqs. (19) to (24) into Eq. (18), we get the following the following system of equations. The coefficients of $\varepsilon , \varepsilon ^2, \varepsilon ^3, \ldots$ are presented in sequence as follows.

4.1 Coefficients of $\varepsilon$

We have the equations for $\alpha _0$ and $\beta _0$ as follows

$$\begin{aligned}&\frac{\partial \alpha _0}{\partial \eta } =0, \qquad \frac{\partial \beta _0}{\partial \xi } =0. \end{aligned}$$

(25)

The solution of Eq. (25) is

$$\begin{aligned}&\alpha _0 = aA(\xi ), \qquad \beta _0 = bB(\eta ). \end{aligned}$$

(26)

In above equation $A(\xi )$ and $B(\eta )$ are arbitrary functions, where a and b in Eqs. (19) to (24) and (26) are proposed which permit us to take $A(0)=1$ and $B(0)=1$.

4.2 Coefficients

We have the equation for $\alpha _1$

$$\begin{aligned}&4\bar{k} \left( \frac{\partial \alpha _1}{\partial \eta } + kaA' \frac{\partial \theta _0}{\partial \eta } \right) + ka \left[ (3aA - 2a R_1 -bB)A' + k^2 H_0^2 \left( \frac{1}{3}+\sigma +\Lambda \right) A''' \right] \nonumber \\&\qquad +\, \bar{k}b \left[ - (aA+bB)B' + \bar{k}^2 H_0^2 \left( \frac{2}{3}+\sigma +\Lambda \right) B'''\right] =0, \end{aligned}$$

(27)

where

$$\begin{aligned} \sigma =M/(\rho H_0),\qquad \Lambda = Q/(\rho g H_0^2) \end{aligned}$$

(28)

are the nondimensional parameters representing the effects of mass and compressive force per unit length of plate, respectively. As $\sigma$ and $\Lambda$ tend to zero, Eq. (27) will reduce to Eq. (20) of Su and Mirie [26]. The terms occurring in Eq. (27) can be further summarized into three parts, namely secular terms, non-local and local terms, which will be analyzed in details as follows.

4.2.1 Secular Terms

In Eq. (27) there are five terms that are independent of $\eta$. After integrating these terms with respect $\eta$, we get the secular attitude. These terms become unbounded with respect to time or space. After setting these terms equal to zero, we obtain

$$\begin{aligned} \left( 3A -2 R_1 \right) aA' + k^2H_0^2 \left( \frac{1}{3}+\sigma +\Lambda \right) A''' =0. \end{aligned}$$

(29)

Let

$$\begin{aligned} R_1 = \frac{1}{2},\qquad kH_0 = \sqrt{3a}. \end{aligned}$$

(30)

After some simplification, Eq. (29) can be written as

$$\begin{aligned} A''' +\left( \frac{3A -1}{\gamma } \right) A'=0, \end{aligned}$$

(31)

where

$$\begin{aligned} \gamma =1+3\sigma +3\Lambda . \end{aligned}$$

(32)

The solution of the above equation can be written as

$$\begin{aligned} A = {{\mathrm{sech}}}^2 \left( \frac{\xi }{2\sqrt{\gamma }}\right) . \end{aligned}$$

(33)

Similarly, we can also write for $\beta$

$$\begin{aligned}&B = {{\mathrm{sech}}}^2 \left( \frac{\eta }{2\sqrt{\gamma }}\right) , \end{aligned}$$

(34)

$$\begin{aligned}&L_1 = \frac{1}{2},\qquad \bar{k}H_0 = \sqrt{3b}. \end{aligned}$$

(35)

4.2.2 Non-local Terms

These terms do not represent any secularity. So we will leave them as they are. Due to them, the resulting equation for $\alpha _1$ comes under an integral. In Eq. (27) we recognize the following two terms in this group. By setting them equal to zero, we obtain

$$\begin{aligned} \left( 4\bar{k}\frac{\partial \theta _0}{\partial \eta }-bB\right) k aA'=0. \end{aligned}$$

(36)

Solving the above equation for $\theta _0$, we get

$$\begin{aligned} \theta _0= \frac{b}{4\bar{k}}\int _{-\infty }^{\eta } B(\eta _1) \text {d}\eta _1. \end{aligned}$$

(37)

Similarly we have

$$\begin{aligned} \varphi _0 = \frac{a}{4k}\int _{+\infty }^{\xi } A(\xi _1) \text {d}\xi _1. \end{aligned}$$

(38)

The first order phase shift in Eqs. (37) and (38) agree with the earlier work presented by Su and Mirie [26].

4.2.3 Local Terms

The remaining part in Eq. (27) can be written as

$$\begin{aligned} \frac{\partial \alpha _1}{\partial \eta } - \frac{b^2}{4} BB' - \frac{ab}{4}AB'+\frac{3b^2}{4}\left( \frac{2}{3}+\sigma +\Lambda \right) B'''. \end{aligned}$$

(39)

Integrating the above equations, we get

$$\begin{aligned} \alpha _1(\xi ,\eta ) = \frac{1}{4}ab AB - c_0 b^2 B+\left( \frac{3c_0}{2}+\frac{1}{8} \right) b^2 B^2+a^2A_1(\xi ), \end{aligned}$$

(40)

where $c_0$ is given in the “Appendix”. Similarly

$$\begin{aligned}&\frac{\partial \beta _1}{\partial \xi } - \frac{a^2}{4} AA' - \frac{ab}{4}A'B+\frac{3a^2}{4}\left( \frac{2}{3}+\sigma +\Lambda \right) A'''=0, \end{aligned}$$

(41)

$$\begin{aligned}&\beta _1(\xi ,\eta )= \frac{1}{4}ab AB - c_0 a^2 A+\left( \frac{3c_0}{2}+\frac{1}{8} \right) a^2 A^2+a^2B_1(\eta ). \end{aligned}$$

(42)

$A_1(\xi )$ and $B_1(\eta )$ are two arbitrary functions which will be determined in the next order of approximation.

4.3 Coefficients of $\varepsilon ^3$

Let

$$\begin{aligned} \Gamma = D/(\rho g H_0^4), \end{aligned}$$

(43)

which is a nondimensional parameter representing the effect of the flexural rigidity of the elastic plate. For the third order, we have the equation for $\alpha _2$, as shown in “Appendix A”. The terms occurring in Eq. (A1) can be further summarized into three parts as follows.

4.3.1 Secular Terms

The secular terms appearing are

$$\begin{aligned} \gamma A_1'' + (3A -1)A_1 =\left( 2R_2 - c_1 \right) A+ c_2 A^2 + c_3 A^3, \end{aligned}$$

(44)

where $c_1$, $c_2$ and $c_3$ are defined in “Appendix”.

The first term on the right-hand side of Eq. (44) becomes unbounded when $\xi \rightarrow \pm \infty$, which shows that the series solution is not asymptotic. Thus, the coefficient of this term must vanish, namely

$$\begin{aligned} R_2 =- \frac{c_1}{2} . \end{aligned}$$

(45)

In Eq. (44) we found that the solution for the wave speed upto the second order is correct. The solution for the rest of the terms can be written as

$$\begin{aligned} A_1 (\xi ) = c_5A -\frac{c_3}{2}A^2. \end{aligned}$$

(46)

Similarly, we have

$$\begin{aligned} B_1 (\eta ) = c_5 B -\frac{c_3}{2}B^2. \end{aligned}$$

(47)

This completes the solution for Eqs. (40) and (42). The homogeneous solution of Eq. (44) is $A'$, but we will drop this term here because we find that when we move to a higher order, the homogeneous term only causes a uniform shift of the origin of $\xi$ which describes a simple phase shift as mentioned in the preceding section.

4.3.2 Non-Local terms

These terms will provide the solution for $\theta _1$ and $\varphi _1$ as

$$\begin{aligned} \theta _1 (\xi , \eta )&= \frac{b}{16\bar{k} } \int _{-\infty }^{\eta } \left[ 4b c_5 -(a+b) - 3a(4-\sigma +3\Lambda ) \right] B \text {d}\eta _1 \nonumber \\&\quad +\, \frac{ab}{16\bar{k} } \int _{-\infty }^{\eta }(37-3\sigma + 12 c_0 +27 \Lambda ) AB \text {d}\eta _1, \end{aligned}$$

(48)

$$\begin{aligned} \varphi _1 (\xi , \eta )&= \frac{a}{16k} \int _{+\infty }^{\xi } \left[ 4a c_5 -(a+b) -3b(4 -\sigma +3\Lambda ) \right] A \text {d}\xi _1 \nonumber \\&\quad +\, \frac{ab}{16k} \int _{+\infty }^{\xi }( 37-3\sigma + 12 c_0+27 \Lambda ) AB \text {d}\xi _1. \end{aligned}$$

(49)

4.3.3 Local Terms

The solution for the local terms can be written as

$$\begin{aligned} \alpha _2&= (c_5b^2+c_6 a^2 )b B^3 + [(c_7bB+c_8 aA )a + c_9 ab +c_{10} a^2] bAB \nonumber \\&\quad +\, (c_{11} b^2+c_{12}ab -c_6 a^2) b B^2 +(c_{13}b^2+c_{14}a^2)b B+a^3 A_2 (\xi ), \end{aligned}$$

(50)

$$\begin{aligned} \beta _2&= (c_5a^2+c_6 b^2 )a A^3 +[(c_7aA+c_8 bB )b + c_9 ab +c_{10} b^2]a BA \nonumber \\&\quad +\, (c_{11} a^2+c_{12}ba-c_5 b^2 )a A^2 +(c_{13}a^2+c_{14}b^2) aA+b^3 B_2 (\eta ), \end{aligned}$$

(51)

where $A_2(\xi )$ and $B_2(\eta )$ are two arbitrary functions which can easily be found in the next order approximation using the same procedure as mentioned above. The constants $c_n$ ($n=4, 5, \ldots 14$) appearing in the above equations are given in “Appendix B”. For our analysis convenience, further calculation stops at the order of $O(\varepsilon ^3)$ and the formulas of $A_2(\xi )$ and $B_2(\eta )$ are omitted.

5 Analytical Solutions of the Problem

The major results obtained in preceding section are as follows.

The surface elevation at the water–plate interface can be obtained with the help of Eq. (17), we get

$$\begin{aligned} \zeta&= \varepsilon (\alpha +\beta ), \end{aligned}$$

(52)

which can be asymptotically given as

$$\begin{aligned} \zeta&= \varepsilon (\alpha _0 + \beta _0)+\varepsilon ^2 (\alpha _1 + \beta _1)+O(\varepsilon ^3), \end{aligned}$$

(53)

where $\alpha _0$ and $\beta _0$ are given in Eq. (26) while $\alpha _1$ and $\beta _1$ in Eqs. (40) and (42). In Eq. (53) the terms which are dependent of $\xi$ and $\eta$ are just the non-uniform phase shifts i.e. at different points of wave the phase shift is different which causes a distortion in wave during collision. For this purpose the terms which are products of $A(\xi )$ and $B(\eta )$ in Eq. (53) must vanish. Therefore the distortion profile can be obtained. After setting $B(\eta )=0$, we get

$$\begin{aligned} \zeta&=\varepsilon aA+\varepsilon ^2 a^2\left[ \frac{1}{2}\left( c_0 +\frac{1}{4} \right) A + A_1 (\xi ) \right] +O(\varepsilon ^3). \end{aligned}$$

(54)

The maximum run-up $\zeta _{\text {max}}$ during the collision process can be obtained by taking $A=B=1$ in Eq. (53), and we get

$$\begin{aligned} \zeta _{\text {max}}&= \zeta \Big |_{A=B=1}. \end{aligned}$$

(55)

The velocity at the bottom U can be obtained from Eq. (17), and we get

$$\begin{aligned} U&= \varepsilon C(\alpha -\beta ). \end{aligned}$$

(56)

Following from Eqs. (30) and (45), the asymptotic solutions for the wave speeds read

$$\begin{aligned} \frac{C_+}{C}&=1+\frac{1}{2}\varepsilon a-\frac{c_1}{2}\varepsilon ^2 a^2 +O(\varepsilon ^3) , \end{aligned}$$

(57)

$$\begin{aligned} \frac{C_-}{C}&=1+\frac{1}{2}\varepsilon b-\frac{c_1}{2}\varepsilon ^2 b^2+O(\varepsilon ^3). \end{aligned}$$

(58)

The phase shift during the collision process reads

$$\begin{aligned} \theta&= \theta _0 + \varepsilon \theta _1 +O(\varepsilon ^2), \qquad \varphi =\varphi _0 + \varepsilon \varphi _1 +O(\varepsilon ^2), \end{aligned}$$

(59)

where $\theta _0$, $\theta _1$, $\varphi _0$, and $\varphi _1$ are given in Eqs. (37), (38), (48), and (49), respectively.

Fig. 1

Three-dimensional view of head-on collision between two solitary waves

Fig. 2

Head-on collision between two solitary waves for different values of $\Gamma$ and $\sigma$. Red line: $\Gamma =0$, $\sigma =0$; Green line: $\Gamma = 0.0725$, $\sigma =0.3668$ (color figure online)

Fig. 3

Head-on collision between two solitary waves for different values of $\Lambda$. Red line: $\Lambda =0$; Green line: $\Lambda =1$ (color figure online)

Fig. 4

Maximum run-up versus wave amplitude. Red line: $\Gamma =0$, $\sigma =0$; Green line: $\Gamma = 0.0725$, $\sigma =0.3668$ (color figure online)

Fig. 5

Maximum run-up versus wave amplitude. Red line: $\Lambda =0$; Green line: $\Lambda =1$ (color figure online)

Fig. 6

Distortion profile. Solid line: Before collision; Dashed line: After collision

Fig. 7

Phase shift vs wave amplitude. Red line: $\Gamma =0$, $\sigma =0$; Green line: $\Gamma = 0.0725$, $\sigma =0.3668$ (color figure online)

Fig. 8

Phase shift vs wave amplitude. Red line: $\Lambda =0$; Green line: $\Lambda =1$ (color figure online)

Fig. 9

Wave speed vs wave amplitude. Red line: $\Gamma =0$, $\sigma =0$; Green line: $\Gamma = 0.0725$, $\sigma =0.3668$ (color figure online)

Fig. 10

Wave speed vs wave amplitude. Red line: $\Lambda =0$; Green line: $\Lambda =1$ (color figure online)

6 Graphical Results and Discussion

In this section, we describe the behavior of all the important governing parameters involved in this hydroelastic wave problem. To analyze it more vigorously, Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 are plotted against multiple values of all the parameters. For instance, we describe the behavior of distortion profile, phase shift, wave speed, water–plate elevation and maximum run-up during a collision. We take the physical parameters $E=10^5$ N m$^{-2}$, $d=0.4$ m, $g=9.8$ m s$^{-2}$, $\rho =10^3$ kg m$^{-3}$, $H_0=1$ m, $\rho _{\text {e}} = 917$ kg m$^{-3}$ and $\Lambda =1$ for the graphical results, which yield $\Gamma =0.0725$ and $\sigma =0.3668$.

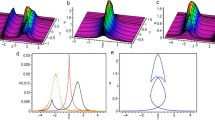
Figure 1 represents the three-dimensional behavior of a pair of solitary waves during the collision process. From this figure we can see that the solitary waves maintain their shapes before and after the colliding process. Figures 2 and 3 are plotted against multiple values of $\Gamma$, $\sigma$ and $\Lambda$. In Fig. 2 we can see that in the presence of a thin elastic plate, the amplitudes of both solitary waves reduce significantly. An increment in $\Gamma$ and/or $\sigma$ reveals the increment in the plate thickness d and Young’s modulus E which are favorable in providing a resistance in the wave profile. Moreover when Young’s modulus increases then deflection in a thin elastic plate becomes more stiffer and a very high rate of reactive forces generated to oppose the deformation of elastic plate. It depicts from Fig. 3 that an increment in the compressive force $\Lambda$ also causes a remarkable reduction in the amplitude of the wave profile.

Figures 4 and 5 represent the maximum run-up amplitude during the collision process which are plotted with the help of Eq. (55). Figure 4 shows the variation of pure gravity waves ($\Gamma =\sigma =0$) and hydroelastic waves ($\Gamma \ne 0$ and/or $\sigma \ne 0$). It is found from this figure that when the nondimensional $\Gamma$ and $\sigma$ parameters increase, the maximum run-up amplitude decreases significantly. However its behavior is similar against the nondimensional parameter $\Lambda$ as shown in Fig. 5.

Figure 6 is sketched to see the behavior of distortion profile before and after collision process. It has been plotted with the help of Eq. (54). Moreover, we can easily observe that the hydroelastic wave profile is symmetric (along the x-axis) before collision process, whereas after the collision a larger tilting occurs and the wave profile push backward along the direction of wave propagation. Moreover, the behavior for the left-going wave is similar as the right-going one.

Figures 7 and 8 are plotted to determine the behavior of phase shift against the multiple values of $\Gamma$, $\sigma$ and $\Lambda$. It is worth mentioning here that the first order phase shift in Eqs. (37) and (38) agrees with the earlier work by Su and Mirie [26]. It can be viewed from Fig. 6 that the presence of hydroelastic waves (i.e. increment in $\Gamma$ and $\sigma$), significantly enhances the phase shift profile. It can be observed from Fig. 8 that an increment in the compressive force $\Lambda$ creates a marked increment in the phase shift profile. Furthermore, in the absence of thin elastic plate (or pure gravity waves) and compression, the present results are in excellent agreement with that of Su and Mirie [26].

Figures 9 and 10 are plotted to analyze the wave speed against the multiple values of $\Gamma$, $\sigma$ and $\Lambda$. It can be seen from Fig. 9 that greater effects of thin elastic plate terms $\gamma$ and $\sigma$ cause a major reduction in the wave speed. However, in Fig. 10 we noticed that the nondimensional parameter $\Lambda$ significantly effects the wave speed and produces marked diminution in the wave speed.

7 Conclusions

Head-on collision between two solitary waves in a thin elastic plate floating on a fluid has been investigated. To observe the effects of collision the Poincaré–Lighthill–Kuo (PLK) method has been used to find the asymptotic series solution. The solution has been calculated upto third order approximation. The physical behavior of all the pertinent parameters are discussed mathematically and graphically for surface elevation, velocity at the bottom, wave speed, phase shift, distortion profile and maximum run-up during collision process.

We found that after collision both the solitary waves preserve their original positions and shapes. From the computational results we also analyze that the amplitudes of both the solitary waves decrease due to the plate deflection. During the head-on collision, we can easily notice that the maximum amplitude decreases when the plate thickness and the compressive forces increase. Another most important point is that when the thickness of plate tends to zero, the solutions are in good agreement with those obtained by Su and Mirie [26] for pure gravity waves. The total phase shift before and after collision for the right- and left-going waves have also been calculated. We also concluded that the distortion in the wave profile produces a smaller tilting and after collision the wave tilts backward in the direction of propagation. The investigation of a present results which is introduced for two-dimensional problems is also applicable for three dimensions with relevant modifications and assumptions.

Appendices

Appendix A: Equation of $O(\epsilon ^3 )$

$$\begin{aligned}&4 \bar{k} \frac{\partial \alpha _2}{\partial \eta } + k\frac{\partial \alpha _1}{\partial \xi } \left( 4 \bar{k} \frac{\partial \theta _0}{\partial \eta } - 2aR_1 + 3\alpha _0 -\beta _0 \right) + \bar{k}\frac{\partial \alpha _1}{\partial \eta } \big (2bR_1+3\alpha _0-\beta _0\big ) \nonumber \\&\quad -\, (\alpha _0 + \beta _0 ) \left( k \frac{\partial \beta _1}{\partial \xi } + \bar{k}\frac{\partial \beta _1}{\partial \eta }\right) + \frac{H_0^2}{3} \left( k^3 \frac{\partial ^3}{\partial \xi ^3} - 2\bar{k}^3\frac{\partial ^3}{\partial \eta ^3} \right) (\alpha _1-\beta _1)\nonumber \\&\quad -\, \bar{k} \frac{\partial \beta _0}{\partial \eta } \left[ -2\bar{k}^2 H_0^2 \frac{\partial ^2 \beta _0}{\partial \eta ^2} + \frac{1}{3}k^3H_0^2\frac{\partial ^3 \varphi _0}{\partial \xi ^3} + k\frac{\partial \varphi _0}{\partial \xi } (\alpha _0 +\beta _0) + \alpha _1+ \beta _1 \right] \nonumber \\&\quad +\, k \frac{\partial \alpha _0}{\partial \xi } \left[ k^2 H_0^2 \frac{\partial ^2 \alpha _0}{\partial \xi ^2} + \bar{k}^2 H_0^2 \frac{\partial ^2 \beta _0}{\partial \eta ^2} - \frac{2}{3}\bar{k}^3H_0^2\frac{\partial ^3 \theta _0}{\partial \eta ^3} \right. \nonumber \\&\quad \left. +\, 4 \bar{k} \frac{\partial \theta _1}{\partial \eta } + 2 \bar{k} R_1 \frac{\partial \theta _0}{\partial \eta } -2a^2 R_2 + \bar{k} \frac{\partial \theta _0}{\partial \eta } (3\alpha _0 - \beta _0 ) + 3 \alpha _1 - \beta _1\right] \nonumber \\&\quad +\, k^3 H_0^2 \frac{\partial ^3 \alpha _0}{\partial \xi ^3 } \left( \frac{1}{2}aR_1 + \beta _0 \right) + k^2 \bar{k}^2H_0^2 \frac{\partial ^2 \alpha _0}{\partial \xi ^2} \frac{\partial ^2 \theta _0}{\partial \eta ^2} + \bar{k}^3 H_0^2\nonumber \\&\quad \times \left( \frac{1}{2} bR_1 + \beta _0 + 2\alpha _0 + k \frac{\partial \varphi _0}{\partial \xi } \right) \nonumber \\&\quad - \,\frac{H_0^4}{30} \left( k^5 \frac{\partial ^5 \alpha _0}{\partial \xi ^5} + \frac{3}{2}\bar{k}^5 \frac{\partial ^5 \beta }{\partial \eta ^5} \right) + \Gamma H_0^4 \left( k^5 \frac{\partial ^5 \alpha _0}{\partial \xi ^5} + \bar{k}^5 \frac{\partial ^5 \beta _0}{\partial \eta ^5} \right) \nonumber \\&\quad +\, \sigma H_0^2 \left\{ \left( k \frac{\partial }{\partial \xi } + \bar{k} \frac{\partial }{\partial \eta } \right) \left[ \left( k^2\frac{\partial ^2 }{\partial \xi ^2} + \bar{k}^2 \frac{\partial ^2}{\partial \eta ^2}\right) (\alpha _1+\beta _1) \right. \right. \nonumber \\&\quad \left. \left. +\, 2\bar{k} k \left( k \frac{\partial \theta _0}{\partial \eta }\frac{\partial ^2 \alpha _0}{\partial \xi ^2} +\bar{k} \frac{\partial \varphi _0}{\partial \xi } \frac{\partial ^2 \beta _0}{\partial \eta ^2} \right) \right] + \bar{k} k \left( k^3 \frac{\partial \theta _0}{\partial \eta } \frac{\partial ^3 \alpha _0}{\partial \xi ^3} + \bar{k}^3 \frac{\partial \varphi _0}{\partial \xi } \frac{\partial ^3 \beta _0}{\partial \eta ^3} \right) \right\} \nonumber \\&\quad +\, \Lambda H_0^2 \left\{ \left( k \frac{\partial }{\partial \xi } + \bar{k} \frac{\partial }{\partial \eta }\right) \left[ \left( k^2 \frac{\partial ^2 }{\partial \xi ^2 } + \bar{k}^2 \frac{\partial ^2}{\partial \eta ^2} \right. \right. +\, 2\bar{k} k \frac{\partial ^2}{\partial \xi \partial \eta }\right) (\alpha _1+\beta _1) \nonumber \\&\quad \left. \left. +\, 2\bar{k} k \left( k \frac{\partial \theta _0}{\partial \eta }\frac{\partial ^2 \alpha _0}{\partial \xi ^2} +\bar{k} \frac{\partial \varphi _0}{\partial \xi } \frac{\partial ^2 \beta _0}{\partial \eta ^2} \right) \right] - \bar{k} k \left( k^3 \frac{\partial \theta _0}{\partial \eta } \frac{\partial ^3 \alpha _0}{\partial \xi ^3} + \bar{k}^3 \frac{\partial \varphi _0}{\partial \xi } \frac{\partial ^3 \beta _0}{\partial \eta ^3} \right) \right\} =0. \end{aligned}$$

(A1)

Appendix B: Expressions of the Coefficients

$$\begin{aligned} c_0&= \frac{3}{4\gamma } \left( \frac{2}{3}+\sigma +\Lambda \right) . \end{aligned}$$

(B1)

$$\begin{aligned} c_1&= \frac{3}{10}-\frac{9\Gamma }{\gamma ^2}+\frac{1}{4\gamma }[4c_0 (3\sigma +3\Lambda -1)-3-2\sigma ], \end{aligned}$$

(B2)

$$\begin{aligned} c_2&= \frac{1}{8\gamma ^2}\left[ 540\Gamma -\gamma \lbrace 17+6\sigma +12\Lambda +4c_0 (45\sigma -15+45\Lambda +2\gamma ) \rbrace \right] , \end{aligned}$$

(B3)

$$\begin{aligned} c_3&= \frac{1}{8\gamma } \left[ -540\Gamma +\gamma \lbrace 25+\gamma +15\gamma (\sigma +\Lambda )+12c_0 (15\sigma -5+15\Lambda +\gamma ) \rbrace \right] , \end{aligned}$$

(B4)

$$\begin{aligned} c_4&=\frac{ 1 }{4}\left( \frac{1}{12}+\frac{11}{2\gamma }+c_0-\frac{c_3}{6}-\frac{5c_3}{4\gamma } \right) , \end{aligned}$$

(B5)

$$\begin{aligned} c_5&=\frac{2}{3}c_2+c_3, \end{aligned}$$

(B6)

$$\begin{aligned} c_6&=\frac{27 }{32 \gamma ^2}, \end{aligned}$$

(B7)

$$\begin{aligned} c_7&= \frac{1}{4} \left( -1+\frac{27}{32\gamma }(\sigma +\Lambda )-\frac{21}{4\gamma } -\frac{9}{2}c_0 -\frac{c_3}{2} \right) , \end{aligned}$$

(B8)

$$\begin{aligned} c_8&= \frac{1}{4} \left( \frac{11}{8}-\frac{9\left( 1-\Lambda +\sigma \right) }{4\gamma }+\frac{3}{2}c_0\right) , \end{aligned}$$

(B9)

$$\begin{aligned} c_9&= \frac{1}{4}\left( \frac{3}{4}+3c_0-\frac{29}{4\gamma }+\frac{9}{4\gamma } (-\Lambda -\sigma )\right) , \end{aligned}$$

(B10)

$$\begin{aligned} c_{10}&= \frac{1}{4}\left( \frac{3}{8\gamma }c_2 +1-c_0+\frac{3}{2\gamma }(1+c_3)+\frac{3}{2\gamma }(\sigma -\Lambda )\right) , \end{aligned}$$

(B11)

$$\begin{aligned} c_{11}&= \frac{1}{4}\left( - \frac{1}{8}+\frac{11}{8\gamma }-\frac{7c_0}{4} +\frac{2c_2}{\gamma }+\frac{8c_3}{\gamma } + \frac{c_4}{2}\right) , \end{aligned}$$

(B12)

$$\begin{aligned} c_{12}&=\frac{1}{32}, \end{aligned}$$

(B13)

$$\begin{aligned} c_{13}&= \frac{1}{4} \left( -\frac{3}{4\gamma }+c_0-\frac{4c_2}{3\gamma }-\frac{2c_3}{\gamma }\right) , \end{aligned}$$

(B14)

$$\begin{aligned} c_{14}&=\frac{9}{80\gamma ^2}. \end{aligned}$$

(B15)