Genetic algorithms with greedy strategy for green batch scheduling on non-identical parallel machines

Abstract

Large scale batch scheduling problems with complex constraints are difficult and time-consuming to solve. Therefore, this paper addresses the green batch scheduling problem on non-identical parallel machines with time-of-use electricity prices. The objective of the problem is to minimise total electricity costs (TEC) in production. Two kinds of algorithms—single-population genetic algorithms (SPGA) and multi-population genetic algorithm (MPGA)—are proposed to solve the problem. In the algorithms, the products are allocated into batches and are then allocated to machines randomly. A greedy strategy is designed to arrange the production sequence and the starting time of the batches. Furthermore, a self-adaptive parameter adjustment strategy is proposed to enhance the adaptability of the algorithm. Computational experiments with CPLEX solver have been conducted to evaluate the performance of the algorithms. On small instances, both SPGA and MPGA can achieve approximate results compared with those obtained by CPLEX, and can also achieve smaller TEC on large instances with less computing time. In addition, the proposed MPGA implemented by parallel computing outperforms SPGA in getting better results with nearly the same computing time.

1 Introduction

The rapid development of many industrial sectors has led to the continuous growth of energy consumption. Although electrical power energy is the main kind of energy in industry, it cannot be stored efficiently: when it has been produced, it is immediately transmitted to the customers. It is particularly important to maintain a balance between the supply and demand for electricity because they constantly change. In this context, scheduling with the integration of industrial production and power system operation has been studied for many years [1, 2], and it has been shown to be effective in reduce the energy consumption or energy cost in production, which is usually called green scheduling. Traditional energy-efficient scheduling models mainly consider the internal parameters of the production. Furthermore, much research on energy-efficient scheduling has been conducted to optimise the quantity of energy consumed in industrial production [3,4,5], However, external factors, such as the modern electricity market policy, are never considered in these models.

In recent years, demand response (DR) is considered to be a most cost-effective and reliable way in the electricity market to maintain the power balance [6, 7], of which one of the most important implementations is time-of-use (TOU) electricity pricing. Unlike traditional energy conservation, TOU electricity pricing is dedicated to motivating electricity users to optimise their energy consumption patterns by avoiding peak hours, and therefore reduce their electricity costs [8]. In recent years, the issue of production scheduling under TOU electricity prices has become an attractive area of research. For the basic single-machine scheduling problem, Mitra et al. [9] studied continuous industrial production planning over 1 week with hourly changes in electricity prices, and they proposed a mixed integer linear programming (MILP) model to formulate this problem. They also discuss models for deterministic and stochastic demand. Fang et al. [10] considered a job scheduling problem to minimise electricity costs under TOU electricity prices, and proposed an algorithm to solve the problem. They highlight that a variable job processing speed is introduced into the implemented production load allocation. Che et al. [11] proposed a continuous-time MILP model and an efficient greedy insertion heuristic algorithm. They reported that the proposed algorithm is highly efficient at solving large scale problems, and has very short computing time. Kurniawan et al. [12] studied a single machine scheduling problem to minimise the total tardiness and cost of electricity under TOU electricity prices. They formulated the problem as an MILP model and used the CPLEX solver to validate the model on small size instances. Furthermore, they proposed a genetic algorithm (GA) to obtain the set of Pareto solutions for large instances. Although single machine scheduling is very common and important in production, the development of integrated production means that single machine scheduling is not good enough to treat multiple production lines or multiple production equipment, which is characterised as scheduling on parallel machines.

Production scheduling on parallel machines under TOU prices has also been studied. Some of these studies simply consider scheduling on two machines [2, 13], while many others focus on scheduling more machines. Ding et al. [14] focused on an efficient MILP formulation of the parallel machine scheduling problem. They proposed a time-interval-based MILP formulation to solve the problem without knowing the exact starting (or stopping) time of every job in each pricing interval, and a column generation heuristic algorithm to solve the problem. Cheng et al. [15] improved the model of [14] by reducing the number of decision variables, thus obtaining greater computational performance. Che et al. [16] studied an energy-conscious unrelated parallel machine scheduling problem under TOU electricity pricing and proposed an MILP model to formulate the problem and a two-stage heuristic algorithm to solve it. Multi-objective parallel machine scheduling problem have been studied [17, 18], many of which have focused on minimising two objectives: first, the traditional performance metric makespan and a green metric; and second, the total electricity cost (TEC). For the optimisation of multi-objective parallel machine scheduling, a heuristic algorithm is usually effective and efficient. In [19, 20], multi-objective scheduling problems with energy consumption threshold were studied and heuristic algorithms, such as meta-heuristic algorithms and multi-population genetic algorithms, were proposed to solve the problem. Hadera et al. [21] investigated a multi-stage parallel machine scheduling problem with energy-cost optimisation, which was generated from practical steel production and extended with minimum-cost network flow. They proposed a bi-level heuristic algorithm that can efficiently solve large scale practical problems.

Many papers only consider a scheduling problem in which products are processed continuously or allocated to machines freely, but never consider batch production. As described in [22], batch scheduling can be defined as arranging products to inseparable production batches, and arranging and sequencing production batches on machines. Batch production is processed in batch mode if small amounts of a large number of products are required. It is particularly common in energy-intensive industries, such as steel, chemicals, food, and so on. Green batch scheduling has also received attraction from academia in recent years. Shrouf et al. [23] focused on the batch scheduling problem on a single machine under TOU electricity prices. Minimising electricity costs and traditional scheduling performance are both considered as the objectives of the optimisation model. The algorithm that they proposed to solve the model is efficient at running the production scheduling in real time. Wang et al. [24] considered minimising energy consumption in heat treatment batch scheduling, but they only considered the optimisation of internal energy utilisation, and not the electricity prices in the energy market. In [25], a bi-objective batch scheduling problem on a single machine was investigated, for which the $\varepsilon$-constraint method was adopted and two heuristic methods were developed to obtain approximate Pareto fronts. This was useful in dealing with large scale real-world problems. Cheng et al. [26] also studied the single-machine batch scheduling problem. In their paper, the load shifting was implemented by switching a machine on and off under TOU prices, while a bi-objective MILP model and a heuristic based $\varepsilon$-constraint algorithm was proposed to implement the optimal scheduling.

In addition to these papers, we would like to point out that the meaning of green scheduling can be expanded from economic aspects to ecological aspects, such as carbon footprint and carbon emission optimisation in green scheduling [27, 28]. The batch scheduling problem is NP-hard even on single machine, while multiple parallel machines make the problem even more complex. Considering the green scheduling under TOU electricity prices, which means allocating the idle time of each batch to avoid on-peak hours, the green batch scheduling becomes a planning problem with mixed continuous and discrete variables but it is hard to find the optimal solution for such as large scale problem. In our previous paper [29], we studied and proposed an MILP optimisation model of the parallel machine batch scheduling problem under TOU electricity prices. The proposed model can be solved by the CPLEX solver but it is too time consuming for larger scale instances. To achieve good solutions in a limited time, more efficient algorithms are required for large scale engineering problems. If the computing resources are sufficient, then some performance acceleration technologies (e.g., parallel computing) can also be integrated into the algorithm.

In the present paper, we propose efficient algorithms for the green parallel machine scheduling problem with the objective of minimising TEC. GA is adopted as the basis of our approach to the algorithm. Products are first assigned to batches and allocated to parallel machines. A greedy strategy is then used to adjust the starting time of the batches to minimise the TEC. Because it is easy to fall into a local optimum for single-population genetic algorithm (SPGA) , we propose another multi-population genetic algorithm (MPGA) to improve the performance.

The main contributions of this work can be summarised as follows: (1) a greedy strategy is designed to adjust the starting time of batches to minimise the total electricity cost; (2) a self-adaptive parameter adjustment strategy is proposed to enhance the adaptability of the algorithm; and (3) a multi-population algorithm is proposed to improve the performance of algorithm and the information exchange between populations is performed to maintain population diversity.

The rest of this paper is organised as follows. Section 2 recalls the problem description and model formulation. The design of the algorithms is proposed in Sect. 3. The results of the computational experiments are provided in Sect. 4. Lastly, we conclude this paper in Sect. 5.

2 Problem description

To clarify the problem, we first recall the model formulation that has been proposed in our previous paper [29]. Generally, the tasks of conventional batch scheduling are to select, group, and sequence products into batches and then allocate the batches to multiple machines to minimise one or more production objectives. In this paper, we consider green scheduling to be optimising batch scheduling to minimise the energy consumption or costs in production. The power load units are considered as the product batches. If there are TOU electricity prices, then the batches are assigned to the time periods when the electricity prices are as low as possible to minimise the total energy cost. In addition, allocating products to the machines that can process it most efficiently also reduces the energy cost. We refer to this kind of problem as green scheduling, and we refer to the other problems that only consider traditional objectives (e.g., makespan or tardiness) as non-green scheduling.

Let us consider the capacity of each production machine. If all the machines have the same capacity (e.g., processing velocity, equipment power, etc.), then we say these machines are identical; otherwise, non-identical.

Table 1 Notation

The notation used in the formulation of the model is presented in Table 1. Five assumptions are defined to detail our problem, as follows:

• There are M parallel machines to process P kinds of products; each kind of product can be processed on any machine.

• The machines are non-identical with different time durations and power demands to process a product.

• There is abundant production capacity so that all products can be processed within the specified time horizon.

• The time horizon is separated into K time periods with different electricity prices; the duration of each period is the same.

• There is maximum power demand constraint on the production, in that we cannot allocate too much production load in one time period.

The objective of the model is to minimise the TEC by optimally planning the batches, assign the batches to machines that have different production capacity, and allocate the starting time periods with high electricity prices. In this context, the problem is formulated as

$$\begin{aligned}&\min \mathrm TEC=\sum _{k\in K}\tau \lambda _k\left( \sum _{n\in M}\sum _{n\in N_m}l_{m,n,k}+l_k^{base} \right) \\&\hbox {s.t.}\nonumber \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{p\in P} X_{m,n,p}\le 1, \quad \forall m \in M, n \in N_m \nonumber \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{m\in M}\sum _{n\in N_m} B_{m,n,p}=D_p, \quad \forall p \in P \end{aligned}$$

(3)

$$\begin{aligned}&U_{m,p}^{min}X_{m,n,p}\le B_{m,n,p}\le U_{m,p}^{max}X_{m,n,p}, p \in P \end{aligned}$$

(4)

$$\begin{aligned}&t_{m,n}^s\le H\cdot \sum _{p\in P} X_{m,n,p}, n \in N_m \end{aligned}$$

(5)

$$\begin{aligned}&o_{m,n,k,p}\le H\cdot X_{m,n,p}, \quad \forall m \in M, n \in N_m, k \in K, p \in P\nonumber \\ \end{aligned}$$

(6)

$$\begin{aligned}&t_{m,n}^s+\alpha _{m,p}X_{m,n,p}+\beta _{m,p}B_{m,n,p}\le H, \nonumber \\&\quad \forall m \in M, n \in N_m, k \in K, p \in P \end{aligned}$$

(7)

$$\begin{aligned}&t_{m,n-1}^s+\alpha _{m,p}X_{m,n-1,p}+\beta _{m,p}B_{m,n-1,p}\le t_{m,n}^s, \nonumber \\&\quad \forall m \in M, n \in N_m, n > 1, p \in P \end{aligned}$$

(8)

$$\begin{aligned}&l_{m,n,k}=\sum _{p\in P}\bar{d}_{m,p}\cdot o_{m,n,k,p}/\tau , \quad \forall m \in M, n \in N_m, k \in K \nonumber \\\end{aligned}$$

(9)

$$\begin{aligned}&\sum _{m\in M}\sum _{1\le n\le N_m} l_{m,n,k}+l_k^{base}\le Q_{md}, \quad k \in K \end{aligned}$$

(10)

In the model, Eq. (1) is the objective function to minimise TEC, which consists of two parts—the cost of production load and the basic load—and it accumulates over time periods. Given TOU prices, the TEC mainly depends on the distribution of production load over the time periods, determined by $l_{m,n,k}$. There are some constraints to be satisfied: Eq. (2) means that each batch on each machine consists of no more than one kind of product. Equation (3) ensures that all products are assigned to batches. Equation (4) restricts the lower and upper bounds of the batch size. Equations (5)–(8) and (11) are constraints on the batch production time. The total production time for each batch consists of preparation time and processing time, and all the batches should be completed within the given time horizon H without overlaps between adjacent batches. The distribution of the load of machine m over the time periods depends on the product processing time, which can be expressed as in Eq. (9). Equation (10) is the constraint of the maximum power demand for industrial electricity users. The production duration of each batch in time period k can be class piecewise function Eq. (11).

$$\begin{aligned} o_{m,n,k}= \left\{ \begin{array}{l@{\quad }l} 0 &{} \text {if }t^s_{m,n}+t^d_{m,n} \le \tau (k-1) \ ,\\ t^d_{m,n} &{} \text {if }\tau (k-1)< t^s_{m,n},\tau k\le t^s_{m,n}+t^d_{m,n} \ ,\\ 0 &{} \text {if }t^s_{m,n}\ge \tau k\ ,\\ \tau &{} \text {if }t^s_{m,n}\le \tau (k-1),\tau k \le t^s_{m,n}+t^d_{m,n}\ ,\\ (t^d_{m,n}-(\tau (k-1)-t^s_{m,n})) &{} \text {if }t^s_{m,n}< \tau (k-1),\tau (k-1)< t^s_{m,n}+t^d_{m,n}<\tau k\ ,\\ (\tau k -t^s_{m,n}) &{} \text {if }\tau (k-1)<t^s_{m,n}<\tau k,\tau k<t^s_{m,n}+t^d_{m,n} \end{array} \right. \end{aligned}$$

(11)

It is known that the parallel-machine batch scheduling problem is NP hard [30], so we try to propose an efficient algorithm to solve large scale problems and compare it with a mathematical programming solver (e.g., CPLEX). It can be seen that Eq. (11) is a piecewise non-linear function. To facilitate MILP solving, the key point of the problem formulation is the linearisation of this equation. The details of the problem formulation and linearisation can be found in [29].

To describe the problem more clearly, a simple example of scheduling solution is presented as Fig. 1. As is shown in the figure, there are two machines—M1 and M2—to produce two different kinds of products. Each rectangular box in the figure represents a production batch, the length of the box represents the production time of the batch, and the two numbers in the box represent the product type and quantity demand. It can be clearly seen that the size and the starting time of batches are changed after optimisation. The production is arranged as far as possible to avoid the on-peak time period, thus to reduce the total electricity cost.

Fig. 1

An example of scheduling solution

3 Methodology

Because it is known that batch scheduling is a classical NP hard problem, it might take a long time to compute an optimal solution to large instances and even to find a feasible solution. How to quickly and reliably search for an approximately optimal solution is important in engineering. GA, which is one of the classical intelligent algorithms for solving complex problem, is adopted as the basis of our method. Because it is easy for a GA to fall into a local optimum, a multi-population algorithm is proposed to solve the problem. In this section, we will introduce the encoding scheme, the genetic operators, the population interaction, and the parameter settings of single-population algorithm and multi-population algorithm.

3.1 Algorithm flow

In this paper, two kinds of algorithms, SPGA and MPGA, are proposed to solve the problem. Figure 2 shows the flowchart of a two-population genetic algorithm. SPGA has the same processes as shown in the figure but only has one population without information between populations. From Fig. 2 it can be seen that the basic operators of each population are the same as for the standard algorithm but two additional methods are used to enhance population diversity and decrease the chance that the algorithm falls into a local optimum. The first additional method is to add some new individuals to the population when a certain number of iterations is reached; the method to generate a new individual is consistent with that in the population initialisation. The second additional method is to exchange information between populations after a certain number of iterations; that is, to let the two populations exchange excellent individuals regularly. In this way, the best individuals in one population are likely to be merged into the other population, so as to implement an elite guided search. In addition, we use a post-processing procedure to treat a violation of a constraint if one happens, and a self-adaptive parameter adjustment strategy to enhance the adaptivity of the algorithm.

Based on the flow of the algorithm and the population updating methods mentioned above, several specific operators and strategies to implement the algorithm have been designed and will be presented in the remaining parts of this section.

Fig. 2

Flowchart of the proposed MPGA

3.2 Chromosome coding and population initialisation

A solution to a batch scheduling problem indicates the allocation of each product to the machines, as well as the processing sequence. In the MPGA, each individual $X_k$ denotes a solution, which is encoded as a vector $M=[m_1,m_2,...,m_M]^T$, where M is the number of machines. The vector $m_i$ represents the batch sequence on machine i. It can be further encoded as an n dimensional vector $[b_1,b_2,...,b_n]$, where n is the number of batches on machine i, and $b_j$ represents a batch. In addition, $b_j$ is a two-dimensional vector with entries of the form [p, B], where p represents the product type and B represents the amount of the product. In this problem, all products should be allocated to batches. Each product can be produced on different machines, but each batch can only be produced on one machine.

Given four machines and four products, Table 2 shows an example of a batch solution, where [2, 53] represents a batch, 2 is the product type, 53 represents the amount of the product, and NA means an empty allocation with no products allocated to the batch.

Table 2 An example of the encoding of a batch solution

In population initialisation, for each specific kind of product, a machine is randomly selected. Then, under the premise that the machine has a batch size constraint $[U_{m,p}^{min},U_{m,p}^{max}]$, the products are randomly assigned to the selected machine. Algorithm 1 shows the detailed process of population initialisation. In addition, each machine has limitations on its production time and the number of product batches. It is necessary to guarantee the feasibility of each solution; that is, all the constraints should be fulfilled during the genetic operations. The details of the satisfaction of the constraints will be provided in Sect. 3.5.

3.3 Production time arrangement with greedy strategy

To calculate the TEC, the production starting time of the batches should be determined first by using Eqs. (1), (9) and (11). Naturally, we know that if the products are arranged as far as possible from on-peak periods, the electricity cost for processing the products will decrease but, at the same time, two problems may appear: the first is how to determine the optimal sequence and starting time of the batches on each machine, and the second is how to coordinate the allocation on parallel machines to satisfy the constraint defined in Eq. (10).

In this context, a greedy strategy is designed to determine the production starting time of the batches, as shown in Algorithm 2, to solve the first problem. The operation is carried out for the machines individually. Given machine m, the batches assigned to the machine are chosen sequentially according to their original order. For a given time period k, we try to put the selected batch n into period k if there is enough idle time, and then the current optimal starting time of batch n can be decided if the TEC for batches $1-n$ is minimised. It should be noted that the successive batches arranged after batch n could be moved if required. After the iterative greedy operation, the sequence and starting time of the batches on machine m are optimally rearranged. Finally, with the assumption that global optimality of production time arrangement on all machines is a set of local optimality on a single machine, $t^s_{m,n}$—which is the decision variable of the staring time—can be determined for the obtained allocation.

For the second problem, when the maximum energy demand constraint in Eq. (10) is violated, the post-processing as described in the next section, Sect. 3.5, will be performed to modify the batch solution encoding.

Fig. 3

Crossover operation (left: before crossing, right: after crossing)

Fig. 4

Mutation operation 1 (left: before mutation, right: after mutation)

Fig. 5

Mutation operation 2 (left: before mutation, right: after mutation)

3.4 Genetic operators

In this part, we will introduce the selection, crossover and mutation operators of the proposed MPGA.

Due to the complexity of the model, when the population is updated, some excellent individuals need to be reserved in the population to guide the direction of the evolution. The widely used roulette selection method [31] is adopted to reserve the elite individuals, and thus to prevent the population from falling into a local optimum.

Table 3 Constraint satisfaction during algorithm process

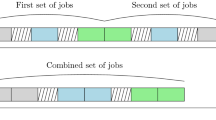
For the crossover operation, the batch allocations in the codes of the individuals are exchanged with the optimal individual according to a dynamic crossover probability. This operation must satisfy the constraint of the product demand for each individual. Figure 3 gives an example of the crossover operation, in which $b_{i,j}$ refers to batch j, which consists of product i. In the example, the batches of product 3 in two individuals are exchanged.

For the mutation operation, to increase the diversity of the populations of individuals, two mutation operators have been designed on the two populations. The first is randomly swapping batches on different machines, and the second is swapping batches on the same machine. Two simple examples of these operations are illustrated in Figs. 4 and 5.

3.5 Constraint satisfaction

In the present paper, the constraints of the model can be classified into two types: the product allocation constraints [i.e., from Eqs. (2) to (4)] and the production time constraints [i.e., Eqs. (5)–(8), and (10)]. In the process of population initialisation and iterative evolution, some constraints may be broken and, therefore, an operation of constraint satisfaction check is required to guarantee the feasibility of the solutions. Equations (9) and (11) are actually decision expressions that depend on the chromosome code: they will not be violated in a genetic operation. Table 3 lists the satisfaction or violation of the constraint in the evolution process.

According to the definitions of the genetic operators, we know that mutation operator 2, which exchanges the sequence of batches on a single machine, and population interaction, which exchanges individuals between populations, will not violate any constraints. In addition, it is easy to conclude from the definitions of the genetic operators that Eqs. (2), (3) and (8) will always be satisfied and will not be broken during the evolution.

Equation (4) will only be broken when the mutation operator 1 is performed; that is, batches are exchanged between different machines, but each machine has its own upper bound and lower bound for its batch size for any given product. When violating the constraint in Eq. (4), the batch size should be adjusted to meet the constraints. If $B_{m,n,p}>U^{max}_{m,p}$, the excess $B_{m,n,p}-U^{max}_{m,p}$ products are randomly allocated to other batches of product p, while other batches satisfy the constraint. If $B_{m,n,p}<U^{min}_{m,p}$, then $U^{min}_{m,p}-B_{m,n,p}$ products will be taken from other batches of product p while no batch violates the batch size constraint.

In the operations of initialisation, crossover, and mutation operator 1, the total production time on each machine is not taken into account, so the batches allocated to a machine may not be finished in the given time horizon. Then the constraints Eqs. (5), (6), and (7) may be broken. In these situations, the overdue batches will be randomly assigned to a machine that has sufficient production capacity to accept the batch. If no machine accepts the batch, then it also needs to resize and transfer some products to other batches so as to arrange that all batches on each machine can be completed within the given time. In addition, for a given time period t, if Eq. (10) is broken, then we randomly select one or more batches that start from period t and move them by increasing their production starting time, as well as the starting time of their successive batches.

3.6 Self-adaptive parameter adjustment

To enhance the adaptability of the algorithm, some of the parameters of the algorithm should not be static but should constantly change with the degree of convergence or the speed of the evolution of the population. In conventional GA, the most direct criterion to judge this is to see whether the optimal individual in the current iteration is better than the previous optimal individual, although this does not always guarantee the global search performance of the algorithm. To facilitate the description of the strategy for the parameter adjustment, the notation is given in Table 4. The parameter adjustment criteria are illustrated in Fig. 6, where the parameters in dashed line boxes are the value to be observed, and those in red solid line boxes are the value to be adjusted while the observation changes. The specific rules for parameter adjustment, as shown in subfigures (a)–(c), are described as follows.

Table 4 Algorithm parameters

Fig. 6

Parameter adjustment criteria

Figure 6a: In the iterative process, when the global optimal individual fitness value repeat number SN increases; that is, the population may be falling into a local optimum, at this point the strategy is to reduce the crossover probability and increase the mutation probability, and vice versa.

Figure 6b: When $|F_{best_1}-F_{best_2}|$—the difference between the two populations—becomes greater and this increases the cross probability, mutation probability, and the number of individuals to exchange during population interaction, and vice versa.

Figure 6c: When the difference between the worst individual and the optimal individual in the population becomes smaller, this means that the population may be falling into a local optimum, and so the mutation probability and the number of new individuals to add should be increased, and vice versa.

Given any parameter v, we use a simple linear rule to adjust its value within the range $[\underline{v},\overline{v}]$. Based on the changing of observed variables or expressions, while v needs to increase, $v=\min \{\overline{v},v+\Delta v\}$, and while v needs to decrease, $v=\max \{\underline{v},v-\Delta v\}$, where $\Delta v$ is the step size for parameter adjustment.

4 Experimental results and analyses

In this section, the results of the computational experiments are provide to evaluate the effectiveness and efficiency of the proposed algorithm. The proposed MPGA will also be compared with CPLEX and SPGA. The MPGA and SPGA algorithms are both implemented in C++ and the computational experiments were conducted on a PC with 3.2GHz CPU and 16.0GB RAM.

4.1 Description of the data and parameter settings

Table 5 Instance data

As shown in Table 5, the dataset used in the present paper consists of seven groups of datasets. The properties of the production machines, product types, and quantities demanded are given. For each dataset, the upper bound of the number of batches on each machine is set to 8. The processing duration and electricity demand for each product on the different machines were generated randomly within a reasonable range.

Table 6 TOU electricity prices and base loads

Table 7 Settings of self-adaptive parameters

Table 8 Scheduling results (Time/(s), TEC/($10^6*\mathrm{CNY}$), gap/($\%$), gap$'$/($\%$))

The TOU electricity price $\lambda _k$ and base load $l_k^{base}$ come from the practical settings applied in an iron and steel mill, the details of the parameters are provided in Table 6. All products should be processed within the given time horizon of 24 h.

The algorithm parameters are set in accordance with our existing knowledge and experimental experiences. The population size of the proposed MPGA is 50, and the number of iterations is 3000 for datasets 1–6, and 5000 for dataset 7. The settings of the self-adaptive parameters are given in Table 7, and they change as introduced in Sect. 3.6. The parameter settings of SPGA and MPGA are the same.

4.2 Experimental results

The objective of the model in this paper is to minimise TEC on the premise of processing all products within a given time horizon. The problems were solved by CPLEX, MPGA and SPGA, and the results are provided in Table 8. In the table, CPLEX0 represents the model with the objective of minimising the makespan and without consideration of the TOU electricity price based DR is solved by CPLEX. This model can be simply expressed as

$$\begin{aligned} \min \max \limits _{m,n,p}(ts_{m,n}+\alpha _{m,p}\cdot X_{m,n,p}+\beta _{m,p}\cdot B_{m,n,p}) \end{aligned}$$

s.t. Equations (2)–(5), (7)–(8), (10).

CPLEX1 indicates that the problem is solved by CPLEX with a computing time limit up to 3600 s, and CPLEX2 denotes using CPLEX to get an approximate solution as MPGA. The MPGA and SPGA algorithms were executed 100 times to compute the mean of the results. It can be clearly seen that the TEC obtained by CPLEX0 without DR is obviously greater than with DR, which is the meaning of the model in this paper.

With a growth of the size of the problem, the solving time needed by CPLEX increases significantly, what leads to this is the increasing number of constraints and variables, particularly the integer variables, which significantly affects the efficiency of solving an MILP. But for the GAs, we can see that the computing time is approximately linearly related to the problem size, and all the instances can be solved within a reasonable computing time.

For MPGA and SPGA, it should be noted that the property gap$'$ is different from gap in CPLEX solving. In this context, gap$'$ represents the difference between the GA based solution and the CPLEX1 solution, which is defined as

$$\begin{aligned} gap'=\frac{F_{AVG}-F_{CPLEX1}}{F_{CPLEX1}} \times 100\%, \end{aligned}$$

where $F_{AVG}$ is the mean TEC over 100 runs of MPGA or SPGA, and $F_{CPLEX1}$ is the result obtained by CPLEX1 when the computing time limit is 3600s.

Fig. 7

Visual chart of scheduling results

Fig. 8

Iterative convergence curves of algorithms a dataset 1, b dataset 4, c dataset 7

From Table 8, we can see that gap$'$ for the MPGA solution ranges from $-\,11.67$ to 5.04%, and for the SPGA solution it is from $-\,9.49$ to 7.5%, where the negative value means the MPGA outperforms CPLEX1, with a smaller TEC. At the same time, with an increase in the size of the problem, MPGA has a more significant advantage in terms of computing time needed to find an approximate solution when compared with CPLEX2. For datasets 1–6, MPGA gets a small gap$'$, which indicates that the MPGA solutions are near to the CPLEX1 solution, and the negative gap$'$ for dataset 7 means a better solution than CPLEX1. In addition, we can also see that the proposed MPGA, which is implemented by parallel programming, outperforms SPGA in getting a smaller TEC on all datasets with no more computing time. The results obtained by the different approaches are also illustrated in Fig. 7, where the bars represent the TEC for the different instances, and the solid lines denote the required computing time. From the figures, we can also conclude that the proposed MPGA can achieve a TEC that approximately same as CPLEX1 on small size instances, but a smaller TEC on large size instances.

The iterative convergence curves of both GAs are given in Fig. 8. For dataset 7, the largest problem size, the iteration is empirically set to 5000, and the others are set to 3000. The figures show that MPGA can achieve smaller fitness value, and has better exploration ability during the middle stage. Overall, SPGA gets earlier maturity that MPGA. These results indicate that our proposed multi-population algorithm is able to improve the algorithm performance. We also find that the fitness difference between early stage and late stage is not very large because the cost saving mainly depends on production time arrangement, while the production time of each batch has been optimised through the greedy strategy while initialising population.

However, our algorithms still have some disadvantages. From our results, we can conclude that, when compared with mathematical programming methods, our methods have great advantage in solving large problems but have no obvious advantage in solving small-scale problems. Another disadvantage is that our methods are essentially a GA-based random search, and the stopping criterion is based on a fixed number of iterations, so there is still a problem in how to evaluate the gap between the current solution and the real optimal solution, and when to stop the iterations. Actually, it could be expected that our algorithms could be more adaptive if some automatic stopping criteria are introduced.

4.3 Batch allocation and load distribution

This paper aims to minimise the TEC by dispatching the production load as much as possible to low-priced time periods. In this section, we try to analyze the feasibility and the energy efficiency of the results. Figures 10, 11 and 12 give the Gantt charts (see subfigure a) and load distribution charts (see subfigure b) for three representative datasets 1, 4 and 7, respectively, where dataset 1 is the smallest size instance, dataset 4 is of medium size, and dataset 7 is the largest. In the Gantt charts, each rectangle box represents a product batch, the batches made up of the same kind of product are filled with the same color. The numbers in each box represent the product type of the batch and its quantity demand; for example, for the first batch on machine 1, the numbers 1,35 mean the batch consists of 35 product 1.

From the Gantt charts it can be summarised that for each kind of product, the amount of products in different batches equals to the quantity demand, and all the batches are finished in given time horizon. In addition, we can see that any adjacent batches on each machine do not overlap in the Gantt charts, which shows that the scheduling results meet the production constraint that defined as Eq. (8). Furthermore, the other constraints, such as batch size constraint, power demand constraint, and so on, are also satisfied for the results. We can now conclude that our scheduling solutions are feasible to meet the production process.

Another problem is the energy efficiency of the results. Unlike conventional energy conservation, which usually reduces the absolute energy consumption, industrial DR under TOU pricing focuses on motivating users to change their production schedule to avoid on-peak time periods, which have significant effects on cutting electricity costs. For each dataset, from whether subfigure (a) or (b) we can see that the product batches are obviously allocated to low-price periods.

In fact, it is natural to think of that the lower saturation of production, the more able it is to avoid the high electricity price periods. To analyze the trend of cost saving versus production saturation, we define two coefficients—ProdSat1 and ProdSat2—to represent the production saturation.

$$\begin{aligned} ProdSat1=\frac{\sum _{k \in K}L_k \cdot \tau }{L_k^{max}\cdot H} \times 100\%, \end{aligned}$$

where $L_k$ is the average power load in time period k, and $L_k^{max}$ is the maximum of $L_k, k\in K$.

$$\begin{aligned} ProdSat2=\frac{minimal makespan}{H} \times 100\%, \end{aligned}$$

ProdSat1 represents the production capacity margin, and ProdSat2 means the production time margin. A cost saving ratio CSR is defined as

$$\begin{aligned} CSR=\frac{F_{CPLEX0}-F_{AVG}}{F_{CPLEX0}} \times 100\%, \end{aligned}$$

Fig. 9

The trend of cost saving versus production saturation

Fig. 10

Scheduling result for dataset 1. a Gantt chart, b load distribution chart

Fig. 11

Scheduling result for dataset 4. a Gantt chart, b load distribution chart

Fig. 12

Scheduling results for dataset 7. a Gantt chart, b load distribution chart

The cost saving ratio and production saturation of all datasets are shown in Fig. 9. It can be seen that the curve of cost saving ratio curves corresponds to ProdSat1 curve closely, basically the curves are symmetrical in vertical direction. At the same time, ProdSat2 is also related to cost saving but it does not reflect the cost saving ratio accurately; for example, the results on datasets 5 and 7 have nearly the same ProdSat2 but the cost saving ratio is very different. This should be due to their different production load although nearly the same makespan. The observed result implies a linear relationship between cost saving ratio and production capacity margin, and indicates that less production saturation, especially ProdSat1, will lead to lower energy costs. This result is also consistent with the experimental results and provides us a good guide to analyze the energy efficiency for different datasets.

In summary, from the figures and analyses we can say that our proposed algorithms guarantee that all products be processed in a given time and can effectively optimise the production starting time of product batches to avoid on-peak time periods, thus reducing the energy cost of the production.

5 Conclusion

In this paper, we studied the green batch production scheduling problem on multiple parallel machines. A single-population algorithm and a multi-population genetic algorithm are proposed to solve the problem efficiently. Our experimental results show that both the SPGA and MPGA can achieve approximate TEC compared with CPLEX on small instances, and smaller TEC on large scale instances with less computing time. In addition, the proposed MPGA implemented by parallel computing outperforms SPGA with no more computing time. However, we agree that parallel programming based MPGA needs more computing resources than SPGA, so people can choose one of them to solve the problem according to different preferences in engineering. Multi-population algorithms with different operation strategies and automatic stopping criteria could be examined in future research to improve performance and strengthen self-adaptive ability.