1 Introduction

Machine learning and big data mining have recently been more attentions by researchers from different research fields [1–3]. Support vector machine (SVM) is based on the statistical learning and structural risk minimization principle [4, 5]. However, it is known that both BP [6] neural network, SVM, and LS-SVM have some challenging issues such as slow learning speed, trivial human intervention and poor computational scalability [5, 7]. A new learning algorithm, i.e., extreme learning machine (ELM) was proposed by Huang et al. [8]. Compared with BP neural networks, SVMs, and LS-SVMs, the ELM have better generalization performance at a much faster learning speed and with least human intervention.

Although ELM has made some achievements, there is still room for improvement. Some scholars are engaged in optimizing the learning algorithm of ELM [42–44]. Han et al. [9] encoded a priori information to improve the function approximation of ELM. Kim et al. [10] introduced a variable projection method to reduce the dimension of the parameter space. Zhu et al. [11] used a differential evolutionary algorithm to select the input weights for the ELM. Some other scholars dedicated themselves to optimize the structure of ELM. Wang et al. [12] properly selected the input weights and bias of ELM in order to improve the performance of ELM. Li et al. [13] proposed a structure-adjustable online ELM learning method, which can adjust the number of hidden layer RBF nodes. Huang et al. [14, 15] proposed an incremental structure ELM, which can increase the number of hidden nodes gradually. Meanwhile, another incremental approach referred to as error minimized extreme learning machine (EM-ELM) was proposed by Feng et al. [16]. All these incremental ELM’s start from a small sized ELM hidden layer, and random hidden node (nodes) are added to the hidden layer. During the growth of networks, the output weights are updated incrementally. On the other hand, an alternative to optimize the structure of ELM is to train a network structure that is larger than necessary and then prune the unnecessarily nodes during the learning. A pruned ELM (PELM) was proposed by Rong et al. [17, 18] as a classification problem. Yoan et al. [19] proposed an optimally pruned extreme learning machine (OP-ELM) methodology. Besides, there are still other attempts to optimize the structure of ELM such as CS-ELM [20] proposed by Lan et al., which used a subset model selection method. Zong et al. [21] presented weighted extreme learning machine for imbalance learning. Fu [22] employed kernel ELM in the field research for the detection of impact location.

In many supervised machine learning algorithms, it is usually required to assume that the training and test data follow the same distribution. However, this assumption does not hold true in many real applications and challenges the traditional learning theories. To deal with such situations, transfer learning, as a new machine learning algorithm, has attracted a lot of attention because it can be a robust classifier with little or even no labeled data from the target domain by using the mass of labeled data from other existing domains (a.k.a., source domains) [23, 24]. Pan et al. [25] proposed a Q learning system for continuous spaces. This is constructed as a regression problem for an ELM. Zhang et al. [26] proposed Domain Adaptation Extreme Learning Machine (DAELM), which learns from a robust classifier in E-nose systems, without loss of the computational efficiency and learning ability of traditional ELM. Huang et al. [27] extend ELMs for both semi-supervised and unsupervised tasks based on the manifold regularization. In the past years, researchers have made substantial contribution to ELM theories and applications in varying fields. Huang et al. [28, 29] studied the general architecture of locally connected ELM and kernel ELM. Tang et al. [30] proposed the multilayer perceptron, extending an ELM-based hierarchical learning framework.

In this paper, this issues will be investigated. Therefore, an algorithm called free sparse transfer learning based on the ELM algorithm (TFSR-ELM) is proposed, which uses a small amount of target tag data and a large amount of source domain old data to build a high-quality classification model. The method takes the advantages of the traditional ELM and overcomes the issue that traditional ELM cannot freely transfer knowledge. In addition, a so-called TFSR-KELM based on the kernel extreme learning machine ELM is proposed as an extension to the TFSR-ELM method for pattern classification problems. Experimental results show the effectiveness of the proposed algorithm.

2 Brief review of the ELM and kernel ELM learning algorithms

In this section, a brief review of the ELM proposed in [31] is given. The essence of ELM is that in ELM the hidden layer need not be tuned. The output function of ELM for generalized SLFNs is

$$\begin{aligned} f_L (x)= & {} \sum _{i=1}^L {\beta _i } h_i (x_j )=\sum _{i=1}^L {\beta _i } h(w_i \cdot x_j +b_i )\nonumber \\= & {} \hbox {h}(x)\beta \quad j=1,\ldots ,N \end{aligned}$$
(1)

where \(w_i \in R^{n}\) is the weight vector connecting the input nodes and the ith hidden node,\(b_i \in R\) is the bias of the ith hidden node, \(\beta _i \in R\) is the weight connecting the ith hidden node and the output node, and \(f_L (x)\in R\) is the output of the SLFN. \(w_i \cdot x_j \) denotes the inner product of \(w_i\) and \(x_j\cdot w_i \) and \(b_i\) are the learning parameters of hidden nodes and they are randomly chosen before learning.

If the SLFN with N hidden nodes can approximate the N samples with zero error, then there exist \(\beta _i \), \(w_i \), and \(b_i\) such that

$$\begin{aligned} \sum _{i=1}^L {\beta _i } h(w_i \cdot x_j +b_i )=t_j, \quad j=1,\ldots ,N \end{aligned}$$
(2)

Equation (2) can be written compactly as

$$\begin{aligned} \mathbf{H} {\varvec{\upbeta }} =\mathbf{T}. \end{aligned}$$
(3)

where

$$\begin{aligned} \mathbf{H}= & {} \left( \! {{\begin{array}{c} {\hbox {h}(x_1 )} \\ \vdots \\ {\hbox {h}(x_N )} \\ \end{array} }} \!\right) \!=\! \left( \! {{\begin{array}{ccc} {h(w_1 ,b_1 ,x_1 )}&{} \cdots &{} {h(w_L ,b_L ,x_1 )} \\ \vdots &{} \ddots &{} \vdots \\ {h(w_1 ,b_N ,x_1 )}&{} \cdots &{} {h(w_L ,b_L ,x_N )} \\ \end{array} }} \!\right) _{N\times L} ,\\ \mathbf{T}= & {} [t_1 ,\ldots ,t_N ]^{T},\quad \text {and}\quad {\varvec{\upbeta }}=[\beta _1 ,\beta _2 ,\ldots ,\beta _L ]^{T}. \end{aligned}$$

Numerous efficient methods can be used to calculate the output weights \(\beta \) including but not limited to orthogonal projection methods, iterative methods [32] and singular value decomposition (SVD) [33].

According to the ridge regression theory [34], one can add a positive value to the diagonal of \(\mathbf{HH}^{T}\); the resultant solution is more stable and tends to have better generalization performance:

$$\begin{aligned} f(x)=\mathbf{H}{\varvec{\upbeta }}=\hbox {h}(x)H^{T}\left( \frac{\mathbf{I}}{C}+\mathbf{HH}^{T}\right) ^{-1}{} \mathbf{T}, \end{aligned}$$
(4)

The feature mapping \(\hbox {h}(x)\) is usually known to the user in ELM. However, if the feature mapping \(\hbox {h}(x)\) is unknown to users, a kernel matrix for ELM can be defined as follows [34]:

$$\begin{aligned} \Omega _{ELM} =\mathbf{HH}^{T}:\Omega _{ELM_{i,j} } =\hbox {h}(x_i )\cdot \hbox {h}(x_j )=K(x_{_i } ,x_j ).\nonumber \\ \end{aligned}$$
(5)

Thus, the output function of kernel ELM classifier can be written compactly as:

$$\begin{aligned} f(x)= & {} \hbox {h}(x)\mathbf{H}^{T}\left( \frac{\mathbf{I}}{C}+\mathbf{HH}^{T}\right) ^{-1}\nonumber \\ \mathbf{T}= & {} \left[ {{\begin{array}{c} {K(x,x_1 )} \\ \vdots \\ {K(x,x_N )} \\ \end{array} }} \right] ^{T}\left( \frac{\mathbf{I}}{C}+\Omega _{ELM} \right) ^{-1}{} \mathbf{T}. \end{aligned}$$
(6)
figure a

3 Proposed learning algorithm

In this section, the overall architecture of the proposed TFSR-ELM is introduced in detail, and a new kernel ELM free sparse representation is presented, this is utilized to determine the basic elements of TFSR-ELM.

3.1 Graph-laplacian regularization

Given a set of N-dimensional data points \(X=\left\{ {x_i } \right\} _{i=1}^N \), we can construct the nearest neighbor graph G with N vertices, where each vertex represents a data point. Let W be the weight matrix of G. If \(x_i\) is among the k-nearest neighbors of \(x_i\), or vice versa, \(W_i =1\), otherwise, \(W_i =0\). We define the degree of \(x_i\) as \(d_i =\sum _{j=1}^m {W_{ij} } ,\) and \(D=diag(d_1 ,\ldots ,d_m )\). Consider the problem of mapping the weighted graph G to sparse representations V,

$$\begin{aligned} \hat{{L}}_N =\frac{1}{2}\sum _{i,j} {(v_i -v_j )^{2}W_{i,j} } =Tr(\hat{{V}}^{T}L\hat{{V}}), \end{aligned}$$
(7)

where \(Tr(\cdot )\) denotes the trace of a matrix and \(L=D-W\) is the Laplacian matrix. By incorporating the Laplacian regularizer (7) into the original sparse representation, we can obtain the following objective function of GraphSC [36]:

$$\begin{aligned}&\mathop {\min }\limits _{B,S} \left\| {X-UV} \right\| _F^2 +Tr(VLV^{T})+\lambda \sum _{i=1}^N {\left\| {v_i } \right\| _1 } \nonumber \\&\qquad s.t.\left\| {u_k } \right\| _2^2 \le 1,k=1,\ldots ,N \end{aligned}$$
(8)

where \(\lambda \ge 0\)is the regularization parameter.

3.2 Unsupervised extreme learning machine

In unsupervised algorithm, the entire training data \(X=\left\{ {x_i } \right\} _{i=1}^N\) are not labeled (N is the number of training patterns) and the target is to find the underlying structure of the original data. When there is no labeled data, the formulation is

$$\begin{aligned} \mathop {\min }\limits _{\beta \in R^{n_l \times n_o }} \frac{1}{2}\left\| \beta \right\| ^{2}+\lambda T_r \left( \beta ^{T}H^{T}LH\beta \right) . \end{aligned}$$
(9)

Note that the above formulation always attains its minimum at \(\beta =0\). As suggested in [35], it is necessary to introduce additional constraints to avoid a degenerated solution. Specifically, the formulation of US-ELM is given by

$$\begin{aligned}&\mathop {\min }\limits _{\beta \in R^{n_l \times n_o }} \frac{1}{2}\left\| \beta \right\| ^{2}+\lambda T_r \left( \beta ^{T}H^{T}LH\beta \right) . \nonumber \\&\qquad s.t.(H\beta )^{T}H\beta =I_{n_o} \end{aligned}$$
(10)

An optimal solution to problem (10) is given by choosing \(\beta \) as the matrix whose columns are eigenvectors (normalized to satisfy the constraint) corresponding to the first \(n_o\) smallest eigenvalues of the generalized eigenvalue problem:

$$\begin{aligned} (I_{n_l } +\lambda H^{T}LH)\nu =\gamma H^{T}H\nu . \end{aligned}$$
(11)

In the algorithm of Laplacian eigenmaps, the first eigenvector is discarded since it is always a constant vector proportional to 1 (corresponding to the smallest eigenvalue 0) [27, 35]. In the US-ELM algorithm, the first eigenvector of (11) also leads to small variations in the embedding and is not useful for data representation. Therefore, it is suggested to abandon this trivial solution as well.

Let \(\gamma _1 ,\gamma _2 ,\ldots ,\gamma _{n_o +1} (\gamma _1 \le \gamma _2 \le \cdots \le \gamma _{n_o +1} )\) be the \((n_o +1)\) smallest eigenvalues of (11) and \(\nu _1 ,\nu _2 ,\ldots ,\nu _{n_o +1}\) be their corresponding eigenvectors. Then, the solution to the output weights \(\beta \) is given by

$$\begin{aligned} \beta ^{*}=\left[ {\nu _2 ^{\prime },\nu _3 ^{\prime },\ldots ,\nu _{n_o +1} ^{\prime }} \right] , \end{aligned}$$
(12)

where \(\nu _i ^{\prime }={\nu _i }/{\left\| {\mathbf{H}\nu _i } \right\| },i=2,\ldots ,n_o +1\) are the normalized eigenvectors. If the number of labeled data is less than the number of hidden neurons, problem (12) is underdetermined. In this case, we have the following alternative formulation by using the same trick as in previous sections:

$$\begin{aligned} (I_u +\lambda LHH^{T})u=\gamma \textit{HH}^{T}u. \end{aligned}$$
(13)

Again, let \(u_1 ,u_2 ,\ldots ,u_{n_o +1}\) be generalized eigenvectors corresponding to the \((n_o +1)\) smallest eigenvalues (13), then the final solution is given by

$$\begin{aligned} \beta ^{*}=H^{T}\left[ {\tilde{u}_2 ,\tilde{u}_3 ,\ldots ,\tilde{u}_{n_o +1} } \right] , \end{aligned}$$
(14)

where \(\tilde{u}_i ={u_i }\big /\left\| {\mathbf{HH}^{T}u_i } \right\| ,i=2,\ldots ,n_o +1\) are the normalized eigenvectors.

Our task is classified, the US-ELM in Algorithm 2:

figure b

3.3 Framework of TFSR-ELM

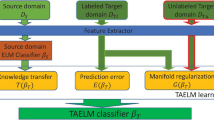
To build an effective association between \(Y_s\) and \(Y_t\), we propose to embed all labels into a latent Euclidean space using a graph-based representation. As a result, the relationship between labels can be represented by the distance between the corresponding prototypes of the labels in the latent space. Furthermore, we show that predictions made by each source classifier can also be mapped into the latent space, which makes the knowledge transfer from source classifiers possible. Finally, a regularization framework is applied to learning an effective classifier for the data classification task. In this manner, the transfer learning framework depends on optimizing the free sparse representation simultaneously by the problem designer, and for this reason it is called “transfer free sparse representation learning” (TFSR-ELM in short). The free sparse representation algorithm is adopted to perform classification in the embedded space. The framework of the proposed TFSR-ELM method is shown in Fig. 1.

The traditional TL-ELM builds a learning model using the training and test data with different distributions that deal with transfer knowledge. The representations learned by TFSR-ELM can be used for building a robust and accurate data classifier. For every class, a US-ELM classifier is introduced, the objective function of which is integrated into (9). US-ELM hyperplane normal vectors for every class are coupled as columns of matrix \(W\in R^{D\times m}\). In addition, all the margins are grouped for the training objects with respect to all the classes into matrix \(\Psi \in \mathbb {R}^{m\times N_l }\).

$$\begin{aligned}&\mathop {\min }\limits _{U,V,W} \left\| {X-UV} \right\| _F^2 +\lambda \sum _{i=1}^N {\left\| {v_i } \right\| _1 } +Tr(V\tilde{M}V^{T})\nonumber \\&\quad +\;\lambda _1 \left( \frac{1}{2}\left\| W \right\| _F^2 +c1^{T}\Psi 1\right) \nonumber \\&\qquad s.t.\quad \left\| {u_k } \right\| _2^2 \le 1,k=1,\ldots ,K, \mathbf{1}-\Psi {\preceq }Y\circ (W^{T}V),\Psi {\succeq }0,\nonumber \\ \end{aligned}$$
(15)

where \(\lambda _1\) is a tuning parameter, c is ELM coefficient, \(\mathbf{1}\) is a matrix of ones, 1 is a vector of ones, \(\circ \) denotes Hadamard product, and \({\preceq }; {\succeq }\) stand for element-wise inequalities.

Fig. 1
figure 1

The framework of proposed TFSR-ELM algorithm

Full size image

A three-step algorithm is proposed for efficiently solving the TFSR-ELM optimization problem. The Lagrangian function for (15) is as follows

$$\begin{aligned}&L(W,\Psi ,U,V,\Gamma ,\Theta ,\nu )=\left\| {X-UV} \right\| _F^2+\lambda \sum _{i=1}^N {\left\| {v_i } \right\| _1 }\nonumber \\&\quad +\;Tr(V\tilde{M}V^{T})+\;\lambda _1\left( \frac{1}{2}\left\| W \right\| _F^2\right) +\sum _{k=1}^K (\left\| {u_k } \right\| _2^2 -1)\nonumber \\&\quad +\;\mathbf{1}^{T}((\lambda _1 c1^{T}+\;\Theta )\Psi +\Gamma \circ (\mathbf{1}-\Psi -Y\circ (W^{T}V)))\mathbf{1}, \end{aligned}$$
(16)

where \(\Gamma ,\Theta \in \mathbb {R}^{m\times N_L },v\in \mathbb {R}^{K}\) are the dual variables associated with corresponding inequality constraints. According to the duality theory, the following problem can be solved:

$$\begin{aligned}&\mathop {\max }\limits _{\Gamma ,\Theta ,\nu } \mathop {\min }\limits _{W,\Psi ,U,V} L(W,\Psi ,U,V,\Gamma ,\Theta ,\nu ) \nonumber \\&\quad s.t.\Gamma {\succeq }0,\Theta {\succeq }0,\nu {\succeq }0. \end{aligned}$$
(17)

The first order optimality conditions over \(W,\Psi \) will have the following form

$$\begin{aligned} W=(\Gamma \circ Y)V^{T},0=(\Gamma \circ Y)\mathbf{1},\Gamma {\preceq }kc, \end{aligned}$$
(18)

By substituting the values of (18) and (16) into (17), we obtain the following optimization problem

$$\begin{aligned}&\mathop {\max }\limits _{\Gamma ,\nu } \mathop {\min }\limits _{U,V} L_D (U,V,\Gamma ,\nu ) \nonumber \\&\quad s.t.(\Gamma \circ Y)\mathbf{1}=0,0{\preceq }\Gamma {\preceq }kc,\nu {\succeq }0, \end{aligned}$$
(19)

where \(L_D (U,V,\Gamma ,\nu )\) has the following form

$$\begin{aligned} L_D (U,V,\Gamma ,\nu )= & {} \left\| {X-UV} \right\| _F^2 +\lambda \sum _{i=1}^N {\left\| {v_i } \right\| _1 } +1^{T}\Gamma 1\nonumber \\&+\;\sum _{k=1}^K {\nu _k } (\left\| {u_k } \right\| _2^2 -1)\nonumber \\&+\;Tr\left( V\left( \tilde{M}-\frac{1}{2}\mathrm{E}\right) V^{T}\right) , \end{aligned}$$
(20)

where \(\mathrm{E}=(\Gamma \circ Y)^{T}(\Gamma \circ Y)\). Problem (20) can be efficiently solved via the following three steps of iterative algorithms.

Free Sparse Codes Learning is done by optimizing

$$\begin{aligned}&\mathop {\min }\limits _V \left\| {X-UV} \right\| _F^2 +\lambda \sum _{i=1}^N {\left\| {\nu _i } \right\| _1 }\nonumber \\&\quad +\;Tr\left( V\left( \tilde{M}-\frac{1}{2}E\right) V^{T}\right) . \end{aligned}$$
(21)

where the dictionary U is fixed. Because equation (21) with \(\hbox {L}_{1}\)-regularization is non-differentiable when \(u_k\) contains 0s, the standard unconstrained optimization algorithms cannot be applied. In the following, an optimization algorithm based on coordinate descent is introduced to solve this problem. It is easy to see that the problem (21) is convex, thus, the global minimum can be achieved. In order to solve the problem by optimization over each \(u_k \), the problem (21) should be rewritten in a vector form.

The reconstruction error \(\left\| {X-UV} \right\| _F^2 \) can be rewritten as follows:

$$\begin{aligned} \sum _{k=1}^N {\left\| {x_k -Uv_k } \right\| ^2 } \end{aligned}$$
(22)

The Laplacian regularizer \(Tr(VLV^{T})(L=\tilde{M}-\frac{1}{2}E)\) is the Laplacian matrix can be rewritten as follows:

$$\begin{aligned} Tr(VLV^{T})= & {} Tr\left( \sum _{k,i=1}^N {L_{ki} v_k v_i^T } \right) \nonumber \\= & {} \sum _{k,i=1}^K {L_{ki} v_{_i }^T v_k } =\sum _{k,i=1}^K {L_{ki} v_{_k }^T v_i } \end{aligned}$$
(23)

Combining (22) and (23), problem (21) can be rewritten as

$$\begin{aligned} \mathop {\min }\limits _V \sum _{i=1}^N {\left\| {x_i -Uv_i } \right\| ^2 } +\lambda \sum _{i=1}^N {\left\| {\nu _i } \right\| _1 } +\sum _{k,i=1}^K {L_{ki} v_{_k }^T v_i } . \end{aligned}$$
(24)

When updating \(\nu _i \), the vectors \(\{\nu _k \}_{k\ne j}\) are fixed. Thus, the following optimization problem is obtained:

$$\begin{aligned} \mathop {\min f(v_i )}\limits _{v_i } =\left\| {x_i -Uv_i } \right\| ^2 +\lambda \sum _{k=1}^j {\left| {v_k^{(j)} } \right| } +L_{ii} v_{_i }^T v_i +v_{_i }^T h_{i},\nonumber \\ \end{aligned}$$
(25)

where \(h_i =2(\sum _{k\ne i} {L_{ik} s_k } )\) and \(s_{_k }^{(j)}\) is the kth coefficient of \(s_k \).

Following the feature-sign search algorithm proposed in [37], Eq. (25) can adopt a subgradient strategy to solve the non-differentiable problem, which uses subgradients of \(f(v_i )\) at non-differentiable points.

Dictionary learning is performed by solving the problem:

$$\begin{aligned}&\mathop {\max }\limits _v \mathop {\min }\limits _U \left( \left\| {X-UV} \right\| _F^2 +\sum _{k=1}^K {v_k (\left\| {u_k } \right\| _2^2 -1)}\right) \nonumber \\&\quad s.t.v{\succeq }0, \end{aligned}$$
(26)

by the iterative optimization method in [36], while fixing the coefficient matrix V. Let \(v=[v_1 ,\ldots ,v_K ]\),and \(v_k\) be the Lagrange multiplier. The problem becomes a least squares problem with quadratic constraints

$$\begin{aligned} \mathop {\min f(U)}\limits _U= & {} \left\| {X-UV} \right\| ^2 +\sum _{k=1}^K {v_k (\left\| {u_k } \right\| ^{2}-1)} , \end{aligned}$$
(27)
$$\begin{aligned} L(U,v)= & {} \left\| {X-UV} \right\| ^2 +Tr(U^{T}U\Lambda )-Tr(\Lambda ) \nonumber \\= & {} Tr(X^{T}X)-2Tr(U^{T}XV^{T}) \nonumber \\&+\;Tr(V^{T}U^{T}UV)+Tr(U^{T}U\Lambda )-Tr(\Lambda )\nonumber \\ \end{aligned}$$
(28)

The optimal solution \(U^{*}\) can be obtained by letting the first-order derivative of (28) to be equal to zero

$$\begin{aligned} U^{*}VV^{T}-XV^{T}+U^{*}\Lambda =0. \end{aligned}$$
(29)

Then, it resolves to

$$\begin{aligned} U^{*}=XV^{T}(VV^{T}+\Lambda )^{-1}. \end{aligned}$$
(30)

Substituting (30) into (28), the Lagrange dual function is

$$\begin{aligned} L(v)= & {} Tr(X^{T}X)-2Tr(XV^{T}(VV^{T}+\Lambda )^{-1}VX^{T}) \nonumber \\&+\;Tr((VV^{T}+\Lambda )^{-1}VX^{T}XV^{T})-Tr(\Lambda ) \end{aligned}$$
(31)

This leads to the following Lagrange dual function:

$$\begin{aligned}&\mathop {\min }\limits _\Lambda Tr(XV^{T}(VV^{T}+\Lambda )^{-1}VX^{T}+Tr(\Lambda ) \nonumber \\&\quad s.t.v{\succeq }0. \end{aligned}$$
(32)

This equation (32) can be solved by using Newton or conjugate gradient algorithm.

Learning Unsupervised ELM. Finally, the optimal classifier parameters are searched:

$$\begin{aligned}&\mathop {\min }\limits _\Gamma \left( \frac{1}{2}Tr(V\mathrm{E}V^{T}-1^{T}\Gamma 1)+\sum _{k=1}^K {v_k (\left\| {u_k } \right\| _2^2 -1)} \right) \nonumber \\&\quad s.t.(\Gamma \circ Y)1=0, \quad 0{\preceq }\Gamma {\preceq }kc, \end{aligned}$$
(33)
figure c

3.4 Framework of TFSR-KELM

Kernel extreme learning machine is based on kernel learning. Specifically, we propose a transfer free sparse representation based on a kernel ELM algorithm which starting from a basic kernel, tries to learn chains of kernel transforms that can produce good kernel matrices for the source tasks. The same sequence of transformations can be then applied to compute the kernel matrix for new related target tasks. This method is applied to the unsupervised and transfer learning.

According to kernel ELM, it can be formulated as:

$$\begin{aligned}&\mathop {\max }\limits _{\Gamma ,\nu } \mathop {\min }\limits _{U,V} L_D (U,V,\Gamma ,\nu ) \nonumber \\&\quad s.t.(\gamma _{KMS} (p,q)\circ Y)\mathbf{1}=0,0{\preceq }\gamma _{KMS} (p,q){\preceq }kc,\nu {\succeq }0, \end{aligned}$$
(34)

The primal of Eq.(34) is defined as

$$\begin{aligned}&\mathop {\min }\limits _\Gamma \left( \frac{1}{2}Tr(V\mathrm{E}V^{T}-1^{T}\Gamma 1)+\sum _{k=1}^K {v_k (\left\| {u_k } \right\| _2^2 -1)} \right) \nonumber \\&\quad s.t.(k_{\sigma /\gamma } (x_i ,x_j )\circ Y)1=0,0{\preceq }k_{\sigma /\gamma } (x_i ,x_j ){\preceq }kc, \end{aligned}$$
(35)

Standard Gaussian kernel (i.e.\(k_{\sigma /\gamma } (x,y)=\exp (-\frac{1}{2(\sigma /{\gamma )}^{2}}\left\| {x-y} \right\| ^{2})\), bandwidth \(\sigma /\gamma )\) is used as the default kernel.

As for multiclass classification problems, the traditional methods, such as one against one (OAO) or one against all (OAA) classification algorithms, decompose a multiclass classification problem into several binary classification problems in. However, these methods suffer from the problem of high computational complexity. For some multiclass classification problems, the optimal solution of TFSR-KELM can be formulated as

$$\begin{aligned}&\mathop {\min }\limits _\Gamma \left( \frac{1}{2}Tr(V\mathrm{E}V^{T}-1^{T}\Gamma 1)+\sum _{k=1}^K {v_k (\left\| {u_k } \right\| _2^2 -1)}\right) \nonumber \\&\quad s.t.(K_s \circ Y)1=0, \quad 0{\preceq }K_s {\preceq }kc, \end{aligned}$$
(36)

Proposed TFSR-KELM algorithm can be summarized as follows.

figure d

4 Experimental results

4.1 Performance evaluation of TFSR-ELM

In this section, in order to evaluate the properties of our framework, we perform the experiments on a non-text dataset obtained from the UCI machine learning repository.

4.1.1 Dataset

UCI dataset The UCI machine learning repository contains Iris, Wine, Segment, Heart, Diabetes, Flare Solar, and Splice dataset (Table 1).

Table 1 UCI data set used in the experiments
Full size table
Fig. 2
figure 2

Sample images in the ORL database

Full size image
Fig. 3
figure 3

Sample images in the YALE database

Full size image

ORL and yale face dataset The ORL face database [38] contains 10 different images for each of the 40 distinctive subjects. Subjects are photographed at different times, with varying lighting conditions, facial expressions and facial details. All images are captured against a dark homogeneous background with the subjects in an upright, frontal position with a small tolerance for side movement, as shown in Fig. 2. The Yale face database [39] contains 165 grayscale images of 15 individuals. There are 11 images per subject, one per different facial expression or configuration: center-light, with glasses, happy, left-light, without glasses, normal, right-light, sad, sleepy, surprised, and winking, as shown in Fig. 3).

MNIST dataset MNIST dataset [41] has a training set of 60,000 examples and a test set of 10,000 examples of size 28 \(\times \) 28 (Fig. 4).

USPS dataset Experiments are conducted on the benchmark USPS handwritten digits dataset. USPS is composed of 7291 training images and 2007 test images of size 16 \(\times \) 16. Each image is represented by a 256-dimensional vector (Fig. 5).

4.1.2 Classification performance assessment

For the UCI categorization data, the different attributes were used to classify the data in a dataset. The number of hidden neurons was set to 1000 for the first two data sets (Iris and Wine), and 2000 for the rest data sets. The hyper-parameter \(\lambda \) was selected from the exponential sequence \(\{10^{-5},10^{0},\ldots ,10^{5}\}\) based on the clustering performance. For US-ELM, TFSR-ELM, the same affinity matrix was used, but the dimension of the embedded space was selected independently. We ran K-means algorithm was run in the original space and the embedded spaces of US-ELM, TFSR-ELM, 200 times independently. There are 200 rounds for all algorithms to get the average accuracy.

Fig. 4
figure 4

Sample images in the MNIST dataset

Full size image

In Table 2, the TFSR-ELM method, delivered more stable results across all the datasets and is highly competitive in most of the data sets. It obtained the best classification accuracy among all methods. Hence, as discussed in the above section, TFSR-ELM algorithm possesses the traditional advantages over other methods in terms of classification accuracy.

Fig. 5
figure 5

Sample images in the USPS dataset

Full size image
Table 2 Performance comparison of the proposed TFSR-ELM
Full size table

As shown in Table 3, TFSR-ELM is obviously more superior than US-ELM in training time for almost all these datasets. Although the TFSR-ELM algorithm has lower training time, its training time is more compared with the traditional ELM algorithm.

To test the performance of US-ELM for noisy data, experiments were conducted on a series of data sets with different levels of noise. Details of the relationship between the noise level and classification accuracy are showed in Table 4. The noise experiment was performed on the Wine data set. The zero mean and different standard deviations of Gaussian noise were added to the training samples. As shown in Table 4, TFSR-ELM is obviously superior than US-ELM in terms of classification accuracy. However, with the increase of noise, the TFSR-ELM is relatively stable. Therefore, it shows very good robustness in terms of noise.

Table 3 Training time (seconds) comparison between K-means, ELM, US-ELM, TFSR-ELM
Full size table
Table 4 The relationship between noise level and classification accuracy
Full size table

4.2 Performance evaluation of TFSR-KELM

In this section, in order to assess the effectiveness of the proposed methods in multi class classification problems, a study in conducted on the performance of the proposed methods TFSR-KELM for face recognition on two benchmarking face databases, namely, Yale and ORL. The target datasets are generated by rotating the original dataset clockwise 3 times by \(10^{0}\), \(30^{0}\), and \(50^{0}\), as shown in Fig. 6. Particularly, the greater the rotation angle is, the more complex will be the resulting problem becomes. Thus three faces learning problems are built for each face dataset.

Because choosing the algorithm parameters for the kernel methods still is a hot field in research, in the algorithm, parameters are generally preset. In order to evaluate the performance of the algorithm, a set of the prior parameters is first given and then the best cross-validation mean rate among the set is used to estimate the generalized accuracy in this work. Five-fold cross validation is used on the training data for parameter selection. Then, the mean of experimental obtained for the testing data is used to evaluate the performance. The overall accuracy (i.e., the percentage of the correctly labeled samples over the total number of samples) is chosen as the reference classification accuracy measure. The performance of TFSR-ELM is compared with K-means, traditional ELM, US-ELM, and TFSR-ELM. For each evaluation, five rounds of experiments are repeated with randomly selected training data, and the average result is recorded as the final classification accuracy in Table 5.

Table 5 Means (%) of classification accuracy(ACC) of all algorithm on Yale and ORL with different rotation angles
Full size table
Fig. 6
figure 6

Face image samples of the Yale and ORL datasets. a Yale faces of object. b Yale faces of object with rotation of \(10^{0}\). c ORL faces of object. d ORL faces of object with rotation of \(10^{0}\)

Full size image

The overall accuracy of LS-SVM is lower than any other classifier for all tasks. With the increase in rotation angle, the classification performance of all classifiers degrades gradually. However, for TFSR-KELM, the performance seems to degrade more slowly than the other methods. Exceptionally, traditional ELM exhibits competitive performance to some extent compared to the other methods, particularly on more complex datasets. As shown in Table 5, the TFSR-KELM method delivers more stable results across all the datasets and is highly competitive for most of the datasets. It obtains the best classification accuracy more times than any other method. Hence, as discussed in the above section, TFSR-KELM possesses overall advantages over other methods in the sense of classification accuracy.

5 Conclusions and future research

The issue of free sparse learning based on transfer ELM was addressed. The basic idea of TFSR-ELM is to use a lot of source data to build a high-quality classification model. Starting from the solution of independent ELMs, it was evident that the addition of a new term in the cost function (which penalizes the diversity between consecutive classifiers) leads to transfer of knowledge. The results showed that the proposed method that uses TFSR-ELM can effectively improve the classification by learning free sparse knowledge and is robust to different sizes of training data.

In addition, a novel transfer free sparse representation kernel extreme learning machine (TFSR-KELM) based on the kernel extreme learning machine was proposed with respect to the TFSR-ELM. Experimental results showed the effectiveness of the proposed algorithm. In the future, a study will be conducted on verify whether this method can be extended to transfer knowledge across different domains. It would be interesting to define a norm between the transformations obtained in such a setting. This norm can be used to decide what type of knowledge could be transferred based on domain similarity.