Introduction

Wind turbine blades are made from a fiber-reinforced composite material, which ensures a light, yet strong structure. A part of the production consists in placing courses of fiber plies in the mold, mainly stitched non-crimp fabric (NCF), followed by the resin infusion process. The NCF plies come in a variety of architectures, e.g. uni- or multi-axial configurations with different areal densities, roving sizes, stitching patterns, etc. The unidirectional (UD) plies are widely used because they enable the fibers to be aligned with the principal loading directions. To improve the handling of the UD plies, a small amount of stabilizing backing material is sometimes added in the transverse direction, held in place with the stitching, thereby forming a so-called quasi-UD.

To be able to predict the outcome of the fiber layup or draping process on double-curved surfaces e.g. in terms of fiber angles and possible wrinkle defects, various simulation models have been developed. The models range in complexity from the simple kinematic models to more advanced nonlinear, dynamic finite element (FE) models. To this end, an understanding of the deformation kinematics and in particular the in-plane shear kinematics is highly important as this deformation is governing for the draping abilities of the fabric and thereby crucial for the modeling [5].

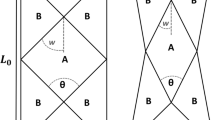
Basically, a fabric deforms kinematically in either pure or simple shear as illustrated in Fig. 1. Pure shear or trellis shear can in many cases accurately describe the behavior of woven fabrics as long as the shear angles are moderate in magnitude. Here, the interwoven rovings simply rotate at their cross-over points. On the other hand, pure UD reinforcements are commonly considered to behave in simple shear, i.e. with the rovings being able to slide relative to each other [17]. In reality, the two deformations are barely distinguishable up to a shear angle of 10∘ [22]. Hereafter, the fabric will tend to behave as either pure or simple shear or in a combination of the two. Simple shear is also sometimes referred to as inter-tow slip or intra-ply slip and is considered an unwanted effect in an otherwise pure shear-dominated deformation.

Fig. 1
figure 1

Pure and simple shear kinematics of fabrics

Full size image

For the kinematic models, both pure and simple shear formulations exist and it is thus necessary to determine what kinematic behavior describes the fabric better. The majority of the developed FE simulation models are based on woven or biaxial fabrics with two fiber families, as this type of reinforcement traditionally is used more in the composite industry but also dedicated UD models exist [4]. To accurately model the fabric behavior, the shear stress vs. shear strain characteristic must be input to the material model. Lastly, for any model it is relevant to know the maximum shear angle the fabric can attain. The above discussion calls for experimental test methods to characterize the shear behavior.

Two tests are commonly used to characterize the shear behavior of fabrics: the picture-frame test and the bias-extension test. The picture-frame test relies on clamping the fabric in a square frame hinged at the corners. During testing, the frame is deformed to a rhomboid to impose a condition of pure shear. However, as noted by Potter [21], the test is less suitable if the fabric’s shear kinematics are not known. For this reason, the present study has applied the bias-extension test. In the test a rectangular specimen with the fibers oriented at ± 45∘ is extended to produce a distinct deformation field in which a shear region exists under certain assumptions. While the test is simple to perform, the processing of the raw test data to a shear stress vs. shear angle curve for the material is more involved. A common data processing procedure is based on a pure shear assumption [5].

Multiple researchers have applied the bias-extension test for shear testing of NCF. Potter [21] tested a glass-carbon hybrid UD crossply prepreg, in which the plies were only held together by the resin. The global deformation was shown to follow the pin-jointed net (PJN) assumption well in terms of global longitudinal and transverse strains. PJN implies that the fibers are in-extensible and can rotate at the cross-over points without sliding, i.e. pure shear. Local discrepancies were, however, observed, e.g. in terms of out-of-plane buckling.

Bel et al. [1] tested a 0/90∘ carbon NCF with a tricot stitch using the bias-extension test. The optical shear measurements revealed that the shear angles were approximately 30% below the kinematic pure shear angles. The difference in absolute terms became large at approximately 20∘ of shear. The authors concluded that this discrepancy was due to inter-tow slip which mainly took place at the interface between the un-sheared and sheared regions of the test specimen.

Schirmaier et al. [24] tested the draping behavior of a carbon UD with a small amount of transverse backing glass fiber. They concluded that the pure shear assumption was invalidated with the material. The results can, however, be used as an aid to parameterize simulation models. See also the related study by Trejo et al. [26].

Pourtier et al. [22] studied a biaxial NCF with both pure and simple shear kinematic assumptions and with different specimen sizes. Measurements of inter-fiber angles were done on the specimens that enabled the distinction between pure and simple shear. The authors concluded that a large specimen would match the pure shear assumption better compared to a smaller specimen which would deform more in simple shear.

The fact that larger specimens match the pure shear kinematics better was also noted by Harrison et al. [9] in a study on woven fabrics which can also experience intra-ply slip. The phenomenon comes down to specimen integrity, i.e. that a larger specimen has more cohesion than a smaller specimen, which thus limits intra-ply slip. Another remark from that study on woven fabrics was, that large specimens tend to wrinkle out-of-plane earlier in the test. This effect can for instance be mitigated using transparent anti-wrinkle plates mounted on either side of the specimen [10].

In Harrison et al. [8] the intra-ply slip occurring during a bias-extension test of a woven fabric was studied and related to the width of the specimen at the half height. Thus, by measuring the width during the test, the slip can be quantified and thus enhance the credibility of the test kinematics up to higher angles of shear.

In summary, the applicability of the bias-extension test and the corresponding data processing to NCF, depends on the architecture of the material. Biaxial NCF with certain stitching patterns will tend to behave like woven fabrics to some extent, but the intra-ply sliding or simple shear deformation can be significant [3]. On the other hand, UD NCF’s are more unpredictable in their nature and will in general not deform in pure shear. Naturally, the right test conditions must be found, i.e. a proper specimen size and a shear angle acquisition method, but this also applies for woven fabrics. To this end, the question arises whether a quasi-UD can be tested and modeled as a biaxial or UD material or perhaps something in between.

In the present study, the bias-extension test is applied to a quasi-UD NCF material to quantify the type of shear kinematic experienced during the test and ultimately determine a shear stress vs. shear strain curve that can be used in a numerical simulation. Different specimen sizes and geometries are tested and the corresponding data processing evaluated. Furthermore, the use of anti-wrinkle plates to suppress out-of-plane wrinkling on the quasi-UD material is also tested in an effort to find the best practice for bias-extension testing of the material. The rest of the paper is organized as follows: “Experimental setup” introduces the quasi-UD material, the experimental test setup, and the data processing. “Experimental results” presents the obtained shear test results. “Comparison with FE model prediction” describes a numerical verification of the experimental approach in the form of a bias-extension test simulation. Lastly the paper is ended with the sections “Discussion” and “Conclusion”.

Experimental setup

This section includes details of the quasi-UD material and the test rig with the corresponding data acquisition and processing.

Material

The quasi-UD material is shown in Fig. 2 and consists of UD glass fibers in the 0∘-direction, stabilized with a layer of ± 80∘ glass backing fibers. Notice, that in reality the backing fibers exhibit significant in-plane waviness. The areal densities of the UD layer and the backing layer are respectively 1322 g/m2 and 60 g/m2. The fibers are held together with a tricot-chain type stitching made from polyester. The total thickness is approximately 1 mm. The fiber mat is coated with a binder material which facilitates pre-consolidation.

Fig. 2
figure 2

The quasi-UD NCF material with the backing side folded over. The edge stitching is visible on the right side. Notice the significant waviness of the backing fibers

Full size image

The bias-extension test

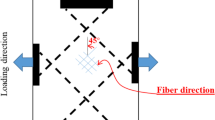
The standard bias-extension test for biaxial fabrics is based on a rectangular specimen with the fibers oriented at ± 45∘ to the edges as sketched in Fig. 3. With the quasi-UD material in this study, the UD rovings are used for orientation reference. The hypothesis is that the material can be considered as a biaxial fabric on a macroscopic level, i.e. with the backing fibers acting as an effective 90∘ family of fibers. The specimen is installed in a universal testing machine with the lower edge clamped while the upper edge is displaced upwards with δ. If the height is at least two times the width and the fabric follows the pin-jointed net assumption, i.e. pure shear, a pure shear zone will theoretically exist in the center of the symmetrically deforming specimen. This zone is denoted C in Fig. 3. Zone A in the figure does not experience shear due to all fibers in that zone being fixed by the clamping while zone B experiences shear with half the shear angle of zone C [16]. If instead the fabric deforms in simple shear, the same three zones can be observed although the specimen deformation is anti-symmetric as sketched to the right in Fig. 3. Furthermore, while zone B is half-sheared, the fiber orientations are not consistent with pure-shear kinematics [22]. From Fig. 3 it can also be observed, that at the same elongation, δ, a specimen undergoing pure shear has a smaller mid-height width and a smaller inter-fiber angle, α, compared to a specimen undergoing simple shear. The shear angle is computed based on the inter-fiber angle:

$$ \begin{array}{@{}rcl@{}} \gamma = 90^{\circ} - \alpha \end{array} $$
(1)

Which is valid for both kinematic theories. For this reason, a specimen in pure shear has a larger shear angle for the same specimen elongation, δ.

Fig. 3
figure 3

Kinematics of the bias-extension test. Left: undeformed. Middle: pure shear. Right: simple shear. CstPS and CstSS indicate the distances that remains constant during respectively pure shear and simple shear cf. Figure 1. The UD rovings run from left to right

Full size image

As discussed in the introduction to this paper, smaller specimens can suffer from loss of cohesion which can also lead to intra-ply slip or simple shear deformation. A larger specimen can of course be tested if the width of the grips is increased accordingly but another approach is to let the specimen width extend beyond the grips [20, 27]. In this study, a standard rectangular specimen of 120 mm × 270 mm is used as the baseline. To test the effect of a larger specimen, a diamond shaped specimen with the same grip-to-grip distance, H0, as the standard specimen is used, see Fig. 4. The diamond shape has the advantage of easier cutting from the roll of fabric and also less material waste. Lastly, a large diamond specimen cut with the full roll width (grip-to-grip distance: 590 mm) is tested to investigate possible size effects. Both the small and large diamond specimens have the edge stitching of the roll on one side with the opposite side having no edge stitching. In this way, the impact of the edge stitching on the specimen cohesion can be investigated. The edge stitching is not expected to have any impact on the specimen deformation apart from the cohesion, but a more detailed investigation could clarify this matter. In Fig. 4 is also indicated the different shear zones of the diamond specimens. These shear zones were determined by a kinematic analysis using a sketch tool in a CAD program.

Fig. 4
figure 4

Specimens cut from the roll of fabric with indication of grip locations: (1): Standard specimen, (2): diamond, (3): large diamond. The different shear zones in the diamond specimens are indicated with letters A, B, C

Full size image

During the initial testing, it was found that the un-tensioned corners of the diamond specimens, i.e. the non-gripped A-zones, would fold out-of-plane during testing. For this reason it was decided to apply the anti-wrinkle plates on the small diamond specimens. The anti-wrinkle plates are made from rectangular transparent acrylic with a thickness of 4.8 mm. They are mounted to the lower, stationary grip after the specimen has been installed and also held together with bolts in each of the four corners. Using spacers, the distance between the plates can be controlled. During the initial testing 3 mm and 5 mm distances were tried and it was concluded that the latter gave the best compromise between suppressing out-of-plane deformation while not affecting the measured load considerably. Thus, all results presented in this paper with anti-wrinkle plates will concern a spacing of 5 mm between the plates.

Obtaining the shear angles

The raw data from the bias-extension test can be processed to normalized shear force, Fsh, vs. shear angle, γ, for a possible comparison with other fabrics or use in a numerical simulation. The shear angles can be kinematically predicted from the specimen dimensions and the crosshead displacement assuming either pure or simple shear. Again referring to Fig. 3, the kinematic relations will be presented in terms of the roving angle, w. The kinematic relations assuming pure shear are well-known and widely used. The inter-fiber angle αPS is given as [5, 22]:

$$ \begin{array}{@{}rcl@{}} \alpha_{\mathrm{P}\mathrm{S}} &=& 2 w_{\mathrm{P}\mathrm{S}}, \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} \qquad w_{\mathrm{P}\mathrm{S}} &=& \arccos\left[\frac{\sqrt{2}}{2} \left( 1 + \frac{\delta}{H_{0}-W_{0}}\right)\right] \end{array} $$
(3)

The inter-fiber angle assuming simple shear, αSS, was derived by Pourtier et al. [22]:

$$ \begin{array}{@{}rcl@{}} &&\alpha_{\mathrm{S}\mathrm{S}} = w_{\mathrm{S}\mathrm{S}} + \arcsin\left( \frac{\sin(w_{\mathrm{S}\mathrm{S}})}{\sqrt{1+\frac{1}{\sin^{2}(w_{\mathrm{S}\mathrm{S}})} - \frac{2}{\tan(w_{\mathrm{S}\mathrm{S}})}}}\right), \end{array} $$
(4)
$$ \begin{array}{@{}rcl@{}} && w_{\mathrm{S}\mathrm{S}} = \arcsin\left( \frac{\sqrt{2} (H_{0} -W_{0})}{2 (H_{0} - W_{0} + \delta)}\right) \end{array} $$
(5)

For both kinematic inter-fiber angle expressions in Eqs. 2 and 4 the shear angle γ can be computed using Eq. 1. As previously discussed, the pure shear kinematics result in a symmetric deformation such that the inter-fiber angle α is twice the roving angle w. On the other hand, simple shear kinematics result in an anti-symmetric deformation for which the inter-fiber angle is the sum of the two terms in Eq. 4 where the first terms is larger than the second.

It is also recommended to optically measure the shear angles as a check [3]. The optical shear angles are determined by analyzing digital images acquired during the test. A widely used method for optical shear angle acquisition is digital image correlation (DIC) [3]. DIC relies on a speckle pattern painted on the surface of the specimen which can be used for cross-correlation. In this study, the Hough transform algorithm is applied which can identify straight lines, i.e. the rovings in the acquired images. For this reason, this method does not use a speckle pattern and is therefore easier to set up experimentally and further, does not affect the force measurements. The main idea is to crop the image to the gauge area (zone C), apply an edge detection algorithm (here the Canny algorithm) and identify straight lines using the Hough transform algorithm. The search space for the lines to identify is among others narrowed down using a minimum length requirement based on the distance between stitches. Details can be found in Krogh et al. [14].

After identifying the roving angles of zone C, the average is computed, i.e. wavg. The next step is to compute the average inter-fiber angle, αavg which can be done with either of the two kinematic theories, i.e. Eqs. 2 and 4. To identify which kinematic theory to apply, the mid-height width of the specimen is also measured optically. As previously noted, a difference in width can be observed between the two types of shear deformation and this width difference can thereby be used to distinguish as first applied by Harrison et al. [8]. The theoretical mid-height width of the rectangular specimen, Wmid (see Fig. 3), can be derived by considering the constant side length of the gauge area, \(L_{c} = \sqrt {2} W_{0} / 2\). Notice that for pure shear kinematics, all four edges of the gauge area remain constant, whereas for simple shear kinematics only two remain constant. The width is computed by using Lc and the roving angle w :

$$ \begin{array}{@{}rcl@{}} W_{\text{mid}} = 2 L_{c} \sin(w) = \sqrt{2} W_{0} \sin(w) \end{array} $$
(6)

Here, the pure shear roving angle wPS, Eq. 3 must be used for pure shear analysis while the simple shear roving angle wSS, Eq. 5 must be used for simple shear analysis.

Obtaining the normalized shear force

A common approach for obtaining the normalized shear force, which is widely used for woven fabrics, is based on an energy equilibrium between the power exerted by the crosshead and the shear deformation energy dissipated in zones C and B. In its original form, the expression was intended for rectangular specimens [5, 15] and here the areas of zones C and B, necessary for calculating the energy contributions, can be determined from the width and the height of the specimen. The shear force expression can be extended with area scaling factors so that it can be applied to other specimen geometries [19]. In this study, the area of zone C and B have been scaled with the factors SC and SB, respectively, where e.g. SC is the ratio between the areas of zone C from the actual specimen and a rectangular specimen. The equation for the normalized shear force, Fsh, becomes:

$$ \begin{array}{@{}rcl@{}} F_{\text{sh}}(\gamma) &= A B - A C F_{\text{sh}}\!\left( \frac{\gamma}{2}\right) \end{array} $$
(7)

The factors A, B and C are calculated as:

$$ \begin{array}{@{}rcl@{}} A &=& \frac{1}{S_{C} (2H_{0}-3W_{0})\cos(\gamma)} \\ B &=& \left( \frac{H_{0}}{W_{0}}-1\right)F \left[\cos\left( \frac{\gamma}{2}\right)-\sin\left( \frac{\gamma}{2}\right)\right]\\ C &=& S_{B} W_{0} \cos\left( \frac{\gamma}{2}\right) \end{array} $$
(8)

F is the crosshead force. The assumptions behind the expression in Eq. 7 are, apart from the kinematics described previously, that the shear angles in each zone are uniform, that the initial state has a perfect orthogonal configuration of the fibers and that the response is rate-independent [5]. In general, the applicability of the expression to UD NCF is not well documented. Simple shear deformation is expected to introduce errors but if the shear angle is measured and the specimen is also undergoing some degree of pure shear, collectively causing specimen elongation, then the error is likely to be small [11].

A point to note about Eq. 7 is that Fsh(γ) depends on the value \(F_{\text {sh}}(\frac {\gamma }{2})\), i.e. its value at the half shear angle. For this reason the expression must be evaluated iteratively, see e.g. Hivet and Duong [12] and Machado et al. [18] for details. The challenge here is that the stability of the classical iterative scheme is affected by introduction of the area scaling factors as also noted by Pierce et al. [19]. To this end, the authors proposed a modification of the initialization. This modification seems rather heuristic for the tested specimen geometry and it is not clear how to adapt it to other geometries. As an alternative to the iterative scheme, Samir and Hamid [23] fitted the expression of the normalized shear force to a 5th degree polynomial by solving five equations in five unknowns at five different values of the shear angle. This approach, however, limits the solution to what can be represented with a fifth degree polynomial and increasing the polynomial order can possibly lead to oscillatory behavior. In this work, the most robust approach was found to be based on a spline fit which is elaborated in the following.

The idea behind the spline fit approach is to determine a piecewise cubic spline function, SFsh(γ) as the solution to Eq. 7, i.e. the normalized shear force as function of the shear angle. An unconstrained optimization algorithm is used to adjust the Nk number knots of the spline such that residuals of normalized shear forces are minimized. The knot positions are evenly distributed on the γ-interval, i.e. \(\gamma _{1},...,\gamma _{N_{k}}\) and the design variables, \(a_{1},...a_{N_{k}}\), will control their corresponding normalized shear force values. Thereby, the i’th knot coordinate is given by (γi,ai). The residuals are calculated for each data point, j = 1,...,Nd as follows:

$$ \begin{array}{@{}rcl@{}} r_{j} = \left[A B - A C S_{\text{Fsh}}\!\left( \frac{\gamma_{j}}{2}\right) \right] - S_{\text{Fsh}}(\gamma_{j}) \end{array} $$
(9)

The expression enclosed in the square brackets corresponds to Eq. 7 in which the value of the normalized shear force at the half shear angle is calculated with the spline fit, i.e. \(S_{\text {Fsh}}\left (\frac {\gamma _{j}}{2}\right )\). The rightmost term is the spline fit evaluated at the j’th data point and thus Eq. 9 must be minimized for all data points:

$$ \begin{array}{@{}rcl@{}} \underset{\mathbf{a}}{\text{minimize}}~& &\frac{1}{N_{d}} \sum\limits_{j=1}^{N_{d}} |r_{j}| \\ \text{s.t.}~~&&a_{i}\geq 0 \quad \forall i=1,...,N_{k} \end{array} $$
(10)

In this way, the average of the residuals is minimized such that all the design variables are positive, i.e. corresponding to positive normalized shear forces. To make sure that the solution predicts zero normalized shear force at zero shear angle, the function value of the first knot is prescribed to 0.0. A value of Nk = 15, i.e. 15 knot positions is used.

Experimental results

The experimental results of the various specimen geometries are presented in this section. The specimens can be seen at an elongation of 15 % in Fig. 5, which will be described in detail later in this section. All tests were carried out in displacement control at a rate of 10 mm/min.

Fig. 5
figure 5

Test specimens at 15 % elongation. a Rectangular, elongated 40 mm. b Diamond without plates, elongated 40 mm. c Diamond with plates, elongated 40 mm (The red lines drawn on the specimen indicate the different shear zones while the blue line traces a roving across the specimen). d Large diamond, elongated 87 mm

Full size image

Force vs crosshead displacement

The measured force from the load cell vs. the displacement of the crosshead of the universal testing machine is presented in Fig. 6 for all the tested specimens. All curves exhibit the same initial trend with a steep increase in the force followed by a near-constant slope. The rectangular specimens continue this trend whereas the diamond specimens gradually increase their slopes. The force levels are quite different which in part can be explained by the differences in specimen areas. It was, however also observed that the backing fibers of the rectangular specimens would tend to be pulled out of the stitches at high values of elongation. This phenomenon can be seen in Fig. 7 and it is an indication that the deformation mechanism is simple shear, i.e. with the UD rovings sliding relative to each other. Only minor pulling-out of the backing fibers was observed with the diamond specimens. The edge stitching kept the backing fibers firmly in place with no apparent impact on the overall deformation. However, merely the larger specimen area was effective in mitigating pull-out as seen in Fig. 8.

Fig. 6
figure 6

Force vs. crosshead displacement for the four specimen configurations

Full size image
Fig. 7
figure 7

Backside of the fiber mat of rectangular specimen at high elongation with slipping of backing fibers visible

Full size image
Fig. 8
figure 8

Backside of fiber mat of diamond w. plates specimen at high elongation (side without edge stitching). The backing fibers remain in their place without slipping

Full size image

Because the fabric is unbalanced, S-shaping of a bias-extension specimen is expected [3]. This deformation overlayed with the anti-symmetric deformation from simple shear can be observed on the rectangular specimen in Fig. 5a.

The diamond specimens can be seen in Fig. 5b (without plates) and 5c (with plates). Obviously there is a big difference between the deformations. The specimen without plates wrinkles in the gage area (onset at approximately 20 mm of displacement) and the free corners fold out-of-plane. The specimen with plates remains almost flat. By means of the lines drawn on the specimen, the effects of in-plane bending stiffness is evident as S-shaping of the rovings. Looking at the measured forces in Fig. 6, it can be seen that the forces of the diamond specimens with plates are not significantly different from those of the diamond specimens without plates. For this reason, and because the out-of-plane deformations inhibited optical analysis after the wrinkle onset, the focus in further the data processing will be on the specimen with plates.

The large diamond specimens (Fig. 5d) exhibited out-of-plane folding / wrinkling to a large extent which even changed mode during the test. This mode change is evident in Fig. 6 as a “soft” force-drop at around 80 mm displacement. The out-of-plane displacements as well as the size of the specimens inhibited optical analysis.

Optical measurements

Videos of the rectangular and diamond w. plates specimens were analyzed optically for shear angles in the gauge area. As previously discussed, the roving angles, w can be measured and with the application of a kinematic theory i.e. Eqs. 2 or 4, the shear angles can be computed. In Fig. 9, the computed shear angles assuming pure shear are presented and plotted against the kinematic pure shear angle which is computed based on the elongation. The ideal “one-to-one” line is also shown. Both types of specimen follow the same initial trend in that they are initially below the ideal line until around 10∘ after which start to follow the line more closely. Slightly before 30∘ the rectangular specimens start to deviate from the line while the diamond specimens stay with the line up to around 45∘. A closer examination of the videos reveal, that the initial deviation is caused by tensioning of the stitches and backing fibers before shear in the gauge area is initiated. This mechanism is probably due to the relatively loose backing fibers and it can thus be observed how rovings at the interface between zone A and C slide relative to each other.

Fig. 9
figure 9

Optical shear analysis assuming pure shear kinematics for rectangular and diamond with plates. The diamond specimens without plates (not shown) showed similar behavior up until the wrinkle onset angle of ≈ 18∘

Full size image

The point where the rectangular specimens separate from the ideal line corresponds to an elongation of approximately 30 mm and by referring to Fig. 6 it can be seen that this point corresponds to the point where the force curves of the rectangular specimens start to flatten. On the other hand, the diamond specimens continue shearing until the point of failure, i.e. with stitches starting to break.

To investigate the behavior of the rectangular specimens more closely, the width at the mid height throughout the test was also extracted from the videos. It is plotted in Fig. 10 together with the theoretical widths predicted by both pure and simple shear kinematics, i.e. using Eq. 6. In the figure it can be seen how the measured widths follow the theoretical pure shear width until a displacement of a little more than 30 mm after which they deviate and continue with the same slope as the theoretical simple shear width. The width measurements thus confirm the previous observations regarding Fig. 9 for the rectangular specimens in terms of a transition from pure to simple shear.

Fig. 10
figure 10

Mid-height width of the rectangular speciemens vs. the crosshead displacement

Full size image

Using the measured mid-height width and the theoretical widths from pure and simple shear, the percentage of pure shear, %PS, can be estimated:

$$ \begin{array}{@{}rcl@{}} \%_{\mathrm{P}\mathrm{S}} = 100 \frac{W_{\text{mid,optical}} - W_{\text{mid,SS}}}{W_{\text{mid,PS}} - W_{\text{mid,SS}}} \end{array} $$
(11)

Thus, if %PS = 100 the prediction is deformation in pure shear whereas if %PS = 0, the estimation is simple shear. The computed pure-shear percentage can then used to scale the kinematic shear angles as well as the optical shear angles:

$$ \begin{array}{@{}rcl@{}} \gamma_{\text{scale}} = \gamma_{\mathrm{P}\mathrm{S}} + (100-\%_{\mathrm{P}\mathrm{S}}) (\gamma_{\mathrm{S}\mathrm{S}} - \gamma_{\mathrm{P}\mathrm{S}}) \end{array} $$
(12)

A result of the shear angle scaling is presented in Fig. 11 in a plot of shear angles vs. crosshead displacement for test specimen #5 (the behavior of the other specimens was similar). The theoretical predictions from pure and simple shear are plotted in black. Notice that the pure shear kinematic angle saturates in 90∘ at around 62 mm, whereas the simple shear kinematic angle continues as a horizontal asymptote. The scaling of the kinematic angles is plotted in green (solid line with circles) and it is seen to follow the theoretical pure shear angles until around 30 mm displacement after which it breaks off and follows the simple shear slope - analogous to what is seen in Fig. 10. The optically measured angles (processed as both pure and simple shear) are plotted as respectively downward and upward pointing triangles with their scaled values plotted as squares - all in red color. It can be seen how the optical pure shear angles are slightly above the kinematic pure shear line at around 20-30 mm of displacement. This effect is likely due to the in-plane bending stiffness (as also seen in Fig. 5c). In general, a reasonable good agreement between the scaled kinematic and optical shear angles is seen. The optical width measurement followed by scaling of kinematic angles could thus be an alternative to the optical shear angle measurement. Attention should be paid to the shear data after pure shear saturation - the validity of the scaling here is questionable. For the further data processing of the rectangular specimens, the scaled optical angles will be used.

Fig. 11
figure 11

Scaling of shear angles based on measured specimen mid-height width. Data from Rectangular, test 5

Full size image

Shear force calculation

The measured load and the shear angles can now be used to compute the normalized shear force for the rectangular, diamond with plates, and large diamond specimens. The results for the rectangular specimens are computed with the scaled optical shear angles (Fig. 11), the diamond with plates specimens are computed with the optical pure shear angles (Fig. 9) and the large diamond specimens are computed with the kinematic shear angles. The latter decision is made due to lack of optical shear angles but can be justified assuming that the large diamond specimens behave like their smaller counterparts, i.e. follow the pure shear kinematics up to around 45∘. The result can be seen in Fig. 12. All specimen curves agree well until a shear angle of 25∘, after which the shear force of the rectangular specimens flatten while the shear force of the diamond specimens rise steeply. As previously discussed, the large diamond specimens exhibited large out-of-plane buckling and thus the discrepancy between the diamond with plates and large diamond specimens was expected. Still, given the large differences in specimen area, it can be concluded that no significant size effects between the two specimen geometries exist. Statistical data of the residuals from the minimization routine in Eq. 11 are presented in Table 1. As seen, the residuals are generally low. The biggest discrepancies could be observed in the beginning and end of the shear angle ranges, where the local changes in the gradient of the normalized shear force was highest.

Fig. 12
figure 12

Normalized shear force vs. shear angle for rectangular, diamond w. plates and large diamond specimens

Full size image
Table 1 Average statistical values of residuals from shear force calculation computed across all specimens in the sample
Full size table

Comparison with FE model prediction

This section presents a numerical simulation of a bias-extension test. The simulation serves two purposes: To test the applicability of a modeling approach developed for two initially orthogonal fiber directions and to verify the computed normalized shear force vs. shear angle curves for the quasi-UD material. The idea is to use the shear data processed from a diamond specimen as input to the model and then simulate a rectangular specimen bias-extension test. Then, the reaction force from the simulation can be compared with the experimentally measured reaction forces of the rectangular specimens. For practical purposes in wind turbine blade manufacturing, the relevant shear angles are below 25∘, which is thus the target in the simulation.

Description of the simulation model

The simulation is carried out in the commercial FE code Abaqus Explicit and makes use of the built-in fabric material model [6]. The fabric material model is developed for fabrics with two fiber directions and stress-strain curves, e.g. from experimental characterization must be input. The deformation modes include fiber tension and compression as well as positive and negative shear. An elaborate description of how to obtain material data input for the material model, including incorporation of out-of-plane bending, can be found in Krogh et al. [13].

In this paper, the focus is on the shear properties and for this reason it was decided to create the model with membrane elements and thereby neglect an accurate description of the out-op-plane behavior. This choice is justified in two ways: First, only minor wrinkling was observed during testing of the rectangular specimens. Second, any out-of-plane displacement is not expected to influence the shear angles and the global reaction force significantly which are the primary interests here. The UD fiber stiffness was chosen to 5 GPa as a balance between keeping the strains in the fiber directions sufficiently low (here max. 0.19 %) while keeping the stable time increment at a reasonable level. Recall that the stable time increment in explicit time integration is inversely proportional to the stiffness of the material and thus this simplification can be made to reduce the computational time [9]. As a further simplification, the stiffness of the other fiber direction in the model, i.e. the effective backing material stiffness, was also set to 5 GPa. In reality, it is much lower and a series of experimental tests would be necessary to determine a proper characteristic. The present setup will result in a symmetrical deformation with PJN-like behavior.

For the experimental shear input to the material model, data from the diamond specimens with plates was used, i.e. seen in Fig. 12. The shear stress is obtained by dividing the normalized shear force, Eq. 7, with the fabric thickness. The data were lightly smoothed and averaged to a single curve before being input to the material models as a series of data points.

The FE model comprises a rectangular fabric with dimensions 120 mm × 270 mm, i.e. equal to the rectangular tested specimens. In the model, the fibers are initially oriented at ± 45∘ to the edges. The ideal mesh from a numerical point of view would have the element edges aligned with the initial fiber directions to avoid in-plane shear locking [28]. Another efficient remedy that can be used with an edge-aligned mesh, is reduced integration together with a stabilization scheme to avoid zero-energy modes [7]. For this reason, the membrane elements used in the model are 4-node elements with reduced integration and hourglass control (Abaqus name: M3D4R).

Numerical results

The result of the simulation is shown in Fig. 13 after displacing the right edge 25 mm with the left edge fixed. From the figure it is clear that the three distinct regions appear. The maximum computed shear angle is 22.4∘, which fits well with the kinematic pure shear angle of 21.2∘. Small wrinkles have formed in the center region C with a maximum out-of-plane displacement of approximately 1.5 mm. The contours of the five rectangular specimens (at the same displacement) have been overlaid using red lines and a good agreement is seen in spite of the slight S-shaping of the experimental test specimens.

Fig. 13
figure 13

Simulation of the bias-extension test in Abaqus at a displacement of 25 mm. The contours indicate the shear angles in degrees. The kinematic pure shear angle is 21.2∘. The contours of the five rectangular specimens have been overlaid using red lines

Full size image

The reaction force of the simulated test (solid red line) is compared with the experimental force-displacement data for the rectangular specimens (solid black line with error bars) in Fig. 14. From the graph is can be seen that the simulation matches the experiment reasonably well up to approximately 25 mm of displacement after which an increase is seen. This point can also be seen in Fig. 6 and corresponds to the elongation where the rectangular specimens start to lose cohesion and deform in simple shear while the diamond specimens keep intact. In general, though, the model seems to be too stiff. A part of this extra stiffness likely comes down to the simplifications made during the modeling, e.g. regarding the backing material stiffness and waviness. However, although the friction contribution from the plates previously was concluded to be small overall (see Fig. 6) the contribution could still be significant at low values of elongation where the forces are likewise low. The same issue was pointed out by Harrison et al. [10]. To investigate this further, the ratios between the averaged reaction forces of the experimental diamond specimens without and with plates were computed over the course of the test and used to scale the simulated reaction force in Fig. 14. The result is shown in the figure as a solid red line with squares which is closer to the experimental data.

Fig. 14
figure 14

Comparison of experimental and simulated values of force vs. displacement of rectangular bias-extension test. The error bars of the experimental data correspond to the min/max values

Full size image

Thus, the data processing is neatly verified in that one specimen geometry (diamond) was processed and used to create the input data to the FE material model which then, when used in the simulation, matches another specimen geometry (rectangular) reasonably well.

Discussion

The results of the paper have indicated that the quasi-UD material predominantly deforms in pure shear although the rectangular specimens exhibit a transition to simple shear at around 25-30∘. This transition is specimen size and shape dependent in that it appears to be related to the pulling-out of backing fibers - something which is mitigated with the extra material surrounding the gauge area in the diamond specimens. However, for practical draping purposes - especially for wind turbine blade production - the deformation kinematics can be assumed to follow pure shear theory. Only for particularly small fiber mats will the simple shear kinematics be relevant but to this end the structural impact of having backing fiber pulled out must also be considered.

Another question is if the high shear angles of 30-40∘ achieved with the bias-extension test can be achieved in a production setting where the fiber mats are mostly draped manually. Thus, the practical shear limit could be considerably lower. A test replicating more closely the draping process in the production setting can clarify this matter.

The FE model showed good agreement with the experimental data but it made use of some simplifying assumptions. If a more accurate description of the simple shear or slip is desired, some more advanced modeling approaches can be found in the literature, see for instance ten Thije et al. [25] or Bel et al. [2].

Conclusion

This paper has presented an investigation of the shear kinematics of a quasi-UD glass fiber material. The material has the majority of the reinforcement fibers in the longitudinal direction with a small amount of transverse ± 80∘ backing fibers. In spite of this unconventional architecture, it is demonstrated using the bias-extension test that the material mostly deforms in pure shear. The mechanism that enables this deformation is rotation of the UD tows and the backing fibers in the stitches with the backing fibers acting as an effective 90∘ family of fibers.

The shear kinematics is however specimen size and shape dependent: The conventional rectangular bias-extension specimen geometry exhibited a transition to simple shear at around 25-30∘ of shear. By applying a diamond geometry which has more stabilizing material surrounding the gauge area in addition to anti-wrinkle plates to suppress out-of-plane wrinkling, primarily pure shear angles up to 45∘ were achieved.

The roving angles were measured optically using a method based on the Hough transform and converted to shear angles using both pure or simple shear kinematics - a necessity when only the UD fibers can be measured. In addition, the mid-height width of the conventional rectangular specimens was also measured which helped identify the transition to simple shear and to compute the percentage of pure shear throughout the test. Using this percentage the pure and simple shear angles could be scaled accordingly.

The bias-extension test was simulated using the fabric material model in Abaqus which is based on two initially orthogonal fiber families. A good agreement with the experimental data was seen which thus verifies the bias-extension data processing. Ultimately, the conclusion is that a model based on pure shear kinematics will be able to predict the draping process up to moderate shear angles, which will find its applicability in the wind turbine blade production.