Introduction

In the last few decades, great progress on studying the metal cutting process has been achieved due to advancements in numerical technologies [1]. On the formation mechanisms of chips, two foundational modeling approaches have formed. The first approach is based on the theory of shear-localized instability. Recht”s model of catastrophic thermoplastic shear [2] provides a good explanation on the shear-localized instability in a serrated chip and the large rate of temperature rise in shear bands [3]. It also gives clear insights into the nonlinear dynamics of cutting from the Hopf bifurcation theory [4] and the dependence of the cutting forces, serration frequency and shear bandwidth on the cutting speeds [5].

The second approach is based on fracture mechanics, which ascribed the serrated chip formation to the cyclic cracking phenomenon [6]. The finite element (FE) models based on ductile fracture theory can better simulate the crack growth behavior along the shear plane during serrated chip formation [7, 8] and the shear-localized instability behavior caused by cyclic cracking [9, 10]. A number of studies also demonstrate the behaviors of the crack propagation from the chip free surface towards the tool tip [11] and the adiabatic shear-localized fracture occurring in the discontinuous chip formation [12].

Recently, a number of new numerical methods based on the meshless technology [13] are used in the simulations of metal cutting. These methods include: the method of smoothed particle hydrodynamics [14, 15], the finite pointset method [16], the natural element method [17] and the constrained natural element method [18]. In addition, other new methods like the volume of solid method [19] and the method based on the concept of generalized stresses [20] have been used.

So far, the main numerical methods used in metal cutting are the Lagrangian, Eulerian, and arbitrary Lagrangian–Eulerian (ALE) methods. The Lagrangian method can simulate both stable and unstable cutting processes [21] and reveal the evolution history of the field variables in the chip [22]. On the one hand, this method requires a pre-setting separation line and corresponding fracture [23] or damage criteria [24] to control the chip separation from the workpiece surface. Typically, the critical values of fracture/damage in the criteria are much smaller than the real values of actual cutting [25]. Thus, the separation line method not only leads to an evident deviation between the simulating results and the actual cutting process, but also restricts the application scope of the method. To characterize the separation behaviors of chip reasonably, a tool indentation method is used to describe the chip separation and breakage behaviors [26, 27].

On the other hand, since the shear-localized deformation of the serrated chip induces a severe mesh distortion, the remeshing technology is applied to eliminate the influence of mesh distortion on the simulation results. Usually, an accurate mesh and remeshing algorithm is needed due to the shear deformation localization and small cut thickness [28]. Correspondingly, remeshing criterion is related to the largest element size, while fracture criterion with the element deletion feature is applied in the simulations of high-speed cutting and the criterion with the remeshing-rezoning methodology in the simulations of conventional cutting. It is worth noting that frequent remeshing can lead to the deterioration of simulation results due to error accumulation [29]. Currently, the progress of remeshing technology makes it possible to model chip formation without pre-setting separation lines [30].

When the Eulerian method is used in the simulation of metal cutting, the plastic deformation of work material is treated as a free flow around the tool tip. The method can represent the flow fields of the plastic deformations of work material. The chip material separation is modeled as a tool indentation process. Since the work material deformation does not induce mesh distortion, remeshing is not required. Thus, this method can have a higher computational efficiency and is suitable for simulating the free flow of a chip material [19]; however, it is not convenient to simulate the unconstrained flow of chip material. Hence, in the modeling of cutting process, the shape of the continuous chip needs to be set in advance [31].

The ALE method [32] combines the advantages of the Lagrangian and Eulerian methods. It can effectively eliminate the influence of mesh distortion and simulate the unconstrained flow of the chip. The ALE mesh can move independently to optimize the mesh arrangement. The method does not require a pre-setting separation line and material failure criteria. The material cracking process governs the separation of the chip material from the workpiece surface [33]. Typically, it requires a mesh motion scheme to describe the free flow of the material around the tool edge [34], the unconstrained flow under various boundary conditions [35], and the chip formation of various shapes [36]. However, the construction of such a mesh motion scheme is a difficult task because the motion between meshes is previously unknown [37]. Therefore, this method is rarely used in the simulations of serrated chip formation during an unstable cutting process [32].

In this work, an improved FE model based on the coupled Eulerian-Lagrangian (CEL) formulation is presented for simulating metal cutting [38]. In the present simulation of metal cutting using this model, the tool and workpiece are assumed to be solid and fluid, and corresponding Lagrangian and Eulerian meshes are set on them, respectively. The plastic deformation and the convective movement of the work material are treated as a free flow and the material separation is modeled by the tool indentation process [26, 27, 39]. Thus, we can very well characterize the transition of chip morphology and the evolution of shear bands, and demonstrate the flow fields of plastic deformation of material in cutting. Recently, this method has been used to perform the simulation of low-speed cutting process since it is convenient to treat the large deformation problem of materials in metal cutting [40]. However, the study does not involve the high-speed cutting process and the shear banding instability behaviors in metal cutting. These topics are addressed in this article.

Hence, this work is intended to serve four aspects: (1) introducing the basic concepts and natures of the CEL FE model for metal cutting, (2) performing a numerical simulation of high-speed cutting process to get better understanding of metal cutting, (3) carrying out a numerical analysis for the shear-localized instability behaviors of chip flow, and (4) conducting an in-depth study on the mesh sensitivity of the CEL model in the application of metal cutting.

The model

The CEL EF model

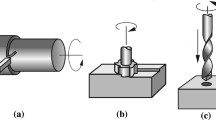
Figure 1a shows the CEL model which imagines the metal orthogonal cutting process as a fluid flow process on a solid boundary, and thus, both Lagrangian and Eulerian meshes are used in this model. The rigid tool is described by the Lagrangian formulation with material mesh. The plastic flow of the work material is described by the Eulerian formulation with spatial mesh. Moreover, a large number of Eulerian air meshes are set for the chip formation. The corresponding dynamic equations of the model can be obtained following the analysis procedure of Bayoumi and Gadala [35]. Figure 1b shows the FE mesh arrangement of the model.

Fig. 1
figure 1

(a) The CEL model for modeling the metal cutting process and (b) the finite element mesh arrangement of this model

Full size image

In the CEL cutting simulation, the work material is assumed to move and the tool is stationary as shown in Fig. 1a. The uncut work material flows into the Eulerian mesh area from the right boundary and the cut work material out of from the left boundary. The developed chips move along the tool rake face and into the air mesh. The boundary conditions of workpiece are given by the horizontal cutting speed. The flow fields of the work material are obtained from the modeling velocity fields. To describe the unconstrained flow of chip free surface, the volume of the solid approach [19] is used. This approach uses the volume fraction of a solid in an Eulerian element cell to construct the free surface shape and location of chips. The evolution of the volume fraction satisfies a transport equation that can be solved numerically. The chip shape and location are prescribed by the volume fraction values from zero to one. The time step consists of a regular Lagrangian step and an Eulerian step. In each time step, the analyses of the stress, strain, heat and mass convection, heat conduction and temperature are performed simultaneously.

The CEL model combines the superiorities of both Lagrangian and Eulerian methods. It eliminates the mesh distortion and the influence of pre-setting separation line in the Lagrangian simulation, and enables to simulate the unconstrained chip flow conveniently. Therefore, using this model, we can not only simulate the stable and unstable cutting processes of metals to study the chip formation mechanisms, but also simulate some special machining processes in applications, for example, the cutting process with the tool chatter (see video file 1) and the cutting process of thin-walled structures (see video file 2). In the two situations, it is almost impossible to perform the simulation of the cutting processes using the Lagrangian method since the pre-setting separation line method is no longer valid.

The dynamic, thermo-mechanical explicit Eulerian analysis is used in the CEL simulation of metal cutting. The 8-node coupled thermo-mechanical linear Eulerian brick element EC3D8RT with reduced integration and hourglass control is used for the discretization of the workpiece and the air meshes, and the Lagrangian element C3D8RT is used for the tool discretization. Compared with the simulation results of standard elements, the calculation error is controlled within 1% for the local quantities of the plastic strain tensor, the von Mises stress, and the hydrostatic pressure. There is almost no effect on global quantities of the cutting force and the chip temperature. The cutting simulation is carried out in the commercial ABAQUS FE code.

Material constitutive models

The Johnson-Cook (J-C) constitutive model [41] describes the effects of strain hardening, rate sensitivity, and thermal softening of work material during cutting and can be represented as:

$$ {\sigma}_p^{eq}=\left[A+B{\left({\varepsilon}_p^{eq}\right)}^n\right]\left(1+C \ln \frac{{\dot{\varepsilon}}_p^{eq}}{{\dot{\varepsilon}}_0}\right)\left[1-{\left(\frac{T-{T}_0}{T_m-{T}_0}\right)}^m\right] $$
(1)

where \( {\upsigma}_p^{eq} \)is the plastic flow stress, \( {\varepsilon}_p^{eq} \)is the equivalent strain, \( {\dot{\varepsilon}}_p^{eq} \) is the equivalent strain rate, and T is the temperature variation. T 0 and T m are the reference and melting temperatures, respectively.

In metal cutting, the hydrostatic pressure at the tool edge is extremely high (>5 GPa) [42]. This results in a large shear strain (10 m/m), a shear strain rate (105–107 1/s), and a shear yield stress (1.5 GPa) in the primary shear zone [43]. Currently, the dynamic torsion test of materials using a Hopkinson bar apparatus cannot reveal these features of metal cutting [40]. To characterize metal cutting, Calamaz et al. [15] proposed the hyperbolic tangent (TANH) material model considering the strain softening. The TANH model has the form:

$$ {\sigma}_p^{eq}=\left[A+B{\left({\varepsilon}_p^{eq}\right)}^n{e}^{-{\left({\varepsilon}_p^{eq}\right)}^a}\right]\left(1+C \ln \frac{{\dot{\varepsilon}}_p^{eq}}{{\dot{\varepsilon}}_0}\right)\left[1-{\left(\frac{T-{T}_0}{T_m-{T}_0}\right)}^m\right]\left[D+\left(1-D\right) \tanh {\left({\varepsilon}_p^{eq}+S\right)}^{-c}\right] $$
(2)

with

$$ D={\left(1-\frac{T}{T_m}\right)}^d,S={\left(\frac{T}{T_m}\right)}^b $$
(3)

where A, B, C, m, and n are the same constants as in the J-C constitutive model, whereas a, b, c, and d are the new material constants in the TANH model.

Figure 2 shows the equivalent flow stress-strain curves of the (adiabatic) J-C model and the TANH model for Ti6Al4V alloy. These material models are dependent on the strain rate and temperatures and have identical hardening behaviors. In the TANH model, the parameter S represents the variation of the strain matching to the peak stress and the exponential factor in the strain hardening term describes the strain softening effect [45]. The TANH model more clearly describes the strain-softening effect caused by the larger strain level on the flow stresses under high temperature environments. The adiabatic J-C model can describe the thermal softening effect at the larger strain level. Both models describe the effect of recrystallization on the flow stresses as the recrystallization of the Ti6Al4V alloy occurs around 1270° K [46]. However, current experimental testing technologies only provide a direct observation for the strain-softening effect in the range of the strain less than 10−1 m/m [44, 47]. This problem has been identified as a pressing research need for high-temperature mechanical properties of materials.

Fig. 2
figure 2

The equivalent flow stress-strain curves of the J-C law and the TANH law at different strain rates and temperatures

Full size image

In this study, the Ti6Al4V alloy work material is assumed to be isotropic and thermoviscoplastic. Both the TANH law and the adiabatic J-C law are used to describe the plastic flow in cutting. The material properties of Ti6Al4V alloy and the constitutive parameters are given in Table 1.

Table 1 The mechanical properties of Ti6Al4V allay [47] and the parameters of the TANH law and the J-C law
Full size table

Contact and friction

In the CEL model, the Eulerian–Lagrangian contact defines the interactions of the tool-chip at the rake face. The interaction behaves as a one-to-one contact between the Lagrangian and Eulerian nodes. The contact algorithm adopted is following that of by Benson and Okazawa [37] and implanted into the commercial ABAQUS code. The location of the tool-chip interface is fixed automatically. For metal cutting, the Coulomb law with a constant friction coefficient describes the tool-chip mechanical contact [48]. Recently, some authors expanded the application of this law. Atkins [49] assumed the friction coefficient to be related to the size and the pressure in the sticking and sliding regions of contact surface. Sima and Özel [45], Zorev [50], and Bahi et al. [51] assumed the friction coefficient to be dependent on the shear stress, cutting speed, and temperature. Wu and Lin [52] represented the friction coefficient as an exponential function of the cutting speed μ = μ 0exp(−ηV C ), in which μ 0 and V C are the Coulomb friction coefficient and the cutting speed, respectively. η is a small parameter. As indicated by the authors that the parameter η can be found in terms of the steady-state cutting condition. Under this circumstance, the friction coefficient μ describes, on average, the sliding behaviors and plastic flow mechanisms on tool rake face. Therefore, η denotes a slight difference between the conditions of the static dry friction and the dynamic contact of cutting process. Figure 3 illustrates the graphs of the friction coefficient versus the cutting speed for different η. This CEL model assumes that the friction coefficient is speed-dependent with η = 0.01.

Fig. 3
figure 3

The relation graphs between the friction coefficient and the cutting speed for different η values

Full size image

Results and discussion

Plastic strain and temperature fields

Figures 4 to 7 illustrate the calculation results of the equivalent plastic strain and the temperature of the chips based on the J-C model and the TANH model. The chip shape transitions from continuous to serrated and then return to continuous are demonstrated as the cutting speed increase. In the stable cutting process with the cutting speed 1 m/s, a continuous chip forms (Fig. 4); and in the unstable cutting process with 20 m/s, a serrated chip forms due to the shear-banding instability of work material in the primary shear zone (Fig. 5). Figure 6 illustrates the modeling result at the cutting speed 2 m/s. It shows that some shear bands have been developed in the chip, and thus denotes a critical state of chip shape transition from continuous to serrated. The calculation results in Fig. 7 show that the shear band evolution has matured and the serrated chip begins to develop when the cutting speed is 3 m/s. In these cases, the peak temperature in the chip reaches the melting point of the work material. In the super-high-speed cutting at the cutting speed 320 m/s, the serrated chip returns into a continuous chip and many immature shear bands are present inside the chip (Fig. 8). By comparing the present results (Fig. 6) and (Fig.8) with the simulation results of Molinari et al. [21], One can see that two critical speed 2 m/s and 320 m/s approach to the Molinari”s modeling results 1.5 m/s and 350 m/s. Evidently, the deviations result from the different formulations of numerical FE models. The atavistic phenomenon of chip shape is attributed to the work material convection effect [21] and the inertia effect [53] to inhibit shear band growth. Furthermore, the present modeling results on the plastic strain fields indicate that large shear strains present in the shear bands and small strain areas present inside the tooth. Under the cutting conditions we are interested in, the peak shear strains obtained with the JC model in the shear bands are much lower in values than that with the TANH model. This indicates that the strain-softening effect of chip material introduced in TANH model has evident influence on the shear banding instability of unstable chip flow in high-speed cutting.

Fig. 4
figure 4

The equivalent plastic strain fields (a, c) and the temperature fields (b, d) correspond to the J-C model (a, b) and the TANH model (c, d), respectively. The cutting speed is equal to 60 m/min (1 m/s)

Full size image
Fig. 5
figure 5

The equivalent plastic strain fields (a, c) and the temperature fields (b, d) correspond to the J-C model (a, b) and the TANH model (c, d), respectively. It shows the critical state of the transition of chip shape from continuous into serrated at the cutting speed of 120 m/min (2 m/s)

Full size image
Fig. 6
figure 6

The equivalent plastic strain fields (a, c) and the temperature fields (b, d) correspond to the J-C model (a, b) and the TANH model (c, d), respectively. The cutting speed is equal to 1200 m/min (20 m/s). In this situation, typical serrated chips develop during the unstable cutting process

Full size image
Fig. 7
figure 7

The equivalent plastic strain fields (a, c) and the temperature fields (b, d) correspond to the J-C model (a, b) and the TANH model (c, d), respectively. The cutting speed is equal to 19,200 m/min (320 m/s). It shows the critical state of chip shape transition from serrated to continuous

Full size image
Fig. 8
figure 8

The streamlines of plastic flow for the work material in the orthogonal cutting process with different cutting speeds. (a) 60 m/min (1 m/s), (b) 1200 m/min (20 m/s) and (c) 19,200 m/min (320 m/s)

Full size image

Figure 8 illustrates the streamlines of the plastic flow of a work material during the orthogonal cutting process. In low-speed cutting (Fig. 8a), the strain-hardening effect governs the plastic flow of the work material and inertia effect is neglected. The inordinate streamlines around the tool edge characterize the unsmooth separation behavior of work material under low-rate loading conditions. In high-speed cutting (Fig. 8b and c), the inertia effect becomes significant. Well-ordered streamlines develop in the work material. We can see in the serrated chip that the shear band induces the sudden change in the streamline orientation in the primary shear zone; whereas in the continuous chips, the change in the streamline orientation is gradual and smooth.

Chip morphology

To characterize the serrated chip shape, Molinari et al. [21] defined the mean shear band spacing, L S , and the segmentation index, S i , as follows:

$$ {L}_S=\frac{1}{2}\left({L}_S^{-}+{L}_S^{+}\right) $$
(4)
$$ {S}_i=\frac{1}{t_2^{+}}\left({t}_2^{+}-{t}_2^{-}\right) $$
(5)

where the meanings of \( {L}_S^{+} \), \( {L}_S^{-} \), \( {t}_2^{+} \), and \( {t}_2^{-} \) are shown in Figure 9, in which the simulating equivalent plastic strain is illustrated for a serrated chip of Ti-6Al-4 V alloy. The cutting speed is 20 m/s, and the cut depth is 100 μm. The parameter S i characterizes the irregular degree of the serrated chip shape. Figure 10 shows the change of S i with the cutting speed. The calculated results based on the CEL approach and the Lagrangian approach [21] have a consistent trend of change. The chip shape strongly depends on the cutting speed in the low-speed unstable cutting process. In the high-speed cutting process, however, the approximated constant S i denotes a weak dependence of chip shape on the cutting speed.

Fig. 9
figure 9

Illustration of mean shear band spacing L S and the segmentation index S i parameters

Full size image
Fig. 10
figure 10

The dependence of the segmentation index S i on the cutting speed

Full size image

Figure 11 shows the change of the shear band spacing with the cutting speed. There is a better consistency between the simulation results obtained in terms of the TANH model and the adiabatic J-C model. The different simulation methods (CEL and Lagrangian) do not produce evident influence on the shear band spacing. In the serrated chip formation, the shear band spacing remains nearly constant as the cutting speed changes. In the low−/high-speed cutting, the sudden increase/decrease of the shear band spacing means initiation and inhibition of the shear bands. This tendency is agreement with the experimental observation of Davies et al. [54].

Fig. 11
figure 11

The relation between the normalized shear band space and the cutting speed

Full size image

Cutting force

Figure 12a presents the calculated cutting and thrust forces using the TANH model and the adiabatic J-C model. The simulated forces have the same oscillating frequency as the results of Sima and Özel [45]. The different slopes of the curve fronts ascribe to the different orientation angles of the FE meshes (see the Weak mesh sensitivity Subsection below). The comparison of the forces with the experimental results [45] in the sense of root mean squares (Table 2) shows that the errors are approximately 8.4% for the cutting force and 21.3% for the thrust force. Figure 12b shows the SEM observations of the longitudinal midsections of a serrated chip. The grains inside the shear bands undergo strong shear flow that causes obvious elongation deformation. The grains inside the chip segmentations experience a small plastic deformation and the initial microstructure of material is retained essentially. In serrated chip formation, the shear-banding instability induces a periodic oscillation of the cutting forces. The minimum value of the cutting forces, corresponding to the peak value of the shear strain in the shear bands, characterizes the mature degree of shear band evolution [14]. The calculated results in Fig. 12a show that the TANH model can better characterize the evolution mechanisms of the shear bands than the adiabatic J-C model.

Fig. 12
figure 12

(a) The time variation regulations of the cutting forces and the thrust forces obtained using the CEL method and the Lagrangian method; (b) the observations from the scanning electron microscope of the longitudinal midsections of a serrated chip

Full size image
Table 2 The root mean squares of the cutting and thrust forces
Full size table

Figure 13 shows the specific cutting forces varying with the cutting speed. When the cutting speed is beyond the transition speed of 3 m/s, the chip flow is unstable and the cutting forces have an identical variation tendency for the TANH and adiabatic J-C material models. When the cutting speed is below 3 m/s, the chip flow is stable. The CEL modeling results predict that the cutting forces increase with increasing cutting speed, which is in agreement with the experimental observations of Atlati et al. [55], but different from the simulation results of Molinari et al. [21]. In low-speed cutting, the plastic deformation of chip material behaves the work hardening which is reflected by the amplitude increases of the cutting force.

Fig. 13
figure 13

The variations of the specific cutting forces with the cutting speed

Full size image

Shear localization deformation

Evolution of shear bands

Figure 14 presents a series of contour maps of the chip equivalent strain at different times. Here, the cutting speed is 20 m/s, the cut depth is 100 μm, and the total cutting time is 0.7 μs. Assuming that the shear band nucleates at time t = 0 (Fig. 14a). At t = 0.187 μs, the shear band grows about 60 μm along the shear plane. The appearance of a slight inflexion on the chip-free surface denotes initiation of a chip segmentation (Fig. 14b). At t = 0.28 μs, the shear band extends to the chip-free surface along a curve path and a new chip segmentation begins to form (Fig. 14c). In this period, the shear band moves upward a distance, Γ, along the tool-chip face (see the inset in Fig. 14). At t = 0.28 μs, the shear fracture occurs along the shear plane, a new surface appears at the chip-free surface (Fig. 14d). By time t = 0.7 μs, a full chip segmentation has developed, and another new shear band begins to nucleate at the tool tip (Fig. 14e). We can see that the CEL model can simulate the serrated chip formation in metal cutting in detail.

Fig. 14
figure 14

The full process of nucleation and evolution of shear bands during serrated chip formation

Full size image

The distance of the shear band moves upward Γ during cutting, as a crucial parameter, can be used to describe the shear-localized instability in the serrated chip. From the discussion above, we can see that Γ is closely related with the chip speed V F , the length of primary shear zone l 1 and is the average propagation speed of the shear band C S . Therefore, we can define an impacting factor with it as below

$$ \varGamma =\varpi \frac{V_F{l}_1}{C_S} $$
(6)

where the coefficient ϖ = 1.25 is determined from the simulation results in Fig. 14. According to the mass conservation law, l 1 V F  = t 1 V C , the dimensionless impacting factor \( \overline{\varGamma} \)is obtained as

$$ \overline{\varGamma}=\varpi \frac{V_C}{C_S} $$
(7)

where \( \overset{-}{\varGamma } \)is related to the ratio of the cutting speed to the propagation speed of the shear band. t 1 represents the cut depth. Figure 15 shows the relationship between the propagation speeds of the shear bands and the cutting speeds, which covers the modeling results of the metal cutting process and the pure shear case [21]. It shows that the loading conditions of high-speed cutting are more favorable to the extension of the shear bands due to larger propagation speeds. The transition speeds in the range of 300–350 m/s and the serrated chip changes into the continuous chip, in agreement with the predictions in previous studies [21, 53].

Fig. 15
figure 15

The relation between the propagation speeds of the shear bands and the cutting speed

Full size image

Split shear bands

The phenomenon of split shear band (Fig. 16a and b) is related to the cutting speed. When the cutting speed is 30 m/s, two split shear bands are observed (Fig. 16c), and at 100 m/s, three split shear bands occur (Fig. 16d). When the first shear band (SB1/SB3) nucleates at the tool tip and grows along a curved path, the shear band moves upward along the tool rake face simultaneously. This leads to the formation of a strong shear flow zone directly below the first shear band. Clearly, the extension of the second shear band SB2/SB4 (Fig. 16c and d) should be along the path of the minimum energy dissipation linking the tool tip and the first shear band. The factor \( \overset{-}{\varGamma } \) characterizes the size of the shear flow zone. \( \overset{-}{\varGamma }=0.06 \)At a cutting speed of 30 m/s, \( \overline{\Gamma}=0.06 \) implies that less deformation energy stored in the shear flow zone is used for the evolution of the second shear band. At 100 m/s, \( \overset{-}{\varGamma }=0.1 \) shows more deformation energy stored in the shear flow zone to be used for the evolution of the second and third shear bands.

Fig. 16
figure 16

The observation of split shear bands in chips: (a) a Ti6Al4V alloy chip; (b) a Ck 45 chip in the quick stop experiment at IEP, Magdeburg [56]. The equivalent strain fields are obtained for the orthogonal cutting of Ti6Al4V alloy with cutting speeds of 30 m/s (c) and 100 m/s (d)

Full size image

The periodic fluctuation of the cutting force represents the repeated shear-banding instability occurring in the serrated chip. Figure 17a shows the cutting force time curves in the case of two split shear bands at a cutting speed of 30 m/s. The peak value of the force labeled by inset 1 corresponds to the first shear band nucleation, and the valley value labeled by inset 2 denotes that the shear band has extended to the chip-free surface. The constant force between insets 2 and 3 denotes the second shear band as it nucleates, extends, and links with the first one. The peak value of the force labeled by inset 4 denotes a new shear band nucleate and insets 4 to 6 denote a new period of the shear band evolution. Similarly, the three split shear bands at a cutting speed of 100 m/s can be discussed in terms of Fig. 17b. We can see in the high-speed cutting that the phenomenon of split shear band obviously reduces the oscillation amplitude of the cutting forces. This is favorable to the improvement of the machined surface integrity.

Fig. 17
figure 17

The cutting force variation with time in situations where there are two split shear bands at a cutting speed of 30 m/s (a) and three split shear bands at a cutting speed of 100 m/s (b)

Full size image

Weak mesh sensitivity

Figures 18a and b show the modeling cutting forces with different mesh sizes and orientation angles, respectively. For a given shear angle φ = 45 degrees, the variations of these mesh geometrical parameters do not lead to the evident variation of the oscillation frequency of cutting force and only induce a slight change of the average values of the cutting forces. This shows that when the CEL model is used in the modeling of metal cutting, it has weak mesh sensitivity that merely influences the calculation accuracy, but does not change the nature of the simulation results.

Fig. 18
figure 18

The curves of cutting forces varying with time for different mesh sizes and a given mesh orientation angle of 30 degrees (a) and for different orientation angles and a given mesh size 3 μm (b). The cutting speed is 30 m/s

Full size image

In FE simulation of metal cutting, the mesh size and orientation angle describe the mesh sensitivity as the shear-localized deformation occurs [53]. In order to get an insight into how the mesh features produce an influence on the shear strain localization in the metal cutting, presently, assume that the meshes of the CEL model have the size L M and orientation angle θ and define the mesh number index in a dimensionless form

$$ {\overline{N}}_{SB}=\overline{N}/\left[ \sin \varphi + \cos \varphi \tan \left(\theta -\varphi \right)\right] $$
(8)

where N and φ denote the mesh number and the shear angle, respectively. \( {\overline{N}}_{SB}={W}_{SB}/{L}_{SB} \),\( \overline{N}={W}_{SB}/{L}_M \) \( \overset{-}{N}={W}_S/L \). W SB is the width of shear bands. L SB is the characteristic size of meshes, which prescripts the geometries of meshes (Fig. 19). The parameter \( {\overline{N}}_{SB} \) \( {\overset{-}{N}}_{SB} \) is the characteristic number of the meshes contained inside the shear bands. The larger \( {\overline{N}}_{SB} \) in value means that the meshes inside the shear bands are divided into more small, which will be propitious to the improvement of computational results. The relation (8) predicts that the reduction of the mesh size or the appropriate orientation angle can improve the simulation results. The optimized mesh size and orientation angle are related to the shear angle.

Fig. 19
figure 19

The definitions of the mesh characteristic size L SB and the mesh orientation angle θ

Full size image

If initial mesh size L M0 decreases to L M /m, the mesh number \( \overline{N} \) will increase m times. If two sides of meshes simultaneously reduces 1/m, the mesh numbers will increase to m 2 times. This implies that an uncontrolled decrease in the mesh size \( \overset{-}{L} \)is apparently impracticable. Here, m = L M0/L M , called the mesh length factor, represents the ratio of reduction of mesh lengths. Furthermore, introducing the mesh angle factor n = φ/θ represents the influence of the orientation angle. In eq. (8), if \( \overline{N} \)is substituted with \( m{\overline{N}}_0 \)in which \( {\overline{N}}_0={W}_{SB}/{L}_{M0} \), and only consider the case of (θ-φ) is small quantity, i.e., the case of the mesh angle approaches to the shear angle, then tan(θ-φ) in (5) can be replaced with φ (1-n)/n. Thus, eq. (8) is rewritten as

$$ {\overline{N}}_{SB}=mn{\overline{N}}_0/ \cos \varphi \left[n \tan \varphi +\left(1-n\right)\varphi \right] $$
(9)

From eq. (9), the relation curves between the parameter\( {\overline{N}}_{SB} \)and the mesh angle θ are shown in Fig. 20. The result illustrates a monotonously decreasing tendency of the parameter\( {\overline{N}}_{SB} \)with an increasing orientation angle θ, and thus a small orientation angle is favorable to improve the computational results. The results in Fig. 21 obtained from eq. (9) indicate that the length factor m is two orders of magnitude greater than the angle factor n for the large m and n values. This shows that the effect of the mesh size is much greater than that of the orientation angle. Note that, as n < 10, the effect of the angle factor n increases rapidly, while as n > 10, the effect tends to steady state. It shows that, as the mesh angle θ varies around the shear angle φ, it produces evident influence on the computational results. These features of the CEL model are different from that of the Lagrangian model of metal cutting [53].

Fig. 20
figure 20

The relation between the dimensionless mesh number index and the mesh orientation angle for different shear angles, where W SB  = 10 μm and L M  = 3 μm

Full size image
Fig. 21
figure 21

The relation between the dimensionless mesh number index and the mesh size fraction m and the orientation fraction n, where W SB  = 10 μm, L M0 = 3 μm and φ = 45 o

Full size image

Summary

This article proposes an improved FE model based on the CEL formulation for the numerical analysis of metal cutting. This model used the Eulerian mesh to describe the workpiece deformation and the air mesh to collect the generated chip. Therefore, it eliminated the mesh distortion and the influence of the separation line method in the Lagrangian approach to better characterize the metal cutting process. The TANH law and the adiabatic J–C law were used to describe the work material plastic flow of a Ti6Al4V alloy. The friction contact at the tool-chip interface was considered speed-dependent.

By CEL simulation of Ti6Al4V alloy cutting, the transitions of chip shape from continuous to serrated and then to continuous were revealed and the corresponding critical speeds determined. The streamlines of plastic flow of work material demonstrated the effect of inertia on chip separation mechanisms and characterized the shear-banding instability in the serrated chip. In the high-speed cutting process, the shape of the serrated chip and the shear band spacing were found to be weakly dependent on the cutting speed. The simulating cutting forces based on the TANH model and the adiabatic J-C model had the same oscillating frequency. However, the TANH model better characterized the evolution of the shear bands. The CEL model reasonably described the work hardening behavior of plastic deformation of work material in stable cutting process. Our study of the split shear bands in high-speed cutting process showed that the phenomenon obviously reduced the oscillation amplitude of the cutting forces and was favorable to the improvement of the machined surface integrity. In the metal cutting simulation, the CEL model exhibited a weak dependence on the mesh geometries.