Influence of out-of-plane compression stress on limit strains in sheet metals

Abstract

The prediction of the forming limits of sheet metals typically assumes plane stress conditions that are really only valid for open die stamping or processes with negligible out-of-plane stresses. In fact, many industrial sheet metal forming processes lead to significant compressive stresses at the sheet surface, and therefore the effects of the through-thickness stress on the formability of sheet metals cannot be ignored. Moreover, predictions of forming limit curves (FLC) that assume plane stress conditions may not be valid when the forming process involves non-negligible out-of-plane stresses. For this reason a new model was developed to predict FLC for general, three-dimensional stress states. Marciniak and Kuczynski (Int J Mech Sci 9:609-620, 1967) first proposed an analytical method to predict the FLC in 1967, known as the MK method, and this approach has been used for decades to accurately predict FLC for plane stress sheet forming applications. In this work, the conventional MK analysis was extended to include the through-thickness principal stress component (σ ₃), and its effect on the formability of different grades of sheet metal was investigated in terms of the ratio of the third to the first principal stress components ($\beta = {{{{\sigma_3}}} \left/ {{{\sigma_1}}} \right.}$). The FLC was predicted for plane stress conditions (β = 0) as well as cases with different compressive through-thickness stress values (β ≠ 0) in order to study the influence of β on the FLC in three-dimensional stress conditions. An analysis was also carried out to determine how the sensitivity of the FLC prediction to the through-thickness stress component changes with variations in the strain hardening coefficient, in the strain rate sensitivity, in plastic anisotropy, in grain size and in sheet thickness. It was found that the out-of-plane stress always has an effect on the position of the FLC in principal strain space. However, the analysis also showed that among the factors considered in this paper, the strain hardening coefficient has the most significant effect on the dependency of FLC to the through-thickness stress, while the strain rate sensitivity coefficient has the least influence on this sensitivity.

Introduction

The poor correlation between the common “cupping” test and the actual performance of sheet metal in industrial forming operations led researchers to look at some more fundamental parameters. A significant breakthrough came in 1963, when Keeler and Backofen [2] reported that during sheet stretching, localized necking required a critical combination of major and minor strains (along two perpendicular directions in the plane of the sheet). Subsequently, this concept was extended by Goodwin [3] to sheet drawing and the resulting curve is known as the Keeler-Goodwin curve or the forming limit curve (FLC). In other words, Keeler developed the right side of the FLC (i.e., positive minor strain), and Goodwin extended the forming limit curve to include negative minor strains.

In order to predict the FLC, Marciniak and Kuczynski [1] proposed that the inhomogeneity of the sheet material could be modeled by a geometric defect in the sheet. In their study, an imperfection in the form of a shallow groove was applied to specimens stretched in equibiaxial tension. The severity of the imperfection was quantified by the ratio of the thickness in the groove to the nominal thickness of the sheet. In general, no reductions in the forming limit would be seen when the value of the imperfection factor is between 0.99 and 1.00. In this model, the initial inhomogeneity of the material develops continuously with plastic deformation until a localized neck eventually appears.

In 1970, Azrin and Backofen [4] subjected a large number of materials to in-plane stretching. They discovered that an imperfection factor of about 0.97 or less was required to obtain agreement between the MK analysis and experimental FLC data. Accordingly, even though the MK method provided a simple predictive model, there was inconsistency between its predictions and experimental data. Similar trends were also observed by Sowerby and Duncan [5] as well as by Marciniak et al. [6]. In addition, Sowerby and Duncan [5] also reported that limit strains predicted with the MK method showed a considerable dependence on material anisotropy.

Ghosh [7] found that material strain rate sensitivity is important during post-uniform deformation. The additional hardening due to strain rate sensitivity plays a significant role in increasing the forming limits by delaying strain localization inside the neck.

The physical soundness and the simplicity of the MK analysis has no doubt been the reason this method has been the most popular theoretical approach for FLC calculation, and it has been used by many researchers, even in recent years: for instance Butuc et al. [8] in 2006, Yoshida et al. [9] in 2007 and Nurcheshmeh and Green [10] in 2010.

The prediction of the FLC of sheet metals traditionally assumes plane stress loading conditions and the effect of the normal stress is usually neglected. Therefore FLC predictions are only strictly valid for open die and free forming processes. However, many metal forming processes lead to the development of non-negligible normal stresses in the sheet when it is formed over a die radius. Through-thickness stresses become even more significant in hydroforming processes, where a pressurized fluid compresses a sheet or a tube against the surface of the die. In many hydroforming applications, the pressure of the forming fluid can generate such high contact pressures that the through-thickness stress exceeds the in-plane stresses. The existence of a significant through-thickness compressive stress creates a hydrostatic stress state that has the potential to increase the formability of the sheet and therefore requires consideration in the prediction of the FLC.

Very few sheet formability studies have taken into account the effect of the normal stress and further research is required in this area. Gotoh et al. [11] presented an analytical expression that predicts an increase in the plane-strain forming limit in strain space due to the presence of through-thickness compressive stresses. They demonstrated theoretically that an out-of-plane stress (even as small as one tenth of the yield stress) can raise the forming limit strain and thus can be effectively used to delay the onset of fracture in press forming. Smith et al. [12] developed a new sheet metal formability model that takes into account the through-thickness normal stress for materials that exhibit planar isotropy. These authors’ model predicts a greater increase in formability due to compressive stresses than that predicted by Gotoh’s model. They also examined the influence of the strain hardening coefficient (n value) on the sensitivity of the FLC to the normal stress.

Finally, Banabic and Soare [13] used the MK analysis to study the influence of fluid pressure normal to the sheet surface on the forming limits of thin, orthotropic sheets. Their model was used to predict the FLC of AA3104-H19 aluminum alloy subject to different fluid pressures ranging from 0 (plane stress condition) to 200 MPa. They showed that the formability of this aluminum alloy improves with the application of a fluid pressure, especially on the right side of the forming limit diagram. Experimental data was available in the plane stress condition which was predicted satisfactory and used to calibrate their model.

In the present paper, a three-dimensional stress state was implemented in a modified version of the MK model to predict FLC with different through-thickness stress values. The imperfection factor was related to the surface roughness and grain size of the sheet and was updated throughout the deformation of the sheet. The imperfection band was oriented perpendicular to the first principal stress, and its rotation was also considered as the sheet was plastically deformed. This modified MK model was validated in plane-stress conditions with experimental FLC data obtained for AISI-1012 steel [14] and it was also compared with other theoretical results obtained by the present authors [10]. The validation of the model for cases that involved through-thickness stresses was done with published experimental FLC data for AA6011 aluminum [15] and STKM-11A steel [16] sheets. The sensitivity of the predicted FLC to the applied out-of-plane stress component was also analyzed as a function of variations in different material properties and the results of this sensitivity analysis will be discussed.

Theoretical approach

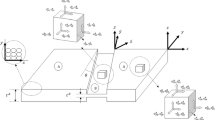
Marciniak and Kuczynski [1, 6] presented a theoretical framework for prediction of FLC that is commonly known as the MK method, which has been shown to predict FLCs with reasonable accuracy. This approach is based on the fact that inhomogeneities are unavoidable in actual sheet materials, and it is assumed that this inherent material inhomogeneity can be modeled as a geometric imperfection in the form of a narrow band (Fig. 1) with a slightly different thickness than the rest of the sheet. Although this approach was originally proposed for plane stress conditions, the current work includes the third stress component in the MK model and is shown as σ ₃ in Fig. 1.

Fig. 1

Thickness imperfection in the MK model

Figure 1 schematically represents a shallow groove on sheet surface, which effectively divides it into two separate regions: region (a) with nominal thickness, and region (b) with the reduced thickness in the groove. The initial imperfection factor of the groove, f ₀, is defined as the thickness ratio between the two regions as follows:

$$ {f_0} = \frac{{t_0^b}}{{t_0^a}} $$

(1)

where t denotes the sheet thickness and subscript ‘0’ denotes the initial state. The thickness difference between these two regions is critical element in the MK theory because the predicted limiting strains are very sensitive to the initial value of the imperfection factor. In most studies, this coefficient is simply assumed to have a fixed value close to 1.0 and that can be adjusted so that the predicted FLC will better fit the experimental data. However, it has been proposed [10] that a more realistic approach would be to relate the initial thickness difference between the two regions to the surface roughness of the sheet. Indeed, research carried out by Stachowicz [17] shows that surface roughness changes with deformation and these changes depend upon initial surface roughness, grain size, and effective plastic strain. By relating the thickness difference between regions (a) and (b) to the surface roughness of the sheet metal, the imperfection factor not only takes on a value that has physical meaning but also the option of adjusting this value so that the predicted FLC can better fit experimental data is eliminated. Stachowicz’s assumption was adopted in this work and the imperfection factor was assumed to change with the deformation of the sheet according to the following relationship:

$$ {f_0} = \frac{{t_0^a - 2\left[ {{R_{{Z0}}} + Cd_0^{{0.5}}\varepsilon_e^b} \right]}}{{t_0^a}} $$

(2a)

$$ f = \frac{{t_0^a - 2\left[ {{R_{{Z0}}} + Cd_0^{{0.5}}\varepsilon_e^b} \right]}}{{t_0^a}}\exp \left( {\varepsilon_3^b - \varepsilon_3^a} \right) $$

(2b)

where R _Z0 is the surface roughness before deformation, C is a material constant, $\varepsilon_e^b$ is the effective strain in region (b), and d ₀ is the material’s initial grain size. Additional details on the calculation of the imperfection factor are provided in the authors’ previous work [10].

In general, the imperfection band is randomly oriented and its orientation can be determined by the angle θ between the groove axis and the direction of the second principal stress (Fig. 1). When plastic deformation begins, this angle will slowly start to change as the groove rotates with respect to the loading axes, and its orientation can affect the limiting strains. In order to obtain FLC predictions with good accuracy, the variations in the groove orientation should therefore be considered in the calculation of the forming limit strains by updating its value at each increment throughout the plastic deformation. This rotation of the imperfection band during deformation was well researched by Sing and Rao [18] and they proposed an empirical formula in which the orientation varies as a function of the true plastic strain increments in region (a) of the sheet as follows:

$$ \tan \left( {\theta + d\theta } \right) = \tan \left( \theta \right)\,\,\frac{{1 + d\varepsilon_1^a}}{{1 + d\varepsilon_2^a}} $$

(3)

where $d\varepsilon_1^a$ and $d\varepsilon_2^a$ are the major and minor principal strains in the nominal area of the sheet, respectively.

A constitutive equation was derived in which the yield function can be expressed in the following general form for isotropic hardening:

$$ f = {\left( {\frac{3}{2}\,{S_{{ij}}}:N:{S_{{ij}}}} \right)^{{1/2}}} - {\sigma_e} $$

(4)

where, S is the deviatoric stress tensor and N is a tensor that describes the anisotropy of the sheet material in terms of the anisotropic constants in Hill’s 1948 yield function [19].

With consideration of the third principal stress component, the three-dimensional plastic potential function was implemented in the MK analysis:

$$ 2h = {\sigma_x}^2 + \left( {F + H} \right){\sigma_y}^2 + \left( {F + G} \right)\sigma_z^2 - 2H{\sigma_x}{\sigma_y} - 2F{\sigma_z}{\sigma_y} - 2G{\sigma_z}{\sigma_x} = {f^2} $$

(5)

where the anisotropic coefficients F, G and H can be calculated from the yield stresses in the principal directions.

Strain hardening is described with the power hardening including strain rate sensitivity effect as follows:

$$ {\sigma_e} = k{\left( {{{\mathop{\varepsilon }\limits^{ \cdot } }_e}} \right)^m}{\left( {{\varepsilon_e} + {\varepsilon_0}} \right)^n}\, $$

(6)

where ε ₀ is a uniform prestrain applied to the sheet, m is the strain-rate sensitivity coefficient, n is the strain-hardening coefficient, σ _e and ε _e are the effective stress and strain, respectively.

The associated flow rule was employed to calculate plastic strain increments as follows:

$$ d{\varepsilon_{{ij}}} = d\lambda \times grad(h) = d\lambda \times \frac{{\partial h}}{{\partial {\sigma_{{ij}}}}} $$

(7)

where dλ is the plastic multiplier and h is the plastic potential function.

There are two main assumptions in the MK analysis. The first one is the geometric compatibility equation expressed as the equality of the tangential plastic strain components inside and outside the imperfection band,

$$ d\varepsilon_{{tt}}^a = d\varepsilon_{{tt}}^b $$

(8)

and the second assumption is the equilibrium of the normal and shear forces across the imperfection, i.e.:

$$ F_{{nn}}^a = F_{{nn}}^b $$

(9a)

$$ F_{{nt}}^a = F_{{nt}}^b $$

(9b)

where subscripts n and t denote the normal and tangential directions of the groove, respectively, and F is the force per unit width, i.e.:

$$ F_{{nn}}^a = \sigma_{{nn}}^a{t^a} $$

(10a)

$$ F_{{nn}}^b = \sigma_{{nn}}^b{t^b} $$

(10b)

$$ F_{{nt}}^a = \sigma_{{nt}}^a{t^a} $$

(10c)

$$ F_{{nt}}^b = \sigma_{{nt}}^b{t^b} $$

(10d)

By combining Eqs. 1, 6 and 10a, 10b the following relation is obtained:

$$ {{{\left[ {\frac{{\sigma_{{nn}}^a}}{{\sigma_e^a}}} \right]}} \left/ {{\left[ {\frac{{\sigma_{{nn}}^b}}{{\sigma_e^b}}} \right]}} \right.} = f\,{{{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^b} \right]^n \times {{\mathop{{\varepsilon_e^b}}\limits^{ \cdot } }^m}} \right)}} \left/ {{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^a} \right]^n \times {{\mathop{{\varepsilon_e^a}}\limits^{ \cdot } }^m}} \right)}} \right.} $$

(11a)

Since the strain rate is defined as $\mathop{{{\varepsilon_e}}}\limits^{ \cdot } = {{{d{\varepsilon_e}}} \left/ {{dt}} \right.}$, it follows that:

$$ {{{\left[ {\frac{{\sigma_{{nn}}^a}}{{\sigma_e^a}}} \right]}} \left/ {{\left[ {\frac{{\sigma_{{nn}}^b}}{{\sigma_e^b}}} \right]}} \right.} = f\,{\left( {\left[ {{\varepsilon_0} + \varepsilon_e^b} \right]/\left[ {{\varepsilon_0} + \varepsilon_e^a} \right]} \right)^n} \times {\left[ {d\varepsilon_e^b/d\varepsilon_e^a} \right]^m} $$

(11b)

Finally, the stress transformation rule leads to the expressions:

$$ \sigma_{{nn}}^a = \sigma_x^a{\cos^2}\left( \theta \right) + \sigma_y^a{\sin^2}\left( \theta \right) $$

(12a)

$$ \sigma_{{nt}}^a = - \left( {\sigma_x^a - \sigma_y^a} \right)\sin \left( \theta \right)\cos \left( \theta \right) = \sigma_x^a\left[ {\left( {\alpha - 1} \right)\sin \left( \theta \right)\cos \left( \theta \right)} \right] $$

(12b)

where α is the ratio of the second true principal stress component (σ ₂) to the first true principal stress component (σ ₁) in the nominal area which indicates the stress path. Expressions similar to Eqs. 12a and 12b can be written for region (b), and using Eqs. 9, 10, and 12 we obtain:

$$ \frac{{\sigma_{{nt}}^b}}{{\sigma_{{nn}}^b}} = \frac{{\sigma_{{nt}}^a}}{{\sigma_{{nn}}^a}} = \frac{{\left( {\alpha - 1} \right)\sin \left( \theta \right)\cos \left( \theta \right)}}{{{{\cos }^2}\left( \theta \right) + \alpha {{\sin }^2}\left( \theta \right)}} $$

(13)

With consideration of the consistency condition, the plastic potential function and the strain transformation rule:

$$ \frac{{d\varepsilon_e^a}}{{\sigma_e^a}}\left\{ {\left[ {\left( {F + H} \right) \times {\alpha^a} - F{\beta^a} - H} \right]\sigma_x^a{{\cos }^2}\theta + \left( {1 - G{\beta^a} - H{\alpha^a}} \right)\sigma_x^a{{\sin }^2}\theta } \right\} = \sigma_x^b\frac{{d\varepsilon_e^b}}{{\sigma_e^b}}\left\{ {\left[ {\left( {F + H} \right) \times {\alpha^b} - F{\beta^b} - H} \right]{{\cos }^2}\theta + \left( {1 - G{\beta^b} - H{\alpha^b}} \right){{\sin }^2}\theta } \right\} $$

(14)

where β is the ratio of the third true stress component to the first true stress component, such that:

$$ \beta = {{{{\sigma_3}}} \left/ {{{\sigma_1} = {{{{\sigma_z}}} \left/ {{{\sigma_x}}} \right.}}} \right.} $$

(15)

By combining Eqs. 11, 13, and 14, the final governing equation was analytically determined as a function of the ratio of the effective plastic strain inside and outside the imperfection band $\eta = {{{\varepsilon_e^b}} \left/ {{\varepsilon_e^a}} \right.}$. This final differential equation indicates the evolution of the effective plastic strain ratio η as the sheet is deformed under a three-dimensional loading condition.

The plastic deformation of the sheet begins as strain increments are imposed along a linear strain path (i.e. for a constant value of $\rho = {{{{\varepsilon_2}}} \left/ {{{\varepsilon_1}}} \right.}$) in the nominal region, and the stress components are calculated from the strain state in the nominal area. Then the strains and stresses in the imperfection region are calculated from the strains and stresses in the nominal area by using the governing equations described above. During the analysis, it is assumed that the normal stress applied on the surface of the sheet or tube is identical for both region (a) and region (b) of the MK model. But since the thickness in region (b) is less than that in the rest of the sheet, the strain rate increases faster in region (b) than in region (a). Moreover, the difference in strain rate between the two regions will intensify as the deformation progresses, and eventually the strains will localize in the imperfection region. It is generally assumed that plastic instability occurs when the effective plastic strain in the imperfection region reaches ten times that in nominal area ($\varepsilon_e^b = 10\,\varepsilon_e^a$). Once the onset of necking takes place, the in-plane plastic strain components in the nominal area ($\varepsilon_1^a$ and $\varepsilon_2^a$) identify a point on the FLC for the specified strain path ρ. In order to generate the entire FLC, the value of the strain ratio ρ is modified and the procedure is repeated for each new strain path. The FLC is thus determined from the limiting strain data obtained for strain paths that vary in increments Δρ = 0.05 from uniaxial tension (ρ = −0.5) to equibiaxial tension (ρ = 1.0).

Experimental validation of the modified MK model

The theoretical MK analysis model presented in the previous section was implemented into a numerical code. This proposed model was then used to predict the FLC of actual sheet and tube materials, both with and without applied normal stresses, in order to validate the numerical code.

Description of materials

The materials that were considered for the validation of the proposed MK model are a low carbon steel (AISI-1012) [14], AA6011 aluminum alloy [15], and STKM-11A steel [16] (the designation of this last steel grade follows the Japanese standard and it is equivalent to an MT1010 steel in the ASTM standard). The mechanical properties of these materials are listed in Table 1. It is also worth noting that in these publications, AISI-1012 refers to a flat stock sheet metal, whereas AA6011 and STKM-11A refer to thin walled tubes.

Table 1 Mechanical properties

Equation 2a was used to calculate the initial imperfection factor value in the MK analysis. It was found that f ₀ = 0.995 for AISI-1012 steel, f ₀ = 0.997 for AA6011 aluminum, and f ₀ = 0.991 for STKM-11A steel.

Validation of the proposed MK model

In order to validate the three-dimensional FLC model described in the previous section, theoretical FLCs were calculated in both plane stress and three-dimensional stress conditions and the predicted FLCs were compared with published experimental data [14–16].

The new model was verified first under plane stress conditions, in the absence of through-thickness stresses (β = 0). Theoretical FLC were compared with the experimental FLC of as-received AISI-1012 sheet steel [14] which were obtained by carrying out stretch forming tests using rectangular and notched blanks of various widths with different conditions of lubrication to achieve a range of strain states $- 0.5 \leqslant \rho = {{{{\varepsilon_2}}} \left/ {{{\varepsilon_1} \leqslant 1.0}} \right.}$. Each blank was electro-etched with a 3.0 mm diameter circle grid and formed over a hemispherical punch until the onset of local necking. The major and minor strains were measured directly from the deformed grids using a profile projector. The FLC predicted with the proposed MK model was also compared with the FLC predicted by a different MK analysis code developed previously by the same authors for purely plane stress conditions [10]. The predicted and experimental FLCs for this grade of steel are shown in Fig. 2.

Fig. 2

Comparison of predicted and experimental FLCs of AISI-1012 steel sheet in-plane stress condition [14]

Figure 2 shows good agreement between the theoretical and experimental FLCs obtained under plane stress conditions, and the developed model predicts the FLC for this steel with acceptable accuracy. Furthermore, it can be seen that the FLC predicted under plane stress conditions with the new three-dimensional model is essentially identical to the FLC predicted with the previous two-dimensional analysis code [10].

The proposed MK analysis model was also verified for more general loading conditions where the out-of-plane stress component is non-negligible (β ≠ 0). This further validation of the three-dimensional MK model was carried out by predicting the FLC of AA6011 aluminum tubes that were hydroformed with up to 15-MPa internal pressure (which corresponds to σ ₃ ≈ 7.5 MPa). Hwang et al. [15] prepared 200-mm long tube specimens with a 1.86-mm wall thickness, and a 51.9-mm outer diameter. The tube specimens were annealed at 410°C for 2 h and then a grid of 5-mm-diameter circles with a spacing of 1-mm was electrochemically etched onto the surface of undeformed tubes for the purpose of strain measurement. Tubes were pressurized in a bulge test apparatus without axial feeding to generate positive minor strains. Other tubes were also pressurized in a hydroforming test machine with axial feeding to generate strain paths with negative minor strains. After the tubes were deformed, the circle grids in the vicinity of the burst were measured by a three-dimensional digital image processing system and the major and minor strains were determined. The limiting strain data from these tests was used to construct the left side of the FLC of these aluminum tubes. The comparison of the predicted and experimental FLCs is shown in Fig. 3.

Fig. 3

Comparison of predicted and experimental FLCs of AA6011 aluminum sheets under 15 MPa internal pressure [15]

It can be seen from Fig. 3 that there is good agreement between the experimental data and the predicted FLC on the left side of the diagram. This may seem surprising considering that the analysis was carried out using Hill’s 1948 yield criterion. Indeed, it is well known that Hill’s quadratic yield function is not suitable for predicting the biaxial behaviour of aluminum alloys and more recent, non-quadratic yield functions have been shown to be much more appropriate [20]. However, it can be seen that the experimental FLC data in Fig. 3 corresponds with deformation modes between plane strain and uniaxial tension, and for such deformation modes the quadratic yield function is capable of predicting reasonably accurate results. Non-quadratic yield functions typically lead to improved predictions of the forming behaviour of aluminum alloys for deformations in biaxial tension, because they are better able to represent the shape of the yield locus between plane strain and balanced biaxial tension: this corresponds with the right side of the FLC for which no experimental data is available. No doubt the predictions of FLC in the region of plane strain would be improved with the use of a non-quadratic yield function.

The proposed model was also validated with another set of experimental limiting strain data for STKM-11A steel presented by Kim et al. [16]. These authors determined the experimental FLC by hydroforming straight tubes with both an axial end-feed force and 56-MPa internal pressure (leading to σ ₃ ≈ 28 MPa). A constant ratio of high internal pressure and relatively low axial force was applied with an end displacement rate of 2.33-mm/s using a PC-based controller. During these experiments, tubes were pressurized until they burst, and the average burst pressure was 56 MPa, with the split occurring parallel with the tube axis and positioned toward the middle of the tube. Strain measurements were taken as near to the fractured edge as possible in order to determine limit strains. Figure 4 shows a comparison of predicted and experimental FLC for negative minor strains.

Fig. 4

Comparison of predicted and experimental FLCs of STKM-11A steel sheet under 56 MPa internal pressure [16]

It can be seen in Fig. 4 that the FLC predicted by the proposed MK analysis lies slightly above the experimental FLC for this grade of steel. This discrepancy between the theoretical and the experimental FLC data is likely due to the fact that experimental strains were not actually measured in local necks since these tubes were allowed to burst, but they were measured in the uniformly deformed material right next to the fractured edge of burst tubes. Therefore these experimental strain data represent a conservative estimation of the actual FLC. Limiting strain data was not available for the right hand side of the diagram because Kim et al. [16] were only able to apply a compressive axial force to the ends of the tubes, whereas a tensile axial force is required to obtain positive minor strains [21].

It is also worth pointing out that the experimental FLC data [14–16] used to validate the current MK model were obtained using the well-known circle grid analysis technique. This technique relies on the measurement of deformed grids on the surface of the specimens as well as the somewhat subjective interpretation about whether necking has begun or not in a specific grid location. This technique is therefore dependent on the experimentalist’s experience and the accuracy of the strain measurements, and therefore it inevitably leads to some variability in the results. According to the author’s experience, the experimental error that can be expected in FLC strain data obtained with the circle grid technique is estimated to be within ±2.5% strain. More advanced techniques are now being used to determine the forming limits of sheet materials with greater repeatability and reproducibility. For instance, digital image correlation is used to measure the strain field across the entire specimen gauge area and numerical interpolation methods are then used to determine the strains at the onset of necking [22–26]. These techniques are very powerful as they can determine limiting strains even for very high strength materials that tend to fracture without necking.

However, although there is some experimental error in the published experimental FLC data [14–16], the comparisons between the predicted and experimental FLC (Figs. 2, 3 and 4) nevertheless show that the proposed three-dimensional MK model provides a good prediction of the FLC, whether the through-thickness stress component is significant or not.

Influence of the through-thickness stress on the FLC

The primary purpose of this work is to study the effect of the through-thickness stress component on the forming limit curve. In this section, the sensitivity of the FLC to the out-of-plane stress component will be studied by applying different levels of through-thickness stress to the surface of AISI-1012 steel sheets. The FLC was predicted for a normal stress ranging from σ ₃ = 0 (plane stress condition) to σ ₃ = 35 MPa. The theoretical results are presented in Fig. 5.

Fig. 5

FLC of AISI-1012 sheet steel predicted as a function of the applied normal stress

It can be seen from Fig. 5 that the FLC is quite sensitive to the normal stress: indeed, the entire FLC is observed to shift up the vertical axis when the applied normal stress increases. The formability of this sheet steel is seen to improve with a normal stress as low as 10 MPa. Furthermore, it is apparent from Fig. 5 that the increase in formability is not proportional to the increase in normal stress: indeed, the rate of increase in formability also increases with the normal stress.

Influence of mechanical properties on the sensitivity of FLC to out-of-plane stresses

In the previous section it was shown (Fig. 5) that the FLC of AISI-1012 sheet steel is dependent on the magnitude of the applied normal stress. Therefore it is also of further interest to determine if this dependence varies from one material to another, and if so, how individual material properties may affect the sensitivity of the FLC to the normal, or through-thickness, stress. The constitutive equations in this three-dimensional version of the MK model are capable of fully describing the elasto-plastic behaviour of sheet materials; therefore it is possible to investigate the effect of individual material parameters on the sensitivity of the FLC to the out-of-plane stress. In this study, the influence of some of the more significant properties of sheet materials—the strain hardening coefficient (n), the strain rate sensitivity (m), the plastic anisotropy coefficients (R), grain size (d ₀) and initial sheet thickness (t ₀) were investigated. Each parameter was therefore modified one by one to observe its effect on the sensitivity of the FLC to increases in the out-of-plane stress, and the results of this study are presented in this section.

Since the work hardening ability of a sheet material is such a significant material property in sheet metal forming, the effect of a change in the strain hardening coefficient is presented first. All the mechanical properties of the AISI-1012 sheet steel (Table 1) were kept unchanged except for the value of the strain hardening coefficient which was doubled from n = 0.35 to n = 0.70. While this change leads to a fictitious material for which the experimental FLC is not readily available, the present three-dimensional version of the MK analysis nevertheless enables us to predict the dependence of the FLC on the applied normal stress. Figure 6 shows the FLC of a very formable sheet material (n = 0.7) for various levels of applied normal stress ranging from σ ₃ = 0 (plane stress) to σ ₃ = 35 MPa.

Fig. 6

FLC of a sheet material that differs from AISI-1012 only by its strain hardening coefficient (n = 0.70), predicted as a function of the applied normal stress

Figure 6 shows that the predicted FLC is almost independent of the applied normal stress for a sheet material with a very high strain hardening coefficient. In order to better visualize the effect of the strain hardening coefficient on the FLC, the vertical shift of the FLC relative to the plane stress condition was plotted as a function of the applied normal stress. More specifically, the percent increase in the limiting major strain in plane strain (FLC₀) due to increases in the out-of-plane stress component was plotted for both materials considered (n = 0.35 and n = 0.70) and shown in Fig. 7. This figure indicates that through-thickness stresses always improve the formability of sheet materials, but the positive effect of the out-of-plane stress is far more significant for lower-formability sheet materials than it is for higher-formability materials.

Fig. 7

Increase in FLC0 as a function of the applied normal stress for two sheet steels that differ only by their strain hardening coefficient (n = 0.35 and n = 0.70)

The next mechanical property considered in this study on the forming limits of sheet metal formed under three-dimensional stress states is the strain rate sensitivity (m). It is well known that positive strain rate sensitivity helps to improve formability by delaying the onset of necking and by strengthening the material as the strain rate increases in the area where strains are localizing. In this investigation, all the mechanical properties of the AISI-1012 sheet steel (Table 1) were kept unchanged except for the strain rate sensitivity which was doubled from m = 0.015 to m = 0.030. The three-dimensional MK model was then used to calculate the FLC for each level of applied normal stress, and the predicted FLCs are plotted in Fig. 8. It is evident from Fig. 8 that the predicted FLC remains very dependent on the through-thickness stress after the strain rate sensitivity was increased by a factor of two. However, comparing Figs. 5 to 8, the sensitivity of the FLC to the through-thickness stress does not appear to have changed significantly.

Fig. 8

FLC of a sheet material that differs from AISI-1012 only by its strain rate sensitivity (m = 0.030) predicted as a function of the applied normal stress

In order to quantify the effect of the strain rate sensitivity (m value) on the dependence of FLC to the normal stress the percentage increase in FLC₀ was plotted as a function of the applied normal stress for both sheet steels (m = 0.015 and m = 0.030), and the results are shown in Fig. 9. It is immediately apparent from this figure that, while formability significantly increases with normal stress for both materials, changes in strain rate sensitivity practically have no effect on the dependence of FLC to the through-thickness stress.

Fig. 9

Increase in FLC0 as a function of the applied normal stress for two sheet steels that differ only by their strain rate sensitivity (m = 0.015 and m = 0.030)

Another mechanical parameter that was considered in this investigation is the anisotropy of the sheet material. It is well known that, according to the MK analysis, variations in anisotropy are seen to have a significant effect on the formability of a sheet material, and this effect is primarily evident on the right hand side of the FLC (i.e. for positive minor strains). Although experimental FLC data do not generally show such an influence of anisotropy on the forming limits [27], the sensitivity of FLC to the applied through-thickness stress was nevertheless calculated for a fictitious material whose mechanical properties are identical to those of AISI-1012 steel except for the anisotropy coefficients; the plastic anisotropy coefficients were doubled from R ₀ = 1.4 to R ₉₀ = 1.35 to R ₀ = 2.8 and R ₉₀ = 2.7. It can be pointed out that, while the anisotropy of this fictitious is expressed in terms of planar anisotropy coefficients (R ₀ and R ₉₀) the level of planar anisotropy is actually low $\left( {\Delta R = \left( {{R_0} + {R_{{90}}} - 2{R_{{45}}}} \right)/2 = 0.85} \right)$, but the normal anisotropy, that is, the through-thickness anisotropy, is quite significant $\left( {\bar{R} = \left( {{R_0} + {R_{{{9}0}}} + {2}{R_{{{45}}}}} \right)/{4} \approx {2}.{42}} \right)$. The FLC of this material was then calculated for increasing levels of applied normal stress and the results are shown in Fig. 10.

Fig. 10

FLC of a sheet material that differs from AISI-1012 only by its plastic anisotropy coefficients (R0 = 2.8 and R90 = 2.7), predicted as a function of the applied normal stress

Figure 10 shows that the formability of a sheet material with significant normal anisotropy also increases with increasing normal stresses. Nevertheless, a comparison of Figs. 5 and 10 seems to indicate that the FLC becomes somewhat less sensitive to the through-thickness stress as normal anisotropy increases. To better evaluate the sensitivity of the FLC to the normal stress for different degrees of normal anisotropy, the percent increase in FLC₀ from the plane stress condition was calculated for both sets of anisotropy coefficients and plotted in Fig. 11.

Fig. 11

Increase in FLC0 as a function of the applied normal stress for two sheet steels that differ only by their plastic anisotropy coefficients (R0 = 1.4 and R90 = 1.35 versus R0 = 2.8 and R90 = 2.7)

Figure 11 indeed supports the observation made from Fig. 10 that, while FLC₀ continues to increase with the normal stress, the rate of increase of FLC₀ is lower for sheet materials with more pronounced normal anisotropy. It can also be observed that the increase in formability is practically proportional to the increase in normal stress for the sheet material with the greater anisotropy.

In this investigation the imperfection factor in the MK analysis was defined, amongst other parameters, as a function of the grain size (d ₀) of the sheet material. It is therefore of interest to determine if the sensitivity of the FLC to the normal stress varies as a function of the grain size. In order to assess the effect of the grain size, the FLC of a fictitious sheet material, identical to the AISI-1012 steel except for its initial grain size that was doubled from 25 μm to 50 μm, were calculated for different values of the applied normal stress. The predicted FLC are plotted in Fig. 12, and once again, it is evident that sheet formability continues to be dependent on the applied normal stress.

Fig. 12

FLC of a sheet material that differs from AISI-1012 only by its grain size (d0 = 50 μm), predicted as a function of the applied normal stress

Similar to the previous cases, the percentage increase in the predicted FLC₀ was plotted as a function of the through-thickness stress for both the AISI-1012 steel and the fictitious material with the increased grain size, and these data are presented in Fig. 13. It appears that when the grain size of the material increases the dependence of FLC on the applied out-of-plane stress decreases somewhat, but the rate of increase in formability still increases with the normal pressure. The initial grain size of the sheet does not appear to a have a significant effect on the dependence of the FLC to the through-thickness stress.

Fig. 13

Increase in FLC0 as a function of the applied normal stress for two sheet steels that differ only by their initial grain size (d0 = 25 μm and d0 = 50 μm)

The sheet material’s initial thickness was the last parameter that was considered in this investigation. Once again, the FLC of a sheet material with identical mechanical properties to those of AISI-1012 steel except for the initial thickness that was reduced by a half from 2.5 mm to 1.25 mm (it did not appear reasonable to predict the FLC for a sheet thickness that was doubled to 5.0 mm), was calculated for different levels of applied normal stress, and the predicted FLC are shown in Fig. 14.

Fig. 14

FLC of a sheet material that differs from AISI-1012 only by its initial thickness (t0 = 1.25 mm), predicted as a function of the applied normal stress

Figure 14 shows that the sheet material with a thinner gauge is still sensitive to the applied normal stress, but that the dependence of the FLC on the through-thickness stress seems to decrease somewhat as the initial sheet thickness drops. Figure 15 confirms that this sensitivity to the through-thickness stress decreases when the sheet thickness decreases, although the actual rate of increase in formability continues to increase slightly with normal stress for this particular material with a 1.25 mm gauge.

Fig. 15

Increase in FLC0 as a function of the applied normal stress for two sheet steels that differ only by their initial thickness (t0 = 1.25 mm and t0 = 2.5 mm)

It should be mentioned, however, that the current model does not address the influence of sheet thickness on limit strains in the presence of significant bending. Indeed, when a sheet is drawn over a punch radius the combination of stretching and bending lead to inhomogeneous through-thickness deformation. Furthermore, the through-thickness strain gradient increases with initial sheet thickness and with the severity of the bend. Ghosh and Hecker [28] showed that an increase in out-of-plane (i.e. bending) deformation tends to delay the onset of necking and shifts the forming limits toward higher strains. Therefore a different approach is required to predict limit strains in cases where there is significant bending [29].

In order to compare the effect of each of these material parameters on the sensitivity of FLC to the through-thickness stress, the percent increase in FLC₀ (compared to the plane stress condition) was plotted in Fig. 16 for each of the factors discussed. It can be seen that variations in the strain hardening coefficient clearly have the most significant effect on the sensitivity of the FLC to the normal stress: the sensitivity to the normal stress increases sharply when the work hardening ability of the material decreases. Similarly, the pressure sensitivity of the FLC increases when the normal anisotropy decreases. Another factor that has a significant effect on the sensitivity of FLC to the normal stress is the initial sheet thickness however its effect is the reverse of that of the other properties: the sensitivity of the FLC to the normal stress increases with the sheet thickness. Finally, any variation in grain size or in strain rate sensitivity does not appear to significantly affect the dependence of FLC on the normal stress unless the normal stress becomes very large (σ ₃ > 30 MPa in this case).

Fig. 16

Increase in FLC0 as a function of the applied normal stress for sheet steels that differ from AISI-1012 by only one mechanical property (see Table 1)

Conclusion

In this research work, the through-thickness stress component was included in the traditional MK analysis to predict FLC in conditions where an out-of-plane stress is applied to the sheet surface. The current model was validated by comparing its predictions to experimental FLC data with different levels of applied normal stress. The FLC of an AISI-1012 steel sheet obtained under plane stress conditions, and the FLC of AA6011 aluminum and STKM-11A steel tubes subjected to various levels of internal pressure were all used to verify the proposed model. A good correlation between the theoretical and experimental FLCs was observed in all three cases.

The current MK model takes into account the effects of material properties such as grain size, surface roughness, and rotation of the initial imperfection. The value of the thickness inhomogeneity was defined as a function of surface roughness and grain size of the sheet material. In addition, the rotation of the imperfection band, the surface roughness and the thickness ratio (f) were updated throughout the loading history. This MK analysis was implemented into a numerical code, and the FLC of AISI-1012 sheet steel was predicted for different values of the applied compressive normal stress. The results obtained from this series of analyses showed that the FLC of a typical sheet steel is very sensitive to the applied normal stress, and the formability of the sheet always improves as the through-thickness stress increases. Therefore whenever it is applicable the addition of, or increase in, through-thickness stress would undoubtedly help to improve the formability of sheet materials in industrial sheet and tube forming processes. In many instances, the rate of increase in formability also increases with the normal stress, providing additional benefit to even small increases in applied normal stress.

Finally, the influence of certain sheet mechanical properties on the sensitivity of FLC to the through-thickness stress was also investigated using this predictive MK analysis code. It was found that the work hardening ability of the material has the greatest influence on the pressure dependence of FLC. Indeed, the dependence of FLC on the applied out-of-plane stress increases significantly as the strain hardening exponent decreases. Similarly, the sensitivity to the normal stress increases as the normal anisotropy ($\bar{R}$) decreases. The grain size and the strain rate sensitivity were found to have only a minor influence on the pressure dependence of the FLC. Finally, the dependence of FLC on the normal stress was seen to increase quite significantly with the thickness of the sheet metal.

All in all, this investigation has shown that, while the dependence of the FLC on the through-thickness stress can vary from one material to another, the stress applied normal to the sheet surface invariably enhances sheet formability. Therefore the pressure dependence of the forming limits of metal sheets and thin-walled tubes cannot be ignored if the forming severity of formed components is to be accurately evaluated and the robustness of forming processes is to be optimized.