1 Introduction

Digital communication systems make use of error correcting codes to reliably transmit information over a noisy channel [1]. Convolutional codes are among the most used ones, with extensive applications in modern wireless communication standards [2–5]. However, the decoding of convolutional codes demands a large amount of processing and energy consumption of a regular wireless digital receiver, which is usually battery powered. For instance, in [6], it is shown that the decoding of a convolutional code, executed by the Viterbi algorithm (VA) [1], accounts for up to 76% of the processing required by a HYPERLAN/2 receiver [4]. In [7], the authors analyse different receiver implementations compatible to the IEEE 802.11 standard [5], showing that the VA accounts for 35% of the overall power consumption.

Moreover, in the last two decades, we had an unimpressive improvement of only 3.5% per year in the nominal battery capacity, while the throughput has increased a million times [8, 9]. Thus, complexity (power) reductions in the decoding of convolutional codes would increase the energy efficiency and lifetime of many wireless devices, being of considerable impact in a number of applications. A survey in the literature shows a series of papers related to this issue; among them, we can cite [10–25]. These works can be divided into three groups: (a) hardware-specific implementations [10–13], (b) sub-optimum decoding methods [14–19] and (c) simpler trellis representations [20–25]. Supported by two recent new paradigms for the implementation of digital communications systems, the software-defined radio model [26] and the cognitive radio concept [27], we concentrate on software-oriented implementations. Therefore, we consider only two of the above options: sub-optimum decoding methods and simpler trellis representations.

Most sub-optimum decoding algorithms were proposed based on the conventional trellis representation of a convolutional code and are similar to the VA. The sub-optimality comes from pruning some of the trellis edges, based on specific criteria. One of the most famous sub-optimum decoding algorithms is the M-algorithm (MA) [14, 15]. The MA achieves a bit error ratio (BER) close to that of the VA with reduced complexity (for an appropriate choice of M) [19]. The reduction in complexity is obtained by expanding only M surviving states per trellis section, instead of expanding all trellis states at each section. Due to this characteristic, the MA is also used when the convolutional code has a large overall constraint length [19] and the application of the optimum VA is prohibitive.

Minimal trellis representation of a convolutional code, introduced in [20] by McEliece and Lin, is an alternative trellis representation for the code, allowing to minimise several theoretical quantities based on the trellis complexity measures defined in [28]. Such a trellis, as opposed to the conventional trellises, has an irregular structure (the number of states and the number of edges emanating from each state are periodically time varying). New minimal trellis codes, with good distance spectrum and fixed complexity of the minimal trellis, have been proposed recently [21, 22]; furthermore, in [29], the authors have shown that the decoding of convolutional codes using the minimal trellis can result in practical implementations with both reduced power consumption and hardware complexity.

In this paper, we combine both approaches, sub-optimum decoding algorithms and simpler trellis representations. More specifically, we design three decoding algorithms based on the MA operating over the minimal trellis, namely modular M-algorithm, proportional M-algorithm and fixed M-algorithm (see Section 3). Each algorithm relies on a different strategy to select the number of states with best metrics in each depth of the trellis. This number can be either fixed or variable when the MA operates over the minimal trellis which establishes distinct trade-off between complexity and performance. We analyse both the computational complexity, in terms of arithmetic operations, and the BER performance for each proposed algorithm over the additive white Gaussian noise (AWGN) channel. Our results show that considerable reductions in complexity can be obtained while achieving a performance close to that of the VA within a given tolerance. Moreover, we show that the proposed algorithms offer a wide range of performance-complexity trade-off which can increase even more the savings in computational complexity. Finally, based on the complexity results, we discuss the applicability of each algorithm in terms of receiver architecture.

The rest of this paper is organised as follows: Some fundamental concepts are introduced in Section 2. The new proposed algorithms are described in Section 3. The BER performance of the new algorithms is numerically investigated in Section 4, while a complexity analysis is carried out in Section 5. Section 6 concludes the paper.

2 Fundamental concepts

Consider a convolutional code C(n, k, ν), where ν, k and n are the overall constraint length, the number of binary inputs and binary outputs, respectively. The code rate is R = k/n. Every such convolutional code can be represented by a semi-infinite trellis which (apart from a short transient in its beginning) is periodic, the shortest period being called a trellis module. In general, a trellis module Φ for a convolutional code C consists of n ′ trellis sections, \(2^{\nu_t}\) states at depth t, \(2^{b_t}\) edges emanating from each state at depth t and l t bits labelling each edge from depth t to depth t + 1, for 0 ≤ t ≤ n ′ − 1.

Two important complexity measures of the computational effort per decoded bit of the VA operating over a specific trellis module are the trellis complexity and the number of merges, which are the number of real additions and real comparisons (normalised by the number of information bits), respectively; the VA has to perform to update the state metrics in each module. The trellis complexity of the module Φ for the code C, denoted by TC(Φ), is [20]

$$ \label{eq_TCM} {\rm TC}(\Phi) = \frac{1}{k} \sum_{t=0}^{n^{\prime}-1} l_t \, 2^{\nu_t + b_t} $$
(1)

symbols per bit. The number of comparisons required at a specific state, in its turn, is the number of edges reaching it minus 1 [30]. Then, the number of comparisons in the module Φ at depth t + 1 is \(2^{\nu_t + b_t} - 2^{\nu_{t+1}}\). So, the merge complexity of the module Φ, denoted by MC(Φ), is

$$ \label{eq_MC} {\rm MC}(\Phi) = \frac{1}{k} \sum_{t=0}^{n^{\prime}-1} 2^{\nu_t + b_t} - 2^{\nu_{t+1} }. $$
(2)

In particular, the conventional trellis module Φconv for a rate R = k/n convolutional code C consists of one trellis section with 2ν initial states and 2ν final states; each initial state is connected by 2k directed edges to final states, and each edge is labelled with n bits. The trellis complexity and the merge complexity of the conventional trellis are \(TC(\Phi_{{\rm con}v}) = (n/k) \, 2^{\nu+k}\) and \({\rm MC}(\Phi_{{\rm con}v}) = 2^\nu(2^k -1)/k\). For instance, consider the C(7,4,4) code with the following generator matrix:

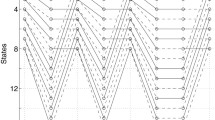
$$ G (D)= \left(\begin{array}{c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c} 1+D &0 &1 &0 &1 &1 &1\\ 0 &1+D &1+D &D &0 &0 &1\\ D &D &D &1 &1 &0 &1\\ 0 &D &0 &D &D &1+D &1\\ \end{array}\right) \label{mat_g} $$
(3)

whose conventional trellis module Φconv is shown in Fig. 1a, with TC(Φconv ) = 448 and MC(Φconv ) = 60. The limiting factor for using the VA, when the trellis module is dense (with many states and edges per state), is the implementation complexity growth.

Fig. 1
figure 1

Conventional a and minimal b trellis modules for the C(7,4,4) convolutional code with generator matrix in Eq. 3. In the minimal trellis, solid edges represent “0” codeword bits while dashed edges represent “1” codeword bits

Full size image

2.1 Minimal trellis

The “minimal” trellis module, Φmin, for convolutional codes was developed in [20]. This “minimal” structure has n ′ = n sections and l t  = 1 bit per edge ∀ t. The state complexity and the edge complexity at depth t will be denoted by \(\widetilde{\nu}_t\) and \(\widetilde{b}_t\), respectively. The state and the edge complexity profiles of the “minimal” trellis module are denoted by \(\widetilde{\boldsymbol{\nu}}=(\widetilde{\nu}_0, \ldots, \widetilde{\nu}_{n-1})\) and \(\widetilde{\boldsymbol{b}}=(\widetilde{b}_0, \ldots, \widetilde{b}_{n-1})\), respectively. This module presents an irregular pattern in each section. For instance, Fig. 1b shows the minimal trellis module for the C(7,4,4) code with generator matrix in Eq. 3. While the single-section conventional trellis module in Fig. 1a has a very regular structure, 16 states with 16 edges leaving each state, each edge labelled by 7 bits, the minimal trellis module in Fig. 1b has n = 7 sections, with 16 or 32 states each. Note that only the first, second, fourth and sixth sections have information bits, i.e. two edges leave each state (\(\tilde{b}_t=1\)).

For the C(7,4,4) code, \(\widetilde{\boldsymbol{\nu}}=(4,4,5,4,4,4,4)\) and \(\widetilde{\boldsymbol{b}}=(1,1,0,1,0,1,0)\); thus, it readily follows from Eqs. 1 and 2 that TC(Φmin) = 48 and MC(Φmin) = 16. It is important to say that the minimal trellis module achieves [28, Theorem 4.26] not only the minimum trellis complexity and the minimum merge complexity but other complexity measures as well, such as maximum number of states and total number of states. Such reduced complexity is our motivation for considering the use of the minimal trellis in this work. However, it is not completely clear whether such a trellis complexity measure directly translates into decoding complexity of reduced complexity decoding algorithms, such as the MA. For that sake, we will compute in Section 5 the number of arithmetic operations required by a specific decoding algorithm, be it over the conventional or the minimal trellis.

2.2 MA over the conventional trellis module

Further reduction of decoding complexity can be attempted by using, besides the simpler trellis representation, sub-optimum algorithms such as the MA [14]. The MA is very similar to the VA, the main difference resting in the fact that the MA calculates the accumulative metric of at most M ≤ 2ν paths along the conventional trellis module.Footnote 1 The MA operating over the conventional trellis can be described by the following steps:

  1. 1.

    Start from the leftmost module of the trellis.

  2. 2.

    Expand all the states metrics stored at depth t − 1 to depth t. Select the surviving edges for each state reached at time t.

  3. 3.

    Select, at most, the M states at time t with the best metrics and discard the others.

  4. 4.

    Store the selected states, their metrics and surviving edges.

  5. 5.

    Repeat steps 2–4 for all trellis modules.

  6. 6.

    Estimate the transmitted sequence by tracebacking from the state with the best final metric.

The main difference between the VA and MA is that the MA selects the M best states before expanding the metrics of these states.

3 MA over the minimal trellis module

When the MA operates over the conventional trellis, the parameter M is fixed; however, since the minimal trellis has a time-varying state profile, the maximum number of states selected in each section of this trellis can be either fixed or variable. We propose three different variants of the MA to operate over the minimal trellis, namely modular M-algorithm (MMA), proportional M-algorithm (PMA) and fixed M-algorithm (FMA). These algorithms differ only in step 3, that is, in the way they select the best states.

The MMA selects the surviving states only in the end of each minimal trellis module. Thus, in the intermediate sections, all expansions are retained. The metrics are expanded up to the end of the module, storing the metrics of all states reached by any surviving edge. Then step 3 of the MMA is thus described as:

  1. 3.

    If this is the last section of the module, store at most the M best states and discard the others; otherwise, store the metrics of all states reached by a surviving edge.

In the PMA, the maximum number of stored states varies according to the number of states in that section. The maximum number of states stored per section is \(2^{\widetilde{\nu}_t}\times \frac{M}{2^{\nu}}\). Recall that \(2^{\widetilde{\nu}_t}\) is the number of states at that section of the minimal trellis, while 2ν is the number of states in the conventional trellis. For instance, if in the MA operating over the conventional trellis the parameter M means a reduction of 50% in the maximum number of stored states, then in the PMA this value of M means a reduction of 50% in the maximum number of states stored in each section of the minimal trellis. Thus, the maximum number of stored states is proportional to the number of states in that section of the minimal trellis. Step 3 of the PMA can be written as:

  1. 3.

    Store at most the \(2^{\widetilde{\nu}_t}\times \frac{M}{2^{\nu}}\) states with the best metric for each section. Discard the others.

In the FMA, up to M states are stored at each section of the minimal trellis, independent of the trellis pattern or section. Step 3 of the FMA can be described as:

  1. 3.

    Store at most the M best states at each section. Discard the others.

4 BER performance

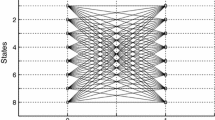
In this section, we numerically investigate the BER performance of the proposed algorithms. In the simulations, the coded blocks were binary phase shift keying (BPSK) modulated, sent over the AWGN channel and decoded by soft decision decoding. We considered the C(7,4,4) code with generator matrix in Eq. 3 and the C(5,3,4) code with generator matrix:

$$ G (D)= \left(\begin{array}{c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c@{\,\,\,}c} 1+D &D &1 &1 &0\\ 0 &1 &1+D & 1+D & 1\\ D+D^2 & D & 0 & 1+D & 1+D \end{array}\right), \label{mat_g5} $$
(4)

whose conventional and minimal trellises are shown in Fig. 2.

Fig. 2
figure 2

Conventional a and minimal b trellis modules for the C(5,3,4) convolutional code with generator matrix in Eq. 4. In the minimal trellis, solid edges represent “0” codeword bits while dashed edges represent “1” codeword bits

Full size image

Figure 3 shows the BER performance of the three new algorithms based on the minimal trellis, as a function of parameter M for a fixed value of the signal-to-noise ratio E b/N 0 (so that the BER is close to 10 − 6), for the C(7,4,4) code. In the figure, it is also shown the performance of the VA over the conventional trellis (or the minimal trellis), which is not a function of M. Note that the performance of the proposed algorithms increase with M, up to the limit where it reaches the performance of the VA.Footnote 2 Figure 4 shows similar results but for the C(5,3,4) code. The performance curves show sometimes a rough behaviour due to the particular dynamics of the proposed algorithms. The increase of only 1 in M may have a huge impact sometimes and almost not any impact in some other cases, also depending on the algorithm. We noted this same behaviour when examining the performance, obtained by simulating the proposed algorithms over other codes.

Fig. 3
figure 3

BER versus M for the proposed algorithms, considering the C(7,4,4) code, soft decision decoding and E b/N 0 = 6 dB

Full size image
Fig. 4
figure 4

BER versus M for the proposed algorithms, considering the C(5,3,4) code, soft decision decoding and E b/N 0 = 6 dB

Full size image

In order to determine the minimal value of M required by each algorithm to achieve a performance close to the VA, we define the tolerance γ, which is the maximum acceptable BER degradation, so that the BER achieved by the sub-optimum decoding algorithm is at most γ above the BER obtained by the VA. For instance, considering the C(7,4,4) code, E b/N 0 = 6 dB, and supposing a tolerance of γ = 10 − 6, the MMA requires M = 6, while the PMA M = 9 and the FMA M = 10. Thus, the MMA requires a smaller number of surviving sates than the PMA and the FMA. But recall that MMA only selects the surviving states at the end of the module, while the PMA and the FMA select them at each section. If the tolerance is increased to γ = 5×10 − 6, then there is a reduction in the required values of M for the MMA from M = 6 to M = 5 and for the FMA from M = 10 to M = 9. Increasing the tolerance even more, to γ = 10 − 5, decreases the required values of M by 1 for all algorithms. Different results are obtained if we consider the C(5,3,4) code at an E b/N 0 = 6 dB. In this case and supposing γ = 10 − 6, the MMA needs M = 6 while the PMA and FMA require M = 10 surviving states. The PMA and the FMA have exactly the same performance because the minimal trellis module for this code has a constant number of states per section, namely 16 states per section. If the tolerance is increased to γ = 5×10 − 6, then the required M is decreased by 1 for all algorithms. By further increasing the tolerance to γ = 10 − 5, there is no change in the required values of M. These results are summarised in Table 1. We observe that different M are required by each algorithm to achieve a performance close to the VA, within a given tolerance. A comparison among the complexity of each algorithm, for each particular required value of M, is performed in the next section.

Table 1 Required value of M for each code for different BER tolerances γ at E b/N 0 = 6 dB
Full size table

5 Complexity analysis

The complexity of a decoding algorithm can be determined in many ways. For instance, in [31], the authors characterise the hardware cost of each operation related to the Viterbi algorithm. Here, we analyse the complexity only as a function of the number of arithmetic operations required by the algorithm, as to be independent of the specific implementation technology or architecture. In this paper, we consider only summations (\({\cal S}\)), multiplications (\({\cal X}\)) and comparisons (\({\cal C}\)). First we consider only the operations required to calculate the accumulated state metrics. Later we take into account the effort required to select the best M states in each section, when needed by the MA and its variants. For the sake of simplicity, memory reads and writes are not taken into account.

Either in the VA, in the MA, or in the proposed algorithms, the first step in decoding is to calculate the edge metrics. These metrics may be calculated by means of the Hamming distance (hard decision decoding) or the Euclidean distance (soft decision decoding). We focus on the case of the Euclidean distance, where when using a constant modulus modulation such as BPSK it is known that the edge metric can be greatly simplified [32]. Supposing the use of a trellis module Φ with parameters ν t , b t and l t in section t, as defined in Section 2, then the edge metric can be calculated as \(\sum_{j=1}^{l_t} y^j_t \cdot x^j_t,\) where \(y^j_t\) is the j-th symbol of the received l t -tuple and \(x^j_t\) is the corresponding edge symbol. Therefore, a total of l t \({\cal X}\) and \(\left( l_t-1 \right)\) \({\cal S}\) are required per edge. Then, the state metrics are expanded, by summing the previous state metrics with the calculated edge metrics. Therefore, one additional summation per edge is required. Furthermore, in order to select the best new state metrics, we have to compare the accumulated metrics of all edges reaching a given state. If \(N_{\rm e}^{it}\) is the number of edges starting in section t and reaching state i in section t + 1, then the total number of operations Λt in the section t of the trellis module Φ, required to calculate the accumulated state metrics, is:

$$ \Lambda^t = \sum_{i=1}^{N_{\rm s}^{t+1}} \, l_t\ N_{\rm e}^{it} ({\cal X}+{\cal S})+(N_{\rm e}^{it}-1) \, {\cal C} \label{comp_phi_t} $$
(5)

where \(N_{\rm s}^{t+1}\) is the number of states in section t + 1 that are reached by edges coming from section t. This analysis is carried out over the n ′ sections. Thus, the number of operations Λ in the module is

$$ \Lambda = \sum_{t=0}^{n^\prime-1}\, \sum_{i=1}^{N_{\rm s}^{t+1}} \, l_t \ N_{\rm e}^{it}\,({\cal X}+{\cal S}) + (N_{\rm e}^{it} -1) \,{\cal C}. \label{comp_phi} $$
(6)

The parameters \(N_{\rm e}^{it}\) and \(N_{\rm s}^{t+1}\) are a function of the state and edge complexity profiles of the trellis module and of the type of algorithm in use. For the VA, \(N_{\rm e}^{it}=\frac{2^{({b}_t+{ \nu}_t)}}{2^{{\nu}_{t+1}}}\) and \(N_{\rm s}^{t+1}=2^{{ \nu}_{t+1}}\). Note that the number of required summations and multiplications matches the non-normalised (multiplied by k) TC(Φ) defined in Eq. 1, while the number of required comparisons matches MC(Φ) in Eq. 2 after the same de-normalisation by k. Equation 6 is specialised for the minimal trellis (n ′ = n, \(l_t=1 \: \forall \: t\)) as

$$ \Lambda_{\rm min} = \sum_{t=0}^{n-1}\, \sum_{i=1}^{N_{\rm s}^{t+1}} \ N_{\rm e}^{it}\,({\cal X}+{\cal S}) + (N_{\rm e}^{it} -1) \,{\cal C}. \label{comp_min} $$
(7)

In the case of the sub-optimum algorithms, as the MA and its variants operating over the minimal trellis proposed in this paper, it is hard to calculate exactly the number of required operations. That is because the number of edges in each section is a random variable, as well as the number of states reached at each trellis section. These random variables can be tracked during the computer simulations, so that the actual average values can be used for calculating the computational complexities. For instance, Table 2 lists \({\bar N}_{\rm s}^{t+1}\), the average number of states in section t + 1, that are reached by edges coming from section t, for the three proposed algorithms, the C(7,4,4) code, E b/N 0 = 6 dB, and using the minimal M for γ = 10 − 6 (M = 6 for MMA, M = 9 for PMA and M = 10 for FMA).

Table 2 \(\bar{N}_{\rm s}^{t+1}\) for C(7,4,4), E b/N 0 = 6 dB and γ = 10 − 6
Full size table

Supposing the use of the minimal trellis, the average number of edges starting in section t and reaching state i in section t + 1, \({\bar N}_{\rm e}^{it}\), can be written as a function of \({\bar N}_{\rm s}^{t}\), M, \({\widetilde b}_t\) and \(\widetilde{\nu}_t\), such that for the MMA, we have:Footnote 3

$$ \label{eq:N_MMA} {\bar N}_{\rm e}^{it}= \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{2^{\widetilde{b}_t}{\bar N}_{\rm s}^t}{{\bar N}_{\rm s}^{t+1}}, & \text{if } 0< t \leq \left(n-1\right) \\[12pt] \displaystyle\dfrac{2^{\widetilde{b}_t}\min \left\{M,{\bar N}_{\rm s}^{t}\right\}}{{\bar N}_{\rm s}^{t+1}}, & \text{if } t=0 \end{array} \right. $$
(8)

for the PMA

$$\label{eq:N_PMA} {\bar N}_{\rm e}^{it}=\frac{2^{\widetilde{b}_t}\min \left\{2^{\widetilde{\nu}_t-\nu}M,{\bar N}_{\rm s}^{t}\right\}}{{\bar N}_{\rm s}^{t+1}} $$
(9)

while for the FMA

$$\label{eq:N_FMA} {\bar N}_{\rm e}^{it}=\frac{2^{\widetilde{b}_t}\min \left\{M,{\bar N}_{\rm s}^{t}\right\}}{{\bar N}_{\rm s}^{t+1}}. $$
(10)

The minimal operator in expressions (9) and (10) appears because, during the operation of the FMA or the PMA, \({\bar N}_{\rm s}^{t}\) can be smaller than the maximum number of surviving states allowed by each algorithm (this is illustrated in Table 2 for the case of the FMA in section t = 2, for instance). Then, we equate from Eqs. 7–10 the average arithmetic complexity of each proposed algorithm over the minimal trellis as

$$ \begin{array}{lll} \Lambda_{\rm min}^{\rm FMA} &=& \sum_{t=0}^{n-1}\, 2^{\widetilde{b}_t}\min \left\{M,{\bar N}_{\rm s}^{t}\right\}\, ({\cal X} + {\cal S}) \: \\ &&+ \: \left(2^{\widetilde{b}_t}\min \left\{M,{\bar N}_{\rm s}^{t}\right\} - {\bar N}_{\rm s}^{t+1}\right)\,{\cal C} \label{comp_FMA} \end{array} $$
(11)
$$ \begin{array}{lll} \Lambda_{\rm min}^{\rm PMA} &=& \sum_{t=0}^{n-1}\,2^{\widetilde{b}_t} \min \left\{2^{\widetilde{\nu}_t-\nu}M,{\bar N}_{\rm s}^{t}\right\} ({\cal X} + {\cal S}) \: \\ &&+ \: \left(2^{\widetilde{b}_t}\min \left\{2^{\widetilde{\nu}_t-\nu}M,{\bar N}_{\rm s}^{t}\right\} - {\bar N}_{\rm s}^{t+1}\right)\,{\cal C} \label{comp_PMA} \end{array} $$
(12)
$$ \Lambda_{\rm min}^{\rm MMA} = \sum_{t=0}^{n-1}\, 2^{\widetilde{b}_t}{\bar N}_{\rm s}^t\, ({\cal X} + {\cal S}) \: + \: \left(2^{\widetilde{b}_t}{\bar N}_{\rm s}^t-{\bar N}_{\rm s}^{t+1}\right)\,{\cal C}. \label{comp_MMA} $$
(13)

Moreover, since the number of states reached at any trellis section varies, the effort to select the best states (when required) also varies. From Table 2, we see that when running the FMA with γ = 10 − 6, for instance, in the first section the best 10 states have to be selected, on average, out of around 14 (\(\bar{N}_{\rm s}^1\) = 14.24 in Table 2), in the second section 10 states have to be selected out of about 20 (\(\bar{N}_{\rm s}^2\) = 19.79) and so on. Such an effort, in terms of comparisons, of selecting the M largest elements within a vector of \(\bar{N}_{\rm s}^{t+1}\) elements can be approximated by [33]:Footnote 4

$$ \label{knuth} \Pi_t(M,\bar{N}_{\rm s}^{t+1})=\bar{N}_{\rm s}^{t+1}-M+\sum_{i=\bar{N}_{\rm s}^{t+1}-M+1}^{\bar{N}_{\rm s}^{t+1}} \log_2 i. $$
(14)

Therefore, in order to fairly compare the proposed algorithms, we have to take into account the effort required to select the best states, an action carried out at each section in the PMA and FMA and only at the end of the module in the MMA. Then, the complexity of the proposed algorithms over the minimal trellis can be written as

$$ \label{comp_total} \Lambda_{\rm min}^{\rm total}=\Lambda_{\rm min}+\left( \sum_{t=0}^{n-1}\Pi_t \right) {\cal C} $$
(15)

where Λmin is calculated according to Eqs. 11–13 and Π t is the average number of comparisons required at section t to select the best states, as defined in Eq. 14, and as function of M, \({\bar N}_{\rm s}^{t+1}\) and to the particular operation of the algorithm.

Based on Eq. 15, we can present the average number of arithmetic operations required by each of the proposed algorithms, considering the minimal value of M given in Table 1 for a given tolerance with respect to the performance of the VA. The values of \(\bar{N}_{\rm s}^t\), t = 0, ⋯ ,n, used in Eqs. 11–15 are obtained by simulations. The case of the C(7,4,4) code is shown in Table 3, while Table 4 deals with the case of the C(5,3,4) code. The number of operations required by the VA, over the conventional (\(\text{VA}_\text{c}\)) and minimal trellises (\(\text{VA}_\text{m}\)), are also shown.

Table 3 Arithmetic operations required for decoding C(7,4,4) at E b/N 0 = 6 dB
Full size table
Table 4 Arithmetic operations required for decoding C(5,3,4) at E b/N 0 = 6 dB
Full size table

From Table 3, we conclude that all algorithms based on the minimal trellis required much less operations than \(\text{VA}_\text{c}\). Moreover, the MMA algorithm requires less \({\cal S}\), \({\cal X}\) and \({\cal C}\) than \(\text{VA}_\text{m}\) for the tolerances γ = 5×10 − 6 and γ = 10 − 5, while requiring less \({\cal S}\) and \({\cal X}\) and basically the same number of \({\cal C}\) than \(\text{VA}_\text{m}\) for a tolerance of γ = 10 − 6. The savings can be considerable, being of 35% in terms of \({\cal S}\) and \({\cal X}\) and of 21% in terms of \({\cal C}\) for the case of γ = 10 − 5. The PMA and FMA can reduce even more the required number of \({\cal S}\) and \({\cal X}\), even to less than half of those of the \(\text{VA}_\text{m}\) (e.g. FMA with γ = 10 − 5), but they require an increase in the number of \({\cal C}\). It is interesting to note that FMA requires less operations than PMA.

Analysing Table 4, we reach similar conclusions, with the PMA and FMA considerably reducing the number of required \({\cal S}\) and \({\cal X}\), while increasing the number of \({\cal C}\) with respect to the \(\text{VA}_\text{m}\).Footnote 5 Again, the MMA requires less \({\cal S}\) and \({\cal X}\) than \(\text{VA}_\text{m}\) for the three tolerances, while requiring basically the same number of \({\cal C}\) than \(\text{VA}_\text{m}\) for γ = 10 − 6 and reducing it for larger γ. The above results explicitly show the performance-complexity trade-off that can be operated by means of the proposed algorithms. Depending on the applications, it may be interesting to lose just a little bit of performance in exchange of a reduced complexity, which may reflect on the device battery lifetime. Moreover, we can also conclude that PMA and FMA are the best option only if summations and multiplications have a cost that is similar to that of comparisons in the specific receiver architecture. However, if comparisons cost more, what is more usual, then MMA would be the best choice among our proposed algorithms.

6 Final comments

In this paper, we proposed sub-optimum decoding algorithms to be used with the minimal trellis associated to the convolutional code. The algorithms are all variations of the M-algorithm, and their operation is matched to characteristics inherent to the minimal trellis. Three algorithms were proposed. Numerical results showed that considerable complexity reductions can be obtained with respect to the Viterbi algorithm operating over the conventional and the minimal trellis, at the cost of a very small reduction in the BER performance. Moreover, the best choice among the proposed algorithms, in terms of complexity reduction, depends on the minimal trellis topology and on the particular receiver architecture. As a future work, we intend to investigate the performance of the proposed algorithms in the fast fading channel (or the Rayleigh channel) scenario.