A Metamodel-Based Analysis of the Sensitivity and Uncertainty of the Response of Chesapeake Bay Salinity and Circulation to Projected Climate Change

Abstract

Numerical models are often used to simulate estuarine physics and water quality under scenarios of future climate conditions. However, representing the wide range of uncertainty about future climate often requires an infeasible number of computationally expensive model simulations. Here, we develop and test a computationally inexpensive statistical model, or metamodel, as a surrogate for numerical model simulations. We show that a metamodel fit using only 12 numerical model simulations of Chesapeake Bay can accurately predict the early summer mean salinity, stratification, and circulation simulated by the numerical model given the input sea level, winter–spring streamflow, and tidal amplitude along the shelf. We then use this metamodel to simulate summer salinity and circulation under sampled probability distributions of projected future mean sea level, streamflow, and tidal amplitudes. The simulations from the metamodel show that future salinity, stratification, and circulation are all likely to be higher than present-day averages. We also use the metamodel to quantify how uncertainty about the model inputs transfers to uncertainty in the output and find that the model projections of salinity and stratification are highly sensitive to uncertainty about future tidal amplitudes along the shelf. This study shows that metamodels are a promising approach for robustly estimating the impacts of future climate change on estuaries.

Introduction

Climate change is likely to produce changes in the temperature, salinity, circulation, and water quality of estuaries and other coastal environments, and it is important to understand what effects these changes will have and whether current practices to manage water quality and the health of estuarine ecosystems are robust against future changes. Because future climate change is difficult to predict, as a result of a myriad of uncertainties including future emissions of greenhouse gases and climate sensitivity, accounting for uncertainty when predicting the impacts of climate change on estuaries and evaluating management strategies is essential. However, most studies on the effects of climate change on estuaries have not accounted for the many sources of uncertainty present nor have they robustly quantified the uncertainty and its greatest sources in their assessments.

Many studies have used model simulations to predict the effects of sea level rise (SLR), and most have used multiple plausible values of SLR to attempt to account for uncertainty. For example, Hong and Shen (2012) and Rice et al. (2012) modeled changes in Chesapeake Bay salinity, stratification, and circulation under three different SLR scenarios and found that SLR caused increased salinity and stratification. Chua and Xu (2014) obtained similar results in their numerical model of San Francisco Bay. Hilton et al. (2008) also predicted increased salinity in the Chesapeake Bay as a result of SLR using both a statistical and a numerical model, Huang et al. (2015) found that sea level rise increased salinity in their model of Apalachicola Bay, and Mulamba et al. (2019) found that sea level rise caused a nonlinear increase in salinity in their model of the St. Johns River. Lee et al. (2017) and Ross et al. (2017) found that sea level rise changed modeled tidal amplitudes and phases in Chesapeake and Delaware Bays, and similarly Ralston et al. (2018) and Ralston and Geyer (2019) found that increased depth from dredging increased tidal range, salinity, and stratification in the Hudson River estuary. A few studies have also examined the effects of changing river discharge: Gibson and Najjar (2000) and Muhling et al. (2018) used statistical models to project changes in mean salinity in the Chesapeake Bay under different scenarios derived from climate model output. They found that model uncertainty, i.e., differences in projected regional changes of temperature and precipitation between climate models, produced uncertainty in future river discharge, which subsequently produced uncertainty about future salinity.

The previously cited studies have not accounted for many of the sources of uncertainty that are present in the climate system and in the models used, and they also did not quantify the uncertainty that they did include. Some of the studies simulated conditions under only a few climate scenarios, in part due to the computational costs of running numerical model simulations (e.g., well over 100 simulations would be required to replicate the combined greenhouse gas and model uncertainty in the CMIP5 climate model dataset). Others of the cited studies have examined how the numerical or statistical model output varies under different levels of only one factor, such as mean sea level (which is simple to perturb). However, this method ignores the large amount of uncertainty that may be contributed by other factors, such as changing streamflow, as well as possible interactions between factors. Most studies using this one-factor method also did not specifically quantify the uncertainty about the chosen input and the resulting uncertainty in the output. Finally, most studies have ignored structural and parametric uncertainty in their estuary models; ignoring this uncertainty could be particularly problematic for biogeochemical models that contain large numbers of uncertain parameters (Hemmings et al. 2015).

A sensitivity and uncertainty analysis is a useful tool for understanding how uncertain the model output is (uncertainty analysis), as well as how and which uncertain model inputs are responsible for the uncertainty in the model output (sensitivity analysis) (Saltelli et al. 2004). Many practitioners consider a sensitivity and uncertainty analysis to be an essential step in the model development and application process (Jakeman et al. 2006; Sin et al. 2009). In this study, we conduct a variance-based sensitivity analysis that determines the contributions of the diverse model inputs to the variance in the model output. If a model input parameter, which is variable in accordance with a specified probability distribution that represents uncertainty about the parameter, produces a large amount of variance in the model output, the model is considered to be sensitive to the parameter. Because sensitivity analysis identifies the input parameters that have the strongest influence on the model output, it has many potential uses including simplifying the model and identifying important areas for future research (Saltelli et al. 2008). However, we are aware of only one study that conducted a quantitative sensitivity analysis on a coastal or estuarine model (Mattern et al. 2013). One reason may be that methods for sensitivity analysis commonly require many numerical model simulations and are infeasible for computationally expensive ocean models.

In other fields of study, computationally inexpensive statistical models have been applied as tools to analyze the sensitivity and uncertainty of large, computationally expensive numerical models. The statistical model, or metamodel or emulator, is fit (or trained) using a limited number of numerical model simulations, and predictions from the statistical model are used to obtain the large number of data points required for a proper sensitivity and uncertainty analysis. Pioneering work in this field was conducted by Sacks et al. (1989), and useful reviews of metamodels and applications to sensitivity and uncertainty analysis are available in Saltelli et al. (2008), Storlie et al. (2009), and Iooss and Lemaître (2015). Climate modeling is one particular field that has widely made use of metamodels. For example, Holden et al. (2010) used a metamodel to calibrate and analyze the sensitivity of an intermediate complexity model, Schleussner et al. (2011) developed a metamodel to analyze the uncertainty surrounding projections of a decline in the Atlantic Meridional Overturning Circulation, and Castruccio et al. (2014) used a metamodel to emulate model temperature and precipitation time series under different CO₂ concentration trajectories. Metamodels have also been used in several studies of coastal and estuarine systems, although none of these studies examined the effects of future climate change. Chen et al. (2018) used artificial neural networks (ANNs) as metamodels to predict salinity and hydrodynamics in San Francisco Bay. van der Merwe et al. (2007) also used an ANN to predict hydrodynamics in the Columbia River estuary. Mattern et al. (2013) used a polynomial chaos expansion, a metamodel method, to analyze the sensitivity and uncertainty of model predictions of hypoxia in the northern Gulf of Mexico. Parker et al. (2019) used Gaussian process regression to predict water levels in an estuary.

There are a few drawbacks to some of the previous methods used to emulate model simulations of estuarine hydrodynamics and biogeochemistry. Due to the large number of parameters involved in an artificial neural network, an ANN is commonly considered to be a “black box” approach—it is difficult to glean an understanding of the natural system from the ANN model fit. ANNs are also particularly vulnerable to overfitting, which results in deceptively high prediction skill when given the input values used to train the model and exceedingly low skill and the inability to generalize when given other values (Razavi et al. 2012). A large number of training simulations may be needed to fit a metamodel using the polynomial chaos expansion approach—for example, Mattern et al. (2013) noted that the number of required simulations scales as an exponential function of the number of inputs, and as a result, the authors fit a separate metamodel for each of the input parameters. Although Mattern et al. (2013) did conduct a sensitivity and uncertainty analysis using their metamodel, because they fit a separate metamodel to each input parameter, they were not able to include the effect of interactions between the input parameters. Chen et al. (2018), van der Merwe et al. (2007), and Parker et al. (2019) did not use their metamodels to conduct a sensitivity and uncertainty analysis and instead focused primarily on evaluating the accuracy of the metamodel predictions and on the computational time saved.

In this study, we examine the use of the Gaussian process (GP) regression as a computationally inexpensive way to emulate climate change simulations from a computationally expensive numerical estuary model and to conduct a sensitivity and uncertainty analysis. Compared to other metamodel approaches that have been applied to coastal and estuarine systems, a Gaussian process metamodel has fewer parameters and the meanings of these parameters are more straightforward, which makes the GP metamodel more interpretable and requires fewer expensive training simulations. Furthermore, oceanographers may find GP metamodels to be especially intuitive as they are analogous to the kriging routines commonly used to interpolate oceanographic observations. To test this approach, we analyze the sensitivity and uncertainty of future salinity and circulation in the Chesapeake Bay. We present a simple test case that focuses on salinity and circulation in the summer, when hypoxia is prevalent in the bay, and that considers only three exogenous variables that are known to affect salinity and circulation and that may change in the future: mean sea level, average streamflow between January and May, and the amplitude of tides along the ocean boundary. The objective is to determine how sensitive circulation and salinity projections are to these three variables and how uncertain future salinity and circulation values are. Although we begin with a relatively simple case, these results may be relevant for future studies that may account for a larger number of uncertain factors and consider more complex model outcomes, such as the size and duration of hypoxic conditions.

Methods

Numerical Model

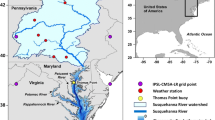
Numerical model simulations were performed using the Finite Volume Coastal Ocean Model (FVCOM) (Chen et al. 2003, 2006). Most aspects of the model configuration, including the horizontal mesh, vertical discretization, bathymetry, and physics options are identical to those described in more detail by Ross et al. (2017). Briefly, the model domain covers both Chesapeake and Delaware Bays and the adjacent Mid-Atlantic Bight, although this paper focuses only on results from Chesapeake Bay (Fig. 1). The numerical model uses the vertical wall assumption: sea level rise does not inundate low-lying land. The model uses ocean boundary conditions from the Hybrid Coordinate Ocean Model (HYCOM) reanalysis (Chassignet et al. 2003, 2007) along with tidal boundary conditions from the Oregon State University TOPEX/Poseidon Global Inverse Solution tide model (TPXO8) (Egbert et al. 1994; Egbert and Erofeeva 2002). Atmospheric wind, radiation, and heat flux forcing are obtained from the North American Regional Reanalysis (NARR) (Mesinger et al. 2006). Freshwater inflows and associated temperatures are determined from US Geological Survey observations for ten rivers, eight of which discharge to the Chesapeake Bay.

Fig. 1

Chesapeake and Delaware Bay portion of the numerical model domain. Colors show the bathymetry of the numerical model. Dots and text show the locations of the 11 selected observation sites in the mesohaline region of Chesapeake Bay

The modeling strategy in this study is to configure the numerical model to approximately simulate “typical” conditions, then see how these conditions change as factors for mean sea level, tidal amplitude, and river discharge are changed. To simulate typical conditions, freshwater discharge for each river was input using a smoothed monthly mean climatology derived from observations during the years 1991 to 2000, which was identified by U.S. Environmental Protection Agency (2010) to be a period of typical hydrological conditions. For atmospheric forcing, the relationship between circulation and wind speed in the Chesapeake Bay is nonmonotonic with varying directional and time dependence (Section 3), so winds cannot be averaged like river discharge. Instead, to obtain a simulation representative of typical conditions, the year 2009 was selected as the source of time-varying atmospheric forcing. 2009 appears to be a typical year from a meteorological perspective; for example, it is the most recent year in which May–June average NARR wind speed and air temperature over the bay were both within 0.5 standard deviations from the 20-year (1999 to 2018) mean. All other aspects of the model configuration are identical to the model used in Ross et al. (2017).

The model was first used to simulate the years 2008 (to spinup) and 2009 (to evaluate the reproduction of climatological conditions). Then, we ran a series of 13 strategically chosen simulations that represent potential realizations of future conditions.

Uncertainty and Projected Changes in Streamflow, Sea Level, and Tidal Range

To simulate the effects of uncertain future conditions, numerical model experiments were performed by repeating the year 2009 simulation with perturbations applied to three model forcing variables that affect salinity and circulation and that may change in the future: mean sea level, tidal boundary conditions, and streamflow. For this simple test case, we neglect changes in wind and other factors that may also change salinity and circulation in the future (Section 3). Our results will thus underestimate uncertainty, but will still capture the effects and associated uncertainty of three major drivers of salinity and circulation and provide a framework for including additional factors in future work. All perturbations were uniformly spread across the range of values that could plausibly be experienced in the year 2050. Perturbations to sea level and streamflow assume that the high Representative Concentration Pathway (RCP) 8.5 greenhouse gas emissions scenario (Riahi et al. 2011) is realized, although conditions under other emissions scenarios are similar in this region in 2050. In all parts of this study, we neglect any correlation between the three exogenous parameters. Although the parameters are likely correlated to some extent, for example, sea level and streamflow change will have some correlation due to temperature dependence, uncertainty for each parameter is also driven by different factors, such as regional oceanographic variability and Antarctic ice sheet contributions for SLR (Kopp et al. 2014) and precipitation parameterizations and internal variability for streamflow change. Similarly, as discussed later in this section, boundary tidal amplitude may also have some correlation with SLR, but we are assuming that uncertainty about the magnitude and direction of the changes represented by the boundary amplitude is significantly greater than the uncertainty due to correlation with uncertain SLR. Accounting for correlations between parameters is also beyond the scope of this study.

Plausible ranges of sea level rise were obtained from the supplementary material of Kopp et al. (2014). We designed the model experiments to cover the plausible ranges for all locations within the model domain, which range from − 8 cm to + 101 cm. We note that we have neglected deep uncertainty about future sea level; i.e., we consider that the (Kopp et al. 2014) probability density is the actual, correct PDF of future sea level. Kopp et al. (2014) also neglected some uncertainty surrounding the response of the Antarctic ice sheet to climate change (DeConto and Pollard 2016), but we avoided most of this uncertainty by focusing on sea level in 2050 rather than in later periods when uncertainty is larger (Bakker et al. 2017; Kopp et al. 2017). We are also assuming that SLR is uniform over the model domain, as in Ross et al. (2017).

Uncertainty about future freshwater inflow into the bay was represented by perturbing the mean streamflow between January and May, because January to May flow has a strong correlation with summertime stratification and hypoxia (Murphy et al. 2011). A rough estimate of plausible values was obtained by examining the range of 29 climate and hydrological model simulations of streamflow from the Susquehanna River produced by the US Bureau of Reclamation (Brekke et al. 2013, 2014). From these results, we estimated that plausible future values could range from 8% lower to 38% higher. Additional information is provided in the supporting information (Section S2). This − 8 to + 38% range also generally encompasses ranges for January–May streamflow change for the Susquehanna River simulated by other models (Irby et al. 2018; Johnson et al. 2012; Seong et al. 2018). The same perturbation was applied to all ten of the rivers in the model; this is a reasonable assumption since projected changes are fairly similar in all of the Chesapeake Bay tributaries, and applying a separate change to each tributary would greatly increase the number of model runs necessary and introduce highly correlated inputs.

Most of the climate and hydrological models project that the largest percent changes in streamflow will occur in January and February with a gradual decrease in the change towards May. This result is consistent with projections of large precipitation increases in winter and the increasing importance of evapotranspiration in warmer months (Najjar et al. 2009). To represent the time dependence of change, each perturbation was applied by multiplying the daily river discharge in the control experiment by a time series of scaling factors. The scaling factors were created by setting a factor of one at the end of May 31, assuming a linear trend in the scaling factor from January through May, and finding the appropriate starting value such that the desired overall perturbation to the January–May average was applied.

The final uncertain parameter we considered was boundary tidal amplitude. It is important to note that some changes in tides due to sea level rise are simulated by the numerical model, and the effects of these changes on salinity and circulation would be accounted for as part of the sensitivity to sea level. However, other changes in tides, such as those caused by basin-scale trends or estuary-shelf-ocean feedbacks, are not included in the model and need to be accounted for as uncertainty in the tidal boundary condition forcing. We also used the tidal boundary condition uncertainty to account for uncertainty about the actual impact of future SLR on changing tides in the bay.

The amplitudes of tidal harmonic constituents in an estuary may vary for several reasons, including sea level rise and feedbacks between the estuary, continental shelf, and open ocean; changes in stratification and internal tides; and changes in the radiational component of solar tides. Woodworth (2010), Müller (2012), Devlin et al. (2018), and Talke and Jay (2020), and Haigh et al. (2020) provide more detailed discussions and additional references. Observations of tidal amplitudes in the study region do in fact contain a variety of trends, and Ross et al. (2017) found that many of the trends were caused by rising sea levels and could be simulated by the numerical model used in this study. However, Ross et al. (2017) also found trends in the observations that are apparently unrelated to sea level rise and are not simulated by the model; they found an average background trend (the trend after subtracting the modeled effect of sea level rise) of − 7.88% century^− 1 in the amplitude of the principal lunar semidiurnal component of the tides (M₂) and a background trend of − 10.05% century^− 1 in the amplitude of the principal solar semidiurnal component (S₂). Although Ross et al. (2017) projected that SLR would increase tidal amplitude in many parts of Chesapeake Bay, global tide model simulations by Schindelegger et al. (2018) predicted that SLR would decrease M₂ amplitude along the majority of the US East Coast. Without accounting for the effect of SLR, Ray (2009) and Müller et al. (2011) found similar negative S₂ amplitude trends at nearly all of the Atlantic Coast sites in their studies. However, Ray (2009) and Müller et al. (2011) found mainly positive M₂ amplitude trends, and Devlin et al. (2018) found an overall positive correlation between increased sea level and observed tidal amplitudes at many stations in the Chesapeake Bay and surrounding region, although increased sea level lowered tidal amplitudes at some stations in the region and along the US East Coast.

In addition to uncertainty about observed tidal trends and whether they have been caused by SLR, there is also uncertainty about whether numerical models can properly simulate the effects of future SLR on tides. The numerical model configuration in this study does not include wetting and drying and inundation of shorelines as sea level rises. Although the model is capable of reproducing historical tides and changes without these features (Ross et al. 2017), the potential for inundation becomes substantial with higher sea level rise amounts, and with these effects included the numerical model predicts a nearly opposite effect of sea level rise on tidal amplitudes in the Chesapeake Bay (Lee et al. 2017). Additionally, because tides are specified along the boundary, the model does not capture potential basin-scale changes or feedbacks between tides in the estuary, shelf, and open ocean. As a result, sea level rise produces negligible changes in tides along the shelf and open ocean in the numerical model used in this study (Ross et al. 2017). However, global model simulations do predict shelf- and basin-scale changes in tides in response to SLR that could propagate to the coastal region and Chesapeake Bay (Pickering et al. 2017; Schindelegger et al. 2018).

To account for uncertainty about historical tidal trends and whether these trends will continue into the future, and whether rising sea levels will produce changes in tides that are not simulated by the numerical model, model simulations were conducted with the amplitudes of all constituents used to generate the tidal boundary conditions perturbed within a range of ± 10%.

Experimental Design, Model Output, and Evaluation

After choosing plausible ranges for the three numerical model input parameters, the model was evaluated at a total of 12 points within the parameter space. The numerical model simulations consisted of an initial set of 9 experiments chosen using a stratified Latin hypercube sample optimized to cover the parameter space uniformly (Pleming and Manteufel 2005; Damblin et al. 2013) followed by 4 additional simulations to take advantage of the remaining computational resources (Fig. 2). One of these 13 model runs using large values for both tidal amplitude scale and SLR encountered a numerical instability and was removed from the remainder of the study, leaving a total of 12 model runs, or 4 times the number of uncertain input parameters.

Fig. 2

Points in streamflow scale, tidal amplitude scale, and sea level rise space where numerical model simulations were run. The unfilled circle indicates a simulation that failed

We calculated four metrics from the numerical model output: mean salinity, vertical and horizontal salinity differences, and the estuarine exchange velocity. Mean salinity is simply vertically averaged salinity. The vertical salinity difference, or stratification, is the difference between the topmost and bottommost model layers. The horizontal salinity difference is the difference in column-mean salinity between the two stations bounding the mesohaline region of the bay (stations 3.2 and 5.5 in Fig. 1). The horizontal difference is a strong proxy for the mean horizontal salinity gradient in the central bay region (the correlation coefficient between the summer mean difference and the gradient determined using linear regression is 0.99 over the 12 model runs), but the difference is simpler to compute and more intuitive than the gradient. The exchange velocity was defined following Chant et al. (2018) as half of the shear of the low-passed longitudinal velocity. We chose these metrics because they provide overall measures of estuarine hydrodynamics and have been examined in other theoretical and modeling studies (Section 3), and because they are also related to the health of the estuarine ecosystem. For example, mean salinity controls the ranges of oyster habitat and diseases (Kimmel et al. 2014), and high salinity stratification produces hypoxia by reducing the downward mixing of oxygenated water (Officer et al. 1984).

All four metrics were calculated at the model output resolution (hourly) for the model points closest to the chosen Chesapeake Bay Program (CBP) water quality database observation stations located in the mesohaline region where stratification and hypoxia often occur (Fig. 1). The metrics were averaged over the 11 stations and over the 59-day period (two lunar months) from May 1 to June 28, a period when stratification is common and hypoxic conditions typically develop.

Finally, the year 2009 control simulation from the numerical model was evaluated by calculating the same four metrics for all observations in the water quality database at the 11 stations. For vertical salinity difference, the measurements closest to the surface and bottom from each vertical profile were used; measurements typically began 1 m below the surface and were taken at 1-m intervals. Metrics were calculated and averaged separately for each 59-day period (May 1 through June 28) from 1984 to 2017 to obtain rough estimates of the climatological probability distribution of each metric. The water quality database does not include observations of velocity, so the exchange velocity metric could not be evaluated.

Metamodel

After running the numerical model at the chosen design points, Gaussian process (GP) metamodels were fit to the model output metrics and used to create the large number of model simulations required for the sensitivity and uncertainty analysis. GP metamodels are analogous to the kriging methods commonly used to interpolate irregularly spaced oceanographic observations; the idea is to use kriging to interpolate the model output from the design points to any number of other points.

The Gaussian process metamodel assumes that the numerical model output Y evaluated at points x in model parameter space can be represented as a Gaussian process, a finite set of random variables with a joint Gaussian distribution (Rasmussen and Williams 2006), that is defined by a mean function m and a covariance function c:

$$ \mathbf{Y}(\mathbf{x}) \sim GP\left( m(\mathbf{x}), c(\mathbf{x}_{i}, \mathbf{x}_{j}) \right) . $$

(1)

After using a small set of numerical model simulations to learn the parameters for the mean and covariance functions, the Gaussian process can be used to predict values of the numerical model output at new points in the numerical model parameter space by combining the mean function at the new points with the covariance between the output at the new points and the output at the training points. A short summary of the mathematical details of the Gaussian process metamodel is provided in Appendix A, and we refer the reader to Rasmussen and Williams (2006) and Roustant et al. (2012) for further details.

A separate GP model was fit for each of the four output variables of interest (Section 3). All models were fit using the DiceKriging package for R (Roustant et al. 2012). The mean function for the models for vertical salinity difference and exchange velocity was a constant value. We included a constant value plus linear trend terms in the mean function for the other two models: the model for mean salinity, which we justify based on previous studies finding roughly linear sensitivity to mean sea level (Hilton et al. 2008; Hong and Shen 2012) and on our interest in estimating the linear sensitivity, and the model for the horizontal salinity difference, which we justify based on expected sensitivity to all of the model inputs (Section 3). For nearly all models, using a linear trend or only a constant value produced similar skill in the cross-validation evaluation (discussed next). The only exception was the model for the horizontal salinity difference, which obtained a poor fit to the numerical model without a linear trend term. All models used a squared exponential as the covariance function, which parameterizes the covariance as a combination of an overall process variance and a separate length scale for each input parameter (Appendix ??).

Overall, the metamodels for the vertical salinity difference and exchange velocity had a total of five parameters that needed to be estimated: the constant mean, the process variance, and the three covariance length scales (one for each of the predictor variables—SLR, tidal amplitude scale, and streamflow scale). The metamodels for mean salinity and horizontal salinity difference also included a linear trend term for each of three predictor variables, bringing the total to eight estimated parameters.

Compared to the amount of data used to fit the metamodel (12 simulations), the number of estimated parameters in the metamodels is large. Larger simulation sizes, on the order of 10 times the number of inputs, are typically considered optimal for fitting metamodels with more inputs than the three used in this study (Loeppky et al. 2009). To verify that predictive skill was obtained with a smaller experimental design, as well as to ensure that the metamodels were not overfit to the data (i.e., that the metamodels have not merely “memorized” the data but have actually learned the relationship between the inputs and output), we evaluated the predictive capability of the metamodels by applying cross-validation. Cross-validation methods are commonly used in statistical modeling and machine learning studies to estimate the error of a model when predicting new data (versus the residual error of a model, which is the error of the model when predicting using the same data that was used to fit the model). These methods work by repeatedly (1) splitting a dataset into “training” and “testing” partitions, (2) fitting a model using the training dataset, (3) generating new predictions using the fitted model and the testing dataset, and (4) calculating an error measure from the difference between the predicted and actual values in the testing dataset. The average of the error measure over a number of cross-validation iterations provides an estimate of the predictive error, and large predictive errors indicate a model that is poor and may be overfitting. For GP models, cross-validation is particularly useful for assessing the predictive ability because the GP predictions perfectly interpolate the training data and the residual error is zero (Marrel et al. 2008).

In this study, we used leave-one-out cross-validation, where only one data point at a time is used in the test dataset and the model is fit to all of the remaining data. The coefficients for the trend term(s) in each metamodel were reestimated during each cross-validation iteration, which improves the error estimates for small sample sizes (Roustant et al. 2012). The covariance parameters were also reestimated. The cross-validation results were evaluated graphically and by computing the Nash-Sutcliffe efficiency (Nash and Sutcliffe 1970):

$$ Q^{2} = 1 - \frac{{\sum}_{i=1}^{n} \left( Y_{i} - \hat{Y_{i}} \right)^{2}}{{\sum}_{i=1}^{n} \left( \overline{Y} - Y_{i} \right)^{2}} $$

(2)

where Y_i is the value simulated by the numerical model, Y¯ is the mean numerical model value, and Y_i ̂ is the metamodel prediction. We also calculated the mean absolute error:

$$ MAE = \frac{1}{n} {\sum}_{i=1}^{n} \left\| \hat{Y_{i}} - Y_{i} \right\| . $$

(3)

Sensitivity and Uncertainty Analysis

The metamodels were used to analyze the sensitivity of the numerical model to the three uncertain parameters. We calculated Sobol’ indices for the first-order and total effects using the methods described in Jansen (1999), Saltelli et al. (2010), and Le Gratiet et al. (2014). Sobol’ indices are based on a decomposition of the variance of the model output into additive functions of the model input. The first-order Sobol’ index is defined as

$$ S_{i} = \frac{V_{X_{i}} \left( E_{X_{-i}}(Y|X_{i}) \right)}{V(Y)} $$

(4)

and the total effect index as

$$ S_{Ti} = \frac{E_{X_{-i}} \left( V_{X_{i}} (Y | X_{-i}) \right)}{V(Y)}. $$

(5)

Y |X_i denotes the model output with factor i fixed, and the function $\phantom {\dot {i} }E_{X_{-i}}$ gives the expected value over all values of the factors that are not fixed. Finally, the function V gives the variance. Therefore, for a given factor, the first-order index gives the expected fraction by which the output variance would be reduced if the factor i was exactly known, while the total index gives the fraction of variance that would remain if all factors except factor i were known (Saltelli et al. 2010). The presence of interactions with other factors is indicated by total indices that are greater than first-order indices (or a sum of first-order indices that is less than 1). Given the small number of parameters in the model used in this study, it would also be feasible to compute all of the intermediate-order indices to precisely determine interactions. However, the results will show that all interactions are negligible. Following Le Gratiet et al. (2014), the Sobol’ indices were calculated from the metamodel output and bootstrapping was used to determine uncertainty. The Sobol’ index calculation used a Monte Carlo approach with metamodel predictions at 2¹⁶ points in predictor (SLR–tidal amplitude scale–streamflow scale) space along with 100 random samples of the metamodel uncertainty at each point and 100 bootstrap samples to determine the uncertainty due to numerical integration. Justification for using 2¹⁶ points is provided in the Supporting Information (Section S4).

The sensitivity and uncertainty analysis requires specifying the probability distributions for each of the factors being analyzed. We based these probability distributions (Fig. 3) on the same information used to assess the plausible ranges of future values. The PDF for future sea level rise, which was derived from the Kopp et al. (2014) values for the Sewells Point location, was a truncated Gaussian distribution with a mean of 43.90 cm, variance of 10.86² cm², and truncations at 3 and 101 cm. The PDF for streamflow change was specified using a triangular distribution over the − 8% to + 38% plausible range. This distribution is a simple approximation that captures our expectation that future streamflow change is more likely to be near the center of the plausible range than near either tail. For the same reason, we also used a triangular distribution to represent uncertainty about future tidal amplitudes. Although the distribution for tidal amplitude spans the ± 10% plausible range, 75% of the probability is contained within ± 5%.

Fig. 3

Probability density (left panels) and cumulative distribution (right panels) functions used in the sensitivity and uncertainty analysis

Results

Numerical Model Control Simulation and Evaluation

The control run of the numerical model successfully reproduces historical mean salinities (Fig. 4); both the mean and mode of the observations are close to the numerical model value. The vertical salinity difference is not simulated as well, with the model value being slightly lower than the range of observed values. This under-prediction of stratification is a common problem in numerical models of Chesapeake Bay (Li et al. 2005; Irby et al. 2016). Some of the errors in the vertical salinity difference may also be a result of errors in the model bathymetry. The numerical model horizontal salinity difference of 12.1 is larger than the largest historical value of 11.5, a bias that is also found in other models Xu et al. (2012), cf. their Table 5). Overall, despite some biases, we consider the model simulations to be sufficiently realistic for the sensitivity and uncertainty analysis. Furthermore, as we are primarily interested in projecting future changes rather than exact future values, some errors in the model historical simulation should not affect the results.

Fig. 4

Mean salinity and vertical and horizontal salinity differences averaged over the 11 selected Chesapeake Bay Program sites in the central Chesapeake Bay (Fig. 1) for the period between May 1 and June 28. Bars show histograms of the observations between 1984 and 2017, and dotted lines show the numerical model simulations

Metamodel Results

Cross-validation shows that the metamodels are capable of predicting the numerical model results with reasonable skill (Fig. 5). For mean salinity and the vertical salinity difference, the efficiency coefficients Q² are above 0.9, and the mean absolute errors (MAEs) are two orders of magnitude smaller than average values. The metamodel for salinity also accurately predicted a salinity value that was more than 1 unit below all other numerical model salinity values. Prediction skill is slightly lower but still reasonable for the exchange velocity: the MAE remains two orders of magnitude less than the mean value, but the Q² metric is closer to 0.8. The skill metric is even lower for the horizontal salinity difference (0.586), although the positive skill and low MAE indicate that this model still has some predictive skill. The horizontal salinity difference may be more challenging to predict as it is determined by salinity at only two stations at opposite ends of the mesohaline region. Overall, the low errors for all variables indicate that despite being fit to only 12 numerical model simulations, the metamodel is a reliable surrogate for the numerical model and can be used for the sensitivity and uncertainty analysis.

Fig. 5

Results from leave-one-out cross-validation of the metamodel. x-axis gives the values simulated by the numerical model. y-axis gives the metamodel prediction when the metamodel was fit to all other points. Solid lines correspond to a perfect match

Figure 6 shows how the metamodel predictions change when only one factor is varied and the other factors are fixed at their present-day values. Table S2 in the supporting information also provides the coefficients of the trend terms in the metamodels. These results show that increased tidal amplitude produces lower mean salinity and stratification. Higher streamflow lowers the mean salinity and increases the horizontal salinity difference. The vertical salinity difference and estuarine circulation may also increase with streamflow. Sea level rise produces a large increase in mean salinity and also increases the stratification and estuarine circulation.

Fig. 6

Results from varying one factor with the other factors fixed at their present-day values. Solid lines denote the metamodel mean prediction, and shaded regions indicate the 95% confidence intervals

Tidal amplitude at the boundary is the largest source of uncertainty for mean salinity, vertical salinity difference, and exchange velocity (Fig. 7), while streamflow dominates the sensitivity and uncertainty of the horizontal salinity difference. Projections for all four variables are at most weakly sensitive to mean sea level. It is important to note that this does not necessarily mean that changes in sea level have a small effect on the metamodel predictions or numerical model output; sea level actually has a fairly large effect on the metamodel predictions in Fig. 6, but our uncertainty about future sea level is smaller than our uncertainty about future streamflow and tidal amplitudes (Fig. 3), so the overall contribution of sea level to the uncertainty is relatively small. Figure 7 shows only the total-effect indices since the first-order effects are essentially the same (Supporting Information Figure S1). This indicates that the interactions between tidal amplitude, mean sea level, and streamflow are negligible.

Fig. 7

Total effect Sobol’ indices for tidal amplitude, sea level, and January-May streamflow. The total effect index indicates the fraction of the variance (or the uncertainty) in the model output that would remain if all factors except the given factor were known (Section 3). Error bars indicate 95% confidence intervals

Given the probabilities for changes in tidal amplitude, streamflow, and sea level considered in this study, the salinity and circulation in the Chesapeake Bay are likely to be different in 2050 (Fig. 8). Increases in mean salinity, vertical salinity difference, and exchange circulation are all very likely, with more than 90% of metamodel predictions exceeding the present-day values. This certainty is consistent with our assumptions that mean sea level and streamflow are likely to increase in the future (Fig. 3) and the metamodel-predicted effects of increases in mean sea level and streamflow (Fig. 6). On the other hand, the horizontal salinity difference is about as likely to increase as it is to decrease, which results from a balance between a larger difference caused by increased streamflow and a smaller difference caused by higher mean sea level.

Fig. 8

Projections of future salinity and circulation in 2050. Gray bars are histograms derived from 10,000 metamodel predictions that sample both input and metamodel uncertainty. Dotted and dashed lines indicate metamodel-derived best estimates of the current and future values, respectively (the best estimate of the future is predicted using the mean of each input PDF). Red dots indicate the 12 numerical model simulations. Percentages in the left and right sides of each panel show the percent of metamodel simulations below and above the current best estimate, respectively

Figure 8 also highlights the challenges of representing uncertainty about future conditions with a limited number of numerical model simulations. For example, even though the 12 training model simulations we used were chosen to cover a wide range of uncertainty, 8.0% of the metamodel predictions of vertical salinity difference are below the lowest numerical model prediction (although some of this uncertainty also comes from the metamodel uncertainty).

Discussion

Consistency with Previous Studies and Theory

The results of our numerical model simulations and metamodel fit with varying values of mean sea level, streamflow, and tidal amplitude are broadly in agreement with expectations from analytical solutions for idealized estuaries and with results from observational and modeling studies of both the Chesapeake Bay and other estuaries. Although a complete investigation of the causes of the sensitivities revealed by the metamodels is beyond the scope of this study, in this section, we compare our results with previous studies to verify that the metamodels have produced physically reasonable results. We compare our results with the classical analytical solutions for the central portion of an estuary at steady state derived by Hansen and Rattray (1965) and expanded and discussed by MacCready (1999), Monismith et al. (2002), MacCready and Geyer (2010), Geyer and MacCready (2014), and others. We also compare our results with the observational study of Newark Bay by Chant et al. (2018) and the observational and modeling study of the lower Hudson River Estuary by Ralston and Geyer (2019).

In some idealized solutions, increasing depth has no effect on the exchange circulation, but it does decrease the horizontal salinity gradient (MacCready and Geyer 2010; Chant et al. 2018). This theory is consistent with the modeling and observational results from Ralston and Geyer (2019), who found that SLR decreased the horizontal salinity gradient and caused a negligible increase in the exchange circulation. On the other hand, in observations of a different estuary, Chant et al. (2018) found that SLR significantly increased the exchange circulation. They proposed that this effect is due to the short length of the estuary that they studied, which prevents the salinity field from completely adjusting to SLR and results in a salinity gradient that is constant or slightly increasing with SLR.

Our results are broadly more consistent with those of Ralston and Geyer (2019): the metamodel fits indicate that SLR likely causes a decrease in the horizontal salinity gradient, but SLR also causes a small increase in the exchange circulation (Fig. 6). It should be noted that metamodel uncertainty is higher for the effect of SLR on the exchange circulation for SLR values above 0.75 m, and the uncertainty for the slope of the effect of SLR on the horizontal salinity gradient is also large. Ralston and Geyer (2019) note that the exchange circulation is theoretically proportional to salinity at the mouth S₀ and river discharge Q_r:

$$ u_{e} \approx \frac{2}{3} \left( \frac{\upbeta g S_{0} Q_{r}}{W} \right)^{1/3} , $$

(6)

with β the saline contraction coefficient, g the gravitational acceleration, and W the width, but they obtained a better fit to their idealized model simulations by replacing the leading coefficient with $\frac {1}{3}$ and replacing S₀ with the local salinity S(x). This scaling also provides a good fit to our model results. Using the January–May average streamflow for Q_r and a width of 15 km, linear regression estimates the leading coefficient in Eq. 6 to be 0.43, between 1/3 and 2/3. This fit has an R² value of 0.84. When using a more general nonlinear least squares regression to also estimate the exponent in Eq. 6, we obtain an estimated exponent of 0.63, closer to 2/3 rather than 1/3, and a leading coefficient of 0.78 with similarly small residual error. It should be noted that the width of the Chesapeake Bay varies significantly, and using other reasonable values for width changes the leading coefficient but not the overall goodness of the fit. The residuals from the first fit have a moderate correlation with mean sea level (R = 0.46), and including an additive sea level term in the linear regression model for Eq. 6 results in a better fit (R² = 0.89; R² adjusted for degrees of freedom also increases) and reduces the leading coefficient to 0.36.

We found that the vertical salinity difference increased slightly with higher mean sea level, a result contrary to classical theory but consistent with that of Ralston and Geyer (2019). However, similar to the case for exchange circulation, the metamodel uncertainty is higher for SLR above 0.75 m. Increased stratification in response to SLR has also been found in model simulations of Chesapeake Bay by Hong and Shen (2012) and San Francisco Bay by Chua and Xu (2014).

Other aspects of our results are consistent with both idealized solutions and other modeling studies. In our metamodel simulations, SLR causes higher mean salinity at a rate of 2.31 m^− 1 (Fig. 6; Table S2). Hilton et al. (2008) simulated summer salinity in the Chesapeake Bay using ROMS and found that the relationship between salinity and mean sea level in the central bay was about 2.5 m^− 1. Also using a different model, Hong and Shen (2012) found a slightly weaker relationship between bay-average salinity and mean sea level of between 1.2 and 2.0 m^− 1. Our model shows a linear scaling between mean salinity and sea level, whereas idealized solutions predict that the salt intrusion length and mean salinity are nonlinear functions of depth (MacCready 1999; Hilton et al. 2008). However, we may not have explored a large enough sea level range to detect a nonlinear scaling.

In our results, higher streamflow lowers the mean salinity and increases the horizontal and vertical salinity differences and the exchange circulation. This result is consistent with both classical solutions and Chant et al. (2018) and Ralston and Geyer (2019). Li et al. (2016) also obtained similar results in their numerical model simulations of Chesapeake Bay. Idealized solutions suggest that the salt intrusion length and the horizontal salinity gradient are proportional to Q^− 1/3 or Q^− 1/7 (Monismith et al. 2002; Ralston et al. 2008), whereas our results show mean salinity and the horizontal salinity difference varying essentially linearly with streamflow. However, we simulated conditions following the spring freshet, and the majority of our simulations of projected climate change included even higher streamflow, so our results are primarily in the region where a nonlinear Q^− 1/3 or Q^− 1/7 dependence would appear to be nearly linear. In addition to being proportional to Q^− 1/3, the length of salt intrusion is also proportional to the inverse of the average tidal velocity $U_{t}^{-1}$ in idealized solutions (Monismith et al. 2002; Ralston and Geyer 2019). Our finding of a stronger sensitivity of mean salinity to tidal amplitude than to streamflow is consistent with this theory.

Higher tidal amplitude is expected to produce greater mixing, but in classical approximations, both the exchange circulation and stratification are not affected by mixing. This insensitivity occurs because although an increase in mixing does initially reduce the exchange circulation and stratification, the resulting weaker circulation increases the horizontal salinity gradient, and eventually balance is restored as the circulation and stratification return to their steady-state values (MacCready and Geyer 2010). Our results are nearly consistent with this theory: we found that higher amplitude reduced the mean salinity, may have increased the horizontal salinity difference (although metamodel uncertainty is high), and caused negligible changes in the exchange circulation. However, in our model, increasing the tidal amplitude significantly reduced the vertical salinity difference.

Neglected Climate Factors and Other Uncertainties

One limitation of the current study is that we have neglected the potential for future changes in typical wind speeds and directions. Wind speed and direction are increasingly being recognized as major factors controlling vertical stratification, circulation, and hypoxia in Chesapeake Bay (Scully 2010a; 2010b; Lee et al. 2013; Du and Shen 2015; Li et al. 2016; Scully 2016). However, changes in wind speed and direction and their impacts are difficult to model. Winds can change rapidly in the study region, and the responses of stratification and hypoxia to changes in wind speed and direction in the Chesapeake Bay are nonmonotonic and have varying time dependence (Li and Li 2011; Xie and Li 2018). As a result, it is necessary to force the numerical model with realistic time series of wind speed and direction; winds cannot be simply averaged like river discharge. Statistical methods could be used to produce stochastic wind speed time series with controllable mean speeds and directions; however, this could also significantly increase the number of ocean model simulations required due to the number of additional parameters introduced and the added random variability.

Observations show that water temperatures in the Chesapeake Bay region have increased during the last century (Preston 2004; Najjar et al. 2010; Ding and Elmore 2015; Rice and Jastram 2015), and this warming trend is likely to continue in the future as greenhouse gas concentrations and atmospheric temperatures also continue to increase. In the present study, we have neglected the impacts of rising temperatures on stratification under the assumption that any temperature changes would be fairly evenly distributed in the relatively shallow bay. However, observations by Preston (2004) do suggest that the Chesapeake Bay bottom water may be warming faster than surface water, so future work may benefit from including temperature changes. Warmer water is also likely to have a significant impact on the bay ecosystem (Najjar et al. 2010; Muhling et al. 2018) and should be included in future work to model these impacts.

The present study has also neglected model structural uncertainty, which could be a large source of uncertainty, particularly in cases of high sea level rise. Lee et al. (2017) showed that modeled changes in tides in Chesapeake and Delaware Bays depend significantly on whether or not the numerical model allows low-lying land to be inundated as sea level rises. Vertical stratification may also depend on the parameterization used to model turbulent mixing, although Li et al. (2005) found that parameterization choice had only a minor impact on simulation of Chesapeake Bay stratification.

Finally, uncertainty about parameters in the numerical ocean model is also ignored in the present study. Parameters that may be worth considering in future studies include the background vertical mixing coefficient (studied by Li et al. (2005)) and the bottom roughness length.

Possible Improvements to Metamodel Methods

It is worth noting that our metamodeling approach, despite being advanced relative to many previous studies in estuarine and coastal regions, is relatively simple compared to methods developed and applied in other fields including climate modeling and statistics. To model the multiple outputs of our estuarine model, we employed what has been termed the “many single-output emulators” method (Conti and O’Hagan 2010). In this method, each output variable is predicted by a completely separate, independent metamodel. However, what Conti and O’Hagan (2010) termed “multi-output” emulators have been developed, which would allow the prediction of the multiple outputs of the estuarine model with a single metamodel (e.g., Conti and O’Hagan (2010), Fricker et al. (2013)). Similarly, we developed metamodels to predict numerical model output that was averaged over both time and space; however, methods for emulating model outputs that vary over time and space have been developed. Methods to emulate model output that varies over space have tended to apply dimensionality reduction methods (i.e., singular value decomposition/principal component analysis) to reduce the large number of grid/mesh points in the numerical model output into a smaller number of orthogonal values that can be easily emulated (e.g., van der Merwe et al. (2007)). However, our approach of averaging the results over time and space makes the metamodels more interpretable and is sufficient for our intent to assess the overall sensitivity of the bay physics to climate change. Finally, the Gaussian process metamodels used in this study fit nearly linear relationships between all of the inputs and outputs (Section 3; Fig. 6). In this case, using simpler multiple linear regression metamodels would be adequate to emulate the numerical model output. We did not choose linear regression models for this study because the relative linearity of the results was not expected a priori.

We expect that our study could also be improved by increasing the number of numerical model simulations used to fit the metamodels. Although the metamodels performed well in cross-validation (Fig. 5), confidence intervals for some of the Sobol’ indices remained large relative to the values of the indices (Fig. 7; Supporting information Section S4). We expect that increasing the numerical model sample size would increase the certainty regarding the metamodel predictions. Increasing the sample size would also help identify areas where the model response is nonlinear or where interactions between terms are present.

A final enhancement to the approach used in this study would be to more robustly quantify the uncertainty about the streamflow and tidal amplitude scales. For both scales, we assumed a triangular PDF with the mode and limits set to rough estimates based on the range of a set of numerical model simulations (for streamflow) and the range of different results reported in the literature (for tidal amplitude). In contrast, the PDF for sea level was obtained from Kopp et al. (2014), who combined a multitude of studies and model experiments that quantified uncertainty about different processes that affect mean sea level to create a final PDF. Although our simple approximations for streamflow and tidal amplitude uncertainty were sufficient to test the value of the metamodeling approach, more robustly quantifying the uncertainty about these parameters would yield more accurate estimates of projected changes and their uncertainties.

Conclusions

Given the assumed probability distributions for future streamflow, mean sea level, and tidal amplitude, future stratification, salinity, and estuarine circulation in the Chesapeake Bay are all likely to be higher than present-day averages in 2050. However, uncertainty about all of the input factors contributes to significant uncertainty in the modeled future conditions. Mean salinity and vertical stratification, which are highly important for biogeochemistry and ecology in the bay, are strongly sensitive to tidal amplitude; however, the effects of uncertainty about tidal amplitude have been examined by only one other study (Lee et al. 2017). Therefore, these results highlight the benefits of conducting a sensitivity and uncertainty analysis and the success of the metamodel approach. Future work should expand the analysis to examine more factors beyond the three used here, including factors related to model structural and parametric uncertainty, and include biogeochemical components. The results also showed that the system was simpler than we initially expected: interactions between the three factors examined were negligible, and the responses of the four variables studied were relatively linear. As a result, future sensitivity and uncertainty analyses may consider simpler methods that do not require the relatively time-consuming building of the metamodels and calculation of the Sobol’ indices.

Appendix A: Details of Gaussian Process Metamodel

We initially treat the model output as the sum of one or more trend terms and a zero-mean Gaussian process:

$$ \mathbf{Y}(\mathbf{x}) = f(\mathbf{x})^{\intercal} \upbeta + GP\left( 0, c(\mathbf{x}_{i}, \mathbf{x}_{j}) \right) $$

(7)

where, for an x consisting of n points in d-dimensional space, f(x)^⊺ is a n × p design matrix for the trend term(s) and β is a p × 1 vector of trend parameters. For a simple intercept only (constant mean, or flat trend), p = 1 and f(x)^⊺ would be a vector of n ones and β the intercept. For a linear trend, these terms are analogous to multiple linear regression, with p = 1 + d, f(x)^⊺ a matrix with rows consisting of a 1 followed by the d coordinates of one point, and β representing the intercept and a slope for each dimension.

The covariance function gives the covariance between the GP at two points x_i and x_j. Under the assumption that the model output is a relatively smooth function of its inputs (Roustant et al. 2012), we modeled the covariance with a squared exponential function:

$$ c(\mathbf{x}_{i}, \mathbf{x}_{j}) = \sigma^{2} {\prod}_{k=1}^{d} \exp \left( -\frac{\left( \mathbf{x}_{i,k} - \mathbf{x}_{j,k} \right)^{2}}{2 {\theta_{k}^{2}}} \right ) $$

(8)

Here, 𝜃_k functions as a length scale that adjusts the distance of the decay of the covariance between model results at different values of factor k, and σ² is a constant known as the process variance.

The separate terms in Eq. 7 can be combined into a single Gaussian process with non-zero mean, and, following Roustant et al. (2012), prediction of the numerical model output Ŷ at a new point x_∗ can be obtained from the expected value of the GP conditional on the n known values of the numerical model simulations Y at points x used to train the metamodel:

$$ E\left[\hat{Y}(\mathbf{x}_{*}) \right] = f(\mathbf{x}_{*})^{\intercal} \hat{\upbeta} + \mathbf{C}_{\mathbf{x}_{*}}^{\intercal} \mathbf{C}_{\mathbf{x}}^{-1} (\mathbf{Y} - \textbf{F} \hat{\upbeta}) $$

(9)

where f(x_∗)^⊺β̂ is the sum of the trend function(s) given estimated values of the coefficients β̂, Cx_∗⊺ is a 1 × n vector of the covariance between the output at the new point and the n training points, Cx− 1 is the inverse of the n × n covariance matrix of the training simulations, Y is a vector of the values of the numerical simulations used for training, and Fβ̂ is a vector of the values of the trend(s) at the training points. Eq. 9 shows that when numerical simulations are near the prediction point in parameter space, and therefore have high covariance, the deviation of the prediction from the trend will be influenced by the deviation of the nearby simulations from the trend. Far away from any numerical simulations used to fit the metamodel, the metamodel prediction will tend to revert towards the value from the trend functions only. Uncertainty about the outcome of the Gaussian process is also typically included when making predictions. See Roustant et al. (2012) for the formulation of the variance of the predicted values. Intuitively, variance is low near points where the numerical model has been run and is large at points far away from known model simulations.