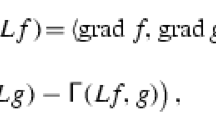On Riemannian Foliations over Positively Curved Manifolds

Abstract

We prove that, under reasonable conditions, odd co-dimension Riemannian foliations cannot occur in positively curved manifolds.

1 Introduction

A basic problem in Riemannian geometry is to construct examples of manifolds with positive sectional curvature. Such examples are sparse in the literature. On the other hand, the set of manifolds with non-negative sectional curvature enjoys large classes: compact Lie groups with bi-invariant metrics, compact symmetric spaces, normal homogeneous spaces, their Cartesian products, and quotients by free isometric group actions.

Such discrepancy suggests that only a very restrictive class of manifolds carries a metric of positive sectional curvature. The question of existence of positively curved metrics still makes sense in the set of manifolds with symmetry (see [26] for a survey), where one might be interested in presenting conditions on the orbits, for instance. This paper establishes a hard obstruction for existence of positive sectional curvature in a special, although interesting, class of metrics that generalizes (principal) symmetries.

Given a compact Riemannian manifold (M, g), a foliation $\mathcal{{F}}$ in (M, g) is said to be Riemannian if its leaves are locally equidistant. Here we only consider non-singular non-trivial foliations, i.e., all leaves have the same positive dimension. We prove:

Theorem 1

Let $\mathcal{{F}}$ be an odd-codimensional Riemannian foliation with bounded holonomy on a compact manifold M. Then M has a vertizontal plane with non-positive sectional curvature.

We say that a foliation has bounded holonomy if there is a constant that uniformly bounds the norms of all holonomy fields with unit initial condition. This class contains principal and associated bundles with compact structure group together with all regular homogeneous foliations defined by proper group actions (see Sect. 3.3).

Theorem 1 lies in two contexts. The first is a generalization of a classical result of Berger: every Killing field in a compact even-dimensional manifold with positive sectional curvature has a zero (see Petersen [19, p. 193] for a proof). Given such a manifold, Theorem 1 recovers Berger’s result by considering the foliation defined by a Killing vector field.

The second context is Wilhelms conjecture. (see, e.g., [1, 3, 7, 13]):

Wilhelm’s Conjecture

Let $\pi : M^{n+k}\rightarrow B^{n}$ be a Riemannian submersion from a compact manifold M with positive sectional curvature. Then $k<n$.

Theorem 1 completely rules out the possibility of a Riemannian submersion with compact holonomy group over an odd-dimensional bases, implying Wilhelm’s Conjecture under these hypothesis (we refer to [10, p. 13] for the definition of holonomy group and Sect. 3.1 and Proposition 3.4 for the relation between compact holonomy group and bounded holonomy).

Theorem 1 also plays a role in a connection between Berger’s result to Wilhelm’s conjecture: if one considers only principal submersions from positively curved spaces, then Berger’s result guarantees that their principal group has rank 1—if not, M would admit a $S^1\times S^1$-action, and thus either M or $M/(S^1\times \{1\})$ is an even-dimensional manifold with a non-vanishing Killing field.¹ We call a Riemannian foliation $\mathcal{{F}}$ principal if the leaves of $\mathcal{{F}}$ coincide with the orbits of an isometric action by a (not-necessarily compact) Lie group G with discrete isotropy groups. Berger’s theorem cannot be directly applied in this situation since the quotient of M by a one-parameter subgroup may be an orbifold or even non-Hausdorff.

Theorem 1 provides a generalization of Berger’s result that handles the foliation case, by considering the Riemannian foliations defined by $\exp (\mathfrak {h}')$ and $\exp (\mathfrak {h})$, where $\mathfrak {h}$ is a maximal abelian subalgebra of $\mathfrak {g}$ and $\mathfrak {h}'$ is a subalgebra of $\mathfrak {h}$ of co-dimension 1. The co-dimension of one of these foliations must be odd.

Corollary 1.1

Let M be a compact Riemannian manifold with positive sectional curvature. If $\mathcal{{F}}$ is a principal Riemannian foliation given by the group G, then the rank of G is equal to 1.

In both cases, the group G is reduced to either $S^1$, SO(3), or $S^3$. In particular, Wilhelm’s conjecture for principal bundles is reduced to the non-existence of free $S^3$- or SO(3)-actions on positively curved 5-manifolds (in any other case, either the co-dimension is odd or bigger than 3).

Another particular case of Theorem 1 is interesting in its own right: the vertical warping of a connection metric, whose proof sheds light on Theorem 1. Let $\mathcal{{F}}$ be a Riemannian foliation on $(M,g_0)$. We call $g_0$ a connection metric if $\mathcal{{F}}$ has totally geodesic leaves with respect to $g_0$. For any basic function $\phi$, we consider a new metric $g_\phi$ defined as

$$\begin{aligned} g_\phi (X+\xi ,X+\xi )=g_0(X,X)+e^{2\phi }g_0(\xi ,\xi ), \end{aligned}$$

(1)

for horizontal X and vertical $\xi$. We prove:

Theorem 2

Let $\mathcal{{F}}$ be a Riemannian foliation in a compact manifold M and $g_0$ be a connection metric. If $g_\phi$ has positive sectional curvature for some $\phi$, then $\mathcal{{F}}$ has a fat point. That is, there is a point $p\in M$ where the image of the O’Neill tensor, $A_X^*\xi$, is non-zero for all non-zero horizontal X and vertical $\xi$.

The notion of fatness was introduced by Weinstein [24] and is a required property for a Riemannian foliation with totally geodesic leaves to have positive sectional curvature, making it a natural concept to appear in Theorem 2. Theorem 2 has two straightforward implications (see Sect. 2 for a proof):

Corollary 1.2

Let $\mathcal{{F}}$ be a Riemannian foliation in a compact manifold M and $g_0$ be a connection metric. If $g_\phi$ has positive sectional curvature for some $\phi$, then

(i):

the co-dimension of $\mathcal{{F}}$ is even,

(ii):

the dimension of M is smaller than twice the co-dimension of $\mathcal{{F}}$.

Item (i) is a strictly weaker version of Theorem 1. Item (ii) states that Wilhelm’s conjecture holds for $\mathcal{{F}}$ (other results related to rigidity of leaf spaces in the presence of curvature bounds are in Guijarro and Wilhelm [12] and Ou and Wilhelm [18]. An example in Kerin [14] shows that Wilhelm’s Conjecture does not hold if positive curvature is required only in an open and dense set).

The proofs of Theorems 1 and 6.5 follow along the same lines of the proof of Berger’s result, but require two different tools. The main tool is dual holonomy fields (Sects. 1.2 and 4), analogous to the virtual Jacobi fields introduced in [23]. The second tool is an auxiliary space, the bundle of infinitesimal holonomy transformations which we introduce through a natural groupoid associated with the horizontal connection (Sect. 3).

The author would like to thank W. Ziller for presenting a related question that motivated Theorem 1, M. Alexandrino, C. Durán, A. Ribeiro, and K. Shankar for their time helping on specific topics. Special thanks goes to C. Durán and anonymous referees for suggestions.

1.1 Notation

We mostly use the notation of Gromoll and Walschap [10]. We follow the usual nomenclature in Riemannian foliations, calling vectors tangent to leaves vertical vectors and vectors orthogonal to leaves horizontal vectors. We denote the space of vertical vectors at $p\in M$ by $\mathcal{{V}}_p$ and the space of horizontal vectors as $\mathcal{{H}}_p$. They define the vector bundles $\mathcal{{V}}$ and $\mathcal{{H}}$, respectively. The upper indexes h and v denote orthogonal projection to $\mathcal{{H}}$ and $\mathcal{{V}}$, respectively.

The geometry of Riemannian foliations is ruled by two tensors introduced by Gray [8] and O’Neill [17]. We use slight modifications of these tensors as in [9] and [10]. Given horizontal vector fields X, Y and a vertical vector field $\xi$, we define

$$\begin{aligned} A_XY=\nabla ^v_XY=\frac{1}{2}[X,Y]^v, \qquad S_X\xi =-\nabla ^v_\xi X. \end{aligned}$$

(2)

The values of A and S at a point p only depend on the values of X, Y and $\xi$ at p, making them genuine tensors. We use the upper index $*$ to denote the adjoint of an operator and ${-*}$ as the inverse of the adjoint, as in [23]. In particular, we define $A^*_X: \mathcal{{V}}\rightarrow \mathcal{{H}}$ as the unique operator satisfying

$$\begin{aligned} \left\langle A^*_X\xi ,Y \right\rangle =\left\langle A_XY,\xi \right\rangle . \end{aligned}$$

All inner products and covariant derivatives are in M. Holonomy fields are denoted by $\xi$ and $\eta$, dual holonomy fields by $\nu$. Vertical vectors are also denoted by $\xi$ and $\nu$ whenever the context is free from ambiguity, otherwise by $\xi _0$ and $\nu _0$.

1.2 Holonomy and Dual Holonomy Fields

Given a horizontal curve c on M, a vector field $\xi$ is called a holonomy field if it is vertical and satisfies

$$\begin{aligned} \nabla _{{\dot{c}}}\xi =-A^*_{{\dot{c}}}\xi -S_{{\dot{c}}}\xi \end{aligned}$$

(3)

(compare Grove and Gromoll [9] or Gromoll and Walschap [10, p. 17]). Holonomy fields realize the derivative of local holonomy transformations: every point $p\in M$ has an open neighborhood $U\ni p$ where the leaves of $\mathcal{{F}}$ coincide with the fibers of a Riemannian submersion $\pi : U\rightarrow V$. Thus given a horizontal curve c, $\pi \circ c$ induces a local holonomy transformations between neighborhoods of c(0) and c(t) on the leaves $L_{c(0)}$ and $L_{c(t)}$, for small t.

Holonomy fields are entirely determined by the horizontal distribution $\mathcal H$ (see e.g., Sect. 3 and Proposition 3.2). In spite of this, lengths of holonomy fields depend very much on the metric along the vertical distribution. To illustrate this statement, consider a principal U(1)-bundle $\pi : M\rightarrow B$ over a Riemanniain manifold (B, g). Given $\omega : TM\rightarrow \mathbb {R}\cong \mathfrak {u}(1)$, a connection 1-form, and $\lambda >0$, M admits the Kaluza–Klein metric

$$\begin{aligned} g(X+\xi ,Y+\eta )=g(d\pi X,d\pi Y)+\lambda \omega (\xi )\omega (\eta ). \end{aligned}$$

One can see that $\mathcal{{F}}=\{\pi ^{-1}(b)~|~b\in B \}$ is a Riemannian foliation with horizontal distribution $\mathcal{{H}}\,{=}\,\ker \omega$. Let c be a horizontal geodesic and $\xi$ an action field. Then $\xi \circ c$ is a holonomy field for every $\lambda$ (Lemma 3.5), but $||\xi (c(t))||=\lambda \omega (\xi (c(t)))$.

In general, holonomy fields are natural generalizations of action fields in principal bundles: if $\mathcal{{F}}$ is given by the fibers of a principal bundle, all holonomy fields are obtained by restricting action fields to horizontal curves (Proposition 3.6). In this case, if M is compact, we can find a uniform bound for the norm of all holonomy fields with unit initial data.

A dual holonomy field is a vertical field $\nu$ that satisfies

$$\begin{aligned} \nabla _{{\dot{c}}}\nu =-A^*_{{\dot{c}}}\nu +S_{{\dot{c}}}\nu . \end{aligned}$$

(4)

When leaves are totally geodesic, the inner product between two holonomy fields is always constant. In this case, one can think of holonomy fields as their own duals. In any other situation, dual holonomy fields are introduced to play this role (see Proposition 4.1).

Dual holonomy fields do sense the metric along the leaves. They arise in an interesting way when one considers integration along horizontal directions (as in Durán and Sperança [5, Theorem 1]).

Although we ask both holonomy and dual holonomy fields to be vertical, a vector field satisfying $\nabla _{{\dot{c}}}^h\xi =-A^*_{{\dot{c}}}\xi$ is vertical as long as it is vertical at a point (see Sect. 3, Remark 3.1). In particular, along a fixed curve, holonomy and dual holonomy fields are in one-to-one correspondence to initial value.

In contrast to virtual Jacobi fields (whose norms can explode), dual holonomy fields are well behaved and also give an interesting expression for the sectional curvature (Propositions 4.1 and 4.2). Both constructions are closely related: in Verdiani and Ziller [23], based on the choice of a family $\mathcal{{J}}=\{J_1,...,J_s\}$ of Jacobi fields, the virtual Jacobi fields associated to $\mathcal{{J}}$ are the family of fields $\{Z_1,...,Z_s\}$ satisfying $\left\langle J_i,Z_j \right\rangle =\delta _{ij}$. The family $\mathcal{{J}}$ is a Lagrangian subspace of Jacobi fields with respect to a natural symplectic form. Such Lagrangian spaces coincide with maximal families of Jacobi fields with self-adjoint Riccati operator in Wilking [25] or [10, p. 45]. Our dual holonomy fields are constructed in the same fashion, but using an special isotropic subspace instead of a Lagrangian one.

As opposed to action fields, both holonomy fields and dual holonomy fields are, in principle, defined only along curves. This leads to the second tool: we introduce the groupoid of infinitesimal holonomy transformations as an auxiliary space, where we can construct global objects similar to action fields, whose restrictions to curves give rise to all holonomy and dual holonomy fields.

The precise definition of bounded holonomy follows below. Riemannian submersions with compact holonomy groups enjoy interesting properties (see Pro–Wilhelm [20] and Tapp [21, 22]). The condition of bounded holonomy is slightly more general and makes sense for foliations. In Sect. 3.3, we prove that it is satisfied for the common classes of Riemannian foliations mentioned in the beginning.

Definition 1.3

We say that a Riemannian foliation has bounded holonomy if there is a constant L such that, for every holonomy field $\xi$ and every t, $||\xi (t)||\le L||\xi (0)||$.

When M is compact, this condition only depends on the horizontal distribution and not on all the involved structures (see Theorem 6.5). We can also observe that a Riemannian foliation has bounded holonomy if and only if its dual holonomy fields satisfy the bound in Definition 1.3 (Lemma 5.2). This is how the boundedness of holonomy comes into the proof of Theorem 1.

The rest of the paper is divided in five sections. In Sect. 2 we prove Theorem 2. In Sect. 3, we construct the groupoid of infinitesimal holonomy transformations and in Sect. 4 the dual holonomy fields. In Sect. 5 we prove the main theorem and in Sect. 6 we explore further the hypothesis and methods. The boundedness of holonomy is only used on Sect. 5.

2 Proof of Theorem 2

In a vertical warping of a connection metric, the function $\phi$ plays the role of the norm of the Killing field in the proof of Berger result (see Petersen [19, p. 193]). We prove Theorem 2 using Gray–O’Neill’s formula for the vertizontal curvatures of M at a maximum of $\phi$.

Since holonomy fields coincides in the metrics $g_0$ and $g_\phi$ (since these two metrics have the same horizontal distribution, it follows from the discussion below Eq. (3)), we can explicitly compute the S-tensor in the metric $g_\phi$. If $\xi$ and $\eta$ are holonomy fields along a horizontal curve c,

$$\begin{aligned} g_{\phi }({\xi (t),\eta (t)})=e^{2\phi }g_0({\xi (t),\eta (t)})=e^{2\phi }g_0({\xi (0),\eta (0)})\,, \end{aligned}$$

since the $g_0$-inner product of two holonomy fields is constant. The S-tensor associated to $g_\phi$, $S^\phi$, is determined by

$$\begin{aligned} 2g_\phi \left( {S^\phi _{{\dot{c}}}\xi ,\eta }\right) =-\frac{\mathrm{{d}}}{\mathrm{{dt}}}g_\phi ({\xi ,\eta }) =-\frac{\mathrm{{d}}}{\mathrm{{dt}}}[e^{2\phi }]g_0({\xi ,\eta })=2g_\phi ({-d\phi ({\dot{c}})\xi ,\eta }). \end{aligned}$$

In particular, at a minimum of $\phi$, $S^\phi \equiv 0$ and the equation for the unreduced sectional curvature of ${\dot{c}}$ and $\xi$ (see [10, p. 28] or 13) becomes

$$\begin{aligned} K(\xi ,\dot{c})=-\frac{1}{2}||\xi ||^2_{g_0}\mathrm{Hess}\, \phi ({\dot{c}},{\dot{c}})+||A^*_{{\dot{c}}}\xi ||^2_{g_\phi }. \end{aligned}$$

(5)

In addition, $\mathrm{Hess}\,\phi$ is non-negative at this point. Therefore, if K is positive, $||A^*_{{\dot{c}}}\xi ||_{g_\phi }^2$ must be non-zero for every non-zero pair $\dot{c},\xi$.

Corollary 1.2 is a direct consequence of linear algebra: both maps $X\mapsto A_X^*\xi$ and $\xi \mapsto A^*_X\xi$ are injective (whenever $\xi \ne 0$ in the first and $X\ne 0$ in the second), and consequently, being the first map skew-symmetric, they imply item (i) and (ii), respectively. Following Florit and Ziller [6], injectivity of $\xi \mapsto A^*_X\xi$ further implies that the dimension of $\mathcal{{V}}$ is bounded from above by the maximum number of linearly independent vector fields on the sphere of dimension $\dim \mathcal{{H}}-1$. $\square$

Two difficulties appear in a general metric (not a vertical warping of a connection metric): there is related function to maximize (as $\phi$) and the Hessian in (5) is replaced by $\left\langle (\nabla _XS)_X\xi ,\xi \right\rangle$, a term much more difficult to control. The aim of the next sections is to overcome such difficulties by constructing a function that plays the role of $\phi$ in a general Riemannian foliation. We introduce this function in Sect. 5. It is not defined on M but in a subset of the groupoid of infinitesimal holonomy transformations.

Theorems 1, 2, and 6.4 suggest that positively curved foliations may carry fat objects such as a fat point, or a horizontal vector with the property we conjecture below:

Conjecture 1

(Strong Wilhelm’s Conjecture) Let $\mathcal{{F}}$ in M be a Riemannian foliation on a compact manifold with positive curvature. Then, it has a horizontal vector X such that $A^*_X$ is injective.

3 The Infinitesimal Holonomy Bundle

Here we present an auxiliary space used in the proof of Theorem 1. The language of groupoids presents itself as a natural language to describe this object. We referee to [16, Chapter 5] for a deeper introduction to the subject.

Foliations usually do not provide holonomy diffeomorphisms between leaves (as in the case of Riemannian submersions—see [10, p. 12]). However, infinitesimal data can be recovered from holonomy fields. For a horizontal curve $c: [0,1]\rightarrow M$, we define $h: \mathcal{{V}}_{c(0)}\rightarrow \mathcal{{V}}_{c(1)}$ as the linear isomorphism given by $h(\xi _0)=\xi (1)$, where $\xi (t)$ is the holonomy field along c with initial condition $\xi (0)=\xi _0$. We call h an infinitesimal holonomy transformation.

Another way to recover the infinitesimal data is using local horizontal lifts. Given $p\in M$, let U be an open neighborhood of p such that the restriction of $\mathcal{{F}}$ to U is realized by a submersion $\pi : U\rightarrow V$.

Given a horizontal curve c on U, we can find a neighborhood of c(0) $U'\subset U$ of the leaf passing through c(0) and a map $\psi : U\times [0,1]\rightarrow M$ such that

• (1) $\psi (x,0)=x$;

• (2) for every $x\in U'$, $t\mapsto \psi (x,t)$ is a horizontal lift of $\pi (c(t))$.

Since c is horizontal, it must be the horizontal lift of $\pi \circ c$ through c(0), and thus $\psi (c(0),t)=c(t)$. Therefore, independent of $U'$, we can always consider $d\psi _{(c(0),1)}: \mathcal{{V}}_{c(0)}\rightarrow \mathcal{{V}}_{c(1)}$ as an infinitesimal holonomy transformation. Such local construction of horizontal lifts, together with the possibility to divide curves into small concatenated curves, shows that the set of $d\phi$’s coincide with the set of holonomy transformations defined in the first paragraph.

Each infinitesimal holonomy transformation is an element in the set

$$\begin{aligned} {{\mathrm{Aut}}}(\mathcal{{V}})=\{h: \mathcal{{V}}_p\rightarrow \mathcal{{V}}_q~|~p,q\in M, h\in {{\mathrm{Iso}}}(\mathcal{{V}}_p,\mathcal{{V}}_q)\} , \end{aligned}$$

(6)

where ${{\mathrm{Iso}}}(\mathcal{{V}}_p,\mathcal{{V}}_q)$ stands for the set of linear isomorphisms between $\mathcal{{V}}_p$ and $\mathcal{{V}}_q$. Composition and inversion of linear transformations endows ${{\mathrm{Aut}}}(\mathcal{{V}})$ with a Lie groupoid structure. A Lie groupoid is a pair of smooth manifolds $\mathcal {G},M$ (also known as the set of arrows and objects) together with two submersions $\sigma ,\tau :\mathcal {G}\rightarrow M$ called the source and target maps; a partially defined multiplication, $(h,h')\mapsto h'h$, defined on pair of elements satisfying $\sigma (h')=\tau (h)$; an inverse map $i:\mathcal {G}\rightarrow \mathcal {G}$; and (in our case) a bi-unit map–a section of both $\sigma$ and $\tau$ that behaves pointwise as a neutral element (since we deal with natural operations on a set of linear maps, we refer to [16] for further details of the general theory.) In the case of ${{\mathrm{Aut}}}(\mathcal V)$, the maps $\sigma ,\tau : {{\mathrm{Aut}}}(\mathcal{{V}})\rightarrow M$ defined on $h: \mathcal{{V}}_p\rightarrow \mathcal{{V}}_q$ by $\sigma (h)=p$ and $\tau (h)=q$ are the source and the target maps, respectively. They, together with the usual composition of linear maps, satisfy the Lie groupoid axioms: given $h, h'\in {{\mathrm{Aut}}}(\mathcal{{V}})$ such that $\sigma (h')=\tau (h)$, then $\sigma (h'h)=\sigma (h)$ and $\tau (h'h)=\tau (h')$; $\tau (h^{-1})=\sigma (h)$ and vice versa; the unit map, $p\mapsto \mathrm{id}_{\mathcal{{V}}_p}$, is a section for both $\sigma$ and $\tau$ and works as a neutral element.

$\mathcal{{E}}$, the collection of all infinitesimal holonomy transformations defined by $\mathcal{{F}}$, is naturally included in ${{\mathrm{Aut}}}(\mathcal{{V}})$ and is closed by composition and inversion: if $h: \mathcal{{V}}_p\rightarrow \mathcal{{V}}_q$ is realized by the horizontal curve c and $h': \mathcal{{V}}_q\rightarrow \mathcal{{V}}_r$ is realized by $c'$, then $h'\circ h$ is realized by the concatenation of c and $c'$; $h^{-1}$ is realized by the curve $\tilde{c}$ defined by $\tilde{c}(t)=c(1-t)$. The unit map $p\mapsto \mathrm{id}_{\mathcal{{V}}_p}$ is realized by constant curves.

We endow ${{\mathrm{Aut}}}(\mathcal{{V}})$ with the topology defined by the submersion $\sigma \times \tau : {{\mathrm{Aut}}}(\mathcal{{V}})\rightarrow M\times M$ along with the operator norm on ${{\mathrm{Iso}}}(\mathcal{{V}}_p,\mathcal{{V}}_q)$ induced by the metric on M. The space $\mathcal{{E}}$ inherits a topology and a groupoid structure from ${{\mathrm{Aut}}}(\mathcal{{V}})$. Smoothness and related questions are discussed in Sect. 6, but neither topology nor differentiability will be used in the proof of Theorem 1.

As usual for groupoids, the restriction of $\tau$ to an orbit of $\mathcal{{E}}$ defines a principal bundle: let $p\in M$ and denote $\mathcal{{E}}_p=\sigma ^{-1}(p)\cap \mathcal{{E}}$. Then $\tau _p=\tau |_{\mathcal{{E}}_p}$ defines a principal bundle over $\tau (\sigma ^{-1}(p))\cap \mathcal{{E}}=L^\#_p$, the dual leaf through p (see Wilking [25] or [10, p. 40] for the definition of dual leaf). The structure group of $\tau _p$, which we denote by $H_p$, is the set of infinitesimal holonomy transformations realized by closed horizontal loops based at p.

Remark 3.1

In contrast to [25], we consider holonomy fields along general horizontal curves instead of broken geodesics. We prefer to deal with the generality of smooth curves since we believe that it expresses better the non-Riemannian nature of (infinitesimal) holonomy transformations. With smooth curves, we still recover the set of infinitesimal holonomy transformations defined by broken geodesics: every broken geodesic can be made a smooth curve by a reparametrization that makes its velocity zero at cusps – since holonomy transformations are defined by their horizontal lifts, they do not depend on the parametrization of their realizing curves.

To further justify how we are considering general curves, we observe that Eq. (3) together with a vertical initial value defines a vertical vector field. As mentioned, this fact is true for any field satisfying $\nabla ^h_{{\dot{c}}} \xi =-A^*_{{\dot{c}}}\xi$ (in particular, dual holonomy fields).

To prove that the equality $\nabla ^h_{{\dot{c}}} \xi =-A^*_{{\dot{c}}}\xi$ preserves the property of being vertical, observe that $\nabla _{{\dot{c}}}^vZ=A_{{\dot{c}}}Z$ for every horizontal field Z, and therefore

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{dt}}}\left\langle \xi ,Z \right\rangle =\left\langle \xi , \nabla _{{\dot{c}}}Z \right\rangle + \left\langle \nabla _{{\dot{c}}}^h\xi ,Z \right\rangle =\left\langle \xi , A_{{\dot{c}}}Z \right\rangle +\left\langle \xi , \nabla ^h_{{\dot{c}}}Z \right\rangle - \left\langle A^*_{{\dot{c}}}\xi ,Z \right\rangle =\left\langle \xi , \nabla ^h_{{\dot{c}}}Z \right\rangle . \end{aligned}$$

On the other hand, one can always obtain a horizontal frame of vector fields satisfying $\nabla _{{\dot{c}}}^hZ=0$ (for instance, we can use local horizontal lifts of parallel vector fields.)

3.1 Examples

Let us give a brief idea of $\mathcal{{E}}_p$ in some cases:

Case 1

If $\mathcal{{F}}$ is given by the fibers of a Riemannian submersion $\bar{\pi }: M\rightarrow B$, its holonomy group at $\bar{\pi }(p)$ acts via diffeomorphisms on the fiber $F=\bar{\pi }^{-1}(\bar{\pi }(p))$ (see [10, p. 13]). In this case, $H_p$ coincides with the image of the isotropy representation of the holonomy group at $\mathcal{{V}}_p=T_pF$.

Case 2

If $\bar{\pi }: M=P\mathop {\rightarrow }\limits ^{\bar{\pi }} B$ is a principal G-bundle, holonomy fields are restrictions of action fields to horizontal curves (see Lemma 3.5 for a proof), i.e., if ${\hat{\xi }}$ is an action field and c is a horizontal curve, $\xi (t)= \hat{\xi }(c(t))$ is a holonomy field along c. In this case, $H_p$ is trivial since

$$\begin{aligned} \xi (0)={\hat{\xi }}(c(0))={\hat{\xi }}(c(1))=\xi (1) \end{aligned}$$

(7)

for every closed horizontal loop c. Furthermore, $\bar{\pi }\circ \tau _p: \mathcal{{E}}_p\rightarrow B$ is isomorphic to the bundle reduction defined by the connection on P (denoted by P(p) in Kobayashi and Nomizu [15, II.7, Theorem 7.1]), which coincides with $L^\#_p$.

Case 3

More generally, for $\bar{\pi }: M\rightarrow B$ a Riemannian submersion with totally geodesic fibers, $\bar{\pi }\circ \tau _p: \mathcal{{E}}_p\rightarrow B$ is isomorphic to the holonomy bundle of the restriction $\bar{\pi }_p=\bar{\pi }|_{L^\#_p}: L_p^\#\rightarrow B$: given a Riemannian submersion $\bar{\pi }$, we can define a principal bundle $\bar{P}$ by fixing a fiber $F=\bar{\pi }^{-1}(b)$ and gathering all holonomy diffeomorphisms induced by curves from b. When the submersion has totally geodesic fibers, all elements of $\bar{P}$ are inside the bundle P defined by all isometries from F to any fiber (see [10, Theorem 2.7.2]). Moreover, P inherits a natural connection from $\bar{\pi }$ and $\bar{P}$ coincides with bundle reduction of P defined by the inherited connection, passing through $\mathrm{id}: F\rightarrow F$ ($\bar{P}=P(\mathrm{id})$ in the notation of [15]). The structure group of $\bar{P}$ is the holonomy group of $\bar{\pi }$ at $\bar{\pi }(p)$, which we denote here by G.

To see how $\mathcal{{E}}_p$ realizes $\bar{P}$, assume that $M=L^\#_p$ and observe that G acts naturally on $\mathcal{{E}}_p$: if $g\in G$ and $h\in \mathcal{{E}}_p$ are realized by the curves $\beta$ and c, respectively, we set $h\cdot g$ as the transformation realized by the concatenation of $\beta$ followed by the lift of $\bar{\pi }\circ c$ to g(p). Equivalently, $h\cdot g=\tilde{h}\circ dg_p$, where $\tilde{h}$ is the infinitesimal holonomy transformation defined by the lift of $\bar{\pi }\circ c$ to g(p). This action is free, since g is an isometry: $\tilde{h}\circ dg_p=h$ if and only if $g(p)=p$ and $dg_p=\mathrm{id}$, and therefore $g=\mathrm{id}$.

Case 4

The arguments in Case 3 remain valid whenever the holonomy group of the submersion is compact (see Theorem 6.5).

These facts are the main motivations for defining $\mathcal{{E}}$ and $\mathcal{{E}}_p$. We give a more detailed example in Sect. 6.1.

3.2 The Natural Action and Horizontal Lifts

The groupoid $\mathcal{{E}}$ acts naturally on vertical vectors. As we shall see, this action gives rise to all holonomy and dual holonomy fields. Let $\pi :\mathcal{{V}}\rightarrow M$ be the bundle of vertical vectors and define

$$\begin{aligned} \zeta :\mathcal{{E}} {\rtimes } \mathcal{{V}}\rightarrow & {} \mathcal{{V}}\nonumber \\ (h,\xi )\mapsto & {} h(\xi ). \end{aligned}$$

(8)

Here $\mathcal{{E}} {\rtimes }\mathcal{{V}}$ is the fibered product

$$\begin{aligned} \mathcal{{E}} {\rtimes } \mathcal{{V}}=\{(h,\xi )\in \mathcal{{E}}\times \mathcal{{V}}~|~ \sigma (h)=\pi (\xi )\}. \end{aligned}$$

Observe that the restriction $\zeta |_{\mathcal{{E}}_p\times \mathcal{{V}}_p}: \mathcal{{E}}_p\times \mathcal{{V}}_p\rightarrow \mathcal{{V}}$ defines $\mathcal{{V}}$ as a linear bundle associated to $\tau _p: \mathcal{{E}}_p\rightarrow L^{\#}_p$.

Holonomy fields give a natural way to lift horizontal curves from M to $\mathcal{{E}}_p$. For any horizontal curve $c: [0,1]\rightarrow M$, we define ${\hat{c}}: I\rightarrow \mathcal{{E}}$ as

$$\begin{aligned} {\hat{c}}(t)\xi _0= \xi (t), \end{aligned}$$

where $\xi$ is the holonomy field along c with initial condition $\xi (0)=\xi _0$. Observe that $\sigma ({\hat{c}}(t))=c(0)$ and $\tau ({\hat{c}}(t))=c(t)$.

Given $h\in \mathcal{{E}}$ and a horizontal curve c starting at $\tau (h)$, we define the $\tau _p$-horizontal lift of c at h as the curve ${\hat{c}}_h: I\rightarrow \mathcal{{E}}_p$ such that ${\hat{c}}_h(t)={\hat{c}}(t)h$. It follows immediately from definition that all holonomy fields on $L_p^\#$ are recovered by these lifts. We state it as a proposition.

Proposition 3.2

Let $h\in \mathcal{{E}}_p$ and c be a horizontal curve with $c(0)=\tau (h)$. Then

• (1) Given $\xi _0\in \mathcal{{V}}_p$, $\xi (t)=\zeta ({\hat{c}}_h(t),\xi _0)$ is a holonomy field along c;

• (2) Given a holonomy field $\xi$ along c, then $\xi (t)=\zeta ({\hat{c}}_h(t),h^{-1}(\xi (0)))={\hat{c}}(t)(\xi (0))$.

3.3 Bounded Holonomy

With Proposition 3.2 at hand, we can give sufficient conditions for bounded holonomy. We begin with an alternative characterization of this property.

Lemma 3.3

$\mathcal{{F}}$ has bounded holonomy if and only if there is a constant L that bounds the operator norm of all elements in $\mathcal{{E}}$. That is, if $||h||\le L$ for every $h\in \mathcal{{E}}$.

Moreover, the operator norm is continuous in $\mathcal{{E}}$ with the topology induced by ${{\mathrm{Aut}}}(\mathcal{{V}})$, since it is continuous in ${{\mathrm{Aut}}}(\mathcal{{V}})$.

Proposition 3.4

Let M be compact and $\mathcal{{F}}$ be the Riemannian foliation given by the fibers of a Riemannian submersion $\bar{\pi }: M\rightarrow B$ with compact structure group. Then $\mathcal{{F}}$ has bounded holonomy.

Proof

Since M is compact, every point in B can be connected to a given point x by a geodesic whose length is less than the diameter of M. Denote the holonomy diffeomorphism defined by a length minimizing geodesic that connects x to y by $\psi ^y$ (the choice of the geodesic is irrelevant). Since the lengths of the geodesics are uniformly bounded, so are $d\psi ^y$ (Tapp [22, Proposition 2.2]). The same is true for the differential of any element in the holonomy group, since the last is contained in a compact structure group. That is, the differentials $d\psi$ are bounded for all $\psi$ in the holonomy group at x.

The proposition follows from the fact that every infinitesimal holonomy transformation can be decomposed as $h=(d\psi ^y)^{-1}d\psi d\psi ^{y'}$ for some $\psi$ in the holonomy group, $y=\pi (\tau (h))$ and $y'=\sigma (h)$. $\square$

When the foliation is given by a subalgebra of Killing fields $\mathfrak {m}$, we prove that all holonomy fields are restrictions of elements of $\mathfrak {m}$ to horizontal curves. This settled, the bound on the norm of elements of $\mathcal{{E}}$ is given in terms of the norms of the Killing fields.

Lemma 3.5

Let $\mathcal{{F}}$ be a Riemannian foliation defined by the action of a Lie algebra $\mathfrak {m}$ of Killing vector fields. Then, for every $\hat{\xi }\in \mathfrak {m}$ and every horizontal curve c, $\xi (t)=\hat{\xi }(c(t))$ is a holonomy field.

Proof

Let $\Xi _\theta$ be the flow of ${\hat{\xi }}\in \mathfrak {m}$. $\mathcal{{V}}$ is preserved by $d\Xi _\theta$ since $\mathcal{{V}}$ is spanned by the Lie algebra $\mathfrak {m}$. Since $\hat{\xi }$ is Killing, $d\Xi _\theta$ also preserves the horizontal distribution. Therefore, if c is a horizontal curve starting at p, $\psi (\theta ,t)=\Xi _\theta (c(t))$ is a collection of horizontal curves. Furthermore, $X=\frac{\partial \psi }{\partial t}$ is a horizontal vector field along the image of $\psi$ which satisfies $[{\hat{\xi }},X]=0$. In particular, $\nabla ^v_X\xi =\nabla ^v_{\xi }X=-S_X \xi$ (and $\nabla ^h_X\xi =-A^*_X\xi$ since $\xi$ is vertical), which proves that $\xi (t)$ satisfies Eq. (3). $\square$

Let $\mathcal{{F}}$ be as in Lemma 3.5. From Lemma 3.5, we conclude that $H_p=\{\mathrm{id}\}$: given a horizontal curve c and a holonomy field $\xi$ on it, then there exists an action field $\hat{\xi }$ such that $\xi (t)=\hat{\xi }(c(t))$ for every t. Therefore, if c is a horizontal loop,

$$\begin{aligned} {\hat{c}}(1)\xi (0)=\xi (1)={\hat{\xi }}(c(1))={\hat{\xi }}(c(0))=\xi (0). \end{aligned}$$

In particular, further assuming that $\mathcal{{F}}$ has only one dual leaf, $\mathcal{{E}}=M\times M$ (note that $H_p$ is the fiber of the submersion $\sigma \times \tau : \mathcal{{E}}\rightarrow M\times M$ at (p, p)), which is a compact subset of ${{\mathrm{Aut}}}(\mathcal{{V}})$ whenever M is compact, providing the bound L in Lemma 3.3. The case of non-trivial dual foliations is treated below.

Proposition 3.6

Let M be compact and $\mathcal{{F}}$ be a Riemannian foliation defined by a Lie algebra $\mathfrak {m}$ of Killing fields. Then $\mathcal{{F}}$ has bounded holonomy.

Proof

Given $p\in M$, denote by $e_p: \mathfrak {m}\rightarrow \mathcal{{V}}_p$ the evaluation map and fix an inner product on $\mathfrak {m}$. Since $\mathfrak {m}$ spans the vertical space at every point, the space

$$\begin{aligned} E=\{(p,\hat{\xi })\in M\times \mathfrak {m}~|~\hat{\xi }\in (\ker e_p)^{\bot } \} \end{aligned}$$

defines a smooth vector bundle over M. We further endow it with the metric induced by $e_p$. Denote the sphere bundle of E by S(E). We can define a function $r: S(E)\rightarrow \mathbb {R}$ as $r(p,{\hat{\xi }})=\max _{q\in M}||{\hat{\xi }}(q)||$. Since r is continuous and S(E) compact, it has a maximum L. Lemma 3.5 guarantees that this is the desired bound. $\square$

4 Dual Holonomy Fields

We give three equivalent characterizations of dual holonomy fields. Given $h\in {{\mathrm{Aut}}}(\mathcal{{V}})$, denote by $h^{-*}$ the inverse of the dual of h.

Proposition 4.1

Let $\nu$ be a vertical field along a horizontal curve c on M. Then, the following conditions are equivalent:

• (1) For any holonomy field $\xi$, $\left\langle \xi (t),\nu (t) \right\rangle$ is constant

• (2) If c is a horizontal curve, then $\nu (t)=\zeta ({\hat{c}}(t)^{-*},\nu (0))=\hat{c}(t)^{-*}\nu _0$

• (3) $\nabla _{{\dot{c}}}\nu =-A^*_{{\dot{c}}}\nu +S_{{\dot{c}}}\nu$.

We call a vertical field satisfying any of these conditions as a dual holonomy field.

Proof

Items (1) and (2) are equivalent since $\xi$ is a holonomy field if and only if $\xi (t)=\zeta (\hat{c}(t),\xi (0))$ (Proposition 3.2). To verify the equivalence between (1) and (3), note that, for a holonomy field $\xi$,

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{dt}}}\left\langle \xi ,\nu \right\rangle =\left\langle \nabla ^v_{{\dot{c}}}\xi ,\nu \right\rangle +\left\langle \xi ,\nabla ^v_{{\dot{c}}}\nu \right\rangle =\left\langle \xi ,\nabla ^v_{{\dot{c}}}\nu -S_{{\dot{c}}}\nu \right\rangle , \end{aligned}$$

(9)

which is zero for all holonomy fields if and only if $\nabla ^v_{{\dot{c}}}\nu =S_{{\dot{c}}}\nu$. Any vertical vector field satisfies $\nabla _{{\dot{c}}}^h\nu =-A^*_{{\dot{c}}}\nu$. $\square$

Item (1) connects dual holonomy fields to the virtual Jacobi fields defined on Verdiani and Ziller [23]. According to item (2), if we define $\bar{\zeta }: \mathcal{{E}} {_\sigma \times _\pi } \mathcal{{V}}\rightarrow \mathcal{{V}}$ as

$$\begin{aligned} \bar{\zeta }(h,\nu )=h^{-*}(\nu ), \end{aligned}$$

(10)

then, in analogy to Proposition 3.2, all dual holonomy fields can be expressed as $\bar{\zeta }({\hat{c}}_h(t),h^*\nu )$. Item (3) provides a useful expression for the sectional curvature of the plane spanned by ${\dot{c}}$ and $\nu$ (Proposition 4.2). We recall that the difference between a holonomy field and a dual holonomy field is (notation-wise) quite small: while holonomy fields are defined as $\xi (t)={\hat{c}}(t)\xi (0)$, dual holonomy fields are defined by $\nu (t)={\hat{c}}(t)^{-*}\nu (0)$.

4.1 The Curvature Equation

Proposition 4.2

Let $\nu$ be a dual holonomy field and $\gamma$ a horizontal geodesic. Then, the unreduced sectional curvature K of the pair $\dot{\gamma }, \nu$ along $\gamma$ is given by

$$\begin{aligned} K(\dot{\gamma },\nu )=\frac{1}{2}\frac{\mathrm{{d}}^2}{\mathrm{{dt}}^2}\Big |_{t=0}||\nu (t)||^2-3||S_{\dot{\gamma }}\nu ||^2+||A^ *_{\dot{\gamma }}\nu ||^2. \end{aligned}$$

(11)

Proof

Recalling Gray–O’Neill’s curvature equations [10, p. 28], we have

$$\begin{aligned} K(\dot{\gamma },\nu )=\left\langle (\nabla _{\dot{\gamma }}S)_{\dot{\gamma }}\nu ,\nu \right\rangle -||S_{\dot{\gamma }}\nu ||^2+||A^*_{\dot{\gamma }}\nu ||^2. \end{aligned}$$

(12)

From the first term, we get

$$\begin{aligned} \left\langle (\nabla _{\dot{\gamma }}S)_{\dot{\gamma }}\nu ,\nu \right\rangle= & {} \frac{\mathrm{{d}}}{\mathrm{{dt}}}\left\langle S_{\dot{\gamma }}\nu ,\nu \right\rangle -\left\langle S_{\dot{\gamma }}\nu ,\nabla _{\dot{\gamma }}\nu \right\rangle -\left\langle S_{\dot{\gamma }}\nabla _{\dot{\gamma }}\nu ,\nu \right\rangle \\= & {} \frac{\mathrm{{d}}}{\mathrm{{dt}}}\left\langle \nabla _{\dot{\gamma }}\nu ,\nu \right\rangle -||S_{\dot{\gamma }}\nu ||^2-\left\langle \nabla _{\dot{\gamma }}^v\nu ,S_{\dot{\gamma }}\nu \right\rangle \\= & {} \frac{1}{2}\frac{\mathrm{{d}}^2}{\mathrm{{dt}}^2}||\nu ||^2-2||S_{\dot{\gamma }}\nu ||^2. \end{aligned}$$

$\square$

The analogous equation for a holonomy field $\xi$ is

$$\begin{aligned} K(\dot{\gamma },\xi )=-\frac{1}{2}\frac{\mathrm{{d}}^2}{\mathrm{{dt}}^2}||\xi ||^2+||S_{\dot{\gamma }}\xi ||^2+||A^ *_{\dot{\gamma }}\xi ||^2. \end{aligned}$$

(13)

The advantage of (11) is the minus sign in front of $||S_{\dot{\gamma }}\nu ||^2$.

5 Proof of Theorem 1

Fix a unitary $\nu _0\in \mathcal{{V}}_p$ and define a real function $\rho _{\nu _0}: \mathcal{{E}}_p\rightarrow \mathbb {R}$ as

$$\begin{aligned} \rho _{\nu _0}(h)=||h^{-*}\nu _0||^2. \end{aligned}$$

(14)

We use this function to replace $\phi$ in the proof of Theorem 1. For instance, at a maximum of $\rho _{\nu _0}$, Eq. (12) guarantees that $\left\langle (\nabla _XS)_X\nu ,\nu \right\rangle$ is non-positive and we can use linear algebra to deal with the A-term.

Theorem 5.1

Suppose that M is compact and $\mathcal{{F}}$ has bounded holonomy. Then, there exists a non-zero $\nu \in \mathcal{{V}}$ such that, for every $X\in \mathcal{{H}}_{\pi (\nu )}$, $K(X,\nu )\le ||A^*_X\nu ||^2$.

Theorem 5.1 guarantees the existence of a vector $\nu \in \mathcal{{V}}$ such that the skew-symmetric map $X\mapsto A_X^*\nu$ is injective whenever M has positive sectional curvature. Thus concluding that the dimension of $\mathcal{{H}}$ must be even. One may wonder whenever it is possible to find a vector X such that $\xi \mapsto A^*_X\xi$ is injective, thus settling Wilhelm’s Conjecture.

Before proving Theorem 5.1, we make a connection between the hypothesis on holonomy and the map $\rho _{\nu _0}$.

Lemma 5.2

A foliation $\mathcal{{F}}$ has bounded holonomy if and only if there are constants $\bar{l}, \bar{L}>0$ such that $l^2||\nu _0||^2\le \rho _{\nu _0}(h)\le L^2||\nu _0||^2$, for all $(h,\nu _0)\in \mathcal{{E}}{_\sigma \times _\pi } \mathcal{{V}}$.

Proof

Let L be a bound for the norm of holonomy fields with unit initial condition. According to Lemma 3.3, $||h||\le L$ for all $h\in \mathcal{{E}}$. On the other hand, since $\mathcal{{E}}$ is closed by inversion, $||(h^*)^{-1}||=||h^{-1}||\le L$, which, together with (2) of Proposition 4.1, make L a bound for all dual holonomy fields with unit initial condition. The constant l can be taken as $L^{-1}$. $\square$

Proof of Theorem 5.1:

Given $\nu \in \mathcal{{V}}_q$ and $X\in \mathcal{{H}}_{q}$, we take advantage of Proposition 4.2 by exploring the function $f(t)=||\nu (t)||^2$, where $\nu (t)$ is the dual holonomy field defined by $\nu$ along the geodesic spanned by X. From Proposition 4.2,

$$\begin{aligned} \frac{1}{2}f''(0)=K(\dot{\gamma },\nu )+3||S_{\dot{\gamma }}\nu ||^2-||A^ *_{\dot{\gamma }}\nu ||^2. \end{aligned}$$

(15)

In particular, we complete the proof by finding $\nu$ that satisfies $f''(0)\le 0$ for each $X\in \mathcal{{H}}_q$. Let $\{h_k\in \mathcal{{E}}_p\}$ be a sequence whose images $\{\rho _{\nu _0}(h_k)\}$ converges to the supremum of $\rho _{\nu _0}$. We shall see that $\nu$ can be taken as any accumulation point for $\{h_k^{-*}\nu _0\}$.

For simplicity, assume for the sequence $\{h_k\}$ above, that $\{h_k^{-*}\nu _0\}$ converges to some $\nu$. The limit, $\nu$, must be non-zero since there are constants $l,L>0$ such that $l\le ||h_k^{-*}||\le L$ (Lemma 5.2).

The proof is finished if $\{h_k\}$ converges to some $h\in \mathcal{{E}}_p$: in this case, $\rho _{\nu _0}(h)$ is a maximum and, for every $X\in \mathcal{{H}}_{\tau (h)}$, the function $f(t)=||\nu (t)||^2$ has a maximum at 0. In the general case, we approximate the function f by similar functions.

Fix $X\in \mathcal{{H}}_{\pi (\nu )}$ and let $\{X_k\in \mathcal{{H}}_{\tau (h_k)}\}$ be a sequence of horizontal vectors converging to X. Consider the family of real functions $\{f_k\}$ defined by $f_k(t)=||\nu _k(t)||^2$, where $\nu _k(t)$ is the dual holonomy field defined by $h_k^{-*}\nu _0$ along $\exp (tX_k)$. The sequence $\{f_k\}$ clearly converges pointwise to f. To conclude that the convergence is $\mathcal{{C}}^r$, $r\ge 2$, observe that the derivatives of $f_k$ are expressed in terms of S and the covariant derivatives of S. Since M is compact, we can uniformly bound any finite number of them.

Assume by contradiction that $f''(0)>2d>0$ for some $X\in \mathcal{{H}}$. Let $k_0$ be big enough so that $f''_k(0)>d$ for $k>k_0$. Then, the Taylor expansion of $f_k$ gives

$$\begin{aligned} f_{k}(\epsilon )=f_{k}(0)+f_{k}'(0)\epsilon +f''_{k}(0)\frac{\epsilon ^2}{2}+O_{k}^{(2)}(\epsilon )\,. \end{aligned}$$

The uniform bound on the derivatives guarantees a uniform bound $|O^{(2)}_k(\epsilon )|<l\epsilon ^3/2$ for all $k>k_0$. In fact, for each k, there is a $c_k\in \mathbb {R}$ such that

$$\begin{aligned} |O^{(2)}_k(\epsilon )|<\left| \frac{f'''_k(c_k)}{3!}\right| |\epsilon |^3. \end{aligned}$$

Now, taking $d/4l<\epsilon <d/2l$, we have

$$\begin{aligned} f_{k}(\epsilon )>f_{k}(0)+f'_{k}(0)\epsilon +\frac{\epsilon ^2}{2}(d-l\epsilon )>f_{k}(0)+f'_{k}(0)\epsilon +\frac{d^3}{64l^2}, \end{aligned}$$

which converges to a value strictly bigger than f(0), unless $f'(0)$ is negative. However, following along the same lines, we conclude that

$$\begin{aligned} f_{k}(-\epsilon )>f_{k}(0)-f'_{k}(0)\epsilon +\frac{d^3}{64l^2} \end{aligned}$$

converges to a value strictly bigger than f(0) if $f'(0)$ is negative. Observing that $f_k(t)=\rho _{\nu _0}({\hat{\gamma }}_{k}(t))$, where ${\hat{\gamma }}_k$ is the $\tau _p$-horizontal lift at $h_k$ of $\gamma _k(t)=\exp (tX_k)$, we contradict the fact that f(0) is a supremum for $\rho _{\nu _0}$. $\square$

6 Final Remarks

6.1 Smoothness of $\mathcal{{E}}$

The foliation $\tilde{\mathcal{{F}}}$, defined on ${{\mathrm{Aut}}}_p(\mathcal{{V}})=\sigma ^{-1}(p)$ by

$$\begin{aligned} \tilde{\mathcal{{F}}}=\{\tau ^{-1}(L)\cap {{\mathrm{Aut}}}_p(\mathcal{{V}})~|~L\in \mathcal{{F}}\}, \end{aligned}$$

is endowed with a natural horizontal distribution by Proposition 3.2. Its dual leaf through $\mathrm{id}\in {{\mathrm{Aut}}}_p(\mathcal{{V}})$ is $\mathcal{{E}}_p$. Thus $\mathcal{{E}}_p$ is an immersed submanifold of ${{\mathrm{Aut}}}_p(\mathcal{{V}})$. Smoothness of the submersion $\tau _p: \mathcal{{E}}_p\rightarrow L^\#_p$ is a much less trivial result—since it falls out of the scope of this paper, we present the details elsewhere.

Considering the differentiability of $\mathcal{{E}}_p$, we believe in the Morse Theory of $\rho _{\nu _0}$ as a genuine approach to generalize Theorem 1 to unbounded holonomy, or even to other problems, such as Wilhelm’s Conjecture.

To further familiarize with the concept of $\mathcal{{E}}$, we take the opportunity to give an example of a foliation where $\mathcal{{E}}_p$ vary along M.

Example 6.1

Let $h: S^7\rightarrow S^4$ be the $S^3$-principal Hopf fibration, where $S^7$ is endowed with the metric of constant sectional curvature 1 and $S^3$ is the quaternionic unit sphere. Denote the principal $S^3$-action as $g\cdot x$ and let $M=S^7{\times _{S^3}}S^3$ be the quotient of $S^7{\times }S^3$ by the $S^3$-action $g\cdot (x,r)=(g\cdot x, grg^{-1})$. Denote the quotient map as $q: S^7{\times } S^3\rightarrow M$. M is naturally an associated bundle, $\pi : M\rightarrow S^4$, with projection $\pi (q(x,r))=h(x)$.

Let $\mathcal{{F}}$ be the foliation on M given by the fibers of $\pi$. The holonomy of $\mathcal{{F}}$ comes from h: if c is a curve in $S^4$ and $c_x$ is its horizontal lift with respect to h with $c_x(0)=x\in S^7$, then $c_{q(x,r)}$, the horizontal lift of c with respect to $\pi$, is given by $c_{q(x,r)}(t)=q(c_x(t),r)$.

Let $\mathfrak {R}: M\rightarrow [-1,1]$ be the map that sends q(x, r) to the real part of r (observe that it only depends on the image of q(x, r), not on r). The level sets of $\mathfrak {R}$ characterizes the dual leaves of $\mathcal{{F}}$: if $q(x,r)\in M$, then $L^\#_{q(x,r)}=\mathfrak {R}^{-1}(\mathfrak {R}(q(x,r)))$. In particular, if $r{\ne } \pm 1$, $\dim L^\#_{q(x,r)}=6$ (moreover, the restriction $\pi |_{L^\#_{q(x,r)}}: L^\#_{q(x,r)}\rightarrow S^4$ is isomorphic to the classical Penrose fibration $\mathbb {C}P^3\rightarrow \mathbb {H}P^1$ described in [4]). On the other hand, $q(S^7{\times }\{\pm 1\})$ is a four-sphere, since $g\cdot (x,\pm 1)=(g\cdot x,\pm 1)$ (thus $q_{S^7{\times }\{\pm 1\}}: S^7{\times }\{\pm 1\}\rightarrow q(S^7{\times }\{\pm 1\})$ is isomorphic to h).

Although such discrepancy may occur among dual leaves, one can identify $\tau _{q(x,r)}: \mathcal{{E}}_{q(x,r)}\rightarrow L^\#_{q(x,r)}$ with $q|_{S^7{\times }\{r\}}: S^7\times \{r\}\rightarrow L^\#_{q(x,r)}$. In particular, although the bundle $\tau _{q(x,r)}$ may vary, every $\mathcal{{E}}_{q(x,r)}$ is diffeomorphic to $S^7$.

Based on Example 6.1, we conjecture:

Conjecture 2

Let $\mathcal{{F}}$ be a Riemannian foliation on M and let ${\mathcal{{F}}}^\mathcal{{E}}$ be the foliation whose leaves are $\mathcal{{E}}_p$. Then $\mathcal{{F}}^\mathcal{{E}}$ is a smooth non-singular foliation. Furthermore, for every $p\in M$, $L^\#_p$ is diffeomorphic to $\mathcal{{E}}_p\times _{H_p} \tilde{L}_p$, for some action of $H_p$ on $\tilde{L}_p$, the universal cover of $L_p$.

Notice that Example 6.1 has bounded holonomy. It may be the case that Conjecture 2 is true only for bounded holonomy.

6.2 A Dual Leaf Theorem

We use the tools developed here to slightly generalize Wilking’s single dual leaf Theorem in the context of bounded holonomy.

Theorem 6.2

Let $\mathcal{{F}}$ be a Riemannian foliation with bounded holonomy and positive vertizontal curvature. Then $\mathcal{{F}}$ has only one dual leaf.

We prove this theorem by giving an Ambrose–Singer type of description for the tangent of the dual leaves. Recall the case of principal bundles, where the Ambrose–Singer theorem describes the tangent to the dual leaf via the curvature two-form $\Omega$ (see Case 2 in 3.1 and Kobayashi–Nomizu [15, II.7, Theorem 7.1]). It states that (after proper identification), the vertical part of $TL^\#_p$ is spanned by $\{\Omega (X,Y)\}$, where X, Y runs through all horizontal vectors on the bundle. The curvature two-form is not present in our context and its best replacement is the Gray–O’Neill’s A-tensor, whose image resides on different fibers of $\mathcal{{V}}$ (making it impossible to get all values together). To get round this situation, we define the set

$$\begin{aligned} \mathcal{{A}}_p=span\{h^{-1}(A_XY)~|~X,Y\in \mathcal{{H}}_{\tau (h)},~h\in \mathcal{{E}}_p\}. \end{aligned}$$

It should be straightforward that $\mathcal{{A}}_p=T_pL^\#_p\cap \mathcal{{V}}_p$ (compare Sect. 2.1 and Lemma 2.1 on Guijarro–Walschap [11]). Given a horizontal curve $c: \mathbb {R}\rightarrow M$, we can define another (possibly much smaller) set:

$$\begin{aligned} \mathcal{{C}}(c)=span\{{\hat{c}}(t)^{-1}(A_{{\dot{c}}(t)}Z)~|~Z\in \mathcal{{H}}_{c(t)}\text { and }t\in \mathbb {R}\}\subset \mathcal{{V}}_{c(0)}. \end{aligned}$$

In a foliation with positive vertizontal curvature and bounded holonomy, we can prove that $\mathcal{{C}}(c)=\mathcal{{V}}_{c(0)}$ (Theorem 6.4).

To prove Theorem 6.4, we follow an idea present in Wilking [25]. Let $\xi$ be a Jacobi holonomy field whose initial value is orthogonal to the dual leaves. In the context of non-negatively curved manifolds, [25] proves that such a holonomy field stays orthogonal to dual leaves. We prove that, in the general case, dual holonomy fields exhibit a similar behavior with respect to $\mathcal{{C}}(c)$ (or $\mathcal{{A}}_p$). For convenience, denote by $c_s$ the curve $c_s(t)=c(s+t)$.

Lemma 6.3

If $\nu _0\,\bot \, \mathcal{{C}}(c)$, then $\nu$, the dual holonomy field defined by $\nu _0$ along c, satisfies $\nu (s)\,\bot \,\mathcal{{C}}(c_s)$. In particular, $A^*_{{\dot{c}}}\nu (s)=0$ for all s.

Proof

The first claim follows by observing that $\mathcal{{C}}(c_s)={\hat{c}}(s)(\mathcal{{C}}(c))$. Moreover, since $A_{{\dot{c}}_s}Z\in \mathcal{{C}}(c_s)$ for all $Z\in \mathcal{{H}}_{c(s)}$, $A^*_{{\dot{c}}_s}\nu (s)=0$. $\square$

Theorem 6.4

Let $\mathcal{{F}}$ be a Riemannian foliation with bounded holonomy and positive vertizontal curvature. Then, for any horizontal geodesic $c: \mathbb {R}\rightarrow M$, $\mathcal{{C}}(c)=\mathcal{{V}}_{c(0)}$.

Proof

Let $\nu$ be a non-zero dual holonomy field as in lemma 6.3. Using (11), we have

$$\begin{aligned} \frac{1}{2}\frac{\mathrm{{d}}^2}{\mathrm{{dt}}^2}||\nu (t)||^2=K({\dot{c}},\nu (t))+3||S_{{\dot{c}}}\nu (t)||^2. \end{aligned}$$

Since $K({\dot{c}},\nu (t))>0$, $||\nu (t)||^2$ is unbounded, contradicting the hypothesis. $\square$

We believe that Theorem 6.4 might help proving Wilhelm’s conjecture.

We follow [2] and call a foliation twisted if it has only one dual leaf. Theorem 6.4 shows that a foliation with bounded holonomy and positive vertizontal curvature is twisted.

6.3 Bounded Holonomy as a Generalization of Compact Holonomy

The aim of this section is to introduce the condition of bounded holonomy as a good replacement in foliations for the property of compact holonomy group, that is only defined on submersions. Here we present a characterization shared by both conditions.

Theorem 6.5

Let $\mathcal{{F}}$ be a twisted Riemannian foliation on a complete manifold $(M,g_0)$. Then $\mathcal{{F}}$ has bounded holonomy if and only if M admits a connection metric $g_1$ such that, for every $X\in \mathcal{{H}}$ and $\xi \in \mathcal{{V}}$,

$$\begin{aligned} g_1(X+\xi ,X+\xi )=g_0(X,X)+g_1(\xi ,\xi ). \end{aligned}$$

Proof

Suppose that $\mathcal{{F}}$ has bounded holonomy. Then, the closure of $H_p$ on $GL(\mathcal{{V}}_p)$ is compact, and thus $\mathcal{{V}}_p$ can be endowed with a $H_p$-invariant inner product $\left\langle , \right\rangle$. Given $h\in \mathcal{{E}}_p$, observe that the metric defined by $\left\langle \xi ,\eta \right\rangle _q=\left\langle h^{-1}\xi ,h^{-1}\eta \right\rangle$ does not depend on the choice of $h\in \tau _p^{-1}(q)$. In fact, if $h,k\in \tau _p^{-1}(q)$,

$$\begin{aligned} \left\langle h^{-1}\xi ,h^{-1}\eta \right\rangle =\left\langle h^{-1}kk^{-1}\xi ,h^{-1}kk^{-1}\eta \right\rangle =\left\langle k^{-1}\xi ,k^{-1}\eta \right\rangle , \end{aligned}$$

since $h^{-1}k\in H_p$.

To see that the foliation is totally geodesic, it is sufficient to check that holonomy fields have constant length along horizontal curves, since, if $\xi (t)$ is a holonomy field along c,

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{dt}}}\left\langle \xi (t),\xi (t) \right\rangle =2\left\langle S_{{\dot{c}}}\xi ,\xi \right\rangle \end{aligned}$$

and $S_{{\dot{c}}}$ is a symmetric operator. However, if $\xi (t)$ is a holonomy field, $\xi (t)={\hat{c}}(t)\xi _0$, for $\xi _0=\xi (0)$. Therefore, recalling that ${\hat{c}}$ is in $\mathcal{{E}}_p$,

$$\begin{aligned} \left\langle \xi (t),\xi (t) \right\rangle _{c(t)}=\left\langle {\hat{c}}(t)^{-1}{\hat{c}}(t)\xi _0,{\hat{c}}(t)^{-1}{\hat{c}}(t)\xi _0 \right\rangle =\left\langle \xi _0,\xi _0 \right\rangle . \end{aligned}$$

$\square$

We observe that the smoothness of the metric constructed in Theorem  6.5 depends on the facts that $\mathcal{{E}}_p\subset {{\mathrm{Aut}}}(\mathcal{{V}})$ is an immersed submanifold and that $\tau _p: \mathcal{{E}}_p\rightarrow M$ is a smooth submersion. However, this settled, Theorem 6.5 guarantees that a Riemannian foliation $\mathcal{{F}}$ with bounded holonomy has a finite dimension Lie group as its holonomy group and its Lie algebra is compact—details will be provided elsewhere.