Toric Kähler–Einstein Metrics and Convex Compact Polytopes

Abstract

We show that any compact convex simple lattice polytope is the moment polytope of a Kähler–Einstein orbifold, unique up to orbifold covering and homothety. We extend the Wang–Zhu Theorem (Wang and Zhu in Adv Math 188:47–103, 2004) giving the existence of a Kähler–Ricci soliton on any toric monotone manifold on any compact convex simple labeled polytope satisfying the combinatoric condition corresponding to monotonicity. We obtain that any compact convex simple polytope admits a set of inward normals, unique up to dilatation, such that there exists a symplectic potential satisfying the Guillemin boundary condition (with respect to these normals) and the Kähler–Einstein equation on . We interpret our result in terms of existence of singular Kähler–Einstein metrics on toric manifolds.

1 Introduction

The question of existence of Kähler–Einstein metrics on compact complex manifold has been subject of intense investigations for the last decades. This problem makes sense on a compact complex manifold $(M^{2n},J)$ with a given Kähler class $\Omega \in H^{2}_{dR}(M)$ for which there is such that $\lambda \Omega =2\pi c_1(M)$. The case $\lambda \le 0$ is non-obstructed and the existence of a Kähler–Einstein metric $(g,\omega )$, with $\omega \in \Omega$ was proved forty years ago [4, 41]. The case $\lambda >0$ proved to be a more difficult question, recently related to a certain notion of stability [10–12, 37] and for which there are various known obstructions, notably the Futaki invariant [19]. In the toric case (the Kähler structure is invariant by the Hamiltonian action of a real torus of dimension ), it follows from the Wang–Zhu Theorem [40] which has been extended to orbifolds [35], that the only obstruction to the existence of Kähler–Einstein metrics on monotone symplectic toric orbifolds (in the sense that there exists $\lambda >0$ such that $\lambda [\omega ]=c_1(M)$) is the vanishing of the Futaki invariant. Through the toric correspondence, finding such orbifolds is a combinatorial problem on labeled polytopes. In the first part of this paper, we prove that any polytope can be labeled to satisfy these two conditions. To give a precise statement, we now recall the main lines of the correspondence.

Symplectic toric compact orbifolds are classified by rational labeled polytopes via the Delzant–Lerman–Tolman correspondence [13, 28]. A labeled polytope is a pair $(P,\nu )$ where $P$ is a simple bounded convex polytope, open in a $n$-dimensional vector space $\mathfrak {t}^*$, $\nu =\{\nu _1, \ldots ,\nu _d\}\subset \mathfrak {t}$ is a set of vectors, inward to $P$, such that if we denote $F_1, \ldots , F_d$ the facets (codimension $1$ face) of $P$, the vector $\nu _k$ is normal to $F_k$ for $k=1, \ldots ,d$ where $d$ is the number of facets. The defining functions of a labeled polytope $(P,\nu )$ are the affine-linear functions $L_1, \ldots , L_d$ on $\mathfrak {t}^*$ such that¹ $P=\{p\in \mathfrak {t}^*\,|\,L_k(p)>0\}$ and $dL_k=\nu _k$. A rational labeled polytope $(P,\nu ,\Lambda )$ is a labeled polytope $(P,\nu )$ and $\Lambda$ a lattice in $\mathfrak {t}$ such that $\nu \subset \Lambda$.

Remark 1.1

If $(P,\nu ,\Lambda )$ is rational, there are (uniquely determined) positive integers $m_1, \ldots ,m_d$ such that $\frac{1}{m_i}\nu _{i}$ are primitive elements of $\Lambda$. Then $(P, m_1, \ldots , m_d)$ is a rational labeled polytope in the sense of Lerman–Tolman [28].

For a given symplectic toric compact orbifold $(M,\omega ,T), \mathfrak {t}$ is the Lie algebra of the torus $T={\mathfrak {t}}\big /{\Lambda }$ and the closure $\overline{P}$ is the image of the moment map. The symplectic properties are encoded in the data $(P,\nu )$. Notably, see [14], monotone symplectic toric orbifolds correspond to what we will call monotone labeled polytopes.

Definition 1.2

We say that $(P,\nu )$ is monotone if there exists $p\in P$ such that $L_1(p)=L_2(p)=\cdots =L_d(p)$. In that case, we call $p$ the preferred point of $(P,\nu )$.

The space of invariant Kähler metrics on $M$ is parameterized by a subspace of convex functions on $P$, the set of symplectic potentials $\mathcal {S}(P,\nu )$, see [2, 3, 15], whose definition we precisely recall in Sect. 2.3. The scalar curvature of the metric $g_u$, associated to $u\in \mathcal {S}(P,\nu )$, is given by the Abreu formula

$$\begin{aligned} S(u)=-\sum _{i,j=1}^n \frac{\partial ^2 u^{ij}}{\partial x_i\partial x_j} \end{aligned}$$

(1)

where $(x_1, \ldots ,x_n)$ are coordinates on $\mathfrak {t}^*$ and $u^{ij}=(\text{ Hess } u)^{-1}$, see [1, 2].

The extremal affine function of $(P,\nu )$, denoted $\mathrm{A}_{(P,\nu )}$, is an affine–linear function on $\mathfrak {t}^*$ which corresponds to the Futaki invariant [19] restricted to the (real) Lie algebra of the torus (the symplectic counterpart of the Futaki invariant as introduced in [26]). In particular, $\mathrm{A}_{(P,\nu )}$ is constant if and only if the Futaki invariant vanishes on $\mathfrak {t}$. The extremal affine function is a useful invariant of $(P,\nu )$ since it satisfies

• $g_u$ is extremal, in the sense of Calabi [8], if and only if $S(u)=\mathrm{A}_{(P,\nu )}$

• $\mathrm{A}_{(P,\nu )}$ is constant, should a constant scalar curvature $T$-invariant compatible Kähler (cscK) metric exist.

In this paper, we prove the following statement.

Theorem 1.3

Given a compact simple convex polytope $\overline{P}$, there exists a set of normals $\nu$, unique up to dilatation, such that $(P,\nu )$ is monotone and has a constant extremal affine function.

In dimension $2$, the existence of such labeling follows from elementary considerations [15].

Remark 1.4

As noticed in [16], labeled polytopes with constant extremal affine function are those for which the centers of mass of $(P,d\varpi )$ and $(\partial P,d\sigma _{\nu })$ coincide, where $d\sigma _{\nu }$ is the volume form on $\partial P$ such that $\nu _k\wedge d\sigma _{\nu }=-d\varpi$ on the facet $F_k$. The set of normals $\nu$ given by Theorem 1.3 is characterized by the fact that the preferred point of $(P,\nu )$ (as a monotone labeled polytope) coincides with the center of mass of $(\partial P,d\sigma _{\nu })$. This last characterization was proved by Mabuchi [31] and used to classify toric complex surfaces admitting a compatible Kähler–Einstein metric: and .

We will see that the set of normals $\nu$ given by Theorem 1.3 can be included in a lattice if and only if $P$ is a lattice polytope (i.e., whose vertices lie in a lattice) and thus, using the Theorem of Wang–Zhu/Shi–Zhu [35, 40] we get

Corollary 1.5

Every (simple convex compact) lattice polytope is the moment polytope of a compact Kähler–Einstein toric orbifold, unique up to dilatation or orbifold covering.

The case where the set of normals $\nu$ given by Theorem 1.3 is not rational motivates us to extend the Wang–Zhu Theorem for general labeled polytopes. More precisely, Wang and Zhu showed in [40] that any Fano toric manifold $(M^{2n},J,T)$ admits a Kähler–Ricci soliton $(g,Z)$, that is, a Kähler metric $g$ and a holomorphic vector field $Z$ such that

$$\begin{aligned} \rho ^g -\lambda \omega ={\mathcal {L}}_Z\omega \end{aligned}$$

(2)

where $\rho ^g$ is the Ricci form of $g, \omega$ the Kähler form $\omega = g(J\cdot ,\cdot )$ and $\lambda = \frac{1}{2n}\,\overline{\text {Scal}}$ with $\overline{\text {Scal}}=\int _{M} \text {Scal}\, \omega ^{n}/\int _M\omega ^n$. In that case, $2\pi c_1(M)=\lambda [\omega ]$. The vector field $Z$ is uniquely determined by the data $(M,[\omega ], T)$ as follows: denoting $p$ the preferred point of the monotone labeled polytope $(P,\nu )$ associated to $(M,[\omega ],T)$, there is a unique linear function on $\mathfrak {t}^*$, $a\in \mathfrak {t}$, such that

$$\begin{aligned} \int _P e^{2a} (f-f(p))d\varpi =0 \end{aligned}$$

(3)

for all . If a holomorphic vector field $Z$ satisfies (2), then $Z\!=\! JX_a-iX_a$, see [39, 40]. The case $a=0$ implies that $Z=0$ and the Kähler-Ricci soliton of Wang–Zhu is a Kähler–Einstein metric.

According to the work of Donaldson [14], a symplectic potential $u\in \mathcal {S}( P,\nu )$ corresponds to a Kähler–Ricci soliton with respect to $\lambda >0$ and $a\in \mathfrak {t}$ if and only if

$$\begin{aligned} \frac{1}{2}\log \det (\text{ Hess } u)_x +\lambda h(x)= a(x) \end{aligned}$$

(4)

where $h$ is the Legendre transform of $u$ (seen as a function on $P$, via the change of variable $x\mapsto (d u)_{x}\in \mathfrak {t}$) and the preferred point of $(P,\nu )$ is the origin.

In fact, the argument of Wang–Zhu holds for any labeled polytope without any deep modification. In order to find appropriate scope for extending their proof in the case when $(P,\nu )$ is not necessarily rational, we consider $P\times \mathfrak {t}$ with its symplectic structure (that is, $P\times \mathfrak {t}\subset \mathfrak {t}^*\times \mathfrak {t}\simeq T^*\mathfrak {t}$) and the $\mathfrak {t}$-Hamiltonian action by translation on the second factor, the moment map being the projection on the first factor. The invariant Kähler metric $g_u$, for a symplectic potential $u\in \mathcal {S}(P,\nu )$, is simply a $\mathfrak {t}$-invariant Kähler metric on $P\times \mathfrak {t}$ with specific behavior along $\partial P\times \mathfrak {t}$. As introduced in [18], see also [14, 15] and Sect. 2.1, for each vertex $p$ of $P$ there is an open toric symplectic manifold $(M_p,\omega _p,T_p)$ depending only on $(P,\nu )$. We point out that, in the rational case, $(M_p,\omega _p,T_p)$ is a uniformizing chart for the orbifold and the boundary condition on symplectic potentials corresponds to the fact that $g_u$ defines a smooth metric on each of the manifolds $(M_p,\omega _p,T_p)$, see Sect. 2.3. In Sect. 5, we notice that the test functions appearing in the proof of Wang–Zhu, behave as functions defined on the compact set $\overline{P}$ while the boundary condition, suitably interpreted, allows us to apply the (local) computations of Yau [41] and Tian–Zhu [39] on each chart $(M_p,\omega _p,T_p)$. Along the way, we have to show that both Yau’s Theorem [41] and Zhu’s Theorem [42] hold, suitably interpreted, in this extended setting.

Theorem 1.6

Let $(P,\nu )$ be a monotone labeled polytope with preferred center $0\in \mathfrak {t}^*$ and compact closure $\overline{P}$. There exists a solution $u\in \mathcal {S}(P,\nu )$ of Eq. (4), so that $g_u$ is a $\mathfrak {t}$-invariant Kähler–Ricci soliton on $P\times \mathfrak {t}$. This solution $u$ is unique in $\mathcal {S}(P,\nu )$ up to addition of an affine-linear function and $g_u$ is Kähler–Einstein if and only if $\mathrm{A}_{(P,\nu )}$ is constant.

A result of Donaldson [15] implies that the set of normals for which there exists a solution of the Abreu equation is open in the set of inward normals of a fixed polytope, see Sect. 6.1. Together with Theorems 1.3 and 1.6, it gives

Corollary 1.7

For each $n$-dimensional polytope $P$, there exists a non-empty open set ${\mathbf{E}}(P)$ of inward normals $\nu$ for which there exists an extremal toric Kähler metric $g_u$ with $u\in \mathcal {S}(P,\nu )$. Moreover, ${\mathbf{E}}(P)$ contains a codimension $n$ subset corresponding to cscK metrics and contains the $1$-dimensional cone of toric Kähler–Einstein metrics. In particular, if there exists a lattice for which $P$ is rational then there exist extremal toric Kähler orbifolds with moment polytope $\overline{P}$.

A compact toric symplectic orbifold $(M,\omega ,T)$ associated to a rational labeled polytope $(P,\nu ,\Lambda )$ is a compactification of $P\times T$ where $T=\mathfrak {t}/\Lambda$ and $P\subset \mathfrak {t}^*$. Consequently, as a straightforward application of Theorems 1.3 and 1.6, we obtain in Sect. 6.3, for any smooth compact toric symplectic manifold, the existence of a toric Kähler–Einstein metric $g_{KE}$ on the open dense subset where the torus acts freely. The singular behavior of $g_{KE}$ along the pre-image of the interior of a facet $F_k$ is conical of angle $2\pi a_k$ where $a_k$ is the ratio between the normal $\nu _k$ and the normal to $F_k$ found in Theorems 1.3. Here, the complex structure and the metric are singular while the symplectic structure is smooth. Using the standard procedure (with Legendre transform) to complexify $P\times T$ the singularity lies along the pre-image of the boundary and we can pass to the more usual setting in the study of conical singularity of metrics (e.g., [17, 38]) where the symplectic form and the metric are singular but not the complex structure. This interpretation is valid for any labeling $\eta$ of $P$ and any toric Kähler metric, in the sense that to any $u\in \mathcal {S}(P,\eta )$ corresponds a $T$-invariant Kähler metric $g_u$ which is smooth on a open dense subset of $M$ and conical along the divisor corresponding to the boundary of $P$. Therefore, Corollary 1.7 provides families of conical extremal Kähler metrics of various type (cscK or not) on each toric symplectic manifold. See Sect. 6.3 for more details.

Theorem 1.6 provides an alternative proof of the Futaki–Ono–Wang Theorem [20]. This theorem establishes the existence of toric Sasaki–Ricci soliton on contact toric manifolds with a (fixed) Reeb vector field satisfying the two conditions:

• the basic first Chern form of the normal bundle of the Reeb foliation is positive,

• the first Chern class of the contact bundle is trivial.

Compact contact toric manifolds with a fixed Reeb vector field are in one-to-one correspondence with labeled polytopes whose defining functions lie in a lattice and satisfy a certain weaker condition than the Delzant condition, see [5, 25, 27]. In this correspondence as well, a compatible toric Sasaki metric is given by a symplectic potential and the scalar curvature is given by the Abreu formula (1), up to an additive constant depending only on the dimension. The hypothesis of the Futaki–Ono–Wang Theorem corresponds to the fact that the associated labeled polytope is monotone, see [20, 32].

For the purpose of this paper, we need to slightly reinterpret the geometry associated to a labeled polytope based on the approach [14, 15, 18]. We do that in the next section. We prove Theorem 1.3 in Sect. 3. In Sect. 4, we introduce the basic analytical tools needed to do geometric analysis in the non-rational case (Sobolev norms, Maximum principle, cohomology, $\ldots$). With these tools in hand, in Sect. 5, we explain why some classical theorems in Kähler geometry, due Yau, Zhu and Tian–Zhu, are valid in this context. Finally, Sect. 6 gathers the geometric applications of our results which are Corollaries 1.5 and 1.7 and the existence of conical extremal Kähler metrics on toric manifold.

2 Labeled Polytopes and Toric Geometry

In what follows, polytopes always refers to simple bounded polytope where simple means that each vertex is the intersection of no more than $n$ facets.

2.1 Symplectic Toric Orbifolds as Compactifications

Let $(M,\omega ,T, \varrho )$ be a compact symplectic toric orbifold, that is, $\varrho : T\hookrightarrow \text{ Ham }(M,\omega )$ embeds $T$ as a subgroup and $2\dim T=\dim M$. We denote $\mathfrak {t}=\text{ Lie } T$. There is a moment map

$$\begin{aligned} x:M\rightarrow \mathfrak {t}^* \end{aligned}$$

which is $T$-invariant and uniquely determined, up to addition of a constant, by the relation $d\langle x,a\rangle =- \omega (X_a,\cdot )$ where $X_a= d_{\mathrm{id}}\varrho (a)$ is the vector field induced by the infinitesimal action of $a\in \mathfrak {t}$. The image of the moment map $\overline{P}={{\mathrm{Im}}}x$ is a compact convex simple polytope.² The weights of the action of the torus on the tangent spaces of fixed points determine a set of vectors $\nu =\{\nu _1, \ldots ,\nu _d\}\subset \mathfrak {t}$ normal to the facets of $P$ and lying in $\Lambda$, the lattice of circle subgroups of $T$, and thus makes $(P,\nu )$ a rational labeled polytope with respect to $\Lambda$ as defined in the introduction. The Delzant–Lerman–Tolman correspondence [13, 28] states that the data $(P,\nu ,\Lambda )$ characterizes $(M,\omega ,T)$ up to a $T$-equivariant symplectomorphism.

In [18], Duistermaat and Pelayo gave a way (alternative to the so-called Delzant construction [13]) to build $(M,\omega ,T)$ from the data $( P, \nu , \Lambda )$ in the smooth case, see also [14]. The idea is based on the fact that $M$ can be seen as a compactification of $P\times T$ prescribed by the combinatorial data of $P$. We slightly adapt this construction here to cover the case of orbifolds and to see where it fails in the non-rational case.

Given a labeled polytope $( P, \nu )$, we denote the set of (closed) faces of $P$ by ${\mathcal {F}}( P)$. The facets of $P$ are still denoted $F_1, \ldots , F_d\in {\mathcal {F}}( P)$. For $F\in {\mathcal {F}}(P)$, denote $I_{F}\subset \{1, \ldots ,d\}$, the set of indices such that $F=\bigcap _{k\in I_F} F_k$. For example, $\overline{ P}\in {\mathcal {F}}( P)$ and $I_{\overline{P}}=\emptyset$. For a vertex $p, I_{\{p\}}$ has $n$ elements and is a lattice in $\mathfrak {t}$. For a face $F\in {\mathcal {F}}_p( P)$, is a subtorus of $T_p={\mathfrak {t}}\big /{\Lambda _p}$ if $p\in F$.

Given a vertex $p$ of $P$, we call ${\mathcal {F}}_p( P)$ the set of faces containing $p$. For $F\in {\mathcal {F}}_p(P)$, we denote $s_p(F)$ the subset of $F$ obtained by removing all the subfaces which do not contain $p$, that is $s_p(F) = \{x\,|\, x\in \mathring{E}, p\in E, E\subset F\}$ where $\mathring{E}$ is the interior of the face $E$ (in $E$). In particular, the interior of a vertex is the vertex itself. Thus, $\bigcup _{F\in {\mathcal {F}}_p(P) } s_p(F)=\bigcup _{F\in {\mathcal {F}}_p(P)}\mathring{F}$ is an open neighborhood of $p$ in $\overline{P}$. Set

where, for $(x,\theta ) \in F\times T_p/T_F$ and $(x',\theta ') \in F'\times T_p/T_{F'}, (x,\theta )\sim (x',\theta ')$ if

• (1) $x=x'$, and

• (2) the equivalence classes of $\theta$ and $\theta '$ in ${T_p}\big /{T_{F\cap F'}}$ coincide.

Here, the first condition implies that $F\cap F'\ne \emptyset$, so $F\cap F'\in {\mathcal {F}}_p( P)$ and $T_{F\cap F'}$ contains $T_F$ and $T_{F'}$ as subgroups. The second condition refers to the fact that ${T_p}\big /{T_{F\cap F'}}$ is the quotient of $T_p/T_F$ by ${T_{F\cap F'}}\big /{T_{F}}$ and the quotient of $T_p/T_{F'}$ by ${T_{F\cap F'}}\big /{T_{F'}}$.

Ordering the normals $\nu _{k_1}, \ldots ,\nu _{k_n}$ ($k_i\in I_{\{p\}}$), we get an identification via which $T_p$ acts on . For an equivariant neighborhood $U_p$ of , the map $\phi _p:U_p\rightarrow M_p$, defined by

$$\begin{aligned} \phi _p(z)= \left[ \left( p + \frac{1}{2}|z_i|^2\nu _{k_i}^*, \left( e^{2\pi \sqrt{-1} \theta _1}, \ldots ,e^{2\pi \sqrt{-1} \theta _n}\right) \right) \right] \end{aligned}$$

(5)

where $z=(|z_1|e^{2\pi \sqrt{-1} \theta _1}, \ldots , |z_n|e^{2\pi \sqrt{-1} \theta _n})$, is a well-defined (i.e., does not depend on the choice of $e^{2\pi \sqrt{-1} \theta _i}$ when $|z_i|=0$) equivariant homeomorphism. The chart $\left( U_p, \phi _p\right)$ provides a (smooth) differential structure to $M_p$.

Now, the cotangent space of $T_p$ is naturally equipped with an exact symplectic form, the differential of the Liouville $1$-form, for which the action of $T_p$ on itself pull-backs to a Hamiltonian action. Given an equivariant trivialization $T^*T_p\simeq \mathfrak {t}^*\times T_p$, the product $P\times T_p$ inherits of the structure of Hamiltonian $T_p$-space whose moment map is simply the projection on the first factor. The chart above extends this structure to give a (non-compact) symplectic toric manifold $(M_p,\omega _p,T_p)$ with moment map $x:M_p \rightarrow \mathfrak {t}^*$ so that $\text{ Im } x= \bigcup _{F\in {\mathcal {F}}_p(P)} \mathring{F}$, see [14, 28].

When $(P,\nu ,\Lambda )$ is rational, $\Lambda _p\subset \Lambda$ for all vertex $p$ and the quotient of $T_p$ by the finite subgroup ${\Lambda }\big /{\Lambda _p}$ is the torus $T={\mathfrak {t}}\big /{\Lambda }$. The quotient map $q_p:T_p\rightarrow T$ gives a way to glue $M_p$ to $P\times T$ providing an orbifold uniformizing chart with structure group ${\Lambda }\big /{\Lambda _p}$. Doing that on all vertices, we obtain the compact symplectic toric orbifold, $(M,\omega ,T)$, associated to $(P,\nu ,\Lambda )$ with moment map $x:M\rightarrow \mathfrak {t}^*$.

Definition 2.1

[13] A rational labeled polytope $(P,\nu ,\Lambda )$ is Delzant if, for each vertex $p, \Lambda _p=\Lambda$. In particular, $(P,\nu ,\Lambda )$ is Delzant if and only if the associated symplectic toric orbifold is a manifold (all orbifold structure groups are trivial).

Remark 2.2

A bigger lattice $\Lambda '\supset \Lambda$ in $\mathfrak {t}$ corresponds to the global quotient by the finite subgroup ${\Lambda '}\big /{\Lambda }$ of $T=\mathfrak {t}/\Lambda$, see [3].

Remark 2.3

If $(P,\nu ,\Lambda )$ is rational, we can replace $\Lambda _p$ by $\Lambda$ in the definition of $T_F$ and set

with the same equivalence relation as above. The topological space $|M|$ is the underlying topological space of $M$ and is a compactification of $P\times T$. The choice of a labeling specifies an orbifold structure on $|M|$ but $|M|$ does not depend on it.

2.2 Action-Angle Coordinates

To a convex polytope $P\subset \mathfrak {t}^*$ one can associate a symplectic manifold $(P\times \mathfrak {t},dx\wedge d\theta )$ where and are any sets of affine coordinates and $dx\wedge d\theta = \sum _{i=1}^n dx_i\wedge d\theta _i$ is (trivially) a symplectic form. More intrinsically, one could consider $T^*P$, the cotangent of the polytope itself (recall that $P$ is open in $\mathfrak {t}^*$), endowed with its canonical symplectic structure. The action of $\mathfrak {t}$ on $P\times \mathfrak {t}$ by translation on the second factor is Hamiltonian with moment map $x:P\times \mathfrak {t}\rightarrow \mathfrak {t}^*$.

Remark 2.4

One can choose $(x,\theta )$ to be dual coordinates (or canonical coordinates) on $\mathfrak {t}^*\times \mathfrak {t}$, defined for a given basis $e_1, \ldots , e_n$ of $\mathfrak {t}$ as $x_i=\langle x, e_i\rangle$ and $\theta _i = \langle \theta , e^*_i\rangle$ where $e_1^*, \ldots , e^*_n$ is the dual basis. Doing so would imply that $dx\wedge d\theta$ is a canonical symplectic form on $\mathfrak {t}\times \mathfrak {t}^*$ corresponding to the differential of the Liouville form on $T^*\mathfrak {t}=\mathfrak {t}\times \mathfrak {t}^*=T^*\mathfrak {t}^*$. However, this is not essential for our purpose since the obvious change of coordinates, say from $\theta$ to $\theta '$, on the second factor identifies the structures $dx\wedge d\theta$ and $dx\wedge d\theta '$.

Given a compact symplectic toric orbifold $(M,\omega ,T, \varrho )$ associated to $(P,\nu ,\Lambda )$, the action-angle coordinates are local coordinates on $\mathring{M}=x^{-1}(P)$ (the subset of $M$ where $T$ acts freely) identifying locally $(\mathring{M},\omega _|)$ with $(P\times \mathfrak {t},dx\wedge d\theta )$. Usually, the existence of such coordinates is proved using a compatible toric Kähler structure which is known to exist by the Delzant construction, see [2, 3, 9]. In view of the construction presented in Sect. 2.1, it is obvious that there is a $T$-equivariant symplectomorphism between $(\mathring{M},\omega _{|_{\mathring{M}}})$ and $(P\times T, dx\wedge d\theta )$. The universal cover of $\mathring{M}$, endowed with the symplectic form induced from $\omega _{|_{\mathring{M}}}$, is symplectomorphic to $(P\times \mathfrak {t},dx\wedge d\theta )$. The action-angle coordinates are $(x,\theta )$ but seen as local coordinates on $\mathring{M}$ on which they satisfies $d\theta _i(X_j):=d\ \theta _i(d_{\mathrm{id}}\varrho (e_j))=\delta _{ij}$.

Remark 2.5

Two compact symplectic toric orbifolds $(M',\omega ',T',\varrho ')$, $(M,\omega ,T,\varrho )$ associated to the same polytope $P$ (assuming the Lie algebra $\mathfrak {t}$ and $\mathfrak {t}'$ are identified but not the lattices) share the same action-angle coordinates in the sense that the symplectic manifolds $(\mathring{M}',\omega '_{|_{\mathring{M}'}})$ and $(\mathring{M},\omega _{|_{\mathring{M}}})$ have a common universal cover on which $\omega '$ and $\omega$ pull back as the same symplectic structure (up to a diffeomorphism).

Proposition 2.6

[1] For any strictly convex function $u\in C^{\infty }(P)$, the metric

$$\begin{aligned} g_{u} = \sum _{i,j} G_{ij}dx_i\otimes dx_j + H_{ij}d\theta _i\otimes d\theta _j, \end{aligned}$$

(6)

with $(G_{ij})=\text{ Hess } u$ and $(H_{ij})=(G_{ij})^{-1}$, is a smooth Kähler structure on $P\times \mathfrak {t}$ compatible with the symplectic form $dx\wedge d\theta$. Conversely, any $\mathfrak {t}$-invariant compatible Kähler structure on $(P\times \mathfrak {t}, dx\wedge d\theta )$ is of this form.

2.3 The Boundary Condition

Here again $(P,\nu )$ is a labeled polytope (with $\overline{P}$ compact, convex and simple) and the functions $L_1, \ldots , L_k$ are the affine-linear functions defining $(P,\nu )$ as $dL_k=\nu _k$ and $P=\{x\in \mathfrak {t}^*| L_k(x)>0,\, k=1, \ldots ,d\}$.

Definition 2.7

A symplectic potential of $(P,\nu )$ is a continuous function $u\in C^0(\overline{P})$ whose restriction to $P$ or to any face’s interior (except vertices), is smooth and strictly convex, and $u-u_o$ is the restriction of a smooth function defined on an open set containing $\overline{P}$ where

$$\begin{aligned} u_o = \frac{1}{2}\sum _{k=1}^d L_k \log L_k \end{aligned}$$

is the Guillemin potential. We denote by $\mathcal {S}(P,\nu )$, the set of symplectic potentials.

The Guillemin potential is a symplectic potential corresponding to the Guillemin metric [22]. Denote the space of real valued affine-linear functions on $P$.

Proposition 2.8

[3, 15] The set of smooth compatible toric (orbifold) Kähler metrics on $(M,\omega ,T)$ is in one-to-one correspondence with the quotient of $\mathcal {S}(P,\nu )$ by , acting by addition. The correspondence is explicit and given by (6).

The smooth compactification of a metric is a local issue. Even though $(P,\nu )$ might not be rational (for any lattice), a symplectic potential $u\in \mathcal {S}(P,\nu )$ defines, via (6), a Kähler metric $g_u$ on $P\times \mathfrak {t}$ which is $\mathfrak {t}$-invariant and thus, for any vertex $p$, defines a Kähler metric, still denoted $g_u$, on $P\times T_p$. The boundary condition implies that $g_u$ is the restriction to $P\times T_p$ of a smooth $T_p$-invariant Kähler metric on $(M_p,\omega _p,T_p)$. Recall that $(M_p,{\Lambda }\big /{\Lambda _p})$ is an orbifold uniformizing chart near the pre-image of a vertex in the rational case and that a smooth orbifold metric is defined as a metric which, on each chart, may be lifted as smooth metric.

Apostolov–Calderbank–Gauduchon–Tønnesen-Friedman gave the following alternative description of the boundary condition.

Proposition 2.9

[3] Given a labeled polytope $(P,\nu )$, a strictly convex function $u\in C^{\infty }(P)$ is a symplectic potential of $(P,\nu )$ if and only if, denoting ${\mathbf{H}}=(\text{ Hess } u)^{-1}$,

• ${\mathbf{H}}$ is the restriction to $P$ of a smooth $S^2\mathfrak {t}^*$-valued function on $\overline{P}$,

• for every $k=1, \ldots , d$, for every $y$ in the interior of the facet $F_k$,

  $$\begin{aligned} {\mathbf{H}}_y (\nu _k, \cdot ) =0\;\;\; \text{ and } \;\;\; d{\mathbf{H}}_y (\nu _k, \nu _k) =2\nu _k, \end{aligned}$$

  (7)

• the restriction of ${\mathbf{H}}$ to the interior of any face $F \subset P$ is a positive definite $S^2(\mathfrak {t}/\mathfrak {t}_F)^*$-valued function.

2.4 The Curvature and the Extremal Affine Function

Fixing any Euclidean volume form $d\varpi$ on $\mathfrak {t}^*$, Donaldson [16] pointed out that the $L^2(P,d\varpi )$-projection of the scalar curvature $S(u)$, given by (1), on the space of affine linear functions, , is independent of the choice of $u\in \mathcal {S}(P,\nu )$. The resulting projection is the extremal affine function of $(P,\nu )$. Indeed, starting from formula (1) for the scalar curvature, integrating by part twice and using the boundary condition 7, we get

$$\begin{aligned} \frac{1}{2}\int _{ P} S(u) x_id\varpi =\!\int _{\partial P} x_id\sigma _{\nu }=: Z_i( P,\nu ) \end{aligned}$$

where $d\sigma _{\nu }$, when restricted to any facet $F_k$, is defined by $\nu _k\wedge d\sigma _{\nu }=-d\varpi$.

Choose a basis $(e_1, \ldots , e_n)$ of $\mathfrak {t}$ and set $x_0= 1, x_1=\langle e_1,\cdot \rangle , \ldots , x_n=\langle e_n,\cdot \rangle$. The extremal affine function of $( P,\nu )$ is $\mathrm{A}_{( P,\nu )}=\sum _{i=0}^n \mathrm{A}_i x_i$ where the vector is the unique solution of the linear system:

$$\begin{aligned}&\sum _{j=0}^n W_{ij}( P)\, \mathrm{A}_j = 2Z_i( P,\nu ),\quad i= 0, \ldots , n \nonumber \\&\text{ with }\quad W_{ij}( P) = \int _{ P} x_ix_jd\varpi \quad \text{ and } \quad Z_i( P,\nu ) =\!\int _{\partial P} x_i d\sigma _{\nu }. \end{aligned}$$

(8)

2.5 Complex Coordinates

For a Kähler structure $(g_u,dx\wedge d\theta ,J_u)$ given by (6) on $P\times \mathfrak {t}$, the set $\{J_uX_1, \ldots ,J_uX_n, X_1, \ldots ,X_n,\}$ is a frame of real holomorphic commutative vector fields providing an identification $\mathfrak {t}\oplus \sqrt{-1}\mathfrak {t}\simeq T_{(x,\theta )}(P\times \mathfrak {t})$ and local holomorphic coordinates $z=t+\sqrt{-1}\theta$ where $dt_i = -d^c\theta _i$.

In the rational case, the complex coordinates $z=t+\sqrt{-1}\theta$ are only local on $\mathring{M}$ and are given by the exponential map, see [14]. Actually, in this context, for a point $y\in \mathring{M}$, the tangent space is naturally identified with the universal cover of $\mathring{M}$ where the covering map is the exponential

As explained in the literature (see, e.g., [9, 14]) we can write $dx\wedge d\theta$ in $z$ coordinates and we find a Kähler potential

$$\begin{aligned} dx\wedge d\theta = \sum _{i,j=1}^n \frac{\partial ^2\phi }{\partial t_i\partial t_j}dt_i\wedge d\theta _j =dd^c\phi . \end{aligned}$$

(9)

In the rational case, $\phi$ is a globally defined function on $\mathfrak {t}$ via the identification provided by the exponential near a point of $\mathring{M}$. Changing the base point corresponds to translate $\phi$ by an affine-linear function of $\mathfrak {t}$. The correspondence between symplectic potentials and Kähler potentials is done via the Legendre transform:

$$\begin{aligned} u(x) = \langle x,t\rangle -\phi (t) \end{aligned}$$

(10)

where $t$ is the unique point of $\mathfrak {t}$ such that $d\phi _t=x$ or inversely $x$ is the unique point of $\mathfrak {t}^*$ such that $du_x=t$. The image of the differential of the Kähler potential is the (open) polytope $P$ (i.e., $P={{\mathrm{Im}}}(t\mapsto d\phi _t)$).

A symplectic potential $u\in \mathcal {S}(P,\nu )$ provides an identification

$$\begin{aligned} \Phi _u : P\times \mathfrak {t}\rightarrow \mathfrak {t}\oplus \sqrt{-1}\mathfrak {t}\end{aligned}$$

via its differential $du:P\rightarrow \mathfrak {t}$ (which is a diffeomorphism since $u$ is strictly convex on $\mathring{M}$) so the coordinates $z=t+\sqrt{-1}\theta$ are globally defined on $P\times \mathfrak {t}$. In the rational case, this identification fits with the fact that both spaces are identified with the universal cover of $\mathring{M}$.

Remark 2.10

The common boundary behavior of symplectic potentials is equivalent to the common asymptotic behavior of Kähler potentials via the identification $du:P\mathop {\rightarrow }\limits ^{\sim }\mathfrak {t}$ or the inverse $d\phi :\mathfrak {t}\mathop {\rightarrow }\limits ^{\sim }P$ (recall that $\frac{\partial ^2\phi }{\partial t_i\partial t_j}(t) =(H_{ij}(x))$ for $du_x=t$). The Guillemin potential $u_o$ gives $du_o = \frac{1}{2} \sum _{k=1}^d (\log L_k +1)\nu _k$. In particular, the normals determine the rate of divergence of $du_o$ when $x\rightarrow \partial P$.

Distinct symplectic potentials $u, u_o\in \mathcal {S}(P,\nu )$ lead to distinct Kähler structures on $\mathfrak {t}\oplus \sqrt{-1}\mathfrak {t}$

$$\begin{aligned} \left( (\Phi _{u_o}^{-1})^*g_{u_o},\, \omega _o = (\Phi _{u_o}^{-1})^*dx\wedge d\theta \right) \;\;\; \text{ and } \;\;\;\left( (\Phi _u^{-1})^*g_u,\, \omega = (\Phi _u^{-1})^*dx\wedge d\theta \right) \end{aligned}$$

compatible with the same complex structure. Denoting $\phi$ and $\phi _o$ the Legendre transform of $u$ and $u_o$ respectively, we have $\omega -\omega _o = dd^c(\phi -\phi _o)$. Going back on $P\times \mathfrak {t}$, using $\Phi _{u_o}^{-1}$ we get

$$\begin{aligned} \left( g_{u_o},\, dx\wedge d\theta , J_{u_o}\right) \;\;\; \text{ and } \;\;\;\left( (\Phi _u^{-1}\circ \Phi _{u_o})^*g_u,\, (\Phi _u^{-1}\circ \Phi _{u_o})^*dx\wedge d\theta , J _{u_o}\right) . \end{aligned}$$

(11)

The map $\Phi _u^{-1}\circ \Phi _{u_o}$ is a $\mathfrak {t}$-invariant smooth diffeomorphism of $\overline{P}\times \mathfrak {t}$ fixing the boundary, thanks to the boundary condition on $u$ and $u_o$. In particular, the function $x\mapsto (\phi -\phi _o)(d(u_o)_x)$ is the restriction to $P$ of a smooth function on $\overline{P}$.

3 Proof of Theorem 1.3

The proof of Theorem 1.3 relies on the following lemma.

Lemma 3.1

Let $( P, \nu )$ be a labeled polytope and let $d\varpi$ be a volume form on $\mathfrak {t}^*$. The linear map defined as

$$\begin{aligned} \Psi _{( P,d\varpi )}(f)= \sum _{k=1}^d \left( \int _{F_k}f d\sigma _{\nu }\right) \nu _k \end{aligned}$$

(12)

does not depend on the set of normals $\nu$ and $\Psi _{( P,d\varpi )}(f) =0$ as soon as $f$ is constant. Moreover, seen as an endomorphism of $\mathfrak {t}$,

$$\begin{aligned} \Psi _{( P,d\varpi )}=-\mathrm{vol}( P,d\varpi )\,\mathrm{Id} \end{aligned}$$

(13)

Proof

The first claim (no dependence on $\nu$) is straightforward. Suppose that $\overline{ P} = \overline{ P}'\cup \overline{ P}''$ such that $F=\overline{ P}'\cap \overline{ P}''$ is a facet in both $P'$ and $P''$. Note that $P'$ and $P''$ induce opposite orientations on $F$. If we choose $v\in \mathfrak {t}$ a normal vector to $F$ inward to $P'$ and denote $d\sigma '$ the form on $F$ such that $v\wedge d\sigma '= -d\varpi$ then $-v\in \mathfrak {t}$ is inward to $P''$ and $-v\wedge -d\sigma '= -d\varpi$. Therefore,

$$\begin{aligned} \Psi _{( P,d\varpi )}(f)= \Psi _{( P',d\varpi )}(f)+\Psi _{( P'',d\varpi )}(f). \end{aligned}$$

By using a triangulation, that is, $n$-simplices $P_{1}, \ldots , P_{N}$ such that $\overline{ P}=\bigcup _{\alpha =1}^N \overline{ P}_{\alpha }$ and $P_{\alpha }\cap P_{\beta }=\emptyset$ if $\alpha \ne \beta$ we get

$$\begin{aligned} \Psi _{( P,d\varpi )}(f)= \sum _{\alpha =1}^N\Psi _{( P_{\alpha },d\varpi )}(f). \end{aligned}$$

(14)

Consider the simplex together with the set of normals $e=\{e_1, \ldots , e_n, e_0 = -\sum _{i=1}^n e_i \}$. Let , we have

$$\begin{aligned} \Psi _{(\Sigma ,dx_1\wedge \cdots \wedge dx_n)}(f)= \sum _{i=1}^n \left( \int _{E_i}f d\sigma -\int _{E_0}f d\sigma \right) e_i \end{aligned}$$

(15)

where for $k=0, \ldots , n, E_k$ denotes the facet normal to $e_k$.

Thus, $\int _{E_i}d\sigma =\int _{E_0}d\sigma = \frac{1}{(n-1)!}$ implies that $\Psi _{(\Sigma ,dx_1\wedge \cdots \wedge dx_n)}(f)=0$ as soon as $f$ is constant.

On the other hand, for each $i=1, \ldots , n$, the invertible affine-linear map

reverses the orientation of , sends $E_i$ to $E_0$ and satisfies $\psi _i^*e_0=e_i$. It follows that $\psi _i^*d\sigma _{|_{E_0}}=-d\sigma _{|_{E_i}}$ and in particular $\int _{E_0}fd\sigma = -\int _{E_i}\psi _i^*(fd\sigma )= \int _{E_i}(f\circ \psi _i ) d\sigma$. Thus, by writing $f$ in coordinates $f(x)=f_0+\sum _{j=1}^n f_jx_j$, Eq. (15) becomes

$$\begin{aligned} \Psi _{(\Sigma ,dx_1\wedge \cdots \wedge dx_n)}(f)&= \sum _{i,j=1, j\ne i}^n f_j \left( \int _{E_i}x_j d\sigma -\int _{E_0}x_j d\sigma \right) e_i -\sum _{i=1}^n f_ie_i\int _{E_0}x_i d\sigma \\&= -\sum _{i=1}^n f_ie_i\int _{E_0}x_i d\sigma . \end{aligned}$$

Observe that for any $i=1, \ldots , n$ the $(n-1)$-form $(-1)^{i+1}x_i \,dx_1\wedge \cdots \wedge \widehat{dx_i}\wedge \cdots \wedge dx_n$ vanishes identically when restricted to the facets $E_1, \ldots ,E_n$ and coincides with $x_id\sigma$ on $E_0$. Hence, we have

$$\begin{aligned} \int _{E_0}x_i d\sigma =(-1)^{i+1}\int _{\Sigma }d \,(x_i \,dx_1\wedge \cdots \wedge \widehat{dx_i}\wedge \cdots \wedge dx_n) =\int _{\Sigma }dx_1\wedge \cdots \wedge dx_n \end{aligned}$$

and, seen as an endomorphism of .

There is only one class of affinely equivalent $n$-simplices: for any $n$-simplex $P_{\alpha } \subset \mathfrak {t}^*$ there is an affine-linear map such that $\phi _{\alpha }( P_{\alpha })= \Sigma$. Hence,

$$\begin{aligned} \Psi _{( P_{\alpha },d\varpi )}&= \phi _{\alpha }^*\circ \Psi _{(\Sigma ,(\phi _{\alpha }^{-1})^*d\varpi )}\circ (\phi ^{-1})^* \nonumber \\&= -\frac{(\phi _{\alpha }^{-1})^*d\varpi }{dx_1\wedge \cdots \wedge dx_n} \text{ vol }(\Sigma ,dx_1\wedge \cdots \wedge dx_n)\text{ Id } \nonumber \\&= -\text{ vol }( P_{\alpha },d\varpi )\text{ Id }. \end{aligned}$$

(16)

The lemma follows then from (14).$\square$

Let $P$ be a $n$-dimensional polytope in a vector space $\mathfrak {t}^*$ of dimension $n$ and denote by $F_1, \ldots ,F_d$ its facets. Up to translation, one can assume that $P$ contains the origin and denote $\nu$ the (unique) set of inward normals for which the defining functions of $(P,\nu )$ satisfies $L_1(0)=\cdots =L_d(0)=1$. The following observation will be useful.

Lemma 3.2

Let $P$ be a polytope of dimension $n$, there is a $(n+1)$-dimensional cone of normals $\nu$ for which $( P,\nu )$ is monotone. Moreover, this cone is parameterized by via the map

$$\begin{aligned} (\lambda ,p)\mapsto \left\{ \frac{\lambda \nu _1}{L_1(p)}, \ldots , \frac{\lambda \nu _d}{L_d(p)}\right\} \end{aligned}$$

where $\nu$ is any given set of normals for $P$ with defining function $L_1, \ldots , L_d$.

To prove Theorem 1.3, we have to show that there exists only one point $p\in P$ such that $\left( P, \left\{ \frac{\nu _1}{L_1(p)}, \ldots , \frac{\nu _d}{L_d(p)}\right\} \right)$ has a constant extremal affine function, see Lemma 3.2.

Notice that any set of normals $\nu (r)$ on $P$ corresponds to a via the variation of normals:

$$\begin{aligned} \nu (r)= \left\{ \frac{1}{r_1}\nu _1, \ldots , \frac{1}{r_d}\nu _d \right\} . \end{aligned}$$

Choose a basis $e_1, \ldots ,e_n$ of $\mathfrak {t}$ and corresponding coordinates $(x_1, \ldots ,x_n)$ on $\mathfrak {t}^*$. By considering the linear system (8), we know that, for a given set of normals $\nu (r), ( P,\nu (r))$ has a constant extremal affine function if and only if

$$\begin{aligned} \mathrm{A}_{( P,\nu (r))}=\mathrm{A}_0 = \frac{Z_0( P,\nu (r))}{W_{00}( P)} \end{aligned}$$

which happens if and only if

$$\begin{aligned} W_{i0}( P)Z_0( P,\nu (r)) = W_{00}( P)Z_i( P,\nu (r)) \;\;\;\;\;\; i= 1, \ldots , n. \end{aligned}$$

(17)

Since $(d\sigma _{\nu (r)})_{|_{F_k}}= r_k(d\sigma _{\nu })_{|_{F_k}}$, the system of Eq. (17) is linear in $r$ and reads,

$$\begin{aligned} W_{i0}( P) \left( \sum _{l} \int _{F_l} d\sigma _{\nu } r_l\right) = W_{00}( P) \sum _{l} \int _{F_l} x_id\sigma _{\nu } r_l \;\;\;\;\;\; i= 1, \ldots , n. \end{aligned}$$

(18)

Notation

Indices $i$ and $j$ run from $1$ to $n$ while indices $k$ and $l$ run from $1$ to $d$.

Observe that, since $\langle \nu _k, x\rangle =-1$ on $F_k$, the vector field $X=\sum _{i=1}^n x_i\frac{\partial }{\partial x_i}$ satisfies

$$\begin{aligned} \iota _Xd\varpi = d\sigma _{\nu } \;\;\;\;\;\; \mathrm{div } X = n \;\;\; \text{ and } \;\;\; \mathrm{div } x_jX = (n+1) x_j. \end{aligned}$$

In particular, $W_{00} = \frac{1}{n} \sum _{k} \int _{F_k} d\sigma _{\nu }, W_{i0} = \frac{1}{n+1} \sum _{k} \int _{F_k} x_id\sigma _{\nu }$ and the system of Eq. (17) for $( P,\nu (r))$ becomes, $i= 1, \ldots , n$,

$$\begin{aligned} \sum _{k,l} \left( n\int _{F_k} x_id\sigma _{\nu } \int _{F_l} d\sigma _{\nu } - (n+1) \int _{F_k} d\sigma _{\nu } \int _{F_l} x_id\sigma _{\nu }\right) r_l =0. \end{aligned}$$

(19)

Since we seek monotone polytopes, by Lemma 3.2, we can restrict our attention to those such that there exists $p\in \mathring{M}$ with

$$\begin{aligned} r =(L_1(p), \ldots , L_d(p)). \end{aligned}$$

The system of Eq. (19) becomes, $i= 1, \ldots , n$,

$$\begin{aligned} \sum _{k,l} \left( n\int _{F_k} x_id\sigma _{\nu } \int _{F_l} d\sigma _{\nu } - (n+1)\int _{F_k} d\sigma _{\nu }\int _{F_l} x_id\sigma _{\nu }\right) (\langle \nu _{l},p\rangle + 1) =0. \end{aligned}$$

(20)

Lemma 3.1 implies that $\sum _{k=1}^d \int _{F_k} d\sigma _{\nu } \nu _k=0$, thus Eq. (20) reads

$$\begin{aligned} \sum _{l} \int _{F_l} x_id\sigma _{\nu } \langle \nu _{l},p\rangle = \frac{-1}{n+1} \sum _{l} \int _{F_l} x_id\sigma _{\nu }. \end{aligned}$$

(21)

The left hand side is just $\langle \Psi _{( P,d\varpi )}(e_i^*),p\rangle$ where $\Psi _{( P,d\varpi )} =-\text{ vol }( P,d\varpi )\text{ Id }$ thanks to Lemma 3.1. This ensures that there is a unique solution $p\in \mathfrak {t}^*$ of the linear system (21) given as

$$\begin{aligned} p&= \frac{1}{(n+1)\text{ vol }( P,d\varpi )}\left( \sum _{l} \int _{F_l} x_1d\sigma _{\nu }, \ldots ,\sum _{l} \int _{F_l} x_nd\sigma _{\nu } \right) \nonumber \\&= \frac{n}{(n+1)\int _{\partial P}d\sigma _{\nu }}\left( \int _{\partial P} x_1d\sigma _{\nu }, \ldots ,\int _{\partial P} x_nd\sigma _{\nu } \right) . \end{aligned}$$

(22)

This solution lies in a segment between the origin and the center of mass of $(\partial P,d\sigma _{\nu })$ and thus lies in $\mathring{ P}$. In conclusion, the labeled polytope $(P,\tilde{\nu })$ with $\tilde{\nu }_i=\frac{\nu _i}{L_i(p)}$ where $p$ is the barycenter of $( P,d\varpi )$ is monotone and has a constant extremal affine function. This prove Theorem 1.3.

Corollary 3.3

The labeled polytope $(P,\nu )$ is monotone with preferred point $p_{\nu }$ and has a constant extremal affine function $A_{(P,\nu )}$ if and only if

$$\begin{aligned} p_{\nu }= \frac{1}{\int _Pd\varpi }\left( \int _Px_1d\varpi , \ldots , \int _Px_nd\varpi \right) =\frac{1}{\int _{\partial P}d\sigma }\left( \int _{\partial P}x_1d\sigma , \ldots , \int _{\partial P}x_nd\sigma \right) . \end{aligned}$$

Another simple corollary of Theorem 1.3 is that the linear space of such that $A_{(P,\nu (r))}$ is constant meets the interior of the positive quadrant of and thus:

Corollary 3.4

Given a polytope $P$, there is a cone of dimension $d-n$ of inward normals $\nu$ such that the extremal affine function $A_{(P,\nu )}$ is constant.

4 Analysis in the Non-rational Case

4.1 Norms and Integration

Remark 4.1

In what follows, any function $f$, defined on $P$ or on $\overline{P}$, is identified with its pull-back on $\overline{P}\times \mathfrak {t}$ and is also denoted $f$. On suitable subsets, we even identify $f$ with the corresponding $T_p$-invariant function on the chart $(M_p,\omega _p,T_p)$ of a vertex $p$.

Fixing an orientation on $\mathfrak {t}^*$, a lattice $\Lambda \subset \mathfrak {t}$ naturally provides a volume form, say $d\varpi _{\Lambda }$, on $\mathfrak {t}^*$ since $\text{ Gl }(\Lambda )\subset \text{ Sl }(\mathfrak {t})$. With the dual volume form $d\varpi _{\Lambda }^*$ on $\mathfrak {t}$, given by the dual lattice, the volume of the torus $T=\mathfrak {t}/\Lambda$ is $(2\pi )^n$. As noticed in [22], given a rational labeled polytope $(P,\nu ,\Lambda )$ associated to the compact symplectic orbifold $(M,\omega ,T)$ with moment map $x:M\rightarrow \mathfrak {t}^*$, Fubini’s Theorem implies that the integration of a $T$-invariant function on $V\subset M$ is the integration of the corresponding function on $x(V)\subset \overline{P}$ times the constant $(2\pi )^n$. Precisely, given an integrable function $f$ on $U\subset P$, assuming $x^{-1}(U)$ is covered by the orbifold uniformizing chart $\left( M_p,{\Lambda }\big /{\Lambda _p},\psi _p\right)$, see Sect. 2.1, we have

$$\begin{aligned} \int _{U}fd\varpi _{\Lambda }&= \frac{1}{(2\pi )^n} \int _{x^{-1}(U)} f \frac{\omega ^n}{n!} = \frac{1}{|\Lambda /\Lambda _p|} \frac{1}{(2\pi )^n} \int _{\psi _p^{-1}(x^{-1}(U))} f \frac{\omega _p^n}{n!}\nonumber \\&= \frac{1}{\int _{T_p}d\varpi _{\Lambda }^*} \int _{\psi _p^{-1}(x^{-1}(U))} f \frac{\omega _p^n}{n!}. \end{aligned}$$

(23)

If we consider only a labeled polytope $(P,\nu )$, there is no preferred lattice but we can arbitrarily choose a volume form $d\varpi =dx_1\wedge \ldots \wedge dx_n$. Formula (23) still holds: for an integrable function $f$ defined on a neighborhood $U$ of a vertex $p$ of $P$, denoting $x:M_p\rightarrow \mathfrak {t}^*$ the moment map of the chart $(M_p,\omega _p,T_p)$,

$$\begin{aligned} \int _Ufd\varpi = \frac{1}{c_p}\int _{x^{-1}(U)}f\frac{\omega _p^n}{n!} \end{aligned}$$

(24)

where is a constant depending on $p$, on $\nu$ and on $d\varpi$. The value (24) does not depend on the vertex $p$.

On the other hand, given $u\in \mathcal {S}(P,\nu )$, the norm of any derivative $|\nabla ^{g_u}\nabla ^{g_u}\cdots \nabla ^{g_u} \psi |_{g_u}$ is a smooth function on $\overline{P}$ as soon as $\psi$ is a smooth $\mathfrak {t}$-invariant function on $\overline{P}\times \mathfrak {t}$. Indeed, $|\nabla ^{g_u}\nabla ^{g_u}\cdots \nabla ^{g_u} \psi |_{g_u}$ is then a $T_p$-invariant function on $M_p$ for each vertex $p$ of $P$ and thus, a smooth function on the image of the moment map of $(M_p,\omega _p,T_p)$ which is $\cup _{F\in {\mathcal {F}}_p(P)}\mathring{F}$, see Sect. 2.1. These smooth continuations (one for each vertex) coincide when overlapping and thus $|\nabla ^{g_u}\nabla ^{g_u}\cdots \nabla ^{g_u} \psi |_{g_u}\in C^{\infty }(\overline{P})$.

The above comments provide a scope for extending standard norms on functional spaces on $\overline{P}$. Namely, given $u\in \mathcal {S}(P,\nu )$ and $d\varpi$, we take the pointwise norms of the derivatives on $P\times \mathfrak {t}$ (or on $M_p$ if applicable) with respect to the Kähler metric $g_u$ while we integrate over $\overline{P}$ using the volume form $d\varpi$. Therefore, we define $L^p$-norms, $C^k$-norms, Hölder norms on suitable spaces of functions on $\overline{P}$ giving rise to the definition of $L^p$-space, $C^k$-space and Sobolev spaces. These spaces do not depend on $d\varpi$ and coincide respectively with their ($T$-invariant) namesake on toric Kähler orbifolds in the rational case. Moreover, even when $(P,\nu )$ is non-rational, they behave as if they were defined on a Kähler compact manifold: Sobolev inequalities, Hölder inequalities, Schauder estimates (for smooth operators on $\overline{P}$), Kondrakov Theorem hold as well, see [23]. Because (24) is (23) in the rational case, a lot of proofs are formally the same.

Remark 4.2

The boundary condition on symplectic potentials recalled in Sect. 2.3, implies that $H=(\text{ Hess } u)^{-1}$ is the restriction of a smooth $S^2\mathfrak {t}^*$-valued function on $\overline{P}$. Thus, as an example of what has been said above, for $f\in C^{\infty }(\overline{P}), g_u(\nabla ^{g_u}f,\nabla ^{g_u}f)= \sum _{i,j=1}^nH_{ij} f_{,i}f_{,j} \in C^{\infty }(\overline{P})$ (with notation (6)).

4.2 Maximum Principle

The Laplace operator of $g_u$ when restricted to the space of $\mathfrak {t}$-invariant functions on $P\times \mathfrak {t}$ is

$$\begin{aligned} \Delta ^{u}_| = \sum _{i,j=1}^n H_{ij}\frac{\partial ^2}{\partial x_j\partial x_i} + \frac{\partial H_{ij}}{\partial x_j}\frac{\partial }{\partial x_i}. \end{aligned}$$

(25)

Thanks to the boundary behavior of $H, \Delta ^{u}_|$ is a smooth operator on $C^{\infty }(\overline{P})$ satisfying

$$\begin{aligned} \int _P h\Delta ^{u} fd\varpi = \int _P \sum _{i,j=1}^nH_{ij} f_{,i}h_{,j} d\varpi =: \langle df,dh \rangle _u. \end{aligned}$$

Moreover, $\Delta ^{u}$ is a symmetric operator on $C^{2}(\overline{P})$ whose kernel consists in constant functions. It is elliptic on $P$ (but not uniformly elliptic). Let see why the Maximum Principle holds in this context as well. If $L_1, \ldots , L_k$ denote the defining affine-linear functions of $P$, the operator $\Delta ^{u}$ is uniformly elliptic on

$$\begin{aligned} P_{\epsilon } =\{x\in \mathfrak {t}^* \,|\, L_k(x)>\epsilon ,\, k=1, \ldots , d\} \end{aligned}$$

for any $\epsilon >0$. The classical Maximum Principle tells us that a function $f \in C^{2}(\overline{P})$ satisfying $-\Delta ^u f\ge 0$ on $P_\epsilon$ attains a maximum on the boundary of $P_\epsilon$. Passing to the limit, we get that $f$ must reach a maximum at a point, say $p$, of $\partial P$ whenever $-\Delta ^u f\ge 0$ on $P$. But if $q$ is a vertex of the face in which lies $p$ (or is $p$ itself if $p$ is a vertex) then $f \in C^{2}(M_q)^{T_q}$ and reaches a maximum at a point in $M_q$ while $-\Delta ^u f\ge 0$ as a function on $M_q$. But $\Delta ^{u}$ is the Laplacian for the Kähler metric $g_u$ on $M_q$. Then, $f$ is constant. In sum, we have the following lemma.

Lemma 4.3

Let $f\in C^2(\overline{P})$ if there exists $u\in \mathcal {S}(P,\nu )$ such that $\Delta ^u f\le 0$ on $P$ then $f$ is constant.

Remark 4.4

Of course the same principle holds for any symmetric operator which is elliptic on $P$ and corresponds to an elliptic operator on each chart $M_p$.

Remark 4.5

Whenever $(P,\nu )$ is rational, to $u\in \mathcal {S}(P,\nu )$ is associated a toric compact Kähler manifold $(M,\omega , g_u T), \Delta ^{u}$ is self-adjoint on the Hilbert space where it is defined, that is $\mathcal {W}^{1,1}(M)$. Now the subset $\mathcal {W}^{1,1}(M)^T$ of $T$-invariant functions is a closed Hilbert subspace and thus, the restriction of $\Delta ^{u}$ is still self-adjoint. This means that the operator $\Delta ^{u}_|$, as written in (25), is self-adjoint on $\mathcal {W}^{1,1}(\overline{P})$. There is no reason for that to fail in the non-rational case.

4.3 A Cohomology Group

A classical approach adopted in Kähler geometry of compact manifolds, is to fix a complex structure $J$ on a compact manifold $M$ and a Kähler class and study the space of compatible Kähler structures $(g,\omega ,J)$ with $\omega \in \Omega$. (This is equivalent to fix $\omega$ instead, by Moser’s Theorem.) This approach makes sense in our setting as well even though the cohomology of $P\times \mathfrak {t}$ is trivial because of the following important fact, explained in [3], due to the combination of a result of Schwarz [34] and the Slice theorem.

Lemma 4.6

Let $(M,\omega ,g,J,T)$ be a compact toric Kähler orbifold with moment polytope $P$ and moment map $x: M\rightarrow \overline{P}$. Then each $T$-invariant $C^k$ function on $M$ is the pull-back by $x$ of a $C^k$ function on $\overline{P}$. In particular, $x$ defines a isomorphism $C^{\infty }(M)^T \simeq C^{\infty }(\overline{P})$.

As a consequence of Lemma 4.6, we get a way to define the Dolbeaut $(1,1)$ cohomology group.

Lemma 4.7

Let $(M,\omega ,g,J,T)$ be a compact toric Kähler orbifold. Two real closed $(1,1)$-forms $\beta ,\beta '$ on $M$ corresponding respectively to potentials $f, h\in C^{\infty }(P)$ (i.e., $\beta =dd^cf, \beta '=dd^cf'$ on $\mathring{M}$) are cohomologous if and only if $f-h \in C^{\infty }(\overline{P})$.

For a given symplectic potential $u\in \mathcal {S}(P,\nu )$, the potential of the Ricci form associated to $g_u$ has been computed in [6], to be

$$\begin{aligned} R_u(x)= \frac{1}{2} \text {log }\,\text {det }\,(\text {Hess }\,u)_{x}. \end{aligned}$$

(26)

Remark 4.8

Thus, using Lemma 4.7, $(M,\omega )$ is monotone with constant $\lambda >0$ if and only if for any symplectic potential $u\in \mathcal {S}(P,\nu ), R_u-\lambda \tilde{\phi }\in C^{\infty }(\overline{P})$ where $\tilde{\phi }(x)=\phi ((du_o)_x)$. This condition makes sense in the non-rational case as well and is equivalent to the fact that $( P,\nu )$ is monotone in the sense of Definition 1.2, see [14].

4.4 Compactifiable Forms

In the rational case, the $1$-forms $dx_1, \ldots , dx_n$ are well-defined on the compact orbifold $M$ and thus a $k$-form $\psi \in \Omega ^k(\overline{P})$ is pulled-back to give a basic $k$-form on $M$. Here basic should be understood as $\mathfrak {t}$-basic, meaning that the contraction of $\psi$ and $d\psi$ by any element $X_v$ with $v\in \mathfrak {t}$ both vanish identically. However, not every $\mathfrak {t}$-invariant $k$-form on $\overline{P}\times \mathfrak {t}$ corresponds to a form that is the restriction of a smooth form on $M$. This is the case for $\psi \in \Omega ^k(\overline{P}\times \mathfrak {t})$ if, for any $k\in \{1, \ldots , d\}$, the contraction of $\psi$ with $\frac{1}{L_k}X_{\nu _k}$ is smooth on $\overline{P}$. To see this, we consider a chart $M_p$ for a vertex $p\in F_k$ and observe that the $1$-forms $|z_i|^2d\theta _i$ are smooth. We call these forms, those who behave as if they were defined on a compact orbifold, compactifiable forms. Let $\psi$ be such a $\mathfrak {t}$-invariant $(2n-1)$-form. Thanks to invariance $d\psi = \sum _{i=1}^n \frac{\partial }{\partial x_i} \psi _i dx\wedge d\theta$ and

$$\begin{aligned} \int _{P} (d\psi )_{|_P} = \int _{P} d \left( \sum _{i=1}^n (-1)^{i+1} \psi _i dx_1\wedge \cdots \wedge \widehat{dx_i} \wedge dx_n\right) = \int _{\partial P} \widehat{\psi } \end{aligned}$$

where $\widehat{\psi } = \sum _{i=1}^n (-1)^{i+1} \psi _i dx_1\wedge \cdots \wedge \widehat{dx_i} \wedge dx_n$. The right hand side is zero since the condition that the contraction of $\psi$ with $\frac{1}{L_k}X_{\nu _k}$ is smooth on $P\cup \mathring{F}_k$ implies that $\widehat{\psi }$ vanishes on $\partial P$. Hence, the integration of an exact compactifiable $2n$-form is zero supporting the evidence that compactifiable forms behave as forms living on a compact manifold.

5 Some Classical Theorems

5.1 Yau’s Theorem

Theorem 5.1

([7, 41]) Given a compact complex manifold $(M,J)$ of Kähler type and a Kähler class $\Omega$, for each $(1,1)$-form $\rho \in 2\pi c_1(M)$ there exists a unique Kähler form $\omega \in \Omega$ such that $\rho$ is the Ricci form of the Kähler structure $(\omega , J)$.

Since the Ricci form only depends on the volume form, Yau’s Theorem reads as: given a smooth function $F\in C^{\infty }(M)$, satisfying $\int _M e^F\omega _o^n =\int _M\omega _o^n$ there exists a unique $\psi \in C^{\infty }(M)$ such that $\int _M\psi \,\omega ^n=0, \omega _o +dd^c \psi >0$ and

$$\begin{aligned} (\omega _o +dd^c \psi )^n =e^F\omega _o^n. \end{aligned}$$

(27)

In terms of potentials, Eq. (27) furnishes a Monge–Ampère type equation. In [7], Calabi showed the uniqueness of solution of this pde and suggested a continuity method to prove the existence. He proved the openness of the set of solutions of (27) while Yau [41] produced a priori estimates. Good references for this proof are also [23, 33].

Let $(P,\nu )$ be a labeled polytope with $P\subset \mathfrak {t}^*$. We fix a symplectic potential $u_o\in \mathcal {S}(P,\nu )$, thus the Kähler structure $(g_o,\omega _o, J)$ on $\mathfrak {t}\oplus i\mathfrak {t}$ ($J$ denote the endomorphism of the tangent bundle induced by $i$), we denote $\rho _o$ its Ricci form and $\phi _o$ the Legendre transform of $u_o$. Thanks to Lemma 4.7 and (26), Yau’s Theorem reads:

Theorem 5.2

Given $R\in C^{\infty } (P)$ such that $R- R_{u_o} \in C^{\infty }(\overline{P})$, there exists $u\in \mathcal {S}(P,\nu )$ such that $R=\frac{1}{2} \text {log }\,\text {det }\,(\text {Hess }\,u)_{x}$ and this solution is unique up to addition by an affine-linear function.

The uniqueness follows from a simple use of the Maximum Principle. To see why this argument holds in our setting, we recall the explanation given in [21]. Denote $\Psi$ the Hermitian endomorphism of the tangent defined by $\omega (X, \Psi (Y))= dd^c\psi (X,Y)$ and $\lambda _1, \ldots , \lambda _n$ its real eigenvalues. Equation (27) is

$$\begin{aligned} \prod _{i=1}^n(1+\lambda _i) =1+\sigma _1(\lambda _1, \ldots , \lambda _n)+ \cdots +\sigma _n(\lambda _1, \ldots , \lambda _n)= e^F\end{aligned}$$

where $\sigma _i$ is the $i$-th symmetric elementary function. In particular, $\omega _o +dd^c \psi >0$ if and only if $1+\lambda _i >0$ for each $i$. Now, since

$$\begin{aligned} \left( \prod _{i=1}^n(1+\lambda _i)\right) ^{\frac{1}{n}} \le \frac{1}{n}\sum _{i=1}^n ((1+\lambda _i))= 1 + \sigma _1(\lambda _1, \ldots , \lambda _n) \end{aligned}$$

and that $\sigma _1=-\Delta ^{g_o} \psi$. We get

$$\begin{aligned} \Delta ^{g_o} \psi \le n(1- e^{\frac{F}{n}}). \end{aligned}$$

(28)

We conclude, using Sect. 4.2, that in our generalized setting as well if there is a solution of Eq. (27) this solution is unique.

With the discussion of Sect. 4, we should be convinced that the proofs of Calabi and Yau are still valid for non-rational labeled polytopes, but we check the details a little bit more. We pass to the complex side of the picture in order to rely on the existing literature on this topic. We consider the path of equations obtained by taking $e^{F_t} = \frac{e^{tF}}{\frac{1}{V_{\Omega }}\int _M e^{tF}d\varpi }$, where $V_{\Omega }= \int _Md\varpi$. The set $S$ of $t\in [0,1]$ such that there exists a solution of Eq. (27) with $F=F_t$ is non-empty, since, at $t=0, \psi \equiv 0$ is a solution.

The linearization of Eq. (27) is

$$\begin{aligned} \dot{F}\mapsto \Delta ^u \dot{F} \end{aligned}$$

as explained in [21, 23, 33]. Hence, the fact that $S$ is open follows the fact that the Laplacian defines an isomorphism of $C_{0,g}^{\infty }(M)=\{f\in C^{\infty }(M)\,|\, \int _M f d\varpi _g=0\}$. The space of invariant functions

$$\begin{aligned} C_{0,g}^{\infty }(M)^T=\left\{ f\in C^{\infty }(M)^T\,|\, \int _M f d\varpi _g=0\right\} =C_{0,d\varpi }^{\infty }(\overline{P}) \end{aligned}$$

is closed under this isomorphism and the Laplacian, when acting on $C_{0,g}^{\infty }(M)^T$, reduced the smooth elliptic operator (25). Thus, the argument is valid on non-rational polytopes as well, see Sect. 4.

To prove that $S$ is a closed subset of $[0,1]$, one needs a priori estimates on solutions of the Monge–Ampère Eq. (27). The estimates were found by Yau in [41]. This is a great piece of work that inspired a lot of subsequent studies. In particular, in [39], Tian and Zhu used and adapted Yau’s ideas to a more complicated equation corresponding to Kähler–Ricci solitons. In Sect. 5.3, we discuss how their study carries in our setting. The uniform bound (the $C^0$ estimate) follows a boot strapping method as explained in [23] and uses only Stokes’s Theorem, Sobolev embedding Theorem, ...that hold in our setting as explained in Sect. 4.

5.2 Zhu’s Theorem

In [42], Zhu considered the following problem: on a compact Fano manifold $(M,J)$, given a Kähler form $\tau \in 2 \pi c_1(M)$ and a holomorphic vector field $Z$ on $M$, does there exist a Kähler metric $(\omega ,g)$ such that

$$\begin{aligned} \rho ^g- \tau ={\mathcal {L}}_Z\omega \end{aligned}$$

(29)

and, if it exists, is it unique ? Zhu proved unicity of solution (up to automorphism) and exhibited necessary and sufficient conditions on the vector field $Z$ for a solution to exist. In the toric case, for a $T$-invariant form $\tau$, these conditions are fulfilled whenever $Z=JX_a-iX_a$ for some $a\in \mathfrak {t}$. Moreover, in this case, the solution is $T$-invariant. Via Lemma 4.7, with the same notation as before (picking a reference metric $\omega _o, \ldots$) Zhu’s result reads as follows

Theorem 5.3

Given a convex function $R\in C^{\infty } (P)$ such that $R- R_{u_o} \in C^{\infty }(\overline{P})$ and $a\in \mathfrak {t}$, there exists $u\in \mathcal {S}(P,\nu )$ such that $R_u - R= a$ and this solution is unique up to addition by an affine-linear function.

In terms of potentials, a solution $\psi$ of Eq. (29), corresponding to $\omega _\psi = \omega _o+dd^c\psi$, satisfies

(30)

where $\theta _Z,f_o\in C^{\infty }(\overline{P})$ satisfies ${\mathcal {L}}_Z\omega _o=dd^c\theta _Z$ and $\rho _o -\tau = dd^cf_o$. He observed that $Z.\psi$ needs to be a real-valued function. In our case, working with $\mathfrak {t}$-invariant functions and holomorphic vector field induced from $\mathfrak {t}\oplus i\mathfrak {t}$ this condition is satisfied. Then using a continuity method Zhu proved uniqueness and existence of solutions assuming that $\tau$ is positive definite $(1,1)$-form. The path of equations he considered starts at the pde corresponding to Yau’s result. So we get the non-emptyness thanks to Yau’s Theorem (which holds in our context by the last section). The proof of openness and uniqueness use standard arguments and facts on compact manifold (Stokes, integration by parts, Maximum Principle, ...). A key ingredient for estimates leading to the closeness part of Zhu’s proof is an a priori bound on $|Z.\psi |$ on compact Kähler manifolds as soon as $({{\mathrm{Im}}}Z).\psi =0$ and $\omega _o +dd^c \psi >0$. The proof of Zhu use classification of complex surfaces and cannot be directly adapted to our generalized setting. However, we only need a weaker result: since $\psi (t)=\phi (t)-\phi _o(t)$ and $Z= JX_a-iX_a$ for some $a\in \mathfrak {t}$, with respect to the coordinates $t+i\theta$, we have

$$\begin{aligned} |(Z.\psi )_t|&= |d\psi (JX_a-iX_a)_t|=\left| \sum _{i=1}^n a_i \left( \frac{\partial \phi }{\partial t_i} - \frac{\partial \phi _o}{\partial t_i}\right) \right| =|\langle a, x\rangle - \langle a, x_o\rangle |\nonumber \\&\le \max \{\langle a, x \rangle \,|\, x\in \overline{P}\} -\min \{\langle a, x_o\rangle \,|\, x_o \in \overline{P}\}. \end{aligned}$$

(31)

This gives the desired bound. For the rest of the estimates, Zhu adapts Yau’s argument and we will see a more complicated version in the next section.

5.3 The Theorem of Wang and Zhu

Theorem 5.4

([40]) Given a compact Fano toric manifold $(M,J,T)$ and $Z_a$ the Kähler-Ricci vector field (where $a\in \mathfrak {t}$ is defined by (3)). For any $\lambda >0$, there exists a unique $T$-invariant Kähler form $\omega \in 2\pi \lambda c_1(M)$ such that $(g,\omega ,J)$ is a Kähler–Ricci soliton with respect to $Z_a$.

Let $(P,\nu )$ be a monotone labeled polytope with preferred point $p\in P$ and $a\in \mathfrak {t}$ be defined by (3). Again, we fix a symplectic potential $u_o\in \mathcal {S}(P,\nu )$ and use the same notation as before.

If $(g,\omega ,J)$ is a Kähler–Ricci soliton with respect to $Z= JX_a-iX_a$ in the sense that it satisfies (2) with $\lambda >0$, one can write

$$\begin{aligned} -dd^c\log \frac{\omega ^n}{\omega _o^n} =dd^c(\theta _Z-f_o +\lambda \psi + Z.\psi ). \end{aligned}$$

(32)

Indeed, this is Eq. (2) with $\rho -\rho _o=-dd^c\log \frac{\omega ^n}{\omega _o^n}$ and $n\lambda \int _{ P}d\varpi = \int _{\partial P}d\sigma _{\nu }$. Wang and Zhu used a continuity method on the modified equation

$$\begin{aligned} (\omega _o +dd^c \psi )^n =e^{f_o-\theta _Z - s\psi -Z.\psi }\omega _o^n \end{aligned}$$

(33)

for a parameter $s\in [0,1]$. The normalization imposed is

$$\begin{aligned} \int _{M}e^{f_o}\omega _o^n=\int _{M}\omega _o^n,\;\;\; \;\;\;\int _{M}e^{\theta _Z+Z.\psi }\omega ^n=\int _{M}e^{f_o -\psi }\omega _o^n=\int _{M}\omega _o^n. \end{aligned}$$

(34)

For $s=0$, the existence of a unique solution is due to Zhu’s result [42], which holds in our context see Sect. 5.2. Again the proof of Wang and Zhu to prove uniqueness of solution and existence under small variation use standard stuff on compact manifold (Stokes, integration by parts, Maximum Principle, ...) that hold in our setting as explained in Sect. 4. The uniform estimate follows from some nice arguments of convexity on the potentials which do not rely on the geometry of $M$, it is clearly explained in [40, §3] and [14, §3.4]. The next lemma, stated and proved in [39] is crucial to get the higher estimates of Wang and Zhu. It is still valid in our generalized setting as we explain below.

Lemma 5.5

Fix $0\le s\le 1$. If $\psi =\phi -\phi _o\in C^{\infty }(\mathfrak {t})$ is a solution of

$$\begin{aligned} (\omega _o +dd^c \psi )^n =e^{f_o-\theta _Z - s\psi -Z.\psi }\omega _o^n \end{aligned}$$

(35)

where $\phi , \phi _o$ are the Legendre transforms of $u$, $u_o\in \mathcal {S}(P,\nu )$ and $\phi _o$ is a potential for $\omega _o$ then a $C^0$ bound on $\psi$ provides $C^2$ and $C^3$ bounds on $\psi$.

Remark 5.6

Note that the normalization (34) only affects $\psi$ up to an additive constant, so the condition ${{\mathrm{Im}}}(t\mapsto (d\phi )_t)= {{\mathrm{Im}}}(t\mapsto (d\phi _o)_t)=P$ is not over determined.

Proof of Lemma 5.5

Equation (35) is (27) with $F$ replaced by $f_o-\theta _Z- s\psi -Z.\psi$. The proof of Tian and Zhu is an adaptation of Yau’s approach. Recall that Zhu gave an a priori bound on $|Z.\psi |$ that still hold in our context Sect. 5.2. Apart from this fact, the arguments of Tian–Zhu are essentially local, using the compactness of the manifold only to get bounds on various continuous functions (depending on $(\omega _o, g_{u_o})$) appearing in the equations. Applying the principle explained in Sect. 4.1 is then enough to claim that the estimates hold in our setting.

We present below the details for getting the second order estimate.

As a first step, a local computation shows that, for solutions of (27), a priori bounds on $|F|$ and $|\Delta ^{g_o} \psi |$ give a priori bounds on $|dd^c\psi |_{g_o}$, see [23, Proposition 5.3.4]. Hence, for solutions of (35), it is sufficient to bound $|\Delta ^{g_o} \psi |$ and $|s\psi + Z.\psi |$. A bound on $|Z.\psi |$ follows from (31). It remains to find a bound on $|\Delta ^{g_o} \psi |$. We only have to find an upper bound to $\Delta ^{g_o} \psi$ since

$$\begin{aligned} 0<\text{ tr }_{\omega _o}(\omega _o+ dd^c \psi ) = n+ \Delta ^{g_o} \psi \end{aligned}$$

where $\text{ tr }_{\omega _o}$ is the trace with respect to $\omega _o$. Tian and Zhu computed that

(36)

at any point $p$, where $\Delta =\Delta ^{g_o}$, are components of the curvature tensor of the metric $g_o$ with respect to holomorphic coordinates, say $z$, chosen at $p$ so that and (this convention is used in local computation mentioned above).

Note that each function appearing in the right hand side of (36) is smooth on $\overline{ P}$. In particular, as a consequence of the boundary condition on symplectic potential (see Proposition 2.9), the function is smooth on $\overline{P}$. Indeed, changing the variables from $t$ to $x$, one gets

(37)

Now, let $p\in \overline{P}$ be a point where the function $\exp (-c\psi )(n+\Delta \psi )$ attains its maximum. Then, using (31) and the compactness of $\overline{P}$, we can show, as Tian and Zhu did, that at this point $p$, there exist $C_1,C_2>0$ such that

$$\begin{aligned} \Delta (-f_o+\theta _Z+\lambda \psi +Z.\psi )\le C_1+C_2(n+\Delta \psi ). \end{aligned}$$

(38)

Inserting this into (36) and using some local formulas (following [41]), there are constants $C_3,C_4,C_5$ independent of $\psi$ such that

$$\begin{aligned} \Delta ^{g}((n+\Delta \psi )\exp (-c\psi ))&\ge - \exp (-c\psi ) (C_3 + C_4(n+\Delta \psi )) \nonumber \\&\quad +C_5\exp (-c\psi +\frac{s}{n-1}\psi )(n+\Delta \psi )^{n/(n-1)}.\qquad \quad \end{aligned}$$

(39)

Then, Yau applied the Maximum Principle: the left hand side of (39) is the Laplacian of a function at its maximum so it must be negative. This argument holds if the maximum is not attained on the boundary of a manifold (which was obviously the case in Yau and Tian–Zhu setting). Actually, it works in our setting as well: if $p\in F \subset \partial P$ where $F$ is a face containing a vertex, say $q$, then the left hand side of (39) is the Laplacian (of a smooth metric $g_u$) of a function defined on $M_q$ (see Sect. 2.3) which attains a local maximum at $p$ so it must be negative. Hence, we get the Tian–Zhu estimate in our generalized setting:

$$\begin{aligned} (n+\Delta \psi _s) \le C (1+ \exp (-s \inf _{M} \psi _s))\exp (-c(\psi _s + \inf _{M}\psi _s)) \end{aligned}$$

(40)

for constants $c,C$ independent of $\psi$.

Following the same argument, the $C^3$-estimate of Tian and Zhu holds as well.$\square$

6 Applications

6.1 Extremal Kähler Equation

Consider the extremal Kähler equation

$$\begin{aligned} S(u)= A_{(P,\nu )} \end{aligned}$$

(41)

for $u\in \mathcal {S}(P,\nu )$ where $S(u)$ is the scalar curvature of $g_u$, given by Abreu’s formula (1). If $u$ is solution of (41), then $g_u$ is an extremal Kähler metric in the sense of Calabi [8]. In [15], Donaldson proved³ that the cokernel of the linearization of the map $u\mapsto S(u)$ in $C^{\infty }(\overline{P})$ is the set of affine linear functions on $\overline{P}$. In particular, denoting ${\mathbf{N}}(P)$ the cone of normals inward to $P$, the linearization of the extension of the scalar curvature map

$$\begin{aligned} S: \bigcup _{\nu \in {\mathbf{N}}(P)} \mathcal {S}(P,\nu )&\longrightarrow C^{\infty }(\overline{P})\nonumber \\ u&\longmapsto S(u) \end{aligned}$$

(42)

is surjective on . Thus, together with the fact that $\bigsqcup _{\nu \in {\mathbf{N}}(P)}\mathcal {S}(P,\nu )$ is path connected, the set ${\mathbf{E}}(P)$ of inward normals $\nu$ for which there exists an extremal Kähler metric $g_u$ with $u\in \mathcal {S}(P,\nu )$ is open in ${\mathbf{N}}(P)$. Gathering this with Theorems 1.3, 1.6 and Corollary 3.4, we get Corollary 1.7.

6.2 Lattice Polytopes and Kähler–Einstein Orbifolds

Lemma 6.1

Let $(P,\nu )$ be a monotone labeled polytope with a constant extremal affine function. Then, is a lattice if and only if $P$ is a lattice polytope.

Proof

One direction is straightforward: if $\nu$ spans a lattice $\Lambda$ there is a toric Kähler–Einstein orbifold with moment polytope $P$ and the general theory tells us that $P$ is a lattice polytope.

Conversely, first observe that the assumption implies that there is a lattice containing both the set of vertices of $P$ and the preferred point $p_{\nu }$. To see this, one can use Corollary 3.3 once $\mathfrak {t}^*$ identified with and the lattice spanned by the vertices with . Denote by $\Lambda ^*\subset \mathfrak {t}^*$ the lattice spanned by $p_{\nu }$ and the vertices of $P$. Use a translation to set $p_{\nu }=0$ (the vertices are still in $\Lambda ^*$) and, up to a dilatation of $\nu$, assume that $L_l=\langle \nu _l,\cdot \rangle +1, l=1, \ldots , d$. Since the origin lies in the interior of the polytope, each facet contains a set of vertices of $P$ which is a (real) linear basis of $\mathfrak {t}^*$. Such a basis lies in $\Lambda ^*$ by assumption and, thus, is a rational linear basis of . This implies that $\langle \nu _l,q \rangle$ is a rational number for each $q\in \Lambda ^*$ and $l=1, \ldots , d$. In particular, there exists such that the set ${m\nu _1, \ldots , m\nu _d}$ is included in the dual lattice of $\Lambda ^*$. $\square$

Corollary 6.2

If $P$ is a polytope with vertices in $\Lambda ^*$, and $\nu$ is a set of normals given by Theorem 1.3 then there exists a real number $s>0$ such that is a sublattice of $\Lambda$, the dual lattice of $\Lambda ^*$.

6.3 Singular Kähler–Einstein Metrics

Consider a Delzant labeled polytope $(P,\eta ,\Lambda )$, see Definition 2.1. The associated compact symplectic toric orbifold $(M,\omega ,T)$ is a smooth manifold (all the orbifold structure groups are trivial). Denote the moment map $x: M\rightarrow \mathfrak {t}^*$ and recall that $T={\mathfrak {t}}\big /{\Lambda }$.

The construction of $(M,\omega ,T)$ of Duistermaat–Pelayo [18], recalled in Sect. 2, allows us to see $M$ as a smooth compactification of $P\times T$. There is an equivariant symplectomorphism between the open subset of $M$ where the torus acts freely, say $\mathring{M}=x^{-1}(P)$, and $P\times T$.

Consider another set $\nu$ of normals inward to $P$ and a symplectic potential $u\in \mathcal {S}(P,\nu )$. The Kähler metric $g_u$ defined by (6) is a $\mathfrak {t}$-invariant smooth Kähler metric on $P\times \mathfrak {t}$ and, thus, defines a smooth Kähler metric, still denoted $g_u$, on $P\times T$, compatible with the symplectic form $dx\wedge d\theta$. Hence, via the equivariant symplectic embedding

$$\begin{aligned} (P\times T, dx\wedge d\theta , T)=(\mathring{M}, \omega _{|_{\mathring{M}}}, T)\subset (M,\omega ,T), \end{aligned}$$

$g_u$ is a smooth Kähler metric on $\mathring{M}$ compatible with the symplectic form $\omega _{|_{\mathring{M}}}$. This metric $g_u$ is not the restriction of a smooth metric on $M$ unless $\nu =\eta$.

Remark 6.3

If $\nu$ spans a sub-lattice of $\Lambda$, the Kähler structure $(g_u,\omega _{|_{\mathring{M}}}, J_u)$ compactifies smoothly (in the orbifold sense) on the orbifold associated to $(P,\nu ,\Lambda ')$.

We now describe the singular behavior of $g_u$ along the toric submanifolds corresponding to the pre-image of the interior of the facets of $P$. For each facet $F_k$, there is a real number $a_k>0$ such that

$$\begin{aligned} a_k\nu _k=\eta _k. \end{aligned}$$

(43)

The type of the singularity along $x^{-1}(\mathring{F}_{k})$ only depends on $a_k$ and to understand which types of singularity may occur we only need to study the possibilities on a sphere. To see this, we can use the alternative definition of $\mathcal {S}(P,\nu )$ of [3], recalled in Sect. 2.3.

Let and $\nu _1= \frac{1}{a}\eta _1$ where $\eta _1$ is the generator of $S^1$. Thus, $(P,\{\eta _1, -\eta _1\})$ is the labeled polytope of the sphere $S^2$ of volume $4\pi$. Let a neighborhood of the origin be a $S^1$-equivariant chart around the south pole $x^{-1}(0)$. With respect to polar coordinates $(r,\theta )$ on $U$ (with the period $2\pi$ given by $\eta _1$ as in (5)), we have $x= \frac{1}{2}r^2$ and $\theta =\theta$. On $(0,2)\times S^1$ the metric $g_u$ is

$$\begin{aligned} g_u=\frac{dx\otimes dx}{2ax +\large {O}(x^2)} +(2ax +\large {O}(x^2))d\theta \otimes d\theta .\quad \end{aligned}$$

(44)

The change of coordinates in the metric (44) gives

$$\begin{aligned} g_u = \frac{1}{a} \left( dr\otimes dr +a^2r^2d\theta \otimes d\theta \right) -\frac{r^2 dr\otimes dr}{a(a +\large {O}(r^2))} + \large {O}(r^4) d\theta \otimes d\theta \end{aligned}$$

(45)

as computed in [3]. The last two terms are smooth and vanish at $r=0$. Therefore

$$\begin{aligned} \text{ if } a&< 1,\, g_u \, \text{ has } \text{ a } \text{ singularity } \text{ of } \text{ conical } \text{ type } \text{ and } \text{ angle } 2a\pi , \nonumber \\ \text{ if } a&= 1,\, g_u \, \text{ is } \text{ smooth },\nonumber \\ \text{ if } a&> 1,\, g_u \, \text{ has } \text{ a } \text{ singularity } \text{ characterized } \text{ by } \text{ a } \text{ large } \text{ angle } 2a\pi >2\pi . \end{aligned}$$

(46)

Consequently, we obtain

Proposition 6.4

Let $(M,\omega , T)$ be a smooth compact symplectic toric manifold associated to the Delzant labeled polytope $(P,\eta ,\Lambda )$. For any set $\nu$ of normals inward to $P$, the symplectic potentials in $\mathcal {S}(P,\nu )$ define $T$-invariant, compatible, Kähler metrics on the open dense subset where the torus acts freely via formula (6). The behavior of these metrics along the pre-image of the interior of the facet $\mathring{F}_k$ only depends on the real number $a_k>0$, defined by $a_k\nu _k=\eta _k$, as in (46).

Proposition 6.5

Let $(M,\omega , T)$ be a smooth compact symplectic toric manifold associated to the Delzant labeled polytope $(P,\eta ,\Lambda )$. Fix $\nu$, a set of inward normals such that $(P,\nu )$ is monotone and has a constant extremal affine function equals to $2n$.

For any $\lambda >0$, there exists a $T$-invariant Kähler–Einstein metric $g_{\lambda }$ smooth on the open dense subset where the torus acts freely, compatible with $\omega$ and with scalar curvature equals to $2n\lambda$. The type of singularity of $g_{\lambda }$ along the pre-image of the interior of the facet $\mathring{F}_k$ is one of the 3 cases of (46) with $a_k$ defined by $\lambda a_k\nu _k=\eta _k$. In particular, for $\lambda$ small enough, the singularity along the pre-image of the interior of any facet is of conical type.

Remark 6.6

Proposition 6.4 gives a way to construct plenty of singular metrics. For instance, a dilatation of the set of normals, $s\nu$ with $s>0$, corresponds in multiplying the volume (with respect to $g_u\in \mathcal {S}(P,s\nu )$) of the orbits of $T$ in $M$ by a factor $s^{\frac{n}{2}}$.

Now, we interpret the Kähler metric $g_u$ has a singular Kähler metric in the usual sense (smooth complex structure and singular symplectic form). Indeed, the singularity of $\Phi _u^{-1}\circ \Phi _{u_o} : P\times \mathfrak {t}\rightarrow P\times \mathfrak {t}$ (see notation (11) in Sect. 2.5) when $u\in \mathcal {S}(P,\nu )$ and $u_o\in \mathcal {S}(P,\eta )$ lies along the boundary $\partial P$ and only depends on the ratio of $\eta$ and $\nu$. That is,

$$\begin{aligned} ((\Phi _u^{-1}\circ \Phi _{u_o})^*g_u, (\Phi _u^{-1}\circ \Phi _{u_o})^*dx\wedge d\theta , J_{u_o}) \end{aligned}$$

is a smooth Kähler metric on $P\times \mathfrak {t}=\mathring{M}$ compatible with $J_{u_o}$ and the complex structure $J_{u_o}$ admits a smooth compactification on $M$. We take back the local setting: , a $S^1$-equivariant chart around the south pole $x^{-1}(0)$ as above, with the polar coordinates $(r,\theta )$ and singular Kähler structure $(g_u,J_u)$ given by (47) for some $a>0$. For our purpose (which is analyzing the local singularity), the smooth Kähler structure $(g_{u_o},dx\wedge d\theta ,J_{u_o})$ can be identified to the standard one on , namely $(dr^2 +r^2d\theta ^2,\omega =rdr\wedge d\theta , i)$, and the smooth part of $g_u$ can be forgotten. We put $g_u =\frac{1}{a}\left( dr\otimes dr +a^2r^2d\theta \otimes d\theta \right)$. Moreover, we don’t need to find explicitly $\Phi _u^{-1}\circ \Phi _{u_o}$ but only a diffeomorphism of $U\backslash \{0\}$ which takes $g_u$ to a metric which is Kähler with respect to the standard complex structure on $U\backslash \{0\}$. Consider $z=r^{1/a}e^{i\theta }$ as in [17] to see that

$$\begin{aligned} a|z|^{2(a-1)}dz\otimes d\bar{z} = \frac{1}{a}\left( dr\otimes dr +a^2r^2d\theta \otimes d\theta \right) - idx\wedge d\theta =g_u -i\omega . \end{aligned}$$

(47)

Up to the multiplicative factor $a$, the $(1,1)$-form

$$\begin{aligned} \omega _a=a|z|^{2(a-1)} i dz\wedge d\bar{z} \end{aligned}$$

is either:

$$\begin{aligned}&\text{ singular } \text{ of } \text{ conical } \text{ type } \text{ and } \text{ angle } 2a\pi , \text{ when } a<1 \nonumber \\&\text{ smooth } \text{ and } \text{ positive } \text{ definite, } \text{ when } a=1 \nonumber \\&\text{ smooth } \text{ but } \text{ not } \text{ positive } \text{ definite, } \text{ when } a>1. \end{aligned}$$

(48)

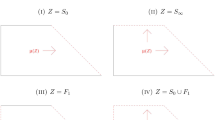
6.4 Singular Kähler–Einstein Metrics on the First Hirzebruch Surface

Let $P$ be the convex hull of the points $(1,0), (1,1), (2,2), (2,0)$ in . Consider the two sets of inward normals:

$$\begin{aligned} \eta&= \left\{ \eta _1= \begin{pmatrix}1\\ 0 \end{pmatrix}, \eta _2= \begin{pmatrix} -1\\ 0 \end{pmatrix}, \eta _3= \begin{pmatrix} 0\\ 1 \end{pmatrix}, \eta _4= \begin{pmatrix} 1\\ -1 \end{pmatrix}\right\} ,\\ \nu (C)&= \left\{ \nu _1= C\frac{7}{5}\begin{pmatrix} 1\\ 0 \end{pmatrix}, \nu _2= C\frac{7}{4}\begin{pmatrix} -1\\ 0 \end{pmatrix},\nu _3= C\begin{pmatrix} 0\\ 1 \end{pmatrix}, \nu _4= C\begin{pmatrix} 1\\ -1 \end{pmatrix} \right\} . \end{aligned}$$

One can check that $(P,\eta )$ satisfies the Delzant condition and corresponds to the first Hirzebruch surface . On the other hand, $(P,\nu (C))$ is monotone and has constant extremal affine function. Actually, see [24], we explicitly know the form of the Kähler–Einstein metric on quadrilaterals in terms of the inverse of the Hessian of the potential: using notation (6), it reads

$$\begin{aligned} (H_{ij})= \frac{x_1}{x_1^2 - x_2}\begin{pmatrix} A(x_1)+ B(x_2/x_1) &{} (x_2/x_1)A(x_1)+ x_1B(x_2/x_1)\\ (x_2/x_1)A(x_1)+ x_1B(x_2/x_1)&{}(x_2/x_1)^2A(x_1)+ x_1^2B(x_2/x_1) \end{pmatrix} \end{aligned}$$

(49)

with

$$\begin{aligned} A(x)&= \frac{-2C}{7}(x-1)(x-2)(2+3x),\nonumber \\ B(y)&= -2Cy(y-1). \end{aligned}$$

(50)

Remark 6.7

The case $C=1$ gives a singularity of angle $2\pi 5/7$ along the section at infinity of which is precisely the angle of singularity obtained by Székelyhidi [36] in the limit case of a construction (using Calabi ansatz) of metrics on satisfying $\text{ Ric }(\omega )\ge \frac{6}{7}\omega$, see also [29, 30].