On Complete Constant Mean Curvature Vertical Multigraphs in $\mathbb{E}(\kappa,\tau)$

Abstract

We prove that any complete surface with constant mean curvature in a homogeneous space $\mathbb{E}(\kappa,\tau)$ which is transversal to the vertical Killing vector field is, in fact, a vertical graph. As a consequence we get that any orientable, parabolic, complete, immersed surface with constant mean curvature H in $\mathbb{E}(\kappa,\tau)$ (different from a horizontal slice in $\mathbb{S}^{2}\times\mathbb{R}$) is either a vertical cylinder or a vertical graph (in both cases, it must be 4H ²+κ≤0).

1 Introduction

The classical theory of constant mean curvature surfaces in 3-manifolds is still an active field of research nowadays. Among all ambient 3-manifolds, the most studied subclass consists of those simply connected with constant sectional curvature, the so-called space forms ($\mathbb{R}^{3}$, $\mathbb{S}^{3}$, or $\mathbb {H}^{3}$). Their isometry group has dimension 6 and acts transitively on their tangent bundle. Apart from the space forms, the most symmetric ones are those simply connected whose isometry group has dimension 4. They are usually denoted by $\mathbb{E}(\kappa,\tau)$, where $\kappa,\tau \in\mathbb{R}$ satisfy κ−4τ ²≠0, and include the Riemannian product manifolds $\mathbb{S}^{2}(\kappa)\times\mathbb{R}$ and $\mathbb{H}^{2}(\kappa )\times\mathbb{R}$ (when τ=0), the Heisenberg space Nil₃ (for κ=0), the universal cover $\widetilde{\mbox{SL}_{2}}(\mathbb{R})$ of the special linear group SL$_{2}(\mathbb{R})$ endowed with some special left-invariant metrics (for κ<0 and τ≠0), and the Berger spheres (for κ>0 and τ≠0). See [3] for more details.

The spaces $\mathbb{E}(\kappa,\tau)$ are characterized by admitting a Riemannian submersion $\pi:\mathbb{E}(\kappa,\tau)\to\mathbb {M}^{2}(\kappa)$ with constant bundle curvature τ, where $\mathbb{M}^{2}(\kappa)$ stands for the simply connected Riemannian surface with constant curvature κ, such that the fibers of π are the integral curves of a unit Killing vector field in $\mathbb{E}(\kappa,\tau)$ (see [12]). In what follows, we will refer to this field as the vertical Killing vector field and it will be denoted by ξ.

In the theory of constant mean curvature surfaces (H-surfaces in the sequel) in $\mathbb{E}(\kappa,\tau)$, vertical multigraphs play an important role. A surface Σ immersed in $\mathbb{E}(\kappa ,\tau)$ is said to be a vertical multigraph if any of the following equivalent conditions hold:

• (a) Σ is transversal to the vertical Killing vector field ξ.

• (b) The surface Σ is orientable and the angle function ν=〈N,ξ〉 has no zeros in Σ, where N is a global unit normal vector field of Σ.

• (c) The projection $\pi_{|\varSigma}:\varSigma\to\mathbb{M} ^{2}(\kappa)$ is a local diffeomorphism.

Conditions (a) and (b) are trivially equivalent, whereas (c) can be deduced from the fact that the absolute value of the Jacobian of π _|Σ equals |ν|.

The need to know whether a vertical H-multigraph is embedded or not often arises in the study of such surfaces. In this paper we solve this problem by proving that they are always vertical graphs (i.e., they intersect at most once each integral curve of ξ), and in particular are embedded, when we additionally assume that the vertical H-multigraph is complete. (We observe that the completeness assumption is needed: A counterexample is given, for example, by the helicoid of $\mathbb{H}^{2}\times\mathbb{R}$ constructed by Nelli and Rosenberg in [17] minus a neighborhood of its axis.) Along these lines, we recall the following known results:

• Hauswirth, Rosenberg, and Spruck proved a half-space theorem for properly embedded $\frac{1}{2}$-surfaces in $\mathbb{H}^{2}\times \mathbb{R}$ and concluded that a complete vertical $\frac{1}{2}$-multigraph in $\mathbb{H}^{2}\times\mathbb{R}$ is always an entire vertical graph (see [10]), i.e., it intersects exactly once each integral curve of ξ. Later on, by using another half-space theorem for properly immersed surfaces in Nil₃, Daniel and Hauswirth [4] proved the same result for minimal vertical multigraphs in Nil₃. Finally, using this theorem by Daniel and Hauswirth, the classification theorem by Fernández and Mira in [7] and the Daniel correspondence [3], it is possible to extend the aforementioned results to prove that a complete vertical H-multigraph in $\mathbb{E}(\kappa,\tau)$ satisfying 4H ²+κ=0 is an entire vertical graph (see also Corollary 4.6.3 in [5] for a complete reference).

• Espinar and Rosenberg proved in [6] that there are no complete vertical H-multigraphs in $\mathbb{H}^{2}\times\mathbb{R}$ for $H>\frac{1}{2}$. In a joint work with Joaquín Pérez (see the proof of Theorem 2 in [13]), the authors proved using a different approach that the only complete vertical H-multigraphs in $\mathbb{E}(\kappa,\tau)$ with 4H ²+κ>0 are the horizontal slices $\mathbb{S}^{2}(\kappa)\times\{t_{0}\}$ in $\mathbb{S}^{2}(\kappa)\times \mathbb{R}$, for any κ>0 (and τ=H=0). The latter result has also been proved in [19].

To obtain the general result stated below, it only remains to study the case 4H ²+κ<0. We highlight that the geometry of an H-surface in the homogeneous spaces $\mathbb{E}(\kappa,\tau)$ varies essentially depending on the sign of 4H ²+κ. For instance, it is known that constant mean curvature spheres exist if, and only if, 4H ²+κ>0; see Theorem 2.5.3 in [5].

Theorem 1

Let Σ be a complete vertical H-multigraph in $\mathbb{E}(\kappa,\tau)$. Then, one of the following statements hold:

• (a) $\mathbb{E}(\kappa,\tau)=\mathbb{S}^{2}(\kappa)\times \mathbb{R}$, H=0, and $\varSigma=\mathbb{S}^{2}(\kappa)\times\{t_{0}\}$, for some $t_{0}\in \mathbb{R}$.

• (b) 4H ²+κ≤0 and Σ is a vertical graph over a domain in $\mathbb{H}^{2}(\kappa)$ whose boundary, if any, consists of complete constant curvature ±2H curves along which the graph takes infinite values. Moreover, if 4H ²+κ=0 then the graph is entire.

We remark that the condition 4H ²+κ=0 in Theorem 1 is not necessary in order to obtain entire vertical H-graphs: Besides horizontal slices, other entire minimal vertical graphs in $\mathbb{H}^{2}\times\mathbb{R}$ have been constructed by Nelli and Rosenberg in [17], by Collin and Rosenberg in [2], and by Mazet, Rosenberg, and the second author in [14]. The reader can also find some examples of rotationally invariant entire vertical H-graphs in $\mathbb {H}^{2}\times\mathbb{R}$ for any $0<H\leq\frac{1}{2}$ in [18]. We also emphasize that there exist many complete vertical H-graphs in $\mathbb{H}^{2}\times\mathbb{R}$ which are not entire:

• On the one hand, Sa Earp [21] and Abresch gave an explicit complete minimal vertical graph defined on half of a hyperbolic plane. In [2, 14], some complete minimal examples in $\mathbb {H}^{2}\times \mathbb{R}$ (which are vertical graphs over simply connected domains bounded by finitely many complete geodesics where the graph has non-bounded boundary data, and/or finitely many arcs at the infinite boundary of $\mathbb{H}^{2}$) are given. Melo constructed in [16] minimal examples in $\widetilde{\mbox{SL}_{2}}(\mathbb{R})$ similar to those in [2].

• On the other hand, Folha and Melo obtained in [9] vertical H-graphs in $\mathbb{H}^{2}\times\mathbb {R}$, with $0<H<\frac{1}{2}$, over simply connected domains bounded by an even number of curves of geodesic curvature ±2H (disposed alternately) over which the graphs go to ±∞.

Let us now explain a consequence of Theorem 1. We consider the stability operator of an orientable H-surface immersed in $\mathbb{E}(\kappa ,\tau)$, given by

$$ L=\Delta+|A|^2+\mbox{Ric}(N), $$

(1.1)

where Δ stands for the Laplacian with respect to the induced metric on Σ, and A and N denote respectively the shape operator and a unit normal vector field of Σ. The surface Σ is said to be stable when −L is a non-negative operator (see [15] for more details on stable H-surfaces). Rosenberg proved in [20] the non-existence of stable H-surfaces in $\mathbb{E}(\kappa,\tau)$ provided that 3H ²+κ>τ ², other than $\mathbb{S}^{2}(\kappa)\times\{t_{0}\}$ in $\mathbb {S}^{2}(\kappa)\times\mathbb{R}$. It is conjectured that the optimal condition for such non-existence result is 4H ²+κ>0. In a joint work with Pérez [13], the authors slightly improve Rosenberg’s bound in the general case and obtain the expected bound under the additional assumption of parabolicity. We recall that a Riemannian manifold Σ is said to be parabolic when the only positive superharmonic functions defined on M are the constant functions. As a direct consequence of Theorem 1 above and Theorem 2 in [13], we get the following nice classification result:

Corollary 2

Let Σ be an orientable, parabolic, complete, stable H-surface in $\mathbb{E}(\kappa,\tau)$. Then, one of the following statements hold:

• (a) $\mathbb{E}(\kappa,\tau)=\mathbb{S}^{2}(\kappa)\times \mathbb{R}$, H=0, and $\varSigma=\mathbb{S}^{2}(\kappa)\times\{t_{0}\}$, for some $t_{0}\in \mathbb{R}$.

• (b) 4H ²+κ≤0 and Σ is either a vertical graph or a vertical cylinder over a complete curve of geodesic curvature 2H in $\mathbb{M}^{2}(\kappa)$.

2 Preliminaries

From now on, Σ will denote a complete vertical H-multigraph in $\mathbb{E}(\kappa,\tau)$, with 4H ²+κ<0. Let us remark that the latter condition implies κ<0, so $\mathbb{E}(\kappa,\tau)$ admits a fibration over $\mathbb{H}^{2}(\kappa)$. By applying a convenient homothety in the metric, there is no loss of generality in supposing that κ=−1. Hence, we can consider the disk $\mathbb{D}(2)=\{(x,y)\in\mathbb{R}^{2}:x^{2}+y^{2}<4\}$ and the model $\mathbb {E}(-1,\tau)=\mathbb{D}(2)\times\mathbb{R}$, endowed with the Riemannian metric

$$\,\mathrm {d}s^2=\lambda^2 \bigl(\,\mathrm {d}x^2+\,\mathrm {d}y^2 \bigr)+ \bigl(\,\mathrm {d}z+\tau\lambda(y\,\mathrm {d}x-x\,\mathrm {d}y) \bigr)^2, $$

where $\lambda:\mathbb{D}(2)\to\mathbb{R}$ is given by $\lambda(x,y)= (1-\tfrac{1}{4}(x^{2}+y^{2}) )^{-1}$. In this model, the Riemannian fibration is nothing but $\pi:\mathbb{E}(-1,\tau)\to\mathbb{H}^{2}$, π(x,y,z)=(x,y), when we identify $\mathbb{H}^{2}\equiv(\mathbb{D}(2),\lambda^{2}(\,\mathrm {d}x^{2}+\,\mathrm {d}y)^{2})$.

Given an open set $\varOmega\subset\mathbb{H}^{2}$ and a function u∈C ^∞(Ω), the graph associated with u is defined as the surface parameterized by

$$F_u:\varOmega\to\mathbb{E}(-1,\tau),\quad F_u(x,y)= \bigl(x,y,u(x,y) \bigr). $$

Let us also fix the following notation, for any R>0:

• Given $x_{0}\in\mathbb{H}^{2}$, we denote by B(x ₀,R) the ball in $\mathbb{H}^{2}$ of center x ₀ and radius R.

• Given p ₀∈Σ, we denote by B _Σ (p ₀,R) the intrinsic ball in Σ of center p ₀ and radius R.

The proof of Theorem 1 relies on some technical results given originally by Hauswirth, Rosenberg, and Spruck in [10]. Although they treat the case $H=\frac{1}{2}$ in $\mathbb{H}^{2}\times\mathbb{R}$, their arguments can be directly generalized to H-surfaces in $\mathbb{E}(\kappa,\tau)$ with 4H ²+κ≤0, giving rise to Lemma 3 below.

Take $x_{0}\in\mathbb{H}^{2}$ and R>0 such that there exists u∈C ^∞(B(x ₀,R)) with F _u (B(x ₀,R))⊂Σ. (As π _|Σ is a local diffeomorphism, this can be done for any x ₀∈π(Σ).) We also fix a unit normal vector field N of Σ so that the angle function ν=〈N,ξ〉 is positive. We observe that ν lies in the kernel of the stability operator of Σ, defined in (1.1); see [1]. Since ν has no zeros, we deduce by a theorem given by Fischer–Colbrie [8] (see Lemma 2.1 in [15]) that Σ is stable. This provides curvature estimates, playing an important role in the proof of Lemma 3.

Suppose that $\hat{x}\in\partial B(x_{0},R)$ satisfies that u cannot be extended to any neighborhood of $\hat{x}$ in $\mathbb{H}^{2}$ as a vertical H-graph. Given a sequence {x _n }⊂B(x ₀,R) converging to $\hat{x}$ and calling p _n =F _u (x _n ), the arguments in [10] can be extended to show that the sequence of surfaces {Σ _n } (where Σ _n results from translating Σ vertically so that p _n is at height zero), converges in the $\mathcal{C}^{2}$-topology to a vertical cylinder π ⁻¹(Γ), for a curve $\varGamma\subset\mathbb{H}^{2}$ of constant geodesic curvature 2H or −2H which is tangent to ∂B(x ₀,R) at $\hat{x}$. Note that the condition 4H ²−1<0 implies that Γ is non-compact.

We denote by N _δ (Γ) the open tubular neighborhood of Γ in $\mathbb{H}^{2}$ of radius δ. Moreover, given $x\in\mathbb{H}^{2}\smallsetminus \varGamma$, we call N _δ (Γ,x)=N _δ (Γ)∩U, where U is the connected component of $\mathbb{H}^{2}\smallsetminus \varGamma$ containing x. By coherence, we denote U=N _∞(Γ,x).

Lemma 3

([10])

In the setting above, suppose that $\hat{x}\in\partial B(x_{0},R)$ satisfies that u cannot be extended to any neighborhood of $\hat{x}$ in $\mathbb{H}^{2}$ as a vertical H-graph. Then, there exist a complete curve $\varGamma\subset\mathbb{H}^{2}$ of constant geodesic curvature 2H or −2H, tangent to ∂B(x ₀,R) at $\hat{x}$, and an open neighborhood N of Γ such that u extends as a vertical H-graph to B(x ₀,R)∪(N∩N _∞(Γ,x ₀)) with infinite constant boundary values along Γ.

Remark 4

In general, Lemma 3 does not hold when N=N _δ (Γ,x ₀) for some constant δ>0 (e.g., see the Jenkins–Serrin type H-graphs [2, 9]). Nevertheless, all the arguments below can be thought of in a sufficiently large compact ball, so in the sequel we can consider N to be equal to N _δ (Γ,x ₀) by restricting N to a tubular neighborhood of Γ of constant radius if necessary.

Remark 5

In our study, we will always find a dichotomy between geodesic curvature 2H or −2H, as well as boundary values +∞ or −∞. Although the arguments below do not depend on these signs, it is worth saying something about the relation between them in order to describe the complete vertical graphs. As mentioned above, it can be shown that the H-multigraphs Σ _n converge uniformly on compact subsets to a vertical cylinder and we are considering the unit normal vector field of Σ which points upwards. By analyzing the normals of Γ in $\mathbb{H}^{2}$ and of π ⁻¹(Γ) in $\mathbb{E}(-1,\tau)$, it is not difficult to realize that if u tends to +∞ (resp. −∞) along Γ, the geodesic curvature of Γ will be 2H (resp. −2H) with respect to the normal vector pointing to the domain of definition of the graph. This fact was proved for minimal surfaces in $\mathbb{H}^{2}\times\mathbb{R}$ by Nelli and Rosenberg in [17]; for H-surfaces in $\mathbb{H}^{2}\times\mathbb{R}$, for 0<H≤1/2, by Hauswirth, Rosenberg, and Spruck in [11]; and for minimal surfaces in $\widetilde{\mathrm{SL}_{2}}(\mathbb{R})$ by Younes in [22].

3 The Proof of Theorem 1

As explained above, we will suppose that Σ is a complete vertical H-multigraph in $\mathbb{E}(-1,\tau)$ with $0\leq H<\frac{1}{2}$, and show that Σ is a vertical graph. The proof relies on the following result.

Proposition 6

Let Σ be a complete vertical H-multigraph in $\mathbb{E}(-1,\tau)$. Given p∈Σ and R>0, there exist an open set $\varOmega\subseteq\mathbb{H}^{2}$ and a function u∈C ^∞(Ω) such that B _Σ (p,R)⊆F _u (Ω).

Note that the fact that Σ is indeed a graph follows from Proposition 6: Reasoning by contradiction, if there existed p,q∈Σ, p≠q, which project by $\pi:\mathbb {E}(-1,\tau)\to \mathbb{H}^{2}$ on the same point, then we could take R bigger than the intrinsic distance from p to q to reach a contradiction. Thus, the rest of this section will be devoted to proving Proposition 6.

From now on, we fix a point p∈Σ and denote x ₀=π(p). The following definition will be useful in the sequel.

Definition 7

We say that $\varOmega\subset\mathbb{H}^{2}$ is admissible if it is a connected open set containing x ₀ for which there exists u∈C ^∞(Ω) such that F _u (Ω)⊂Σ and F _u (x ₀)=p.

If $\varOmega\subset\mathbb{H}^{2}$ is admissible, then the function u in the definition above is unique, and we will call it the function associated with Ω. The technique we will use to prove Proposition 6 consists of enlarging gradually an initial admissible domain until it eventually contains the projection of an arbitrarily large intrinsic ball.

As ν>0, there exists a neighborhood of p in Σ which projects one-to-one to a ball B(x ₀,ρ), for some ρ>0. In other words, there exists ρ>0 such that B(x ₀,ρ) is admissible. Let us consider

$$ R_0=\sup \bigl\{ \rho>0:B(x_0,\rho)\text{ is admissible} \bigr\}. $$

(3.1)

If R ₀=+∞, Proposition 6 follows trivially for such a point p, so we assume R ₀<+∞. This implies that B(x ₀,R ₀) is a maximal admissible ball, and it will play the role of our initial domain.

Lemma 8

Let Ω be an admissible domain such that ∂Ω is a piecewise C ²-embedded curve. Suppose that there exists $\hat{x}$ in a regular arc of ∂Ω such that Ω cannot be extended as an admissible domain to any neighborhood of $\hat{x}$. Then:

• (i) The geodesic curvature of ∂Ω at $\hat{x}$ with respect to its inner normal vector is at least −2H.

• (ii) There exists a curve $\varGamma\subset\mathbb{H}^{2}$ with constant geodesic curvature 2H or −2H, tangent to ∂Ω at $\hat{x}$, and there exist δ>0, y∈Ω, and a function v∈C ^∞(N _δ (Γ,y)) such that:

  • (a) The function v has constant boundary values +∞ or −∞ along Γ.

  • (b) Given r>0, we have $U_{r}=N_{\delta}(\varGamma,y)\cap B(\hat{x},r)\cap\varOmega\neq \varnothing$ and there exists r ₀>0 such that u=v in U _r for 0<r<r ₀.

Proof of Lemma 8

Let us consider a geodesic ball $B(y,\rho)\subset\mathbb{H}^{2}$ contained in Ω and tangent to ∂Ω at $\hat{x}$. Lemma 3 guarantees the existence of a curve $\varGamma\subset\mathbb{H}^{2}$ with constant geodesic curvature 2H or −2H, tangent to ∂B(y,ρ) at $\hat{x}$, and δ>0 such that the H-graph over B(y,ρ) can be extended to an H-graph over B(y,ρ)∪N _δ (Γ,y). Let us define v as the restriction of such an extension to N _δ (Γ,y). It can be easily shown that Γ, δ, y, and v satisfy the conditions in item (ii). The uniqueness of prolongation ensures that Ω must be contained in N _∞(Γ,y), from where the estimation for the geodesic curvature of ∂Ω given in item (i) follows. □

We will prove (see Lemma 11 for R=R ₀ and $\mathcal{C}=\emptyset$) that the set of points in ∂B(x ₀,R ₀) such that u cannot be extended to any neighborhood of them as a vertical H-graph is finite. So we can denote them as x ₁,…,x _r . Lemma 8 guarantees that, given j∈{1,…,r}, there exists a curve $\varGamma_{j}\subset\mathbb{H}^{2}$ of constant geodesic curvature 2H or −2H which is tangent to ∂B(x ₀,R ₀) at x _j , such that u can be extended to $B(x_{0},R_{0})\cup N_{\delta_{j}}(\varGamma_{j},x_{0})$, for some δ _j >0. The next step in the proof of Proposition 6 will consist of showing that the curves Γ ₁,…,Γ _r are disjoint. Then we will be able to extend the initial ball B(x ₀,R ₀) to a new admissible domain $\varOmega=B(x_{0},R_{0})\cup(\bigcup_{j=1}^{r}N_{\delta}(\varGamma_{j},x_{0}))$, for some δ≤min{δ _j :j=1,…,r}. The function associated with such Ω will have boundary values +∞ or −∞ along each of the Γ _j (depending on the sign of its geodesic curvature). Therefore, for a further extension of Ω we will work in $\bigcap_{j=1}^{r}N_{\infty}(\varGamma_{j},x_{0})$, i.e., we will extend Ω in the direction of ∂Ω∩∂B(x ₀,R ₀). As this process will be iterated, we describe a general situation for the extension procedure.

Definition 9

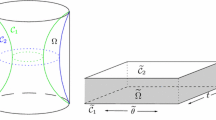
Let $\mathcal{C}$ be a finite family of curves in $\mathbb{H}^{2}$, each one with constant geodesic curvature 2H or −2H. We will say that $\mathcal{C}$ is in general position for some radius R>0 when the following three conditions are satisfied:

• (a) Each $\varGamma\in\mathcal{C}$ intersects the closed ball $\overline{B}(x_{0},R)$ and x ₀∉Γ.

• (b) $\partial\varOmega_{\mathcal{C}}\cap\varGamma\neq \emptyset$ for every $\varGamma\in\mathcal{C}$, where

  $$ \varOmega_{\mathcal{C}}=B(x_0,R)\cap \biggl( \bigcap _{\varGamma\in\mathcal{C}} N_\infty(\varGamma,x_0) \biggr). $$

  (3.2)

• (c) No intersection point of curves in $\mathcal{C}$ lies on $\overline{B}(x_{0},R)$.

(We recall that N _∞(Γ,x ₀) is the open connected component of $\mathbb{H}^{2}\smallsetminus \varGamma$ containing x ₀.) See Fig. 1, which depicts some examples. It is clear that the family of curves {Γ ₁,…,Γ _r } in the discussion above is in general position for the radius R ₀. This condition will be preserved under the successive steps for enlarging the admissible domain. The next lemma gives some information about a family of curves in general position.

Fig. 1

Three families of four curves in $\mathbb{H}^{2}$. The associated domain $\varOmega_{\mathcal{C}}$ with respect to the disk (in light gray) has been colored in darker gray. The family on the left is in general position with respect to the disk whereas conditions (a) and (c) in the definition fail for the one in the middle, and condition (b) does not hold for the one on the right

Lemma 10

Let $\mathcal{C}$ be a finite family of curves in general position for a radius R>0. Suppose that $\varOmega_{\mathcal{C}}$, defined by (3.2), is an admissible domain and that, for any $\varGamma\in\mathcal{C}$, there exists a vertical H-graph v over N _δ (Γ,x ₀), for some δ>0, with constant infinite boundary values along Γ, which coincides with the function u associated with $\varOmega_{\mathcal{C}}$ on $\varOmega_{\mathcal{C}}\cap N_{\delta}(\varGamma,x_{0})$. Then:

• (a) Any two curves in $\mathcal{C}$ are disjoint.

• (b) There exists δ′>0 so that $\varOmega_{\mathcal{C}}\cup(\bigcup_{\varGamma\in\mathcal{C}}N_{\delta'}(\varGamma,x_{0}))$ is admissible.

Proof of Lemma 10

Reasoning by contradiction, let us suppose that there exists a point $\widetilde{x}\in\varGamma_{1}\cap\varGamma_{2}$ for some $\varGamma_{1},\varGamma_{2}\in\mathcal{C}$. Condition (c) in Definition 9 tells us that $\widetilde{x}\notin\overline{B}(x_{0},R)$. We can take a continuous family {D _t } _t∈[0,ℓ) of geodesic balls in $\mathbb{H}^{2}$ satisfying the following three conditions:

• (1) D ₀⊂B(x ₀,R).

• (2) ∂D _t is tangent to Γ ₁ and Γ ₂, for any t∈[0,ℓ).

• (3) The radius of D _t strictly decreases with respect to t, and D _t converges to the point $\widetilde{x}$ when t→ℓ.

Let us call, respectively, x ₁ and x ₂ the points in Γ ₁ and Γ ₂ which are closest to x ₀. Denote by T an open triangle with vertices $\widetilde{x}$, x ₁, and x ₂, which has two sides lying on Γ ₁ and Γ ₂ and the third one is a curve interior to $\varOmega_{\mathcal{C}}$ joining x ₁ and x ₂. Let us denote by Λ _t ⊂∂D _t the intersection of $\varOmega_{\mathcal{C}}\cup T$ with the longest of the two curves in which ∂D _t is divided by Γ ₁ and Γ ₂. Then $\varOmega_{\mathcal{C}}\cup T=\varOmega_{\mathcal{C}}\cup(\bigcup _{[0,\ell)} \varLambda_{t})$ (see Fig. 2).

Fig. 2

Left: Three curves in general position, two of which intersect at $\widetilde{x}\notin\overline{B}(x_{0},R)$. Right: $\varOmega_{\mathcal{C}}\cup T$ have been magnified (T in darker gray) and some of the curves Λ _t which cover T up to $\widetilde{x}$ are shown

Let r∈[0,ℓ] be the supreme of the values of t∈[0,ℓ) for which the function u associated with $\varOmega_{\mathcal{C}}$ can be extended as an H-graph on $\varOmega_{\mathcal{C}}\cup(\bigcup_{s\in[0,t]}\varLambda_{s})$. Note that r>0 since the graph can be extended to $\varOmega_{\mathcal{C}}\cup N_{\varepsilon}(\varGamma_{i},x_{0})$, for i∈{1,2} and some ε>0, and the curves Λ _s lie on the union of these two open sets for small values of s. Moreover, it must be r=ℓ: Otherwise there would exist a point in Λ _r such that u cannot be extended to any neighborhood of it as an H-graph. But Λ _r has constant geodesic curvature smaller than −1<−2H with respect to the normal pointing to $\varOmega_{\mathcal{C}}\cup(\bigcup_{s\in[0,r]}\varLambda_{s})$, contradicting Lemma 8.

Hence we have proved that $\varOmega_{1}=\varOmega_{\mathcal{C}}\cup T$ is admissible, and the extension u ₁ of u over Ω ₁ has non-bounded values in the part of ∂Ω ₁ lying on Γ ₁∪Γ ₂. Nonetheless, the graph u can also be extended to u ₂ defined over $\varOmega_{2}=\varOmega_{\mathcal{C}}\cup N_{\varepsilon}(\varGamma_{1},x_{0})$. Thus u ₁=u ₂ in Ω ₁∩Ω ₂, by uniqueness of the analytic prolongation. This is a contradiction because u ₂ has bounded values in Γ ₂∩N _ε (Γ ₁,x ₀)⊂∂(Ω ₁∩Ω ₂) whereas u ₁ does not. Such a contradiction proves (a). Item (b) also follows from the previous argument. □

Let us now prove that, apart from the curves along which the graph takes infinite boundary values, the number of points in the boundary of the corresponding domain which do not admit an extension to any neighborhood of them is finite at any step of the extension procedure.

Lemma 11

Let $\mathcal{C}$ be a finite family of curves in general position for some radius R>0. Suppose that $\varOmega_{\mathcal{C}}$ is admissible and the function u associated with $\varOmega_{\mathcal{C}}$ takes constant infinite boundary values along the curves in $\mathcal{C}$. Then the set A(R) of points in $\partial\varOmega_{\mathcal{C}}\cap\partial B(x_{0},R)$ such that u cannot be extended to any neighborhood of them as an H-graph is finite.

Proof of Lemma 11

Since $\mathcal{C}$ is finite, $\partial\varOmega_{\mathcal{C}}\cap\partial B(x_{0},R)$ consists of finitely many regular arcs. Their endpoints belong to A(R), but they are finitely many and, by Lemma 8, it is known that the graph can be extended as an H-graph to a neighborhood in $\mathbb{H}^{2}$ of any point in a neighborhood in $\partial\varOmega_{\mathcal{C}}\cap\partial B(x_{0},R)$ of any of them. Thus we will not consider such endpoints.

Lemma 8 also says that the rest of the points in A(R) are isolated. On the other hand, it is easy to check that A(R) is closed: We suppose there exists a sequence {x _n } in A(R) converging to x _∞∉A(R). Such a point x _∞ must be interior to one of the arcs in $\partial\varOmega _{\mathcal{C}}\cap\partial B(x_{0},R)$ because of the discussion above. Then u admits an extension to a neighborhood of x _∞ in $\mathbb {H}^{2}$. But x _n lies in such a neighborhood for n large enough, a contradiction.

Hence A(R) is closed, consists of isolated points, and is contained in the compact set ∂B(x ₀,R), so it is finite. □

We now have all the ingredients to prove the desired result.

Proof of Proposition 6

Repeating the argument leading to Eq. (3.1) and provided that R ₀<+∞ (otherwise we would be done), we can consider the maximal admissible ball B(x ₀,R ₀). Lemma 11 guarantees the existence of a finite collection of points in ∂B(x ₀,R ₀) such that B(x ₀,R ₀) cannot be extended in an admissible way to any neighborhood of any of them. Hence, there exists a finite family $\mathcal{C}_{0}$ of complete curves with constant geodesic curvature 2H or −2H, each one tangent to ∂B(x ₀,R ₀) at one of those points, under the conditions of Lemma 8. The family $\mathcal{C}_{0}$ is in general position. Then Lemma 10 says that the curves in $\mathcal{C}_{0}$ are disjoint and that there exists δ>0 such that the domain $\varOmega'=\varOmega_{\mathcal{C}_{0}}\cup(\bigcup_{\varGamma\in \mathcal{C}_{0}}N_{\delta}(\varGamma,x_{0}))$ is admissible.

Moreover, the initial graph can be extended to a neighborhood of any point interior to ∂Ω′∩∂B(x ₀,R ₀), so we can define the supremum of R>R ₀ satisfying that $B(x_{0},R)\cap(\bigcap_{\varGamma\in\mathcal{C}_{0}} N_{\infty}(\varGamma ,x_{0}))$ is admissible, called R ₁. If R ₁<+∞, then let us consider the admissible domain $\varOmega_{1}=B(x_{0},R_{1})\cap(\bigcap_{\varGamma\in \mathcal{C}_{0}} N_{\infty}(\varGamma,x_{0}))$. By the definition of R ₁, there will be points in the interior of ∂Ω ₁∩∂B(x ₀,R ₁) for which Ω ₁ cannot be extended in an admissible way to any neighborhood of any of them. By Lemma 11, these points are finitely many, and we can apply Lemma 8 to obtain a new family $\mathcal{C}_{1}\supset\mathcal{C}_{0}$ in general position for the radius R ₁. Note that $\mathcal{C}_{1}-\mathcal{C}_{0}\neq\emptyset$.

This procedure can be iterated to get a strictly increasing sequence (possibly finite) of radii {R _n } in such a way that, for any n, there exists $\mathcal{C}_{n}$, a family of curves in general position for R _n , with $\mathcal{C}_{n-1}\subsetneq\mathcal{C}_{n}$. Besides, the arguments above show that the domain

$$\varOmega_{\mathcal{C}_n}=B(x_0,R_n)\cap \biggl(\bigcap _{\varGamma\in\mathcal{C}_n}N_\infty(\varGamma,x_0) \biggr), $$

is admissible, $\varOmega_{\mathcal{C}_{n-1}}\subset\varOmega _{\mathcal{C}_{n}}$, and the associate function u _n extends u _n−1. Note that there exists δ _n >0 such that $\varOmega_{\mathcal{C}_{n}}$ can be extended to the admissible domain $\varOmega_{\mathcal{C}_{n}}\cup(\bigcup_{\varGamma\in\mathcal{C}_{n}}N_{\delta_{n}}(\varGamma,x_{0}))$, by item (b) of Lemma 10.

In this situation, there are two possibilities: Either $R_{n_{0}}=+\infty$ for some n ₀≥0 (and we would be done since Σ would be a complete vertical graph), or the sequence {R _n } has infinitely many terms. Suppose we are in the latter case. Then we claim that lim{R _n }=+∞. In order to prove this, we observe that the curves in $\mathcal{C}_{n}$ are all disjoint by Lemma 10. If R _∞=lim{R _n }<+∞, we would have an infinite family of disjoint curves (infinite, as each $\mathcal{C}_{n}$ strictly contains $\mathcal{C}_{n-1}$), each one with constant geodesic curvature 2H or −2H and intersecting the compact ball $\overline{B}(x_{0},R_{\infty})$. But this situation is impossible by condition (b) in Definition 9 (it tells us that, when we fix one of such curves, Γ, the rest of them must lie in one of the two components of $\mathbb{H}^{2}\smallsetminus \varGamma$).

Given $n\in\mathbb{N}$, the open set $O_{n}=F_{u_{n}}(\varOmega _{\mathcal{C}_{n}})\subset\varSigma$ satisfies that π(∂O _n )⊂∂B(x ₀,R _n ), since u _n has boundary values ±∞ on the curves of $\mathcal{C}_{n}$. Then we get that the length of any piecewise regular curve α:[a,b]→Σ with α(a)=p and α(b)∈∂O _n is bigger than R _n , as the projected curve π∘α in $\mathbb{H}^{2}$ is shorter than α. Thus, the distance in Σ from p to ∂O _n is at least R _n , so $B_{\varSigma}(p,R_{n})\subset F_{u}(\varOmega _{\mathcal{C}_{n}})$ and we are done since R _n is arbitrarily large. □