Optimization Analysis of Microgravity Experimental Facility for the Deployable Structures Based on Force Balance Method

Abstract

Ground-based microgravity experiment facility for large deployable structures based on the force balance was used in deployment function experiments and profile precision estimations. Considering how to exert the balance force in an accurate and efficient way to reduce its adverse effects and improve the realism of the simulated space environment. In this paper, a deformation displacement model of deployable structures under the effects of balance forces and gravity was established based on the finite element theory. The effects of the number, and the distribution form, of balance forces on deformation displacement of deployable structures were examined, and the optimal values of balance forces were derived using the genetic algorithm. The results shows that the effectiveness of the ground-based microgravity experiment facility for large deployable structures can be significantly improved by appropriately selecting the number and the distribution form of balance forces, and optimizing the values of balance forces.

Introduction

The large deployable structure is the main component of space exploration mission, has been widely used in resources exploration, electronic reconnaissance, deep space exploration and other key national core technology areas (Guo et al. 2019; Yin et al. 2018; Hu et al. 2015). There are many factors that affect its deployable process including contains a large number of parts, friction, clearance. Moreover, the microgravity environment has a great influence on materials, structures, electromagnetism etc. (Wang et al. 2019). Hence, it is difficult to predict the development process and eliminate all kinds of faults directly through theoretical analysis. However, it is extremely expensive to launch the equipment into the space environment for experiments. Considering the experimental cost and feasibility, most large apace deployable structures adopt ground simulation experiments for functional verification (Mengliang 2007).

The simulation method of microgravity environment mainly includes motion balance method, force balance method and hybrid simulation method (Zhu et al. 2018; Wen-Hui et al. 2014). There are free falling body method (Watanabe et al. 1998; Liu et al. 2018) and parabolic body method (Krutyansky et al. 2019) in the motion balance method, which simulates the weightless environment by making the experimental object obtain the motion acceleration in the same magnitude and direction as the gravitational acceleration. However, motion balance method is not suitable for microgravity experiments of the deployable structure because of short simulation time, high energy consumption, and the influence of air resistance in high speed motion. The force balance method includes water float method, suspension method and air flotation method (Qi et al. 2011), by applying different forms of force to balance the effects of gravity. Part of the balance force is used to offset the influence of gravity field, and the other part will produce additional external forces that affect the driving force and precision of the deployable structure. The force balance method has been widely used because of its advantages in controllable experimental process, relatively low cost and simple operation, though it can’t completely eliminate the influence of gravity on the experimental process; Hybrid simulation method (Zaussinger et al. 2019; Xu et al. 2009) is a space environment simulation method that combines physical experiments with computer simulation experiments. In order to achieve a more accurate simulation results of the space environment, the parameter characteristics measured from the physical prototype should be compared and analyzed with those obtained from the simulation experiments. The simulation model parameters of the test object in the zero-gravity environment are modified. Stewart 6-dof experimental platform developed by Dubowsky (Dubowsky et al. 1994) and the ground simulation system for space robots established by the University of Delaware (Agrawal et al. 1996) are belong to hybrid simulation method. This method does not require physical equipment for microgravity environment simulation, nor does it need to test the whole equipment, however, the experimental process is relatively complex, which makes it difficult to establish the simulation model of complex equipment.

The suspension-based force balance method has been wide used in microgravity experiments of the deployable structure. Guoliang (Guoliang et al. 2018) proposed an active suspension method to unload the gravity of a hoop truss structure in the ground. A 4.8 m diameter deployable reflector model was tested by the suspension method at the NTT radio systems laboratory in Japan to verify the correctness of the design and analysis (Mitsugi et al. 2000). Jorgensen et al. (2005) used a simple low-stiffness suspension system and videometry to measure the angular displacement of the deploying panel ground tests; Mitsubishi Electric Corporation developed an expansion experiment system using maglev slider for the expansion experiment of large deployable mesh reflector (Sugimoto et al. 1997). Qiang et al. designed an experimental test rig for eliminate the gravity effects to validate the dynamics numerical examples of space deployable structures (Tian et al. 2015).

In order to improve the efficiency of microgravity experimental device based on suspended force balance method, it is necessary to construct the mechanical model, which considered the number and the distribution form of balance forces. The finite element method (FEM) can well describe the stress characteristics of large truss structures, the FEM has made a long-term development in the fields of aerospace, civil engineering and mechanical manufacturing (Rohit et al. 2018). E.A. Thornton used FEM to study the effects of temperature changes in space on space antennas (Thornton et al. 1982). Wang et al. analyzed the stress and deformation on structure with large span and large load, proposed an optimization scheme using finite element software (Wang et al. 2011). Lindner D K proposed an algorithm from the finite element method to consider the detection, location and estimation (DLE) of damage on a space truss (Lindner et al. 2013).

The large sizes of deployable support structures are usually latticed-shell shaped, deformation can easily occur under the effect of imbalanced forces. Therefore, structural deformation displacement is highly sensitive to imbalanced forces, which can be used as an indicator representing the plausibility of balance forces to accurately evaluating the outcomes of gravity balance. Additionally, the profile precision of structures that corresponds to structural deformation displacement can be used as an indicator to guide the optimization of balance forces, and thus reduce the effect of gravity on profile precision.

This paper is organized as follows. In Sect. 2, the construction of the total stiffness matrix is described, and the overall static model of the deployable structure is obtained. The third section introduces the microgravity experimental equipment, and the nodal displacement of the deployable structure under gravity and equilibrium force is obtained based on the research content of the second chapter. The fourth section compared the advantages and disadvantages of classical optimization algorithm and genetic algorithm, then constructed a genetic algorithm-based optimization model using maximum node deformation displacement as an evaluation indicator. The fifth section compares the deformation outcomes of the deployable structure under different numbers and distribution forms of balance forces, evaluates the effectiveness of the method based on the optimization result of type 6, and validates the correctness of the results based on simulation results.

Static Model of the Deployable Structure Based on the FEM

Three-Dimensional Beam Elements

This part, giving the three-dimensional beam elements based on the FEM, as showing in Fig. 1, three-dimensional beam elements have 2 node displacement, $\delta ={\left[{\delta}_i^T{\delta}_j^T\right]}^T$, there are 12 degree of freedoms, each node consists of three position displacement (u, v, w) and three rotational displacement (θ_x, θ_y, θ_z), which are defined in local coordinates.

Fig. 1

The three-dimensional beam elements

According to the displacement of node i and j, the displacement of an arbitrary point r_p, in the whole beam element, can be obtained by interpolation function.

$$ {r}_p=\left[\begin{array}{c}u\\ {}v\\ {}w\end{array}\right]=N\left(x,y,z\right)\delta . $$

(1)

Here, N(x, y, z) is shape function, the form follows Pascal Triangle (Beuchler & Schöberl, 2006). The relationship between displacement field and strain field in elastic body can be expressed by Eq. (2).

$$ \left\{\varepsilon \right\}=\frac{\partial {r}_p\left(x,y,z\right)}{\partial x\left(x,y,z\right)}=\frac{\partial N\left(x,y,z\right)}{\partial x\left(x,y,z\right)}\delta = B\delta $$

(2)

According to the principle of minimum potential energy, of all possible displacements that satisfy the displacement boundary conditions, and Eq. (3) gives the relationship between node load and node displacement in static equilibrium. The specific derivation process can be referred to the literature (Bathe 2006).

$$ {K}^e{\delta}^e-{s}^e=0 $$

(3)

K^e is element stiffness matrix, s^e is panel load and δ^e is node displacement, all of them defined in local coordinates, which can be transformed to the global coordinate system by the rotation matrix of pose R^e (Pan and Wei 2019).

Construct the Deployable Structure Based on Blockset

The deployable structure as shown in Fig. 2 uses four-plane intersection deployable module (FIDM) to form basic sub-rings, which in series along the arc direction and the cylindrical direction respectively. The basic sub-ring consists of three different kinds of subrings, BUD (Basic Unit on the Directrix), MBUG (Main Basic Unit on the Generatrix) and ABUG (Assistant Basic Units on the Generatrix), and the geometry of the same subring is identical.

Fig. 2

The deployable structure

There are 25 main driver modules and 16 auxiliary driver modules as show in Fig. 3. Local frame O_zi(i = 1~25) of main driver modules and local frame O_fj(j = 1~16) of auxiliary driver modules were established. The rotation matrix R^k(k = 1, ⋯, 41) between local coordinate system and global coordinate system can be obtained by coordinate transformation.

Fig. 3

Local frame of the deployable structure

The main driver module is composed of BUD and MBUM, and the auxiliary driver module is composed of ABUM. Introduce the blockset shown in Table 1.

Table 1 Blocksets

Here, blockset H_l = [h_l1 h_l2 h_l3 h_l4](l = 1, …, 10),

$$ \left\{\begin{array}{l}{h}_{lj}=0,\mathrm{with}\mathrm{out}\kern0.5em \mathrm{subring}.\\ {}{h}_{lj}=1,\mathrm{with}\kern0.5em \mathrm{BUD}\kern0.5em \mathrm{subring}.\\ {}{h}_{lj}=2,\mathrm{with}\kern0.5em \mathrm{MBUM}\kern0.5em \mathrm{subring}.\\ {}{h}_{lj}=3,\mathrm{with}\kern0.5em \mathrm{ABUM}\kern0.5em \mathrm{subring}.\end{array}\right. $$

And, constructed the deployable structure based on blockset can be expressed as Fig. 4.

Fig. 4

The deployable structure based on blockset

Blockset

For different types of blockset, H_l(l = 1, ⋯, 10), is composed of three subrings BUD, MBUM and ABUM. In order to number the beam elements conveniently, the connection points of each member on three subrings, including hinge constraint points and rigid constraint points, are discretized as finite element nodes.

The number of each beam element and the node number corresponding to the element in the three subrings are shown in Fig. 5. Here, the red number represents the beam element number and the black number represents the node number. As shown in the Fig. 5, solid points represent rigid constraints, and hollow points represent hinged constraints. It is necessary to point out that, the node 6 on three subrings, beam no.5 and beam no.6 are rigidly connected, beam no.5 and beam no.18 are hinged constraint. Similarly, beam no.17 and beam no.19 connected with node 16 are rigidly connected, and beam no.16 and beam no.17 are hinged.

Fig. 5

Three subrings

The sequence of beam element number and node number in different blockset can be obtained by combining the above three subrings in different ways. Here, take blockset H₄ as an example to explore the corresponding relationship between beam element and node in blockset. Blockset H₄ consists of two BUD subrings and two MBUM subrings, considering that the splicing between different blocksets has overlapping nodes, some beam elements and corresponding nodes in h_i2 and h_i3 subring need to be deleted, as the blue line and point shown in Table 2.

Table 2 Blockset of H₄

There are 61 beams and 48 nodes in blockset H₄, the corresponding relationship between beam element and node can be seen in the Appendix. The beam element numbers and corresponding node numbers in other types of blockset can be acquired, then the blockset module shown in Fig. 4 can be assembled to obtain the corresponding relationship between all beam elements and nodes of the deployable structure. Table 3 shows the number of beam elements and nodes in different blockset.

Table 3 The number of beam elements and nodes in different blockset

Total Stiffness Matrix and Statics Model

In order to obtain the total stiffness matrix, the stiffness matrix of the element is first described as ${K}_{ie}^{mn}$ according to the beam number and node number, here, subscript i is the beam element number, superscript (m, n) is the node number at both ends of the beam element. Then stiffness matrix in global coordinate system, ${\overline{K}}_i^{mn}$, can obtain by introducing the corresponding beam element cosine matrix R^ie. Next, based on the beam element number and the corresponding node number, ${\overline{K}}_i^{mn}$ is promoted to K_i, which consistent with the dimension of the total stiffness matrix. Finally, the total stiffness matrix is obtained by adding up the stiffness of all elements.

The total stiffness matrix [K] in the global coordinate system can be obtained by the above process, show in Fig. 6. The equilibrium equation of developable structure under external force can be expressed by the total stiffness matrix as,

Fig. 6

Set of total stiffness matrices

$$ \left\{\boldsymbol{Q}\right\}=\left[\mathbf{K}\right]\left\{\varDelta \right\} $$

(4)

{Q} represents the node load, which is formed by the theory of static equivalence principle of the external force on the deployable structure, and {∆} represents the node deformation under the action of the node load {Q}.

Microgravity Experimental Facility and Mechanical Model of Balance Force

Microgravity Experimental Facility

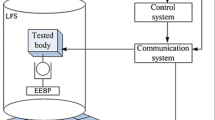
A cylindrical reticulated shell deployable mechanism was studies in this paper, which consists of a large number of slender beams. The length of the cylindrical is 12 m, directrix is 12.8m, the envelope space of the closed form is (1.41 × 1.35 × 1.87) m³. There is only gravity and equilibrant after the deployable structure was fully extended and self-balanced. The three-dimensional configuration and microgravity experimental facility is shown in Fig. 7 and Fig. 8, respectively.

Fig. 7

Development trajectory of the deployable structure

Fig. 8

Microgravity experimental facility

The cylindrical reticulated shell deployable mechanism, in state of suspended, only one column, which the basic unit in the plane where the central bus is located is in the same plane as the equilibrium force (the tension generated by the lifting wire at the lifting point), the rest of will be subjected to the horizontal component of the equilibrium force. It’s hard to obtain good balance effect through directly determine the equilibrium force by experience. However, it is worth mentioning that different distribution strategies of equilibrium force will have varying degrees of negative impact on ground experiment. Therefore, it is necessary to put forward a method automatically select distribution strategy of equilibrium force, which can reduce the negative influence degree to improve the reliability of the ground experiment.

Mechanical Model of Balance Force

The schematic diagram of the developable structure under gravity and equilibrant is shown in Fig. 9.

Fig. 9

Static model of the deployable structure with equilibrium force

The gravity and the equilibrium force are respectively equivalent to the node load {Q^g} and {Q^T} through the theory of static equivalence principle, then the node load vector containing gravity and equilibrant is {Q^T + g} = {Q^g} + {Q^T}. The node deformation vector, {∆^g + T}, is obtained based on the statics model of developable structure constructed in chapter 2, Eq. (4).

$$ \left\{{\varDelta}^{\mathrm{g}+\mathrm{T}}\right\}={\left[\mathbf{K}\right]}^{-1}\left\{{\boldsymbol{Q}}^{T+\mathrm{g}}\right\} $$

(5)

Optimization Model of Balance Force

According to Eq. (5), the load constraint of developable structure in microgravity environment is,

$$ \left\{\begin{array}{l}\left\{{\boldsymbol{Q}}^{\mathrm{g}}\right\}=\boldsymbol{\xi} \\ {}\left\{{\boldsymbol{Q}}^{\mathrm{T}}\right\}=\mathbf{0}\end{array}\right. $$

(6)

Here, the nodal load equivalent to gravity is a tiny vector ξ, and equilibrium node load vector is 0, hence {∆^g + T} is also a tiny vector.

$$ \left\{{\varDelta}^{\mathrm{g}+\mathrm{T}}\right\}=\left\{{\delta}_1,{\delta}_2,\dots, {\delta}_{\mathbf{J}}\right\} $$

(7)

J is the total number of nodes, so there must be a tiny amount η to make Eq. (8) true.

$$ \max \left({\delta}_i,i\in \mathbf{J}\right)\le \eta $$

(8)

Therefore, the maximum node deformation of developable structure can be used as an optimization criterion to measure the rationality of the distribution of equilibrium force. And the smaller the maximum node deformation of developable structure is, the better the effect of microgravity device will be.

Salar (Salar et al. 2019) points out that GA (genetic algorithm) are strong at searching for improvement, and they are not limited by restrictive assumptions about the search space. Luo (Xu-Quan 2007) compared the advantages and disadvantages of GA and traditional optimization algorithm and comes to the same conclusion as Salar. Feifei and Fei (2016) points out that GA has significant advantages in solving the optimal solution of multi-constraint problems. Zhifan (2003) compared the gradient algorithm with the GA and pointed out that although the gradient algorithm has a strong local search ability, while it is difficult to obtain the global optimal solution. Genetic algorithm adopts the idea of biological evolution, which can keep approaching the target value, through automatically modify the input variables according to the desired optimization target. The whole optimization process does not involve the specific parameter relationship between variables and objective functions. This method can be used to find the optimal equilibrium force distribution automatically.

According to the foregoing analysis, the goal of optimizing the equilibrium force is to reduce the maximum node deformation of the deployable structure, thus, the objective function is,

$$ \min \left[{Displacement}^{\mathrm{max}}\left({T}_{m1},{T}_{m1},\dots, {T}_{mn}\right)\right] $$

(9)

Here, Displacement^max is the maximum displacement of the deployable structure, it can also be expressed as max(δ_i, i ∈ J), under the combined action of gravity and equilibrium force. T_mi is the equilibrium force at lifting point i, and the number of lifting points is n.

The sum of all the equilibrium forces, including the balance force generated by the counterweight and the balance force at the constraint point, acting on the lifting point shall be the same as the gravity applied to the deployable structure in the ideal case. Therefore, the total equilibrium force can’t be changed when adjusting, that is to say, equilibrium force should be satisfied the Eq. (10).

$$ \left\{\begin{array}{c}\sum \limits_{i=1}^n{T}_{mi}={\sum}_{i=1}^n{T}_{mi}^{\hbox{'}}={M}_s\mathrm{g}\\ {}{T}_{mi}\ge 0,{T}_{mi}^{\hbox{'}}\ge 0\end{array}\right. $$

(10)

${\mathrm{T}}_{\mathrm{mi}}^{\prime }$ is the equilibrium force at lifting point i after adjusting, M_s is the mass of the deployable structure, the acceleration of gravity is g. With Eq. (9) as the objective function, Eq. (10) as the constraint conditions, the optimization process is as follows:

• 1. {T_mi| i = 1~n} is a relatively reasonable equilibrium force is proposed according to experience, and the mechanical model of the deployable structure, the function (5), was constructed;

• 2. [−| ΔT_mi|  ,  | ΔT_mi| ] is the floating range allowed by the lifting force, N kinds of solutions are given at random, $\left\{{\left\{{T}_{mi}^{\prime}\right\}}_j|i=1\sim n,j=1\sim N\right\}$, which forms the initial population. The adjusted lifting force is obtained according to Eq. (11).

$$ \left\{\begin{array}{l}{T}_{mi}^{\hbox{'}}={T}_{mi}+{\mathit{\operatorname{rand}}}_i\left|\varDelta {T}_{mi}\right|\\ {}s.t.\left(\sum \limits_i^n{\mathit{\operatorname{rand}}}_i=0,{\mathit{\operatorname{rand}}}_i\in \left[-1,1\right]\right)\end{array}\right. $$

(11)

Here, rand_i is a uniform random number in the range of [−1, 1];

• 3. Obtaining the maximum displacement information of the deployable structure by introducing ${\left\{{T}_{mi}^{\prime}\right\}}_j$ into the FEM model, repeated this process until the maximum displacement, which all the deployable structures corresponding to the initial population, {Displacement^max_j| j = 1~N} is obtained;

• 4. Calculate the value of fitness function based on {Displacement^max_j| j = 1~N}, and according to it, the roulette model was used to screen the individuals, the population composed of relatively superior individuals was obtained;

• 5. The next generation of species was formed, through the selected populations were cross-mutated and retained some optimal individuals according to a certain probability. It’s worth mentioning that, the quasivid model proposed by Eigen (Eigen and Schuster 1977), individuals in a population spontaneously evolve to a quasivid model;

• 6. Repeat steps (3) to (5), until the floating value of the maximum node deformation of the developable structure tends to be stable, that is, the maximum deformation difference value between any two generations later is less than the given precision tol (this paper tol = 0.001mm), and the population converges, the optimal equilibrium force distribution scheme is obtained.

Strategies and Optimization Results Analysis

Through the fourth chapter of comparative analysis, this paper selects the genetic algorithm. Considering the complex relationship between the equilibrium force and the deployable structure makes the algorithm search in the global scope slow down. Therefore, selecting a reasonable initial value of the equilibrium force can improve the search efficiency and precision of the optimal solution.

Total mass of the deployable structure is M_s = 279.35 kg, adopts equal distribution method when determining the initial equilibrium force because the small curvature of the cylindrical surface fitted by the deployable structure. Considering the symmetry of the cylindrical surface, the following six groups of equilibrium force strategies are adopted in this paper as showing in table 4.

Table 4 Strategies of equilibrium force

The red points represent the equilibrium force applied, and the black circle is the additional constraint for limit the translational of the deployable structure. The following Table 5 shows the maximum displacement of the six strategies under the initial equilibrium force distribution.

As shown in the Table 5, the initial displacement gradually decreases with the increase of number of lifting points. Compare strategy 2 with strategy 3, the same number of lifting points are arranged in different ways, which also have an effect on the displacement. The more evenly the lifting points are distributed, the better effect of microgravity experimental facility is.

Table 5 The maximum displacement

The equilibrium force of strategy 6 is adopted in order to obtain a higher optimization effect. There are 45 lifting points, which initial equilibrant value of each lifting point is 60.8N, and it’s symmetric about column 5. Lin proposed an adaptive genetic algorithm to avoid local optimal solution, this paper adopts the parameters selected by Lin and the implementation process of genetic algorithm can be referred to the literature (Salar et al. 2019). So the population size was set to 50 and the genetic algebra to 300, the convergence process is shown in Fig. 10.

Fig. 10

Convergence process of GA

Figure 11 shows difference value of the maximum displacement between adjacent algebras, indicated the population converges to 196th generation and the optimal solution are obtained. The maximum displacement of the deployable structure is 1.76mm after optimization (less than the initial plan 51.4%), which has a significant optimization effect. The optimal equilibrium force distribution show in Fig. 12, the final optimal equilibrium force value at each suspension point is shown in Table 6.

Fig. 11

Difference value of the maximum displacement between adjacent algebras

Fig. 12

The optimal equilibrium force distribution. The cyan solid point is the applied point of equilibrium force, there are 5 rows and 9 columns, and there are 45 equilibrium forces

Table 6 The final optimal equilibrium force value (N)

The maximum change of equilibrant value from the original scheme is only 0.85N, on the one hand, which indicates the rationality of the initial distribution scheme. The sensitivity of large deployable structure to equilibrium force is further illustrated. Therefore, in order to obtain a high-performance microgravity experimental system, reasonable arrangement for the distribution and value of equilibrium force is important. On the other hand, that indicated the presence of a strong stochastic dependence, so considering the optimal distribution of the points of application of the forces themselves is important in the future.

Figure 13 shows the accuracy measurement points of the deployable structure, where the point number of row i and column j is Node (i, j) = 9(i − 1) + j, row 5 and column 6 is Node (5, 6) = 42.

Fig. 13

Accuracy measurement points of the deployable structure

Figure 14 shows the displacement of accuracy measurement points of the deployable structure, which due to the equilibrium force is given according to Table 6. To verify the correctness of the results, the simulation results of commercial software PATRAN are used as reference, the displacement result is shown in Fig. 15.

Fig. 14

The results of FEM method

Fig. 15

The simulation results of PATRAN

The maximum displacement is 1.78 mm, almost equal the FEM model, and the displacement of each node is basically consistent with the change trend. The displacement mainly occurs at the node without the lifting point, the displacement is symmetric about the fifth column, the further away from column 5, the greater the displacement. According to the use of symmetrical back suspension, the inclination angle between the plane of each column and the ground, which increases with the distance from the fifth column. Therefore, it can be concluded that the component force of gravity perpendicular to the plane is the main cause of the displacement. The displacement caused by this factor is difficult to be effectively improved by changing the equilibrium force. If the displacement of the structure can be further reduced effectively, the nodes on the even-numbered rows should be added to increase the equilibrium force. However, this will lead to too many lifting points and too small spacing of lifting wires and sliders, which will reduce the reliability of the system and increase the cost.

Conclusions

The static model of the deployable structure under the action of gravity and equilibrium force is proposed in this paper based on the finite element theory. Then, the maximum deformation of the deployable structure with six different strategies is analyzed. The results show that the deployable structure has smaller the initial maximum deformation and better the balance effect when the number of lifting points increases; Finally, strategy 6 is selected as the optimization model and the optimization results are given, which are verified by finite element software; This paper shows that the distribution of equilibrium force has significant influence on the effect of microgravity experimental equipment. In order to obtain efficient ground experiment results, it is necessary to analyze the number and the distribution form of balance forces.

During ground unrolling experiments, the deployable structure will inevitably generate internal forces due to the gravity and the equilibrium force, which likely to cause uneven stress on the beam, resulting in excessive stress on the local beam, lead to instability, development process is stuck and other dangerous conditions. Therefore, the internal force of each beam during the expansion process can be further studied. Under the condition that measurement accuracy of the deployable structure is guaranteed after the final full expansion, focusing the follow-up research to make the stress of each beam uniform and ensure the high reliability of deployable structure.

Appendix

Table 7 The beam element numbers and corresponding node numbers