Introduction

Transport properties in the liquid phase are of prime importance to understand the processes of microstructure formation during solidification. Above the liquidus temperature, the viscosity, which is a measure of the liquid’s resistance against macroscopic shear stresses, is usually connected to the molecular transport via the Stokes-Einstein equation. Since the nucleation and growth of solids from the liquid involves atomic diffusion, knowledge of the temperature dependence of viscosity is of interest. This property is also of interest for glass formation since vitrification is possible when nucleation of crystals can be avoided.

Cu50Zr50 is a congruently melting alloy that solidifies via dendrite growth without constitutional undercooling (Galenko et al. 2017). It is an ideal model system for the investigation of the solidification process, which is determined by the redistribution of heat at the solidification front and the atomic attachment kinetics at the interface.

Investigations of liquid’s thermophysical properties, crystal nucleation and growth demand for a freely suspended sample, which is (nearly) free from external forces under controllable flow conditions (laminar or turbulent) (Fecht and Wunderlich 2017; Tamaru et al. 2018; Mirsandi et al. 2015; Liu et al. 2016; Jiang and Zhao 2018). Such measurements are possible under microgravity conditions.

The melting and solidification of a levitated sample during containerless processing offer the possibility to avoid contact of the sample with a container. This reduces heterogeneous nucleation and allows studies of metastable supercooled liquids far below their liquidus temperatures. In this study, we applied the oscillating drop method (Fecht and Wunderlich 2017; Fecht et al. 2008; Eckler et al. 1991; Egry 1991) to measure the surface tension and viscosity of a Cu50Zr50 sample levitated by an electromagnetic levitator (EML) under microgravity aboard the International Space Station (ISS). Compared to electrostatic levitation (ESL) (Paradis et al. 2002; Ishikawa et al. 2005; Mauro and Kelton 2011) and acoustic or aerodynamic levitation (Trinh 1985; Weber et al. 1994), electromagnetic levitation (EML) enables the stable positioning of a very wide range of electrically conductive samples. The possibility to use larger samples under microgravity (typically 6–8 mm in diameter) reduces the influence of mass loss on the measurements. Due to the different sample sizes, the influence of sample evaporation is typically more notable in electrostatic or acoustic levitation (especially at higher temperatures) than in EML.

In the oscillating drop method, a levitating liquid droplet is subjected to a pulsed electromagnetic dipole field to induce surface oscillations. The surface oscillation frequency is determined by the surface tension, liquid density, and sample radius. Under terrestrial conditions, a spherical droplet levitated by an electromagnetic field is deformed due to gravitational forces, which leads to a split of the surface oscillation frequency. However, this can be corrected by the Cummings correction (Cummings and Blackburn 1991). The measurement of viscosity under 1-g conditions is usually impossible by using the EML technique due to the large forces needed to position the sample, which already lead to strong heating and non-laminar flows in the sample.

The measurements presented here were performed in the material science laboratory electromagnetic levitator (ISS-EML) in the European space laboratory Columbus on board the International Space Station.

Experiment

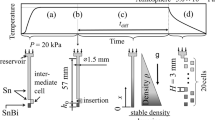
The flight sample (Batch-2, sample #21) for the ISS-EML was prepared from high purity copper (Cu) (99,9999% slugs from Alfa Aesar) and zirconium (Zr) (99.97% bar from Smart Elements). The sample (1 g in mass, 6.5 mm diameter) was prepared by arc melting in an Ar 6 N atmosphere. Before processing, the sample was placed in the coil system of the ISS-EML under high vacuum (≈ 10−8 Torr) and held in position by a quadrupole rf-field. Due to the micro-gravity environment, only small fields are necessary to keep the sample positioned, which therefore does not result in notable sample heating. Sample heating is performed separately by an overlaid dipole rf-field, that also leads to a slight elongation of the liquid sample along the coil axis. Initially, the sample was heated to about 1400 K (191 K above the liquidus temperature), and the heater was turned off to cool the sample in the supercooled liquid state until crystallization. A typical melting/cooling cycle is shown in Fig. 1. The kink in the temperature-time profile around 1150 K is due to a change in the heater voltage and the rapid rise around 980 K is due to crystallization. In order to measure surface tension and viscosity, short heater pulses were applied (see spikes in the heater voltage in Fig. 1) to excite surface oscillations at a few specific temperatures. The oscillation of the sample was recorded by a high-speed camera at 200 Hz, which was mounted radially, perpendicular to the coil axis. The recording frequency was more than 5 times higher than the surface oscillation frequency. A pyrometer, mounted axially, allowed monitoring of the sample temperature.

Fig. 1
figure 1

Typical temperature-time diagram (left axis) together with the heater control voltage (dashed line, right axis) during a thermal cycle. The sudden rise in temperature, marked by an arrow, indicates crystallization

Full size image

Data Analyses

Surface Tension

A liquid droplet can exhibit surface oscillations, especially when initiated by an initial droplet deformation. The time dependent sample radius R(t,ϑ,φ) can be expressed by

$$ R\left(t,\vartheta, \varphi \right)={\sum}_l{\sum}_{m=-l}^{+l}{a}_{l,m}(t)\ {Y}_{l,m}\left(\vartheta, \varphi \right) $$
(1)

with coefficients al,m(t) and spherical harmonics Yl,m of order l with m = ±l, …, ±1, 0. For the Y2,m harmonic, the m = ±2, ±1, 0 modes are degenerate under micro-g, i.e., they exhibit the same surface oscillation frequency. The axisymmetric oscillation mode along the axial direction, Y2,0 is dominant since the viscous damping of the higher order modes is stronger (Basaran 1992; Mashayek and Ashgriz 1998), resulting effectively in a single mode of oscillation. The surface oscillation frequency ω0for the Y2,m modes is related to the surface tension, σ, by Rayleigh’s equation (Rayleigh 1879)

$$ {\omega}_0=\sqrt{\frac{8\sigma }{a^3\rho }} $$
(2)

where the surface tension is represented by σ, the mass density by ρ and the equilibrium radius of the droplet by a. Edge detection algorithms (Schneider et al. 2008) were applied to the video images to obtain e.g. the projected sample area A and the sample radii RX, RY in X- and Y-direction. The equilibrium radius a is calculated from the projected sample area as \( a=\sqrt{\raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.} \). From this, the relative time dependent shape deformations in X- and Y-directions (δX and δY) of the sample were determined by high-pass filtering of the sample radii RX, RY in X- and Y-directions, normalized by the equilibrium radius a (δi = Ri/a, for i = X,Y).

By performing discrete Fourier transformations on these signals, the oscillation spectrum, and hence the oscillation frequency was obtained. We calculated the frequency spectra from time windows of one second after a pulse was applied, which were shifted in steps of 0.5 s along the time axis to obtain the surface oscillation frequencies as a function of temperature.

Deformation of a Rotating Sphere

The frequencies obtained from the method just discussed, will, however not reveal the correct surface tension when the sample rotates. The surface tension acting on a force-free liquid droplet leads to a pressure p0 on the surface of the droplet. Hence, the boundary condition of a liquid droplet is given by (Chandrasekhar 1965, Meyer and van der Veen 1989)

$$ \sigma \overrightarrow{\nabla}\overrightarrow{n}={p}_0 $$
(3)

where σ is the surface tension and →n is the vector normal to the surface. In a rotating liquid droplet, the force acting on an infinitely small mass element at a distance r from the rotational axis must be counteracted by the force exerted on the mass element by the surface tension. The pressure inside the droplet is then given as

$$ p={p}_0+\frac{1}{2}\rho {\varOmega}^2{r}^2 $$
(4)

where Ω is the angular rotation frequency of the droplet. By transforming the problem to cylindrical coordinates, Chandrasekhar derived an expression for the shape of the droplet as a function of rotational frequencies (Chandrasekhar 1965), which was confirmed subsequently (Meyer and van der Veen 1989). The polar radius of a two-dimensional projection of a rotating liquid droplet is expressed by

$$ F(r)={\int}_r^1\frac{\left(1-C\right)x+C{x}^3}{\sqrt{1-{\left(\left(1-C\right)x+C{x}^3\right)}^2}} dx $$
(5)

in units of the equatorial radius with the only parameter C, given by (Chandrasekhar 1965; Meyer and van der Veen 1989)

$$ C=\frac{\varOmega^2\rho {a}^3}{8\sigma }=\frac{\varOmega^2}{\omega_0^2} $$
(6)

F(0) is equivalent to the aspect ratio (the ratio between the short and long axis) of the rotating droplet.

In Fig. 2, the droplet aspect ratio is shown as a function of C. In the ISS experiments, the aspect ratio could be obtained from the video images. Specifically, the sample edges were fitted with an ellipse and the length of the long (La) and short axis (Lb) were determined. After a low-pass filtering to remove the surface oscillations, the aspect ratio Lb/La was calculated. Without solving Eq. 5 for C, the aspect ratio, F(0), could be used to obtain C graphically from Fig. 2.

Fig. 2
figure 2

Aspect ratio of a rotating droplet as a function of the parameter C = Ω2/ω02

Full size image

Frequency Shift of a Rotating Sphere

As was derived by Busse (1984) and experimentally verified by Annamalai et al. (1985) and others, the frequency of surface oscillations of liquid droplets shifts due to sample rotation. For axisymmetric oscillation of the Y2,0 mode, the observed oscillation frequency ω is given as (Busse 1984; Annamalai et al. 1985)

$$ \omega ={\omega}_0\left(1+\frac{16}{21}\frac{\varOmega^2}{{\omega_0}^2}\right) $$
(7)

where ω0 is the oscillation frequency in the absence of sample rotation. By discrete Fourier transformation, the oscillation spectrum and the oscillation frequency can be determined from the oscillation measures (δX and δY). By combining Eqs. 5–7, thereby eliminating the rotation frequency, one can arrive at an expression for the oscillation frequency, ω0, in the absence of rotation

$$ {\omega}_0=\frac{21\upomega}{16C+21} $$
(8)

This enables the determination of surface tension even in the presence of strong sample rotation.

Rayleigh’s equation (Eq. 2) is only valid for small amplitude oscillations (Rayleigh 1879; Tsamopoulos and Brown 1983). The surface oscillation frequency decreases with the square of the amplitude (Tsamopoulos and Brown 1983) for large oscillations. This effect is negligible if the sample deformation is not too high (Xiao et al. 2018) or can otherwise be corrected with the polynomial fitting approach introduced by Xiao et al. (2018). In the present study, the initial shape deformation after the pulse excitations, and hence the initial oscillation amplitudes were all below 1.5%. Therefore, the effect of deformation induced frequency shifts were safely neglected.

Data from the 4th thermal cycle was corrected following eq. (8). Figure 4 shows a representative time series of the sample’s relative deformation during the first and second thermal cycles, measured in the X-direction δX (high-pass filtered), together with a frequency spectrum.

Viscosity

Under the assumption of laminar flows inside the liquid droplet, the amplitude, R(t), of the surface oscillations decays exponentially with time (R(t) = R0 exp.(−t/τ)) due to viscous damping. The damping time constant τ is related to the viscosity η by the Lamb equation (Lamb 1975)

$$ \tau =\frac{3}{20\pi}\frac{m}{a}{\eta}^{-1} $$
(9)

for a sample of mass m. The finite fluidity of a droplet does not change the Rayleigh frequency of the surface oscillations as long as the viscosity is small enough (1/τ < < ω) (Fecht and Wunderlich 2017; Mashayek and Ashgriz 1998; Chandrasekhar 1959; Reid 1960).

Often, the measured time series does not show a purely exponential decay. This may be due to several reasons: (1) the edge detection algorithm may lead to small fluctuations of the measured radius, and (2) slight periodic movements of the sample along the view direction may lead to small defocusing of the image and, therefore, a noise in the edge detection. Most of these disturbances can be removed by high-pass filtering of the signals. Phase jumps between the degenerate Y2,m-modes and sample rotations or precessions may lead to an amplitude modulation of the oscillation. Since the signal modulation due to sample precession and rotation is a purely kinematic effect, in simple cases this can be dealt with by proper modeling (Wunderlich and Mohr 2018).

Results

Viscosity and surface tension were measured during four thermal cycles. In the first two cycles (cycle 1 and 2), the sample did not show significant rotation. Therefore, the oscillation frequencies at different temperatures could be determined in the conventional manner and the surface tension estimated from Eq. 1. However, a strongly deformed oblate shaped sample was observed in cycles 3 and 4. In cycle 3, the angle of the sample rotation axis towards the viewing direction did slightly change during data acquisition. This made the estimation of the aspect ratio difficult. In cycle 4, the oblate shape developed slowly over the progression of the cycle, perhaps because it was released to the positioning field while it was already rotating. Fortunately, the rotation axis of the sample was perfectly aligned perpendicular to the view direction of the radial camera. Hence, we could use the data of cycle 4 to obtain additional surface oscillation data from the rotating and oscillating droplet. Figure 3 presents the surface tension as a function of temperature. It also shows the uncorrected (Eq. (2)) and corrected (Eq. (8)) surface tension data from cycle 4. During the progression of the thermal cycle 4, the rotation frequency of the sample increased from about 4 Hz to 10 Hz. From a linear fit of the correct data from the three thermal cycles (1,2, and 4), the temperature dependent surface tension σ(T) was obtained as:

$$ \sigma (T)=\left(1.58\pm 0.01\right)\mathrm{N}/\mathrm{m}-\left(3.1\pm 0.6\right)\times {10}^{-4}\ \mathrm{N}/\mathrm{m}\times \mathrm{K}\ \left(T-1209\ \mathrm{K}\right) $$
(10)
Fig. 3
figure 3

Surface tension of Cu50Zr50 as a function of temperature, measured during three thermal cycles

Full size image
Fig. 4
figure 4

a Representative unmodulated decay of surface oscillations, following a pulse excitation b Fourier transformation of the signal, showing a single peak, fitted by a Lorentzian function

Full size image
Fig. 5
figure 5

The measured viscosities (triangles) follow an Arrhenius relation (straight line)

Full size image
Fig. 6
figure 6

Comparison of viscosities from the present measurements (blue diamonds) with the ground-based ESL-studies (Mauro et al. 2014) (purple squares), simulated MD results (Zhang et al. 2015) (green diamond) and the value predicted by the CFM model at 1473 K (Novakovic et al. 2004) (red triangle)

Full size image

Since theory does not predict an appreciable change in the decay time due to sample rotation (Watanabe 2010; Lee 1986), we considered all four cycles for the determination of the viscosity. In order to obtain the damping time constant τ, the amplitude modulation was fit by an exponential decay, \( R(t)\propto {\mathrm{e}}^{-\frac{t}{\tau }} \). The obtained damping time constant τ was used in conjunction with the Lamb equation (Eq. 9) to determine the viscosity. Within the investigated temperature range of 1250 K – 1425 K, the viscosity can be expressed by an Arrhenius law of η(T) = η0 · exp(EA/kBT) as shown in Fig. 5.

From the Arrhenius fit we obtain η0 = (0.08 ± 0.02) mPa·s and an activation energy EA = (0.58 ± 0.03) eV. The relatively small scatter of data, even when taken from rotating and non-rotating sample during thermal cycles, confirm that sample rotation had a negligible influence on the decay time. A similar fit of the viscosity data taken in ground-based ESL experiments in the same temperature range (Mauro et al. 2014) give η0 = (0.028 ± 0.01) mPa·s and EA = (0.65 ± 0.02) eV, which are similar, but slightly different to that obtained from the ISS experiments. As shown in Fig. 6, the two experimental data sets are also in reasonable agreement with the MD simulation data (Zhang et al. 2015), as well as with the compound formation model (CFM) of Novakovic et al. (2004).

Discussion

The presented method for the determination of surface tension of rotating liquid droplets delivers the correct surface tension. This can be seen by comparing the surface tension determined from the non-rotating droplet in cycle 1 and 2 with the rotating droplet in cycle 4 (see Fig. 3). This confirms that reliable surface tension data may be obtained even when the droplet is rotating, which is often a common problem in levitation experiments.

The measured surface tension of Cu50Zr50 is 10% higher than the reported values from ground-based sessile drop experiments (Krasovskyy et al. 2005) and about 15% higher than the surface tension of a Cu46Zr54 liquid measured in electrostatic levitation (ESL) (Herlach 2006) experiments. They are, however, in good agreement with prediction from the compound formation model (CFM) (Novakovic et al. 2004).

Several models enable the prediction of the surface tensions of alloy liquids from the surface tensions of the constituent elements. For such an analysis, reliable data for the elemental liquids are required. There seems to be a wide scatter in the literature data for the surface tension of both Cu and Zr. From the literature data reported by ten different groups, Keene (1993) suggested an expression, σCu(T) = 1.374 N/m – 2.6·10−4 N/m·K (T – 1085 °C). This is higher than the values measured by ground based electromagnetic levitation by Schmitz et al. (2009), σCu(T) = (1.30 ± 0.01) N/m – (2.64 ± 0.9) ·10−4 N/m·K (T- 1358 K). Similar values were obtained by Amore et al. (2011) obtaining σCu(T) = 1.33 N/m – 2.3 ·10−4 N/m·K (T- 1358 K) by the oscillating drop method in a ground based electromagnetic levitator. The surface tension measurements of Brillo et al. (2014) in a ground based electromagnetic levitator revealed very similar values of σCu(T) = 1.334 N/m – 2.6 ·10−4 N/m·K (T- 1358 K).

The scatter of data can be understood by possible influences of residual oxygen (Gallois and Lupis 1981) or other impurities, such as sulphur (Baes and Kellog 1953), on the surface tension of copper.

Surface tension data for zirconium are even more scattered, especially in its temperature dependency. Compared to σZr(T) = 1.46 N/m – 2.44·10−4 N/m·K (T – 2128 K) by Rhim et al. (1999), the data from two other groups are σZr(T) = 1.51 N/m – 3.7·10−4 N/m·K (T – 2128 K) (Frohberg et al. 1998), and σZr(T) = 1.50 N/m – 1.1·10−4 N/m·K (T – 2128 K) (Paradis et al. 2002).

The scarcity of surface tension data can be understood by the high solution reactivity of liquid zirconium that makes the measurement with container-based methods impossible. Similar to the situation for copper, the scatter in the surface tension data for zirconium can also be due to oxygen adsorption/segregation. Therefore, comparing the surface tension for the alloy liquid from those for the elemental liquids is unreliable.

Quantitative comparison of the viscosity data with the elemental liquids using semi-empirical models is also difficult. Due to the vastly different liquidus temperatures of the alloys from the elemental metals, their viscosities are measured over different temperature regimes. The melting points of Zr (2124 K) and Cu (1357 K) are much higher than the melting point of Cu50Zr50 (1209 K); the available literature data for viscosity of liquid Zr exists only for T > 1800 K, which is far above the measured temperature range for Cu50Zr50.

In addition, due to the existence of many intermetallic clusters in the Cu-Zr liquids (Mauro et al. 2014), comparison with the elemental liquids become problematic. As was shown experimentally by Holland-Moritz et al. (2012), and also predicted by several molecular dynamics simulations (Zhang et al. 2015; Hao et al. 2010), a variety of different aggregate structures exists in the Cu-Zr melt. The ab initio molecular dynamics simulation of liquid Cu-Zr melts by Zhang et al. (Zhang et al. 2015) predicts dynamic heterogeneity in the liquids from the different packing of clusters. Icosahedrally packed clusters can form stiff, relatively immobile regions, while clusters with lower symmetry can lead to collective, string like atomic movements (Zhang et al. 2015). The simulated data from this study have been plotted in Fig. 6, which are in fair agreement with the data from the ESL (Mauro et al. 2014) and EML (this work) experiments. A CFM model by Novakovic et al. (2004) also predicts the viscosity data at 1473 K, which is in good agreement with the measurements (Fig. 6).

Conclusions

The excellent stability of microgravity conditions on board the ISS build a stable environment for the verification of ground based measurements of surface tension and viscosity. The resulting data quality enables the study of effects, such as sample rotations, on the measurement results, without the influence of gravity. This is more difficult to study in the short process cycles of parabolic flights (~ 20 s). Furthermore, measurements of other thermophysical properties, such as the specific heat capacity or effective thermal conductivity of a melt are only possible in a microgravity environment such as the ISS, which allows much longer experiment cycles than other microgravity platforms (Fecht and Wunderlich 2017).

The surface tension and viscosity of Cu50Zr50 was measured on oscillating droplets using the containerless electromagnetic levitation technique under micro-gravity on board the International Space Station. Theoretical work of Busse (1984) and Chandrasekhar (1965) was successfully applied to obtain a correction for the surface oscillation frequency for a rotating liquid sphere with a-priori unknown rotation frequency. This enables the analysis of a larger amount of measurement data, increasing the information yield of the experiments.

The measured surface tension is intermediate between those for elemental Cu and Zr liquids. However, due to the large scatter in the temperature dependence of the surface tension for the elemental liquids, they could not be used for comparison with those from the present measurements for Cu50Zr50. The viscosity of Cu50Zr50 is in agreement with those measured by Mauro et al. (2014) using the ground-based ESL technique. Also predictions from the simulation models, such as MD simulations by Zhang et al. (2015) and the CFM model by Novakovic et al. (2004), are in good agreement with the measured data.