Introduction

Under the background of fluid management in space, there are relatively many researches about the flow in a fan-shaped asymmetry interior corner under microgravity. The gravitational force in the microgravity environment is very weak, which can even be ignored. So the surface tension has become the key factor that influences the fluid behavior. Fluid behavior is related to the shape of interface and container, and the interior corner is an important factor (Qi and Rui 2007). Under microgravity, the fluid will be redistributed when flowing along the container’s interior corner, which is called capillary flow in interior corner (Li et al. 2013). Currently, capillary flow is widely studied. The reason is that the interior corner provides a “pipeline” for fluid flow. What’s more, this behavior is spontaneous. Container with such interior corner is usually used for fluid management in the aerospace engineering. For example the application of reservoir and deflector in fuel tank is based on the theory of capillary flow in interior corner.

Fig. 1
figure 1

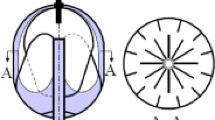
Schematic model of heavily vaned VTRE tank showing fluid location in low-gravity environment. Tank is partially filled with liquid as is shown at left. (Nardin and Weislogel, 2005)

Full size image

Most studies of capillary flow are done in interior corner with V-shape. The size of interior corner along the container’s axis is fixed. But due to the machining question, it is hard to make a sharp corner. The corner is always round. In 1990, Concus and Finn (1990) found that with the increase of radius of the rounded corner, the critical contact angle, predicted by Concus-Finn condition, would decrease. In other words it is more likely for fluids to have a stable interface configuration. Assuming that the transitional rounded corner and the interface of the liquid are concentric, Ransohoff and Radke (1988) make a theoretical analysis and think that the resistance coefficient is a function that associates interior corner, the static contact angle, the thickness of fluid layer, and the radius of the rounded corner. Due to the thickness of liquid layer and the radius of the transitional rounded corner vary in the process of flow, the resistance coefficient changes quickly in the flowing direction. So the capillary-driven flow near transitional rounded corner is very complicated, which was proved by Dong and Chatzis (1995) in 1995. Chen et al. (2006, 2007) obtain a suitable equation of flow resistance coefficient by nondimensionalization. They provide the approximate solution of the capillary-driven flow in the transitional corner and verify the result through drop tower experiment, which shows that the rounded corner will lower the rate of fluid climbing in interior corner. Through drop-tower experiment Xu et al. (2013) study the process of flow in capillary of different dimension and section shape, which is dominated by surface tension. They analyze and compare the experimental results. With analytical method, Li et al. (2012) analyze the capillary flow in asymmetric interior corner consisting of straight vane and curved wall, and put forward a concept of equivalent interior corner angle. They establish governing equations of interior corner flow, and then calculate the flow in the interior corner. Basing on the homotopy analysis method, Li et al. (2013) studies the approximate analytical solution of the capillary flow, and give an expression of series solution. Kostoglou et al. (2016) study the problem of steady-state and transient condensation on axisymmetric narrow fins under the combined action of gravity. It is found that the film thickness is finite at the tip of a fin with zero local slope. Weislogel and Nardin (2005) study capillary driven flows within planar interior corners where the wetting properties of the fluid differ between the two faces that form the interior corner. The microgravity fluid transport experiment set-up with two capillary channels is developed for the experimental investigation of capillary channel flow by using drop tower (Chen et al. 2016). The capillary channel flow has three typical flow patterns: subcritical flow, supercritical flow and critical flow in both the symmetrical channel and asymmetrical channel.

Table 1 The Properties of the Liquid Physical
Full size table

With the development of satellite technology and demand of on-orbit servicing, the vane-type surface-tension tank is widely used. Its working principle is based on the flow driven by capillary in interior corner. The diagram of its structure is shown in Fig. 1 (Nardin and Weislogel 2005). Deflectors are fixed vertically on the inner tank wall and cylinder along the container axis respectively. The value of interior corner formed by the deflector and cylinder stays constant and symmetrical. The inner wall is arc-shape. So the interior corner formed by deflector and the tank wall is not symmetric. This asymmetric interior corner is called the fan-shaped asymmetric corner. Currently, there are not many system researches of capillary flow in the fan-shaped asymmetric corner. As a preliminary exploratory study, based on literature extensively, we take a numerical simulation of the capillary flow in the fan-shape asymmetric corner with FLOW-3D. This is a fundamental research and can provide preliminary exploration and technical support for space science experiment in the future. This is also useful to fluid management in space and to accurately predicting and controlling fluid behavior.

Introduction to FLOW-3D and Simulation Parameter Setting

FLOW-3D, based on method of VOF (volume of fluid), can precisely simulate the free surface. This method introduces a function in flow field for tracking the moving surface. The generalized minimal residual method (GMRES) is adopted for solving. The GMRES was developed by Saad and Schultz in 1986. It is an iterative method used for the numerical solution of large scale equations. This method can provide highly accurate solution of multidimensional equations of high order. And the solving process is based on the Galerkin method. Galerkin method is widely used in CFD (Ajmani et al. 1994; Hong et al. 1998).

The Governing Equations

Governing equations of capillary flow under microgravity are:

$$\nabla \cdot \boldsymbol{\nu}=0 $$
$$ \frac{\partial \boldsymbol{\nu}}{\partial t}+\boldsymbol{\nu}\cdot \nabla \boldsymbol{\nu}=-\frac{1}{\rho} \nabla p+\frac{\mu} {\rho} {\Delta} \boldsymbol{\nu}+\boldsymbol{g}-\boldsymbol{f} $$
(1)
$$\frac{\partial F}{\partial t}+\boldsymbol{\nu}\cdot \nabla F=0 $$

In these equations, v is the velocity vector of the fluid. g is the acceleration vector of gravitation. f is the liquid-gas surface tension. p is the pressure. ρ is the fluid density. μ is the dynamic viscosity coefficient of the fluid. F =F(x,y,z) is a function of liquid volume. The function represents the volume fraction of liquid in the computational domain. The value of F varies from 0 to 1. For a certain grid, F =1 denotes that the grid is fully occupied by the liquid; F =0 denotes that there is no liquid. If 0 < F <1, the grid is partially filled with liquid.

The formulation of the moving contact line boundary condition is the case of fluid statics where the condition

$$ \mathbf{n} \mathbf{\cdot}\mathbf{k} = \cos\theta $$
(2)

is applied

The 𝜃 is the static contact angle of the fluid-solid pair, k is the inward normal to the container walls, and n is the outward unit normal to the free surface of liquid.

Specific values need to be input through boundary condition option when flow-3D is used to calculate.

Computational Physical Model

In this paper, we adopt geometric models, as is shown in Fig. 2a. The shape of cross section is a sector. The size of central angle is 2α, and initial liquid height is h z. As the container is an symmetric structure, we do simulation experiment by using half model.

Fig. 2
figure 2

The structure diagram of geometric model

Full size image

The cross section of the half model is shown in Fig. 2b. The radius of r sector is R and α represents half size of central angle. The contact angle is 𝜃 1 on the OA wall and 𝜃 2 is a contact angle on the AB wall. The interior corner formed by OA wall and AB wall is fan-shaped asymmetric corner. In microgravity environment, the liquid climbs along the wall. The rising height of liquid equals the distance from apex of climbing to the initial liquid surface. L represents the climbing height of liquid.

Parameter Setting

When calculating, we need to consider the effects of the residual acceleration. According to the data from the microgravity laboratory, the microgravity lasts 5s and the residual acceleration is 5 × 10−3 g 0. A grid block is divided by uniform mesh. Figure 3 shows the different values of rising height with different grid size. From Fig. 3, we can learn that when grid size is less than 0.4mm, the computational error caused by grid size can be ignored. Of course, the smaller the grid size is, the more time computational calculation needs. Considering efficiency and accuracy, we choose 0.32mm as grid size in the following research.

Fig. 3
figure 3

The climbing height of liquid under different mesh size

Full size image

Results and Analysis

Comparison Between Numerical Results and Experimental Results

In order to verify the feasibility of the numerical simulation program, we simulate the capillary flow under microgravity with two different types of silicone oil, and compare the data with these obtained by drop tower in literature (Zhang 2013). The value of microgravity with single capsule is 10−3 g 0. The container model is similar to Fig. 2a. In accord with the experimental conditions, we select 1.5cs and 10cs silicone oil as the experimental medium. Physical properties are shown in Table 1. Here, σ represents the surface tension coefficient, ρ is the density, . μ is the dynamic viscosity, ν is the kinematic viscosity, and 𝜃 is the static contact angle.

In this calculation, the initial height h z = 0.1m, the gravitational acceleration is 0.0098m/s2. The simulation time is identical with drop tower experiment. The time is 3.6s. Figure 4 shows the rising height of 10cs silicone oil in fan-shaped asymmetric interior corner at different time when we do a simulation with FLOW-3D.

Fig. 4
figure 4

The simulation consequence of rising height in asymmetry interior corner at different time(10cs silicone)

Full size image

Figure 5 shows the rising height of different silicone oil, 1.5cs and 10cs, in asymmetry interior corner, and compares the simulation result with experiment result.

Fig. 5
figure 5

The data comparison of the rising height in asymmetry interior corner

Full size image

Compared with drop tower experiment, the data of rising height, obtained from numerical simulation, has some slight differences, as is shown in Fig. 5. The main reason is that the experimental data are extracted manually, which has a visual error and cause the data error. In addition, during the drop tower experiment, the liquid forms an upper meniscus under the action of surface tension and static pressure before liquid is in the micro-gravitational condition. This process is ignored by numerical simulation. Here we just make a simulation of capillary flow under microgravity environment after drop capsule is released. But the trend of the capillary flow and the rising height of liquid at different time are roughly same. That verifies the correctness and the effectiveness of the numerical simulation of capillary flow in fan-shaped asymmetric interior corner under microgravity. That also provides technical support for further studying the capillary flow in fan-shaped asymmetric interior corner under microgravity.

Exploring the Concus-Finn conditions for the Flow in Fan-Shaped Asymmetry Interior Corner

About the static equilibrium surface in sharp corner, Concus and Finn (Concus and Finn 1994) first proposed the Concus-Finn condition that satisfied the calculation of flow in interior corner. 𝜃 is the contact angle and α is half interior corner angle. If 𝜃+α>90° , there is always a boundary and single-valued equilibrium surface at the interior corner of the container. When 𝜃+α< 90° (Concus-Finn condition), there is a solution of the equilibrium surface under gravity environment, but it is not bounded. From the physical point, there is a stable interface but the thin liquid layer spreads over interior corner. In the weightless condition, there is no the solution of the equilibrium surface, which means if the length of the edge of interior corner is infinite, the liquid will spread along the edge of interior corner endlessly. Concus-Finn theory has been confirmed by drop tower (Hou 2009) and some related microgravity experiment in space shuttles (Concus et al. 2000), and become an important theoretical basis for many subsequent related experiments. By changing the contact angle 𝜃 1, 𝜃 2 and getting the rising height, we explore the Concus-Finn condition that the capillary flow in fan-shaped asymmetry interior corner should satisfy. In order to comprehensively explore the Concus-Finn condition, we chose the central angle 2α = 70° and 90° . For the capillary flow in the sharp corner, if the condition is not satisfied, that is to say, contact angle on plane 𝜃 1> 90° - α, we observe what effects the contact angle 𝜃 2 has on the rising height in fan-shaped asymmetry interior corner through changing the contact angle 𝜃 2. After a certain time, if the leading edge can’t reach a stable state, the flow in asymmetry interior corner satisfies the Concus-Finn condition; if the leading edge reaches a stable state, it does not satisfy the Concus-Finn condition. Basing on the analysis above, we chose the central angle 2α = 70° and 90° and the container radius R = 60mm. The select of viscosity, surface tension and density of experiment medium is based on 10cs silicone. And the initial height is h z = 0.05m. The contact angle parameter is shown in Table 2.

Table 2 Parameter selection (10cs silicone oil)
Full size table

According to the parameter above, we can analyze what effects the change of contact angle has on the rising height in fan-shaped asymmetric interior corner.

According to the data in Fig. 6, we observe that the rising height decreases with the increase of contact angle. As is shown in Fig. 6a and c, when central angle 2α = 70° and 90° , 𝜃 1 = 60° and 𝜃 2> 30° , the rising of the liquid in fan-shaped asymmetric interior corner tends to be in equilibrium, and the liquid in the container forms a stable surface. When 𝜃 2≤ 30°, the leading edge of the liquid cannot reach to a stable state and would continually rise. Here 𝜃 1+𝜃 2< 90°, it is not related to central angle 2α. Similarly, from the Fig. 6b and d, when 𝜃 1 = 65° and 𝜃 2> 35° , the rising in fan-shaped asymmetry interior corner trends to be in equilibrium. When 𝜃 2≤35° and 𝜃 1+𝜃 2< 90° the rising height of the liquid increases with time and is not related to central angle 2α From the analysis above, we get that the Concus-Finn condition of the capillary flow in fan-shaped asymmetric interior corner. The Concus-Finn condition is 𝜃 1+𝜃 2< 90°.

Fig. 6
figure 6

The rising height of fluid with different size of contact angle

Full size image

The effects of Different Parameters on the Rising Height

When The Concus-Finn condition is satisfied we chose five different group of contact angle (1) 𝜃 1 = 𝜃 2 = 0° (2) 𝜃 1 = 0° 𝜃 2 = 20° (3) 𝜃 1 = 0° 𝜃 2 = 40° (4) 𝜃 1 = 207°, 𝜃 2 = 0° (5) 𝜃 1 = 40°, 𝜃 2 = 0°. And then we study the effect of the initial liquid height h z , the dynamic viscosity μ, the surface tension coefficient σ, the density ρ, the container center angle 2α and the radius R on the capillary flow. The parameters are shown in Table 3.

Table 3 Preferences
Full size table

The Effect of Initial Liquid Height on Rising Height

Through the group I in Table 3 we can study the effect of initial height on the rising height in fan-shaped asymmetric interior corner, as is shown in Fig. 7.

Fig. 7
figure 7

The rising height of the liquid with different initial liquid height

Full size image

According to the Fig. 7 when the initial height h z varies and contact angle keeps unchanged, the rising height is almost the same at the same time So when other parameters keep unchanged, the initial height has no effect on the rising height. As the container has the same cross-sectional area, the volume of the initial liquid has no effect on the rising height. In order to save the computational time, we choose h z = 0.05m.

The Effect of Dynamic Viscosity on Rising Height

Choosing the group II in Table 3, we can analyze, with different contact angles, the effect of liquid viscosity on the rising height in fan-shaped asymmetry interior corner.

According to the Fig. 8 we take the same contact angle in the same container. We find that the rising height decreases with the increase of viscosity, and that with the increase of time, the viscosity has larger effect on the height of leading edge. The main reason is that with increase of time the gravity and inertia almost don’t work. The rising height is mainly determined by the interaction of resistance caused by viscosity, the surface tension and capillary-driven force When the coefficients of surface tension and the contact angle keep unchanged, driving force does not vary. With the increase of dynamic viscosity the resistance of the rising liquid increases, and the rising speed decreases. Meanwhile the rising height will decrease. In addition, the size of contact angle also has a great influence on the rising height With the increase of contact angle, the capillary driving force and the rising height will decrease.

Fig. 8
figure 8

The rising height with different viscosity

Full size image

The Effect of Surface Tension Coefficient on Rising Height

According to the group III in Table 3, we can study the effect of changing the surface tension coefficient on the rising height, as is shown in Fig. 9.

Fig. 9
figure 9

The rising height under different surface tension coefficient

Full size image

In the Fig. 9 we take the same contact angle in the same container. At the same time the rising height increases significantly with the increase of surface tension The main reason is that when the liquid viscosity and contact angle don’t change, the increase of surface tension coefficient would lead to the increase of driving force of the rising liquid. As a result, the rising speed and height will increase.

The Effect of Liquid’s Density on Rising Height

Choosing the group IV in Table 3, we can find out the effect of density on the rising height in fan-shaped asymmetry interior corner with different contact angles, as is shown in Fig. 10.

Fig. 10
figure 10

The rising height under different liquid’s density

Full size image

From Fig. 10 we observe that the rising height decreases with the increase of density when we take the same contact angle in the same container at the same time. But the range is relatively narrow. We can explain this with the definition of the Bond number, Bo =ρgl 2/ σ. When other conditions are the same, the less the value of ρ and Bo is, the stronger the surface tension is. The increase of surface tension leads to the increase of driving force. Meanwhile the rising speed and height increase with the increase of driving force. However, due to Bo<<1, the density has little effect on the Bo So the difference of rising height under different densities is not obvious.

The Effect of the Container’s Central Angle on Rising Height

According to the group V in Table 3, with different contact angle we can learn the effect of container’s central angle on the rising height in fan-shaped asymmetry interior corner, as is shown in Fig. 11.

Fig. 11
figure 11

The climbing height under different viscosity

Full size image

According to the (a), (b), (d) in Fig11 when the contact angle is small, the rising height tends to increase with the increase of central angle. And the increase is obvious when the central angle is small. When central angle is large, for example the central angle is greater than 60° in Fig. 11a, the increase of rising height is not obvious It’s the same situation with Fig. 11d and e. The reason is that when the central angle is small, the two capillary flow in fan-shaped asymmetric interior corner would have a coupling. It is also called the cross flow. The smaller central angle is, the more obvious the phenomenon is. Then the higher the liquid rise in the central angle the lower the rising height is in fan-shaped asymmetry interior corner. When the central angle increased to a certain extent, the coupling is reduced to a weaker state. The change of the central angle has a little effect on the capillary flow when other conditions are same. When the contact angle is large, as is shown in (c) and (e) in Fig. 11, the rising height increases with the increase of the contact angle.

The Effect of Container’s Radius on Rising Height

According to the group VI in Table 3, we can learn the effect of container’s radius on the rising height with different contact angles, as is shown in Fig. 12.

Fig. 12
figure 12

The rising height with different container’s radius

Full size image

From the Fig. 12, we take same contact angle in the same container. When R ≥ 60mm the change of the container’s radius almost has no effect on the rising height. When R< 60mm, the smaller the container’s radius is, the lower the rising height is. This is because when the radius is small, the capillary flow in fan-shaped asymmetry interior corner of the container will couple with the capillary flow in the sharp corner, which is called cross flow. The smaller the radius is, the more obvious the phenomenon is. And the capillary flows in three interior corners will influence each other. When the container radius increases to a certain extent, the influence becomes weak. When other conditions are same, the change of the container‘s radius has little effect on the flow of the liquid.

The Effect of Contact Angles

Based on the research above, we can learn the effect of a parameter on rising height It basically has the same varying trend with different contact angles. Now we learn the effects of contact angle on rising height. The experimental medium is 10cs The initial height h z = 0.05m central angle of the container 2α = 90° and radius R = 60mm.

According to Fig. 13 the rising height decreases with the increase of contact angle But the contact angle 𝜃 2 on arc wall has a greater influence than the contact angle 𝜃 1 on straight wall. Therefore, if we want to reduce the rising height of capillary flow when managing liquid surface, we can use different materials for the arc wall and straight wall, which will make the contact angel 𝜃 2 larger than the 𝜃 1.

Fig. 13
figure 13

The rising height of the liquid under different contact angles

Full size image

The Research on the Initial Width in Fan-Shaped Asymmetry Interior Corner

The initial width of liquid surface H is a very important parameter for researching the capillary flow in fan-shaped asymmetry interior corner under microgravity environment. Weislogel (1996) observed that there is a constant width in capillary flow in V-shape interior corner by a series of drop tower experiments, which is called the initial width of liquid surface. In this section, we find that there is also an initial width of liquid surface H in fan-shaped asymmetric interior corner, as is shown in Fig. 14. Figure 14 displays the rising curves at t = 05s, 1.0s, 1.5s, 2.0s, 2.5s, 3.0s, 3.5s, 4.0s, 4.5s, 5.0s; and curves have an intersection point Aat different time, which corresponds to the initial width of liquid surface H.

Fig. 14
figure 14

The simulations of capillary flow with FLOW-3D. xis the radial direction of the vessel and zis the axial direction

Full size image

In this section we focus on the effects of different parameters on initial width H. The results are shown in the following Tables 4–9.

Table 4 The effect of the initial liquid’s height h z on characteristic meniscus width H
Full size table
Table 5 The effect of dynamic viscosity on characteristic meniscus width H (μ = 9.350×10−3Pa ⋅s)
Full size table
Table 6 The effect of surface tension of the liquid on characteristic meniscus width H (σ = 20.1×10−3N/m)
Full size table
Table 7 The effect of the density on characteristic meniscus width H (ρ = 935kg/m)
Full size table
Table 8 The effect of the central angle on characteristic meniscus width H
Full size table
Table 9 The effect of the container’s radius on characteristic meniscus height H
Full size table

According to the Tables 4–9, with the varying of parameters of experimental medium and container, there is an initial width of liquid surface for most fan-shaped asymmetric interior corners. For the model with small central angles, the result of numerical simulation is not satisfied and there is no obvious initial liquid width. When we take the same group of contact angle, the initial width of liquid surface H will increase with the increase of dynamic viscosity, central angle and radius, and decrease with the increase of surface tension. The varying of liquid initial height h z and liquid density has little effect on initial width H. When the initial liquid height and liquid density vary, the H gets the minimum value when the contact angle 𝜃 1 = 0° , 𝜃 2 = 40° . H gets the maximum value when 𝜃 1 = 40° , 𝜃 2 = 0° . As the other three set of contact angle vary in the group, the value of H is almost keep unchanged. The research in this section provides an important parameter for theoretical research on capillary flow in fan-shaped asymmetric interior corner.

Conclusion

The article studies the numerical simulation of capillary flow in fan-shaped asymmetric interior corner under microgravity. We infer that the Concus-Finn condition about the capillary flow in fan-shaped asymmetric interior corner is 𝜃 1+𝜃 2< 90° . When the Concus-Finn condition satisfied, we study the effects of different parameters on rising height and initial height. And we find when we take a set of contact angle, the rising height increases with the increasing of the surface tension, container radius and central angle, and decreases with the increasing of the dynamic viscosity, the density and the contact angle. But the contact angle of arc wall has a greater influence on decreasing scale than the contact angle of straight wall. The initial liquid height has no effect on the rising height. In addition, we find that the capillary flow in fan-shaped asymmetry interior corner is the same as the capillary flow in V-shape constant interior corner. There also is an initial width of liquid surface. It increases with the increasing of the dynamic viscosity, central angle and the radius, and decreases with the increasing of surface tension. However, the varying of the initial height and density has no effect on initial width of liquid surface H. It provides an important parameter for the theoretical study on the capillary flow in fan-shaped asymmetry interior corner. In the follow-up space experiment and theoretical analysis, researchers can make a further study on the capillary flow in fan-shaped asymmetry interior corner under microgravity based on this paper.