Introduction

Non-equilibrium fluctuations (NEFs) are dramatically different from equilibrium ones (EFs), because of the coupling of the driving gradient with spontaneous velocity fluctuations (Ortiz de Zárate and Sengers 2006). This results in a huge amplification of NEFs that is way more efficient for long wavelength fluctuations. Indeed, the intensity of NEFs exhibits a power-law divergence as \(I\left ( q \right )\propto q^{-4}\), q = 2σ/λ being the fluctuation wave number inversely proportional to the wave length λof the fluctuation. This divergence is prevented only by the effect of gravity (Segrè and Sengers 1993; Vailati and Giglio 1998, 1997) and by the vertical confinement determined by the final size of the sample (Ortiz de Zárate et al. 2006). These two reducing effects also impact the dynamics of NEFs. In a stable configuration, gravity accelerates very large fluctuations in moving them towards iso-dense layers (Croccolo et al. 2006, 2007), while confinement acts in combination with gravity slowing down even larger fluctuations, as shown recently (Giraudet et al. 2015). Recently, also simulations studies have pointed out the importance of NE fluctuations in diffusive processes (Donev et al. 2011; Balboa Usabiaga and et al. 2012; Donev et al. 2014; Delong et al. 2014).

The GRADFLEX experiment, flown in 2007 onboard the Russian satellite FOTON-M3, aimed at showing the full power-law divergence of the intensity of NEFs upon removal of the gravity force. This result was fully achieved both qualitatively, as can be appreciated from the published images (Vailati et al. 2011) and videos (ESA website), and quantitatively, as shown in the published papers (Vailati et al. 2011; Takacs and et al. 2011; Cerbino et al. 2015).

Many other space-based experiments have pointed out the importance of diffusive processes especially in microgravity conditions (De Lucas and et al. 1989; Snell and Helliwell 2005; Barmatz et al. 2007; Beysens 2014; Hegseth et al. 2014; Shevtsova 2010; Shevtsova et al. 2011, 2014).

One interesting aspect of NEFs is that their analysis provides direct access to the transport coefficients associated to the physical processes involved, like diffusion or thermodiffusion (the so-called Soret effect). This peculiarity has been capitalized in the past for measuring fluid transport properties such as the mass diffusion and the Soret coefficients (Croccolo et al. 2012; Giraudet et al. 2014), but can be, in principle, further extended to other properties such as thermal diffusivity or viscosity. In the cited papers fluid properties were obtained on ground by the analysis of the dynamics of concentration NEFs. More specifically, the evaluation of the time decay for different wave numbers by means of dynamic Shadowgraph allows getting the mass diffusion coefficient from the behavior of fluctuations at large wave vectors, where fluctuations are dominated by diffusion. At the same time, the Soret coefficient can be obtained by evaluating the experimental solutal Rayleigh number \(Ra_{s} ={\beta g\nabla cL^{4}} /{\left ( {\upsilon D} \right )}\) that is related to the wave number where time decay shows a distinct maximum, marking the transition from a regime for relaxation of the fluctuations dominated by diffusion, to one dominated by buoyancy (Croccolo et al. 2007, 2012). Here \(\beta =\left ( {1 /\rho } \right )\cdot \left ( {{\partial \rho }/{\partial c}} \right )\) is the solutal expansion coefficient, ρthe fluid density, cthe weight fraction concentration of the denser component of the mixture, gthe gravitational acceleration, ∇cthe amplitude of the concentration gradient, Lthe vertical extension of the sample, υthe kinematic viscosity and Dthe mass diffusion coefficient. While the same approach can be used in the absence of gravity for measuring the mass diffusion coefficient, one cannot get the Soret coefficient because the maximum in the time decay disappears, as the solutal Rayleigh number R a s vanishes.

Here we propose an alternative procedure to obtain the value of the Soret coefficient in microgravity. Our procedure relies on the simultaneous determination of the intensity of the temperature and concentration NEFs and on the fact that solutal fluctuations are generated by a concentration gradient driven by the imposed temperature gradient through the Soret effect. The Soret coefficient S T is proportional to the ratio between the concentration gradient and the applied temperature one:

$$ {\Delta} c=-S_{T} c_{o} \left( {1-c_{o} } \right){\Delta} T, $$
(1)

where Δcis the concentration difference between the top and the bottom of the cell, c 0 the equilibrium concentration of the denser component, ΔT the temperature difference between the top and the bottom of the cell. In this article we describe how to obtain a reliable measurement of the thermal diffusion ratio \(k_{T} =T\,\,S_{T} c_{o} \left ( {1-c_{o} } \right )\), which is proportional to the Soret coefficient.

The remainder of the paper is organized as follows: Section “Theory and Methods” reports the theory and methods relevant to the analysis, in section “Results and Discussion” we provide results and discussion and in section “Conclusions” conclusions are drawn.

Theory and Methods

Thermodiffusion

When a thermal gradient is applied to a multi-component mixture, the different species undergo partial separation, which is contrasted by mass diffusion. The separation of the species is commonly named thermodiffusion or Soret effect (Soret 1879; de Groot and Mazur 1984). This situation ends up at a steady state determined by a balance between Fickean diffusion and thermodiffusion when the corresponding fluxes are identical in the intensity and opposite in the direction, so that the total mass flux is zero \(\vec {{J}}=\vec {{J}}_{Soret} +\vec {{J}}_{diffusion} =0\). Imposing that the total mass flux is zero leads to Eq. 1, at steady state. The Soret effect can be thus conveniently utilized for generating a precisely controllable and, in the case of small temperature differences, linear concentration gradient in a fluid mixture by applying a temperature one.

Non-Equilibrium Fluctuations

The theory of non-equilibrium fluctuations has been elegantly described in the book by Ortiz de Zárate and Sengers (Ortiz de Zárate and Sengers 2006) and in references therein. Here we just would like to recall the main equations that will be used in the following. In particular we are interested in a recent development of the theory that includes realistic boundary conditions in the case when gravity is removed (Ortiz de Zárate et al. 2015) the case relevant to the analysis of the GRADFLEX experiment. The assumption g = 0 led the authors derive an analytical solution for the dynamic structure factor of solutal NEFs :

$$ S\left( {\omega ,q} \right)=\frac{k_{B} T}{\rho }\frac{\left( {\nabla c} \right)^{2}}{\upsilon Dq^{4}}\frac{2Dq^{2}}{\omega^{2}+D^{2}q^{4}}\left[ {1+\frac{4\left( {1-\cosh \tilde{{q}}} \right)}{\tilde{{q}}\left( {\tilde{{q}}+\sinh \tilde{{q}}} \right)}} \right], $$
(2)

where k B is the Boltzmann constant, T the average temperature, \(\tilde {{q}}=qL_{\mathrm {}}\)the dimensionless wave number and Lthe vertical extension of the sample. This equation contains the main result that the dynamics of NEFs in microgravity show only diffusive behavior. Therefore the time constant can be expressed as a function of the wave number \(\tau \left ( q \right )\) as:

$$ \tau \left( q \right)=\frac{1}{Dq^{2}}. $$
(3)

This behavior has been experimentally observed during the GRADFLEX experiment (Vailati et al. 2011; Cerbino et al. 2015).

For temperature fluctuations an exact theory including confinement effects is not available, but one can derive the exact expression of the intensity of NE fluctuations in the limit of large wave numbers (Ortiz de Zárate and Sengers 2006)

$$ \frac{{S_{TT}^{NE}}^{\infty}}{S_{TT}^{E} }=\frac{c_{p} \left( {\nabla T} \right)^{2}}{T\alpha_{T} \left( {\alpha_{T} +\upsilon } \right)}L^{4}, $$
(4)

where c p is the heat capacity at constant pressure, α T the thermal diffusivity and:

$$ S_{TT}^{E} =\frac{k_{B} T^{2}}{\rho c_{p} }, $$
(5)

is the intensity of the thermal fluctuations at equilibrium, independent of the wave number. For NE concentration fluctuations, by integrating Eq. 2 over the temporal frequencies and in the limit of large wave numbers, one gets:

$$ {S_{cc}^{NE}}^{\infty }=\frac{k_{B} T}{\rho }\frac{\left( {\nabla c} \right)^{2}}{\upsilon D}L^{4}. $$
(6)

The ratio \({{S_{cc}^{NE}}^{\infty }}/{{S_{TT}^{NE}}^{\infty }}\) can thus be deduced from Eqs. 4–6:

$$\left( {\frac{S_{cc} }{S_{TT} }} \right)^{NE,\infty }=\frac{\left( {\nabla c} \right)^{2}}{\upsilon D}\frac{\alpha_{T} \left( {\alpha_{T} +\upsilon } \right)}{\left( {\nabla T} \right)^{2}}. $$

By including the definition of the Soret coefficient provided by Eq. 1 one finally obtains:

$$\begin{array}{@{}rcl@{}} \left( {\frac{S_{cc} }{S_{TT} }} \right)^{NE,\infty }&=&\frac{\alpha_{T} \left( {\alpha_{T} +\upsilon } \right)}{\upsilon D}\left[ {c_{0} \left( {1-c_{0} } \right)S_{T} } \right]^{2}\\&=&\frac{\alpha_{T} \left( {\alpha_{T} +\upsilon } \right)}{\upsilon D}\frac{{k_{T}^{2}}}{T^{2}}\approx \frac{\alpha_{T} }{D}\frac{{k_{T}^{2}}}{T^{2}}.\\ \end{array} $$
(7)

From Eq. 7 one can thus obtain k T after measuring the ratio \({{S_{cc}^{NE}}^{\infty }}/{{S_{TT}^{NE}}^{\infty }}\) and knowing the two other quantities α T and D. It’s worth noting that only the amplitude of k T can be retrieved with no information about its sign.

GRADFLEX Experiment

The GRADFLEX experiment (Vailati et al. 2006) was actually composed of two distinct parts, one analyzing the behavior of temperature fluctuations in a simple fluid and another one analyzing solutal fluctuations in a binary mixture. Here we report and discuss only results from the latter experiment. The binary mixture under investigation is a colloidal suspension of polystyrene (PS) with a molecular weight of 9,100g/mol at a weak concentration of 1.8%w/w dissolved in pure toluene. The small concentration allows considering the limit of dilute sample and neglecting interactions between the polymer chains.

Experimental Procedures

The sample was confined by two 12-mm-thick sapphire windows placed at a distance of 1mm. The temperature of each window was controlled independently by using an annular Thermo Electric Device governed by a Proportional Integral Derivative (PID) servo loop. The sample was also laterally confined by a flat Viton gasket with an inner diameter of 25mm. The measurement of the temperature was performed immediately outside the sapphire plates in order to minimize the time delay to the temperature PID controllers, thus resulting in a very efficient temperature control with an RMS of about 10mK over 24 hours. Further details about the design of the apparatus can be found in literature (Vailati et al. 2006, 2011).

A series of experiments was performed consisting in the application of three temperature differences (nominally 5, 10 and 20K) and awaiting the mass diffusion time needed for the system to evolve to the stationary state τ s = L 2/D = 5000s.

During the steady state series of images were acquired with constant time delay of Δt = 10s.

Optical Setup

The optical technique utilized is that of quantitative Shadowgraph (Settles 2001; Trainoff and Cannell 2002; Croccolo and Brogioli 2011) that allows both imaging of what happens inside the cell as well as light scattering measurements by means of statistical analysis of the acquired images. The optical setup consisted of a super-luminous light emitting diode at a wavelength of 680±10nm coupled to a mono-mode fiber. The diverging beam exiting the fiber is steered by a mirror and collimated by an achromatic doublet lens. The collimated beam passes through the sample recording phase modulations due to fluctuations of the refractive index and then through a relay lens before impinging onto the CCD camera detector.

Image Analysis

Images have been analysed by means of two different approaches: the first one is the Differential Dynamic Algorithm that is able to extract the intermediate scattering function (ISF) by analysing differences of images with increasing time delay; the second one is Thermal Gradient Analysis that we introduce here and that relies on the analysis of static power spectra for thermal gradients to retrieve the static signal of non-equilibrium fluctuations. In the following the two methods are described in more details.

a) Differential Dynamic Algorithm

The Differential Dynamic Algorithm has been introduced in 2006 for the analysis of Shadowgraph and Schlieren images during ground-based free diffusion experiments of isothermal binary mixtures (Croccolo et al. 2006, 2007). The principle has been further applied to other near field optical techniques (Cerbino and Trappe 2008; Cerbino and Vailati 2009; Giavazzi and Cerbino 2014).

The main idea is that of calculating the structure function of the fluctuations of the image intensity, which is calculated as (Croccolo et al. 2006):

$$ C_{m} \left( {\vec{{q}},{\Delta} t} \right)=\left\langle {\left| {I\left( {\vec{{q}},t+{\Delta} t} \right)-I\left( {\vec{{q}},t} \right)} \right|^{2}} \right\rangle_{t} , $$
(8)

where \(I\left ( {\vec {{q}},t} \right )\) is the image intensity upon 2D-spatial Fourier transform and Δt the varying temporal delay between considered images.

This signal is further investigated for each available wave vector as a function of the time delay Δtbetween images by fitting through the following equation:

$$ C_{m} \left( {q,{\Delta} t} \right)=2\left( {A_{DDA} \left( q \right)\left( {1-f\left( {q,{\Delta} t} \right)} \right)+B_{DDA} \left( q \right)} \right), $$
(9)

where \(A(q)=S\left ( q \right )\cdot T\left ( q \right )\) represents the static power spectrum as the product of the optical transfer function \(T\left ( q \right )\) and the static power spectrum of the concentration fluctuations \(S\left ( q \right )\). A DDA(q) is thus the measured amplitude of the decaying signal: in our experimental conditions this is equivalent to the concentration fluctuations, because thermal ones decay too fast to be captured at the acquisition rate of the CCD camera. Here q represents the wave number, i.e. the amplitude of the wave vector \(\vec {{q}}\) after azimuthal averaging. Finally, \(B_{DDA} \left ( q \right )\) represents the background noise of the DDA analysis that includes also all the signals that decay faster than the acquisition delay time, like thermal fluctuations, as stated above (Cerbino et al. 2015).

From this kind of analysis one gets access to the Intermediate Scattering Function (ISF) of the system. In many cases a single exponential decay is a realistic assumption for the ISF of NEFs, as will be discussed further in the next section, so one can assume:

$$ f\left( {q,{\Delta} t} \right)=\exp \left[ {-\frac{\Delta t}{\tau \left( q \right)}} \right]. $$
(10)

Fitting of Eqs. 9 and 10 can thus provide the value of the time decay of the fluctuations for every wave number q. In the case of a microgravity experiment recent theories confirm the prediction of a pure diffusive behavior of concentration NE fluctuations, even in the presence of non-negligible confinement effects, so that the time decay is expected to be described by Eq. 3 (Ortiz de Zárate et al. 2015). A fitting of the experimental data of \(\tau \left ( q \right )\) as a function of the wave number can thus provide a quantitative measurement of the mass diffusion coefficient.

b) Thermal Gradient Analysis

As stated in the previous paragraph, one can get the static power spectrum of fluctuations A(q) directly from the DDA analysis, but the efficiency of this procedure is limited when the intensity of fluctuations is very small or when the time decays become smaller than the time acquisition step of the CCD camera, like it is the case here for fluctuations of wave number larger than about 200cm −1. In this paper we introduce thus a different approach that takes into account simultaneously the results obtained for the three applied thermal gradients. From the acquired images one can get information about the static power spectrum of fluctuations by directly measuring the quantity (Brogioli et al. 2000; Trainoff and Cannell 2002):

$$ S_{m} \left( {\vec{{q}}} \right)=\left\langle {\left| {I\left( {\vec{{q}},t} \right)-I_{0} \left( {\vec{{q}},t} \right)} \right|^{2}} \right\rangle_{t} , $$
(11)

where \(I_{0} \left ( {\vec {{q}},t} \right )=\left \langle {I\left ( {\vec {{q}},t} \right )} \right \rangle _{t} \) is the FFT of the background image. The measured static power spectrum can also be expressed as:

$$ S_{m} \left( q \right)=A_{stat} \left( q \right)+B_{stat} \left( q \right), $$
(12)

where \(A_{stat} (q)=S_{stat} \left ( q \right )\cdot T\left ( q \right )\) represents the measured static power spectrum as the product of the optical transfer function \(T\left ( q \right )\) and the static power spectrum of the NE fluctuations \(S_{stat} \left ( q \right )=S_{s} \left ( q \right )+S_{t} \left ( q \right )\), including both temperature and solutal ones. Contrary to the DDA analysis, the TGA provides the statics of the signal so that it is independent of the frame rate of the CCD camera, therefore both the solutal and thermal signals are measured.\(_{\mathrm {}}B_{stat} \left ( q \right )\) here represents the background noise of the ‘statics’ related to all the sources of noise such as the CCD camera and the entire electronic system. It’s worth pointing out that the intensity of solutal fluctuations is expected to be much larger than that of the temperature ones, as it will be shown in the Discussion section. Therefore, we can assume that the static signal is mostly determined by solutal fluctuations \(S_{stat} \left ( q \right )\approx S_{s} \left ( q \right )\). Theoretical models predict a quadratic dependence of the structure factor from the temperature difference (see Eqs. 4 and 6):

$$ S_{m} \left( {q,{\Delta} T} \right)=a_{TGA} \left( q \right)\cdot {\Delta} T^{2}+B_{TGA} \left( q \right). $$
(13)

Here the term \(a_{TGA} \left ( q \right )\) is a sort of normalized static power spectrum that factors out the dependence from the three different thermal gradients used in the actual GRADFLEX experiment. Of course the amplitude \(A_{TGA} \left ( q \right )\) can eventually be recovered for any temperature gradient by calculating \(A_{TGA} \left ( q \right )=a_{TGA} \left ( q \right )\cdot {\Delta } T^{2}\). Finally, the background obtained by the TGA analysis would, in principle, identify with the one mentioned in the static power spectrum: \(B_{stat} \left ( q \right )=B_{TGA} \left ( q \right )\).

Results and Discussion

In the following, we report results of the analysis of the images obtained by the GRADFLEX mixture experiment. The images acquired during the flight have been stored on dedicated solid state disks that have been recovered after the FOTON M3 satellite reentry. The raw data of Shadowgraph images contain both measurements of the optical background \(I_{0} \left ( {\vec {{q}},t} \right )=\left \langle {I\left ( {\vec {{q}},t} \right )} \right \rangle _{t} \) not evolving in time, and the fluctuating signal that is related to refractive index fluctuations within the sample. In Fig. 1 we report four false colors images of differences of images taken at steady state at different delay times of 10, 100, 1000 and 10000s.

Fig. 1
figure 1

False colors visualization of NE concentration fluctuations in microgravity. Data shown are for the maximum nominal temperature gradient at the steady-state of the thermodiffusion process. The side of each image is 13 mm

Full size image

Clearly, the contrast of the images is steadily increasing with the delay time. Also a sort of characteristic size is somewhat recognizable within the images, which is a signature of the transfer function of the shadowgraph technique. This can be further appreciated in Fig. 4 when the power spectrum of differences of images is presented.

Evaluation of the Mass Diffusion Coefficient by DDA Analysis

From shadowgraph images the structure function \(C_{m} \left ( {q,{\Delta } t} \right )\) has been calculated as per Eq. 8 for all the wave numbers available in our optical setup. In Fig. 2, three examples of structure functions are plotted against the time delay between images for three different wave numbers. The data points are normalized between 0 and 1 to facilitate comparison.

Fig. 2
figure 2

Structure function \(C_{m} \left ( {q,{\Delta } t} \right )\) as a function of the time delay Δt for three different wave numbers q. Symbols stand for experimental data, while lines are the result of fitting with Eqs. 9 and 10

Full size image

The decay times of fluctuations are determined by fitting the data at each wave number by means of Eqs. 9 and 10 with the three free parameters defined above: A DDA(q), \(\tau \left ( q \right )\) and \(B_{DDA} \left ( q \right )\). The resulting time decays are plotted in Fig. 3 as a function of the wave number q. The data plotted in Fig. 3 represent the runs with nominal temperature difference of 20K, but equivalent results have been obtained for the other two temperature gradients.

Fig. 3
figure 3

Time decays \(\tau \left ( q \right )\) for the largest temperature gradient. The dashed blue line corresponds to the CCD delay time. The solid red line corresponds to the fitting with Eq. 3 using D as the only fitting parameter

Full size image

The time decays in microgravity conditions should be well described by pure diffusive time constants mentioned above (Ortiz de Zárate et al. 2015), see Eq. 3. By fitting resulting time decays through Eq. 3 with the mass diffusion coefficient D as the only free parameter one gets the value D = (2.03±0.04)x10 −6 cm 2/s in agreement with available data for the investigated mixture of PS in toluene (Vailati et al. 2011; Rauch and Kohler 2002, 2003).

Evaluation of the Statics by the TGA and Comparison with the DDA

The static power spectrum \(S_{m} \left ( q \right )_{\mathrm {}}\)of NE fluctuations has also been evaluated by Eq. 11 for the three different temperature gradients applied in the GRADFLEX mixture experiment. Results are shown in Fig. 4. Note that the plot is in log-log scale and that the typical oscillations due to the Shadowgraph transfer function are clearly visible. The signal is due to both solutal and thermal NE fluctuations, even if the solutal contribution is expected to be dominant. Here we also assume that the contribution of equilibrium fluctuations is contained into the background noise in the investigated range of wave numbers.

Fig. 4
figure 4

Static power spectrum\(_{\mathrm {\thinspace }}S_{m} \left ( q \right )\)for three temperature differences and the background resulting from fitting data through Eq. 13 as explained in the text

Full size image

These data are then fitted through Eq. 13 for each wave number with \(a_{TGA} \left ( q \right )\) and \(B_{TGA} \left ( q \right )_{\mathrm {}}\)as free parameters. The values of the obtained background are plotted in Fig. 4 for direct comparison to the signal. The oscillations typical of the Shadowgraph technique are not present in the background signal.

The results for the quantity \(A_{TGA} \left ( q \right )=a_{TGA} \left ( q \right )\cdot {\Delta } T^{2}\) are shown in Fig. 5 calculated for the maximum thermal gradient together with the results of \(A_{DDA} \left ( q \right )\) obtained by means of the DDA algorithm. Clearly, the DDA algorithm fails in retrieving a satisfactory estimate of \(A_{DDA} \left ( q \right )\) at wave numbers larger than about 200cm −1. It should be stressed again that the signal obtained by means of the DDA analysis (black line in Fig. 5) is originated by concentration fluctuations only, while the one obtained by the TGA analysis is the sum of the signal for solutal and thermal fluctuations. Actually in the DDA analysis and for the present experimental conditions, the signal of thermal fluctuations ends up in the background term \(B_{DDA} \left ( q \right )\) because its decay is too fast with respect to the image acquisition rate. Results for \(B_{DDA} \left ( q \right )\) are shown in Fig. 6 for the three temperature differences.

Fig. 5
figure 5

Comparison between the quantity \(A_{TGA} \left ( q \right )=a_{TGA} \left ( q \right )\cdot {\Delta } T^{2}\) obtained through the TGA analysis and \(A_{DDA} \left ( q \right )\) as obtained through the DDA one

Full size image
Fig. 6
figure 6

DDA background \(B_{DDA} \left ( q \right )\) for the three temperature differences and the background resulting from fitting data through Eq. 13 as explained in the text

Full size image

By comparing Figs. 4 and 6 one can note that the intensity of thermal fluctuations is only roughly 5% of the total intensity, which justifies the assumption that solutal fluctuations are the main contribution of the signal. Therefore, we are now in the position of performing again the TGA analysis on the data of \(B_{DDA} \left ( q \right )\) shown in Fig. 6 in order to recover the static power spectrum of non-equilibrium thermal fluctuations only. We term the resulting parameter \(a_{TGA,th} \left ( q \right )_{\mathrm {}}\)to distinguish from the one previously obtained. The resulting \(A_{therm} \left ( q \right )=a_{TGA,th} \left ( q \right )\cdot {\Delta } T^{2}\) is shown in Fig. 7 together with the result previously obtained for solutal fluctuations.

Fig. 7
figure 7

Static power spectra for the solutal \(a_{TGA} \left ( q \right )\) and thermal \(A_{therm} \left ( q \right )\) NEFs

Full size image

Again we stress that the intensity of the signal of thermal fluctuations is roughly one order of magnitude smaller than that of solutal NEFs. Also we note that the quality of the signal for thermal fluctuations is worst because of the poorer signal to noise ratio. For thermal fluctuations data become almost unreliable outside the wave number range 40÷150cm −1. Vertical blue lines in Fig. 7 mark the mentioned range. To obtain further information about the static power spectrum of NEFs \(S\left ( q \right )\) one should divide the two signals shown in Fig. 7 by the shadowgraph transfer function \(T\left ( q \right )\), as done in (Vailati et al. 2011). This step requires a fine calibration of the optical technique, which introduces a number of undetermined sources of error. If one aims at retrieving the thermal diffusion ratio k T, an alternative approach is that of calculating the ratio:

$$ \frac{A_{TGA} \left( q \right)}{A_{therm} \left( q \right)}=\frac{S_{sol} \left( q \right)\cdot T\left( q \right)}{S_{th} \left( q \right)\cdot T\left( q \right)}=\frac{S_{sol} \left( q \right)}{S_{th} \left( q \right)}. $$
(14)

We recall that in the limit of large wave vectors this ratio should be equal to the result obtained in Eq. 7. One can further perform a fitting of the obtained data points in the wave number range around 100 cm −1 using k T as fitting parameter in order to get an estimate of its value.

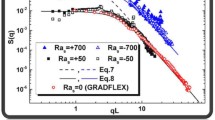
In Fig. 8 results of the ratio provided by Eq. 14 are shown as blue circle open symbols together with the theoretical prediction as a red continuous line and with the fitted value for large wave numbers. The theoretical curve is provided by the ratio of the theoretical predictions reported in Fig. 3 of (Cerbino et al. 2015), where the concentration intensity comes from a recent paper (Ortiz de Zárate et al. 2015) and the thermal one can be retrieved from the classical book (Ortiz de Zárate and Sengers 2006). The resulting value for the ratio is about 14 that results in a thermal diffusion ratio of \(k_{T} =\left ( {1.0\pm 0.2} \right )\times 10^{-3}K^{-1}\), in agreement with literature (Vailati et al. 2011; Rauch and Kohler 2002, 2003). We stress out here that the ratios provided by Eqs. 7 and 14 do not depend from the applied temperature difference. Therefore, the procedure for the determination of the thermal diffusion ratio described here relies on a powerful self-referencing method that works flawlessly even in the absence of the knowledge of the temperature gradient imposed to the sample. Moreover, the shadowgraph technique used by the method does not require any delicate optical alignment. These two features make the method proposed here a rugged solution ideal for the determination of transport coefficients under harsh conditions or in hostile environments.

Fig. 8
figure 8

Ratio of the static signal for solutal and thermal fluctuations. The dashed line represents the asymptotic value at large wave vectors

Full size image

Conclusions

In this paper we provide a further analysis of the images acquired during the GRADFLEX experiment in order to quantitatively measure the mass diffusion coefficient and the thermal diffusion ratio of a binary mixture of PS in toluene at weak concentration. These results confirm quantitatively the fact that the analysis of NE fluctuations can be efficiently performed by means of light scattering techniques like the shadowgraph able to detect wave numbers as small as 10/cm, thus getting access to the physical phenomena involved in the thermodiffusion process and providing a sound measurement of transport properties of the system.

Different image analysis procedures have been applied confirming previously published data. In particular a simple self-referencing method is proposed to measure both the mass diffusion coefficient and the thermal diffusion ratio. Remarkably, the method proposed by us does not require performing optical and thermal calibrations.