Introduction

For majority of fluids, surface tension is a decreasing function of temperature, hence any thermal non-uniformity inevitably generates a surface flow transporting warm fluid and aiming at eliminating cooler regions. A fluid motion driven by surface tension differences resulting from thermal gradients along a fluid-gas interface is called thermocapillary (Marangoni) convection. This type of flows is very common in numerous technological processes and industrial applications, in which e.g., evaporation or welding are involved, and is of great importance to chemical engineers.

Attention to the thermocapillary flows and their hydrodynamic stability has been spawned by the prospect of processing materials by containerless methods to avoid contamination from crucible walls. Particularly, containerless growth of semiconductor crystals by the so-called floating zone technique in space has been considered as a way to reduce convection in crystal melts in order to produce high-quality homogeneous materials, highly anticipated by the electronics industry. The expected homogeneity, however, has not been acquired and it has been blamed on presence of buoyancy. Eliminating it did not resolve the problem and it has been understood that the reason for the azimuthally variable properties of the crystals was not buoyancy but Marangoni convection (Chang and Wilcox 1976). Though buoyant forces are strongly reduced in microgravity, thermocapillary effect at the interface is the dominant mechanism to drive fluid motion.

We study a non-isothermal liquid column, a liquid bridge, that represents a half of a floating zone. In the studied system, a temperature difference between the supporting disks is imposed. At small values of the temperature gradient, the flow settles into a form of a two-dimensional toroidal cell. The two-dimensional roll becomes unstable as soon as the temperature gradient achieves a critical value, and the flow becomes three-dimensional, either steady or oscillatory. The type, pulsating or not, of the supercritical flow is defined by the balance between heat conduction (dominant for low Pr numbers) and heat convection (dominant for high Pr numbers).

In the present paper, ΔT cr refers to the temperature difference for the onset of three-dimensional convection characterized by oscillating temperature disturbances. A liquid bridge is an example of a complex dynamical system displaying many interesting non-linear phenomena, such as chaos (Melnikov et al. 2004; Ueno et al. 2003).

It was shown by Schwabe and Scharmann (1979), and by Chun and Wuest (1979) that the hydrothermal instability in a liquid bridge sets in through a supercritical Hopf bifurcation. Both the critical temperature difference and the regime of the supercritical flow are defined by the physical properties of the fluid the liquid bridge is made of, as well as are dependent on the geometry of the system (liquid volume, the ratio of the height to the radius of the column - aspect ratio Γ) and on ambient conditions (properties of the surrounding gas, gravity, vibrations, to name a few). In a liquid with a high Prandtl number (Pr = ν/k, kinematic viscosity ν to thermal diffusivity k ratio), the hydrothermal instability is oscillatory and a hydrothermal wave, either traveling in the azimuthal direction or standing, is initiated. The three-dimensional supercritical flow has a modal structure with integer number m of pairs of hot and cold patterns visible when the perturbed temperature field is visualized (see e.g. Shevtsova et al. (2003)). m is called the azimuthal wave number. The perturbations can be visualized by subtracting the two-dimensional temperature field, obtained by averaging the temperature in the azimuthal direction, from the full three-dimensional solution.

Both theoretical (see e.g. Kuhlmann (1999)-Lappa (2005)) and experimental (Preisser et al. 1983; Shevtsova et al. 1999) studies on the onset of instability and the identification of the flow regimes in liquid bridges are being performed over several decades. The critical temperature difference, or suitably defined the critical thermocapillary Reynolds number Re cr ∝ΔT cr , and the wave number m were calculated and measured for different liquids, including liquid bridges with non-cylindrical free surface (Shevtsova and Legros 1998).

It is worth mentioning separately a number of works on the effect of heat exchange through interface on hydrothermal stability of a Marangoni flow ((Kamotani et al. 2003) - (Shevtsova et al. 2013)), which is a very important aspect in many technological applications, such as surface tension-driven and buoyancy convection inside evaporating droplets. It was found (Shevtsova et al. 2005; Ueno et al. 2010; Gaponenko and Shevtsova 2012; Melnikov and Shevtsova 2014) the strength of the effect of the heat transport through the interface on the stability of the thermocapillary flow strongly depends on the rate of heat exchange (the Biot number), temperature and velocity profiles in the gaseous phase, and on the physical properties of the liquid.

In the current effort, we study influence of thermal conditions in the gas phase surrounding a liquid bridge on stability of the Marangoni flow. The heat is carried away (or towards in case of heating) from the fluid by convection, conduction and radiation. Experimentally, the local heat flux is proportional to the temperature difference between the fluid and the surrounding gas that we call the ambient temperature. Changing temperature in the gas phase changes the amount of transported heat per unit time. The experimental setup, used for the present work, allows us prescribing and maintaining a uniform ambient temperature far away from the interface, at the distance of about 30 times of the radius of the liquid zone.

Computer modeling has been employed to confirm/support the experimental findings. In addition to the experimental conditions, thermally insulated free surface and a linear temperature distribution in the gas phase were considered.

Experimental apparatus and conditions

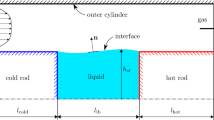
The experimental setup, shown in Fig. 1, was designed and built by Prof. Schwabe and his co-workers from University of Giessen in Germany. The liquid bridge of a radius of 3mm is created inside a chamber of a large volume, which serves to isolate the liquid bridge from the disturbing convection in the laboratory. The chamber has thick walls with the inner diameter of approximately 100mm, and it has four glass windows for optical observation from the side. The upper rod is made of sapphire, and the bottom brass rod is placed exactly beneath the upper one. The transparent top rod allows us to have a top view on the flow field. The two rods have a specially treated edges allowing creating a liquid bridge of a relatively large volume. The bottom rod was coated with EGC-1700 liquid to prevent leakage of n-decane. For the undertaken experimental work, in order to avoid undesired buoyant convection, the top rod was heated and the bottom plate was kept at the constant temperature of T c = 20 °C by using thermostatic baths. During each experimental run, the wall of the chamber T out was maintained at a constant temperature using a thermostatic bath. It allowed us to study different external conditions by varying T out between 10 and 40 °C. The liquid bridge was formed by injecting the liquid through the circular inlet of a very small radius at the center of the bottom rod.

Fig. 1
figure 1

Experimental setup: a sketch showing the liquid bridge and the external chamber, b a photograph of two rods between which a liquid bridge is created

Full size image

We used type K Chromel-Alumel thermocouples (with a sensitivity of approximately 41μV/°C and a good accuracy of about 0.75 % at room temperature) to control the temperatures at both rods, of the chamber and to record temperature oscillations. Besides the obvious importance of maintaining the imposed ΔT constant, the temperature of the chamber T out is another important factor to control as it is capable of influencing the experimental conditions via heat exchange between the fluid and air inside the chamber. In order to avoid this influence, it has always been thermally stabilized and controlled.

The thermocouples have been calibrated using the thermally regulated water cooling system. The thermocouple, used for measuring local temperature of the liquid, was not supposed to interfere the convection in fluid. For this reason, it has been installed at approximately the middle of the liquid column, and approximately 0.25 mm away from the liquid-gas interface in air. This installation allowed us to avoid creating mechanical disturbances into the fluid flow. In order to have a fast response of the thermocouple to changes of temperature, the thermocouple was very thin with the tip of approximately 40 microns. The distance d between the rods is adjustable allowing us to study different aspect ratios.

The working liquid is n-decane (molecular formula C 10 H 22), which is an evaporating liquid (Yasnou et al. 2012), (Melnikov et al. 2013). The evaporation rate was monitored using the same approach as in (Melnikov et al. 2013) and the losses of the liquid volume were continuously compensated through the bottom cold rod using an automatic syringe pump. As the evaporation rate was found to be growing with the increase of the imposed temperature difference, the higher T h was imposed the more we had to compensate. Simple estimations showed that the velocity of the injected liquid at the inlet did not exceed 40 microns per second and the thermocapillary flow was not disturbed by this procedure.

We were visualizing the flow field with the help of two types of particles injected into the liquid bridge: (1) gold-coated acrylic particles of 15 microns in diameter, whose density is 1470 kg/m3; (2) hollow glass microspheres (Eccospheres) of different diameters between 20 and 100 microns having the density of 790 kg/m3 (Melnikov et al. 2013). Two cameras were used: one for the top view with a frame rate of 30 fps; the other for the side view.

Experimental procedure

As the first step, special care was taken about adjusting the experimental setup in the strictly horizontal position. A careful alignment of the rods was done using computer image processing.

As the second step, an image of a plumb-line was acquired and analyzed to ensure that the camera was positioned vertically. The optical distortion produced by the lens were negligible.

Each experiment consisted of the following steps:

  1. (i)

    Careful cleaning and drying the liquid bridge cell. The rods were coated with the anti-wetting EGC-1700 agent and were dried.

  2. (ii)

    Creating a liquid bridge of the desired volume by injecting the necessary amount of liquid from the syringe. The experiments were performed for different volume ratios. The injected liquid volume was always checked.

  3. (iii)

    Establishing a required temperature of the chamber’s wall. We were waiting for about 60 minutes for the temperature to stabilize.

  4. (iv)

    Heating and cooling the rods. We were waiting for about 20 minutes to allow the temperatures to reach the steady state and to thermocapillary flow to establish. The imposed temperature difference ΔT was varied between 3 and 13 K.

  5. (v)

    Recording local temperature of the fluid.

  6. (vi)

    Recording top view images during 20–30 seconds by a camera. A small amount of particles has been added to the liquid for observing the flow pattern.

Experimental observations

Keeping the chamber’s wall temperature at 25 °C, values of critical temperature difference were measured within a wide range of liquid volume. To calculate ΔT cr we used the fact that the amplitude of temperature oscillations increases as a square root of the distance from the bifurcation point, i.e. A 2∼(ΔT−ΔT cr ). Thus, calculating the amplitude at several supercritical values of ΔT one can find the critical temperature difference. For completing this procedure, several measurements at sub-critical values of ΔT were done to measure the offset. As there are always random thermal disturbances and fluctuations present in the flow and thermocouples, while having a short response time, never have the absolute accuracy, the temperature records always contain noise that must be filtered off. The experimentally calculated offset for the amplitude of temperature oscillations was small, about 0.01–0.02 °C.

Figure 2 shows findings for a wide range of liquid bridge volume. Critical temperature difference is plotted versus volume ratio Vr, which is the ratio of the injected fluid volume to the volume of the cylinder πR 2 d. For the study, the temperature of the chamber’s wall T out was kept at 25 °C.

Fig. 2
figure 2

Stability diagram: experimentally measured critical temperature difference versus fluid volume ratio. Temperature at the wall of the chamber was stabilized at 25 °C

Full size image

Though, the change of the critical temperature difference is not very big, there are two branches of the stability diagram. One observes the flow stabilization at about Vr = 0.9 where the value of ΔT cr becomes relatively high. At first, we have associated the two branches with different flow structures, as it occurred in the experiments of (Shevtsova et al. 2003).

To prove it, the flow structure was visualized and quantified using small particles denser than the fluid. In those cases, where the particles accumulated in a coherent structure (PAS) (Melnikov et al. 2011; Pushkin et al. 2012; Melnikov et al. 2013), we could find the mode m of the supercritical flow. A PAS may be formed under certain conditions; they are imposing strong requirements on the flow to be characterized by a strong one-mode periodic traveling wave. Figure 3 presents some examples of the particles accumulation structures recorded for 4 different volume ratios. Though a PAS was not always formed, we could identify a m = 2 traveling wave for the volume ratios between 0.82 and 1.05.

Fig. 3
figure 3

Experimental snapshots of particles distributions for different fluid volume ratios: a - 0.87, b - 0.92, c - 0.98, d - 1.05. Temperature at the wall of the chamber was stabilized at 25°C. The particles are seen as black specks. Here the mode of the flow m is 2

Full size image

To check how the external thermal conditions can affect the onset of instability, a set of experiments has been performed in which T out was varied between 10 (strong cooling) and 40°C (strong heating).

The observations prove that increasing the external temperature results in a weak stabilization of the thermocapillary flow. The critical temperature difference slightly rises, as shown in Fig. 4. The slope, however, depends on the liquid volume. Whereas the ΔT cr versus T out curve is concave for Vr = 0.98 and 1.05, it is convex for Vr = 0.92. Figure 4 shows the following trend: the larger volume of the liquid bridge, the stronger the effect of the ambient temperature. The similar behavior was previously observed in the experiments with silicone oils (Kamotani et al. 2003; Shevtsova et al. 2005). Varying the temperature of the wall of the chamber did not result in changing the mode m = 2 of the flow. As it will be seen below in Chapter 2, this result appears to be crucial for drawing a conclusion about the actual temperature distribution in air inside the chamber.

Fig. 4
figure 4

Experimentally measured critical temperature difference versus temperature at the wall of the chamber for different liquid volume ratios

Full size image

The critical conditions were not the only interest of the study. Another question was related to how the dynamics of the flow change while one moves farther away from the critical point as ΔT increases. To trace the transitions occurred in the system, the frequency of temperature oscillations were analyzed. Any significant change of the dynamics is expected to be seen on frequency curves.

The frequency of temperature oscillations depends on ΔT and the temperature at the chamber’s wall T out seems to have a weak effect on it. As Fig. 5 shows, this dependency is not the same for any volume ratio. However, just after the onset of instability, the frequency is always decreasing with the increase of ΔT for the three studied volume ratios as is shown in Fig. 5.

Fig. 5
figure 5

Fundamental frequency as a function of temperature difference ΔT observed at different ambient temperatures at the external wall of the chamber: T out =10 (circles), 25 (squares) and 40 °C (triangles). Experiments were performed for three different volume ratios Vr: a - 0.92, b - 0.98, c - 1.05

Full size image

The fundamental frequency curves versus ΔT for Vr = 0.98 and 1.05 are rather smooth, but we have found a strong frequency drop in a liquid bridge of 0.92 volume ratio. The two fundamental frequencies belonging to the two curves (at small and at high values of ΔT in Fig. 5a) are not commensurate, hence corresponding to two different regimes characterized by different wave numbers. The oscillations observed right after the critical point are of a very high frequency. The m = 2 mode exists immediately after the frequency drop; it was confirmed by the observations of a PAS. No PAS was formed before it, and for this reason we cannot say anything about the mode of the flow there. The value of ΔT, at which the frequency drop occurs, depends on T out . The higher the temperature at the external chamber’s wall the larger ΔT of the drop.

To identify changes in the system’s dynamics, not revealed by the frequency plots, a chaos analysis was performed.

Chaos analysis

Several approaches to quantify the degree of ”noisiness” of a signal have been proposed. For the problem of hydrothermal instability in a liquid bridge, Shevtsova et al. (Shevtsova et al. 2003) and Melnikov et al. (Melnikov et al. 2004; 2005) have successfully applied the Shannon concept of entropy to the time series of temperature.

In the present paper, in order to apply nonlinear analysis to the experimental data, we use a different method based on the Takens embedding theorem (Takens 1981) to transform the time-series, recorded for temperature, into a pseudo-phase space. After the reconstruction, the level of the deterministic dynamics (order of chaos) of the system is evaluated. We employ the translation error E trans to characterize the non-linearity of the flow. We adopted the approach of Wayland et al. (Wayland et al. 1993) to calculate E trans . First, an experimental attractor should be constructed from the given experimental time series (s(t 1), s(t 2), ..., s(t N )). The attractor is a sequence of vectors x(t i ) defined as:

$$x(t_{i}) = (s(t_{i}), s(t_{i} + \tau), ..., s(t_{i} + (D - 1) \tau)), \ i = 1, ..., N - (D - 1) \tau, $$

where the time lag τ and the embedding dimension D are to be found. The translation error is calculated as

$$ E_{trans} = {1 \over k + 1} \sum\limits_{i=0}^{k} {| v_{i} - <v>|^{2} \over | <v>|^{2}}, \ <v>= {1 \over k + 1} \sum\limits_{i=0}^{k} v_{i}, $$
(1)

where v i = x(t i + τ)−x(t i ) is the translation vector, and |v| denotes the Euclidean length of the vector v. k is the number of the neighboring points. For the present analysis, k = 4.

The higher the stochasticity of the system, the larger the translation error. Generally, its value for the stochastic (random) data is close to 1, whereas that of the deterministic data (a limit cycle) is close to 0. Values of E trans in the range between 0 and 0.1 correspond to deterministic time series, range between 0.1 and 0.5 - to the chronological noise. The translation error represents the colored noise when its value reaches 0.5 or more.

We use the method proposed by Cao (Cao 1997) to estimate the dimension D of the embedded space. We do not supply further details of the algorithm of the calculation of E trans , but only show the results of its implementation to the experimentally recorded time-series.

Many experiments have been processed in order to obtain the dimension D. In the majority of cases, the minimum embedding dimension is equal to 6 or 7, except a small amount of experiments were its value reached 9.

Figure 6 summarizes the results of the chaos analysis performed for three volumes when T out = 25 °C. The insertions show the corresponding phase portraits of the system in the pseudo-phase space (T(t), T(t+τ), T(t+2τ)). It is only in the most slender of the three liquid bridge that E trans exceeds 0.1 (triangles in Fig. 6). The point, where the translation error sharply decreases again, coincides with the mode change observed in Fig. 5a. Therefore, bifurcation of another spatial mode of the flow is preceded by a generation of a spectral noise. This is seen in Fig. 7 presenting the temperature oscillations and the corresponding power spectrum. The oscillations are irregular with a quite noisy spectrum.

Fig. 6
figure 6

Translation error as a function of temperature difference calculated for the temperature oscillations in liquid bridge of three volume ratios: Vr = 0.92 (triangles), 0.98 (squares) and 1.05 (circles). There are two regions, delimited by E trans . Bellow approximately 0.01 the oscillations are periodic, above approximately 0.1 the oscillations are aperiodic. At the intermediate values of the translation error they are characterized by a spectrum with several commensurate frequencies. The insertions are the phase portraits of the system characteristic for the corresponding regimes

Full size image

In the liquid bridges of the higher volume ratios, no spectral noise was recorded. The small peak of E trans in case of Vr = 1.05 between ΔT = 9 and 9.5K (circles in Fig. 6) is rather insignificant, although the trajectory of the system in the pseudo-phase space becomes more complicated (see the insertions in Fig. 6).

Fourier analysis made for the temperature oscillations within this range of ΔT explains what happens there. Figure 8 shows the temperature oscillations together with the corresponding power spectrum of the signal for the ”fat” liquid bridge at ΔT = 8.85K. In the parameters space, where the translation error grows, a second frequency appears. The two frequencies are commensurate, and it results in characteristic ”beatings”.

Fig. 7
figure 7

Temperature time-series (a) and the corresponding power spectrum (b) for Vr = 0.92 at ΔT = 8.80 °C corresponding to upper insert in Fig. 6 characterized by E trans > 0.1. The spectrum is noisy

Full size image

Summarizing the results in Fig. 6, it turns out that the shape of the liquid-gas interface has a significant impact of the trajectory of the system in the phase space. The used quantity E trans characterizes the quality of the traveling wave. This parameter plays an important role in the non-linear dynamics, e.g. for determination of the parameters space where PAS exits.

Fig. 8
figure 8

Temperature time-series (a) and the corresponding power spectrum (b) for Vr = 1.05 at ΔT = 8.85°C corresponding to lower insert in Fig. 6 characterized by E trans ∈(0.01, 0.1). The spectrum is composed of two commensurate frequencies

Full size image

Model

Governing equations and boundary conditions

To model the experiment, we consider a flow in a cylindrical liquid bridge, i.e. Vr = 1.0, of radius R = 3.0mm and of d = 2.58mm in height (thus the aspect ratio is d/R = 0.86). The interface is assumes cylindrical and straight, as is sketched in Fig. 9. The temperatures T h and T c (T h > T c ) are prescribed at the upper and lower walls respectively, yielding the temperature difference ΔT = T h −T c . Density ρ, surface tension σ, and kinematic viscosity ν of the liquid are taken as linear functions of the temperature:

$$\begin{array}{@{}rcl@{}} && \rho(T)=\rho_{0}-\rho_{0} \beta (T - T_{0}), \hskip 0.5cm \beta= - {1 \over \rho_{0}} {\partial \rho \over \partial T} \ , \\ && \sigma (T) = \sigma_{0} - \sigma_{T} (T - T_{0}), \hskip 0.5cm \sigma_{T} = - {\partial \sigma \over \partial T} \ , \\ && \nu (T) = \nu_{0} + \nu_{T} (T - T_{0}), \hskip 0.5cm \nu_{T} = {\partial \nu \over \partial T} \ . \end{array} $$

where subscript 0 indicates the quantities at the reference temperature T 0 = T c .

Fig. 9
figure 9

Liquid bridge

Full size image

The governing dimensionless Navier-Stokes, continuity and energy equations for an incompressible fluid are:

$$\begin{array}{@{}rcl@{}} && \frac{\partial \textbf{V}}{\partial t} + (\textbf{V}\cdot \nabla) \textbf{V} = - \nabla P + R_{\nu} \cdot 2\textbf{S} \times \nabla {\Theta}\\ &&{\kern6.35pc}+ (1 + R_{\nu} {\Theta} ) \nabla^{2} \textbf{V}+ \vec e_{z} \, Gr \, {\Theta} , \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} && \nabla \cdot \textbf{V} \hskip 0.1cm = \hskip 0.1cm 0, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} && \frac{\partial {\Theta} }{\partial t} + \textbf{V} \cdot \nabla {\Theta} \hskip 0.1cm = \hskip 0.1cm \frac{1}{Pr} \nabla^{2} {\Theta}, \end{array} $$
(4)

where V = (V r , V φ , V z ) is velocity, Θ=(T−T 0)/ΔT is temperature and t is time, S is the strain rate tensor. The scales for the radial and axial coordinates are the radius R and the height d of the liquid column, respectively. The scales for time, velocity and pressure are t ch = d 2/ν 0, V ch = ν 0/d and \(P_{ch} = \rho _{0} V_{ch}^{2}\). ∇ is the nabla operator.

The rigid walls are inert, impermeable, no-slip boundaries held at constant temperatures:

V(r, φ, z = 0, t)= V(r, φ, z = 1, t)=0 and Θ(r, φ, z = 0, t)=0, Θ(r, φ, z = 1, t)=1.

The interface is a stress-free non-insulated surface:

$$\begin{array}{@{}rcl@{}} V_{r} = 0, \quad \!2[ 1 \, +\, R_{\nu} {\Theta} ] \mathbf{S} \cdot \mathbf{e_{r}} \, +\, Re \left(\mathbf{e_{z}} \partial_{z} \, +\, \mathbf{e_{\phi}} \frac{1}{r} \partial_{\phi} \right) {\Theta} = 0, \\ \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \partial {\Theta} / \partial r = - Bi ({\Theta} - {\Theta}_{\textit{amb}}) \end{array} $$
(6)

where Bi is the Biot number and Θ amb is the dimensionless temperature of the gas near the interface defined as Θ amb = (T amb −T 0)/ΔT. As seen from Eq. 6, the heat exchange between the liquid and the gas is controlled by both the Biot number and the temperature profile in the gas. The Biot number is a dimensionless parameter whose value depends not only on the properties of the media but also on features of the flow (Shevtsova et al. 2003).

There are the following non-dimensional parameters. Three of them, the Grashof number, Gr, the ”thermocapillary” Reynolds number, Re, and the viscosity contrast, R ν , are proportional to ΔT:

$$ Gr = \frac{g\beta{\Delta} T d^{3}}{\nu_{0}^{2}}, \hskip 0.3cm Re = \frac{\sigma_{T} {\Delta} T d}{ \rho_{0} {\nu_{0}^{2}}}, \hskip 0.3cm R_{\nu} = \frac{\nu_{T} {\Delta} T}{\nu_{0}}, $$

The others are the Prandtl and Biot numbers and the aspect ratio

$$ Pr = \frac{\nu_{0}}{k}, \hskip 0.3cm Bi = \frac{h R}{\lambda}, \hskip 0.3cm {\Gamma}=\frac{d}{R}. $$

where k, β are thermal diffusivity, thermal expansion coefficient, λ is the thermal conductivity of the liquid. h is the convection heat transfer coefficient and g is the Earth gravity. Properties of n-decane are given in Table 1.

Table 1 Physical properties of n-decane at working temperature
Full size table

We adopt the numerical approach of (Shevtsova et al. 2001) on a staggered mesh, which is non-uniform both in the radial and axial directions. The computational grid is filling the physical domain with 100 intervals in the radial and in the axial directions and with 32 intervals in the azimuthal direction. Description of the numerical method and code validation could be found in (Melnikov et al. 2004).

Heat transfer model

There are three major mechanisms involved in transport of heat through the interface - convective, radiative and evaporative. They will have an impact on the resulting Biot number. In the following analysis, neither thermal radiation nor evaporation are considered. The value of Bi is estimated using the expression of (Kays and Crawford 1980) for a forced laminar convection. The ambient gas is entrained by the Marangoni flow along the interface, and the absolute value of the velocity of the fluid at the interface averaged over the surface is chosen as the characteristic velocity of the gas phase:

$$V_{i} = {1 \over 2 \pi} \left| \int_{0}^{2 \pi} {\int_{0}^{1}} \, V_{z} (r = 1) d \varphi \, d z \right|.$$

The average heat transfer coefficient over the length d in a forced laminar convection is estimated as:

$$ h = 0.664 \ Re_{\textit{air}}^{1/2} \ Pr_{\textit{air}}^{1/3} \ {\lambda_{\textit{air}} \over d}, $$
(7)

where Re air = V i d/ν air is the Reynolds number in gas phase, the Prandtl number of air is Pr air =0.713.

The calculations performed for the thermally insulated interface at the onset of instability resulted in V i ≈70, thus yielding Re air ≈5.3. Setting Re air to this small value ensures the laminar regime of convection in air. Finally, using Equation (7) one obtains h = 13.6 and Bi = 0.31. Accounting for the disregarded mechanisms of heat transfer will inevitably increase the value of Bi. Without being able to supply the real value of the Biot number in the experiment, the modeling was performed for a vast region of Bi ∈ [0, 1].

Results of computer modeling

To model the experiments, along with the thermally insulated interface, different profiles of T amb were considered:

  • 1 - T amb = const and varied between 10 and 40 °C;

  • 2 - linear T amb = T c + ΔTz (°C), T c = 20 ° C.

As we consider the liquid bridge of Vr = 1, the results of the calculations are compared with the experimental ones for the closest liquid volume, i.e. for Vr = 0.98. The critical temperature difference was calculated with an accuracy of 0.1 °C.

The computer modeling brought both discoveries and questions. A comparison between the CFD simulations and the experiments for the critical conditions is shown in Fig. 10. Dashed and solid lines represent the stability curves for Bi = 0.25 and 0.5 (shown by dashed and solid lines in Fig. 10), while the experimental data are plotted by diamond symbols. The results reveal the noticeable reduction of the stability of the two-dimensional flow with the increase of ambient temperature in air. At the same time, imposing the linear temperature profile in the gas phase results in a slight increase of the critical temperature difference with respect to that at Bi = 0 (compare dotted and dashed-dotted curves in Fig. 10) that is similar to the experimental observations.

Fig. 10
figure 10

Critical temperature difference obtained via computer modeling of flow in liquid bridge of Γ=0.86 with Bi = 0.25 (black dashed line) and 0.5 (black solid line) at different thermal conditions in the ambient gas and compared to the experimentally measured values (red diamond symbols) for liquid bridge of volume ratio 0.98. Blue dotted and green dashed-dotted lines correspond to linear temperature profile in the gas T c + ΔTz and adiabatic interface (Bi = 0), correspondingly. For the modeling, T out is equal to the ambient temperature in the gas phase T amb

Full size image

As shown in Fig. 11, the flow is continuously destabilizing with the increase of T amb (while keeping the value of Bi constant). Varying values of Bi between 0 and 1 for the linear profile in the gas phase and for T amb ≤ 25 °C (room temperature) reveales a stabilization of the thermocapillary flow. When the gas is cold, increasing the rate of the heat transfer (value of Bi) results in a very strong stabilization of the flow: ΔT cr =9.6 and 14.4° C for Bi = 0.5 and 1, respectively.

Fig. 11
figure 11

Critical temperature difference obtained via computer modeling of flow in liquid bridge of Γ=0.86 at various thermal conditions in the ambient gas: linear profile T c + ΔTz (blue dotted line), 10 °C (red solid line), 25 °C (black dashed line) and 40 °C (green dashed-dotted line). The lines represent the fits through the calculated points at Bi = 0, 0.25, 0.5 and 1. Only a part of the solid curve is shown due to the very strong growth of the critical Reynolds number in case of the strong cooling at T amb = 10 °C

Full size image

The stability diagram for T amb = 40 °C is different from those for the other cases (see Fig. 11). When the air is hot, the critical temperature difference starts decreasing, and is growing after reaching a minimum at about Bi = 0.5. The stability curve for T amb = 40 °C has a small peak at about Bi = 0.35. It is a consequence of a change of the critical wave number m of the flow, which will be explained below. The value of ΔT cr at Bi = 0.5 is very close to the one found experimentally.

One may argue that the critical temperature difference for Bi = 0 (shown as dashed-dotted line in Fig. 10) is not far from the experimental one either, and thus the heat flux was negligible in the experiments. However, agreement with the experimental observations will require the similar mode m = 2 of the supercritical flow, and this is where all the simulated cases, except the one with T amb = 40 °C, fail (see a summary of the computational results in Table 2).

Table 2 Critical mode m of the flow in case of insulated interface and for Bi ∈ [0, 1] under different surrounding conditions at the interface. T c =20° C
Full size table

Figure 12 shows snapshots of disturbances (perturbations) of temperature field made for two weakly supercritical cases at ΔT = 8 °C: (a) thermally insulated interface, (b) interface surrounded by hot ambient air at T amb = 40 °C when Bi = 0.5. The disturbances are defined as deviations of the three-dimensional field from the azimuthally averaged solution (its axisymmetric part). They are calculated and visualized to determine the azimuthal wave number (see e.g. (Shevtsova et al. 2001)):

$$ f^{*} \, =\, f (r, \varphi, z, t) \, -\, \bar{f} (r, z, t), \! \quad \bar{f} \, =\, \frac{1}{2 \pi}\! \int_{0}^{2 \pi}\! f\! (r, \varphi, z, t) d \varphi, $$
(8)

f is any physical variable, e.g. temperature or velocity. f ∗ does not show the complete perturbations but only their three-dimensional parts.

Fig. 12
figure 12

(Color online) Snapshots of deviations of temperature field Θ∗ from the azimuthally averaged solution in supercritical regime near the critical point: a insulated interface, i.e. Bi = 0; b T amb = 40 ° C and Bi = 0.5. Mid-gray and darkest gray (red and blue) indicate hot and cold regions, respectively

Full size image

There are three pairs of hot-cold patterns visible at the cross section and at the interface in the case of thermally insulated free surface, whereas for T amb = 40 °C there are two pairs, corresponding to m = 2 - the mode that was observed experimentally (see Fig. 3c). The experimental mode was confirmed only when T amb = 40 °C and Bi > 0.35 (as shown in Table 2). It is for this reason that the linear temperature profile in gas is also ruled out.

No mode change was observed between Bi = 0 and 1 for the considered cases, except at T amb = 40 °C as is mentioned above. It is always 3 for the linear profile, cold gas and room temperature. In case of the hot environment, the mode is 2 between Bi = 0.35 and 1. This is another indication on that the temperature in the ambient gas phase in the experimental chamber was high and rather homogeneous. Changing T out had no effect on the structure of the thermocapillary flow in the experiments. The homogeneity of the gas temperature was probably due to the Marangoni flow entraining the hot air downwards.

Discussion

As was shown above, there is a number of disagreements between the model and the experiment. A question arises whether some of them can be neglected or should be worked on to be reduced. For example, as can be seen in Fig. 10, the experimental and theoretical stability diagrams have different slopes. Or, while the mode m = 2 was observed in the experiments at any considered T out , the calculations confirmed the experimental findings only at T amb = 40 °C and Bi > 0.35, and they revealed m = 3 mode for the other cases.

This discussion merely serves to emphasize that discrepancies between the two sets of data rule out the model. It should rather be stated that whenever a disagreement occurs between model and experiment, its possible reasons in both the experiment, the model, or both must be considered.

There are a few reasons of the divergences between the results of the computer modeling and the experimental data. We have to recall that a number of features of the problem were neglected in the ad hoc model. Among them are the deformations of the interface, which are always non-zero on ground, and the transport processes taking place in ambient gas. Our model is one-phase laminar flow of incompressible fluid, and the heat flux through the interface is calculated by Eq. 6 under the assumptions of T amb = T out , an idealized temperature profile in gas and the Biot number to be independent of the coordinates. These are, however, straightforward and strong simplifications. In reality, it is already a separate problem of how to measure the distribution of the heat flux and which locations should be chosen to measure the temperature of gas phase to be considered as T amb .

The shape of the interface, related to the liquid volume, affects the critical conditions as shown in Fig. 2. The maximal impact of Vr on T cr , however, does not exceed 6 % over the range of Vr = 0.75−1.05, whereas the calculated values of the critical temperature difference are larger than the corresponding experimental ones (for T out = 10 °C the difference attains its maximum of 37 %). Therefore, it seems most likely that the discrepancy originates either in the ambient temperature distribution in the gas phase unknown from the experiment or in the value of the Biot number considered as uniform, i.e. constant along the entire interface, and independent of the external temperature T out .

It is possible that changing the temperature at the external wall of the experimental chamber did not change much the gas temperature near the interface due to a number of reasons. It could be, e.g., because of the boundary being far away from the liquid bridge (the distance between the wall and the interface is 33 times the radius of the bridge), and/or due to the features of the design of the experimental setup visible on the right picture of Fig. 1 (it is discussed below).

Shevtsova et al. (2005) and Tiwari and Nishino (2010) experimentally measured temperature distribution in air near the interface for thermocapillary convection in liquid bridges of aspect ratios of 1 and 1.2 made of 5 and 10 cSt silicone oils. It was shown there is a thermal boundary layer in air near the free-surface with a large thermal gradient, and the ambient temperature reached a more or less constant value at approximately 6−7 times of the radius of the liquid bridge away from the interface. Therefore, the obtained experimental data were processed and are shown in Fig. 10 as the circle symbols (we call it processed experiment). In frame of this approach, T amb was assumed constant and recalculated at the point located 7R = 21mm away from the free surface. The temperature at the free surface is estimated as T s = T c + 0.7ΔT cr (Shevtsova et al. 2003), whereas the temperature in the gas beyond the boundary layer is assumed to be changing linearly between the free surface and the external wall. The latter is 97 mm away from the interface. Hence,

$$T_{\textit{amb}} = T_{s} + (T_{\textit{out}} - T_{s}) {21 (\text{mm}) \over 97 (\text{mm})}.$$

Doing so noticeably contracts the experimental points in Fig. 10 and increases the growth rate of the critical temperature difference against T out .

The design of the setup, of course, affects the temperature inside the chamber. The cold and hot boundaries spread beyond the edges of the rods. Moreover, the liquid bridge is confined between two horizontal disks of a large radius. The present configuration makes the experimental conditions similar to those studied in (Tiwari and Nishino 2006; 2010) with presence of two horizontal partition boundaries, which were shown to be capable of affecting the critical conditions of the flow.

As for the value of the Biot number, the parameter quantifying the rate of the heat exchange, variations of T out will affect the gas flow induced by buoyancy, which, in turn, will modify the convection heat transfer coefficient h (Kays and Crawford 1980; Bejan and Kraus 2003) (it is proportional to \(V_{\textit {air}}^{0.5}\) and |T out −T s |0.25, where V air is the characteristic velocity of air, which at the same time is entrained by the fluid flow and driven by buoyancy due to the horizontal temperature gradient in the chamber).

Conclusions

The present work reports on results of both experimental and theoretical study of the influence of heat transfer on the stability of a flow, caused by a combined effect of thermocapillary forces and buoyancy, in a liquid bridge differentially heated at the opposite boundaries.

We have measured the critical temperature difference in liquid bridges of different volume ratios varied between 0.7 and 1.05. One of the findings for the considered system (liquid bridge of n-decane with Pr = 13.5) is that the liquid volume, i.e. the curvature of the interface, has a weak effect on the critical parameters. The highest value of the imposed temperature difference, at which the onset of temperature oscillations occurs, was measured in a liquid bridge of volume ratio of 0.9. It is only about 10 % and 6 % larger than those obtained at 0.7 and 1.05 volume ratios respectively.

Volume ratio, however, is capable in changing the dynamics of the flow. In a thin liquid bridge of volume ratio 0.92, we have observed non-periodic oscillations within an extensive range of ΔT, whereas the oscillations were regular and periodic in a fat liquid bridge.

The mode of the supercritical flow was found via observing particles accumulation structures in the flow, which was forming in the range of the volume ratios between 0.87 and 1.05. Over this range, the mode was always 2.

It was found that changing the temperature at the rigid wall of the experimental chamber, which was about 10 mm away from the liquid-gas interface, results in stabilization of the flow and the critical temperature difference slightly increases.

To support the experimental observations, a set of three-dimensional computer modeling was performed. It is crucial that the heat flux through the interface be properly accounted for in order to reproduce the experimental results. The heat transfer was modeled by the Newton’s law. It was shown that the ambient temperature inside the chamber had to be high and the Biot number greater than 0.35 to have a good agreement with the experimental data.

It was obtained that the spatial structure of the supercritical flow is quite susceptible to change of the experimental conditions in the surrounding air. Increasing temperature of surrounding gas results in changing the wave number. It does not occur, however, when the Biot number is small.

The calculations revealed that increasing the rate of the heat transfer through the interface (value of the Biot number) stabilizes the thermocapillary flow when the interface is cooled. Increasing the ambient temperature in the gas phase has an ambiguous impact on the stability of the flow. The stability diagram has a pronounced minimum at about Bi = 0.5.

The performed modeling has shown how important it is to consider the heat transfer through the interface in order to reproduce the experimental observations. The presented analysis clearly demonstrates that neglecting heat transfer through the liquid-gas interface may lead to inconsistent results.