1 Introduction

As a result of the recent financial crisis the relevance of the Efficient Market Hypothesis (EMH) has been questioned, on the grounds that it overlooks important issues such as information asymmetry, non-rational behaviour, moral hazard and adverse selection. An alternative paradigm is the so-called Fractal Market Hypothesis (FMH – see Mandelbrot, 1972, and Peters, 1994), according to which stock prices are non-linear and the normal distribution (a basic assumption of the EMH) cannot be used to explain their movements given the presence of “fat tails”. Within this framework one of the key characteristics of many financial time series is their degree of persistence, namely time dependence which might imply the presence of both short- and long-memory properties. However, this strand of the literature has produced mixed evidence. Further, only limited research has examined whether financial crises amount to a regime shift affecting the degree of persistence of stock markets.

This paper uses two different approaches (i.e. R/S analysis and fractional integration) to estimate persistence in the Ukrainian stock market. In particular, we show that its degree was not the same at different stages of the financial crisis of 2007–2009. We also show that data smoothing does not improve the R/S method. Our findings have important implications for trading strategies and macro-prudential policies.

According to the EMH, it should not be possible to make systematic profits based on historical stock prices and therefore prices should follow a random walk process, which implies an order of integration of 1 and uncorrelated disturbances or in case of R/S analysis that the Hurst exponent should be equal to 0.5. In this paper we show that the degree of integration of Ukrainian stock market prices is significantly higher than 1 in both the level and the volatility series, which is a clear indication of inefficiency in the market. We also show that the degree of persistence, measured with the Hurst exponent, is unstable and in general much higher than 0.5. This result is robust to using different methods and sample periods.

The layout of the paper is the following. Section 2 contains a brief literature review. Section 3 describes the data and outlines the Hurst exponent method as well as the I (d) techniques used for the analysis. Section 4 presents the empirical results. Section 5 provides some concluding remarks.

2 Literature review

Mandelbrot (1972) was the first to provide evidence of persistence and long memory in financial markets. Greene and Fielitz (1977) found long-term dependence in stock prices in the NY stock exchange. Booth et al. (1982) also reported that some financial series have long memory. Helms et al. (1984) found it for the price of futures (see also Peters, 1991, 1994).

Lo (1991) showed that often evidence of long memory might in fact reflect short-memory components that have been overlooked (see also Fung and Lo, 1993; Cheung and Lai, 1993; Crato, 1994). Long memory in stock markets was reported by Greene and Fielitz (1977), Peters (1991, 1994), Onali and Goddard (2011), Alvo et al. (2011), Lento (2013), Niere (2013), while the opposite was reported by Lo (1991), Jacobsen (1995), Berg and Lyhagen (1998), Crato and Ray (2000), Batten et al. (2005) and Serletis and Rosenberg (2007)). Some other authors have claimed that the degree of persistence changes over time (Corazza and Malliaris (2002), Glenn (2007) and others).

This paper contributes to the above literature by examining the long memory property of the Ukrainian stock market by investigating its order of integration using non-parametric, as well as semi-parametric and parametric methods.

In the case of the emerging economies there is clearer evidence of long memory and persistence in stock markets. Some examples are the studies by Niere (2013), who analysed 6 Asian countries (Indonesia, Malaysia, Philippines, Singapore, Thailand, Vietnam); Matteo et al. (2005), who examined the cases of Russia, Indonesia and Peru, Zunino et al. (2009), who focused on Latin America, and Anoruo and Gil-Alana (2011), who find evidence of long memory in both stock prices and their volatility in a group of African countries, Finally, Gil-Alana and Yaya (2014) examine persistence and asymmetric volatility in the Nigerian bull and bear stock markets.

Los (2003) suggested using the Hurst exponent, created by the hydrologist Hurst (1951), for measuring persistence. Cajueiro and Tabak (2005) showed that the higher the Hurst exponent is, the lower the efficiency of the market is. Grech and Mazur (2004) and Grech and Pamula (2008) investigated the connection between the Hurst exponent and market crashes. R/S analysis and fractional integration are the most popular methods for measuring persistence but they have both produced inconclusive results.

3 Data and methodology

The R/S method was originally applied by Hurst (1951) in hydrological research and improved by Mandelbrot (1972), Peters (1991, 1994) and others analysing the fractal nature of financial markets. Compared with other approaches it is relatively simple and suitable for programming as well as visual interpretation.

For each sub-period range R (the difference between the maximum and minimum index within the sub-period), the standard deviation S and their average ratio are calculated. The length of the sub-period is increased and the calculation repeated until the size of the sub-period is equal to that of the original series. As a result, each sub-period is determined by the average value of R/S. The least square method is applied to these values and a regression is run, obtaining an estimate of the angle of the regression line. This estimate is a measure of the Hurst exponent, which is an indicator of market persistence. More details are provided below.

  1. 1.

    We start with a time series of length M and transform it into one of length N = M - 1 using logs and converting stock prices into stock returns:

    $$ {N}_i= \log \left(\frac{Y_{t+1}}{Y_t}\right),\kern0.72em t=1,2,3,\dots \kern0.24em \left(M-1\right) $$
    (1)
  2. 2.

    We divide this period into contiguous A sub-periods with length n, so that A n = N, then we identify each sub-period as I a , given the fact that a = 1, 2, 3. . ., A. Each element I a is represented as N k with k = 1, 2, 3. . ., N. For each I a with length n the average e a is defined as:

    $$ {e}_a=\frac{1}{n}\;{\displaystyle \sum_{k=1}^n{N}_{k,a},\kern0.6em k=1,2,3,\dots N},\kern0.6em a=1,2,3\dots, A $$
    (2)
  3. 3.

    Accumulated deviations X k,a from the average e a for each sub-period I a are defined as

    $$ {X}_{k,a}={\displaystyle \sum_{i=1}^k\Big({N}_{i,a}}-{e}_a\Big) $$
    (3)

    The range is defined as the maximum index X k,a minus the minimum X k,a , within each sub-period (I a ):

    $$ {R}_{Ia}= \max \left({X}_{k,a}\right)- \min \left({X}_{k,a}\right),\kern0.6em 1\le k\le \kern0.36em n. $$
    (4)
  4. 4.

    The standard deviation S Ia is calculated for each sub-period I a

    $$ {S}_{Ia}=\kern0.48em {\left(\left(\frac{1}{n}\right){\displaystyle \sum_{k=1}^n{\left({N}_{k,a}-{e}_a\right)}^2}\right)}^{0,5} $$
    (5)
  5. 5.

    Each range R Ia is normalized by dividing by the corresponding S Ia . Therefore, the re-normalized scale during each sub-period I a is R Ia /S Ia . In the step 2 above, we obtained adjacent sub-periods of length n. Thus, the average R/S for length n is defined as:

    $$ {\left(R/S\right)}_n=\kern0.36em \left(1/A\right){\displaystyle \sum_{i=1}^A\left({R}_{Ia}/{S}_{Ia}\right)} $$
    (6)
  6. 6.

    The length n is increased to the next higher level, (M - 1)/n, and must be an integer number. In this case, we use n-indexes that include the initial and ending points of the time series, and Steps 1–6 are repeated until n = (M - 1)/2.

  7. 7.

    Now we can use least square to estimate the equation log (R/S) = log (c) + Hlog (n). The angle of the regression line is an estimate of the Hurst exponent H. This can be defined over the interval [0, 1], and is calculated within the boundaries specified in Table 1.

    Table 1 Hurst exponent interval characteristics
    Full size table

On the basis of the values of the Hurst exponent, the data can be classified as follows:

  • 0 ≤ H < 0.5 – the data are fractal, the EMH is confirmed, the distribution has fat tails, the series are antipersistent, returns are negatively correlated, there is pink noise with frequent changes in the direction of price movements, trading in the market is riskier for individual participants;

  • H = 0.5 – the data are random, the EMH is confirmed, asset prices follow a random Brownian motion (Wiener process), the series are normally distributed, returns are uncorrelated (no memory in the series), they are a white noise, traders cannot «beat» the market using any trading strategy

  • 0.5 < H ≤ 1 – the data are fractal, the EMH is confirmed, the distribution has fat tails, the series are persistent, returns are positively correlated, there is black noise and a trend in the market.

An important step in the R/S analysis is the verification of the results by calculating the Hurst exponent for randomly mixed data. In theory, these should be a random time series with a Нurst exponent equal to 0.5. In this paper, we will carry out a number of additional checks, including:

  • Generation of random data;

  • Generation of an artificial trend (persistent series);

  • Generation of an artificial anti-persistent series.

In order to analyse persistence, in addition to the Hurst exponent and the R/S analysis we also estimate parametric/semiparametric models based on fractional integration or I (d) models of the form:

$$ {\left(1\kern0.36em -L\right)}^d{x}_t\kern0.48em =\kern0.36em {u}_t, \kern0.6em t\kern0.48em =\kern0.48em 0, \pm 1, \kern0.24em \dots, $$
(7)

where d can be any real value, L is the lag-operator (Lxt = xt−1) and ut is I (0), defined for our purposes as a covariance stationary process with a spectral density function that is positive and finite at the zero frequency. Note that H and d are related through the equality H = d – 0.5.

In the semiparametric model no specification is assumed for ut, while the parametric one is fully specified. For the former, the most commonly employed specification is based on the log-periodogram (see Geweke and Porter-Hudak 1983). This method was later extended and improved by many authors including Künsch (1986), Robinson (1995a), Hurvich and Ray (1995), Velasco (1999a, 2000) and Shimotsu and Phillips (2002). In this paper, however, we will employ another semiparametric method: it is essentially a local ‘Whittle estimator’ in the frequency domain, which uses a band of frequencies that degenerates to zero. The estimator is implicitly defined by:

$$ \widehat{d}=\kern0.36em \arg \kern0.24em \min {}_d\kern0.36em \left( \log \kern0.36em \overline{C(d)}\kern0.48em -\kern0.36em 2\kern0.24em d\kern0.36em \frac{1}{m}{\displaystyle \sum_{s=1}^m \log \kern0.36em {\lambda}_s}\right)\kern0.24em , $$
(8)
$$ \overline{C(d)\;}\kern0.36em =\kern0.48em \frac{1}{m}\kern0.36em {\displaystyle \sum_{s=1}^mI\left({\lambda}_{\;s}\right)\kern0.24em {\lambda}_{\;s}^{\kern0.24em 2\;d}},\kern2.04em {\lambda}_s=\frac{2\kern0.24em \pi\;s}{T}, \kern2.16em \frac{m}{T}\to 0, $$

where m is a bandwidth parameter, and I (λs) is the periodogram of the raw time series, xt, given by:

$$ I\left({\lambda}_s\right)\kern0.36em =\kern0.36em \frac{1}{2\;\pi\;T\;}\;{\left|{\displaystyle \sum_{t=1}^T{x}_t\;{e}^{i\;{\lambda}_st}}\right|}^2, $$

and d ∈ (−0.5, 0.5). Under finiteness of the fourth moment and other mild conditions, Robinson (1995b) proved that.

$$ \sqrt{m\;}\;\left(\widehat{d}\kern0.36em -\kern0.36em {d}_o\right)\kern0.48em {\to}_d\kern0.48em N\left(0,\kern0.24em 1/4\right)\kern0.96em as\kern0.36em T\to \kern0.36em \infty, $$

where do is the true value of d. This estimator is robust to a certain degree of conditional heteroscedasticity and is more efficient than other more recent semiparametric competitors. Other recent refinements of this procedure can be found in Velasco (1999b), Velasco and Robinson (2000), Phillips and Shimotsu (2004, 2005) and Abadir et al. (2007).

Estimating d parametrically along with the other model parameters can be done in the frequency domain or in the time domain. In the former, Sowell (1992) analysed the exact maximum likelihood estimator of the parameters of the ARFIMA model, using a recursive procedure that allows a quick evaluation of the likelihood function. Other parametric methods for estimating d based on the frequency domain were proposed, among others, by Fox and Taqqu (1986) and Dahlhaus (1989) (see also Robinson, 1994 and Lobato and Velasco, 2007 for Wald and LM parametric tests based on the Whittle function).

Two of the main Ukrainian stock market indexes, namely the PFTS and UX indices respectively, are used for the empirical analysis. The sample period goes from 2001 to 2013 for PFTS and from 2008 to 2013 for UX. For most of the calculations we used the UX index, which is most frequently used nowadays to analyse the Ukrainian stock market, since the UX series, only starting in 2008, is relatively short. The different periods considered include that of the inflation “bubble” and market overheating, which created the preconditions for the crisis in 2007, the peak of the crisis at the end of 2008 and in the early part of 2009, and its attenuation towards the end of 2009 and in 2010 (Fig. 1).

Fig. 1
figure 1

Periodisation of financial crisis 2007–2009

Full size image

The peak of the crisis is defined on the basis of the dynamics of the CBOE Volatility Index (VIX), which is calculated from 1993 using the S & P 500 prices of options in the Chicago Stock Exchange, one of the largest organized trading platforms. It should be noticed that peaks of market volatility at 89.53 and 81.48 were observed during the announcement of the bankruptcy of Lehman Brothers and AIG in September - October 2008 with an overall increase in volatility in the second half of 2008. At the same time the decision to restructure the AIG debt led to better investment expectations of market participants and to a fall of the VIX index to 39.33 (Fig. 2).

Fig. 2
figure 2

Dynamics of the VIX Index in 2007–2010

Full size image

Also important is the choice of the interval of the fluctuations to analyse, i.e. 5, 30, 60 min, one day, 1 week, 1 month. We decided to focus on the 1-day interval, because higher frequency data generates significant fluctuations of fractals, and lower frequency data lose their analytical potential.

We incorporate data smoothing into the R/S analysis and test the following hypothesis: data smoothing (filtration) lowers the level of “noise” in the data and reduces the influence of abnormal returns; smoothing makes the data closer to the real state of the market.

We use the following simple methods:

  1. 1

    Smoothing with moving averages (simple moving average (SMA) and weighted moving average (WMA) with periods 2 and 5);

  2. 2

    Smoothing with the Irwin criterion.

The analysis is conducted for the Ukrainian stock market index (UX) over the period 2008–2013. Overall we analysed 1300 daily returns. As a control group we chose daily closes of UX (unfiltered data) and a set of randomly generated data. The estimates of the Hurst exponent for the mixed data sets are used as a criterion for the adequacy of the results.

The first stage is the visual analysis of both unfiltered and filtered data. The results are presented in Figs. 3, 4, 5, 6, 7 and 8. The behavior of the series does not change dramatically after filtering (smoothing), but the level of “noise” decreases. In terms of fractal theory, visual inspection reveals a decrease of the fractal dimension.

Fig. 3
figure 3

Visual interpretation of filtered and unfiltered UX data: SMA filtration

Full size image
Fig. 4
figure 4

Visual interpretation of filtered and unfiltered UX data: WMA filtration

Full size image
Fig. 5
figure 5

Visual interpretation of filtered and unfiltered UX data: Irwin filtration

Full size image
Fig. 6
figure 6

Visual interpretation of filtered and unfiltered randomly generated data: SMA filtration

Full size image
Fig. 7
figure 7

Visual interpretation of filtered and unfiltered randomly generated data: WMA filtration

Full size image
Fig. 8
figure 8

Visual interpretation of filtered and unfiltered randomly generated data: Irwin filtration

Full size image

To confirm that the properties of the time series are the same and we only neutralise the level of unnecessary “noise”, we filtered randomly generated data sets for which the fractal dimension should remain the same. However, visual inspection (see Figs. 6–8) shows that the fractal dimension of the randomly generated data set also changes after filtering.

To corroborate the visual analysis we calculate the Hurst exponent for each type of filter.

As can be seen from Table 2, filtering the data leads to over-estimating the Hurst exponent. The longer the averaging period (the bigger the level of filtering) the higher the Hurst exponent is, indicating dependency of the latter on the former.

Table 2 Hurst exponent estimation for different variants of data filtration
Full size table

The clearest sign of the inadequacy of the data filtering is the behaviour of the Hurst exponent calculated for the random variables: it should be close to 0.5 and constant, but in the presence of filtering it increases automatically and proportionally depending on the averaging period.

Irwin’s method also generates overestimates of the Hurst exponent and therefore is inappropriate as well. Overall, it appears that data smoothing artificially increases the Hurst exponent, and therefore further calculations will be based on the original data sets.

One more possible modification of the R/S analysis is the use of aliquant numbers of groups, i.e. computing the Hurst exponent for all possible groups. The results are presented in Table 3.

Table 3 Hurst exponent estimates with standard methodology (aliquot number of groups) and modified (aliquant number of groups) for different data sets
Full size table

Both the real financial data and the randomly generated ones suggest that the use of aliquant numbers of groups leads to overestimates of the Hurst exponent. Nevertheless, using them might be appropriate in the case of small data sets, but a correction of 0.03–0.05 should be made depending on the value of the Hurst exponent (the bigger it is the bigger the correction should be). Given these results, the standard methodology will be used below to estimate the Hurst exponent.

4 Empirical results

As a first stage of the analysis we estimate persistence of two Ukrainian stock market indices over the full sample (UX: 2008–2013, PFTS: 2001–2013). The results in Table 4 show that the Hurst exponent for both indexes is significantly higher than 0.5. (it is equal to 0.66), which is evidence of persistence and long memory. Therefore it appears that the Ukrainian stock market is inefficient and asset prices can be forecast, thereby gaining abnormal profits.

Table 4 Full-sample analysis of Ukrainian stock market persistence
Full size table

Next, we estimate persistence during the financial crisis. We checked different window sizes and found that 300 (close to one calendar year) is the most appropriate on the basis of the behaviour of the Hurst exponent: for narrower windows its volatility increases dramatically, whilst for wider ones it is almost constant, and therefore the dynamics are not apparent.

Having calculated the first value of the Hurst exponent (for example, that for the date 13.07.2007 corresponds to the period from 21.04.2005 till 13.07.2007), each of the following ones is obtained by shifting forward the “data window”. The chosen size of the shift is 10, which provides a sufficient number of estimates to analyse the behaviour of the Hurst exponent. Therefore the second value is calculated for 27.07.2006 and characterises the market over the period 10.05.2005 till 27.07.2006, and so on. As a result we obtain 170 control points (Hurst exponent estimates) for different sub-samples characterised by various degrees of persistence in the Ukrainian stock market over the period 2005–2013 (see Fig. 9).

Fig. 9
figure 9

Dynamics of Hurst exponent during 2003–2013 (calculated on PFTS data with “data window” = 300, shift = 10)

Full size image

Our results imply that the Ukrainian stock market is inefficient and persistent. Further, persistence is not constant over the whole sample, but increased during the crisis. Therefore, it is possible to devise trading strategies to beat the market and obtain abnormal profits For example, a high level of persistence suggests using trend-based trading strategies. Exploiting market anomalies can also generate speculative profits. The evidence concerning the changing degree of persistence can also be used to create an early warning system for regulators for the purpose of macro-prudential supervision.

Finally, the volatility of the Hurst exponent during the crisis can be interpreted in terms of investors’ sentiment, namely as an indication of less optimistic expectations and increasing uncertainty about future developments.

4.1 Semiparametric/parametric methods for the UX index

Next we focus on the UX index. Fig. 10 displays four time series plots for prices and returns, as well as the squared and absolute returns. Figs. 11 and 12 display respectively the correlograms and periodograms of each series. They suggest that the UX index is nonstationary. This can also be inferred from the correlogram and periodogram of the series in the top half of Figs. 11 and 12. Stock returns might be stationary but there is still some degree of dependence in the data as indicated by the significant values of the correlograms of stock returns in Fig. 11. Finally, the correlograms of the absolute and the squared returns also indicate high time dependence in the series.

Fig. 10
figure 10

Time series UX data

Full size image
Fig. 11
figure 11

Correlograms The thick lines refer to the 95% confidence band for the null hypothesis of no autocorrelation

Full size image
Fig. 12
figure 12

Periodograms The horizontal axis refers to the discrete Fourier frequencies λj = 2πj/T, j = 1, …, T/2

Full size image

Table 5 reports the estimates of d based on a parametric approach. The model considered is the following:

Table 5 Estimates of d and 95% confidence intervals
Full size table

y t  = α + β t + x t , (1 − L)d x t  = u t , t = 1, 2, …,

where yt stands for the (logged) stock market prices, assuming that the disturbances ut are in turn a) white noise, b) autoregressive (AR (1), and c) of the Bloomfield-type, the latter being a non-parametric approach that produces autocorrelations decaying exponentially as in the AR case.

We consider the three standard cases of i) no deterministic terms (α = β = 0 above), ii) with an intercept (i.e., β = 0), and iii) with an intercept and a linear time trend. The most relevant case is the one with an intercept. The reason is that the t-values imply that the coefficients on the linear time trends are not statistically significant in all cases, unlike those on the intercept. We have used a Whittle estimator of d (Dahlhaus, 1989) along with the parametric testing procedure of Robinson (1994).

The results indicate that for the log UX series the estimated value of d is significantly higher than 1 independently of the way of modelling the I (0) disturbances. As for the absolute and squared returns, the estimates are all significantly positive, ranging between 0.251 and 0.313.

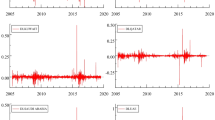
Figure 13 focuses on the semiparametric approach of Robinson (1995b), extended later by many authors, including Abadir et al. (2007). Given the nonstationary nature of the UX series, first-differenced data are used for the estimation, then adding 1 to the estimated values to obtain the orders of integration of the series. When using the Abadir et al., (2007) approach, which is an extension of Robinson (1995a) that does not impose stationarity, the estimates were almost identical to those reported in the paper, and similar results were obtained with log-periodogram type estimators. Along with the estimates we also present the 95% confidence bands corresponding to the I (1) hypothesis for the UX data and the I (0) hypothesis for the absolute/squared returns. We display the estimates for the whole range of values of the bandwidth parameter m = 1, .,, T/2 (horizontal axe in the plots in Fig. 13).Footnote 1 It can be seen that the values are above the I (1) interval in the majority of cases, which is consistent with the parametric results reported in Table 5. For the absolute and squared returns, the estimates are practically all significantly above the I (0) interval, implying long memory behaviour. Overall, these results confirm the parametric ones. The estimated value of d is slightly above 1 for the log stock market prices, and significantly above 0 (thus implying long memory) for both squared and absolute returns.

Fig. 13
figure 13

Semiparametric Whittle estimates of d The horizontal axis concerns the bandwidth parameter while the vertical one refers to the estimated value of d. The bold lines correspond to the 95% confidence interval for the I (1) (a) and the I (0) (b and c) hypotheses

Full size image

Figure 14 presents the stability results. We computed the estimates of d with two different approaches: a recursive one, initially using a sample of 300 observations, and then adding ten more observations each time, and a rolling one with a moving window of 300 observations. Again this was done for both prices and absolute/squared returns. Persistence appears to decrease over time, especially for the volatility series.

Fig. 14
figure 14

Stability results based on recursive estimates

Full size image

5 Conclusions

This paper uses both the Hurst exponent and parametric/semiparametric fractional integration methods to analyse the long-memory properties of two Ukrainian stock market indices, namely the PFTS and UX indices. The evidence suggests that this market is inefficient and that persistence was not constant over time; in particular, it increased during the recent financial crisis, when the market became less efficient/more predictable and more vulnerable to anomalies. These findings support the FMH paradigm rather than the EMH for the Ukrainian stock market.

A time-varying degree of persistence, as measured by the Hurst exponent, implies that trading strategies might have to be revised. For example high persistence suggests using trend-based strategies, as well as exploiting market anomalies, such as the January, day of the week, end of the month, and holidays effects. Thus, the Hurst exponent can be used to create customized trading strategies in financial markets.

The analysis of market persistence also provides information about expectations and can be useful for macro-prudential purposes. Specifically, the Hurst exponent can be interpreted as a “fear” index, which reflects the current market conditions, expectations about future developments, the degree of uncertainty (volatility), and investors’ sentiment in general – the higher the exponent, the less efficient the market is. Finally, our study also shows that data smoothing is not advisable in the context of R/S analysis.