Blood flow analysis in tapered stenosed arteries with the influence of heat and mass transfer

Abstract

A non-Newtonian fluid model is used to investigate the 2D pulsatile blood flow through a tapered artery with stenosis. The mixed convection effects of heat and mass transfer are also taken into account. By applying non-dimensionalization and radial coordinate transformation, we simplify the system in a tube. Under the finite difference scheme, numerical solutions are calculated for velocity, temperature concentration, resistance, impedance, wall shear stress and shearing stress at the stenosis throat. Finally, Quantitative analysis is carried out.

1 Introduction

The human cardiovascular system is the internal transport of fluids with multiple branches of the arteries in which is a complex blood circulates. The work concerning about bio-fluid dynamical aspects of the human cardiovascular system has gained much attention in recent years with respect to the diagnosis and the genesis of atherosclerosis. Among the various cardiovascular diseases, stenosis is a major one which affects the flow of blood in the arteries. It is associated with pressure distribution, shear stress at the wall and resistance to blood flow. Reasonable analysis and simulations may help clinic a lot. Thus, the study of blood flow through stenosed arteries is of considerable significance [11, 21].

Several researchers [30, 32] examined and analyzed the blood flow through a stenosed artery and investigated the effect of physical parameters on blood flow through an arterial stenosis. The effect of tapering on the physiologically important parameters such as wall shear stress, flow rate and resistance to flow has been studied by Bloch [7]. Ku [16], and Kumar [17] discussed the diagnosis and treatment of cardiovascular diseases.

In all the investigations above, blood was treated as classical Newtonian fluid in which the constitutive equation is established by

$$\begin{aligned} \tau = \mu \frac{\mathrm {d}u}{\mathrm {d}y}, \end{aligned}$$

where $\tau$ is the shearing stress, $\frac{\mathrm {d}u}{\mathrm {d}y}$ is the shear rate of the fluid and $\mu$ is the viscosity.

However, It has been pointed out that in some diseased conditions, blood exhibits remarkable non-Newtonian properties since it has been seen through several experiments that most of the biological fluids exhibit rheology of non-Newtonian characteristics [18, 26, 28]. Therefore, the interest has been non-Newtonian fluid in stenosed artery in recent years.

During past decades, numerous investigators focused on different types of fluid in stenosed artery. Ismail et al. [15] and Nadeem et al. [22] studied blood flow through a tapered artery with a stenosis by Power law fluid model

$$\begin{aligned} \tau = \mu (\dot{\gamma })^{m - 1} \dot{\gamma }, \end{aligned}$$

(1)

where the consistency $\mu$ is the characteristics of each polymer and

$$\begin{aligned} \dot{\gamma } = \sqrt{ \frac{1}{2} \sum \nolimits _{i}\sum \nolimits _{j} \dot{\gamma _{ij}} \dot{\gamma _{ij}} } = \sqrt{ \frac{1}{2} \varPi }, \end{aligned}$$

$\dot{\gamma _{ij}}, i,j = 1, 2, 3$ are the rate of strain tensor component. Chaturani and Samy [10] presented Casson fluid for blood flow through a normal artery with a stenosis by perturbation method:

$$\begin{aligned} \left| \tau \right| ^\frac{1}{2}= \left\{ \begin{aligned}&\left| \tau _0 \right| ^{\frac{1}{2}} + \mu \left| \frac{\partial u}{\partial r} \right| ^\frac{1}{2},&\quad \left| \tau \right| \ge \left| \tau _{0} \right| , \\&\frac{\partial u}{\partial r} = 0,&\quad \left| \tau \right| \le \left| \tau _{0} \right| , \end{aligned} \right. \end{aligned}$$

(2)

The relation (2)$_{2}$ corresponds to the vanishing of the velocity gradients in regions in which the shear stress is less than the yield stress. Ali et al. [6] and Zaman et al. [33] captured the rheology of blood by utilizing Sisko fluid model:

$$\begin{aligned} \tau = \left( \mu _{\infty } + (\mu _{0} - \mu _{\infty }) \left[ 1 + \varGamma ^2 \varPi ^2 \right] ^{n - \frac{1}{2}} \right) A_1, \end{aligned}$$

(3)

where $\mu _{\infty }$ is the infinite shear rate viscosity, $\mu _{0}$ is the zero shear rate viscosity, $\varGamma$ is the time constant, n is the power law index, $A_1$ is the first Rivilin-Ericksen tensor given as $A_1 = \nabla u + (\nabla u)^T$ and $\varPi = \sqrt{\frac{1}{2}\mathrm {tr}(A_1^2)}$. Ellahi et al. [12] investigated the blood flow as Jeffrey fluid in a catherized tapered artery with the suspension of nanoparticles:

$$\begin{aligned} \tau = \frac{\mu }{1+\lambda _1} \left( \dot{\gamma } + \lambda _2^* \ddot{\gamma } \right) . \end{aligned}$$

(4)

Akbar [2,3,4] modelled blood with Carreau fluid, Walter’s B fluid and Sutterby fluid model through a tapered artery with a stenosis, respectively and she also discussed Williamson fluid with pseudoplastic characteristics [5].

At the same time, the system was been more complex under the background of medicine and physic. Mekheimer and El Kot [20] considered blood flow as Sisko fluid and examined the influence of heat and mass transfer; Waqas et al. [31] modeled and analyzed the generalized Burgers fluid subject to Cattaneo–Christov heat flux model; Sankar [25] treated blood as Casson fluid and analyzed the effects of magnetic field through a stenosed artery; Tripathi et al. [29] developed couple stress biofluids with electro-magneto-hydrodynamic properties; Noreen, Waheed and Hussanan [23] studied the flow of magneto-hydrodynamic nanofluid through an asymmetric microfluidic channel under an applied axial electric field by considering the impacts of wall flexibility, Joule heating and upper/lower wall zeta potentials.

In 1992, Luo and Kuang [18] proposed a new constitutive relation of non-Newtonian fluid which has the property of shear thinning. The constitutive equation is as follows:

$$\begin{aligned} \begin{aligned}&\bar{\tau }=\bar{\tau }_{0}+\eta _{2}\bar{\dot{\gamma }}^{\frac{1}{2}}+\eta _{1}\bar{\dot{\gamma }},\quad \bar{\tau }\ge \bar{\tau }_{0}\\&\bar{\dot{\gamma }}=0,\quad \bar{\tau }<\bar{\tau }_{0}, \end{aligned} \end{aligned}$$

(5)

where $\bar{\tau }_{0}$, $\eta _{1}$ and $\eta _{2}$ are functions of hematocrit, plasma viscosity and other chemical variable respectively and $\bar{\dot{\gamma }}=\sqrt{\frac{\bar{\varPi }}{2}}$ denotes the shear rate of the fluid, $\bar{\varPi }$ is the second covariant of the system. Moreover, Luo and Kuang [18] made the experimental verification of the K–L model. The results showed that the experimental data fit quite well with the K–L model (5), so the model can be used to describe blood flow. It is quite a different constitutive relationship of non-Newtonian fluid and no one has treated it as blood flow in a stenosed artery.

Motivated by the researches above, we model blood as the K–L model and investigate the heat and mass transfer of blood flow. First, we examine the fluid equation with heat and mass transfer by the constitutive equation of K–L model and choose one geometry of stenosed artery. Then, we use the basic parameters to nondimensionalize the system for further study. Moreover, in order to discrete the system conveniently, we apply the radial coordinate transformation. Finally, we get the numerical solution of velocity, flow rate, resistance and wall shear stress at the stenosis throat by finite difference method [9, 14, 24].

The paper is arranged as follows. Section 2 gives the formulation of the problem including fluid equations, constitutive equation and geometry of tapered stenosed artery. Section 3 does the nondimensionalization. Section 4 transfers fluid equations by radial coordinate transformation and gives the relation between axial velocity and radial velocity. Section 5 shows the numerical approximation iteration by finite difference method. Section 6 provides the numerical results by graphics.

2 Formulation of the problem

2.1 Geometry of stenosed artery

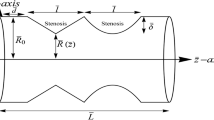
In our work, the artery is considered as a tube which is thin, elastic, cylindrical and tapered. It also has overlapping stenosis in the vessel axisymmetricly. To illustrate the blood artery, we would take the cylindrical polar coordinates system. We denote one point in the system by $(r, \theta , z)$, in which z-axis is taken along the axis of the artery, r and $\theta$ are radial and circumferential directions respectively. According to [8, 15], we introduce the geometry of stenosis as follows

$$\begin{aligned} \bar{R}\left( \bar{z},\bar{t}\right) =\left\{ \begin{aligned}&\left[ \left( m\bar{z}+d_{0}\right) -\frac{\tau _{m}\cos (\psi )\left( \bar{z}-\bar{d}\right) }{\bar{l}_{0}} \bar{\zeta } \right] \bar{a}_{1}(\bar{t}),\quad \bar{d}\le \bar{z}\le \bar{d}+\frac{3}{2}\bar{l}_{0},\\&\left( m\bar{z}+d_{0}\right) \bar{a}_{1}(\bar{t}),\quad \mathrm {Otherwise}.\\ \end{aligned} \right. \end{aligned}$$

Fig. 1

Geometry of the stenosed artery

where $\bar{\zeta } = 11-\frac{94\left( \bar{z}-\bar{d}\right) }{3\bar{l}_{0}}+\frac{32\left( \bar{z}-\bar{d}\right) ^{2}}{\bar{l}_{0}^{2}}-\frac{32\left( \bar{z}-\bar{d}\right) ^{3}}{3\bar{l}_{0}^{3}}$, $\bar{R}\left( \bar{z},\bar{t}\right)$ denotes the radius of the artery; $\frac{3\bar{l}_{0}}{2}$ is the length of overlapping stenosis, $\psi$ is the angle of tapering; $\bar{d}$ is the location of the stenosis; $\bar{L}$ represents the finite length of arterial segment; The slope of the tapered vessel is taken by $m=\tan (\psi )$ and the critical height of the stenosis is given by $\tau _{m}$. The time-variant parameter $\bar{a}_{1}(\bar{t})$ can be writen as $\bar{a}_{1}(\bar{t})=1+k_{r}\cos (\bar{\omega } \bar{t}-\phi )$, where $k_{r}$ denotes some parameter related to amplitude and $\phi$ denotes the phase angle. Specificly, we can see the geometry in Fig. 1.

2.2 Flow equations

The blood flow is concerned as an type of incompressible viscous fluid system in which we consider the thermal diffusion and mass transfer which can be applied to illustrate the blood flow with drug.

The continuity equation

$$\begin{aligned} \frac{\partial \bar{u}}{\partial \bar{r}}+\frac{\bar{u}}{\bar{r}}+\frac{\partial \bar{w}}{\partial \bar{z}}=0, \end{aligned}$$

(6)

The momentum equations

$$\begin{aligned} \rho \left( \frac{\partial \bar{u}}{\partial \bar{t}}+\bar{u}\frac{\partial \bar{u}}{\partial \bar{r}}+\bar{w}\frac{\partial \bar{u}}{\partial \bar{z}}\right)= & {} -\frac{\partial \bar{p}}{\partial \bar{r}}+\left( \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left( \bar{r}\bar{\tau }_{rr}\right) +\frac{\partial }{\partial \bar{r}}\bar{\tau }_{rz}\right) ,\end{aligned}$$

(7)

$$\begin{aligned} \rho \left( \frac{\partial \bar{w}}{\partial \bar{t}}+\bar{w}\frac{\partial \bar{w}}{\partial \bar{r}}+\bar{w}\frac{\partial \bar{w}}{\partial \bar{z}}\right)= & {} -\frac{\partial \bar{p}}{\partial \bar{z}}+\left( \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left( \bar{r}\bar{\tau }_{rz}\right) +\frac{\partial }{\partial \bar{r}}\bar{\tau }_{zz}\right) \nonumber \\&+\,\rho \bar{g}\bar{\alpha }\left( \bar{T}-\bar{T}_{0}\right) +\rho \bar{g}\bar{\alpha }\left( \bar{C}-\bar{C}_{0}\right) , \end{aligned}$$

(8)

The energy equation

$$\begin{aligned} \begin{aligned} \rho c_{p}\left( \frac{\partial \bar{T}}{\partial \bar{t}}+\bar{u}\frac{\partial \bar{T}}{\partial \bar{r}}+\bar{w}\frac{\partial \bar{T}}{\partial \bar{z}}\right)&=\bar{\tau }_{rr}\frac{\partial \bar{u}}{\partial \bar{r}}+\bar{\tau }_{rz}\frac{\partial \bar{w}}{\partial \bar{r}}+\bar{\tau }_{rz}\frac{\partial \bar{u}}{\partial \bar{z}}+\bar{\tau }_{zz}\frac{\partial \bar{w}}{\partial \bar{z}}\\&\quad +k\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{r}^2}+\frac{1}{r}\frac{\partial \bar{T}}{\partial \bar{r}}+\frac{\partial ^{2}\bar{T}}{\partial \bar{z}^{2}}\right) , \end{aligned} \end{aligned}$$

(9)

and The mass concentration equation

$$\begin{aligned} \begin{aligned} \left( \frac{\partial \bar{C}}{\partial \bar{t}}+\bar{u}\frac{\partial \bar{C}}{\partial \bar{r}}+\bar{w}\frac{\partial \bar{C}}{\partial \bar{z}}\right)&=D\left( \frac{\partial ^{2}\bar{C}}{\partial \bar{r}^2}+\frac{1}{r}\frac{\partial \bar{C}}{\partial \bar{r}}+\frac{\partial ^{2}\bar{C}}{\partial \bar{z}^{2}}\right) \\&\quad +\frac{DK_{T}}{T_{m}}\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{r}^2}+\frac{1}{r}\frac{\partial \bar{T}}{\partial \bar{r}}+\frac{\partial ^{2}\bar{T}}{\partial \bar{z}^{2}}\right) , \end{aligned} \end{aligned}$$

(10)

where $\rho$ denotes the density of fluid, $\bar{p}$ is the fluid pressure. To make a distinction, we define $\bar{u}$ and $\bar{w}$ as the velocity components in radial and axial directions respectively. $\bar{T}$ refers to the temperature and $\bar{C}$ is defined as the concentration of mass. Moreover, we denote the thermal conductivity by k, the specific heat at constant pressure by $c_{p}$, also we define the medium’s temperature as $T_{m}$, the thermal-diffusion ratio and the coefficients of mass diffusivity as D and $K_{T}$ respectively.

From (5), it can be deduced that

$$\begin{aligned} \left\{ \begin{aligned}&\bar{\tau }_{zz}=2\bar{\eta }(\bar{\dot{\gamma }})\left( \frac{\partial \bar{w}}{\partial \bar{z}}\right) \\&\bar{\tau }_{rr}=2\bar{\eta }(\bar{\dot{\gamma }})\left( \frac{\partial \bar{u}}{\partial \bar{r}}\right) \\&\bar{\tau }_{rz}=\bar{\eta }(\bar{\dot{\gamma }})\left( \frac{\partial \bar{w}}{\partial \bar{r}}+\frac{\partial \bar{u}}{\partial \bar{z}}\right) \end{aligned} \right. \end{aligned}$$

where $\bar{\eta }(\bar{\dot{\gamma }})=\frac{\bar{\tau }}{\bar{\dot{\gamma }}}$ represents the apparent viscosity.

It is known that blood flow is pulsatile. As [27] stated, the pressure gradient with dimension can be writen as [27]

$$\begin{aligned} -\frac{\partial \bar{p}}{\partial \bar{z}}=\bar{A}_{0}+\bar{A}_{1}\cos \bar{\omega } \bar{t},\qquad t>0. \end{aligned}$$

where $\bar{A}_{0}$ denotes the amplitude in the case of the steady state while $\bar{A}_{1}$ represent the amplitude in the case of the pulsatile blood flow. $\bar{\omega }$ is the angular frequency defined by $\bar{\omega }=2\pi \bar{f}_{p}$ where $\bar{f}_{p}$ is the frequency of pulse.

2.3 Initial and Boundary conditions

The initial value for velocity is given by [27],

$$\begin{aligned} \begin{aligned}&\bar{w}(r,z,0)=\left( \frac{\bar{A}_{0}+\bar{A}_{1}}{4\eta _{1}}\right) \left[ d_{0}^{2}-\left( \frac{\bar{r}}{d_{0}}\right) ^2\right] ,\\&\bar{u}(r,z,0)=0,\ \bar{T}(r,z,0)=\bar{T}_{0},\ \bar{C}(r,z,0)=\bar{C}_{0}. \end{aligned} \end{aligned}$$

The boundary conditions are

$$\begin{aligned} \begin{aligned}&\bar{u}(\bar{r},\bar{z},\bar{t})=0,\ \frac{\partial \bar{w}}{\partial \bar{r}}(\bar{r},\bar{z},\bar{t})=0,\ \frac{\partial \bar{T}}{\partial \bar{r}}(\bar{r},\bar{z},\bar{t})=0,\ \frac{\partial \bar{C}}{\partial \bar{r}}(\bar{r},\bar{z},\bar{t})=0,\quad \bar{r}=0,\\&\bar{u}(\bar{r},\bar{z},\bar{t})=\frac{\partial \bar{R}}{\partial \bar{t}},\ \bar{w}(\bar{r},\bar{z},\bar{t})=0,\ \bar{T}(\bar{r},\bar{z},\bar{t})=0,\ \bar{C}(\bar{r},\bar{z},\bar{t})=0,\quad \bar{r}=\bar{R}(\bar{z},\bar{t}), \end{aligned} \end{aligned}$$

3 Non-dimensionalization

Let us introduce non-dimensional quantities as follows:

$$\begin{aligned} \begin{aligned} r&=\frac{\bar{r}}{d_{0}},\quad z=\frac{\bar{z}}{d_{0}},\quad R=\frac{\bar{R}}{d_{0}},\quad u=\frac{\bar{u}}{u_{0}},\quad w=\frac{\bar{w}}{u_{0}},\quad t=\bar{\omega }\bar{t},\quad p=\frac{d_{0}}{u_{0}\eta _{1}}\bar{p}, \\ \tau _{0}&=\frac{d_{0}}{u_{0}\eta _{1}}\bar{\tau }_{0},\quad \tau _{rr}=\frac{d_{0}}{u_{0}\eta _{1}}\bar{\tau }_{rr},\quad \tau _{zz}=\frac{d_{0}}{u_{0}\eta _{1}}\bar{\tau }_{zz},\quad \tau _{rz}=\frac{d_{0}}{u_{0}\eta _{1}}\bar{\tau }_{rz},\\ \alpha ^{2}&=\frac{\rho d_{0}^{2}\bar{\omega }}{\eta _{1}},\quad T=\frac{\bar{T}-\bar{T}_{0}}{\bar{T}_{0}},\quad C=\frac{\bar{C}-\bar{C}_{0}}{\bar{C}_{0}},\quad \mathrm {Re}=\frac{\rho d_{0}u_{0}}{\eta _{1}},\quad \mathrm {E_{c}}=\frac{u_{0}^{2}}{c_{p}\bar{T}_{0}},\\ \mathrm {P_{r}}&=\frac{c_{p}\eta _{1}}{k},\quad \mathrm {S_{r}}=\frac{\rho DK_{T}\bar{T}_{0}}{\eta _{1}T_{m}\bar{C}_{0}},\quad \mathrm {S_{c}}=\frac{\eta _{1}}{D\rho },\quad \mathrm {G_{r}}=\frac{g\bar{\alpha } d_{0}^3 \bar{T}_{0}}{\eta _{1}^{2}},\quad \mathrm {G_{c}}=\frac{g\bar{\alpha } d_{0}^3 \bar{C}_{0}}{\eta _{1}^{2}}, \\ A_{0}&=\frac{d_{0}^{2}}{u_{0}\eta _{1}}\bar{A}_{0},\quad A_{1}=\frac{d_{0}^{2}}{u_{0}\eta _{1}}\bar{A}_{1},\ \end{aligned}\nonumber \\ \end{aligned}$$

(11)

where $d_{0}$ is the fixed radius of the normal artery positioned in the non-stenotic region, $u_{0}$ denotes the average velocity of flow in the uniform artery, $\bar{T}_{0}\ \mathrm {and}\ \bar{C}_{0}$ are average temperature of the fluid and concentration of mass respectively. $\mathrm {P_{r}}$ is the Prandtl number, $\mathrm {S_{r}}$ is Soret number, $\mathrm {E_{c}}$ is Eckert number, $\mathrm {S_{c}}$ is Schmidt number, $\mathrm {G_{r}}$ is Grashof number and $\mathrm {G_{c}}$ is solutal Grashof number.

As non-dimensional quantities are shown in Eq. (11), the dimensionless geometry of stenosed artery is

$$\begin{aligned} R\left( z,t\right) =\left\{ \begin{aligned}&\left[ \left( mz+d_{0}\right) -\frac{\tau _{m}\cos (\psi )\left( z-d\right) }{l_{0}}\zeta \right] a_{1}(t),\quad d\le z\le d+\frac{3}{2}l_{0},\\&\left( mz+d_{0}\right) a_{1}(t),\quad \mathrm {Otherwise}.\\ \end{aligned} \right. \end{aligned}$$

where $\zeta = 11-\frac{94\left( z-d\right) }{3l_{0}}+\frac{32\left( z-d\right) ^{2}}{l_{0}^{2}}-\frac{32\left( z-d\right) ^{3}}{3l_{0}^{3}}$ and $a_{1}(t)=1+k_{r}\cos (t-\phi )$.

Similarly, making use of (11) along with Eq. (6)–(10), one obtains that

$$\begin{aligned}&\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(12)

$$\begin{aligned}&\alpha ^{2}\frac{\partial u}{\partial t}+\mathrm {Re}\left( u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right) =-\frac{\partial p}{\partial r}+\left[ \frac{\partial }{\partial r}\left( r\tau _{rr}\right) +\frac{\partial }{\partial z}\left( \tau _{rz}\right) \right] , \end{aligned}$$

(13)

$$\begin{aligned}&\alpha ^{2}\frac{\partial w}{\partial t}+\mathrm {Re}\left( u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right) =-\frac{\partial p}{\partial z}+\left[ \frac{\partial }{\partial r}\left( r\tau _{rz}\right) +\frac{\partial }{\partial z}\left( \tau _{zz}\right) \right] \nonumber \\&\quad +\,\mathrm {G_{r}}T+\mathrm {G_{c}}C, \end{aligned}$$

(14)

$$\begin{aligned}&\alpha ^{2}\frac{\partial T}{\partial t}+\mathrm {Re}\left( u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\right) \nonumber \\&\quad =\mathrm {E_{c}}\left( \tau _{rr}\frac{\partial u}{\partial r}+\tau _{rz}\frac{\partial w}{\partial r}+\tau _{rz}\frac{\partial u}{\partial z}+\tau _{zz}\frac{\partial w}{\partial z}\right) \nonumber \\&\qquad +\frac{1}{\mathrm {P_{r}}}\left( \frac{\partial ^{2} T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2} T}{\partial z^{2}}\right) , \end{aligned}$$

(15)

$$\begin{aligned}&\alpha ^{2}\frac{\partial C}{\partial t}+\mathrm {Re}\left( u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}\right) =\frac{1}{\mathrm {S_{c}}}\left( \frac{\partial ^{2} C}{\partial r^{2}}+\frac{1}{r}\frac{\partial C}{\partial r}+\frac{\partial ^{2} C}{\partial z^{2}}\right) \nonumber \\&\quad +\,\mathrm {S_{r}}\left( \frac{\partial ^{2} T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2} T}{\partial z^{2}}\right) , \end{aligned}$$

(16)

in which the dimensionless stress components are

$$\begin{aligned} \tau _{zz}= & {} 2\eta (\dot{\gamma })\left( \frac{\partial w}{\partial z}\right) ,\\ \tau _{rr}= & {} 2\eta (\dot{\gamma })\left( \frac{\partial u}{\partial r}\right) ,\\ \tau _{rz}= & {} \eta (\dot{\gamma })\left( \frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}\right) ,\\ \eta (\dot{\gamma })= & {} \frac{\tau _{0}+l\dot{\gamma }^{\frac{1}{2}}+\dot{\gamma }}{\dot{\gamma }},\quad l=\frac{\eta _{2}}{\eta _{1}}\left( \frac{d_{0}}{u_{0}}\right) ^{\frac{1}{2}},\\ \dot{\gamma }^{2}= & {} 2\left[ \left( \frac{\partial u}{\partial r}\right) ^{2}+\left( \frac{u}{r}\right) ^{2}+\left( \frac{\partial w}{\partial z}\right) ^{2}\right] +\left( \frac{\partial u}{\partial z}+\frac{\partial w}{\partial r}\right) ^{2}. \end{aligned}$$

Moreover, the dimensionless pressure gradient $-\frac{\partial p}{\partial z}$ in Eq. (14) is as follows:

$$\begin{aligned} -\frac{\partial p}{\partial z}=A_{0}+A_{1}\cos \omega t,\qquad t>0. \end{aligned}$$

Correspondingly, the initial conditions are

$$\begin{aligned} \begin{aligned} w(r,z,0)&=\left( \frac{A_{0}+A_{1}}{4}\right) \left[ 1-\left( \frac{r}{d_{0}}\right) ^2\right] ,\\ u(r,z,0)&=0,\ T(r,z,0)=0,\ C(r,z,0)=0. \end{aligned} \end{aligned}$$

(17)

The boundary conditions are

$$\begin{aligned} \begin{aligned} u(r,z,t)&=0,\ \frac{\partial w}{\partial r}(r,z,t)=0,\ \frac{\partial T}{\partial r}(r,z,t)=0,\ \frac{\partial C}{\partial r}(r,z,t)=0,\quad r=0,\\ u(r,z,t)&=\frac{\partial R}{\partial t},\ w(r,z,t)=0,\ T(r,z,t)=0,\ C(r,z,t)=0,\quad r=R(z,t). \end{aligned}\nonumber \\ \end{aligned}$$

(18)

4 Radial coordinate transformation

As the vessel wall varies in time, we introduce the radial coordinate transformation $\xi =\frac{r}{R(z,t)}$, which was given by [6, 8, 19], to fix the vessel. Under the transformation, Eq. (12), (14)–(16) take the form as follows:

$$\begin{aligned}&\frac{1}{R}\frac{\partial u}{\partial \xi }+\frac{u}{\xi R}+\frac{\partial w}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial w}{\partial \xi }=0, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial w}{\partial t}= & {} \frac{\xi }{R}\frac{\partial R}{\partial t}\frac{\partial w}{\partial \xi }+\frac{\mathrm {Re}}{\alpha ^{2}}\left( -\frac{u}{R}\frac{\partial w}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}w\frac{\partial w}{\partial \xi }-w\frac{\partial w}{\partial \xi }\right) \nonumber \\&-\,\frac{1}{\alpha ^{2}}\frac{\partial p}{\partial z}+\frac{1}{\alpha ^{2}}\left( \frac{1}{\xi R}\tau _{\xi z}+\frac{1}{R}\frac{\partial \tau _{\xi z}}{\partial \xi }-\frac{\partial \tau _{zz}}{\partial z}+\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial \tau _{zz}}{\partial z}\right) \nonumber \\&+\,\mathrm {G_{r}}T+\mathrm {G_{c}}C, \end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial T}{\partial t}= & {} \frac{\xi }{R}\frac{\partial R}{\partial t}\frac{\partial T}{\partial \xi }+\frac{\mathrm {Re}}{\alpha ^{2}}\left( -\frac{u}{R}\frac{\partial T}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}w\frac{\partial T}{\partial \xi }-w\frac{\partial T}{\partial \xi }\right) \nonumber \\&+\,\frac{\mathrm {E_{c}}}{\alpha ^{2}}\left[ \frac{\tau _{\xi \xi }}{R}\frac{\partial u}{\partial \xi }+\frac{\tau _{\xi z}}{R}\frac{\partial w}{\partial \xi }+\tau _{\xi z}\left( \frac{\partial u}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial u}{\partial \xi }\right) \right. \nonumber \\&\left. +\,\tau _{z z}\left( \frac{\partial w}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial w}{\partial \xi }\right) \right] \nonumber \\&+\,\frac{\mathrm {1}}{\alpha ^{2}\mathrm {P_{r}}}\left[ \frac{1}{R^{2}}\frac{\partial ^{2} T}{\partial \xi ^{2}}+\frac{1}{\xi R^{2}}\frac{\partial T}{\partial \xi }+\frac{\partial ^{2} T}{\partial z^{2}}\right. \nonumber \\&\left. -\left( -\frac{\xi }{R^{2}}\frac{\partial R}{\partial z}\frac{\partial T}{\partial \xi }+\frac{\xi }{R}\frac{\partial ^{2} R}{\partial z^{2}}\frac{\partial T}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial ^{2} T}{\partial \xi ^{2}}\right) \right] , \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial C}{\partial t}= & {} \frac{\xi }{R}\frac{\partial R}{\partial t}\frac{\partial C}{\partial \xi }+\frac{\mathrm {Re}}{\alpha ^{2}}\left( -\frac{u}{R}\frac{\partial C}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}w\frac{\partial C}{\partial \xi }-w\frac{\partial C}{\partial \xi }\right) \nonumber \\&+\,\frac{\mathrm {S_{r}}}{\alpha ^{2}}\left[ \frac{1}{R^{2}}\frac{\partial ^{2} T}{\partial \xi ^{2}}+\frac{1}{\xi R^{2}}\frac{\partial T}{\partial \xi }+\frac{\partial ^{2} T}{\partial z^{2}}\right. \nonumber \\&\left. -\left( -\frac{\xi }{R^{2}}\frac{\partial R}{\partial z}\frac{\partial T}{\partial \xi }+\frac{\xi }{R}\frac{\partial ^{2} R}{\partial z^{2}}\frac{\partial T}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial ^{2} T}{\partial \xi ^{2}}\right) \right] \nonumber \\&+\,\frac{1}{\alpha ^{2}\mathrm {S_{c}}}\left[ \frac{1}{R^{2}}\frac{\partial ^{2} C}{\partial \xi ^{2}}+\frac{1}{\xi R^{2}}\frac{\partial C}{\partial \xi }+\frac{\partial ^{2} C}{\partial z^{2}}\right. \nonumber \\&\left. -\left( -\frac{\xi }{R^{2}}\frac{\partial R}{\partial z}\frac{\partial C}{\partial \xi }+\frac{\xi }{R}\frac{\partial ^{2} R}{\partial z^{2}}\frac{\partial C}{\partial \xi }+\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial ^{2} C}{\partial \xi ^{2}}\right) \right] , \end{aligned}$$

(22)

where stress components are

$$\begin{aligned} \tau _{zz}&=2\eta (\dot{\gamma })\left( \frac{\partial w}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial w}{\partial \xi }\right) ,\\ \tau _{\xi \xi }&=2\eta (\dot{\gamma })\left( \frac{1}{R}\frac{\partial u}{\partial \xi }\right) ,\\ \tau _{\xi z}&=\eta (\dot{\gamma })\left( \frac{\partial u}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial u}{\partial \xi }+\frac{1}{R}\frac{\partial w}{\partial \xi }\right) ,\\ \eta (\dot{\gamma })&=\frac{\tau _{0}+l\dot{\gamma }^{\frac{1}{2}}+\dot{\gamma }}{\dot{\gamma }},\quad l=\frac{\eta _{2}}{\eta _{1}}\left( \frac{d_{0}}{u_{0}}\right) ^{\frac{1}{2}},\\ \dot{\gamma }^{2}&=2\left[ \left( \frac{\partial u}{\partial \xi }\frac{1}{R}\right) ^{2}+\left( \frac{u}{\xi R}\right) ^{2}+\left( \frac{\partial w}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial w}{\partial \xi }\right) ^{2}\right] \\&\quad +\left( \frac{\partial u}{\partial z}-\frac{\xi }{R}\frac{\partial R}{\partial z}\frac{\partial u}{\partial \xi }+\frac{1}{R}\frac{\partial w}{\partial \xi }\right) ^{2}. \end{aligned}$$

Multiplying Eq. (19) by $\xi R$ and integrating with respect to $\xi$ from 0 to $\xi$, we get

$$\begin{aligned} u(\xi ,z,t)=\xi \frac{\partial R}{\partial \xi }w-\frac{R}{\xi }\int _{0}^{\xi }\xi \frac{\partial w}{\partial z}d\xi -\frac{2}{\xi }\int _{0}^{\xi }\xi wd\xi , \end{aligned}$$

(23)

for $\xi =1$, using the boundary conditions. (23) becomes

$$\begin{aligned} -\int _{0}^{1}\xi \frac{\partial w}{\partial \xi }d\xi =\int _{0}^{1}\xi \left[ \frac{2}{R}\frac{\partial R}{\partial z}w+\frac{1}{R}\frac{\partial R}{\partial t}f(\xi )\right] d\xi , \end{aligned}$$

(24)

where $f(\xi )$ is an arbitrary function satisfying $\int _{0}^{1}\xi f(\xi )d\xi =1$. Thus, we set $f(\xi )=4\left( \xi ^{2}-1\right)$. Combining (24), we have

$$\begin{aligned} \frac{\partial w}{\partial z}=-\frac{2}{R}\frac{\partial R}{\partial z}w+\frac{4}{R}\left( \xi ^{2}-1\right) \frac{\partial R}{\partial t}, \end{aligned}$$

(25)

substituting (25) into (23), we finally arrive at

$$\begin{aligned} u(\xi ,z,t)=\xi \left[ \frac{\partial R}{\partial z}w+\frac{\partial R}{\partial t}\left( 2-\xi ^{2}\right) \right] . \end{aligned}$$

(26)

Conditions (17) and (18) can be written as

$$\begin{aligned} \begin{aligned} w(\xi ,z,0)&=\left( \frac{A_{0}+A_{1}}{4}\right) \left[ 1-\left( \frac{\xi R}{d_{0}}\right) ^2\right] ,\\ u(\xi ,z,0)&=0,\ T(\xi ,z,0)=0,\ C(\xi ,z,0)=0.\\ u(\xi ,z,t)&=0,\ \frac{\partial w}{\partial \xi }(\xi ,z,t)=0,\ \frac{\partial T}{\partial \xi }(\xi ,z,t)=0,\ \frac{\partial C}{\partial \xi }(\xi ,z,t)=0,\quad r=0,\\ u(\xi ,z,t)&=\frac{\partial R}{\partial t},\ w(\xi ,z,t)=0,\ T(\xi ,z,t)=0,\ C(\xi ,z,t)=0,\quad r=R(z,t), \end{aligned} \end{aligned}$$

5 Numerical approximation

In this section, finite difference method is applied to solve the problem. Specifically, central difference scheme is carried out in spatial dimension while forward difference scheme is adapted in time dimension as in following manner ( Difference of u, T, C with relevant derivatives and $Q, \varLambda , \tau _w$ can also be obtained by similar expression ):

$$\begin{aligned} \left( w_{\xi }\right) _{i,j}^{k}= & {} \frac{\partial w}{\partial \xi }=\frac{\left( w\right) _{i,j+1}^{k}-\left( w\right) _{i,j-1}^{k}}{2\varDelta \xi },\\ \left( w_{z}\right) _{i,j}^{k}= & {} \frac{\partial w}{\partial z}=\frac{\left( w\right) _{i+1,j}^{k}-\left( w\right) _{i-1,j}^{k}}{2\varDelta z},\\ \frac{\partial w}{\partial t}= & {} \frac{\left( w\right) _{i,j}^{k+1}-\left( w\right) _{i,j}^{k}}{\varDelta t},\\ \left( w_{\xi \xi }\right) _{i,j}^{k}= & {} \frac{\partial ^{2}w}{\partial \xi ^{2}}=\frac{\left( w\right) _{i,j+1}^{k}-\left( w\right) _{i,j}^{k}+\left( w\right) _{i,j-1}^{k}}{\left( \varDelta \xi \right) ^{2}},\\ \left( w_{z z}\right) _{i,j}^{k}= & {} \frac{\partial ^{2}w}{\partial z^{2}}=\frac{\left( w\right) _{i+1,j}^{k}-\left( w\right) _{i,j}^{k}+\left( w\right) _{i-1,j}^{k}}{\left( \varDelta z\right) ^{2}},\\ \left( w_{\xi z}\right) _{i,j}^{k}= & {} \frac{\partial ^{2}w}{\partial \xi \partial z}=\frac{\left( w\right) _{i+1,j+1}^{k}-\left( w\right) _{i-1,j+1}^{k}-\left( w\right) _{i+1,j-1}^{k}+\left( w\right) _{i-1,j-1}^{k}}{4\varDelta \xi \varDelta z}, \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{aligned}&\xi _{j}=\left( j-1\right) \varDelta \xi , \qquad \left( j=1,2,\ldots ,N+1\right) ,\ \xi _{N+1}=1,\\&z_{i}=\left( i-1\right) \varDelta z, \qquad \left( i=1,2,\ldots ,M+1\right) ,\\&t_{k}=\left( k-1\right) \varDelta t, \qquad \left( k=1,2,\ldots \right) . \end{aligned} \right. \end{aligned}$$

For more specific expressions of numerical scheme, readers are refered to [9, 14, 24, 25].

6 Results and discussion

In this section, graphical results are displayed and The quantitative effects of parameters are discussed. As in [10, 14], we have parameters that

$$\begin{aligned} \begin{aligned} d_{0}&=1,\ A_{0}=1,\quad A_{1}=0.2A_{0},\quad \phi =0,\quad k_{r}=0.05\\ f_{p}&=1.2,\quad L_{0}=15,\quad d=7,\quad L=30.\ \\ \end{aligned} \end{aligned}$$

We take $\varDelta \xi =0.1$ along the radial direction and $\varDelta z=0.1$ along the axial direction. What’s more, to make sure the convergence of the solution, time step is $\varDelta t=0.001$. By using MATLAB programming, we obtain the numerical solutions for velocity, flow rate, shear stress, resistive impedance, temperature, and concentration distributions with respect to various system parameters.

6.1 Velocity distribution

Figure 2 shows the velocity distribution with regard to different values of $\psi$ and $\tau _{m}$ with $z=10, t=0.2, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{r}}=1.5, \mathrm {G_{c}}=1$. Under the assumption that the blood vessel is axial symmetric, it is obviously that blood flow velocity reaches the maximum value at the center of the artery from Fig. 2. With the increase of maximum depth of the stenosis $\tau _{m}$, the velocity of blood increases remarkably while it will decrease as the angle of tapered vessel increases. We can also conclude that the velocity varies like a parabolic function at $\xi$. Thus, reducing the stenosis in the blood vessel is so important that dredging the vessels will decelerate the blood velocity and consequently, reducing the risk of disease.

Fixing the critical height of stenosis at $\tau _{m}=0.3d_{0}$ and varying $\mathrm {G_{r}}$ and $\mathrm {G_{c}}$, we have different velocity profile with different $\mathrm {G_{r}}$ and $\mathrm {G_{c}}$ on Fig. 3. Thus, we can obtain that the velocity increase with the rise of Grashof number $\mathrm {G_{r}}$ and solutal Grashof number $\mathrm {G_{c}}$ which represent the heat effects and mass effect on fluid respectively. That means with the growth of temperature and concentration, the velocity will increase a lot correspondingly.

6.2 Flow rate

Figure 4 illustrates the profiles for volumetric flow rate in stenosed artery under three different taper angles and $\mathrm {G}_{r}$ with $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000,\tau _{0}=1, l=4, \mathrm {E_{c}}=0.3, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{c}}=1.5$. It can be seen that the volumetric flow rate distribution is shaped like the geometry of the stenosis, which demostrates that the flow rate dropped at the beginning of the stenosis and reaches to its Minimum at the stenosis critical height. What’s more, when the tapered angle increases, the flow rate grows up considerably. It can also be obtained in Fig. 4 that as thermodynamics parameter Grashof number $\mathrm {G_{r}}$ increases, the flow rate grows up.

Figure 5 shows that under the effect of the mass transfer in fluid which can be illustrated by solutal Grashof number $\mathrm {G_{c}}$, the flow rate will have a different increases as $\mathrm {G_{c}}$ increases. The positive feedback can guide people to take effective action to enhance the flow rate.

Fig. 2

Variation of axial velocity for $z=10, t=0.2, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{r}}=1.5, \mathrm {G_{c}}=1.5$

Fig. 3

Variation of axial velocity for $z=10, t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3$

Fig. 4

Variation of flow rate for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000,\tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{c}}=1.5$

Fig. 5

Variation of flow rate for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{r}}=1.5$

6.3 Wall shear stress

Figures 6 and 7 are presented to demonstrate the variation of the shear stress at stenosis for different tapered angle with Grashof number $\mathrm {G_{r}}$ and solutal Grashof number $\mathrm {G_{c}}$ with $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000,\tau _{0}=1, l=4, \mathrm {E_{c}}=0.3, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3$. It is observed that the wall shear stress appears diverging tapering with tapered angle $\psi > 0$, converging tapering with tapered angle $\psi < 0$ and non-tapered artery with tapered angle $\psi = 0$. What’s more, with an increase in $\mathrm {G_{r}}$, $\mathrm {G_{c}}$, the wall shear stress decrease a lot, which means that temperature and concentration profile have a negative effect on wall shear stress.

Fig. 6

Variation of wall shear stress for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{c}}=1.5$

Fig. 7

Variation of wall shear stress for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{r}}=1.5$

Fig. 8

Variation of flow resistance for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{c}}=1.5$

Fig. 9

Variation of flow resistance for $t=0.2, \tau _{m}=0.3d_{0}, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3, \mathrm {G_{r}}=1.5$

6.4 Flow resistance

Figures 8 and 9 reveal the flow resistance profile for different values of $\psi$, $\mathrm {G_{r}}$ and $\mathrm {G_{c}}$ with $z=10, t=0.2, \mathrm {Re}=1000, \alpha ^2=2000, \tau _{0}=1, l=4, \mathrm {E_{c}}=0.4, \mathrm {P_{r}}=3, \mathrm {S_{r}}=3, \mathrm {S_{c}}=3$. It is obviously that blood flow resistance reaches the maximum value at the critical height point of the stenosis from Figs. 8 and 9. The shape of the resistance distribution is like the opposition of flow rate as in Fig. 4. Moreover, when Grashof number $\mathrm {G_{r}}$ and solutal Grashof number $\mathrm {G_{c}}$ grows, the flow resistance reduces and it will decreases as the angle of tapered vessel increases.

Fig. 10

Axial velocity profiles measured at different times [1]

Fig. 11

The experimental (o) and numerical (–) results of the axial velocity profiles [13]

Remark 1

From [1, 13], we have found several experimental results as showed in Figs. 10 and 11. Figures 10 and 11 illustrated the parabolic trend of the axial blood velocity which is consistent with our results in Fig. 2 and so with other the blood rheology properties. That means our model and simulations are credible.

7 Conclusion

Based on the above analysis, we can summarize several fluid dynamical properties of blood, which flows through tapered narrow arteries with time-dependent overlapping stenosis under heat and mass transfer. Several blood rheology properties such as the axial velocity of blood, flow rate, wall shear stress and resistance to flow are determined by the stenosis, different degrees of taperness, heat transfer and mass transfer. The major results of the present investigation are:

• When the maximum depth of the stenosis $\tau _{m}$ grows, the axial velocity of blood increases while it will decrease as the angle of tapered vessel increases.

• With the growth of Grashof number $\mathrm {G_{r}}$ and solutal Grashof number $\mathrm {G_{c}}$, the flow rate will increase a lot correspondingly, which means the positive feedback of heat and mass transfer on the velocity profile of blood.

• The distribution of wall shear stress with regard to z-axis shaped like the distribution of flow rate and have similar response from different tapered angle and Grashof number $\mathrm {G_{r}}$ and solutal Grashof number $\mathrm {G_{c}}$.

• Since the flow rate is higher in the former than in the latter, it can be observed that the resistive impedance in a diverging tapering is less than those in a converging tapering.

• It is seen that the flow resistance decrease when the Grashof number and solutal Grashof number increases, which means the negative feedback of heat and mass transfer on the blood resistance.

In our work, we apply a different constitutive equation in fluid equations. The analytical results show numerous relationships between various rheology properties, thus, may provide some quantitative guidance in clinical analysis.