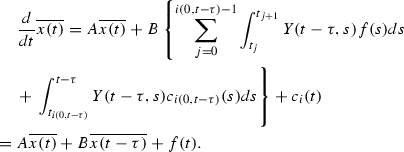1 Introduction

In recent decades, there are only few development on seeking explicit formula of solution to delay differential/discrete equations by introducing continuous/discrete delayed exponential matrix [1, 2]. One of the most advantages of continuous/discrete delayed exponential matrix is to help transferring the classical idea to represent the solution of linear ODEs into linear delay differential/discrete equations. For more continued works, one can refer to existence and stability of solutions to several classes of delay differential/discrete equations [3,4,5,6,7,8,9,10,11,12,13] and some relative controllability problems [14,15,16,17].

Impulsive delay differential equations are widely used to characterize the situation subject to abrupt changes in their states depending on the previous time interval. For more recent development of theory and application, one can refer to [18,19,20,21] for the determined case and reference therein. Next, we also remark that there are interesting work on impulsive stochastic delay differential equations with Markovian jump [22,23,24,25,26,27,28], where the classical approach are used to address the exponential stability problem. More precisely, Lyapunov–Krasovskii functional, stochastic version Razumikhin technique as well as linear matrix inequalities technique are utilized to derive the sufficient conditions to ensure the exponential stability of the trivial solution in the mean square.

In general, it is difficult to derive explicit presentation of solution without knowing impulsive delayed Cauchy matrix even for linear impulsive delay differential equations by adopting the similar idea to derive a solution involving impulsive Cauchy matrix [29, p.108, (3.3)] for linear impulsive differential equations.

In this paper, we firstly introduce impulsive delayed Cauchy matrix and seek the formula of solutions for the following linear impulsive delay differential equations

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\dot{x}(t)=Ax(t)+Bx(t-\tau ),~\quad t\ge 0,~\tau >0,~t\ne t_{i},\\&\Delta x(t_{i})=C_{i}x(t_{i}),~\quad i=1,2,\ldots ,\\&x(t)=\varphi (t),~-\tau \le t\le 0, \end{aligned} \right. \end{aligned} \end{aligned}$$
(1)

where \(A,B,C_{i}\) be constant \(n\times n\) matrices, \(AB=BA\), \(AC_{i}=C_{i}A\) and \(BC_{i}=C_{i}B\) for each \(i=1,2,\ldots \), \(\varphi \in C_{\tau }^1:= C^1([-\tau ,0],\mathbb {R}^n)\), and \(x(t)\in \mathbb {R}^{n}\), and time sequences \(\{t_{k}\}^{\infty }_{k=1}\) satisfy \(0=t_{0}<t_{1}<\cdots< t_{k}<\cdots \), impulsive conditions \(\Delta x(t_{k}):=x(t_{k}^{+})-x(t_{k}^{-})\), \(x(t_{k}^{+})=\lim \limits _{\epsilon \rightarrow 0^{+}}x(t_{k}+\epsilon )\) and \(x(t_{k}^{-})=x(t_{k})\) represent respectively the right and left limits of x(t) at \(t=t_{k}\) and \(\lim \limits _{k\rightarrow +\infty }t_{k}=\infty \).

Secondly, we seek the possible presentation of solutions to linear impulsive nonhomogeneous delay differential equations

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\dot{x}(t)=Ax(t)+Bx(t-\tau )+f(t),~\quad t\ge 0,~\tau >0,~t\ne t_{i},~f\in C(\mathbb {R}^{+},\mathbb {R}^{n}),\\&\Delta x(t_{i})=C_{i}x(t_{i}),~\quad i=1,2,\ldots ,\\&x(t)=\varphi (t),~-\tau \le t\le 0. \end{aligned} \right. \end{aligned} \end{aligned}$$
(2)

We would like to point that the main innovation is to derive the impulsive delayed Cauchy matrix for (1) and give its norm estimation. Further, we obtain explicit formula of solutions to (1) and (2) by virtue of new constructed impulsive delayed Cauchy matrix. Moreover, we present two sufficient conditions to guarantee the trivial solution to (1) is locally asymptotically stable. Next, we extend to show that the trivial solution to impulsive delay differential equations with nonlinear term is locally asymptotically stable. Finally, we make two numerically examples to illustrate our theoretical result.

The rest of the paper is organized as follows. In Sect. 2, we recall some notations and definitions, and give the concept on impulsive delayed Cauchy matrix and its norm estimation, and show that is the fundamental matrix for linear impulsive delay differential equations. In Sect. 3, we give the explicit formulas of solutions to linear impulsive homogeneous/nonhomogeneous delay differential equations via impulsive delayed Cauchy matrix and the variation of constants method. In Sect. 4, sufficient conditions ensuring local asymptotical stability of solutions are presented. Examples are given to illustrate our theoretical results in final section.

2 Preliminaries

For any \(x\in \mathbb {R}^n\) and \(A\in \mathbb {R}^{n\times n}\), we introduce vector norm \(\Vert x\Vert =\max _{1\le i \le n} |x_{i}|\) and matrix norm \(\Vert A\Vert =\max _{1\le i \le n}\sum _{j=1}^{n} |a_{ij}|\) respectively, where \(x_{i}\) and \(a_{ij}\) are the elements of the vector x and matrix A. Let \(L(\mathbb {R}^n)\) be the space of bounded linear operators in \(\mathbb {R}^n\). Denote by \(C(\mathbb {R}^{+}, \mathbb {R}^n)\) the Banach space of vector-value bounded continuous functions from \(\mathbb {R}^{+}\rightarrow \mathbb {R}^n\) endowed with the norm \(\Vert x\Vert _{C}=\sup _{t\in \mathbb {R}^{+}}\Vert x(t)\Vert \). We introduce a space \(C^1(\mathbb {R}^{+}, \mathbb {R}^n)=\{x\in C(\mathbb {R}^{+}, \mathbb {R}^n): \dot{x}\in C(\mathbb {R}^{+}, \mathbb {R}^n) \}\). Denote \(PC(\mathbb {R}^{+},\mathbb {R}^n):=\{x:\mathbb {R}^{+} \rightarrow \mathbb {R}^n:x\in C((t_{i},t_{i+1}],\mathbb {R}^n) \}\) and \(PC^1(\mathbb {R}^{+},\mathbb {R}^n):=\{x:\mathbb {R}^{+} \rightarrow \mathbb {R}^n:\dot{x}\in PC(\mathbb {R}^{+},\mathbb {R}^n)\}\).

Definition 2.1

A function \(x\in C^1([-\tau ,0],\mathbb {R}^n)\cup PC^1(\mathbb {R}^{+},\mathbb {R}^n)\) is called the solution of (1) (or (2)) if x satisfies \(x(t)=\varphi (t)\) for \(-\tau \le t\le 0\) and the first and second equations in (1) (or (2)).

Definition 2.2

(see [1, (11)] or [5, (11)]) \(e_{\tau }^{Bt}:\mathbb {R}\rightarrow \mathbb {R}^{n\times n}\) is called delayed matrix exponential if

$$\begin{aligned} e_{\tau }^{Bt}= \begin{aligned} \left\{ \begin{aligned}&\Theta ,~~~~~t<-\tau ,~\tau >0,\\&I,~~~-\tau \le t<0, \\&I+Bt+B^2\frac{(t-\tau )^2}{2}+\cdots +B^k\frac{(t-(k-1)\tau )^k}{k!},~~(k-1)\tau \le t<k\tau ,~k=1,2,\ldots , \end{aligned} \right. \end{aligned}\nonumber \\ \end{aligned}$$
(3)

where B is a constant \(n\times n\) matrix, \(\Theta \) and I are the zero and identity matrices, respectively.

Lemma 2.3

(see [1, Lemma 4] or [5, p.2253]) For all \(t\in \mathbb {R}\), \( \frac{d}{dt}e_{\tau }^{Bt}= Be_{\tau }^{B(t-\tau )}. \)

Lemma 2.4

(see [8, Lemma 12]) If \(\Vert B\Vert \le \alpha e^{\alpha \tau }\), \(\alpha \in \mathbb {R}^{+}\), then \( \Vert e_{\tau }^{B(t-\tau )}\Vert \le e^{\alpha t},~t\in \mathbb {R}. \)

Lemma 2.5

(see [30, 2.28, p.44]) Let \(A\in L(\mathbb {R}^n)\). For any \(\varepsilon >0\), there is a norm on \(\mathbb {R}^n\) such that \(\Vert A\Vert \le \rho (A)+{\varepsilon }\), where \(\rho (A)\) is the spectral radius of A.

Lemma 2.6

(see [29, (3.7), p.109]) Let \(A\in L(\mathbb {R}^n)\) and \(\alpha (A)=\max \{\mathfrak {R}\lambda \mid \lambda \in \sigma (A)\}\). For any \(\varepsilon >0\), there are \(K\ge 1\) such that \( \Vert e^{At}\Vert \le K e^{(\alpha (A)+\varepsilon )t} \) for any \(t\ge 0\). Here \(\sigma (A)\) is the spectrum of A.

In what follows, we introduce a concept of impulsive delay matrix function, an extension of delay matrix function for linear delay differential equations, which help us to seek explicit formula of solutions to impulsive delay differential equations.

By virtue of delayed matrix exponential (3), we define \(Y(\cdot ,\cdot ):\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}^{n\times n}\) and

$$\begin{aligned} Y(t,s)=e^{A(t-s)}X(t,s+\tau ),~t>s, \end{aligned}$$
(4)

where

$$\begin{aligned} X(t,s)=e_{\tau }^{B_1(t-s)}+ \sum \limits _{s-\tau<t_{j}<t}C_{j}e_{\tau }^{B_{1}(t-\tau -t_{j})}X(t_{j},s), \quad B_{1}=e^{-A\tau }B. \end{aligned}$$

Here, we call \(Y(\cdot ,\cdot )\) defined in (4) as impulsive delayed Cauchy matrix associated with (1).

Remark 2.7

Obviously, \(Y(t,t)=X(t,t+\tau )=e_{\tau }^{B_1(t-t-\tau )}=I,\) and \(Y(t,s)=e^{A(t-s)}X(t,s+\tau )=e^{A(t-s)}e_{\tau }^{B_1(t-s-\tau )}=\Theta ,~t<s.\)

Lemma 2.8

Impulsive delayed Cauchy matrix \(Y(\cdot ,\cdot )\) is the fundamental matrix of (1).

Proof

We divide our proof into two steps.

Step 1 We verify that \(Y(\cdot ,\cdot )\) satisfies differential equation \(\frac{d}{dt}Y(t,s)= AY(t,s)+BY(t-\tau ,s),~t\in (t_i,t_{i+1}].\) In fact, having differentiated Y(t, s) for \(t\in (t_i,t_{i+1}]\) and \(t>s\), by using Lemma 2.3, we obtain

$$\begin{aligned}&\frac{d}{dt}Y(t,s) = Ae^{A(t-s)}X(t,s+\tau )+e^{A(t-s)}\bigg \{B_1e_{\tau }^{B_1(t-2\tau -s)}\nonumber \\&\qquad +\;B_1 \sum \limits _{s<t_{j}<t}C_{j}e_{\tau }^{B_{1}(t-2\tau -t_{j})}X(t_{j},s+\tau )\bigg \}\\&\quad = AY(t,s)+Be^{A(t-\tau -s)}\bigg \{e_{\tau }^{B_1(t-2\tau -s)}+ \sum \limits _{s<t_{j}<t-\tau }C_{j}e_{\tau }^{B_{1}(t-2\tau -t_{j})}X(t_{j},s+\tau )\bigg \}\\&\quad = AY(t,s)+BY(t-\tau ,s). \end{aligned}$$

Step 2 We verify that \(Y(t_{i}^{+},s)-Y(t_{i}^{-},s)= C_{i}Y(t_{i},s).\) Note that \(e_{\tau }^{Bt^{+}}=e_{\tau }^{Bt^{-}}\) for all \(t>-\tau \), then

$$\begin{aligned}&Y(t_{i}^{+},s) = e^{A(t_{i}^{+}-s)}\bigg \{e_{\tau }^{B_1(t_{i}^{+}-\tau -s)}+ \sum \limits _{s<t_{j}<t_{i}^{+}}C_{j}e_{\tau }^{B_{1}(t_{i}^{+}-\tau -t_{j})}X(t_{j},s+\tau )\bigg \}\\= & {} e^{A(t_{i}^{-}-s)}\bigg \{e_{\tau }^{B_1(t_{i}^{-}-\tau -s)}+ \sum \limits _{s<t_{j}<t_{i}^{-}}C_{j}e_{\tau }^{B_{1}(t_{i}^{-}-\tau -t_{j})}X(t_{j},s+\tau )\\&+\;C_{i}e_{\tau }^{B_{1}(t_{i}^{+}-\tau -t_{i})}X(t_{i},s+\tau )\bigg \}\\= & {} e^{A(t_{i}^{-}-s)}X(t_{i}^{-},s+\tau )+C_{i}e^{A(t_{i}^{-}-s)}X(t_{i},s+\tau ) = Y(t_{i}^{-},s)+C_{i}Y(t_{i},s). \end{aligned}$$

This ends the proof. \(\square \)

To give the norm estimation of \(Y(\cdot ,\cdot )\), we first consider the norm estimation of \(B_{1}=e^{-A\tau }B\).

For a given \(B_{1}\), one can find a \(\alpha \in \mathbb {R}^{+}\) such that

$$\begin{aligned} \Vert B_{1}\Vert \le \alpha e^{\alpha \tau }. \end{aligned}$$
(5)

In fact, by Lemmas 2.5 and 2.6, we have \(\Vert B_{1}\Vert =\Vert e^{-A\tau }B\Vert \le K(\rho (B)+\varepsilon )e^{(\alpha (-A)+\varepsilon )\tau }.\) Choosing \(\alpha \ge \max {\{K(\rho (B)+\varepsilon ), \alpha (-A)+\varepsilon \}},~\varepsilon >0\), then we obtain (5). In addition, we can calculate the parameter \(\alpha \) for a given matrix by using MATLAB software.

Lemma 2.9

For any \(\varepsilon >0\) there exits \(K\ge 1\) such that

$$\begin{aligned} \Vert X(t,s)\Vert \le \bigg (\prod _{s-\tau<t_{j}<t}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{\alpha (t+\tau -s)}, \end{aligned}$$
(6)

and

$$\begin{aligned} \Vert Y(t,s)\Vert \le K\bigg (\prod _{s<t_{j}<t}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{(\alpha (A)+\alpha +\varepsilon )(t-s)}. \end{aligned}$$
(7)

Proof

Without loss of generality, we suppose that \(t_{m}<s-\tau \le t_{m+1}\) and \(t_{m+n}<t\le t_{m+n+1},~m,n=0,1,2,\ldots \). Next, we apply mathematical introduction to complete our proof.

  1. (i)

    For \(n=0\), by Lemma 2.4 via (5),

    $$\begin{aligned} \Vert X(t,s)\Vert \le \Vert e_{\tau }^{B_1(t-s)}\Vert \le e^{\alpha (t+\tau -s)}. \end{aligned}$$
  2. (ii)

    For \(n=1\), by Lemmas 2.4 and 2.5 via (5), we have

    $$\begin{aligned} \Vert X(t,s)\Vert\le & {} \bigg \Vert e_{\tau }^{B_1(t-s)}+C_{m+1}e_{\tau }^{B_{1}(t-\tau -t_{m+1})}X(t_{m+1},s)\bigg \Vert \\\le & {} e^{\alpha (t+\tau -s)}+(\rho (C_{m+1})+\varepsilon )e^{\alpha (t-t_{m+1})}e^{\alpha (t_{m+1}+\tau -s)}\\\le & {} (\rho (C_{m+1})+1+\varepsilon )e^{\alpha (t+\tau -s)}. \end{aligned}$$
  3. (iii)

    Let \(i:=i(0,t)\) be the number of the impulsive points which belong to (0, t). For \(n=k\), suppose that

    $$\begin{aligned} \Vert X(t,s)\Vert \le \bigg (\prod _{j=m+1}^{m+k}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{\alpha (t+\tau -s)} = \bigg (\prod _{s-\tau<t_{j}<t}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{\alpha (t+\tau -s)}. \end{aligned}$$
  4. (iv)

    For \(n=k+1\), by Lemmas 2.4 and 2.5 via (5) again,

    $$\begin{aligned} \Vert X(t,s)\Vert\le & {} \left\| e_{\tau }^{B_1(t-s)}+\sum \limits _{s-\tau<t_{j}<t}C_{j}e_{\tau }^{B_{1}(t-\tau -t_{j})}X(t_{j},s)\right\| \\\le & {} e^{\alpha (t+\tau -s)}+\sum \limits _{j=m+1}^{m+k+1}(\rho (C_{j})+\varepsilon )e^{\alpha (t-t_{j})}\bigg (\prod _{r=m+1}^{j-1}(\rho (C_{r})\\&+\;1+\varepsilon )\bigg ) e^{\alpha (t_{j}+\tau -s)}\\\le & {} \bigg (1+\sum \limits _{j=m+1}^{m+k+1}(\rho (C_{j})+\varepsilon )\prod _{r=m+1}^{j-1}(\rho (C_{r})+1+\varepsilon )\bigg )e^{\alpha (t+\tau -s)}\\= & {} \bigg (\prod _{j=m+1}^{m+k+1}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{\alpha (t+\tau -s)}\\= & {} \bigg (\prod _{s-\tau<t_{j}<t}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{\alpha (t+\tau -s)}. \end{aligned}$$

    Linking mathematical induction, one can obtain (6). Finally, using (4) and (6) via Lemma 2.6, one can derive (7) immediately. The proof is finished.\(\square \)

3 Representation of solutions

In this section, we seek explicit formula of solutions to linear impulsive nonhomogeneous delay system by adopting the classical ideas to find solution of linear impulsive ODEs.

We drive explicit formula of solutions to linear impulsive homogeneous delay system.

Theorem 3.1

The solution of (1) has the form

$$\begin{aligned} x(t)=Y(t,-\tau )\varphi (-\tau ) +\int _{-\tau }^0Y(t,s)[\dot{\varphi }(s)-A\varphi (s)]ds,~t\ge -\tau . \end{aligned}$$
(8)

Proof

Concerning on the solution of (1) and Lemma 2.8, one should search in the form

$$\begin{aligned} x(t)=Y(t,-\tau )c +\int _{-\tau }^0Y(t,s)g(s)ds, \end{aligned}$$

where c is an unknown constants, g(t) is an unknown continuously differentiable function. Moreover, it satisfies initial condition \(x(t)=\varphi (t),-\tau \le t\le 0\), i.e.,

$$\begin{aligned} x(t)=Y(t,-\tau )c +\int _{-\tau }^0Y(t,s)g(s)ds:=\varphi (t), \quad -\tau \le t\le 0. \end{aligned}$$

Let \(t=-\tau \), we have

$$\begin{aligned} Y(-\tau ,s)= \begin{aligned} \left\{ \begin{aligned}&\Theta ,\quad -\tau <s\le 0,\\&I,\quad \, s=-\tau . \end{aligned} \right. \end{aligned} \end{aligned}$$

Thus \(c=\varphi (-\tau ).\) Since \(-\tau \le t\le 0\), one obtains

$$\begin{aligned} Y(t,s)=e^{A(t-s)}e_{\tau }^{B_{1}(t-\tau -s)}= \begin{aligned} \left\{ \begin{aligned}&\Theta ,~~t<s\le 0,\\&e^{A(t-s)},-\tau \le s\le t. \end{aligned} \right. \end{aligned} \end{aligned}$$

Thus on interval \(-\tau \le t\le 0\), one can derive that

$$\begin{aligned} \varphi (t)= & {} Y(t,-\tau )\varphi (-\tau )+\int _{-\tau }^0Y(t,s)g(s)ds\nonumber \\= & {} Y(t,-\tau )\varphi (-\tau )+\int _{-\tau }^tY(t,s)g(s)ds+\int _{t}^0Y(t,s)g(s)ds\nonumber \\= & {} e^{A(t+\tau )}\varphi (-\tau )+\int _{-\tau }^te^{A(t-s)}g(s)ds. \end{aligned}$$
(9)

Having differentiated (9), we obtain

$$\begin{aligned} \dot{\varphi }(t)=Ae^{A(t+\tau )}\varphi (-\tau )+A\int _{-\tau }^te^{A(t-s)}g(s)ds+g(t)=A\varphi (t)+g(t). \end{aligned}$$

Therefore,

$$\begin{aligned} g(t)=\dot{\varphi }(t)-A\varphi (t). \end{aligned}$$

The desired result holds. \(\square \)

Next, the solution of (2) can be written as a sum \(x(t)=x_{0}(t)+\overline{x(t)}\), where \(x_{0}(t)\) is a solution of (1) and \(\overline{x(t)}\) is a solution of (2) satisfying zero initial condition.

The following result show us how to derive the formula of \(\overline{x(\cdot )}\).

Theorem 3.2

The solution \(\overline{x(t)}\) of (2) satisfying zero initial condition, has a form

$$\begin{aligned} \overline{x(t)}=\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Y(t,s)f(s)ds +\int _{t_{i}}^t Y(t,s)f(s)ds,~t\ge 0. \end{aligned}$$
(10)

Proof

By using method of variation of constants, one will search \(\overline{x(t)}\) in the following form

$$\begin{aligned} \overline{x(t)}=\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Y(t,s)c_{j}(s)ds +\int _{t_{i}}^t Y(t,s)c_{i}(s)ds, \end{aligned}$$
(11)

where \(c_{j}(t),~j=0,1,\ldots ,i(0,t)\) is an unknown vector function. We divide our proofs into several steps as follows:

  1. (i)

    For any \(0<t\le t_{1}\), we have \(\overline{x(t)}=\int _{0}^t Y(t,s)c_{0}(s)ds.\) Let us differentiate \(\overline{x(t)}\) to obtain

    $$\begin{aligned} \frac{d}{dt}\overline{x(t)}= & {} A\overline{x(t)}+B\int _{0}^{t-\tau } Y(t-\tau ,s)c_{0}(s)ds\\&+B\int _{t-\tau }^{t} Y(t-\tau ,s)c_{0}(s)ds+c_{0}(t)\\= & {} A\overline{x(t)}+B\overline{x(t-\tau )}+f(t). \end{aligned}$$

    From Remark 2.7, we know, \(Y(t-\tau ,s)=\Theta ,~s>t-\tau \), then

    $$\begin{aligned} c_{0}(t)=f(t). \end{aligned}$$
  2. (ii)

    For any \(t_{1}<t\le t_{2}\), we have

    $$\begin{aligned} \overline{x(t)}=\int _{0}^{t_{1}} Y(t,s)f(s)ds+\int _{t_{1}}^t Y(t,s)c_{1}(s)ds. \end{aligned}$$

    Let us differentiate \(\overline{x(t)}\) again to obtain

    $$\begin{aligned} \frac{d}{dt}\overline{x(t)}= & {} \int _{0}^{t_{1}} [AY(t,s)+BY(t-\tau ,s)]f(s)ds\\&+\;\int _{t_{1}}^t [AY(t,s)+BY(t-\tau ,s)]c_{1}(s)ds+c_{1}(t)\\= & {} A\overline{x(t)}+B\overline{x(t-\tau )}+f(t), \end{aligned}$$

    which implies that

    $$\begin{aligned} c_{1}(t)=f(t). \end{aligned}$$
  3. (iii)

    Suppose that \(c_{i-1}(t)=f(t)\) holds on subintervals \((t_{i-1},t_{i}], ~i=2,3\ldots \). For any \(t_{i}<t\le t_{i+1}\), we have

    $$\begin{aligned} \overline{x(t)}=\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Y(t,s)f(s)ds +\int _{t_{i}}^t Y(t,s)c_{i}(s)ds. \end{aligned}$$

    Let us differentiate \(\overline{x(t)}\) again to obtain

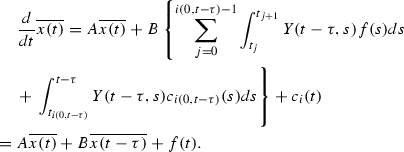
    This yields that \(c_{i}(t)=f(t)\). According to the mathematical induction, one can obtain \(c_{i}(t)=f(t),~i=1,2\ldots .\) Linking with (11), (10) is derived. \(\square \)

Corollary 3.3

The solution of (2) has the form

$$\begin{aligned} x(t)= & {} Y(t,-\tau )\varphi (-\tau ) +\int _{-\tau }^0Y(t,s)[\dot{\varphi }(s)-A\varphi (s)]ds\nonumber \\&+\;\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Y(t,s)f(s)ds +\int _{t_{i}}^t Y(t,s)f(s)ds. \end{aligned}$$
(12)

4 Asymptotical stability results

In this section, we discuss asymptotical stability of trivial solution of (1).

Definition 4.1

The trivial solution of (1) is called locally asymptotically stable, if there exists \(\delta >0\) such that \(\Vert \varphi \Vert _{1}:=\max _{[-\tau ,0]}\Vert \varphi (t)\Vert +\max _{[-\tau ,0]}\Vert \dot{\varphi }(t)\Vert <\delta \), the following holds:

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert x(t)\Vert =0. \end{aligned}$$

To prove our main results on the stability of trivial solution, we introduce the following conditions.

\((H_{1})\) Suppose that the distance between the impulsive points \({t_k}\) and \({t_{k+1}}\) satisfies

$$\begin{aligned} 0<\theta _{1}\le t_{k+1}-t_{k}\le \theta _{2}, \quad k=0,1,2\ldots , \end{aligned}$$

and set

$$\begin{aligned} \theta =\left\{ \begin{aligned} \theta _{1},~\alpha (A)+\alpha <0,\\ \theta _{2},~\alpha (A)+\alpha \ge 0, \end{aligned} \right. \end{aligned}$$

for some \(\alpha \) given in (5).

\((H_{2})\) Let \(\eta _{1}:=\alpha (A)+\alpha +\frac{1}{\theta }\ln (\rho (C)+1)\), where \(\rho (C):=\max \{\rho (C_{j}):j=1,\ldots ,i(0,t)\}\) and assume that \(\eta _{1}<0.\)

\((H_{3})\) There exists a positive constant p such that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\frac{i(0,t)}{t}=p. \end{aligned}$$

\((H_{4})\) Suppose that \(\eta _{2}<0\), where

$$\begin{aligned} \eta _{2}:=\alpha (A)+\alpha +p\ln (\rho (C)+1). \end{aligned}$$
(13)

Now, we are ready to state our first stability result for trivial solution of (1).

Theorem 4.2

If \((H_{1})\) and \((H_{2})\) are satisfied, then the trivial solution of (1) is locally asymptotically stable.

Proof

Using (8), Lemma 2.9 and Theorem 3.1, we have

$$\begin{aligned} \Vert x(t)\Vert\le & {} \Vert Y(t,-\tau )\Vert \Vert \varphi (-\tau )\Vert +\int _{-\tau }^0\Vert Y(t,s)\Vert \Vert \dot{\varphi }(s)-A\varphi (s)\Vert ds\nonumber \\\le & {} K\bigg (\prod _{j=1}^{i}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{(\alpha (A)+\alpha +\varepsilon )(t+\tau )}\Vert \varphi (-\tau )\Vert \nonumber \\&+\;\int _{-\tau }^0K\bigg (\prod _{j=1}^{i}(\rho (C_{j})+1+\varepsilon )\bigg ) e^{(\alpha (A)+\alpha +\varepsilon )(t-s)}\Vert \dot{\varphi }(s)-A\varphi (s)\Vert ds\nonumber \\\le & {} M e^{(\alpha (A)+\alpha +\varepsilon )t}(\rho (C)+1+\varepsilon )^{i(0,t)}\nonumber \\= & {} M e^{(\alpha (A)+\alpha +\varepsilon )(t-t_{i(0,t)})}e^{(\alpha (A)+\alpha +\varepsilon )t_{i(0,t)}}(\rho (C)+1+\varepsilon )^{i(0,t)}\nonumber \\\le & {} M e^{(\alpha (A)+\alpha +\varepsilon )\theta }e^{(\alpha (A)+\alpha +\varepsilon ) i(0,t)\theta }(\rho (C)+1+\varepsilon )^{i(0,t)}\nonumber \\= & {} Me^{(\alpha (A)+\alpha +\varepsilon )\theta }[e^{(\alpha (A)+\alpha +\varepsilon )\theta }(\rho (C)+1+\varepsilon )]^{i(0,t)}, \end{aligned}$$
(14)

where

$$\begin{aligned} M:=K(e^{(\alpha (A)+\alpha +\varepsilon )\tau }\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0 e^{-(\alpha (A)+\alpha +\varepsilon )s}\Vert \dot{\varphi }(s)-A\varphi (s)\Vert ds)>0. \end{aligned}$$

It follows from the condition \((H_{2})\) that one can choose \(\varepsilon >0\) such that

$$\begin{aligned} e^{(\alpha (A)+\alpha +\varepsilon )\theta }(\rho (C)+1+\varepsilon )\le e^{\frac{\theta \eta _{1}}{2}}<1. \end{aligned}$$

Then (14) gives

$$\begin{aligned} \Vert x(t)\Vert \le Me^{(\alpha (A)+\alpha +\varepsilon )\theta }e^{\frac{\theta \eta _{1}}{2} i(0,t)}\rightarrow 0~\text{ for }~t\rightarrow \infty (\text{ implies } i(0,t)\rightarrow \infty ). \end{aligned}$$

The proof is completed. \(\square \)

Next, we give second stability result for trivial solution of (1).

Theorem 4.3

If \((H_{3})\) and \((H_{4})\) are satisfied, then the trivial solution of (1) is locally asymptotically stable.

Proof

The proof is similar to Theorem 4.2, so we only give the details of main differences. Note that \((H_{3})\), we have \(i(0,t)< t(p+\varepsilon )\), \(\varepsilon >0\) arbitrarily small. Linking the formula (14), one has

$$\begin{aligned} \Vert x(t)\Vert\le & {} Me^{(\alpha (A)+\alpha +\varepsilon )t}(\rho (C)+1+\varepsilon )^{i(0,t)}\\\le & {} Me^{[\alpha (A)+\alpha +\varepsilon +(p+\varepsilon )\ln (\rho (C)+1+\varepsilon )]t}. \end{aligned}$$

By virtue of \((H_{4})\) we can find \(\varepsilon \) such that

$$\begin{aligned} \Vert x(t)\Vert \le Me^{[\alpha (A)+\alpha +\varepsilon +(p+\varepsilon )\ln (\rho (C)+1+\varepsilon )]t} \le M e^{\frac{\eta _{2}}{2}t}\rightarrow 0~\text{ as }~t\rightarrow \infty . \end{aligned}$$

The desired result holds. \(\square \)

To end this section, we extend the above results to nonlinear case. Consider the following linear impulsive delay system with nonlinear term

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\dot{x}(t)=Ax(t)+Bx(t-\tau )+f(x(t)),~\quad t\ge 0, \tau >0, t\ne t_{i},\\&x(t)=\varphi (t),~-\tau \le t\le 0,\\&\Delta x(t_{i})=C_{i}x(t_{i}),~i=1,2,\ldots , \end{aligned} \right. \end{aligned} \end{aligned}$$
(15)

where \(f\in C(\mathbb {R}^{n},\mathbb {R}^{n})\).

We impose the following additional assumptions:

\((H_{5})\) Suppose exists \(l > 0\) such that \(\Vert f (x)\Vert < l\Vert x\Vert .\)

\((H_{6})\) Suppose that \(Kl+\frac{\eta _{2}}{2}<0,\) where \(\eta _{2}\) is defined in (13).

Theorem 4.4

Assume that \((H_{3})\), \((H_{5})\) and \((H_{6})\) are satisfied. Then the trivial solution of (15) is locally asymptotically stable.

Proof

By Corollary 3.3, any solution of (15) should have the form

$$\begin{aligned} x(t)= & {} Y(t,-\tau )\varphi (-\tau ) +\int _{-\tau }^0Y(t,s)[\varphi '(s)-A\varphi (s)]ds \nonumber \\&+\;\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Y(t,s)f(x(s))ds +\int _{t_{i}}^t Y(t,s)f(x(s))ds. \end{aligned}$$
(16)

By the conditions of \((H_{3})\), (7) reduces to

$$\begin{aligned} \Vert Y(t,s)\Vert\le & {} K(\rho (C)+1+\varepsilon )^{i(s,t)} e^{(\alpha (A)+\alpha +\varepsilon )(t-s)}\nonumber \\\le & {} Ke^{[\alpha (A)+\alpha +\varepsilon +(p+\varepsilon )\ln (\rho (C)+1+\varepsilon )](t-s)}\nonumber \\\le & {} Ke^{\frac{\eta _{2}}{2}(t-s)}. \end{aligned}$$
(17)

Taking norm in two sides of (16) via (17) and \((H_{5})\), one has

$$\begin{aligned} \Vert x(t)\Vert\le & {} Ke^{\frac{\eta _{2}}{2}(t+\tau )}\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0Ke^{\frac{\eta _{2}}{2}(t-s)}\Vert \varphi '(s)-A\varphi (s)\Vert ds \\&+\sum \limits _{j=0}^{i-1}\int _{t_{j}}^{t_{j+1}}Ke^{\frac{\eta _{2}}{2}(t-s)}l\Vert x(s)\Vert ds +\int _{t_{i}}^t Ke^{\frac{\eta _{2}}{2}(t-s)}l\Vert x(s)\Vert ds. \end{aligned}$$

This yields that

$$\begin{aligned} e^{-\frac{\eta _{2}}{2}t}\Vert x(t)\Vert\le & {} Ke^{\frac{\eta _{2}}{2}\tau }\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0Ke^{-\frac{\eta _{2}}{2}s}\Vert \varphi '(s)-A\varphi (s)\Vert ds \\&+Kl\int _{0}^{t}e^{-\frac{\eta _{2}}{2}s}\Vert x(s)\Vert ds. \end{aligned}$$

Let

$$\begin{aligned} T=Ke^{\frac{\eta _{2}}{2}\tau }\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0Ke^{-\frac{\eta _{2}}{2}s}\Vert \varphi '(s)-A\varphi (s)\Vert ds>0. \end{aligned}$$

By using the well-known classical Gronwall inequality (see [31, Theorem 1]), we have

$$\begin{aligned} e^{-\frac{\eta _{2}}{2}t}\Vert x(t)\Vert \le Te^{Klt}, \end{aligned}$$

which yields that

$$\begin{aligned} \Vert x(t)\Vert \le Te^{(Kl+\frac{\eta _{2}}{2})t}\rightarrow 0~~\text{ as }~~t\rightarrow \infty \end{aligned}$$

due to \((H_{6})\). The proof is finished. \(\square \)

5 Examples

In this section, we give two examples to illustrate our above theoretical results. Here, we use MATLAB software to compute some parameters and draw the figures for the examples.

Example 5.1

Consider (1) with \(\tau =0.2\) and

$$\begin{aligned} A= \left( \begin{array}{cc} -3 &{}\quad 0 \\ 0 &{}\quad -2.5\\ \end{array} \right) ,\quad B= \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 0.8 \\ \end{array} \right) ,\quad C_{j}= \left( \begin{array}{cc} 2+\frac{1}{j} &{}\quad 0 \\ 0 &{}\quad 2 \\ \end{array} \right) , \quad j=1,2,\ldots ,\nonumber \\ \end{aligned}$$
(18)

and

$$\begin{aligned} \varphi (t)= \left( \begin{array}{cc} 0.3\\ 0.4 \\ \end{array} \right) , \quad i(0,t)=\left[ \frac{t+1}{2}\right] , \end{aligned}$$
(19)

where [x] is the biggest integer less than real x.

Obviously, \(AB=BA\), \(AC_{j}=C_{j}A\), \(BC_{j}=C_{j}B\), \(j=1,2,\ldots ,\) and \(\alpha (A)=-2.5\), \(\rho (C)=3\). Next, \(\Vert e^{At}\Vert =e^{-2.5t}\le Ke^{(\alpha (A)+\varepsilon )t}\), where \(K=1\) and \(\varepsilon >0\). By computation, \(\Vert \varphi \Vert _{1}=0.4=\Vert \varphi (-\tau )\Vert <\delta :=0.41\), \(p=\lim \limits _{t\rightarrow \infty }\frac{i(0,t)}{t}=\lim \limits _{t\rightarrow \infty }\frac{[\frac{t+1}{2}]}{t}=\frac{1}{2}.\) Next, by using MATLAB software, we obtain

$$\begin{aligned} \Vert B_1\Vert =\Vert e^{-A\tau }B\Vert =\left\| \left( \begin{array}{cc} 1.8221 &{}\quad 0 \\ 0 &{}\quad 1.3190 \\ \end{array} \right) \right\| \le \alpha e^{0.2\alpha }, \quad choose~\alpha =1.3821,\\ M\ge K(e^{(\alpha (A)+\alpha )\tau }\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0 e^{-(\alpha (A)+\alpha )s}\Vert \varphi '(s)-A\varphi (s)\Vert ds)=0.5440>0, \end{aligned}$$

and

$$\begin{aligned} \eta _{2}=\alpha (A)+\alpha +p\ln (\rho (C)+1)=-0.4248<0. \end{aligned}$$

Now all the conditions of Theorem 4.3 are satisfied. Thus,

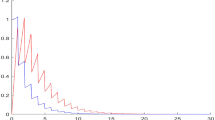
$$\begin{aligned} \Vert x(t)\Vert \le M e^{\frac{\eta _{2}}{2}t}=Me^{-0.2124t}\rightarrow 0~\text{ as }~t\rightarrow \infty , \end{aligned}$$

that is, the trivial solution of (1); (18); (19) is locally asymptotically stable (see Fig. 1).

Fig. 1
figure 1

The state response x(t) of (1);(18);(19)

Full size image
Fig. 2
figure 2

The state response x(t) of (15); (19); (20)

Full size image

Example 5.2

Consider (15) with \(\tau =0.2\) and

$$\begin{aligned}&A= \left( \begin{array}{cc} -3.3 &{}\quad 0 \\ 0 &{}\quad -3.3 \\ \end{array} \right) , \quad f(x(t))= \left( \begin{array}{cc} 0.5\sin x_{1}\\ 0.5\sin x_{2} \\ \end{array} \right) \nonumber \\&B= \left( \begin{array}{cc} 0.8 &{}\quad 0.2 \\ 0 &{}\quad 0.6 \\ \end{array} \right) ,\quad C_{j}= \left( \begin{array}{cc} 3 &{}\quad 0.5 \\ 0 &{}\quad 2.5 \\ \end{array} \right) , \quad j=1,2,\ldots , \end{aligned}$$
(20)

and \(\varphi \), i(0, t) are defined in (19).

By the calculation, \(AB= \left( \begin{array}{cc} -2.64 &{} -0.66 \\ 0 &{} -1.98 \\ \end{array} \right) =BA\), \(AC_{j}= \left( \begin{array}{cc} -9.9 &{} -1.65 \\ 0 &{} -8.25 \\ \end{array} \right) =C_{j}A\),

\(BC_{j}= \left( \begin{array}{cc} 2.4 &{} 0.9 \\ 0 &{} 1.5 \\ \end{array} \right) =C_{j}B,~j=1,2,\ldots .\)

Obviously, \(\alpha (A)=-3.3\). and \(\Vert e^{At}\Vert =e^{-3.3t}\le Ke^{(\alpha (A)+\varepsilon )t}\), where \(K=1\) and \(\varepsilon >0\). In addition, \(\Vert f(x)\Vert < l\Vert x\Vert \), we can choose \(l=0.5\). Next, by using MATLAB software, we obtain

$$\begin{aligned} \Vert B_1\Vert =\Vert e^{-A\tau }B\Vert =\left\| \left( \begin{array}{cc} 1.5478 &{}\quad 03870 \\ 0 &{}\quad 1.1609 \\ \end{array} \right) \right\| \le \alpha e^{0.2\alpha }, \quad and \; choose~\alpha =1.4483. \end{aligned}$$

Moreover, \(\eta _{2}=\alpha (A)+\alpha +p\ln (\rho (C)+1)=-1.1586\), thus,

$$\begin{aligned} T=Ke^{\frac{\eta _{2}}{2}\tau }\Vert \varphi (-\tau )\Vert +\int _{-\tau }^0Ke^{-\frac{\eta _{2}}{2}s}\Vert \varphi '(s)-A\varphi (s)\Vert ds=0.6228>0. \end{aligned}$$

Note that \(Kl+\frac{\eta _{2}}{2}=-0.0793<0.\) Now all the conditions of Theorem 4.4 are satisfied. Then,

$$\begin{aligned} \Vert x(t)\Vert \le Te^{(Kl+\frac{\eta _{2}}{2})t}=0.6228e^{-0.0793t}\rightarrow 0~\text{ as }~t\rightarrow \infty , \end{aligned}$$

that is, the trivial solution of (15); (19); (20) is locally asymptotically stable (see Fig. 2).