1. Introduction

Conventional black-box regression models such as auto-regressive, auto-regressive moving average and the likes are linear models, which were widely used for hydrological forecasting (Abrahart and See 2000; Guang-Te and Singh 1994; Mondal and Wasimi 2006). Based on a basic necessity of being stationary, these models have limited ability to predict non-linear hydrologic time series (Nourani et al. 2011). It is the reason behind a great deal of research into the application of artificial intelligence (AI) techniques in hydrological forecasting. Artificial neural network (ANN) is one of the most popular AI techniques, which has been employed in various fields of hydrological forecasting and successful results have been reported (Altunkaynak 2007; Aytek et al. 2008; Besaw et al. 2010; Can et al. 2012; Dahamshe and Aksoy 2009; Kakahaji et al. 2013; Taormina et al. 2012). A comprehensive review concerning the application of neural networks in river forecasting was presented by Abrahart et al. (2012).

Both short-term and long-term streamflow predictions are required to plan, operate and optimize the activities associated with water resource system (Kisi 2010). Each of them has their own benefits and applications in operational hydrology. Monthly period prediction, as a long-term or transition from short- to long-term period, is useful for many water resource applications such as environmental protection, drought management, and optimal reservoir operation (Wang et al. 2009). However; Short-term forecasts, with lead times of hours or days, are necessary for flood warning systems and real-time reservoir operation (Chang et al. 2004). Based upon the aim of forecasting issue, different kinds of daily, monthly, and annual streamflow prediction models were developed individually by researchers without considering the efficiency of the proposed model in other time horizons and successful results were reported. For instance, genetic programing model (Makkeasorn et al. 2008), wavelet regression model (Kücük and Agiralioglu 2006, Kisi 2010), stand-alone wavelet and cross-wavelet model (Adamowski 2008), and wavelet-ANN model (Kisi 2009, Krishna 2013) were suggested for daily streamflow forecasting. Moreover, an adaptive-network-based fuzzy inference system (Lin et al. 2005), a single station neuro-wavelet model (Cannas et al. 2006), and a wavelet predictor–corrector model (Zhou et al. 2008) were also suggested for monthly streamflow prediction. Coulibaly and Burn (2004) used wavelet analysis method with climatic patterns for both describing inter-annual features and quantifying the temporal variability of Canadian annual streamflow. Their results indicated that streamflow regionalization can be refined based on their wavelet spectra.

As known, streamflow series are highly non-stationary and quasi-periodic signals contaminated by various noises at different flow levels (Wu et al. 2009a). Unsatisfactory prediction results of ANN models have been widely reported for this kind of signals (Cannas et al. 2006; Nourani et al. 2011). ANN models were not also performed good enough in the case of runoff-runoff streamflow prediction due to the lagged prediction effect, which has been mentioned by some researchers (Chang et al. 2007; De Vos and Rientjes 2005; Muttil and Chau 2006; Wu et al 2009a). In such cases, application of data pre-processing methods, such as moving average, singular spectrum analysis, and continues/discrete wavelet transform (WT) integrated with ANN models have been suggested to improve the accuracy of the model (Adamowski and Sun 2010; Cannas et al. 2006; Kisi 2008; Krishna 2013; Niu and Sivakumar 2013; Nourani et al. 2011, Wu et al. 2009b). Application of the abovementioned data pre-processing methods along with some other feasible alternatives was discussed in detail by Chau and Wu (2011).

Our review in the relevant literature showed that hybrid single-station daily/monthly streamflow prediction models have received tremendous attention of researches (e.g. Cannas et al. 2006; Adamowski 2008; Kisi 2009; Shiri and Kisi 2010; Krishna 2013). however, at the best of our knowledge, generalization of NW techniques in successive–station monthly streamflow prediction was not discussed. Thus, the main challenge of this study is to investigate the effect of wavelet-based data pre-processing method on the performance of ANN-based successive-station monthly streamflow predictions models in a perennial river. The successive-station prediction strategy using a pair of upstream-downstream records tends to decrease the lagged prediction effect of commonly proposed single-station runoff-runoff modes, while the wavelet component of the model provides a powerful tool to capture the non-stationary feature of the process. Following this, in the first phase of the current research, we put forward eight black-box ANN-based prediction models using streamflow records from two successive gauging stations on Çoruh River, Turkey. Typical three-layer feed-forward neural network (FFNN) algorithm has been applied to develop the best structure for each model. In the second phase, we applied discrete wavelet decomposition procedure to generate our NW models. Finally, a comparative efficiency analysis between ad hoc FFNN and hybrid NW models has been done in terms of accuracy and simplicity.

Overview of FFNN

FFNN is one of the commonly used ANN techniques that typically involve three parts (American Society of Civil Engineers, ASCE Task committee 2000): including input layers with a number of input nodes, one or several hidden layers, and a number of output nodes. The number of hidden layers and nodes in each layer are two key design parameters. The input nodes do not perform any transformation upon the input data sets. They only send their initial weighted values to the nodes in the hidden layer. The hidden layer nodes typically receive the weighted inputs from the input layer or a previous hidden layer, perform their transformations on it and pass the output to the next adjacent layer which is generally another hidden layer or the output layer. The output layer consists of nodes that receive the hidden-layer outputs and send it to the modeller. Initial weight values are progressively corrected during a training process (at each iteration) that compares predicted outputs with corresponding observations and back-propagates any errors to determine the fitting weights which is required to minimize the errors.

A critical issue in ANN modeling is to avoid likely undertraining and overtraining problems. In the former situation, the network may not be possible to fully detect all attributes of a complex time series, while overtraining may reduce the model capacity for generalization properties. Application of cross-validation or selection of appropriate number of neurons in hidden layer using the trial-and-error procedure with a confined training iteration number (epoch), which were commonly suggested to prevent these problems (Cannas et al. 2006; Elshorbagy et al. 2010a; Wu et al. 2009b; Kisi 2008; Krishna 2013, Nourani et al. 2008 and 2009; Principe et al 2000). The design issues, training mechanisms and application of FFNN in hydrological studies have been the subject of different studies (ASCE Task committee 2000, Abrahart et al. 2012) and the explicit expression for an output value of a three-layered FFNN networks is given by (Nourani et al. 2013). Therefore, to avoid duplication, we only introduced the main concepts of the FFNN here. The FFNN modelling attributes used in this study will be given in Section 5.1.

Wavelet transform

Wavelet transforms (WT) have recently begun to be used as a beneficial data pre-processing tool for hydrological time series. The term wavelet means small wave. The wave refers to the condition that it is oscillatory and the smallness refers to the condition that the function is of finite length (Cannas et al. 2006). By a WT, a time series decomposes into multiple levels of details, sub-time series, which provide an interpretation of the original time series structure and history in both the time and frequency domains using a few coefficients (Nourani et al. 2013). Wavelets are waving-like mathematical functions with amplitude begin at zero, increases, and then decreases back to zero. Figure 1 represents three types of the most popular wavelet functions. As it clear from the figure, a wavelet tends to be irregular and asymmetric unlike the sine waves (Ozger, 2010).

Fig. 1
figure 1

Schematics of a Harr wavelet, b db4 wavelet, and c Meyer Hat wavelet

Full size image

WT appears to be more effective tool than the Fourier transform (FT) in studying non-stationary time series (Partal and Kücük 2006; Partal and Kisi 2007). The main advantage of WT is their ability to simultaneously obtain information on the location and frequency of a signal, while FT separates a time series in to sine waves of various frequencies, WT separates it into shifted and scaled waves using a predefined (or mother) wavelet (Ozger, 2010). WT Advantages compared to FT was discussed in detail by Sifuzzaman et al. (2009).

Continuous wavelet transforms (CWT)

In mathematics, an integral transform (Tf) is particular kind of mathematical linear operator, which has the following form:

$$ \mathrm{Tf}\left(\mathrm{u}\right)={\displaystyle {\int}_{\mathrm{t}1}^{\mathrm{t}2}\mathrm{K}\left(\mathrm{t},\mathrm{u}\right)}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} $$
(1)

where f(t) is an square-integrable function such as a continuous time series and K is a two variable, t and u, function called kernel.

According to Eq. 1, any integral transform is specified by a choice of the kernel function. If function K is chosen as wavelet function, then CWT is (Mallat, 1998):

$$ \mathrm{T}\left(\mathrm{a},\mathrm{b}\right)=\frac{1}{\sqrt{\left|\mathrm{a}\right|}}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\uppsi}^{\ast }}\left(\frac{\mathrm{t}-\mathrm{b}}{\mathrm{a}}\right)\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} $$
(2)

where T(a, b) is the wavelet coefficients, ψ (t) is a mother wavelet function, in time and frequency domain, and * denotes operation of complex conjugate.

The parameter a, is scaling factor which acts as a dilation (a > 1) or a contradiction (a < 1) coefficient of the mother wavelet. When the scaling factor is less than 1, the mother wavelet is more contracted which results more detailed sub-time series. In contrast, the scaling factor greater than 1 means the stretched mother wavelet which results less detail sub-time series. The parameter b is the translation (or position) value and also called time factor of the mother wavelet, which allows the study of the signal f(t) locally around the time b (Kücük and agiralioglu, 2006). The main property of wavelets is localized in both time (b) and frequency (a) whereas the Fourier transform is only localized in frequency.

The CWT calculation produce N2 coefficients from a data set of length N; hence redundant information is locked up within the coefficients which may or may not be a desirable property (Addison et al., 2001; Krishna 2013). As an alternative, the discrete wavelet transform is usually preferred for practical applications in hydrological time series decomposition (Rajaee et al., 2011; Rathinasamy and Khosa, 2012).

Discrete wavelet transforms (DWT)

Hydrologic data usually are recorded in discrete time intervals. Hence, DWT is preferred to CWT for practical applications (Nourani et al. 2013). The wavelet function in its discrete form can be represented as:

$$ {\uppsi}_{\mathrm{a},\mathrm{b}}\left(\mathrm{t}\right)=\frac{1}{\sqrt{\mathrm{a}}}\uppsi \left(\frac{\mathrm{t}-\mathrm{b}}{\mathrm{a}}\right) $$
(3)

where a and b are scaling and position parameters, respectively.

In DWT, wavelet coefficients are commonly calculated at every dyadic step, i.e. the operation of WT is carried out at dyadic dilation (a = 2m) and integer translations (b = 2mn); where m and n are integers that control the wavelet dilation and translation respectively. Therefore, the dyadic wavelet function can be obtained by Eq. (4) and DWT coefficients, Ti (m, n), for a time series such as f (t) can be defined as Eq. (5).

$$ {\uppsi}_{\mathrm{m},\mathrm{n}}\left(\mathrm{t}\right)={2}^{-\mathrm{m}/2}\uppsi \left({2}^{-\mathrm{m}}-\mathrm{n}\right) $$
(4)
$$ {\mathrm{T}}_i\left(\mathrm{m},\mathrm{n}\right)={\displaystyle \sum_{\mathrm{i}=0}^{\mathrm{N}-1}{\uppsi}_{\mathrm{i}}}.\left(\mathrm{t}\right){\mathrm{f}}_{\mathrm{i}}\left(\mathrm{t}\right)={2}^{-\mathrm{m}/2}{\displaystyle \sum_{\mathrm{i}=0}^{\mathrm{N}-1}\uppsi \Big(\left({2}^{-\mathrm{m}}-\mathrm{n}\right){\mathrm{f}}_{\mathrm{i}}\left(\mathrm{t}\right)} $$
(5)

Study area and data

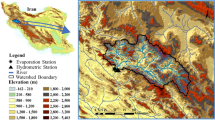
Our study area is Çoruh River, the perennial river in eastern Black Sea region, Turkey (Fig. 2). The river springs from Mescit Mountains in Bayburt and reaches the Black Sea in Batum City of Georgia after a course of 431 kms. Mean annual flow of the river before leaving Turkey’s border is about 200 m3/s. General characteristics of the river catchment were already described by Can et al. (2012).

Fig. 2
figure 2

Location of study area (Çoruh River Catchment)

Full size image

The reliability of any hydrological prediction model will be crucially dependent on the quality of the underlying data. It is therefore important that sufficient attention is placed on gathering good quality data before they are used in prediction analysis. There are 11 successive gauging stations, with deferent recording time period, on the main course of the Çoruh River. Respect to the spatial and temporal consistency of the stations, we selected our study gauges (Fig. 2 stations 2322 and 2315) and observation period (1972–2000) from available data in such a way that provide both the longest and the most reliable records concurrently. Monthly streamflow time series of stations at 29-year period has been depicted in Fig. 3. Table 1 presents the statistical characteristics of the relevant data.

Fig. 3
figure 3

Monthly streamflow time series for the 29-year period

Full size image
Table 1 The monthly statistical parameters of observed streamflow data
Full size table

Çoruh is a shared river between Turkey and Georgia. Monthly streamflow prediction at the lower reach of the river, trans-boundary reach, will help both countries’ water recourses managers make suitable decisions in dry or wet spells or to resolve probable conflicts about sharing of river water.

Prior to the training of our ANN and NW models, the normalization was applied for the data. The main goal of data normalization is to scale the data within a certain range in order to minimize bias within the neural networks. In this study, we applied the following formula for the min-max normalization method (Eq. (6)). This formula rescales target values to lie within a range of 0.1 to 1.0 and produces the arithmetic mean of target values larger than that of common min-max normalization method and at the same time being closer to the mean of activation factor (=0.5 in our networks). In commonly used min-max normalization method with a range of 0.0 to 1.0 (Priddy and Keller 2005), inefficient learning process of ANN is reported (Sajikumar and Thandaveswara 1999; Tahershamsi et al. 2012).

$$ {\mathrm{X}}_{\mathrm{n}}=0.1+0.8\times \left(\frac{\mathrm{X}}{{\mathrm{X}}_{\max }-{\mathrm{X}}_{\min }}\right) $$
(6)

where Xn = normalized value of X, Xmax = maximum value and Xmin = minimum value of each variable of the original data.

After training, the model that yields the best results in terms of Nash-Sutcliffe efficiency (NSE) and root mean squared error (RMSE) can be selected as the most efficient model. NSE (Eq. (7)) is a normalized indicator of the model’s ability to predict about the 1:1 line between observed and predicted data. RMSE (Eq. (8)) measures the root average of the squares of errors. The error is the amount by which the value implied by the estimator differs from the target or quantity to be estimated.

$$ \mathrm{NSE}=1-\frac{{\displaystyle \sum_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{obs}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{pre}}\right)}^2}}{{\displaystyle \sum_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{obs}}-{\mathrm{X}}_{\mathrm{mean}}^{\mathrm{obs}}\right)}^2}} $$
(7)
$$ \mathrm{RMSE}=\sqrt{\frac{{\displaystyle \sum_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{obs}}-{\mathrm{X}}_{\mathrm{i}}^{\mathrm{pre}}\right)}^2}}{\mathrm{n}}} $$
(8)

where X obs i = observed value of X, X pre i = predicted value X obs mean = mean value of observed data and n = number of observed data.

Proposed models and results

At many of the hydrological modeling studies, modelers have developed different empirical relationships between input and output variables based upon single- or multi-step-ahead forecasting scenarios (Chang et al. 2007; Kisi 2004 and 2008; Krishna 2013; Nourani et al. 2009 and 2012). Sudheer et al. (2002) suggested a statistical procedure, based on cross-correlation, autocorrelation and partial autocorrelation properties of the time series for identifying the appropriate input vector for the model. However, Modarres (2009) showed that global statistics are insufficient indicators for the best ANN. In this study, a number of successive-station combinations (Models (1) to (8)) were trained and compared with each other to identify the appropriate input vector. Such an identification methodology has previously applied by Kisi (2004 and 2007) for single-statin daily and monthly streamflow prediction. The structure of the proposed models expressed as follows.

  1. (1)

    Model (1) Dt = f(Dt-1, εt)

  2. (2)

    Model (2) Dt = f(Ut, εt)

  3. (3)

    Model (3) Dt = f(Dt-1, Ut, εt)

  4. (4)

    Model (4) Dt = f(Ut-1, Dt-1, εt)

  5. (5)

    Model (5) Dt = f(Ut-1,Ut, Dt-1, εt)

  6. (6)

    Model (6) Dt = f(Ut-1, Ut, Dt-2, Dt-1, εt)

  7. (7)

    Model (7) Dt = f(Ut-2, Ut-1 , Dt-2, Dt-1, εt)

  8. (8)

    Model (8) Dt = f(Ut-2,Ut-1,Ut,Dt-2,Dt-1, εt)

where D t and Ut represent downstream and upstream monthly streamflow respectively and εt is an uncertainty term (to be minimized).

FFNN modelling results

Our data record is composed of 348 monthly streamflow observations at each station. Due to the temporal consequence of hydrological process, such as streamflow between gauging stations, it is recommended to use the first part of observed time series for training and the rest for the verification (Kisi 2007; Krishna 2013; Nourani et al. 2012). In this study, the first 70 and the rest 30 percentage of 348 observations were selected for training and validation of the networks, respectively. Therefore, the entire data set were divided into two subsets. The statistical parameters of each subset were presented in Table 2.

Table 2 Statistical parameters of subsets
Full size table

At the first stage of streamflow prediction, several three-layer FFNNs with the sigmoid transfer function in hidden layer and linear transfer function in output layer has been developed as a nonlinear modelling structure. It has been proved that three-layer FFNNs are satisfied for the hydrological forecasting (ASCE Task committee 2000; Chau et al. 2005; Nourani et al. 2008; Rezaeianzadeh 2013a). The three-layer FFNN network, which is well known as universal approximator (Hornik et al. 1989), is probably the most popular ANN in the case of nonlinear mapping (Tahershamsi et al. 2012, Krishna 2013). The satisfactory application of the sigmoid and linear transfer functions in hidden and output layers, respectively for streamflow prediction was extensively reported (e.g. Chang et al. 2007, Krishna 2013; Rezaeianzadeh et al. 2013b). Following the structure definition, we trained our models using the Levenberg-Marquardt (LM) algorithm with a useful toolbox available in the MATLAB® software. The LM is one of the Newtonian optimization techniques and more powerful than conventional gradient descent techniques (Kisi, 2007), which widely used in FFNNs (Haykin, 1999). The successful implementation of LM algorithm to train ANN-based hourly, daily, and monthly streamflow prediction models is frequently reported (e.g. De Vos and Rientjes 2005; Chau et al. 2005; Cannas et al. 2006; Kisi 2010)

As broadly suggested in the literature (e.g. Cheng et al. 2005; Chang et al. 2007; Taormina et al. 2012), in this research, a fixed number of input nodes, equals to the number of input time series at each model, a single hidden layer with dynamic nodes varying from 1 to 10 with a step size of 1 in each trial, and one output node (the desired output) was adopted to train the proposed models. Determination of optimum number of neurons in hidden layer is an important aspect of an efficient network. As it mentioned previously, in order to check any under- or over-fitting problem during the training process, a commonly suggested trial-and-error approach (Kisi 2008) is utilized to select the optimum number of neurons in the hidden layer. If the number of nodes in the hidden layer is too small, the network may not have sufficient degrees of freedom to learn the process correctly. On the contrary, if it is too high, the training will take a long time and the network may sometimes overfit (Kisi 2004). Cannas et al. (2006) found that the optimal FFNN models are constructed with a few number of hidden neurons. As it mentioned previously, in present study, the upper hidden neurons threshold was adopted to be 10. The mean square error value at validation step in each trial is used as a criterion for selecting the optimal number of hidden neurons. No significant improvement in model performance was found when the number of hidden neurons was increased from the limit, which is similar to the experiences of other researchers (Cheng et al. 2005; Cannas et al. 2006; Wu et al. 2009b). Results of the best FFNN structure for each model and their performance levels have been tabulated in Table 3. Scatterplots of the best predictions compared to their corresponding observed values were illustrated in Fig. 4.

Table 3 Performance comparison of FFNN and NW techniques at validation period
Full size table
Fig. 4
figure 4

Comparison of dimensionless predicated streamflow for the Calibrations and validations by different models; a Model 1, b Model 2, c Model 3, d Model 4, e Model 5, f Model 6, g Model 7, h Model 8

Full size image

NW modelling results

The proposed NW models are hybrid-ANN models, which mean the pre-processed data via wavelet transform, are entered to the ANN model in order to improve the accuracy of the formerly structured FFNN models. The schematic structure of the proposed NW model is illustrated in Fig. 5. The structure includes two phases. In the pre-processing phase, the original monthly streamflow time series including Dt, Ut and their previous observations are decomposed into sub-series of approximations (A) and details (D) through the high-pass and low-pass filter coefficients of a chosen mother wavelet. In this manner each sub-series may represent a special level of the temporal characteristics of the original input time series. Appropriate mother wavelet may be selected in this phase according to shape pattern similarity between the mother wavelet and the investigated time series (Onderka et al. 2013). The Brute-force search method can also be applied as an alternative to choose an appropriate mother wavelet (Nourani et al. 2013).

Fig. 5
figure 5

Schematic view of proposed NW model

Full size image

Our time series is characterized by a very irregular signal shape, fast decaying and oscillating, thus an irregular mother wavelet, the Daubechies wavelet with four vanishing moments (db4, Fig. 1b) was selected for use (Daubechies, 1990). Nourani et al. (2011) compared the effect of db4 with three different irregular mother wavelets, comprising Haar, Sym3 and Coif1 wavelets, on daily and monthly streamflow prediction and showed that the db4 provides the best performance. The effective application of the db4 for decomposition of non-stationary monthly streamflow time series has also been reported by Cannas et al. (2006). Therefore, in the present study, we applied dyadic DWT with the db4 mother wavelet at different resolution modes (i.e. 2, 4, 8, 16, and 32-month mode) to decompose the original observed streamflow time series. Each resolution demonstrates specific time feature of the investigated time series. In decomposition level 5 (i.e. dyadic dilation a = 32), there is five details (or resolution modes) and one approximation sub-signal. We wrote a special code to use the MATLAB® software for NW simulation in this research. For instance, the approximation (a5) and detail sub- series (d1 through d5) for the streamflow time series of downstream station has been illustrated in Fig. 6.

Fig. 6
figure 6

Approximation and detail sub-series of streamflow at station 2315

Full size image

In the second phase, simulation phase, at first, the three-layer FFNN models are built afresh such that the sub-series, a5 and d1 through d5 in our experiment, of the original time series are the input neurons to the FFNN. Then, training and validation process are performed using the input sub-series to determine output time series. The number of input layer neurons was determined according to the used decomposition level and the output layer neuron was a fixed one. Results for the best NW structure and their performance level compared to those of FFNN are presented in Table 3.

Discussion

The efficiency results of the best developed FFNN and NW models for all proposed combinations are compared in Table 3 using NSE and RMSE indices at the validation period. It can be implied from the table that Model (1) resulted in the lowest achieved performance level. Suggested decomposition process did not also provide any noteworthy improvement in the results of corresponding FFNN. It may be because of introducing insufficient lag time (input neurons) to the models. It indicated that this single-step-ahead monthly streamflow prediction scenario could not provide a suitable prediction model for the river.

Based upon aforementioned successive-station prediction strategy, in the second scenario upstream data records was considered as input neurons instead of increasing in the lag-time of downstream station records. Model (2), provides a downstream flow prediction scenario using only simultaneous upstream station records. Although it makes a considerable improvement in the performance levels of corresponding NW-based model compared with those of Model (1), it does not provide a suitable streamflow prediction model yet (NSE = 0.482). The reason is obviously related to the fact that the mean monthly flow in the study reach has a spatially increasing regime which is also distinguishable in Fig. 3. Comparing with all other scenarios, Model (2) shows that the highest effect of wavelet decomposition on the accuracy of FFNN models occurs in this case. It is due to the fact that temporal characteristics of the downstream time series are thought to be highly simultaneously correlated with time features of upstream sub-series. The results of these first two models also indicated the necessity of additional forecasting lead time and/or efficient input variables.

The first combination of upstream and downstream flow, Model (3), resulted in significant improvement in the performance levels. It implies that that existing sub-basins between the stations have considerable physical effects (i.e., increasing drainage area) on the occurrence of flow at downstream station. This is the reason why we intentionally keep downstream flow at time (t-1), Dt-1, in constructing of the other combinations (Models (4) to (8)). Similar to Model (1), Although NW slightly outperformed FFNN; wavelet decomposition technique did not provide considerable improvement for the ad hoc FFNN in Model (3). It may be due to the presence of inefficient decomposed sub-series within the input nodes of NW. Therefore, it is suggested that suitable filtering strategies would be implemented on the choice of effective decomposed sub-series in future studies. For instance, correlation between decomposed sub-series with original input time series can be used to distinguish the effective discrete wavelet components (Krishna 2013).

Models (4) to (8) represent five effective prediction successive-station combinations with high performance levels, which all perform similar to each other. NW provided comparatively better outcomes than FFNN in all cases. Due to remarkable coherence between the observed and predicted values in these models, there is a very strict competition among them to be chosen as an optimum streamflow prediction model of the river. From Table 3, it is observed that Models (4) and (5) are the most appropriate combinations for streamflow prediction by FFNN and NW. Both of them use downstream and upstream flows at time (t-1) (Dt-1 and Ut-1); however, the former also contains an extra input variable namely upstream flow at time (t) (Ut). Adding one more variable into the input layer of Model (4) intentionally, resulted in imperceptible improvement in FFNN and reduction in NW efficiency. Such a diminishing accuracy is also observed in NW results of Models (6) to (8). This drawback of NW might be due to increasing number of input neurons. Adding one more input variable in our FFNN models generates six more input sub-signals within the corresponding NW structure that significantly increases the complexity of the model. It is important to note that inevitable errors of each input series (sub-series) magnify the total error of the NW, and thus the model efficiency diminishes. Therefore, we suggest the NW modellers to be very careful when selecting the input variables whether or not it is inefficient or efficient multivariable NW model.

The efficiency values of NW-based Model (4) (RMSE = 0.032 and NSE = 0.962) demonstrate that successive-station strategy using only 1-month lag provides the most accurate monthly streamflow prediction model on Çoruh River. It provides more than 60 percentage improvement in NSE value of single-station-1-month-ahead model (i.e. Model (1)). It is why in single-station runoff-runoff models application of at least 3 to 4 lag-times in order to achieve the best modelling structure were commonly recommended (Wu et al. 2009a, b; Kisi 2010; Shiri and Kisi 2010).

Considering all the aforementioned results and the concept of simplicity and applicability as a main issue in modelling, Model (4) has been selected as the best monthly streamflow prediction at station 2315 on Çoruh River. In order to present detailed comparison between the NW and FFNN models, the scatterplots and the plots of the observed and predicted time series of 1-month-ahead forecast for Çoruh River (Model (4)) at validation period were illustrated in Figs. 7 and 8, respectively. The residuals of the models have also depicted in the Fig. 8b.

Fig. 7
figure 7

Scatter plots of predicted data at validation period (station 2315)

Full size image
Fig. 8
figure 8

Predicted and observed monthly streamflow (a) and prediction residuals (b) at station 2315 for validation period

Full size image

These figures show the high ability of both proposed FFNN and NW models to predict the low and medium monthly streamflow (150 < Dt < 400 m3/s). NW is more capable of capturing local extremes (i.e. minima and maxima), global maximums (or annual peaks) than FFNN and generated 5m3/s mean absolute error less than those of FFNN which warrant its superiority to FFNN in overall sense. Furthermore, Fig. 8 shows that some of the FFNN model’s timing of the peaks is lagged. This lagged prediction effect is the result of using antecedent observed values as FFNN inputs without considering any data pre-processing approach, which is consistent with the findings of other researchers (De Vos and Rientjes 2005; Wu et al. 2009a, b). It reveals the fact that the chosen mother wavelet, db4, has performed well as expected.

Conclusion

In this study, we attempted to investigate how and how much a wavelet-based data pre-processing method can improve the performance of the common tree-layer FFNN models in successive-station monthly streamflow prediction. For this aim, we firstly developed eight different FFNN prediction models using historical observations from two successive gauging stations on Çoruh River, Turkey. Then, we tried to optimize our models via a discrete wavelet transform method. Wavelet-transformed data in conjunction with ANN structures generated our proposed hybrid NW models that were capable of capturing useful information about history of the observations on various time resolution levels with the use of only a few coefficients.

The obtained results indicated a promising role of NW in successive-station monthly streamflow prediction, which led all FFNN models to more accurate predictions. Our proposed NW model provides flexible choice of mother wavelet selection to decompose the input time series. The results showed that Daubechies mother wavelet with four vanishing moments provides acceptable outcomes for monthly streamflow decomposition. Therefore, its application to decompose similar monthly streamflow signals is suggested. The comparative analysis between different input combinations pointed out that only 1 month-lagged records of both downstream and upstream stations are enough to establish the best prediction model for the study catchment.

Owing to our study limited to the implementation of a distinct catchment data, applying this approach to pairs of stations from different catchments is suggested to strengthen these conclusions. We evaluated a single ANN algorithm along with a single db4 mother wavelet in order to propose our NW model. Other ANN techniques, such as generalized regression and/or radial basis function algorithms using different mother wavelets (e.g., Harr, Mayer, and others) can also be investigated in order to improve the efficiency of NW-based successive-station streamflow prediction models.