Introduction

Invasive species are thought to be one of the greatest causes of loss of biodiversity in the world (Williamson 1999). Many different aspects of invasions have been object of attention in the last decades. Among those, the spatial dynamics of invasions is one aspect that has attracted a great amount of interest (Shigesada and Kawasaki 1997). The mathematical theory to understand and predict how invasions take place has been being studied to a great extent, and features a variety of mathematical formulations, from reaction–diffusion to integrodifference equation models. Although the assumptions behind each treatment may be different, there are some general results, such as that – in the absence of Allee effects – the spread velocity depends only on dispersal capacity and net reproductive rate at low densities (Kot et al 1996).

Comparison of models with data is in general harmed by the lack of observations about the main parameters present in the models. Although growth ratios can in many cases be inferred from laboratory experiments, the dispersal ability of a given species is difficult to determine. Frequently, models are adjusted to data by fitting the parameters related to dispersal. However, this weakens the model’s validity and precludes testing the model. In this paper we overcome these difficulties in a specific case: we give a model where the parameters determining the speed of invasion are completely fixed by either laboratory experiments or by field observations. With the velocity determined by the parametrized model, we test the predictions in a geographically distinct region, relying on historical data.

Around 1975, Chrysomya albiceps (Calliphoridae), a blowfly species, was brought from Africa to South America by Angolan refugees during the Civil War (Guimarães et al 1978). Although there are records of previous introductions (Baumgartner and Greenberg 1984), only on that occasion the species was established. Afterwards, C. albiceps invaded South America tropical regions in the following decade, displacing other native blowfly species.

Blowflies, as many insects, are stage-structured species. The larval phase accounts for the population regulation, as the population level is essentially determined by the resource availability (in this case, carrion). On the other hand, dispersal is related to the adult stage.

In this paper, we propose a model incorporating stage-structure and dispersal that is capable of predicting the speed of invasion for blowflies of the C. albiceps species using as input parameters fertility and survival data, measured in laboratory, and one-generation dispersal data, assessed by means of capture-recapture techniques in an experiment performed in the 80’s in South Africa. This provides us with a definite speed that is not fitted to the realized invasion, so we are able to compare it to the actual speed of invasion observed in South America.

Although the data used in this case mixes laboratory experiments with field data of different geographical locations, the results about the invasion speed are close to the observed velocity, a point which renews hope that even simple models, taking care of biological particulars and noisy data, can provide meaningful information about the dynamics of invasions.

Finally, we point out that the model presented below also displays an interesting mathematical structure, which has already been seen in previous works, (Kot 1992; Andersen 1991). In fact, as the dynamical stage of the model shows a bifurcation route to chaos, when space is incorporated the resulting model reveals the formation of spatial non-stationary structures.

The model

C. albiceps life cycle consists of egg-larvae-adult stages. The female adults deposit large masses of eggs onto carrion or feces, that are consumed by the larvae after eclosion, which go through three instars before emerging as adults, which are able to fly and search for new carcasses.

These blowflies are known to display intraguild predation as well as cannibalism in the larval stage (Ullyett 1950), which contributes to a strong density dependence during the larval period with overcompensation (Godoy et al 2001), that is, declining recruitment with increasing density of larvae, affecting both survival and fertility rates.

Successful invasive species are expected to be regulated by bottom-up processes: the release from predatory pressure in a given region – taking the species out of a self-regulated community – makes the population level dependent on the available resources (Sakai et al 2001). This fact simplifies the mathematical modeling of invasions, as relevant results can be obtained by means of single-species models.

The local dynamics

Let us begin by building our model presenting the local dynamics equations. We consider a simple, two-stage difference model, following the results of Prout (Prout and McChesney 1985). It accounts for growth and competition for resources in the larval stage, without any spatial dynamics yet:

$$ u_{t} = S^* v_t\, e^{-s v_t} \quad , $$
(1)
$$ v_{t+T} = \frac{1}{2} F^* u_t\, e^{-f v_t} \quad . $$
(2)

In the above equations u represents adult female population density and v the larval density. S * and F * are to be interpreted as maximum survival and fertility rates, while s and f are related to density effects on those rates. Also, each time step corresponds to a complete generation time, the egg-to-egg interval T.

C. albiceps is a semelparous species, that is, it oviposits only once. Also, it feeds on ephemeral resources, so that competition tends to be important only between individuals of the same generation. This indicates that the assumption of discrete time dynamics is a sensible choice.

The spatial dynamics

We proceed by introducing spatial dynamics into the model through a redistribution kernel K(x, x′; y, y′). In the case at hand, only the adult population is responsible for the dispersal, since the spread of larvae occurs at a much smaller scale. The redistribution kernel should thus describe the contribution of adults emerging at (x′,y′) at time t to the larvae at (x,y) at the next next generation (at time t + T), through oviposition. Adopting a discrete-time, continuous space description, the equations will read (Kot 1992):

$$ u_{t}(x,y) = S^* v_t(x,y)\, e^{-s v_t(x,y)}, $$
(3)
$$ \begin{array}{rll} v_{t+T}(x,y) &=& \frac{1}{2} F^* \iint u_t(x',y') \\ && \times \ e^{-f v_t(x',y')} K(x, x'; y, y') dx'dy' ~ , \end{array} $$
(4)

where the parameters are the same as in Eqs. 1 and 2.

Spatial homogeneity

In the above equation we have assumed that the parameters F *, S *, s and f do not depend on the spatial location. This cannot be true on every spatial scale as, for instance, f and s are related to the carrying capacities which, in turn, are related to the availability of resources. We certainly have fragmentation at small scale, since carcasses are distributed heterogeneously in space, but the invasion’s spatial scale is much larger than that. In view of that, we will treat space as homogeneous, taking all parameters as averaged, which corresponds to the homogenization limit (Shigesada et al 1986). Accordingly, variability in small spatial scale is not to be predicted by our model.

Spatial heterogeneity on a larger scale may still be of relevance, but for that the problem would have to satisfy two conditions (Pachepsky and Levine 2011): (a) discrete number of individuals, that is, insufficient size of propagules, such that it is necessary that the population build up in order to be able to go forward; and (b) completely inhospitable barriers between patches. None of them are verified, since (a) a single – female – blowfly may propagate the invasion, having a very high recruitment, such that the number of propagules is always as high as it can be; and (b) blowflies are generalists, feeding on all kinds of decaying organic material, from feces to carcasses, so that they are able to survive in most places (Richards et al 2009).

Ricker-like model

The system of equations can be rewritten as a single equation for larvae only, where adults are not explicitly modeled, but may be seem as a means of propagation from one generation to the next:

$$ \begin{array}{rll} v_{t+T}(x,y) &=& \frac{1}{2} F^* S^* \iint v_t(x^\prime,y^\prime) \\ &&\times \ e^{-(f+s) v_t(x^\prime,y^\prime)} K(x, x^\prime; y, y^\prime) dx^\prime dy^\prime ~. \end{array} $$
(5)

It is clear that this model is of the Ricker form (Ricker 1954), so its local dynamics, which is well known (May and Oster 1976), exhibits complex behavior for high values of the product S * F *, presenting a period-doubling bifurcations route to chaos as the product of those parameters increases.

The redistribution kernel

In order to progress, an assumption has to be made about the form of the redistribution kernel. We will consider, in what follows, two cases. First, we will look to the one-dimensional case. This will allow us to get a simplified view of the dynamics and use previous results to calculate the speed of the invasion front. Next, we will look to the two-dimensional case on the semi-plane, with zero-flux conditions on the border. This represents additional biological realism, as the actual invasion process for C.albiceps in the Neotropics was initiated at a coastal zone and directed inland.

For the one-dimensional case, we make the simplifying assumption that the redistribution kernel is Gaussian. Even though it is usually argued that real populations tend to show leptokurtic kernels (Okubo and Levin 1989; Neubert et al 1995; Kot et al 1996), we seek to keep behavior-related assumptions to a minimum, though keeping in mind that we may be underestimating dispersal. Such choice yields the following model:

$$ \begin{array}{rll} v_{t+T}(x) &=& \frac{F^* S^*}{2 \sqrt{\pi} \sigma} \int_{-\infty}^{+\infty} v_t(x^\prime) \\ &&\times \ e^{-(s+f) v_t(x')}\, e^{-(x-x')^2/\sigma^2} dx' ~, \end{array} $$
(6)

where now we have another parameter, σ, which measures the typical distance an adult individual roams before ovipositing. On this interpretation, we neglect the effect of another female oviposition besides the first.

For the two-dimensional case, we assume independence of the x and y directions. This allows us to consider a product kernel, \(K(x, x^\prime; y, y^\prime) = K_x(x, x^\prime) K_y(y, y^\prime) \). Considering the semi-plane defined by x ≥ 0, the kernel reads:

$$ K_y(y, y^\prime) = \frac{1}{\sigma \sqrt{\pi}}\, e^{-\frac{(y-y^\prime)^2}{\sigma^2}} $$
(7)
$$ K_x(x, x^\prime) = \begin{cases} \dfrac{1}{\sigma \sqrt{\pi}} \left[ e^{-\frac{(x-x^\prime)^2}{\sigma^2}} + e^{-\frac{(x+x^\prime)^2}{\sigma^2}}\right] \text{ if } x^\prime \geq 0~,\\ 0 \text{, otherwise.} \end{cases} $$
(8)

\(K_y(y,y^\prime)\) is the Gaussian kernel in the unbounded direction. The expression for \(K_x(x,x^\prime)\) can be derived under the same assumptions used to derive a Gaussian kernel, but with a reflexive boundary at x = 0. Indeed, both expressions can be obtained from the assumption that the underlying process is Markovian, with equal probabilities in each direction (Chandrasekhar 1943). We note furthermore that with this kernel, the integral appearing in Eq. 5 is not a convolution anymore, as \(K_x(x,x^\prime)\) does not depend only on the difference x − x′.

Results

One-dimensional case

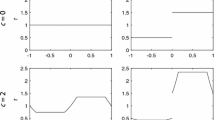
The model defined by the kernel given in Eq. 6 leads to complex spatial and temporal dynamics for sufficiently large F * and S * parameters as can be seen in Fig. 1. This was to be expected, since the local dynamics already showed such complex behavior (Kot 1992; Andersen 1991). The population density oscillates irregularly both in space – if we look at a “snapshot” in time – and in time – given a fixed spatial location. It is not, however, our intention to reassess the typical dynamics of the Prout model. Rather, we proceed to consider the spatial effects that are connected to observations.

Fig. 1
figure 1

Population density evolution, with realistic parameters for C. albiceps invasion: F * S * = 130, s + f = 0.1 and σ = 10.8. In the first plot we show the initial condition, a small, localized population

Full size image

We turn now to the calculation of the speed of invasion. As in many models with the same ingredients, dispersal and nonlinearity, we have essentially two solutions – one is the null solution, and the other shows complex dynamics, (Kot 1992). Connecting both of them, there is a wave front. After a short interval, the speed of invasion converges to a constant, as can be seen by numerically integrating the equations. We point out that the spatial scale is fixed by the parameter σ, so that the space units are fixed with respect to it, and so it is expected that the invasion speed should be proportional to σ, as it will indeed turn out.

The upper bound of the velocity, c, of the front of invasion in terms of the model parameters was given by Kot et al (1996):

$$ c = \sigma \sqrt{\log{\frac{F^* S^*}{2}}} $$
(9)

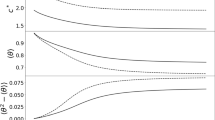
For sake of completeness, in Fig. 2 we display also how the maximum fertility and survival rates affect invasion velocity.

Fig. 2
figure 2

Analytical upper bound for the invasion speed as a function of the parameter’s product F * S *, for both one and two-dimensional cases

Full size image

It is worthy to emphasize that the front velocity does not depend on the parameters f and s. These parameters measure fertility and survival drop rates when population density increases, that come into play only at higher densities and do not interfere in the velocity of invasion. We note, however, that it has been argued recently that density dependence can play a role in spread velocity (Pachepsky and Levine 2011) when the landscape is fragmented and populations are discrete, that is, when the approximation of continuously varying, infinitesimal populations is not sensible.

Two-dimensional case

The two-dimensional case has been treated numerically and the solution is displayed in Fig. 3. The results have been obtained using realistic parameters estimated in the next section.

Fig. 3
figure 3

Solution of the two-dimensional model results, with F * S * = 130, s + f = 0.1 and σ = 8. We can see the front of invasion expanding in one generation, as well as a pattern of peaks and valleys in the region already occupied by the population. At t = 0 the initial condition consists of a localized population around the origin

Full size image

In Appendix B we show that, although theory in general predicts that the upper bound for invasion velocities is lower in two-dimensional domains than in one-dimensional ones (Fort 2007), the Gaussian kernel is a special case in which both velocities are the same. We show that this happens in general when the kernel is separable, id est when the probability of displacement in each direction is independent of the displacement in the other direction.

In the full nonlinear case, we show numerically that, after a transient, the distance travelled per generation along any ray with origin in (0,0), is constant. Therefore the invasion speed is also constant, and indeed has the same value as in the one-dimensional case. This is in agreement with what the results of Appendix B suggest.

The general aspect of the spatial configuration of the solutions corresponds to non-stationary patterns with a spatially complex dynamics, just as in the one-dimensional case, Fig. 1. In the next section we comment on the actual detectability of such patterns.

Parameter estimates and comparison with observations

In this section, we reuse data from the literature to feed the model developed in the last section in order to obtain a prediction of the velocity of invasion. In using and analyzing that data, it is crucial to bear in mind that predictability may be hindered by “founder effects” (Melbourne and Hastings 2009), so that the variability of the relevant life-history traits must be taken into account. In that spirit, what we provide is a range of values for the invasion speed.

Godoy et. al. (Godoy et al 2001) measured fertility and survival data for C. albiceps, finding S * to be approximately 0.5±0.1 and F * 260±40 total eggs/female in 10 days. They also validate the Ricker form of the local population dynamics, although the parameters f and s found are related to the amount of resources used in their particular experiment.

To estimate σ, we use data from a capture-recapture field experiment which was conducted in South Africa in 1985 (Braack and Retief 1986). It consisted in the release of 16,000 radioactively marked C. albiceps blowflies in a certain point and the subsequent recapture, after 5 to 7 days, in large traps spread throughout the field at different distances from the release point. We rework the published data taking into account the local habitat preference as well as the sampling effort, as detailed in the Appendix A. We then proceed to calculate σ fitting the best Gaussian with a least squares method, shown in Fig. 4, along with the histogram of the data treated as described. The estimative is rough, given the limitations of the measurement, but it is taken on the field instead of in the lab, so the data is more likely to reflect the characteristics of the in natura population.

Fig. 4
figure 4

Least squares fit of analyzed dispersal data from (Braack and Retief 1986). Dotted lines indicate minimum and maximum acceptable width parameter

Full size image

Figure 4 shows that σ is about 10.8 km, in the range 7 − 14 km. Using these value for σ along with the data for F * and S *, we find that the velocity per generation is about 20 km/generation, with the range between 14 and 30 km/generation.

To calculate the actual velocity, we need to estimate the generational time of the blowflies in the field. Laboratory experiments show that time from hatching to eclosion is highly dependent on temperature, ranging from 10 to 30 days for temperatures between 17 and 25°C (Al-Misned et al 2002; Richards et al 2008). Also, from the field experiment performed by Braack in the Kruger Park (RSA) (Braack and Retief 1986), which presents temperatures similar to the State of São Paulo, we can estimate that the flying stage lasts between 5 and 10 days, which leads to an egg-to-egg time of 15 to 35 days (Table 1).

Table 1 Summary of parameter ranges used
Full size table

Using the previous results and taking into account these estimates for generational time, our models predict dispersal velocity between 0.4 and 2.0 km/day for C. albiceps invasion in the Neotropics.

In order to compare these results with the actual invasion in the Neotropics, we resort to historical data published in the 70’s and early 80’s. Baumgartner and Greenberg (1984) estimated C. albiceps invasion velocity between 1.5 and 1.8km/day. We also retrieved data stating the first observation of C. albiceps in 73 locations in Brazil (Guimarães et al 1979). This allows us to estimate the upper bound for the invasion velocity, which turns out to be 2.0km/day. The estimated range that we had calculated above, between 0.4 and 2.0km/day, is in agreement with the actual invasion speeds.

Finally, we notice that the spatio-temporal patterns observed in the dynamics of the models (see, for instance, Figs. 1 and 3 are not expected to be observable in field experiments, as they occur in a spatial scale close to σ, which is the scale in which the homogenization limit, discussed in Section “The model”, breaks down.

Conclusions and final comments

Invasive species present a rich variety of situations where the use of mathematical models is helpful to provide a theoretical setting, allowing to assess questions such as invasibility and the dynamics of actual invasions.

The results that we have obtained combine laboratory parameters (fertility and survival) with dispersal data from a field experiment for one-generation, leading to prediction of the invasion speed of the species. The agreement of this result with the velocity of an actual invasion in another geographical range is by no means trivial. The combination of data obtained at different spatial and temporal scales could have hampered the applicability of the models. Indeed, that has been the case, for instance, with the model predictions for an invasive shrub in North America studied by Neubert and Parker (2004). Although observations connected to the pattern of spread have showed agreement with theory (Nash et al 1995; Kot et al 1996; Mistro et al 2005), quantitative predictions have seldom been tested. Even in continuous time models, more often it is the spread pattern, such as a front of constant velocity, that has been verified, but see Giuggioli et al. (2005).

The fact that the model predictions are supported by data is probably related to the generalist behavior of the C. albiceps species with respect to the use of habitat, being found in wide climatic and geographical ranges (Richards et al 2009). This not only makes the application of data collected in Africa to the Neotropics sensible, but also strengthens the case for the assumption of homogeneous space, as in the models presented above. The spatially homogeneous model yielded consistent results at a scale of 102-103 kilometers.

In this work we have introduced a two-dimensional redistribution kernel defined on the semi-plane, thus breaking radial symmetry of the equations. With the assumption of a completely reflexive boundary, the solutions of the model, obtained numerically, give results similar to the one-dimensional case, although the invasion speed is slightly larger. To our knowledge, two-dimensional kernels have been explored only in a few cases, as for example in Lindström et al. (2011).