Dynamical behavior of a stochastic Nicholson’s blowflies model with distributed delay and degenerate diffusion

Abstract

The mathematical model with time delay is often more practical because it is subject to current and past state. What remains unclear are the details, such as how time delay and sudden environmental changes influence the dynamic behavior of systems. The purpose of this paper is to analyze the long-time behavior of a stochastic Nicholson’s blowflies model, which includes distributed delay and degenerate diffusion. The application of the Markov semigroups theory is to prove that there exists a unique stationary distribution. What’s more, the expression of probability density function around the unique positive equilibrium of the deterministic model is briefly described under a certain condition. The results of this paper can be used to find that the weaker white noise can guarantee the existence of a unique stationary distribution and the stronger mortality rate can cause the extinction of Nicholson’s blowflies. Some numerical examples are also given to explain the effect of the white noise.

1 Introduction

In recent decades, using biological models to study the survival problem of populations is a extraordinary significant method and a hot topic of concern. In particular, attention is concentrated on qualitative analysis of population model by many mathematicians and biologists. Besides, Nicholson’s blowflies model belongs to a class of biological systems and its analog equation is more consistent with the experimental data [1]. Therefore, it is more realistic to study the dynamic behavior of Nicholson’s blowflies model.

To the best of our knowledge, since Gurney et al. [1] presented Nicholson’s blowflies model, which explains Nicholson’s blowflies data more accurately, the model and its modifications have been widely studied [1,2,3,4,5]. For example, Zhu et al. [2] discussed the global existence of positive solution for a stochastic Nicholson’s blowflies model with regime switching and obtained path estimation. Xiong et al. [3] investigated the global exponential stability of positive pseudo-almost periodic solution. Next, we will explain why it is more meaningful to build Nicholson’s blowflies model with distributed delay and white noise.

On the one hand, when modeling ecosystem dynamics, it is desirable to take into account models that not only depend on the current situation but also on their past state. The above model cannot explain such phenomenon [1,2,3,4,5], while the time delay can better describe this phenomenon [6,7,8,9]. Nevertheless, it is difficult to analyze the long-time behavior of discrete time-delay equations. Hence, we use distributed delay to characterize the dynamic behavior of discrete delay equations. For instance, Wang et al. [6] studied the asymptotic stability of the positive equilibrium for a Lotka–Volterra predator–prey system of population allelopathy with distributed delay and proved Hopf bifurcations. Al-Omari et al. [8] analyzed global stability in a population competition system with distributed delay and harvesting. However, the difference between this paper and the above articles is that we study the long-term behavior of Nicholson’s blowflies model.

On the other hand, few people assume that the environment is constant in real life. Due to the influence of environmental factors (such as weather, food supply and so on.), it is reasonable and practical to investigate the biological system with environmental noise. Many scholars analyzed the time-delay model with random noise [10,11,12]. For example, Hu et al. [10] proved that there is a global almost surely positive solution and obtained asymptotic path estimation of the solution for a stochastic Lotka–Volterra system with unbounded distributed delay. Liu et al. [11] discussed long-time behavior for a stochastic logistic model with distributed delay. Even though, as far as we know, very few studies have been done to think over the influence of distributed delay and environmental noise into Nicholson’s blowflies model.

The originality of this paper is as follows: (i) The white noise and distributed delay are all taken into account in the Nicholson’s blowflies model. (ii) Extinction and asymptotic stability for a stochastic Nicholson’s blowflies model with distributed delay is solved. (iii) The expression of the probability density function around the positive equilibrium point of the deterministic system is obtained. In addition, the questions addressed of this paper are as follows: (i) What are the conditions for the existence of probability density function around the positive equilibrium point of the deterministic system? (ii) How does the white noise affect the growth of Nicholson’s blowflies?

To answer the above questions, the layout of this paper is as follows: the second part mostly formulates the stochastic Nicholson’s blowflies model with distributed delay and some preliminaries are put forward. In Sect. 3, we present the main results for the strong kernel case, which include the existence and uniqueness of globally positive solution, extinction of Nicholson’s blowflies, asymptotic stability and probability density function of Nicholson’s blowflies model. In Sect. 4, there are some results for the weak kernel. In Sect. 5, we make simulations to confirm our results. Section 6 concludes the paper.

2 The model formulation and some preliminaries

We first formulate a stochastic Nicholson’s blowflies model with distributed delay in Sect. 2.1.

2.1 The model formulation

A classic Nicholson’s blowflies model was presented by Gurney et al. [1] as follows:

$$\begin{aligned} dX(t) =\left[ -\delta X(t) +pX(t-\tau )e^{-aX(t-\tau )}\right] dt, \end{aligned}$$

(1)

with initial conditions $X(s)=\phi (s)$, for $s\in [-\tau ,0]$, $\phi \in C([-\tau ,0],[0,+\infty ))$, $\phi (0)>0$. All parameters in model (1) are assumed to be positive and listed in the Table 1.

Table 1 List of parameters and their meanings in model (1)

Noting that the Nicholson’s blowflies model (1) is a discrete delay equation, but it is not easy for a discrete delay equation to analyze its long-time behavior. To better explain the dynamic behavior of the model (1), we introduce continuous time delay into the model (1) is as follows:

$$\begin{aligned} dX(t)= & {} \left[ -\delta X(t) +p\int _{-\infty }^{t}f(t-s)X(s)e^{-aX(s)}\mathrm{d}s\right] \nonumber \\&dt, \end{aligned}$$

(2)

where the kernel $f:[0,\infty )\rightarrow [0,\infty )$ is a function of time. The article [13] of Macdonald demonstrated that the distribution delay obeys Gamma distribution, that is,

$$\begin{aligned} f(t)=\frac{t^{n}\alpha ^{n+1}e^{-\alpha t}}{n!},~t\in (0,\infty ), \end{aligned}$$

with $\alpha >0$ and $n\ge 0$. As is known to all, we get a strong kernel for $n=1$ while weak kernel for $n=0$, i.e.,

$$\begin{aligned} (i)~f(t)= & {} \alpha ^{2}te^{-\alpha t}~~(n=1),~~~~~ \nonumber \\ (ii)~f(t)= & {} \alpha e^{-\alpha t}~~(n=0). \end{aligned}$$

Define

$$\begin{aligned} \begin{aligned} Y(t)&=\int _{-\infty }^{t}\alpha ^{2}(t-s)e^{-\alpha (t-s)}X(s)e^{-aX(s)}\mathrm{d}s,\\ Z(t)&=\int _{-\infty }^{t}\alpha e^{-\alpha (t-s)}X(s)e^{-aX(s)}\mathrm{d}s, \end{aligned} \end{aligned}$$

according to the linear chain technique, then the following equivalent system of the above system (2) is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dX(t) &{}=\left[ -\delta X(t) +pY(t)\right] dt,\\ dY(t) &{}=\alpha \left[ Z(t)-Y(t)\right] dt,\\ dZ(t) &{}=\alpha \left[ X(t)e^{-aX(t)}-Z(t)\right] dt. \end{aligned} \end{array}\right. } \end{aligned}$$

(3)

If $\delta <p$, then there exists a unique positive equilibrium point:

$$\begin{aligned} E^{*}= & {} (X^{*},Y^{*},Z^{*})\\= & {} \left( -\frac{1}{a}\ln \frac{\delta }{p},-\frac{\delta }{ap}\ln \frac{\delta }{p},-\frac{\delta }{ap}\ln \frac{\delta }{p}\right) . \end{aligned}$$

Model (3) is unavoidable affected by external environment factors due to the randomness of real life. We consider that the per capita adult mortality daily rate $\delta$ is subject to the white noise. Thus, $\delta$ is replaced by $\delta -\sigma \dot{B}(t)$ , where B(t) is a one-dimensional standard Brownian motion and $\sigma ^{2}$ is the white noise intensity. The deterministic Nicholson’s blowflies model with distributed delay can be transformed into the following stochastic model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dX(t) &{}=\left[ -\delta X(t) +pY(t)\right] dt+\sigma X(t)dB(t),\\ dY(t) &{}=\alpha \left[ Z(t)-Y(t)\right] dt,\\ dZ(t) &{}=\alpha \left[ X(t)e^{-aX(t)}-Z(t)\right] dt. \end{aligned} \end{array}\right. } \end{aligned}$$

(4)

We will present the following desirable definitions and lemmas in Sect. 2.2 after we formulate the stochastic model with distributed delay.

2.2 Some preliminaries

We define $(\Omega , \mathcal {F}, \{\mathcal {F}_{t}\}_{t\ge 0}, \mathbb {P})$ be a complete probability space with a natural filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions (i.e., it is increasing and right continuous while $\mathcal {F}_{0}$ contains all $\mathbb {P}$-null sets), and B(t) is defined on this complete filtrated probability space. Define

$$\begin{aligned} \mathbb {R}_{+}^{3}=\{(X,Y,Z)\in \mathbb {R}^{3}:~X>0,~Y>0,~Z>0\}. \end{aligned}$$

Consider the n-dimensional SDE:

$$\begin{aligned} d\hat{X}(t) = \tilde{b}(\hat{X}(t),t)dt + g(\hat{X}(t),t)dB(t), \end{aligned}$$

(5)

with its initial value $\hat{X}(0) = \hat{X}_{0} \in \mathbb {R}^{n}$. Let $C^{2,1}(\mathbb {R}^{n} \times [t_{0},\infty ); \mathbb {R}_{+})$ be the family of all nonnegative real-valued functions $V(\hat{X}, t)$ defined on $\mathbb {R}^{n} \times [t_{0},\infty )$ which satisfies continuously twice differentiable in $\hat{X}$ and once in t. The differential operator L of Eq. (5) is defined as

$$\begin{aligned}&L=\frac{\partial }{\partial t}+\sum _{r=1}^{r}\tilde{b}_{r}(\hat{X}(t),t)\frac{\partial }{\partial \hat{X}_{i}}\\&\quad \qquad +\frac{1}{2}\sum _{i,j=1}^{r}[g^{T}(\hat{X}(t),t)g(\hat{X}(t),t)]_{ij}\frac{\partial ^{2}}{\partial \hat{X}_{i}\partial \hat{X}_{j}}. \end{aligned}$$

If L acts on a function $V\in C^{2,1}(\mathbb {R}^{n} \times [t_{0},\infty ); \mathbb {R}_{+})$, then

$$\begin{aligned}&LV(\hat{X},t)= V_{t}(\hat{X},t)+V_{\hat{X}}(\hat{X},t)\tilde{b}(\hat{X}(t),t)\\&\quad +\frac{1}{2}trace[g^{T}(\hat{X}(t),t)V_{\hat{X}\hat{X}}g(\hat{X}(t),t)], \end{aligned}$$

where $V_{t}=\frac{\partial V}{\partial t}$, $V_{\hat{X}}=(\frac{\partial V}{\partial \hat{X}_{1}},\frac{\partial V}{\partial \hat{X}_{2}},\ldots ,\frac{\partial V}{\partial \hat{X}_{n}})$ and $V_{\hat{X}\hat{X}}=(\frac{\partial ^{2}V}{\partial \hat{X}_{i}\partial \hat{X}_{j}})_{n\times n}$.

Lemma 2.1

[2] If $F(x)=xe^{-ax}$, $\forall a>0, x>0$, then $F(x)\le \frac{1}{ae}$.

2.2.1 Markov semigroup

Next, some fundamental definitions and results with regard to Markov semigroup are proposed.

Define $\mathbb {X}=\mathbb {R}_{+}^{3}$, $\Sigma =\mathbb {D}$ be the $\sigma$-algebra of Borel subsets of $\mathbb {X}$ and m be a Lebesgue measure of the space $(\mathbb {X}, \Sigma )$. Let $\mathbb {D}$ contain all densities, i.e.,

$$\begin{aligned} \mathbb {D}=\{g\in L^{1}:g\ge 0,~\Vert g\Vert =1\}, \end{aligned}$$

where $\Vert \cdot \Vert$ is the norm of the Lebesgue measure space $L^{1}=L^{1}(\mathbb {X}, \Sigma , m)$. If $P(\mathbb {D})\subset \mathbb {D}$, then a linear mapping $P:L^{1}\rightarrow L^{1}$ is known as Markov operator [14].

Definition 2.2

[15] If there is a measurable function $k: \mathbb {X}\times \mathbb {X}\rightarrow [0, \infty )$ satisfying

$$\begin{aligned} \int _{\mathbb {X}}k(\mathbf {x}, \mathbf {y})m(\mathrm{d}\mathbf {x})=1,~~~ \forall ~ \mathbf {y}\in \mathbb {X}, \end{aligned}$$

then

$$\begin{aligned} Pg(\mathbf {x})=\int _{\mathbb {X}}k(\mathbf {x}, \mathbf {y})g(\mathbf {y})m(\mathrm{d}\mathbf {y}), \end{aligned}$$

P is called an integral Markov operator and the function k a kernel.

A family of Markov operators $\{P(t)\}_{t\ge 0}$ which satisfies the following three conditions:

(1):

$P(0)=Id$ (Id is the identity matrix);

(2):

$P(t+s)=P(t)P(s)$ for every $s, t\ge 0$;

(3):

$\forall g\in L^1$, the function $t\mapsto P(t)g$ is continuous concerning the $L^1$-norm; is known as a Markov semigroup.

Definition 2.3

[15] A Markov semigroup $\{P(t)\}_{t\ge 0}$ is known as asymptotically stable if there is an invariant density $g*$ satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert P(t)g-g*\Vert =0,~~\forall g\in \mathbb {D}. \end{aligned}$$

Definition 2.4

[15] A Markov semigroup $\{P(t)\}_{t\ge 0}$ is known as sweeping concerning a set $A \in \Sigma$ if

$$\begin{aligned} \lim _{t\rightarrow \infty } P(t)g(\mathbb {X})m(d\mathbb {X})=0,~~\forall g \in \mathbb {D}. \end{aligned}$$

Lemma 2.5

[15] Assume that $\{P(t)\}_{t\ge 0}$ be an integral Markov semigroup with the continuous kernel $k(t, \mathbf {x}, \mathbf {y})$ for $t>0$ of satisfying $\int _{\mathbb {X}}k(t, \mathbf {x}, \mathbf {y})m(\mathrm{d}\mathbf {x})=1$ for all $y\in \mathbb {X}$. If

$$\begin{aligned} \int _0^\infty P(t)g(\mathbf {x})\mathrm{d}t>0,~~\forall g\in \mathbb {D}~~a.e. \end{aligned}$$

Then the Markov semigroup is asymptotically stable or is sweeping concerning compact sets.

If a Markov semigroup $\{P(t)\}_{t\ge 0}$ is asymptotically stable or is sweeping for a sufficiently large family sets, then its property is known as the Foguel alternative.

2.2.2 Fokker–Planck equation

Denote the transition probability function by $\mathscr {P}(t, x, y,z, A)$, for any $A\in \Sigma$ and the diffusion process (X(t), Y(t), Z(t)), i.e.,

$$\begin{aligned} \mathscr {P}(t, x, y, z, A)=\text {Prob}\{(X(t), Y(t), Z(t))\in A\}, \end{aligned}$$

where (X(t), Y(t), Z(t)) of (4) is a solution with the initial condition $(X(0), Y(0), Z(0))=(x, y, z)$. If $t>0$, the distribution of (X(t), Y(t), Z(t)) is absolutely continuous with regard to the Lebesgue measure, then there is also a density U(t, x, y, z) of (X(t), Y(t), Z(t)) which satisfies the following Fokker–Planck equation [16]:

$$\begin{aligned}&\frac{\partial U}{\partial t}=\frac{\sigma ^2}{2}\frac{\partial ^2(x^2 U)}{\partial x^2}-\frac{\partial (f_1(x, y, z)U)}{\partial x}\nonumber \\&\quad -\frac{\partial (f_2(x, y, z)U)}{\partial y}-\frac{\partial (f_3(x, y, z)U)}{\partial z}, \end{aligned}$$

(6)

where

$$\begin{aligned} f_1(x, y, z)= & {} -\delta x +py,~ f_2s(x, y, z)=\alpha (z-y)~\text{ and }\\ f_3(x, y, z)= & {} \alpha (xe^{-ax}-z). \end{aligned}$$

A Markov semigroup related to (6) is briefly described now. Let $P(t)V(x, y, z)=U(t, x, y, z)$, $\forall ~V\in \mathbb {D}$. Based on the operator P(t) is a contraction on $\mathbb {D}$, it can be extended to a contraction on $L^1$. The operators $\{P(t)\}_{t\ge 0}$ can form a Markov semigroup. The infinitesimal generator of $\{P(t)\}_{t\ge 0}$ is denoted by $\mathscr {A}$, i.e.,

$$\begin{aligned}&\mathscr {A}V=\frac{\sigma ^2}{2}\frac{\partial ^2(x^2 V)}{\partial x^2} -\frac{\partial (f_1(x, y, z)V)}{\partial x}\\&\qquad \qquad -\frac{\partial (f_2(x, y, z)V)}{\partial y}-\frac{\partial (f_3(x, y, z)V)}{\partial z}. \end{aligned}$$

The adjoint operator of $\mathscr {A}$ is:

$$\begin{aligned}&\mathscr {A}^*V=\frac{\sigma ^2}{2}\frac{\partial ^2(x^2 V)}{\partial x^2}+\frac{\partial (f_1(x, y, z)V)}{\partial x}\nonumber \\&\qquad \qquad +\frac{\partial (f_2(x, y, z)V)}{\partial y}+\frac{\partial (f_3(x, y, z)V)}{\partial z}. \end{aligned}$$

(7)

3 Main results in the strong kernel case

Firstly, the existence and uniqueness of globally positive solution of (4) is discussed, then investigating the long-term behavior of the model (4) is desirable.

3.1 Existence and uniqueness of globally positive solution

Theorem 3.1

For any initial value $(X(0), Y(0), Z(0))\in \mathbb {R}_{+}^{3}$, there exists a unique solution of the system (4) with the strong kernel, which will remain in $\mathbb {R}_{+}^{3}$ with probability one.

Proof

The proof is similar to that in [2, 17, 18]. Here we omit it. $\square$

The aim of this theorem is to prove the population X(t) of the stochastic system (4) becomes extinct.

3.2 Extinction

Theorem 3.2

Let (X(t), Y(t), Z(t)) be a solution of the stochastic system (4) with the strong kernel, for any given initial value $(X(0), Y(0), Z(0))\in \mathbb {R}_{+}^{3}$. If $p<\delta$, then

$$\begin{aligned} \lim _{t\rightarrow \infty }X(t)=0,~\lim _{t\rightarrow \infty }Y(t)=0~\text{ and }~\lim _{t\rightarrow \infty }Z(t)=0~a.s. \end{aligned}$$

That is to say, the population X(t) of the stochastic system (4) becomes extinct with probability one.

Proof

Let

$$\begin{aligned} \lambda (\omega _{1},\omega _{2},\omega _{3})=(\omega _{1},\omega _{2},\omega _{3})M_{0}, \end{aligned}$$

where

$$\begin{aligned} \lambda= & {} \root 3 \of {\frac{p}{\delta }},~(\omega _{1},\omega _{2},\omega _{3})=(1,\lambda ^{2},\lambda )~\text{ and }~\\ M_{0}= & {} \begin{pmatrix} 0~\frac{p}{\delta }~0 \\ 0~0~1 \\ 1~0~0 \\ \end{pmatrix}. \end{aligned}$$

Define a $C^{2}$-function $V_{1}(t)$: $\mathbb {R}_{+}^{3}\rightarrow \mathbb {R}_{+}$

$$\begin{aligned} V_{1}(t)=c_{1}X(t)+c_{2}Y(t)+c_{3}Z(t), \end{aligned}$$

where $c_{1}=\frac{\omega _{1}}{\delta }$, $c_{2}=\frac{\omega _{2}}{\alpha }$ and $c_{3}=\frac{\omega _{3}}{\alpha }$. Using Itô’s formula [19] to system (4) leads to

$$\begin{aligned} d(\log V_{1}(t))=L(\log V_{1}(t))dt+\frac{c_{1}\sigma X(t)}{V_{1}(t)}dB(t), \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{aligned} L(\log V_{1}(t))&=\frac{1}{V_{1}(t)}\bigg (c_{1}(-\delta X(t)+pY(t))\\&\quad +c_{2}\alpha (Z(t)-Y(t))+c_{3}\alpha (X(t)e^{-aX(t)}\\&\quad -Z(t))\bigg )-\frac{c_{1}^{2}\sigma ^{2} X^{2}(t)}{2V_{1}^{2}(t)}\\&\le \frac{1}{V_{1}(t)}\bigg (c_{1}(-\delta X(t)+pY(t))\\&\quad +c_{2}\alpha (Z(t)-Y(t))+c_{3}\alpha (X(t)-Z(t))\bigg )\\&=\frac{1}{V_{1}(t)}(\omega _{1}, \omega _{2}, \omega _{3})\\&\bigg [\begin{pmatrix} 0~\frac{p}{\delta }~0 \\ 0~0~1 \\ 1~0~0 \\ \end{pmatrix}-\begin{pmatrix} 1~0~0 \\ 0~1~0 \\ 0~0~1 \\ \end{pmatrix}\bigg ]\begin{pmatrix} X(t) \\ Y(t) \\ Z(t)\\ \end{pmatrix}\\&=\frac{1}{V_{1}(t)}(\lambda -1)(\omega _{1}X(t)\\&\quad +\omega _{2}Y(t)+ \omega _{3}Z(t))\\&\le \min \{\delta ,\alpha \}(\lambda -1). \end{aligned}\nonumber \\ \end{aligned}$$

(9)

Substituting (9) into (8) yields

$$\begin{aligned} d(\log V_{1}(t))\le & {} \min \{\delta ,\alpha \}(\lambda -1)dt\nonumber \\&+\frac{c_{1}\sigma X(t)}{V_{1}(t)}dB(t). \end{aligned}$$

(10)

Integrating it from 0 to t and dividing t on both sides, we obtain

$$\begin{aligned}&\frac{\log V_{1}(t)}{t}\le \frac{\log V_{1}(0)}{t}+\min \{\delta ,\alpha \}(\lambda -1)\nonumber \\&\quad + \frac{1}{t} \int _0^t \frac{c_{1}\sigma X(s)}{V_{1}(s)}\mathrm{d}B(s), \end{aligned}$$

(11)

where let $M(t)=\int _0^t \frac{c_{1}\sigma X(s)}{V_{1}(s)}\mathrm{d}B(s)$, which is a local martingale with $M(0) = 0$. Moreover, using the strong law of large numbers [19] yields

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M(t)}{t}=0 ~a.s. \end{aligned}$$

(12)

Since $p<\delta$, $\lambda =\root 3 \of {\frac{p}{\delta }}<1$, substituting (12) into (11) and then taking the superior limit, we obtain

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\log V_{1}(t)}{t}\le \min \{\delta ,\alpha \}(\lambda -1)<0~~a.s., \end{aligned}$$

therefore,

$$\begin{aligned}&\lim _{t\rightarrow \infty }\frac{\log X(t)}{t}=0,~\lim _{t\rightarrow \infty }\frac{\log Y(t)}{t}=0~\text{ and }\\&~\lim _{t\rightarrow \infty }\frac{\log Z(t)}{t}=0~a.s., \end{aligned}$$

which means that

$$\begin{aligned} \lim _{t\rightarrow \infty }X(t)=0,~\lim _{t\rightarrow \infty }Y(t)=0~\text{ and }~\lim _{t\rightarrow \infty }Z(t)=0~a.s. \end{aligned}$$

In other words, the population X(t) is arrived at becoming extinct with probability one. $\square$

Next, we discuss the existence of a unique stable stationary distribution.

3.3 Asymptotic stability

Theorem 3.3

Let (X(t), Y(t), Z(t)) be a solution of the stochastic system (4) with the strong kernel. The distribution of (X(t), Y(t), Z(t)) has a density U(t, x, y, z), $\forall t > 0$. If $p>\delta +\frac{\sigma ^{2}}{2}$, then there is a unique density $U^{*}(x, y, z)$ satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }\iint _{\mathbb {R}_{+}^{3}}|U(t, x, y, z)-U^{*}(x, y, z)|\mathrm{d}x\mathrm{d}y\mathrm{d}z=0. \end{aligned}$$

The proof of the above Theorem 3.3 consists of the following steps:

• (1) Based on the H$\ddot{o}$rmander condition [14], it indicates that the kernel function of the process $(X(t), Y(t), Z(t))$ is absolutely continuous.

• (2) According to support theorems [20], we prove that the kernel function is positive on $\mathbb {R}_{+}^{3}$.

• (3) We demonstrate that the Markov semigroup is asymptotically stable or is sweeping with respect to compact sets by Lemma 2.5.

• (4) Since there exists a Khasminski$\breve{i}$ function, we exclude sweeping.

Next, to accommodate the above steps, we therefore give the following Lemmas 3.4–3.7.

Lemma 3.4

For every $(x_{0}, y_{0}, z_{0}) \in \mathbb {X}$ and $t > 0$, the transition probability function $\mathbb {P}(t, x_{0}, y_{0}, z_{0}, A)$ has a continuous density $k(t, x, y, z; x_{0}, y_{0}, z_{0})$ with regard to Lebesgue measure.

Proof

If $\mathbf {a}(x)\in \mathbb {R}_{+}^{3}$ and $~\mathbf {b}(x)\in \mathbb {R}_{+}^{3}$ are vector fields, then the Lie bracket $[\mathbf {a},\mathbf {b}]$ is a vector field expressed by

$$\begin{aligned} {[}\mathbf {a},\mathbf {b}]_{j}(x)=\sum _{i=1}^{3}\bigg (a_{i}\frac{\partial b_{j}}{\partial x_{i}}-b_{i}\frac{\partial a_{j}}{\partial x_{i}}\bigg ),~j=1,2,3. \end{aligned}$$

Let

$$\begin{aligned}&\mathbf {a}(X, Y, Z)= \begin{pmatrix} -\delta X+pY \\ \alpha (Z-Y) \\ \alpha (Xe^{-aX}-Z) \end{pmatrix} ~~\text {and}~~\\&\quad \mathbf {b}(X, Y, Z)= \begin{pmatrix} \sigma X \\ 0 \\ 0 \end{pmatrix}. \end{aligned}$$

Then Lie bracket $[\mathbf {a},\mathbf {b}]$ is given by

$$\begin{aligned} \mathbf {a}_1\triangleq [\mathbf {a},\mathbf {b}]= \sigma \bigg (pY,0,-\alpha e^{-aX}(X-aX^{2})\bigg )^{T} \end{aligned}$$

and

$$\begin{aligned} \mathbf {a}_2\triangleq [\mathbf {a},\mathbf {a}_1]=\bigg (B_{1},B_{2},B_{3}\bigg )^{T}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} B_{1}&=\sigma p(\delta -\alpha )Y+\alpha Z,\\ B_{2}&=\alpha ^{2}\sigma e^{-aX}(X-aX^{2})~~\text {and}\\ B_{3}&=(-\delta X+pY)(a\alpha \sigma e^{-aX}(X-aX^{2})\\&\quad - \alpha \sigma e^{-aX}(1-2aX)-\alpha \sigma pYe^{-aX}(1-aX)\\&\quad -\alpha ^{2}\sigma e^{-aX}(X-aX^{2})), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned}&|\mathbf {b}~\mathbf {a}_1~\mathbf {a}_2|= \left| \begin{array}{ccc} \sigma X &{}\sigma pY&{}B_{1}\\ 0 &{}0&{}B_{2}\\ 0&{}-\sigma \alpha e^{-aX}(X-aX^{2})&{}B_{3} \end{array}\right| \\&\quad =\sigma ^{2}\alpha ^{2} e^{-2aX}(X-aX^{2})^{2}X. \end{aligned}$$

Thus, $\mathbf {b},~\mathbf {a}_1~\text {and}~\mathbf {a}_2$ are linearly independent on $\mathbb {R}_{+}^{3}$. Then for each $(X, Y, Z)\in \mathbb {R}_{+}^{3}$, where $X\ne \frac{1}{a}$, the vector $\mathbf {b},~\mathbf {a}_1~\text {and}~\mathbf {a}_2$ span the space $\mathbb {R}_{+}^{3}$. Based on the Hörmander Theorem [21], the transition probability function $\mathscr {P}(t, x_0, y_0, z_0, A)$ has a continuous density $k(t, x, y, z; x_0, y_0, z_0)$, i.e., $k\in C^\infty ((0, \infty )\times \mathbb {R}_{+}^{3}\times \mathbb {R}_{+}^{3})$. $\square$

Lemma 3.5

For every $(x_{1}, y_{1}, z_{1})\in \mathbb {R}_{+}^{3}$ and $(x_{2}, y_{2}, z_{2})\in \mathbb {R}_{+}^{3}$, there exists $T > 0$ such that $k(T, x_{2}, y_{2}, z_{2}; x_{1}, y_{1}, z_{1})>0$.

Proof

The method of verifying the positivity of k can be adopted, based on support theorems [20]. To use the support theorems, we first give Stratonovich version of Itô’s form (4):

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dX(t) &{}=\left[ -(\delta +\frac{1}{2}\sigma ^{2})X(t) +pY(t)\right] dt\\ &{}\quad +\sigma X(t)\circ dB(t),\\ dY(t) &{}=\alpha \left[ Z(t)-Y(t)\right] dt,\\ dZ(t) &{}=\alpha \left[ X(t)e^{-aX(t)}-Z(t)\right] dt. \end{aligned} \end{array}\right. } \end{aligned}$$

(13)

Next, we fix a point $(x_0, y_0, z_0)\in \mathbb {X}$ and a function $\phi \in L^2([0, T]; \mathbb {R})$ and the integral system is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} X_\phi (t)&{}= x_0+\int _0^t[-(\delta +\frac{1}{2}\sigma ^{2}) X_\phi (s) +pY_\phi (s)\\ &{}\quad +\sigma X_\phi (s)\phi ]\mathrm{d}s,\\ Y_\phi (t)&{}= y_0+\int _0^t\alpha \left[ Z_\phi (s)-Y_\phi (s)\right] \mathrm{d}s,\\ Z_\phi (t)&{}= z_0+\int _0^t\alpha \left[ X_\phi (s)e^{-aX_\phi (s)}-Z_\phi (s)\right] \mathrm{d}s. \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(14)

Let $\mathbf {N}=(x, y, z)^T$, $\mathbf {N}_0=(x_0, y_0, z_0)^T$, denote $D_{\mathbf {N}_0; \phi }$ be the Fréchet derivative of the function $h{\mapsto }\mathbf {N}_{\phi +h}(T): L^2([0, T]; \mathbb {R})\rightarrow \mathbb {X}$. If the rank of the Fréchet derivative $D_{\mathbf {N}_0; \phi }$ is full rank for some $\phi \in L^2([0, T]; \mathbb {R})$, then $k(T, x, y, z; x_0, y_0, z_0)>0$ for $\mathbf {N}=\mathbf {N}_\phi (T)$ holds. Let

$$\begin{aligned} \Psi (t)=\mathbf {f'}(\mathbf {N}_\phi (t))+\phi \mathbf {g'}(\mathbf {N}_\phi (t)), \end{aligned}$$

where $\mathbf {f'}$ and $\mathbf {g'}$ are the Jacobians of

$$\begin{aligned} f= \begin{pmatrix} -(\delta +\frac{\sigma ^{2}}{2})x+py\\ \alpha (z-y)\\ \alpha (xe^{-ax}-z) \end{pmatrix} ~~\text {and}~~ g= \begin{pmatrix} \sigma x\\ 0\\ 0 \end{pmatrix}, \end{aligned}$$

respectively. Let $Q(t, t_0)~(0\le t_0\le t\le T)$ be a matrix function satisfies $Q(t_0, t_0)=Id$, $\frac{\partial Q(t, t_0)}{\partial t}=\Psi (t)Q(t, t_0)$, then

$$\begin{aligned} D_{\mathbf {N}_0; \phi }h=\int _0^TQ(T, s)g(s)h(s)\mathrm{d}s. \end{aligned}$$

Step 1: To illustrate the rank of $D_{\mathbf {N}_0; \phi }$ is 3. Let $\varepsilon \in (0, T)$ and $h(t)=\frac{\chi _{[T-\varepsilon , T]}(t)}{x_\phi (t)}~(t\in [0, T])$, where $\chi$ is the indicative function on $[T-\varepsilon , T]$. In the light of Taylor expansion, namely,

$$\begin{aligned}&Q(T, s)= Id+\Psi (T)(s-T)\\&\quad +\frac{1}{2}\Psi ^2(T)(s-T)^2+o((s-T)^2). \end{aligned}$$

Therefore,

$$\begin{aligned} D_{\mathbf {N}_0; \phi }h=\varepsilon \mathbf {v}-\frac{1}{2}\varepsilon ^2\Psi (T)\mathbf {v}+\frac{1}{6}\varepsilon ^3\Psi ^2(T)\mathbf {v}+o(\varepsilon ^3), \end{aligned}$$

where $\mathbf {v}=(-\sigma ,0,0)^{T}$, then compute

$$\begin{aligned}&\Psi (T)\mathbf {v}=\sigma \begin{pmatrix} -(\delta +\frac{\sigma ^{2}}{2})+\alpha \phi &{}p&{}0\\ 0&{}-\alpha &{}\alpha \\ \alpha e^{-ax}(1-ax)&{}0&{}-\alpha \end{pmatrix} \begin{pmatrix} \sigma \\ 0\\ 0 \end{pmatrix}\\&\quad =\begin{pmatrix} \sigma (-(\delta +\frac{\sigma ^{2}}{2})+\alpha \phi )\\ 0\\ \sigma \alpha e^{-ax}(1-ax) \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned}&\Psi ^2(T)\mathbf {v}=\sigma \begin{pmatrix} -(\delta +\frac{\sigma ^{2}}{2})+\alpha \phi &{}p&{}0\\ 0&{}-\alpha &{}\alpha \\ \alpha e^{-ax}(1-ax)&{}0&{}-\alpha \end{pmatrix}\\&\quad =\begin{pmatrix} \sigma (-(\delta +\frac{\sigma ^{2}}{2})+\alpha \phi )\\ 0\\ \sigma \alpha e^{-ax}(1-ax) \end{pmatrix}\\&\quad =\begin{pmatrix} \sigma H\\ \sigma \alpha ^{2} K\\ \sigma \alpha K(H-\alpha ) \end{pmatrix}, \end{aligned}$$

where $H=-(\delta +\frac{\sigma ^{2}}{2})+\alpha \phi$ and $K=e^{-ax}(1-ax)$, thus

$$\begin{aligned}&|\mathbf {v}~~\Psi (T)\mathbf {v}~~\Psi ^2(T)\mathbf {v}|= \left| \begin{array}{ccc} \sigma &{}\sigma H&{}\sigma H^{2}\\ 0 &{}0&{}\sigma \alpha ^{2} K\\ 0&{}\sigma \alpha K&{}\sigma \alpha K(H-\alpha ) \end{array}\right| \nonumber \\&\quad =-\sigma ^{3}\alpha ^{3} e^{-2aX}(1-aX)^{2}<0, \end{aligned}$$

where $X\ne \frac{1}{a}$, so $\mathbf {v}$, $\Psi (T)\mathbf {v}$ and $\Psi ^2(T)\mathbf {v}$ are linearly independent. Therefore, the rank of $D_{\mathbf {N}_0; \phi }$ is 3.

Step 2: Firstly, we claim that there exists a control function $\phi$ and $T>0$ such that $\mathbf {X}_\phi (0)=\mathbf {X}_0$, $\mathbf {X}_\phi (T)=\mathbf {X}$ for any two points $\mathbf {X}_0\in \mathbb {R}_{+}^{3}$ and $\mathbf {X}\in \mathbb {R}_{+}^{3}$ holds, then system (14) can be replaced by the following differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} X'_\phi (t)=-(\delta +\frac{1}{2}\sigma ^{2}) X_\phi (t) +pY_\phi (t)+\sigma X_\phi (t)\phi ,\\ Y'_\phi (t)=\alpha \left[ Z_\phi (t)-Y_\phi (t)\right] ,\\ Z'_\phi (t)=\alpha \left[ X_\phi (t)e^{-aX_\phi (t)}-Z_\phi (t)\right] . \end{array}\right. } \end{aligned}$$

(15)

To construct the function $\phi$, first of all, we find a positive constant T and a $C^{3}$-function $Y_{\phi }$: $[0,T] \rightarrow (0,+\infty )$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha Z_\phi (t)=Y'_\phi (t)+\alpha Y_\phi (t)>0,\\ X_\phi (t) e^{-aX_\phi (t)}=Y''_\phi (t)+2\alpha Y'_\phi (t)+\alpha ^{2}Y_\phi (t)>0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(16)

and the following boundary value conditions are met:

$$\begin{aligned} \begin{aligned}&Y_{\phi }(0)=y_{1},Y_{\phi }(T)=y_{2},\\&Y'_{\phi }(0)=\alpha (z_{1}-y_{1})\triangleq C_{1},Y'_{\phi }(T)=\alpha (z_{2}-y_{2})\triangleq D_{1},\\&Y''_{\phi }(0)=\alpha (z'_{1}-y'_{1})=\alpha ^{2}(x_1e^{-ax_1}-2z_{1}+y_{1})\triangleq C_{2},\\&Y''_{\phi }(T)=\alpha (z'_{2}-y'_{2})=\alpha ^{2}(x_2e^{-ax_2}-2z_{2}+y_{2})\triangleq D_{2}. \end{aligned} \end{aligned}$$

(17)

Next we separate the construction of the function $Y_\phi$ on three subintervals $[0, \varepsilon _{1}]$, $[\varepsilon _{1}, T-\varepsilon _{2}]$ and $[T-\varepsilon _{2}, T]$, where $0<\varepsilon _{1},\varepsilon _{2}<\frac{T}{2}$, will be determined later. We choose the $C^3$-function $Y_\phi$ on $[0, \varepsilon _{1}]$ as follows:

$$\begin{aligned} Y_\phi (t)=y_{1}+C_{1}t+\frac{C_{2}}{2}t^{2}+At^{3},~\forall t\in [0, \varepsilon _{1}], \end{aligned}$$

(18)

where the coefficients $C_{1},~C_{2}~\text {and}~y_{1}$ are given in (17), then the coefficient A satisfies

$$\begin{aligned}&Z_\phi '(\varepsilon _{1})=\frac{1}{\alpha }Y^{''}_\phi (\varepsilon _{1})+Y^{'}_\phi (\varepsilon _{1})\\&\quad =\frac{1}{\alpha }(C_{2}+6A\varepsilon _{1}) +C_{1}+C_{2}\varepsilon _{1}+3A\varepsilon _{1}^{2}=0, \end{aligned}$$

thus,

$$\begin{aligned} A=-\frac{C_{2}+\alpha C_{1}+\alpha C_{2}\varepsilon _{1}}{\sigma \varepsilon _{1}+3\sigma \varepsilon _{1}^{2}}. \end{aligned}$$

When $t=0$, $Y_{\phi }(0)=y_{1},~Y'_{\phi }(0)=C_{1},~Y''_{\phi }(0)=C_{2}$ from (18), namely, the conditions (17) hold. Next, we intend to prove (16). Due to

$$\begin{aligned} \begin{aligned}&\alpha Z_\phi (0)=Y'_\phi (0)+Y_\phi (0)=C_{1}+\alpha y_{1}>0,\\&X_\phi (0) e^{-aX_\phi (0)}=Y''_\phi (0)+2\alpha Y'_\phi (0)+\alpha ^{2}Y_\phi (0)\\&\quad =C_{2}+2\alpha C_{1}+\alpha ^{2} y_{1}>0, \end{aligned} \end{aligned}$$

then there is a sufficiently small $\varepsilon _{1}\in (0,\frac{C_{1}+\alpha y_{1}}{|C_{2}|})$ such that for $t\in (0, \varepsilon _{1})$,

$$\begin{aligned} \begin{aligned}&Y'_\phi (t)+\alpha Y_\phi (t)=A\alpha t^{3}\\&\quad +(3A+\frac{C_{2}}{2}\alpha )t^{2}+(C_{2}+C_{1}\alpha )t+C_{1}+\alpha y_{1}>0,\\&G_{1}(t)\triangleq A\alpha ^{2}t^{3}+(6\alpha A+\frac{C_{2}}{2}\alpha ^{2})t^{2}\\&\quad +(2\alpha C_{2}+\alpha ^{2}C_{1})t+C_{2}+2\alpha C_{1}+\alpha ^{2} y_{1}>0,\\&G_{2}(t)\triangleq A\alpha ^{2}t^{3}+(6\alpha A+\frac{C_{2}}{2}\alpha ^{2})t^{2} +(2\alpha C_{2}\\&\quad +\alpha ^{2}C_{1})t+\alpha (C_{1}+\alpha y_{1})-\alpha C_{2}\varepsilon _{1}>0. \end{aligned} \end{aligned}$$

(19)

According to (19), the first inequality of (16) is satisfied. And the second inequality of (16) also holds since

$$\begin{aligned} Y''_\phi (t)+2\alpha Y'_\phi (t)+\alpha ^{2}Y_\phi (t) = 6At + G_{1}(t). \end{aligned}$$

It can be discussed in two cases.

$\mathbf {Case~1.}$ If $C_{2}+\alpha C_{1}+\alpha C_{2}\varepsilon _{1}\le 0$, i.e., $A \ge 0$, then

$$\begin{aligned}&Y''_\phi (t)+2\alpha Y'_\phi (t)+\alpha ^{2}Y_\phi (t) = 6At \nonumber \\&\quad + G_{1}(t)\ge G_{1}(t)>0~\text {by }{(19)}. \end{aligned}$$

$\mathbf {Case~2.}$ If $C_{2}+\alpha C_{1}+\alpha C_{2}\varepsilon _{1}>0$, then

$$\begin{aligned}&!`Y''_\phi (t)+2\alpha Y'_\phi (t)+\alpha ^{2}Y_\phi (t)\\&\quad = 6At + G_{1}(t)\ge 6A\varepsilon _{1}+G_{1}(t)\\&\ge -(C_{2}+\alpha C_{1}+\alpha C_{2}\varepsilon _{1}) +G_{1}(t)=G_{2}(t)>0~\text {by } {(19)}. \end{aligned}$$

Thus, $Y_\phi (t)$ satisfies (16) and (17) for $t\in [0,\varepsilon _{1}]$. The same proof for $t\in [T-\varepsilon _{2}, T]$, we also find a $C^3$-function $Y_\phi (t)$: $[T-\varepsilon _{2}, T]\rightarrow (0, \infty )$ such that

$$\begin{aligned} Y_\phi (T)= & {} y_1, ~~Y'_\phi (T)=C_{1},~~\\ Y''_\phi (T)= & {} C_{2},~~Z'_\phi (\varepsilon _{2})=0, \end{aligned}$$

and $Y_\phi (t)$ satisfies inequalities (16) for $t\in [T-\varepsilon _{2}, T]$. We choose T sufficiently large and extend the function $Y_\phi (t): [0, \varepsilon _{1}]\cup [T-\varepsilon _{2}, T] \rightarrow (0,\infty )$ to a $C^3$-function $Y_\phi (t)$ defined on [0, T] such that (15)–(17) hold.

Then from the second and the third equations of (15), two $C^1$-function $Z_\phi (t)$ and $X_\phi (t)$ can be found to satisfy (16) and (17), respectively. Finally there is a continuous control function $\phi$ which can be determined from the first equation of (15). This completes the proof. $\square$

Lemma 3.6

The Markov semigroup $\{P(t)\}_{t\ge 0}$ is asymptotically stable or is sweeping concerning compact sets.

Proof

Based on the result of Lemma 3.4, it shows that $\{P(t)\}_{t\ge 0}$ is an integral Markov semigroup, which has a continuous density k(t, x, y, z) for $t>0$. By Lemma 3.5, we know for every $g\in \mathbb {D}$,

$$\begin{aligned} \int _0^\infty P(t)g\mathrm{d}t>0, ~\text {a.s.}~ \text {on} ~\mathbb {R}_{+}^{3}, \end{aligned}$$

due to $k(t, x, y, z)>0$ and $P(t)g=\int _{\mathbb {R}_{+}^{3}}k(t, \mathbf {x})g(\mathbf {x})m(\mathrm{d}\mathbf {x})$, where $\mathbf {x}=(x,y,z)$. Therefore, according to Lemma 2.5, the Markov semigroup $\{P(t)\}_{t\ge 0}$ is asymptotically stable or is sweeping concerning compact sets. $\square$

Lemma 3.7

If $p>\delta +\frac{\sigma ^{2}}{2}$, then the Markov semigroup $\{P(t)\}_{t\ge 0}$ is asymptotically stable.

Proof

By virtue of the Lemma 3.6, it implies that the semigroup $\{P(t)\}_{t\ge 0}$ satisfies the Foguel alternative. In order to exclude sweeping, we construct a nonnegative $C^2$-function V and a closed set $\Gamma \in \mathbb {R}_{+}^{3}$ such that

$$\begin{aligned} \sup _{(X, Y, Z)\in \mathbb {R}_{+}^{3}\setminus \Gamma }\mathscr {A}^*V<0, \end{aligned}$$

where the $C^2$-function V is known as Khasminskiĭ function [22].

Define a nonnegative $C^2$-function V by

$$\begin{aligned} \begin{aligned} V(X, Y, Z)&=M\bigg (-\log X-\frac{p}{\alpha }\log Y\\&\quad -\frac{p}{\alpha }\log Z\bigg )-\log Y-\log Z\\&\quad +\frac{1}{\theta +1}\bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta +1}\\&:=V_2-\log Y-\log Z+V_3, \end{aligned} \end{aligned}$$

where M and $0<\theta <1$ will be determined later. First, by Lemma 2.1, we compute

$$\begin{aligned} \mathscr {A}^*V_2&= M\bigg (\delta +\frac{\sigma ^{2}}{2}+2p-\left( p\frac{Y}{X}+p\frac{Z}{Y}+p\frac{Xe^{-aX}}{Z}\right) \bigg )\nonumber \\&\le M\bigg (\delta +\frac{\sigma ^{2}}{2}+2p-3\left( p^{3}\frac{Y}{X}\cdot \frac{Z}{Y}\cdot \frac{Xe^{-aX}}{Z}\right) ^{\frac{1}{3}}\bigg )\nonumber \\&=M\bigg (\delta +\frac{\sigma ^{2}}{2}+2p-3pe^{-\frac{aX}{3}}\bigg )\nonumber \\&= M\bigg (\delta +\frac{\sigma ^{2}}{2}+2p-3p+3p\bigg (1-e^{-\frac{aX}{3}}\bigg )\bigg )\nonumber \\&\le M\bigg (-p+\delta +\frac{\sigma ^{2}}{2}+paX\bigg ). \end{aligned}$$

(20)

$$\begin{aligned} \mathscr {A}^*V_3&= \bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta }\nonumber \\&\bigg (-\delta X+pY+2p(Z-Y)+3p(Xe^{-aX}-Z)\bigg ) \nonumber \\&\quad +\frac{\theta }{2}\sigma ^{2}X^{2}\bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta -1}\nonumber \\&\le \bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta }\bigg (-\delta X-pY-pZ\nonumber \\&\quad +\frac{3p}{ae}\bigg ) +\frac{\theta }{2}\sigma ^{2}X^{2}\bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta -1}\nonumber \\&\le -\delta X^{\theta +1}-\frac{2^{\theta }p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}\nonumber \\&\quad -\frac{3^{\theta }p^{\theta +1}}{\alpha ^{\theta }}Z^{\theta +1} +\frac{3p}{ae}\bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta }\nonumber \\&\quad +\frac{\theta }{2}\sigma ^{2}X^{\theta +1}\le -\frac{1}{2}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}\nonumber \\&\quad -\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}-\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1} +B. \end{aligned}$$

(21)

And

$$\begin{aligned} \mathscr {A}^*(-\log Y-\log Z)=2\alpha -\alpha \frac{Z}{Y}-\alpha \frac{Xe^{-aX}}{Z}, \end{aligned}$$

(22)

where

$$\begin{aligned}&B=\sup _{(X,Y,Z)\in \mathbb {R}_{+}^{3}}\bigg \{-\frac{1}{2}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}\\&\quad -\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1} -\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1}\\&\quad +\frac{3p}{ae}\bigg (X+\frac{2p}{\alpha }Y+\frac{3p}{\alpha }Z\bigg )^{\theta }\bigg \}, \end{aligned}$$

and $\delta -\frac{\theta }{2}\sigma ^{2}>0$, i.e., $0<\theta <\frac{2\delta }{\sigma ^{2}}$.

Combining (20)–(22), we obtain

$$\begin{aligned} \begin{aligned} \mathscr {A}^*V&= \mathscr {A}^*V_2+\mathscr {A}^*(-\log Y-\log Z)+\mathscr {A}^*V_3\\&\le M\bigg (-p+\delta +\frac{\sigma ^{2}}{2}+paX\bigg )\\&\quad +2\alpha +B-\alpha \frac{Z}{Y}-\alpha \frac{Xe^{-aX}}{Z}\\&\quad -\frac{1}{2}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}-\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}\\&\quad -\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1}= -M\mu +2\alpha +B+MpaX \\&\quad -\alpha \frac{Xe^{-aX}}{Z}-\alpha \frac{Z}{Y}-\frac{1}{2}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}\\&\quad -\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}-\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1}\\&\le -2+MpaX-\alpha \frac{Xe^{-aX}}{Z} -\alpha \frac{Z}{Y}\\&\quad -\frac{1}{4}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1} -\frac{1}{4}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}\\&\quad -\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}-\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1}, \end{aligned} \end{aligned}$$

(23)

where $\mu =p-\delta -\frac{\sigma ^{2}}{2}>0$, M is a positive constant satisfying $-M\mu +2\alpha +B\le -2$.

Define a bounded closed set €

$$\begin{aligned}&\Gamma =\Big \{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~\epsilon _{1}\le X\le \frac{1}{\epsilon _{1}},~\epsilon _{2}\le \nonumber \\&X\le \frac{1}{\epsilon _{2}},~\epsilon _{3}\le X\le \frac{1}{\epsilon _{3}}\Big \}, \end{aligned}$$

(24)

where $0<\epsilon _{1},~\epsilon _{2},~\epsilon _{3}<1$ are sufficient small real numbers. In the set $\mathbb {R}_{+}^{3}\setminus \Gamma$, $\epsilon _{1},~\epsilon _{2}~\text {and}~\epsilon _{3}$ satisfy the following conditions:

$$\begin{aligned} \begin{aligned}&0<\epsilon _{1}\le \min \bigg \{\root \theta +1 \of {\frac{\delta -\frac{\theta }{2}\sigma ^{2}}{4(H+1)}},~\frac{1}{Mpa}\bigg \},\\&0<\epsilon _{3}\le \min \bigg \{\frac{3p}{\alpha }\root \theta +1 \of {\frac{\alpha }{6(H+1)}},~\epsilon _{1}^{2}e^{-\frac{a}{\epsilon _{1}}}\bigg \},\\&0<\epsilon _{2}\le \min \bigg \{\frac{2p}{\alpha }\root \theta +1 \of {\frac{\alpha }{4(H+1)}},~\frac{\alpha \epsilon _{3}}{1+H}\bigg \}, \end{aligned} \end{aligned}$$

(25)

where

$$\begin{aligned} H=\max _{X\in (0,+\infty )}\bigg \{-2+MpaX-\frac{1}{4}(\delta -\frac{\theta }{2}\sigma ^{2}) X^{\theta +1}\bigg \}. \end{aligned}$$

For the convenience of the following discussion, we will divide $\Gamma ^{c}=\mathbb {R}_{+}^{3}\setminus \Gamma$ into six domains:

$$\begin{aligned} \begin{aligned}&\Gamma ^{1}=\Big \{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~X>\frac{1}{\epsilon _{1}}\Big \},\\&~\Gamma ^{2}=\Big \{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~Y>\frac{1}{\epsilon _{2}}\Big \},\\&~\Gamma ^{3}=\Big \{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~Z>\frac{1}{\epsilon _{3}}\Big \},\\&\Gamma ^{4}=\{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~0<X<\epsilon _{1}\},\\&~\Gamma ^{5}=\{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~\epsilon _{1}\le X\le \frac{1}{\epsilon _{1}},~0<Z<\epsilon _{3}\},\\&\Gamma ^{6}=\{(X, Y, Z)\in \mathbb {R}_{+}^{3}|~\epsilon _{1}\le X\le \frac{1}{\epsilon _{1}},\\&\epsilon _{3}\le Z\le \frac{1}{\epsilon _{3}},~0<Y<\epsilon _{2}\}, \end{aligned} \end{aligned}$$

clearly, $\Gamma ^{c}=\Gamma ^{1}\cup \Gamma ^{2}\cup \Gamma ^{3}\cup \Gamma ^{4}\cup \Gamma ^{5}\cup \Gamma ^{6}$. Next, we will prove that $\mathscr {A}^*V\le -1$ for any $(X, Y, Z) \in \Gamma ^{c}$, this is equivalent to proving $\mathscr {A}^*V\le -1$ in the above six domains, respectively. We discuss it in six cases.

$\mathbf {Case~1.}$ If $(X,Y,Z)\in \Gamma ^{1}$, then

$$\begin{aligned}&\mathscr {A}^*V\le H-\frac{\delta -\frac{\theta }{2}\sigma ^{2}}{4}X^{\theta +1}\\&\quad \le H-\frac{\delta -\frac{\theta }{2}\sigma ^{2}}{4\epsilon _{1}^{\theta +1}}\le -1, ~\text {by the first inequality of }{(25)}. \end{aligned}$$

$\mathbf {Case~2.}$ If $(X,Y,Z)\in \Gamma ^{2}$, then

$$\begin{aligned}&\mathscr {A}^*V\le H-\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }}Y^{\theta +1}\\&\quad \le H-\frac{2^{\theta -1}p^{\theta +1}}{\alpha ^{\theta }\epsilon _{2}^{\theta +1}}\le -1,\\&\qquad ~\text {by the third inequality of }{(25)}. \end{aligned}$$

$\mathbf {Case~3.}$ If $(X,Y,Z)\in \Gamma ^{3}$, then

$$\begin{aligned}&\mathscr {A}^*V\le H-\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }}Z^{\theta +1}\\&\quad \le H-\frac{3^{\theta }p^{\theta +1}}{2\alpha ^{\theta }\epsilon _{3}^{\theta +1}}\le -1,\\&\qquad ~\text {by the second inequality of }{(25)}. \end{aligned}$$

$\mathbf {Case~4.}$ If $(X,Y,Z)\in \Gamma ^{4}$, then

$$\begin{aligned}&\mathscr {A}^*V\le -2+MpaX\\&\quad \le -2+Mpa\epsilon _{1}\le -1, ~\\&\qquad \text {by the first inequality of }{(25)}. \end{aligned}$$

$\mathbf {Case~5.}$ If $(X,Y,Z)\in \Gamma ^{5}$, then

$$\begin{aligned}&\mathscr {A}^*V\le H-\alpha \frac{Xe^{-aX}}{Z}=H-\alpha \frac{X}{Z}\frac{1}{e^{aX}}\\&\quad \le H-\alpha \frac{\epsilon _{1}}{\epsilon _{3}}\frac{1}{e^{\frac{a}{\epsilon _{1}}}}\le -1,\\&\qquad ~\text {by the second inequality of }{(25)}. \end{aligned}$$

$\mathbf {Case~6.}$ If $(X,Y,Z)\in \Gamma ^{6}$, then

$$\begin{aligned}&\mathscr {A}^*V\le H-\alpha \frac{Z}{Y}\le H-\alpha \frac{\epsilon _{3}}{\epsilon _{2}}\\&\quad \le -1, ~\text {by the third inequality of }{(25)}. \end{aligned}$$

To summarize, there exists a closed set $\Gamma \in \mathbb {R}_{+}^{3}$ such that

$$\begin{aligned} \sup _{(X, Y, Z)\in \mathbb {R}_{+}^{3}\setminus \Gamma }\mathscr {A}^*V\le -1<0. \end{aligned}$$

According to [22], we know that the existence of a Khasminskiĭ function shows that the semigroup $\{P(t)\}_{t\ge 0}$ exclude sweeping from the set $\Gamma$. By Lemma 2.5, we can get that the semigroup $\{P(t)\}_{t\ge 0}$ is asymptotically stable. $\square$

3.4 Probability density function

In this part, we will give the probability density function of quasi-stationary distribution near the positive equilibrium point of the model (4) with the strong kernel.

First, let $u=X-X^{*},~v=Y-Y^{*}$ and $w=Z-Z^{*}$, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} du &{}= \left[ -\delta (u+X^{*}) +p(v+Y^{*})\right] dt+\sigma (u+X^{*})dB(t),\\ dv &{}= \alpha \left[ (w+Z^{*})-(v+Y^{*})\right] dt,\\ dw &{}= \alpha \left[ (u+X^{*})e^{-a(u+X^{*})}-(w+Z^{*})\right] dt. \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(26)

The system (26) can be approximately expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} du &{}= (-a_{11} u +a_{12}v)dt+\sigma X^{*}dB(t),\\ dv &{}= (-a_{21}v+a_{21}w)dt,\\ dw &{}= (a_{31}u-a_{33}w)dt, \end{aligned} \end{array}\right. } \end{aligned}$$

(27)

where $a_{11}=\delta ,~a_{12}=p,~a_{21}=\alpha ,~a_{31}=\alpha (1-aX^{*})e^{-aX^{*}}=\frac{\alpha \delta }{p}(1+\ln \frac{\delta }{p})$ and $a_{33}=\alpha$.

Now we give the existence theorem and specific form of the probability density function of the linear system (27) of (4).

Theorem 3.8

If

$$\begin{aligned} \delta <p~\text {and}~\delta \alpha ^{2}(5+\ln \frac{\delta }{p})+\alpha (2\alpha ^{2}+\delta ^{2})>0, \end{aligned}$$

then the distribution of the solution (u, v, w) of system (27) has a density function $\Phi (u, v, w)$ which takes the following form

$$\begin{aligned} \Phi (u, v, w)=(2\pi )^{-\frac{3}{2}}|\Sigma |^{-\frac{1}{2}}e^{-\frac{1}{2}(u, v, w)\Sigma ^{-1}(u, v, w)^{T}}, \end{aligned}$$

and corresponding to the marginal probability density function

$$\begin{aligned} \Psi (u)=\frac{1}{\sqrt{2\pi }\sigma _{1}}e^{-\frac{u^{2}}{2\sigma _{1}^{2}}}, \end{aligned}$$

where $\Sigma$ denotes the covariance matrix of (u, v, w), $\Sigma ^{-1}=\frac{2}{\sigma ^{2}\alpha ^{2}(1-aX^{*})^{2}e^{-2aX^{*}}}(d_{ij} )_{3\times 3}$, $d_{ij} (i, j = 1, 2, 3)$ and $\sigma _{1}$ are defined as below.

Proof

Let $y=w-v$, by (27), then

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dy&{}= [a_{31}u-(a_{21}+a_{33})y-a_{33}v]dt,\\ dv&{}= a_{21}ydt. \end{aligned} \end{array}\right. } \end{aligned}$$

Let $x=a_{31}u-(a_{21}+a_{33})y-a_{33}v$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dx&{}= -(A_{11}x+A_{12}y+A_{13}v)dt+\sigma a_{31} X^{*}dB(t),\\ dy&{}= xdt,\\ dv&{}= a_{21}ydt, \end{aligned} \end{array}\right. } \end{aligned}$$

(28)

where $A_{11}=a_{11}+a_{21}+a_{33}=\delta +2\alpha >0$, $A_{12}=a_{11}a_{21}+a_{11}a_{33}+a_{21}a_{33}=2\delta \alpha +\alpha ^{2}>0$, $A_{13}=a_{11}a_{33}-a_{12}a_{31}=-\delta \alpha \ln \frac{\delta }{p}>0$. U(x, y, v) be the density function of (x, y, v), which can be approximated by the following Fokker–Planck equation:

$$\begin{aligned}&0=\frac{\rho ^2}{2}\frac{\partial ^2U}{\partial x^2}-\frac{\partial [-(A_{11}x-A_{12}y-A_{13}v)U]}{\partial x}\\&\quad -\frac{\partial (xU)}{\partial y}-\frac{\partial (a_{21}yU)}{\partial v}, \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned} 0&= \bigg (\frac{\partial }{\partial y}-\frac{A_{12}}{\theta _{22}}\frac{\partial }{\partial y}\bigg ) \bigg [\frac{\rho ^2}{2}\frac{\partial U}{\partial x}+(\theta _{11}x+\theta _{13}v)U\bigg ]\\&\quad +\bigg (\frac{A_{12}}{\theta _{22}}\frac{\partial }{\partial x}-\frac{a_{21}}{\theta _{22}}\frac{\partial }{\partial v}\bigg )\bigg [\frac{\rho ^2}{2} \frac{\partial U}{\partial y}+\theta _{22}xU\bigg ]\\&\quad +\frac{a_{21}}{\theta _{22}}\frac{\partial }{\partial y} \bigg [\frac{\rho ^2}{2} \frac{\partial U}{\partial v}+(\theta _{31}x+\theta _{33}v)U\bigg ], \end{aligned} \end{aligned}$$

where $\theta _{12}=\theta _{21}=\theta _{23}=\theta _{32}=0$. From the above equation, we get,

$$\begin{aligned}&\theta _{11}=A_{11}>0,~\theta _{13}=A_{13}>0,~\theta _{31}=\frac{A_{11}A_{12}-\theta _{22}}{a_{21}},\\&\theta _{33}=\frac{A_{12}A_{13}}{a_{21}}>0, \end{aligned}$$

on account of

$$\begin{aligned} \theta _{22}= & {} A_{11}A_{12}-a_{21}A_{13}=\delta \alpha ^{2}\left( 5+\ln \frac{\delta }{p}\right) \\&+\,\alpha (2\alpha ^{2}+\delta ^{2})>0. \end{aligned}$$

Obviously, $\theta _{ij}=\theta _{ji}$ and the matrix $\theta = (\theta _{ij} )_{3\times 3}~(i, j = 1, 2, 3)$ is positive definite owing to $\theta _{11}\theta _{22}\theta _{33}-\theta _{13}^{2}\theta _{22}=\theta _{22}^{2}\frac{A_{13}}{a_{21}}>0$. The joint density function of (x, y, v) is as follows:

$$\begin{aligned}&U(x, y, v)=Ce^{-\frac{1}{\rho ^2}(\theta _{22}x^{2}+\theta _{22}y^{2}+\theta _{33}v^{2}+2\theta _{13}xv)}\\&\quad =Ce^{-\frac{1}{\rho ^2}(x, y, v)\theta (x, y, v)^{T}}, \end{aligned}$$

where C is a positive constant satisfying $\iiint _{\mathbb {R}_{+}^{3}}U(x, y, v)\mathrm{d}x\mathrm{d}y\mathrm{d}v= 1$ and

$$\begin{aligned} \begin{pmatrix} x\\ y\\ v \end{pmatrix} = \begin{pmatrix} a_{31}&{}a_{21}&{} -(a_{21}+a_{33})\\ 0&{}-1&{}1\\ 0&{}1&{}0 \end{pmatrix} \begin{pmatrix} u\\ v\\ w \end{pmatrix} \triangleq A\begin{pmatrix} u\\ v\\ w \end{pmatrix}. \end{aligned}$$

Thus, the Gaussian density function corresponding to (u, v, w) is as follows:

$$\begin{aligned} \Phi (u, v, w)=C'e^{-\frac{1}{\rho ^2}(u, v, w)A^{T}\theta A(u, v, w)^{T}}, \end{aligned}$$

where $C'$ is a positive constant satisfying $\iiint _{\mathbb {R}_{+}^{3}}\Phi (u, v, w)\mathrm{d}u\mathrm{d}v\mathrm{d}w= 1$.

$$\begin{aligned} \Sigma ^{-1}= & {} \frac{2}{\rho ^2}A^{T}\theta A\triangleq \frac{2}{\rho ^2}\\ D= & {} \frac{2}{\sigma ^{2}\alpha ^{2}(1-aX^{*})^{2}e^{-2aX^{*}}}(d_{ij})_{3\times 3}, \end{aligned}$$

where $\Sigma$ denotes the covariance matrix of (u, v, w). Apparently, the matrix $\Sigma ^{-1}$ is positive definite, then $\Sigma$ is also positive definite matrix. Therefore, $d_{ij} = d_{ji}~(i, j = 1, 2, 3)$. Direct calculation leads to that

$$\begin{aligned} d_{11}&=a_{31}^{2}\theta _{11}=\frac{\delta ^{2}\alpha ^{2}}{p^{2}}(2\alpha +\delta )\left( 1+\ln \frac{\delta }{p}\right) ^{2},\\ d_{12}&=a_{31}(a_{21}\theta _{11}+\theta _{13})\\&=\frac{\delta \alpha ^{2}}{p}(1+\ln \frac{\delta }{p})\left( 2\alpha +\delta -\delta \ln \frac{\delta }{p}\right) ,\\ d_{13}&=-\theta _{11}a_{31}(a_{21}+a_{33})\\&=-\frac{2\delta \alpha ^{2}}{p}(2\alpha +\delta )\left( 1+\ln \frac{\delta }{p}\right) ,\\ d_{22}&=a_{21}(a_{21}\theta _{11}+2\theta _{31})+\theta _{22}+\theta _{33}\\&=2\alpha (2\alpha ^{2}+3\delta \alpha +\delta ^{2}) -\delta (\alpha ^{2}+2\delta +\alpha )\ln \frac{\delta }{p},\\ d_{23}&=-(a_{21}+a_{33})(a_{21}\theta _{11}+\theta _{31})-\theta _{22}\\&=-\alpha \left( 6\alpha ^{2}+7\delta \alpha +2\alpha ^{2}-\delta \alpha \ln \frac{\delta }{p}\right) ,\\ d_{33}&=\theta _{11}(a_{21}+a_{33})^{2}+\theta _{22}\\&=\alpha \left( 10\alpha ^{2}+9\delta \alpha +2\delta ^{2}+\delta \alpha \ln \frac{\delta }{p}\right) . \end{aligned}$$

Then we have

$$\begin{aligned} \Phi (u, v, w)=(2\pi )^{-\frac{3}{2}}|\Sigma |^{-\frac{1}{2}}e^{-\frac{1}{2}(u, v, w)\Sigma ^{-1}(u, v, w)^{T}}. \end{aligned}$$

The marginal probability density function is expressed by

$$\begin{aligned} \Psi (u)=\frac{1}{\sqrt{2\pi }\sigma _{1}}e^{-\frac{u^{2}}{2\sigma _{1}^{2}}}. \end{aligned}$$

So, let’s try to find $\sigma _{1}^{2}$, we have

$$\begin{aligned} \Sigma =\bigg (\frac{2}{\rho ^{2}}A^{T}\theta A\bigg )^{-1}=\frac{\rho ^{2}}{2}A^{-1}\theta ^{-1} (A^{-1})^{T}. \end{aligned}$$

We know that $\sigma _{1}^{2}$ is the element in the first row and the first column of the covariance matrix, direct calculation, we get

$$\begin{aligned} \begin{aligned} \sigma _{1}^{2}&=\frac{\rho ^{2}}{2}\frac{\theta _{33}}{a_{31}^{2}(\theta _{11}\theta _{33}-\theta _{13}^{2})}\\&=\frac{\sigma ^{2}(2\delta +\alpha )}{2a^{2}[(2\delta +\alpha )(2\delta +\alpha +\delta \alpha ^{2}\ln \frac{\delta }{p})]}. \end{aligned} \end{aligned}$$

$\square$

Fig. 1

The path of X(t) for the stochastic Nicholson’s blowflies model (4) (blue line) and its corresponding deterministic model (red line) with initial parameters $(X(0), Y(0), Z(0)) = (0.05, 0.01, 0.01)$ under different noise intensities $\sigma =0.10$, $\sigma =0.13$, $\sigma =0.16$ and $\sigma =0.19$. (Color figure online)

Fig. 2

Figures on the left-hand side show solution in the total number of Nicholson’s blowflies X(t) resulting from Eq. (4) (blue line) and its corresponding deterministic model (red line), with initial conditions $(X(0), Y(0), Z(0)) = (0.05, 0.01, 0.01)$ under different noise intensities $\sigma =0.1$ (a), $\sigma =0.2$ (c) and $\sigma =0.3$ (e). Figures on the right-hand side present histograms of the probability density function of X(100) with three different values of $\sigma :~\sigma =0.1$ (b), $\sigma =0.2$ (d) and $\sigma =0.3$ (f). (Color figure online)

4 Main results in the weak kernel case

When $n=0$, f(t) is weak kernel, i.e., $f(t)=\alpha e^{-\alpha t}.$

Define

$$\begin{aligned} Y(t)=\int _{-\infty }^{t}\alpha e^{-\alpha (t-s)}X(s)e^{-aX(s)}\mathrm{d}s, \end{aligned}$$

considering the actual situation, white noise is also added into (2), then system (2) with weak kernel and environment noise is becoming:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} dX(t) &{}= \left[ -\delta X(t) +pY(t)\right] dt+\sigma X(t)dB(t),\\ dY(t) &{}= \alpha \left[ X(t)e^{-aX(t)}-Y(t)\right] dt. \end{aligned} \end{array}\right. } \end{aligned}$$

(29)

Using same methods similar to Sect. 3, we have come to the following conclusions directly:

Theorem 4.1

There exists a unique solution of the system (29) with the weak kernel, for any initial value $(X(0), Y(0))\in \mathbb {R}_{+}^{2}$, which will remain in $\mathbb {R}_{+}^{2}$ with probability one.

Theorem 4.2

Let (X(t), Y(t)) be a solution of the stochastic system (29) with the weak kernel, for any given initial value $(X(0), Y(0))\in \mathbb {R}_{+}^{2}$. If $p<\delta$, then

$$\begin{aligned} \lim _{t\rightarrow \infty }X(t)=0~\text{ and }~\lim _{t\rightarrow \infty }Y(t)=0~a.s. \end{aligned}$$

Theorem 4.3

Let (X(t), Y(t)) be a solution of the stochastic system (29) with the weak kernel. The distribution of (X(t), Y(t)) has a density U(t, x, y), $\forall t > 0$. If $p>\delta +\frac{\sigma ^{2}}{2}$, then there is a unique density $U^{*}(x, y)$ satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }\iint _{\mathbb {R}_{+}^{2}}|U(t, x, y)-U^{*}(x, y)|\mathrm{d}x\mathrm{d}y=0. \end{aligned}$$

5 Numerical simulations

Using Milstein’s method [23], the discretized equation of model (4) is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} X_{k+1} &{}= X_k + \left( - \delta X_k +pY_k \right) \Delta t +\sigma X_k\sqrt{\Delta t} \xi _k\\ &{}\quad + \frac{1}{2}\sigma ^2X_k (\xi _k^2-1)\Delta t, \\ Y_{k+1} &{}= Y_k + \alpha \left( Z_k - Y_k \right) \Delta t, \\ Z_{k+1} &{}= Z_k + \alpha \left( X_k e^{-aX_k} - Z_k \right) \Delta t, \end{aligned} \end{array}\right. } \end{aligned}$$

where $\xi _k^2 ~(k=1,2,\ldots )$ are independent Gaussian random variables N(0, 1). Next, we give two numerical examples to support our results.

5.1 Extinction

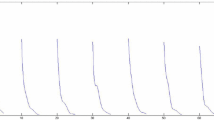
Using the software MATLAB, we choose right parameters $\delta =0.3$, $p=0.1$, $a=2$ and the strong kernel coefficient $\alpha =0.4$. For the deterministic system (3) and the stochastic model (4), we find that the Nicholson’s blowflies X(t) will eventually die out, which is consistent with the result of Theorem 3.2 (see Fig. 1). Compared with the four pictures (a), (b), (c) and (b) in Fig. 1, it can be observed that the extinction of the Nicholson’s blowflies X(t) will be accelerated with the increase of noise intensity $\sigma$.

5.2 Asymptotic stability

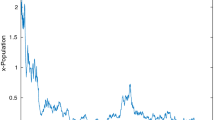
For the sake of testing the existence of a stationary distribution, we choose $\delta =0.3$, $p=0.7$, $a=2$ and $\alpha =0.4$. For deterministic system (3), there exists a locally asymptotically stable (see the left-hand side of Fig. 2), where positive equilibrium is $E^{*}=(0.4236,0.1816,0.1816)$. We find that there exists a stationary distribution and a higher $\sigma$ generates larger fluctuations of X(t). The distribution of X(t) is positively skewed with the noise increases as shown in Fig. 2.

6 Conclusion

In this paper, we formulate a stochastic Nicholson’s blowflies model with distributed delay by using the linear chain technique. The main objective of this paper is to discuss the long-time behavior of Nicholson’s blowflies model. Firstly, the existence and uniqueness of globally positive solution for the stochastic Nicholson’s blowflies model is obtained. Then, the sufficient conditions for the stochastic extinction of Eq. (4) are established. Generally speaking, due to the diffusion matrix is degenerate, the uniform elliptic condition is invalid. So, using Markov semigroup theory, the existence of a unique stationary distribution of the model (4) is derived. Finally, particular attention is given to the expression of the density function around the positive equilibrium of the deterministic system. Since the corresponding Fokker–Planck equation is three-dimensional, the previous method is invalid. While this paper fills this gap. In order to answer the questions mentioned in the introduction, we state the main results as follows:

• (i) Theorem 3.2 gives the conclusion of extinction that if $p<\delta$, then

  $$\begin{aligned}&\lim _{t\rightarrow \infty }X(t)=0,~\lim _{t\rightarrow \infty }Y(t)=0~\text{ and }~\\&\lim _{t\rightarrow \infty }Z(t)=0~a.s. \end{aligned}$$

  That is to say, the population X(t) of the stochastic system (4) becomes extinct with probability one.

• (ii) According to Theorem 3.3, the condition for stationary distribution is $p>\delta +\frac{\sigma ^{2}}{2}$.

• (iii) Through Theorem 3.8, the conditions for the existence of probability density function is

  $$\begin{aligned} \delta <p~\text {and}~\delta \alpha ^{2}(5+\ln \frac{\delta }{p})+\alpha (2\alpha ^{2}+\delta ^{2})>0. \end{aligned}$$

  Many interesting questions deserve further discussion. For example, a more complex model with Markovian switching is proposed to consider the positive recurrence of the system. We’ll leave this for future work.