A theoretical model linking interspecific variation in density dependence to species abundances

Abstract

Understanding the factors that govern the commonness and rarity of individual species is a central challenge in community ecology. Empirical studies have often found that abundance is related to traits associated with competitive ability and suitability to the local environment and, more recently, also to negative conspecific density dependence. Here, we construct a theoretical framework to show how a species’ abundance is, in general, expected to be dependent on its per-capita growth rate when rare and the rate at which its growth rate declines with increasing abundance (strength of stabilization). We argue that per-capita growth rate when rare can be interpreted as competitive ability and that strength of stabilization largely reflects negative conspecific inhibition. We then analyze a simple spatially implicit model in which each species is defined by three parameters that affect its juvenile survival: its generalized competitive effect on others, its generalized response to competition, and an additional negative effect on conspecifics. This model facilitates the stable coexistence of an arbitrarily large number of species and qualitatively reproduces empirical relationships between abundance, competitive ability, and negative conspecific density dependence. Our results provide theoretical support for the combined roles of competitive ability and negative density dependence in the determination of species abundances in real ecosystems, and suggest new avenues of research for understanding abundance in models and in real communities.

Introduction

What determines species diversity in ecological communities is a major unanswered scientific question (Pennisi 2005). Two interrelated aspects of species diversity are species richness and relative abundance. Existing models, such as the lognormal and the neutral models, can provide good statistical fits to empirical patterns of relative abundance for an ensemble of species (Volkov et al. 2007; McGill 2003; Chisholm and Pacala 2010). However, these models do not allow us to predict the relative abundance of individual species.

Empirical studies have shown that abundance tends to be correlated with two factors: conspecific density dependence and traits related to competitive ability. Competitive ability is generally defined as the ability to extract a limiting resource or to use a limiting resource efficiently. For example, in Minnesota grasslands, plant species with higher competitive ability, measured as lower values for nitrogen (the equilibrium level to which they reduce this limiting resource in monoculture), had higher abundances in multi-species plots (Fargione and Tilman 2006). A number of other studies have also found that plant species with traits leading to more efficient use or uptake of the limiting resource tend to have higher abundances (Mamolos et al. 1995; Tsialtas et al. 2001; Theodose et al. 1996).

The second factor correlated empirically with relative abundances is negative conspecific density dependence, by which we mean the rate at which species’ per-capita growth rates decline with increasing abundance. In plant communities, species with stronger negative impacts on conspecifics tend to be less abundant (Klironomos 2002; Mangan et al. 2010; Comita et al. 2010). In general, conspecific negative density dependence reflects intraspecific competition and/or apparent competition that is stronger than interspecific competition and/or apparent competition. Among plants, it is variously attributed to the influence of host-specific natural enemies and to more intense resource competition. Soil-borne pathogens have been specifically linked to negative density dependence in a number of systems (Klironomos 2002; Mangan et al. 2010; Bell et al. 2006). Negative density dependence is also a general mechanism of coexistence in animals, although a similar link between negative density dependence and relative abundance has yet to be demonstrated in this case (Amarasekare 2009).

The empirical correlations between abundance, competitive ability, and negative density dependence have received little attention in the theoretical literature (although see the simulation model in Mangan et al. 2010). Models of resource competition do predict that species having lower R* values (i.e., more competitive species) should be more successful (Tilman 1990; Tilman et al. 1982). However, under pure R* theory, this does not lead to stable coexistence because the species with the lowest R* is predicted to competitively exclude all species with higher R* values. Stable coexistence requires a mechanism that makes intraspecific effects more negative than interspecific effects and thereby creates negative conspecific density dependence (Chesson 2000).

A logical starting point for investigating the relationship between abundance, competitive ability, and negative density dependence is the theoretical literature on stable coexistence (Levin 1970). Stable coexistence means that species tend to recover from perturbations that lower their abundance (Chesson 2000). Species are predicted to coexist when stabilizing forces, such as niche differences, limit interspecific competition and are sufficiently strong to overcome differences in inherent fitness between species (Chesson 2000; Adler et al. 2007). Where stabilization is insufficient to overcome differences in intrinsic fitness, competitive exclusion results instead. Neutral models (Hubbell 2001) correspond to the extreme case in which species have the same intrinsic fitness and there is no stabilization. Previous theoretical studies have investigated how the addition of a constant level of negative density dependence can affect species abundance distributions and species–area curves (Chave et al. 2002; Volkov et al. 2005) but have not evaluated the impacts of variation in density dependence among species.

By parameterizing a coexistence model in terms of competitive abilities and negative conspecific density dependence of individual species, it should be possible to derive coexistence conditions and equilibrium abundances in terms of these parameters. One difficulty in analyzing such a model is that a species’ abundance can depend to a large extent on its location in parameter space relative to other species (e.g., Tilman 1994; Muller-Landau 2010), thereby obscuring any relationship between abundance and absolute parameter values. Nevertheless, we hypothesize that the relationship of abundance to negative density dependence and competitive ability may be strong enough to emerge consistently from different theoretical models regardless of the underlying structure.

Our approach in this paper is to analyze the relationship between relative abundance and negative density dependence in a simple model. As discussed above, there is an extensive theoretical literature on the relationship between coexistence and negative density dependence, and we could have chosen many different models as our starting point (e.g., the Monod model (Grover 1990) or the Lotka–Volterra model). The model that we use is based on Chesson’s (2000) framework and is chosen for its simplicity, generality, and analytical tractability. We first present a general graphical description of the model to illustrate how invasion growth rate and strength of stabilization are conceptually related to equilibrium abundance. We then turn to the analytical model that is parameterized in terms of negative conspecific density dependence and competitive response, and we derive formulas for equilibrium abundance, invasion growth rate, and strength of stabilization for each species. We also determine coexistence and invasion criteria, and we analyze the stability of equilibria. Our formulas reveal the theoretical relationship of abundance to the parameters representing negative density dependence and competitive response. We investigate this relationship further by assembling communities and conducting numerical simulations. We close with a discussion of the implications for understanding species abundances in real communities and of avenues for future research.

General framework

In communities that exhibit coexistence of multiple species, all species have, by definition, positive per-capita growth rates when rare (Chesson 2000; Levin 2000). A direct corollary of this is that all species have negative average per-capita growth rates when near monodominance. As a first-order approximation, we can assume that the average per-capita growth rate of each species decreases monotonically as abundance increases, declining to zero at the species’ equilibrium abundance and then becoming negative at higher values of abundance. In general, this picture may be complicated by factors such as Allee effects, which cause per-capita growth rates to be negative when the species is rare, or by limit cycles and chaotic dynamics, which prevent species from reaching equilibrium abundances. We ignore these complicating factors in the framework that follows, but our qualitative insights should be robust to their inclusion.

First, we focus on the simple case in which the decline in per-capita growth with increasing abundance for every species is linear. The dynamics of a species can then be fully described by any two of the following three quantities: the invasion growth rate $\widehat{r}$ (per-capita growth rate when rare), the stabilization Z (decrease in per-capita growth with increasing abundance), and the equilibrium abundance $\overline p$ (Fig. 1). The three parameters are related by $\overline p = - \widehat{r}/Z$.

Fig. 1

Conceptual graphical model of the relationship between equilibrium abundance ($\overline p$; horizontal intercept), per-capita growth rate when rare ($\widehat{r}$; vertical intercept) and strength of stabilization (Z; magnitude of the slope) for a single species. For simplicity, the relationship between the growth rate and abundance is assumed to be linear in the graphical model, as discussed in the text

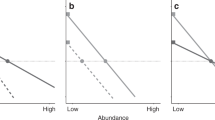
Within this framework, we can examine the dynamics of multi-species communities graphically. Consider first the special case in which species vary in their strength of stabilization but not in their invasion growth rates. In this case, relative abundances are fully determined by stabilization (Fig. 2a). Next consider the case in which species vary in their invasion growth rates but not in their strength of stabilization: relative abundances are now fully determined by the invasion growth rates (Fig. 2b). Lastly, consider the case in which both stabilization and invasion growth rate vary: relative abundances now depend on both (Fig. 2c).

Fig. 2

Conceptual graphical model of the relationship between equilibrium abundance (horizontal intercept), per-capita growth rate when rare (vertical intercept), and strength of stabilization (magnitude of the slope) for multiple coexisting species. For simplicity, the relationship between the growth rate and abundance is assumed to be linear for each species in the graphical model, as discussed in the text; a shows four species with equal per-capita growth rate when rare but different strengths of stabilization; b shows four species with different per-capita growth rates when rare but equal strength of stabilization; and c shows four species with different per-capita growth rates and different strengths of stabilization

Thus, we can see conceptually that equilibrium abundances should be related to both invasion growth rate and competitive ability. To motivate the analytical model to be introduced in the next section, we observe that insofar as differences in invasion growth rate reflect differences in competitive ability (Adler et al. 2007) and stabilization reflects conspecific inhibition, abundance should be related to competitive ability and conspecific inhibition.

Model

We develop a spatially implicit discrete-time model in which species differ in their generalized competitive effects on other species, in their responses to competition, and in their additional negative influences on (or responses to) conspecifics. We denote the relative abundance of species i at time t as p _i,t . A proportion m ∈ (0,1) of adults dies per unit time step, and new individuals are recruited into the community. The recruitment and survival of new individuals are governed by a lottery among juveniles, which is influenced by the relative abundances of adults in the community.

The master equation governing the dynamical behavior of the system is

$$ {p_{{i,t}}}_{{ + {1}}} = \left( {{1} - m} \right){p_{{i,t}}} + m{p_{{i,t}}}\sum\nolimits_{{_{{{ }j}}}} {\frac{{{s_{{ij}}}{p_{{j,t}}}}}{{{\Sigma_k}{s_{{kj}}}{p_{{k,t}}}}}}, $$

(1)

where S _ij  ∈ (0,1) is the probability of survival of juveniles of species i under species j, and the upper and lower bounds of the summations (here and throughout) are 1 and n (Note that for motile animal communities, the product p _i,t p _j,t could be interpreted as the contact rate of species i and j and the parameter S _ij could be interpreted as a mass-action coefficient). Competitive effects, competitive responses, and negative conspecific density dependence together determine juvenile survival, with S _ij  = α _j β _i for i ≠ j, and S _ii  = α _i β _i (1 − η _i ), with α _i , β _i , η _i  ∈ (0,1). We interpret α _i as a measure of the effect of species i on other species: small values of α _i correspond to a strong effect of species i on other species (e.g., a tree that casts deep shade). The parameter β _i is a measure of the competitive response of species i: small values of β _i correspond to species that do poorly in the presence of competition (e.g., light-demanding species). The parameter η _i is a measure of conspecific inhibition: high values of η _i correspond to strong conspecific inhibition and thus stronger negative density dependence. This model just described is a niche model with stable coexistence facilitated by conspecific negative density dependence (non-zero η _i parameters). In this model, the parameter β _i is a measure of intrinsic fitness: it determines the relative growth rates of the species in the absence of stabilizing forces (Chesson 2000; Appendix I). If stabilization is removed from the model (i.e., if all the parameters η _i are zero, thus setting intraspecific effects equal to interspecific effects), then the species with highest intrinsic fitness (β _i ) will competitively exclude all other species, and species with equal intrinsic fitness will exhibit neutral coexistence (Appendix I).

Because the p _i,t represents relative abundances and because ${\sum_i}{p_i}_{{,t + 1}} = {\sum_i}{p_{{i,t}}}$ from (1), we can assume without loss of generality, the initial condition ${\sum_i}{p_{{i,0}}} = 1$. Also, from (1) we can see that p _i,t + 1 ≥ 0, which, in conjunction with ${\sum_i}{p_{{i,t}}} = 1$ implies p _i,t + 1 ≤ 1, so the behavior of the master equation is sensible in that it constrains the relative abundances to be between 0 and 1. Substituting the expressions for S _ij into the master equation gives

$$ {p_{{i,t + 1}}} = (1 - m){p_{{i,t}}} + m\left\{ {\frac{{ - {\alpha_i}{\beta_i}{\eta_i}{p_{{i,t}}}}}{{\left( {{\sum_k}{\alpha_i}{\beta_k}{p_{{k,t}}}} \right) - {\alpha_i}{\beta_i}{\eta_i}{p_{{i,t}}}}}{p_{{i,t}}} + {\beta_i}{p_{{i,t}}}{\sum_j}\frac{{{\alpha_j}{p_{{j,t}}}}}{{\left( {{\sum_k}{\alpha_j}{\beta_k}{p_{{k,t}}}} \right) - {\alpha_j}{\beta_j}{\eta_j}{p_{{j,t}}}}}} \right\} $$

(2)

We also define:

$$ f({{\bf p}}) = \mathop{\sum }\limits_k {\beta_k}{p_{{k,t}}} > 0 $$

and

$$ g({{\bf p}}) = \mathop{\sum }\limits_j \frac{{{\alpha_j}{p_{{j,t}}}}}{{\left( {{\sum_k}{\alpha_j}{\beta_k}{p_{{k,t}}}} \right) - {\alpha_j}{\beta_j}{\eta_j}{p_{{j,t}}}}} = \mathop{\sum }\limits_j \frac{{{p_{{j,t}}}}}{{f({{\bf p}}) - {\beta_j}{\eta_j}{p_{{j,t}}}}} $$

so the master equation becomes:

$$ {p_{{i,t + 1}}} = \left( {1 - m} \right){p_{{i,t}}} + m{p_{{i,t}}}\left\{ {\frac{{ - {\beta_i}{\eta_i}{p_{{i,t}}}}}{{f\left( {{\bf p}} \right) - {\beta_i}{\eta_i}{p_{{i,t}}}}} + {\beta_i}g\left( {{\bf p}} \right)} \right\} $$

Equilibrium abundances

We seek an equilibrium in which all of the n species are extant $\left( {{{\overline p }_i} > 0} \right)$. To solve for the equilibrium, we set ${p_{{i,t + 1}}} = {p_{{i,t}}} = {\overline p_i}$ and divide through by ${\overline p_i}$:

$$ 1 = \frac{{ - {\beta_i}{\eta_i}{p_{{i,t}}}}}{{f\left( {{\bf p}} \right) - {\beta_i}{\eta_i}{p_{{i,t}}}}} + {\beta_i}g\left( {\overline {{\bf p}} } \right) $$

This gives:

$$ {\overline p_i} = f\left( {\overline {{\bf p}} } \right)\frac{1}{{{\beta_i}{\eta_i}}}\left( {1 - \frac{1}{{{\beta_i}g\left( {\overline {{\bf p}} } \right)}}} \right) $$

(3)

To evaluate $g\left( {\overline {{\bf p}} } \right)$, we multiply both sides of (3) by β _i and sum:

$$ \mathop{\sum }\limits_i {\beta_i}{\overline p_i} = \left( {\mathop{\sum }\limits_k {\beta_k}{{\overline p }_k}} \right)\mathop{\sum }\limits_i \left\{ {\frac{1}{{{\beta_i}{\eta_i}}}\left( {{\beta_i} - \frac{1}{{g\left( {\overline {{\bf p}} } \right)}}} \right)} \right\} $$

which gives:

$$ g\left( {\overline {{\bf p}} } \right) = \frac{{{\Sigma_i}\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {{\Sigma_i}\frac{1}{{{\eta_i}}}} \right) - 1}} > 0. $$

Also, from the constraint ${\Sigma_i}{\overline p_i} = 1$, we can express $f\left( {\overline {{\bf p}} } \right)$ (which is effectively a normalization constant) as

$$ f\left( {\overline {{\bf p}} } \right) = {\left[ {\mathop{\sum }\limits_i \frac{1}{{{\beta_i}{\eta_i}}}\left( {1 - \frac{1}{{{\beta_i}g\left( {\overline {{\bf p}} } \right)}}} \right)} \right]^{{ - 1}}} $$

For the equilibrium (3) to exist in a sensible way, we need all ${\overline p_i} > 0$, so ${\beta_i}g\left( {\overline {{\bf p}} } \right) > 1$.This leads to the existence criterion:

$$ {\beta_i} > \frac{{\left( {{\sum_j}\frac{1}{{{\eta_j}}}} \right) - 1}}{{{\sum_j}\frac{1}{{{\beta_j}{\eta_j}}}}} $$

which can be rearranged to give:

$$ {\beta_i} > \frac{{\left( {{\sum_{{j \ne i}}}\frac{1}{{{\eta_j}}}} \right) - 1}}{{{\sum_{{j \ne i}}}\frac{1}{{{\beta_j}{\eta_j}}}}}. $$

(4)

The coexistence condition can also be expressed as:

$$ {\sum_j}\frac{1}{{{\eta_j}}}\left( {1 - \frac{{{\beta_{{\min }}}}}{{{\beta_j}}}} \right) < 1, $$

(5)

where β _min = min _i (β _i ). If there are only two species, the existence criterion (4) reduces to s ₁₂ > s ₂₂ and s ₂₁ > s ₁₁. That is, species 1 survives better under species 2 than species 2 does under itself, and similarly, species 2 survives better under species 1 than species 1 does under itself. Each species has a greater negative effect on itself than on the other species, consistent with standard coexistence conditions. Note that as we add more species, the left-hand side of (5) increases monotonically, and conversely, as we remove species, the left-hand side of (5) decreases monotonically. One consequence of this is that if n species can coexist, then so can any subset of these species.

From equation (3), it is immediately clear that a species’ equilibrium abundance is inversely related to the degree to which the species inhibits its conspecifics (${\overline p_i}$ is proportional to 1/η _i ). Equilibrium abundance is also positive related to competitive response, β _i : if two species inhibit conspecifics equally (η _i  = η _j ), then the one with the higher competitive response will be more abundant (i.e., ${\beta_i} > {\beta_j} \Rightarrow {\overline p_i} > {\overline p_j}$). To see this, suppose β ₁  > β ₂ and η ₁ = η ₂ = η and observe that $g\left( {\overline {{\bf p}} } \right)$ declines monotonically with the addition of more species to the system (Appendix II), so that:

$$ g\left( {\overline {{\bf p}} } \right) = \frac{{{\sum_i}\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {{\sum_i}\frac{1}{{{\eta_i}}}} \right) - 1}} < \frac{{\frac{1}{\eta }\left( {\frac{1}{{{\beta_1}}} + \frac{1}{{{\beta_2}}}} \right)}}{{\frac{1}{\eta } + \frac{1}{\eta } - 1}} < \frac{1}{{{\beta_1}}} + \frac{1}{{{\beta_2}}} = \frac{{\frac{{{\beta_1}}}{{{\beta_2}}} - \frac{{{\beta_2}}}{{{\beta_1}}}}}{{{\beta_1} - {\beta_2}}} $$

and then:

$$ \left( {{\beta_1} - {\beta_2}} \right) < \frac{1}{{g\left( {\overline {{\bf p}} } \right)}}\left( {\frac{{{\beta_1}}}{{{\beta_2}}} - \frac{{{\beta_2}}}{{{\beta_1}}}} \right) $$

$$ \frac{1}{{{\beta_1}}}\left( {1 - \frac{1}{{{\beta_1}g\left( {\overline {{\bf p}} } \right)}}} \right) > \frac{1}{{{\beta_2}}}\left( {1 - \frac{1}{{{\beta_2}g\left( {\overline {{\bf p}} } \right)}}} \right) $$

which, using the definition of ${\overline p_i}$, immediately leads to ${\overline p_1} > {\overline p_2}$ (remembering that η ₁ = η ₂ by assumption).

Stability of the equilibrium

Let M be the Jacobian matrix of partial derivatives with entries ${m_{{ij}}} = {\left. {\frac{{\partial {F_i}}}{{\partial {p_j}}}} \right|_{{\overline p }}}$, where ${p_{{i,t + 1}}} = {F_i}\left( {{{{\bf p}}_{{{\bf t}}}}} \right)$ as defined above. The equilibrium $\overline {{\bf p}}$ defined by (3) is locally stable if and only if all eigenvalues λ _i of the matrix M satisfy $\left| {{\lambda_i}} \right| < 1$. The one-species case is trivial because the initial condition is ${\overline p_1} = 1$ and it immediately follows from (1) that ${\overline p_{{1,t}}} = 1$ for all t. In the two-species case, the dynamics of the second species are redundant because of the constraint that p ₁ + p ₂ = 1, so we only need to check that

$$ \left| {{\lambda _{1}}} \right| = \left| {{{\left. {\frac{{\partial {F_{1}}}}{{\partial {p_{1}}}}} \right|}_{{\overline {{\bf p}} }}}} \right| < 1 $$

This reduces to:

$$ - 1 < \frac{{ - 2Bm + A}}{A} < 1 $$

where $B = \left( {{a_1}\left( {{\beta_2} - {\beta_1}} \right) + {a_1}{\beta_1}{\eta_1}} \right)\left( {{a_2}\left( {{\beta_1} - {\beta_2}} \right) + {a_2}{\beta_2}{\eta_2}} \right)\left( {{a_2}\beta_1^2{a_1}{\eta_1} + {a_1}\beta_2^2{a_2}{\eta_2} - {a_1}{a_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right) > 0\;and\;A = 2{\left( {{a_1}{a_2}{\beta_1}{\beta_2}\left( {{\eta_1} + {\eta_2} - {\eta_1}{\eta_2}} \right)} \right)^2} > 0$. So the conditions become just m < A/B ≡ m _crit. It can be shown (Appendix III) that m _crit > 1 and so the two-species equilibrium is always locally stable, assuming only that it exists, because 0 < m < 1. We conjecture that $\overline {{\bf p}}$ is also locally stable for the n-species case (see Appendix IV for the Jacobian for the n-species case). Simulations further suggest that the equilibrium $\overline {{\bf p}}$ defined by (3) is in fact globally stable (e.g., Fig. 3).

Fig. 3

Trajectories of the relative abundances of individual species in a typical community governed by the master equation (2). The community of n = 100 species was assembled using condition (4), with β ₁ = 0.999 and subsequent β _i  = 0.01β _L  + 0.99β _U . The parameters a _i and η _i were drawn from uniform random distributions on (0,1) Initial abundances were also drawn from uniform random distributions on (0,1) and then normalized to sum to 1. Only the 10 species with highest equilibrium abundances (${\overline p_i}$) are shown

Invasion growth rates

The expression for the growth rate of species i when rare in our model is:

$$ {\widehat{r}_i} = \mathop{{\lim }}\limits_{{{p_{{i,t}}} \to 0}} \frac{{{p_{{i,t + 1}}} - {p_{{i,t}}}}}{{{p_{{i,t}}}}} = \mathop{{\lim }}\limits_{{{p_{{i,t}}} \to 0}} \left[ {m{\beta_i}g\left( {{\bf p}} \right) - \frac{{mf\left( {{\bf p}} \right)}}{{f\left( {{\bf p}} \right) - {\beta_i}{\eta_i}{p_{{i,t}}}}}} \right] = m{\beta_i}g\left( {{\bf p}} \right) - m $$

which depends only on the competitive response, or intrinsic fitness, β _i and not on the competitive effect a _i or conspecific inhibition η _i (η _i vanishes in the expression for $g\left( {{\bf p}} \right)$ because we are assuming ${p_{{i,t}}} \to 0$). Note that this is consistent with our general framework, under which differences in invasion growth rates are expected to reflect differences in intrinsic fitness. We require ${\widehat{r}_i} > 0$, so:

$$ {\beta_i} > \frac{1}{{g\left( {{\bf p}} \right)}} = \frac{1}{{{\sum_{{j \ne i}}}\frac{{{p_{{j,t}}}}}{{f\left( {{\bf p}} \right) - {\beta_j}{\eta_j}{p_{{j,t}}}}}}} $$

If all of the other species j ≠ i are at equilibrium, then the invasion condition becomes:

$$ {\beta_i} > \frac{1}{{g\left( {{{{\bf p}}_{{ - i}}}} \right)}} = \frac{{\left( {{\Sigma_{{j \ne i}}}\frac{1}{{{\eta_j}}}} \right) - 1}}{{{\Sigma_{{j \ne i}}}\frac{1}{{{\beta_j}{\eta_j}}}}} $$

where $g\left( {{{{\bf p}}_{{ - i}}}} \right)$ is evaluated at the equilibrium for the n − 1 species excluding species i, which is the same as the coexistence condition (4). So any species can invade when rare, assuming that it can potentially coexist with the other species and that the other species are at equilibrium.

Strength of stabilization

If species i invades a system in which the other n − 1 species are initially at their equilibrium, the relationship between the growth rate and the abundance of species i can be approximated by the linear equation:

$$ {r_i} \approx {\widehat{r}_i} - \frac{{{{\widehat{r}}_i}}}{{{{\overline p }_i}}}{p_i} $$

(6)

The linear approximation appears to be reasonable for most systems, as we will later show in simulations. The slope represents the strength of stabilization and is given by:

$$ Z \equiv - \frac{{{{\widehat{r}}_i}}}{{{{\bar{p}}_i}}} = - m{\eta_i}\beta_i^2\frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}\left( {\frac{{{\beta_i}g\left( {{{{\bf p}}_{{ - i}}}} \right) - 1}}{{{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1}}} \right) $$

(7)

As expected, the strength of stabilization is proportional to the conspecific feedback (η _i ). The relationship between the strength of stabilization and the competitive response (β _i ) is more subtle. For systems with many species (large n), the ratio $\left( {{\beta_i}g\left( {{{{\bf p}}_{{ - i}}}} \right) - 1} \right)/\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right)$ approaches 1, in which case the strength of stabilization should be proportional to the square of β _i , but this effect is difficult to reproduce in simulations.

Assembling communities

Our model facilitates the theoretical coexistence of arbitrarily many species, as we now prove by induction. Without loss of generality, we add species to the community in order of decreasing β _i . First, we construct a community with only one species for which the parameters a ₁, β ₁, and η ₁ for the first species are set to any values, subject to the restriction a ₁, β ₁, η ₁ ∈ (0,1). We know from the work above that condition (4) holds for this one-species system, so the equilibrium exists and is stable (although only neutrally stable for the one-species case). Now assume that we have a system with n species for which condition (4) holds, which means that:

$$ {\beta_L} \equiv \frac{{\left( {\sum_{{j = 1}}^n\frac{1}{{{\eta_j}}}} \right) - 1}}{{\sum_{{j = 1}}^n\frac{1}{{{\beta_j}{\eta_j}}}}} < \min \left\{ {{\beta_i}:1 \leqslant i \leqslant n} \right\} \equiv {\beta_U} $$

(8)

Let us choose ${\beta_{{n + 1}}} \in \left( {{\beta_L},{\beta_U}} \right)$ and arbitrary α _n + 1 and $η_{n + 1}$. Now:

$$ \frac{{\left( {\sum_{{j = 1}}^n\frac{1}{{{\eta_j}}}} \right) - 1}}{{\sum_{{j = 1}}^n\frac{1}{{{\beta_j}{\eta_j}}}}} < {\beta_{{n + 1}}} $$

$$ \Rightarrow \left( {\mathop{\sum }\limits_{{j = 1}}^n \frac{1}{{{\eta_j}}}} \right) - 1 + \frac{1}{{{\eta_{{n + 1}}}}} < {\beta_{{n + 1}}}\left( {\mathop{\sum }\limits_{{j = 1}}^n \frac{1}{{{\beta_j}{\eta_j}}}} \right) + {\beta_{{n + 1}}}\frac{1}{{{\beta_{{n + 1}}}{\eta_{{n + 1}}}}} $$

$$ \Rightarrow \frac{{\left( {\sum_{{j = 1}}^{{n + 1}}\frac{1}{{{\eta_j}}}} \right) - 1}}{{\sum_{{j = 1}}^{{n + 1}}\frac{1}{{{\beta_j}{\eta_j}}}}} < {\beta_{{n + 1}}} $$

and so condition (4) holds for the system with n + 1 species also. As we add new species, it is easily shown that β _L increases and β _U decreases, so the possible range for β _n + 1 shrinks but never to zero. We emphasize that this assembly rule is general: any potential community of coexisting species in our model can be assembled in this way.

We can also consider the special case of assembling communities in which all species have the same conspecific inhibition (i.e., η _i  = η _j  = η). In this case, we know from (5) that the condition for coexistence is:

$$ \eta > {\eta_{{\min }}} = n - {\beta_{{\min }}}{\sum_j}\frac{1}{{{\beta_j}}} $$

(9)

The interpretation of this condition is that given a set of competitive response parameters (β _i ), we can calculate the minimum conspecific inhibition required to facilitate coexistence of all species. It is quite possible for η _min > 1 in (9), in which case coexistence is impossible because of the restriction that η ∈ (0,1).

We can consider another special case in which conspecific inhibition (η _i ) is again constant and the competitive responses (β _i ) are drawn from a uniform random distribution on [β _lo, β _hi]. In this case, the expected value of η _min in inequality (9) is:

$$ E\left( {{\eta_{{\min }}}} \right) = n - {\beta_{{\min }}}\sum\limits_{{j = 1}}^n E \left( {\frac{1}{{{\beta_j}}}} \right) \approx n - {\beta_{\rm{lo}}}\sum\limits_{{j = 1}}^n E \left( {\frac{1}{{{\beta_j}}}} \right) = n\left( {1 - \frac{{\ln (x)}}{{x - 1}}} \right) > 0, $$

where x = β _hi/β _lo and the approximation is valid if n is sufficiently large. The maximum number of species that can coexist under this scheme is then given approximately by:

$$ n < {n_{{\max }}} \approx \frac{\eta }{{\left( {1 - \frac{{\ln (x)}}{{x - 1}}} \right)}} $$

Determinants of abundance, invasion growth rate, and stabilization in simulated communities

We constructed communities numerically according to the rule given by (8) and confirmed that these communities do indeed exhibit coexistence between arbitrarily many species (to the limits of numerical precision) (e.g., Fig. 3). They also exhibit the theoretical relationships between abundances ${\overline p_i}$ and the model parameters discussed earlier: abundance is uncorrelated with competitive effect (α _i ), positively correlated with competitive response (β _i ), and negatively correlated with conspecific inhibition (η _i ) (Fig. 4a–c).

Fig. 4

Relationship of equilibrium abundances (${\overline p_i}$; a–c), invasion growth rate (${\widehat{r}_i}$; d–f), and strength of stabilization (Z; panels g–i) to model parameters for the community described in the legend of Fig. 3. a, d, g Strength of competitive effects (α _i ; note that low values of α _i indicate strong effects; R ² = 0.000, p = 0.839;R ² = 0.008; p = 0.371; R ² = 0.007; p = 0.398). b, e, h Strength of competitive response (β _i ; R ²  = 0.294, p < 0.001; R ² = 1.000, p < 0.001, R ² = 0.003, p = 0.612). c, f, i Strength of conspecific inhibition (η _i ; R ² = 0.498, p < 0.001, R ² = 0.001, p = 0.770; R ² = 1.000, p < 0.001)

The numerical simulations also confirmed that the invasion growth rate is positively related to competitive response (intrinsic fitness; β _i ) but unrelated to the other parameters (Fig. 4d–f) and that strength of stabilization is strongly correlated with conspecific inhibition (η _i ) (Fig. 4g–i). As expected, equilibrium abundance is then correlated with both invasion growth rate and strength of stabilization (Fig. 5). Furthermore, the relationship between the per-capita growth rate and abundance was approximately linear for most species in most simulated communities (confirming the validity of (6)), although the linear approximation was worse for the more abundant species (Fig. 6), especially in species-poor communities (not shown).

Fig. 5

Relationship of equilibrium abundance (${\overline p_i}$) to invasion growth rate (${\widehat{r}_i}$) and strength of stabilization (Z _i ) for the community described in the legend of Fig. 3. a Equilibrium abundance versus invasion growth rate (R ² = 0.302, p < 0.001). b Equilibrium abundance versus strength of stabilization (R ² = 0.486, p < 0.001)

Fig. 6

Growth rate versus relative abundance for the system described in the legend of Fig. 3. Each solid curve represents the trajectory of an individual species invading the system when the other n − 1 species are initially at their equilibrium relative abundances. Each dotted line is the linear approximation (6) to the corresponding trajectory. Only the 10 most abundant (highest ${\widehat{p}_i}$) species are shown

It should be noted that the general patterns discussed above can be sensitive to the method used to choose the a _i , β _i , and η _i parameters: it is possible, for example, to make abundance ${\overline p_i}$ positively related to conspecific inhibition (η _i ) by introducing positive correlations between η _i and competitive response (β _i ).

Discussion

The theoretical model that we have presented here illustrates why, in practice, one might expect abundance to be positively related to competitive ability and negatively related to conspecific inhibition. We have built on previous conceptual work that describes how species coexistence is regulated by invasion growth rates and stabilization (Adler et al. 2007; Chesson 2000), by observing that high equilibrium abundances are generally associated with high invasion growth rates and low stabilization and that, in turn, invasion growth rates relate to competitive ability (or, equivalently, intrinsic fitness) and stabilization relates to conspecific inhibition. An important observation from our model is that a species’ invasion growth rate and the strength of the stabilization to which it is subjected are contextual, in the sense that they are determined not only by the species’ own parameters but also by those of all the other species in the community. In real ecosystems, invasion growth rates and the strength of stabilization of individual species are also both expected to vary with environmental conditions, in conjunction with variation in equilibrium abundance and, ultimately, presence in the community.

The theoretical work here was inspired in particular by recent data from tropical plant communities (Comita et al. 2010; Mangan et al. 2010). Differences in juvenile survival depending on the species identity of neighbors are the key to our model and can be interpreted in terms of differential seedling survival in soils under conspecific versus heterospecific adults as measured by Mangan et al. (2010), and to differential seedling survival as a function of local conspecific neighbor density as measured by Comita et al. (2010). Our model characterizes conspecific inhibition with one parameter per species and competitive ability with another parameter per species. The competitive ability parameter expresses a general influence of species traits on survival. The model demonstrates how the two parameters (local inhibition and competitive ability) can jointly influence abundance. The relative importance of the two parameters in determining relative abundances depends on the degree to which each varies among species and on how they covary.

A standard interpretation of conspecific inhibition in models such as ours, as well as in the empirical studies that inspired our model, is in terms of natural enemies, but there are other possible causes of conspecific inhibition. Stronger negative effects of conspecifics than of heterospecifics on per-capita population growth are a general feature of all stabilizing mechanisms (i.e., all niche mechanisms) and are not unique to natural enemies (Chesson 2000). Differentiation in resource use, for example, can also produce such patterns. Thus, empirical observations of conspecific inhibition alone are not sufficient to implicate natural enemies. Specific tests such as the disappearance of this inhibition when enemies are removed are needed to establish the role of enemies in maintaining abundances in real ecosystems (Carson 2008; Klironomos 2002; Bell et al. 2006; Mangan et al. 2010). As noted above, our model was formulated with plant communities in mind, but the model is sufficiently abstract to generalize to any community of organisms in which conspecific inhibition operates (e.g., animal communities; Amarasekare 2009).

Conspecific inhibition, in general, and host-specific natural enemies, in particular, effectively create a niche space that has as many dimensions as there are species present. Theoretically, if there are no other fitness differences among species, conspecific inhibition can enable the coexistence of arbitrary numbers of species (Armstrong 1989). However, as we have shown here, theory also shows that the contribution of conspecific inhibition to coexistence is limited to a surprising degree by variation in fitness among species. As the number of species increases, conspecific inhibition is associated with ever weaker stabilization because the average relative abundances of each species in the community are necessarily lower and, hence, individuals encounter fewer conspecifics. Consequently, species with relatively low invasion growth rate that could previously persist in the community can be knocked out as species richness increases because the stabilization forces acting on other, more abundant, species become weaker. This decrease in the strength of stabilization forces as species richness increases seems to be fairly general. For example, species richness (n) is often in the denominator in expressions for Chesson’s stabilizing forces (Chesson 2000).

The near-linearity of per-capita growth versus abundance observed in our model (Fig. 6) is a consequence of the global nature of our spatially implicit model, in which the probability that a recruit of one species lands near an individual of another species is simply proportional to both species’ overall relative abundance in the community. We expect that a spatially explicit model with local dispersal and local inhibition would result in a growth versus abundance curve with a more concave shape because individuals that were relatively rare overall would generally not be as rare locally and so juveniles would be subject to higher conspecific densities. The effects of localized dispersal and inhibition on coexistence vary among models and depend on the magnitude of conspecific inhibition as well as the scales of dispersal and inhibition (Muller-Landau and Adler 2007; Adler and Muller-Landau 2005).

In future, it would be interesting to conduct similar analyses of other coexistence models to explore the generality of our findings. The structure of our model is essentially a competitive hierarchy in which negative conspecific density dependence stabilizes coexistence among species with inherent fitness differences. Conspecific inhibition is, almost by definition, the only niche mechanism that can lead to stabilization, but as noted above, it can take a variety of forms and would need to be measured differently in different models. For example, our general framework could be applied to the classic Lotka–Volterra competition model or to models based on it (Rees and Westoby 1997; Adler et al. 2007) by making the competition coefficients functions of species-specific competitive effect, competitive response, and conspecific inhibition. We expect that such analyses would exhibit similar patterns to ours (e.g., positive relationships between abundance and the magnitude of negative density dependence). In other models, however, such as habitat partitioning models, the expected relationship of conspecific inhibition to model parameters is less obvious. Explicit derivation of the invasion growth rates, strength of stabilization, and equilibrium abundances for these models, and examination of their relationships to model parameters (similar to our analysis here), would provide insights into the implications of the underlying mechanisms for community assembly, structure, and dynamics. A goal of such analyses should be to express invasion growth rates and strength of stabilization in terms of parameters that are empirically measurable. In our case, both competitive response and conspecific inhibition can, in principle, be measured experimentally (Levine and HilleRisLambers 2009) or estimated from observational data (Adler et al. 2010; Adler et al. 2006).

By using a model to show how abundances can be related to competitive response and conspecific inhibition (negative density dependence), we have provided a theoretical basis for recently observed empirical patterns (Comita et al. 2010; Mangan et al. 2010) and we have laid the framework for more realistic models. A major limitation of our model is that it ignores issues of scale and spatial variation that are critical for the maintenance of biodiversity (Levin 2000). We can reasonably expect that competitive response and conspecific inhibition (and hence invasion growth rate and strength of stabilization) will vary across a landscape and will also vary depending on the scale at which we measure them. This variation in turn generates spatial variation in abundances: a species may be common regionally but rare locally, or rare at one location and common in another. Exploring how these issues play out in a more sophisticated spatially explicit model is a priority for future research.

Appendices

Appendix I: Coexistence in the absence of negative density dependence

We investigate coexistence in our model in the absence of negative density dependence (i.e., η _i  = 0). In this case, the master equation becomes:

$$ {p_{{i,t + 1}}} = \left( {1 - m} \right){p_{{i,t}}} + m{p_{{i,t}}}{\beta_i}g\left( {{\bf p}} \right) $$

It can be seen from this equation that β _i represents intrinsic fitness because it measures differences in relative growth rates in the absence of stabilizing forces (Chesson 2000). To solve for equilibrium, we let ${p_{{i,t + 1}}} = {p_{{i,t}}} = {\overline p_i}$. Assuming that ${\overline p_i} \ne 0$, we have:

$$ {\beta_i}g\left( {{\bf p}} \right) = 1 $$

$$ {\beta_i}\mathop{\sum }\limits_j \frac{{{p_{{j,t}}}}}{{f\left( {{\bf p}} \right)}} = 1 $$

$$ {\beta_i} = \mathop{\sum }\limits_j {\beta_k}{p_k} $$

which means that every species that persists at equilibrium must have an identical value of β _i . The master equation then degenerates to:

$$ {p_{{i,t + 1}}} = {p_{{i,t}}} $$

meaning that species will persist at their initial abundances. This model is clearly only neutrally stable.

Appendix II: Mathematical details from equilibrium abundances section

We want to show that $g\left( {\overline {{\bf p}} } \right)$ declines monotonically with the addition of more (stably coexisting) species to the system defined by (2). Start with a system of n (stably coexisting) species with equilibrium relative abundances ${\overline {{\bf p}}_n}$, so that:

$$ g\left( {{{\overline {{\bf p}} }_n}} \right) = \frac{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} $$

Now add another (stably coexisting) species to the system so that there are n + 1 species and:

$$ g\left( {{{\overline {{\bf p}} }_{{n + 1}}}} \right) = \frac{{\frac{1}{{{\beta_{{n + 1}}}{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} $$

We know from the coexistence condition (4) that:

$$ {\beta_{{n + 1}}} > \frac{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}}{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}. $$

This in turn implies that:

$$ \frac{1}{{{\beta_{{n + 1}}}}} < \frac{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} = g\left( {{{\overline {{\bf p}} }_n}} \right) $$

and thus:

$$ g\left( {{{\overline {{\bf p}} }_{{n + 1}}}} \right) = \frac{{\frac{1}{{{\beta_{{n + 1}}}{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} < \frac{{\frac{{g\left( {{{\overline {{\bf p}} }_n}} \right)}}{{{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} = g\left( {{{\overline {{\bf p}} }_n}} \right), $$

where the final equality follows from

$$ a = \frac{b}{c} \Rightarrow a = \frac{{\frac{a}{x} + b}}{{\frac{1}{x} + c}} $$

for any x.

Appendix III: Local stability analysis for the two-species case

We complete the stability analysis for the two-species case started in the main text. Let ${\eta_i} = {\gamma_i}/{\alpha_i}{\beta_i}$. We want to show that

$$ {m_{\rm{crit}}} = \frac{{2{{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)}^2}}}{{\left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right)}} > 1. $$

Note that the three factors in the denominator of m _crit are positive and the parenthetic expression in the numerator is positive too because:

$$ {\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2} = {\alpha_2}{\beta_2}{\gamma_1} + {\gamma_2}{s_{{11}}} $$

Now let:

$$ A = 2{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)^2} > 0 $$

$$ B = \left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right) > 0 $$

So we have:

$$ \matrix{ {A - B = 2{{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)}^2}} \hfill \cr { - \left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right)} \hfill \cr { = - \left\{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_2}\left( {{\beta_1} + {\beta_2}} \right){\gamma_1} + {\alpha_1}\left( {{\beta_1} + {\beta_2}} \right){\gamma_2} - {\gamma_1}{\gamma_2}} \right\}} \hfill \cr { \times \left\{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_1}\left( { - 2{\beta_1} + {\beta_2}} \right){\gamma_2} + {\gamma_1}\left( {{\alpha_2}\left( {{\beta_1} - 2{\beta_2}} \right) + 2{\gamma_2}} \right)} \right\}} \hfill \cr }<!end array> $$

The first factor in braces here is positive because:

$$ \matrix{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_2}{\beta_1}{\gamma_1} + {\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} + {\alpha_1}{\beta_2}{\gamma_2} - {\gamma_1}{\gamma_2}} \hfill \cr { = \left\{ {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right\} + \left\{ {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right\}} \hfill \cr { = \left\{ {\left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)} \right\}} \hfill \cr { + 2\left\{ {{\alpha_1}{\beta_1}{\alpha_2}{\beta_2} - \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)} \right\}} \hfill \cr { = \left( {{s_{{21}}} - {s_{{11}}}} \right)\left( {{s_{{12}}} - {s_{{22}}}} \right) + 2\left\{ {{\alpha_1}{\beta_1}{\alpha_2}{\beta_2} - \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)} \right\} > 0} \hfill \cr }<!end array> $$

The second factor in the expression for A − B is negative because:

$$ \matrix{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_1}\left( { - 2{\beta_1} + {\beta_2}} \right){\gamma_2} + {\gamma_1}\left( {{\alpha_2}\left( {{\beta_1} - 2{\beta_2}} \right) + 2{\gamma_2}} \right)} \hfill \cr { = \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2} - {\alpha_2}{\beta_1}} \right) + \left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)\left( {{\alpha_1}{\beta_1} - {\gamma_1} - {\alpha_1}{\beta_2}} \right)} \hfill \cr { = {s_{{11}}}\left( {{s_{{22}}} - {s_{{12}}}} \right) + {s_{{22}}}\left( {{s_{{11}}} - {s_{{21}}}} \right) < 0} \hfill \cr }<!end array> $$

and so $A - B > 0$. We know that B is positive, so ${m_{\rm{crit}}} = A/B > 1$.

Appendix IV: Jacobian for the general case

We want to compute the Jacobian A evaluated at the equilibrium (3) of the dynamical system defined by (2). Let ${\eta_i} = {\gamma_i}/{\alpha_i}{\beta_i}$. To do this, we require the partial derivatives of the expression on the right hand side of the master equation (2):

$$ {F_i}\left( {{\bf p}} \right) = \left( {1 - m} \right){p_i} + m{p_i}\left\{ {\frac{{ - {\gamma_i}{p_i}}}{{{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}}} + {\beta_i}g\left( {{\bf p}} \right)} \right\} $$

where

$$ f\left( {{\bf p}} \right) = \sum\limits_k {{\beta_k}{p_k}} $$

and so

$$ \frac{{\partial f}}{{\partial {p_i}}} = {\beta_i} $$

and

$$ g\left( {{\bf p}} \right) = \sum\limits_j {\frac{{{\alpha_j}p_j}}{{\left( {{\Sigma_k}{\alpha_j}{\beta_k}{p_k}} \right) - {\gamma_j}{p_j}}}} = \sum\limits_j {\frac{{{\alpha_j}{p_j}}}{{{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}}}} $$

and so

$$ \matrix{ {\frac{{\partial g}}{{\partial {p_i}}} = \frac{{\alpha_i^2}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}\left( {f\left( {{\bf p}} \right) - {p_i}\frac{{\partial f}}{{\partial {p_i}}}} \right) - \frac{{\partial f}}{{\partial {p_i}}}\sum\limits_{{j \ne i}} {\frac{{\alpha_j^2{p_j}}}{{{{\left( {{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}} \right)}^2}}}} } \hfill \cr { = \frac{{\alpha_i^2\left( {{\bf p}} \right)}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}} - {\beta_i}\sum\limits_j {\frac{{\alpha_j^2{p_j}}}{{{{\left( {{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}} \right)}^2}}}} } \hfill \cr }<!end array> $$

These expressions can be used to compute the partial derivatives of F _i :

$$ \frac{{\partial {F_i}}}{{\partial {p_i}}} = 1 + m\left\{ {\frac{{ - {\alpha_i}f\left( {{\bf p}} \right)}}{{{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}}} + {\beta_i}g\left( {{\bf p}} \right) + {p_i}\left[ {\frac{{{\alpha_i}{\gamma_i}}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}\left( {{p_i}{\beta_i} - f\left( {{\bf p}} \right)} \right) + {\beta_i}\frac{{\partial g}}{{\partial {p_i}}}} \right]} \right\} $$

and

$$ \frac{{\partial {F_i}}}{{\partial {p_j}}} = m{p_i}\left\{ {\frac{{{\alpha_i}{\gamma_i}}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}{p_i}{\beta_j} + {\beta_i}\frac{{\partial g}}{{\partial {p_j}}}} \right\} $$

for $i \ne j$. Note that:

$$ \sum\limits_{{i = 1}}^n {\frac{{\partial {F_i}}}{{\partial {p_j}}}} = 1 $$

for any j. Intuitively, this follows because the F _i just represent all of the p _i and time t + 1 and the net change in these with a change in p _j is just one.

Now at, ${{\bf p}} = \overline {{\bf p}}$, we have:

$$ {\overline p_i} = f\left( {\overline {{\bf p}} } \right)\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {1 - \frac{1}{{{\beta_i}g\left( {\overline {{\bf p}} } \right)}}} \right) $$

and so:

$$ {\left. {\frac{{\partial g}}{{\partial {p_i}}}} \right|_{{\overline {{\bf p}} }}} = \mathop{\beta }\nolimits_i^2 \frac{{g{{\left( {\overline {{\bf p}} } \right)}^2}}}{{f\left( {\overline {{\bf p}} } \right)}} - \mathop{\beta }\nolimits_i \frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}h\left( {\overline {{\bf p}} } \right) $$

where

$$ h\left( {\overline {{\bf p}} } \right) = \sum\limits_k {\left\{ {\frac{{{\alpha_k}{\beta_k}}}{{{\gamma_k}}}\left( {{\beta_k}g\left( {\overline {{\bf p}} } \right) - 1} \right)} \right\}} $$

and:

$$ {\left. {\frac{{\partial {F_i}}}{{\partial {p_j}}}} \right|_{{\overline {{\bf p}} }}} = m\frac{{{\alpha_i}}}{{{\gamma_i}}} - \left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_j}\left\{ {\left( {{\beta_i} + {\beta_j}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} $$

for i ≠ j, and

$$ \eqalign{ {\left. {\frac{{\partial {F_i}}}{{\partial {p_i}}}} \right|_{{\overline {{\bf p}} }}} = 1 + m{p_i}\beta_i^2\left\{ {\frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1 - \frac{{{\gamma_i}}}{{{\alpha_i}}}g\left( {\overline {{\bf p}} } \right)} \right) + \left( {{\beta_i}\frac{{g{{\left( {\overline {{\bf p}} } \right)}^2}}}{{f\left( {\overline {{\bf p}} } \right)}} - \frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}h\left( {\overline {{\bf p}} } \right)} \right)} \right\} = \hfill \cr = 1 + m\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_i}\left\{ {\left( {2{\beta_i} - \frac{{{\gamma_i}}}{{{\alpha_i}}}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} \hfill \cr }<!endgathered> $$

We can then write a general expression for the entries of the Jacobian A:

$$ {a_{{ij}}}{\left. { = \frac{{\partial {F_i}}}{{\partial {p_j}}}} \right|_{{\overline {{\bf p}} }}} = {\delta_{{ij}}} + m\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_j}\left\{ {\left( {{\beta_i} + {\beta_j} - {\delta_{{ij}}}\frac{{{\gamma_i}}}{{{\alpha_i}}}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} $$

where δ _ij is the Kronecker delta. Note that ${\beta_i}g\left( {\overline {{\bf p}} } \right) - 1 > 0$ because this is a necessary and sufficient condition for coexistence, as discussed in the main text.