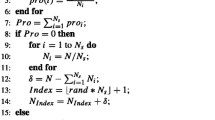1 Introduction

The success of evolution in nature outstrips that of evolutionary computing even though it is based on the same principles. This can be attributed primarily to the abundance of resources in nature, such as time and memory, which are constrained in a computer system. This is especially true in the case of systems which involve human interactivity, such as interactive evolutionary computation (IEC). Consequently, accelerating evolutionary computation (EC) is necessary for many EC applications to improve the performance of their target systems. Consider the case of an IEC that optimizes a target system based on the IEC user’s subjective evaluations; user fatigue is a serious problem limiting such a system’s practical application. Multiple trials for accelerating IEC and EC have therefore been proposed [12, 23].

One of the methods taken for accelerating EC is to approximate the fitness landscape and apply an elite strategy [22]. If the search space is high dimensional, non-linear, non-differentiable and non-convex, conventional approximation methods encounter difficulties dealing with the complex space, and the best solution is to reduce the search space dimension. This kind of dimensionality reduction strategy was originally proposed in Pei and Takagi [10, 13] and applied to the traveling salesman problem in a real-world application [11].

We have used interpolation or approximation methods to obtain the fitness landscape in a dimensionally reduced search space [10, 13]. Reaching the global optimum from the elite is easier in the regression space. Although it may not be the actual global optimum, it may be a neighbor to the global optimum in the original search space. Finding the actual global optimum from the elite is therefore an easier task. Here, regression space refers to a lower dimensional space consisting of k dimensional (k-D) axes of the original n-D axes, where we use k = 1 in this paper. In other words, individuals are projected onto the k-D space to simplify finding the elite. This elitism does not destroy the original EC search space so much by approximation, but can accelerate the IEC and EC convergence with less computational cost by conducting the elite search in the n regression spaces of k-D (k = 1).

We extend our previous works [10, 13] and present a comprehensive investigation of our proposal through the series of experiments which we present in this paper. Specifically, we investigate: (1) accelerated convergence of our proposals in a simulated IEC user model. (2) the computational cost of our proposal in comparison to the work in [22] for ordinary EC, and (3) EC acceleration performance for higher dimensional benchmark tasks. A Gaussian mixture model with different dimensions and 34 well-known benchmark functions are employed in our experiments. Some related analysis and discussions are involved in each investigation. From a framework viewpoint, this method can be embedded in any IEC and EC algorithm in order to obtain accelerated convergence. The investigation of the above-listed three topics contributes to this paper’s originality.

Following this introductory section, an overview of methods used for accelerating EC is reported in Sect. 2 We introduce the interpolation and approximation methods which relate to our study in Sect. 3. In Sect. 4, we explain in detail our proposed method is enabled by a technique for reducing the dimensionality of the search space, and we show how the elite can be obtained from regression search spaces. In Sects. 5 and 6, IEC and EC are experimental evaluated using a Gaussian mixture model with various different dimensions and 34 benchmark functions, and their results and related topics are analyzed and discussed. Finally, we discuss some general issues in Sect. 7 and conclude with the performance of our proposed methods presented here and discuss some open topics, further opportunities and future works in Sect. 8.

2 Conventional techniques

There are many complex optimization tasks in many areas that involve combinatorial, dynamic, severely non-linear, non-differentiable, and non-convex space problems. Although EC is a good metaheuristic optimization tool for them, its search performance for such complex tasks naturally decreases. EC usually finds areas of better fitness easily and quickly, however, finding the global optimum accurately may be time-consuming. Several conventional accelerating EC convergence methods have been proposed to solve this problem [12]. They include approximating the fitness landscape [15, 16, 22], adaptive evolution control methods [6], developing new mechanisms embedded into existent EC algorithms [14], information fusion methods [5, 8, 27] and so on.

Using the EC landscape information directly is a promising method for EC acceleration. A single-peak function is used to obtain the landscape of the original search space [Eq. (1)], and an elite individual is found from the peak of that landscape’s curve to accelerate the EC search [22]. This method can be considered both high return and low risk; the elite is obtained from a fitted single-peak function and the worst fitness individual is simultaneously removed from the population, which does not significantly destroy the original search space. It is, however, costly to fit the single peak function in a high dimensional search space with the requirement that it needs at least 2D + 1 individuals in the fitting process, where D is the number of dimensions of the problem. Our proposed methods obtain the fitness landscape in lower dimensional search spaces, and thus significantly reduce the computational cost in the fitting stage. In this paper, we compare our proposed methods with the method in [22].

$$ f(X) = \sum_{i=1}^n a_i(x_i-b_i)+c $$
(1)

Adaptive evolution control methods [6] control and self-adaptively tune the EC parameters, such as operator rate, or use a dynamic search strategy to balance global exploration and local exploitation such that EC performance is enhanced. In differential evolution, there have been some novel strategies proposed in recent years, such as SaDE [18], JADE [20], jDE [1] and JASaDE [4].

Information fusion methods are an important acceleration method. In this case, EC is fused with other optimization techniques to change the search strategy, to decide the search direction, or to choose high priority individuals, etc. These fusion techniques include local search [2, 24, 27], simulated annealing [8], artificial neuron networks [5, 7], and others too numerous to mention here.

3 Approximating the fitness landscape by interpolation and approximation

3.1 Regression function

The computation of each EC generation produces a set of discrete individuals and their corresponding fitness \({(x_i,y_i), i=0,1,\ldots,m}\), but the analytical expression relating the two cannot be known. We make the data regression curve for the required function from the given category \(\Upphi\).

Because there must be some errors in the observed discrete data, we do not require interpolated or approximated curves pass through all the discrete points exactly, but rather that it approaches the original curve at its discrete points, i.e. near x i , as much as possible.

We let the function \({\varphi(x)}\) belong to \(\Upphi\), and \({\delta_{i}} = {\varphi(x_i)- y_i}\) be the error at \({\varphi(x_i)}\), such that the error vector is \({\delta=(\delta_0,\delta_{1},\ldots,\delta_m)^T}\). In the regression calculation process, we let the norm of the vector ||δ|| be minimized. For a different norm, we can construct a different regression function. The function series is shown in Eq. (2).

$$ \Upphi=Span\{\varphi_0(x),\varphi_1(x),\ldots,\varphi_n(x)\} $$
(2)

The members in Eq. (2), i.e. \(\varphi_0(x),\varphi_1(x), \ldots, \varphi_n(x)\), are linearly independent in the interval [a, b], where the nodes x i are contained. Any type of function \(\varphi(x)\) can be expressed as Eq. (3).

$$ \varphi(x) = a_{0}\varphi_{0}(x) + a_{1}\varphi_1(x)+\cdots+a_n\varphi_n(x) $$
(3)

The EC search space is complex for some nonlinear, non-differentiable, and non-convex space problems. The regression process brings additional cost to the EC, so a better solution is to select a simple function as the regression function to reduce its additional cost. A polynomial function is suitable for regression computing, so in this paper, we select it as the regression function in our interpolation and approximation methods.

3.2 Lagrange interpolation method

The Lagrange interpolation polynomial has the characteristic of being linear and unique. For one dimensional data from individuals \({x_0}, {x_1}, \ldots, {x_n}\), we can set up an n degree polynomial \({l_0(x)},{l_1(x)}, \ldots, {l_n(x)}\). We set its type as l i (x j ) = δ ij , where the form of δ ij is as shown in Eq. (4).

$$ \delta_{ij} = \left\{ \begin{array}{ll} 0 & \rm{if}\, i=j \\ 1 & \rm{if}\, i\not=j \end{array} \right. $$
(4)

From the definition of l k (x), we can obtain Eq. (5), which is the n degree interpolation polynomial, where l i (x) is an nth degree polynomial. The relationships of the Lagrange interpolation polynomial are shown in Eqs. (5), (6), (7) and (8).

$$ p_n(x)=\sum_{k=0}^{n} l_k(x)y_k=y_{i} $$
(5)
$$ l_k(x)=a(x-x_{0})\ldots(x-x_{k-1})(x-x_{k+1})\ldots(x-x_n) $$
(6)

When l k (x k ) = 1,

$$ a=[(x_k-x_0)\ldots(x_k-x_{k-1})(x_k-x_{k+1})\ldots(x_k-x_n)]^{-1} $$
(7)

i.e.,

$$ l(x)= \prod_{i=1,i\not=k}^n \frac{(x-x_i)}{(x_k-x_i)} $$
(8)

Equations (8) and (9) are the n degree Lagrange interpolation basis function and the n degree Lagrange interpolation polynomial, respectively.

$$ L_n(x)= \sum_{k=0}^n l_k(x)y_k,\quad i=0,1,\ldots,n $$
(9)

In this paper, we use the binomial Lagrange interpolation polynomial as the simplified regression search space expression, and use the three individuals with relative better fitness as the interpolation points to obtain the concrete regression function. The concrete interpolation polynomial is as in Eq. (10). The Lagrange interpolation method is used to find the parameters of Eq. (10).

$$ L(x)=\sum_{k=1}^{3} \left\{ \prod_{i=1,i\not=k}^3\frac{(x-x_i)}{(x_k-x_i)} \right\} y_{k} $$
(10)

3.3 Least squares approximation method

As is mentioned above, we want to minimize the norm of the error vector \(\delta=(\delta_0,\delta_1,\ldots,\delta_m)^{T}\). If we use the 2-norm form vector as the error vector, the calculation process is simplified. When one calculates the error vector norm for the 2-norm, the approximation method is referred to as the least squares method. Given data in the form of the function series, i.e., Eq. (2), we want to find a function that lets the error 2-norm vector be minimized, namely, Eq. (11).

$$ ||\delta^*||^2_2=\sum^m_{i=0} \delta^{*2}_{i}=\sum^m_{i=0}[\varphi^*(x_i)-y_i]^2=\min_{\varphi(x)\in\Upphi}||\delta^*||^{2}_{2} $$
(11)

The approximation function is shown in Eq. (12).

$$ \varphi^*(x)=a^*_0\varphi_0(x)+a^*_1\varphi_1(x)+\cdots+a^{*}_{n}\varphi_n(x) $$
(12)

If we can obtain \({\varphi_0(x), \varphi_1(x), \ldots, \varphi_n(x)}\), the system will be orthogonal, i.e. \({(\varphi_{i},\varphi_{j})=0 (i\not=j)}\), and the coefficient matrix equations will form a diagonal matrix [Eq. (13)].

$$ a^{*}_{k} = \frac{(f,\varphi_{k})}{(\varphi_{k},\varphi_{k})} $$
(13)

So the approximation function is as in Eq. (14).

$$ \varphi^*(x) = \sum_{i=0}^{n} \frac{(f,\varphi_i)}{(\varphi_{i}, \varphi_{i})}\varphi_{i}(x). $$
(14)

Similar to the use of Lagrange interpolation in Sect. 3.2 to obtain a regression search space by interpolation, here we use a linear function to obtain a linear approximation of the regression search space. The concrete expression is shown in Eq. (15).

$$ \left( {\begin{array}{l} (\varphi_{0} \varphi_{0} )\quad (\varphi_{0} \varphi_{1}) \\ (\varphi _1 \varphi _0 )\quad (\varphi _1 \varphi _1 ) \\ \end{array}} \right) \left({\begin{array}{l} D \\ E \\ \end{array}} \right)=\left({\begin{array}{l} y_0 \\ y_1 \\ \end{array}}\right) $$
(15)

The approximation process is used to obtain the parameters D and E in Eq. (15) such that the regression search space may be defined in a linear space.

4 Obtaining elite from regression search spaces by dimensionality reduction to accelerate IEC and EC searches

4.1 Dimensionality reduction method

It is not easy for conventional interpolation or approximation methods to find an accurate regression search space corresponding to the original multi-dimensional space. An alternative method is to reduce the dimensionality of the original search space and find approximate curve expressions in the lower dimensional spaces. However, if the parameter variables of the fitness function are dependent, when they are separated into the lower dimensional space, the dimensionality reduction method will destroy the original search space information and the dependent parameter variables’ relationships. Although there is a risk that some information will be lost when reducing the search space dimensionality, it is easy to interpolate or approximate the search space to obtain landscape information in lower dimensional search spaces with e.g. one or two dimensions of the original search space.

Our method for reducing the dimensionality of the searching space uses only one of the n parameter axes at a time instead of all n parameter axes, and projects individuals onto each 1-D regression space. The landscape of the n-D parameter space is given by a fitness function, \(y=f(x_1,x_{2},\ldots,x_n)\), and the fitness value of the m-th individual are given by Eq. (16).

$$ y_m=f(x_{1m},x_{2m},\ldots,x_{nm})\, (m=1,2,\ldots,M) $$
(16)

There are M individuals with n-D parameter variables. We project the individuals onto the n 1-D spaces in i-th dimension as follows.

$$ (x_{i1},y_1) (x_{i2},y_2) \ldots (x_{im},y_m) $$

Each of the n 1-D regression spaces has M projected individuals. The original search space and dimensionally reduced search space are shown in Fig. 2. The dimensionality reduction method simplifies the regression computations, and it is easy to obtain a regression search space in lower dimension, which can be helpful in situations which involve a higher dimensional nonlinear search space.

4.2 Method for simplifying the regression space landscape to select an elite

We interpolate or approximate the landscape of each 1-D regression space using the projected M individuals and select elite from the n approximated 1-D landscape shapes. In this paper, we test two methods for approximating the 1-D regression search spaces; in the first method we use a binomial Lagrange interpolation and in the other linear least squares approximation. The elite is generated from the resulting approximated shapes.

Finding the elite corresponds to a kind of local search in the area where relatively better individuals exist in the original search space. The global optimum is expected to be near this area and we may be able to find it with a probability higher than chance [22]. So the elite selection method is a critical step in the proposed acceleration processes.

As the elite obtained by the two different elite selection methods is different, it is expected that the acceleration performance will also differ. Further, the regression EC search space obtained by approximation or interpolation has its own characteristics and particularities, and we must use an efficient method to obtain an elite from this simplified search space after analyzing its characteristics.

Binomial Lagrange interpolation simplifies a regression space with a nonlinear curve, and it is easy to obtain its inflection point from its gradient, using the inflection point as the elite. The linear least squares approximation uses a linear function to approximate the regression space. Its gradient is either descent or ascent. Lacking an inflection point, a safer method, taking into account both descent and ascent, is to select the average point of the linear approximation line as the elite (see Fig. 1).

Fig. 1
figure 1

New elite selection methods from a regression search space. Left by Lagrange interpolation method; Right by least squares approximation method

Full size image
Fig. 2
figure 2

Method for synthesizing elite. This proposed method represents a novel local search method for accelerating IEC/EC convergence

Full size image

Our proposed methods replace the worst individual in each generation with an elite selected as above. Although we cannot deny the small possibility that the global optimum is located near the worst individual, the possibility that the worst individual will become a parent in the next generation is also low; removing the worst individual therefore presents the least risk and is a reasonable choice.

4.3 Method for synthesizing elite

The methods in Sect. 4.2 select n elite points in n 1-D regression spaces, respectively: \({x_{1-elite}}, {x_{2-elite}},\ldots,\) and x n-elite . The n-D elite used for accelerating IEC/EC convergence in the next generation is obtained as follows:

$$ {\rm New\,Elite} = (x_{1-elite}, x_{2-elite}, ..,x_{n-elite}). $$

It is easier to calculate elite in a lower dimensional space than a higher dimensional space. Although we use 1-D as the lower dimensional space in this paper, in general the method need not be restricted to 1-D.

Once a new elite has been obtained, there are two methods for how it can be handled. In one cautious method, the fitness value of this elite is calculated to determine whether the new elite is really useful for acceleration, and in the other straightforward method, the new elite is inserted into the next IEC/EC iteration process without any prior consideration or judgment. In our proposed methods, we choose the first method. If the fitness of elite is better than the worst one, we place it into the next generation.

Our proposed method is based on the hypothesis that (1) elite calculated by interpolation or approximation from relatively better individuals will also have good fitness; (2) synthesizing an n-D elite from n elite points in n 1-D regression spaces will also produce a good elite; (3) the probability of the global optimum being located near to the synthesized elite is high. (see Fig. 2)

In general, this proposed method represents a novel local search method for accelerating IEC/EC convergence, and it is this method that represents this paper’s principal original contribution.

5 IEC experimental evaluations and analysis

5.1 Methods for comparison

Table 1 shows our proposed methods along with conventional methods for comparison. We use differential evolution (DE) [17] in our experiments. As mentioned above, our proposed methods can be embedded as a framework in any IEC or EC algorithm to accelerate its search and is not limited to DE.

Table 1 Conventional methods and our proposed methods used for experimental comparison
Full size table

5.2 IEC user model and experimental conditions

Experimental evaluations frequently demand many repeated experiments under the same conditions, and evaluations with an IEC user model is necessary for this case rather than a real human IEC user. Our IEC user model [9] was designed based on the four specifications of (1) a relatively simple fitness landscape, (2) a multi-modal fitness landscape, (3) a big valley structure, and (4) parametrically controllability of the shape and complexity of the fitness landscape. The rationale of (1) is that although a human IEC user cannot distinguish differences less than the differential threshold of perceptions, he or she can nevertheless obtain practical solutions. The rationale of (2) is the observation that there are graphics, design, music, and others expressions for which fitness values are high but their expressions are quite different. That of the (3) is that an IEC user can reach the global optimum area easily in spite of (2). The feature of the (4) is essential to conduct experiments with gradually changed several fitness landscapes.

A Gaussian mixture model (GMM) was established as pseudo-IEC user to simulate the user’s evaluation in [21]. The GMM consists of different means, variances and peaks mixed together to express the characteristics of a human user conducting an IEC evaluation experiment. We use a GMM for evaluation in this section. Concretely, we combine four Gaussian functions (k = 4) and realize the characteristics expressed by Eqs. (17, 18, 19, 20) in 3 dimensions (3-D), 5-D, 7-D, and 10-D. Fig. 3 is a 3-D example of a Gaussian mixture model.

Fig. 3
figure 3

3-D view of a Gaussian mixture model

Full size image

The big difference between an IEC user model and ordinary fitness functions is the implementation of the (a) relative and (b) discrete fitness evaluations of a human user. A human IEC user compares given individuals relatively and, unlike a fitness function, does not give absolute fitness. He or she also cannot give precise fitness values but rather assigns discrete ones, e.g. 1–5 points, every generation, while ordinary fitness functions give continuous values. When the difference between individuals is less than the minimum discrete fitness range, i.e. an evaluation threshold, a human IEC user cannot distinguish the difference, and it becomes fitness noise that must be realized by an IEC user model.

The IDE user simulation in this section randomly chooses either a trial vector or a target vector and leaves it as offspring in the next generation when the difference of their fitness values is less than a certain value to simulate the unavailability of a human IDE user’s comparison; we set the difference threshold as 1/50 of the difference between the maximum and minimum fitness values present in the population for each generation.

$$ GMM(x)=\sum_{i=0}^{k} {a_i\exp\left({ -\sum_{j=0}^{n}{\frac{(x_{ij}-\mu_{ij})^2}{2\sigma_{ij}^2}}}\right)} $$
(17)
$$ \sigma = \left(\begin{array}{cccccccccc} 1.5 & 1.5 &1.5 &1.5 &1.5 &1.5 &1.5 &1.5 &1.5 &1.5\\ 2 &2 &2 &2 &2 &2 &2 &2 &2 &2 \\ 1 &1 &1 &1 &1 &1 &1 &1 &1 &1 \\ 2 &2 &2 &2 &2 &2 &2 &2 &2 &2 \end{array}\right) $$
(18)
$$ \mu = \left (\begin{array}{cccccccccc} -1 & 1.5 &-2 &2.5 & -1 &1.5 &-2 &2.5 &-1 &1.5\\ 0 &-2 &3 &1 &0 &-2 &3 &1 &0 &-2\\ -2.5 & -2& 1.5& 3.5&-2.5 & -2& 1.5& 3.5&-2.5 & -2\\ -2 &1 &-1 &3 &-2 &1 &-1 &3 & -2 &1 \end{array}\right) $$
(19)
$$ a_i = \left( \begin{array}{cccc} 3.1,& 3.4, & 4.1, & 3 \end{array} \right)^{T} $$
(20)

IDE parameters are set as the Table 2. Population size, 20, is used to reflect a realistic choice for IEC experiments with a real human user.

Table 2 IEC experiment parameter settings
Full size table

5.3 Evaluations of our proposal

Figure 4 shows the average convergence curves of the best fitness values for 50 trial runs of IDE-LS and IDE-LR with their competitors using GMM with 3-D, 5-D, 7-D and 10-D. Table 3 shows the average fitness value at the 20th generation.

Fig. 4
figure 4

Average convergence curves of 50 trial runs for a 3-D, b 5-D, c 7-D and d 10-D Gaussian mixture model with population size of 20

Full size image
Table 3 Average fitness value at 20th generation of 3-D, 5-D, 7-D and 10-D Gaussian mixture models (pseudo-IDE user)
Full size table

From these results it can be seen that, in general, our proposed methods are able to accelerate all Gaussian mixture models, i.e., our proposed methods are significantly better than canonical IDE, with the exception of the IDE-LR method applied to a 3-D model. This indicates that our proposed acceleration methods can be effectively used in some IEC applications. However, for some cases, our proposed methods are not more effective than the previously proposed acceleration method.

To obtain an estimate of the performance of our proposed acceleration methods under real IEC application conditions, we conducted IEC evaluation experiments with 20 individuals per generation. In Table 3, it can be seen that the acceleration performance improves with higher dimensions, i.e. the 10-D, 7-D and 5-D GMM with 20 individuals are more efficient than in the 3-D case. This indicates that our proposed methods increase the diversity of the population in higher dimensions more significantly than in lower dimensions. When the dimension of the GMM is higher, our proposed methods seem to offer the same performance.

Compared with the IDE-TA method, all of our proposed methods outperform it, except IDE-LS applied in the 7-D modal case. The proposed method IDE-LS and IDE-LR can perform significantly better than IDE-TB in lower dimensional problems (3-D and 5-D) and IDE-TN in higher dimensional problems (7-D and 10-D), respectively. These observations indicate that our proposed methods may work better than IDE-(TB, TN, TA) when the distribution of individuals in a search space has less diversity, while IDE-(TB, TN, TA) have better performance even in such cases.

6 EC experimental evaluations and analysis

6.1 Benchmark functions and experimental conditions

We evaluate our proposed methods with 34 benchmark functions. Our proposed methods aim to reduce IDE user fatigue by accelerating IDE search. However, their applicability is not limited to IEC; they can be used for any EC search with fitness functions. Information about some of these functions and their related parameters can be found in literature [3, 19, 25], and [26]. See definitions, search ranges of optimization parameters, and characteristics of the benchmark functions in Table 4.

Table 4 Benchmark functions used in experimental evaluations, where Range is the scale of the parameters, n is the dimension of the function and C is the function’s characteristics, respectively
Full size table

Some evaluation indexes for comparing our proposed methods applied to EC are average fitness value until convergence is reached in the maximum search generation, Wilcoxon signed-rank test at the maximum search generation and the total time cost statistics and analysis, which can show us to what degree our proposed methods are time-saving.

EC experimental parameters are set as shown in Table 5. We use differential evolution (DE/best/1/bin) as the optimization method to evaluate the methods. The evaluation is conducted under difficult search conditions; only 100 individuals search 50-D/30-D functions for which the search parameter ranges are expanded, and the other uses 30 individuals.

Table 5 EC experiment parameter settings
Full size table

6.2 Evaluations of our proposal

Convergence characteristics of the 34 benchmark functions are shown in Tables 6 and 7. In the tables, Wilcoxon signed-rank tests are applied between our proposed methods with canonical DE and previous acceleration methods [22]. As was previously mentioned, for higher dimensional problems (F21–F34), the previous acceleration methods require the # of population size must be 2D + 1 = 2 × 50 = 101, which exceeds the experimental settings, so our proposed methods can be applied to such higher dimensional problems but the previous methods cannot. This demonstrates one advantage of our proposed methods.

Table 6 Average fitness value of F1–F20 benchmark functions
Full size table
Table 7 Average fitness value of F21–F34 benchmark functions
Full size table

The proposed methods converge faster than the conventional methods at the same generation for both lower and higher dimensional problems except for a few functions. This effect cannot be observed for F3, F5, F7, F8, F23, F28, F31, F32 and F34 functions because there are no significant differences between canonical DE and DE with either of our proposed methods. Our proposed method’s acceleration performance look similar, and if there is any difference, the superiority depends on the task being performed. From the Wilcoxon signed-rank tests comparison of our proposed methods with previous acceleration methods, the performance of our proposed methods is better than one of them in F2, F3, F4, F10, F11, F12, F14, F15, F16, F18, F19 and F20 in lower dimension problems. The DE-LS method’s performance is better than that of DE-LR method in comparison with previous mentioned acceleration methods, i.e. DE-TB, DE-TN and DE-TA. For higher dimensional benchmark functions (F21–F34), our proposed methods also show the capability to accelerate EC search, except in some cases, and even to problems with shifted and rotated characteristics.

6.3 Discussion on acceleration performance

With the exception of F3, F5 F7 and F8, our proposed methods can accelerate all lower dimensional benchmark functions. There were no cases where the proposed methods were significantly poorer than canonical DE. Although our proposed acceleration methods use a dimensionality reduction technique to obtain new elite in a lower dimensional search space, which would seem to imply more efficiency in problems with the characteristic of variable separability (i.e. F1, F4, F6, F10, F14 and F18), the experimental results show that DE-LR and DE-LS also exhibit better performance when the variables are non-separable (i.e. F2, F9, F11–F13, F15–F17, F19 and F20). For uni-modal and multi-modal problems, the experimental results indicate that our proposed methods have the same capability to accelerate these two kinds of problems.

As the global optimum of F3 is on the edge of a searching space, the elite obtained around the global optimum by function approximation may be located outside of the searching range. Our experiment does not use the elite in this case, and the DE using our proposed methods becomes identical to canonical DE. This would explain why there is no significant difference between DE-N, DE-LR and DE-LS.

F7 is made by putting multiple sine curves on a sloped plane that is otherwise similar to F3. The difficulty with this task is that the minimum point, i.e. the global optimum, is located near the maximum point of the plane and there are local minimums around the global optimum. When local minimums and the global optimum are located close together, the elite obtained from an approximated curve may be located in a gap between these peaks and its fitness may be poor. This may be a reason why the performance of our proposed methods is the same as with canonical DE.

F4 is a quartic function with Gaussian noise and has its global optimum in the center of the searching space. Although it is a multi-modal function due to the quartic function and fluctuations due to noise, the influence of the noise is relatively small and its whole shape is close to a quadratic function such as in F1. Elite from an approximated function using individuals that fluctuate slightly should be located in the center, and the performance of DE-LR and DE-LS should be better, as with F1, while that of canonical DE is negatively influenced by the fluctuations. This may explain the good performance of our proposed method with F4.

For higher dimensional problems (F21–F34), our proposed methods are also effective except F23, F28, F31, F32 and F34; most of them have complex fitness landscapes with a rotation characteristic. As rotated fitness landscape changes the real location of global optimum dramatically, our projected one-dimensional landscape can not use other dimensional search space information collaboratively. Obtained elite are not correct in each lower dimension. Maybe this is the reason why our proposed methods are ineffective in those benchmark tasks.

Except in special cases, the performance of DE-LR and DE-LS are better than that of DE-TN. This demonstrates that the original search space landscape fitted by those individuals with the lowest distance from the best individual is not accurate as a regression of the original search space; i.e. individuals near the best individual are not necessarily in regions of better fit in the original search space.

6.4 Discussion on computational complexity

Reducing computational cost is the greatest feature offered by our methods. This method of approximating landscapes and using the peak of an approximated function belongs to the same category as [22], but we extend that work by introducing projection onto a 1-D space, synthesizing an elite from the elites on multiple 1-D functions, and thus further reducing computational cost. Let’s examine the efficiency of the methods by calculating the time cost (see Table 8).

Table 8 Average cost time of each method for one time running (Unit: ms)
Full size table

We calculate the run times of 50 trials of DE-N, DE-LR, DE-LS, DE-TB, DE-TN and DE-TA, and obtain the average running time cost of one computation. The system used to run the experiment is powered by a Core2 Duo 2GHz CPU with 1GB RAM running Windows XP (SP2).

The table shows that the time cost of our proposed methods is more than canonical DE and less than the previous acceleration methods. The time cost of our proposed method is almost the same for one benchmark function. The three previous acceleration methods are costly for one benchmark function. We can conclude that our proposed methods save the time cost of optimization when compared to the previous acceleration methods.

To further evaluate the significance of our proposed methods as compared with the previous methods, we conduct a time cost variance analysis with the time cost data sample from our tests. Before calculating the F distribution value of the multiple groups’ sample time cost data for significance evaluation, we should check whether the sample data fit a normal distribution in theory. For a large data set (data >30 samples), it must fit a normal distribution in accordance with the Central Limit Theorem. We use the Jarque–Bera test to check each time cost data set for goodness-of-fit to a normal distribution, and for abnormal data we smooth it for fitting to a normal distribution. We calculate the F value for each of the lower dimensional benchmark functions (F1–F20) in Table 9 with r = 5, n = 250. F 0.05(r − 1, n − r) = F 0.05(4, 245), i.e, \({F_{0.05}(4, \infty)} = {2.37}\). From Table 9, it can be seen that all the F values are greater than 2.37, indicating that our proposed method’s time cost means differ significantly from those of the previous methods.

Table 9 Confidence interval and F value for the 20 benchmark functions
Full size table

From Tables 8 and 9, we can conclude that the proposed methods can significantly save time over previous methods. A comparison of DE-(LR and LS) with DE-(TB, TN and TA) shows that our proposed acceleration methods seem more beneficial than previous ones. However, before the regression and fitting process, it is necessary to select the sample data. In the selection process, there are more searching and sorting operations, and these take as much as or even more time than the regression and fitting processing. This shows how essential selection of sample data is when accelerating EC from a landscape obtained from its search space. This, improving the performance of data selection, will be a subject of our future research.

7 Discussion of general issues related to our proposal

7.1 Regression function selection for landscape approximation

Approximation function selection is a critical issue in the approximation of the IEC/EC landscape. From a practical viewpoint, we should select an appropriate approximation function after analyzing the characteristics of the IEC/EC landscape. In this study, we reviewed related regression methods used to approximate IEC/EC landscapes in Sect. 3, and selected binomial Lagrange interpolation and linear least squares approximation as the regression methods for our study.

The regression search space approximated by binomial Lagrange interpolation and linear least squares approximation are nonlinear and linear, respectively. The characteristic of the nonlinear space is that it is ruleless, which is a feature common to most IEC/EC search spaces. Binomial Lagrange interpolation is a method that can be used to obtain nonlinear landscape information about the IEC/EC search space and we can find new elite in this nonlinear regression space. Maybe there is a rule between the new elite and the global optimum in the regression search space, and we can obtain it by chance. The linear function least squares method approximates some linear relationship between each individual and its fitness in the local search space. If the search space of some IEC/EC application is linear, we can obtain the IEC/EC search space’s linear relationship from the linear function approximation. We can also obtain the global optimum from the new elite in the regression linear space.

How to obtain the approximated IEC/EC search space is a promising research direction. In our study, we tried to use nonlinear and linear curve expressions to approximate the IEC/EC search space, to obtain the approximation relationship between the approximated and the original IEC/EC search space, and to find the global optimum from the new elite by chance. However, the approximation process influences the performance of the IEC/EC algorithms, so using an efficient approximation method is another topic to be considered when designing accelerated IEC/EC algorithms. We should use the lowest possible degree of interpolation and approximation functions in the lowest possible dimensional spaces to reduce the time cost required for the entire IEC/EC algorithm.

7.2 Regression model establishment and usage

The experimental results in this study show that both linear (DE-LS) models and nonlinear (DE-LR) models can be used to efficiently accelerate IEC/EC convergence. However, sign tests indicate that the methods are mostly effective in the initial generations [10], and an alternative solution is to use this kind of acceleration method to speed IEC/EC convergence only in those early generations.

Constructing and selecting different models to better approximate the IEC/EC search space is a worthwhile topic for further research. To achieve optimal performance, we should choose approximation methods that are suited to the characteristics of the search space. For regression in the discrete domain, a more powerful tool than continuous domain Lagrange interpolation and least squares approximation is required. To find how best to approximate the search space in the discrete domain is a valuable research topic.

Another point deserving special attention is the method used for dimensionality reduction. The objective of the dimensionality reduction is to simplify the computation of the search space regression by performing it in a lower dimension. The dimensionality reduction loses much search space information, however, such as the relationship between the parameters in non-separable problems. How we can reduce the search space dimension as much as possible while simultaneously preserving the necessary search space information for the next generation of the search is a challenging problem for further research into the dimensionality reduction method.

The new elite selection method is also a key step in the acceleration process. The elite selection method is determined by the different search space regression methods. They can be categorized as linear and nonlinear models, corresponding to the classification method of the regression model. A new elite selection method should be determined by analyzing the characteristics of the regression model.

7.3 Data sampling technique

It is necessary to sample the data to obtain the original search space information which is used in the approximation processes. The data sampling technique determines the quality of the approximation model, indirectly influencing the model usage and obtained elite. Several data sampling methods have been proposed. These include best data strategy, distance nearest data strategy, whole data strategy and random data strategy. For comparison of those sample studies, we discuss the advantages and disadvantages of the methods as follows.

First, obtaining suitable data for the approximation of the IEC/EC landscape requires time in searching and sorting operations. With a view to maximizing performance and saving time, we need to select an easy way to obtain the sample data. Secondly, from the experimental results, the distance nearest data strategy is more costly than any of the other sampling data strategies. The acceleration performance of the approximation model combined with distance nearest data is not as good as the others. So with a view to practical applications, the distance nearest data strategy exhibits low performance. Third, our proposed acceleration methods that use the best data strategy to approximate the model in the lower search space perform better than the previous acceleration methods in some cases. However, if we select a data sampling strategy which is even more time efficient and does not require searching and sorting, such as the random data strategy, the performance of our proposed methods may be further improved. This is a direction for further research.

7.4 Limitations

Additional time is required to approximate the IEC/EC search space when using our proposed acceleration methods, so the IEC/EC algorithm’s computational complexity is increased. The performance issue is the biggest problem for the application of our acceleration methods. Although our proposed methods exhibit performance that is better than the previously proposed acceleration methods, performance remains a critical issue when looking to apply the method. When this acceleration is used in a concrete application, we must consider the issue of performance and find a balance between algorithm computational complexity and the speed of convergence.

Population diversity is the key consideration for obtaining the final global optimum in IEC/EC. Acceleration methods can lead to a premature convergence on a local optimum in some special landscape conditions. When a nearly identical elite is inserted generation after generation, our proposed method can lead to premature convergence. The issue of elite insertion strategy selection is a topic of considerable importance when applying our proposed acceleration methods to concrete IEC/EC applications.

8 Conclusion and future work

We proposed IEC/EC convergence be accelerated by using a dimensionality reduction technique in approximating the fitness landscape. The novel feature in these acceleration methods was to use elite synthesized from elite points found in lower dimensional spaces. The main contribution of this study was utilizing the notion of dimensionality reduction for approximating the fitness landscape to accelerate IEC/EC searches. Our experimental evaluations with a Gaussian mixture model and 34 benchmark functions showed that the proposed methods can accelerate IEC and EC searches with lower computational cost. The acceleration performance can be obtained in both lower and higher dimensional problems, especially when the landscape of the tasks takes on a roughly big valley structure. We also analyzed the relationship between the performance of the proposed methods and the landscape shapes.

Theoretical research is but one part of this scientific research; the ultimate objective of our research is to apply this novel method and technique to actual applications with societal benefit. We conducted simulation evaluations to compare characteristics of several methods with multiple different initializations under the same experimental conditions. In the next step, we should quantitatively evaluate IEC user fatigue and collect basic experimental data together with the convergence experiments’ results in this paper. After that, we need to conduct human subjective tests with human IEC users, evaluate user fatigue and acceleration performance synthetically, and conclude the evaluation of the proposed methods. It is important to obtain conclusions through its application and thus find new directions by which we can improve our work. We expect these developments will occur on topics such as the selection of the linear or nonlinear model, the actual interpolation or approximation methods used and the expression of the regression space. We will continue conducting research on those topics in the future.