1 Introduction

The performances of engineering processes and thermal devices are always affected by irreversible losses that lead to increase of entropy and decrease of thermal efficiency. Thus the important factors are to be determined to minimize the entropy generation and maximize the flow system efficiency. To analyse the irreversibilities in the form of entropy generation, the second law of thermodynamics is applied. The factors that are responsible for the irreversibility are heat transfer across finite temperature gradients, characteristic of convective heat transfer and viscous dissipation. Most of the energy-related applications such as cooling of modern electronic systems, solar power collectors and geothermal energy systems depend on entropy generation. The concept of entropy generation rate in flow and thermal systems was introduced by Bejan [1]. It is observed that the thermal system efficiency is enhanced by minimizing the entropy generation of the system [2,3,4].

The flow through ducts or pipes is frequently used in fluid distribution networks, cooling and heating applications. The study of entropy generation within the fluid volume is important in understanding the fluid flow in any process, which is helpful to optimize the entropy generation or the quality of energy to be preserved in any process. Several researchers investigated the entropy generation of fluid flows in pipes. In [5], the author examined the influence of temperature-dependent viscosity with heating process on entropy generation due to turbulent flow in a pipe. An analytical method was proposed in [6] to investigate the entropy generation in the pipe flow by considering different pipe wall temperatures and flow Reynolds numbers. The effect of uniform wall heat flux boundary condition was analysed [7] on entropy generation in a circular pipe as a two-dimensional flow. The entropy generation in a circular pipe of non-Newtonian fluid flow was developed [8] with varying viscosity and it was noticed that the entropy generation number is affected by the non-Newtonian parameter especially near the pipe wall. The entropy generation in a circular pipe was calculated in [9], using the non-Newtonian fluid flow model with constant viscosity and it was observed that the entropy generation increases on increasing the modified Stanton number and dimensionless inlet wall to fluid temperature difference. A numerical study was reported in [10] to investigate both the first and the second law of thermodynamics for thermally developing forced convection in a circular tube filled by a saturated porous medium, with uniform wall temperature and effects of viscous dissipation. In [11], a review was presented on entropy generation for the fully developed ice slurry pipe flow and it was found that as the dimensionless group parameter or mass fraction of ice increases, the volumetric average entropy generation number increases. The effect of viscosity parameters on entropy generation for Hagen–Poiseuille flow in a pipe was investigated in [12] due to fluid friction and heat transfer. The effect of heat flux distribution on entropy generation due to both heat transfer and friction was presented in [13]. Ref. [14] leads to the conclusion that minimum entropy generation aspects must be considered to minimize the irreversibility and to enhance the performance of the heat pipe while designing. The dimensionless entropy generation was estimated in [15] for a laminar flow through a circular tube immersed in an isothermal fluid. The presence of irreversibility inside a porous vertical pipe was analysed in [16] to investigate the entropy generation. In [17], a numerical method was proposed to discuss the fluid flow and heat transfer in pipes partly occupied with porous medium and to evaluate the entropy generation.

The flow of fluids over boundaries of porous materials have many applications in practice, such as transpiration cooling, boundary layer control and biomedical engineering as well as drinking water treatment. In general, in many heat transfer processes, the local wall heat flux is a linear function of the local wall temperature. This phenomenon is found in the temperature boundary condition of the third kind. Recently, a novel mechanism for the heating process has drawn the involvement of many researchers, namely, convective boundary condition (CBC), where heat is supplied to the convecting fluid through a bounding surface with a finite heat capacity. Further, this results in the heat transfer rate through the surface being proportional to the local difference in temperature with the ambient conditions. Besides, it is more general and realistic, particularly in various technologies and industrial operations such as transpiration cooling process, textile drying and laser pulse heating. The effect of variable viscosity and convective heating on the entropy generation due to flow in a MHD channel with permeable walls was reported in [18]. The entropy generation for nano-fluid flow over a vertical porous channel was studied in [19] with convective heating under MHD effect. The entropy generation minimization method was applied in [20] to the optimization of MHD flow that takes place in a porous channel with slip flow and convective boundary conditions. It is noticed that the minimum entropy generation is found for the optimum values of Hartman number, Prandtl number, Biot number, suction/injection Reynolds number and Eckert number.

Several fluids used in engineering and industrial processes, such as poly-liquid foams and geological materials, exhibit flow properties that cannot be explained by Newtonian fluid flow model. To explain the behaviour of such fluids, different models have been introduced. Among these, micropolar fluids [21] have distinct features, such as the local structure effects, which are microscopic and micro-motion of elements of the fluid, the presence of stresses due to couple, body couples and non-symmetric stress tensor. Micropolar fluids are the fluids with microstructure. The flow characteristics of haematological and colloidal suspensions, polymeric additives, liquid crystals, geomorphological sediments, lubricants, etc. accurately resemble the micropolar fluids. The aspect of rotation of fluid particles in micropolar fluid model is governed by an independent kinematic vector called the microrotation vector, which makes it different from other non-Newtonian fluids.

Thus, in the present paper the micropolar fluid is used to investigate the entropy generation numerically in a porous inclined circular pipe. The governing equations in cylindrical polar coordinate system are simplified and numerically solved using a spectral quasi-linearization method (SQLM) to obtain the entropy generation and Bejan number in a circular pipe.

2 Mathematical formulation

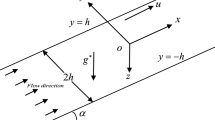
Consider the steady axisymmetric fully developed laminar incompressible micropolar fluid through an infinite length pipe of circular cross section with porous walls (see figure 1). The radius of the pipe is a and the pressure gradient is assumed to be constant. The pipe is inclined with an angle \(\alpha \). Choose the cylindrical polar coordinate system (\(r,\theta ,z\)), where z-axis is the direction of fluid flow. The flow depends on r only since the flow is fully developed and the pipe is of infinite length. The z component of the velocity vector does not vanish but the transpiration cross-flow velocity \(w_0\) remains constant, where \(w_0<0\) is the velocity of the suction and \(w_0>0\) is the velocity of the injection. The surface of the pipe is convectively heated with a hot fluid that provides a heat transfer coefficient h. Assume that the temperature of the hot fluid is \(T_2\) and the ambient temperature is \(T_1\).

Figure 1
figure 1

Schematic diagram of the problem.

Full size image

Based on these assumptions, the governing equations [22, 23] of micropolar fluid flow and heat transfer in the absence of body force and body couple are as follows.

2.1 Continuity equation:

$$\begin{aligned} \frac{\partial u}{\partial z}=0. \end{aligned}$$
(1)

2.2 Momentum equation:

$$\begin{aligned} -\frac{\partial p}{\partial z}+\frac{\kappa }{r} \left[ \sigma +r \frac{d\sigma }{dr}\right] +(\mu +\kappa )\left[ \frac{d^2u}{dr^2}+\frac{1}{r}\frac{du}{dr}\right] + \rho g^* \beta (T-T_1)\sin \alpha = \rho w_0 \frac{du}{dr}. \end{aligned}$$
(2)

2.3 Angular momentum equation:

$$\begin{aligned} -2\kappa \sigma -\kappa \frac{du}{dr}+\gamma \left[ \frac{d^2\sigma }{dr^2}+\frac{1}{r}\frac{d\sigma }{dr}-\frac{\sigma }{r^2}\right] = \rho j^*w_0\frac{d\sigma }{dr}. \end{aligned}$$
(3)

2.4 Energy equation:

$$\begin{aligned}&K_f\left[ \frac{d^2T}{dr^2}+\frac{1}{r}\frac{dT}{dr}\right] +\left(\mu +\frac{\kappa }{2}\right)\left( \frac{du}{dr}\right) ^2 -2\beta \frac{\sigma }{r}\frac{d\sigma }{dr} +\frac{\kappa }{2}\left[ \frac{du}{dr}+2\sigma \right] ^2\nonumber \\&\quad + \gamma \left[ \left( \frac{d\sigma }{dr}\right) ^2+\frac{\sigma ^2}{r^2}\right] = \rho C_p w_0\frac{dT}{dr} \end{aligned}$$
(4)

where u(r) is the component of velocity in the flow direction, \(\sigma \) the microrotation component, T is the temperature, \(\rho \) is the density, p is the pressure of the fluid, \(\mu \) is the dynamic viscosity, \(\kappa \) is the vortex viscosity, \(\gamma \) is the spin-gradient viscosity, \(g^*\) is the acceleration due to gravity, \(\beta \) is the coefficient of thermal expansion and \(K_f\) the thermal conductivity. The boundary conditions are proposed as follows:

$$\begin{aligned} \frac{du}{dr} =0, \,\, \sigma =0, \,\, \frac{dT}{dr}=0, \,\, \text{ at }\,\, r = 0 \end{aligned}$$
(5a)
$$\begin{aligned} u = 0, \,\,\sigma =0, \,\, -K_f\frac{dT}{dr}=h(T-T_1) ,\,\, \text{ at }\,\, r = a \end{aligned}$$
(5b)

where h is the heat transfer coefficient.

Introducing the following dimensionless quantities:

$$\begin{aligned} r = a \eta ,\,\, u = u_0f(\eta ),\,\, \sigma = \frac{u_0}{a}g(\eta ),\,\,\theta (\eta ) = \frac{T-T_1}{T_2-T_1} \end{aligned}$$
(6)

in Eqs. (2)–(4), we get the following non-linear system of differential equations:

$$\begin{aligned}&\frac{1}{1-N}\left( f''+\frac{1}{\eta }f'\right) +\frac{N}{1-N}\left( g'+\frac{1}{\eta }g\right) +g_s\sin (\alpha ) \theta -A = Rf' \end{aligned}$$
(7)
$$\begin{aligned}&\frac{N(2-N)}{m^2(1-N)}\left( g''+\frac{1}{\eta }g'-\frac{1}{\eta ^2}g\right) -\frac{2N}{1-N}g -\frac{N}{1-N}f'= Ra_jg' \end{aligned}$$
(8)
$$\begin{aligned}&\theta ''+\frac{1}{\eta }\theta '+Br\left[ \frac{2-N}{2(1-N)}f'^2+\frac{1}{2}\frac{N}{1-N}\left( f'+2g\right) ^2 \right. \left. -\frac{2B}{\eta }gg'\right] \nonumber \\&\quad +Br\frac{N(2-N)}{m^2(1-N)}\left( g'^2+\frac{1}{\eta ^2}g^2\right) = PrR\theta ' \end{aligned}$$
(9)

where primes denote differentiation with respect to \(\eta \), \(N = \frac{\kappa }{\kappa +\mu }\) is coupling number, \(Gr = \frac{\rho ^2g*\beta (T_2-T_1)a^3}{\mu ^2}\) is the Grashof number, \(Re = \frac{\rho u_0a}{\mu }\) is the Reynolds number, \(g_s = \frac{Gr}{Re}\) is the buoyancy parameter, \(R=\frac{\rho w_0a}{\mu }\) is the suction/injection parameter, \(A = \frac{a^2}{\mu u_0}\frac{dp}{dZ}\) is the constant pressure gradient, \(m^2 = \frac{a^2\kappa (2\mu +\kappa )}{\gamma (\mu +\kappa )}\) is the micropolar parameter, \(a_j= \frac{j}{a^2}\) is the micro-inertia parameter, \(Br = \frac{\mu u_0^2}{K_f(T_2-T_1)}\) is the Brinkman number, \(B = \frac{\beta }{\mu a^2}\) is the material constant and \(Pr = \frac{\mu C_p}{K_f}\) is the Prandtl number.

The corresponding boundary conditions are

$$\begin{aligned} f'(\eta ) = 0, \,\, g(\eta ) = 0, \,\, \theta '(\eta ) = 0,\,\, \text{ at }\,\, \eta = 0 \end{aligned}$$
(10a)
$$\begin{aligned} f(\eta ) = 0, \,\, g (\eta ) = 0, \,\, \theta '(\eta )+Bi\theta (\eta ) =0, \,\, \text{ at }\,\, \eta = 1 \end{aligned}$$
(10b)

where \(Bi=\frac{ah}{K_f}\) is the Biot number.

3 Method of solution

The system of Eqs. (7)–(9) along with the boundary conditions (10) are solved using the SQLM [24,25,26], which was coined by Motsa. The quasilinearization method (QLM) is a generalization of the Newton–Raphson method [27] for solving nonlinear boundary value problems. In this method the iteration scheme is obtained by linearizing the nonlinear component of a differential equation using the Taylor series expansion. Chebyshev spectral method is then used to solve the resulting linearized system of equations.

Let \(f_{r}\), \(g_{r}\) and \(\theta _{r}\) be an approximate current solution and \(f_{r+1}\), \(g_{r+1}\) and \(\theta _{r+1}\) be an improved solution of the system of equations (7)–(9). By taking Taylor’s series expansion of non-linear terms in (7)–(9) around the current solution and neglecting the second and higher order derivative terms, we get the linearized equations as follows:

$$\begin{aligned}&a_{1,r}f_{r+1}''+a_{2,r}f_{r+1}'+a_{3,r}g_{r+1}'+Ng_{r+1} + a_{4,r}\theta _{r+1} = a_{5,r} \end{aligned}$$
(11)
$$\begin{aligned}&-b_{1,r}f_{r+1}'+b_{2,r}g_{r+1}''+ b_{3,r}g_{r+1}'-b_{4,r}g_{r+1} =0 \end{aligned}$$
(12)
$$\begin{aligned}&c_{1,r}f_{r+1}'+c_{2,r}g_{r+1}'+c_{3,r}g_{r+1}+c_{4,r}\theta _{r+1}''+c_{5,r}\theta _{r+1}' = c_{6,r} \end{aligned}$$
(13)

where the coefficients \(a_{s,r},\, s = 1,2,...\) are known functions calculated from previous iterations and are defined as follows:

$$\begin{aligned} &{a_{1,r} = \eta , \quad a_{2,r} = 1-\eta (1-N)R, \quad a_{3,r} = N\eta , \quad a_{4,r} = g_s\eta (1-N)\sin (\alpha ),}\\ & {a_{5,r} = A\eta (1-N), \quad b_{1,r} = N\eta ^2, \quad b_{2,r} = \frac{N(2-N)}{m^2}\eta ^2,}\\ &{b_{3,r} = \frac{N(2-N)}{m^2}\eta -(1-N)Ra_j\eta ^2, \quad b_{4,r} = 2N\eta ^2+\frac{N(2-N)}{m^2}},\\ & {c_{1,r} = 2Br\eta ^2 (f_r'+N g_r), \quad c_{2,r} = -2BBr(1-N)\eta g_r+\frac{2N(2-N)}{m^2}Br\eta ^2 g_r',}\\ & {c_{3,r} = 4BrN\eta ^2g_r+2BrN\eta ^2f_r'-2BBr(1-N)\eta g_r' +\frac{2N(2-N)}{m^2}Brg_r,}\\ & {c_{4,r} = \eta ^2(1-N), \quad c_{5,r} = \eta (1-N)-PrR\eta ^2(1-N)},\\ & {c_{6,r} = Br\left[ \eta ^2f_r'^2+\frac{N}{2}\eta ^2 f_r'^2+2N\eta ^2g_r^2+2N\eta ^2f_r'g_r-2B(1-N)\eta g_rg_r'+\frac{N(2-N)}{m^2}\eta ^2g_r'^2+ \frac{N(2-N)}{m^2}g_r^2\right] }. \end{aligned}$$

The Chebyshev spectral collocation method [28] is used to solve these linearized equations (11)–(13). Approximations are performed using the Chebyshev interpolating polynomials for the unknown functions; further, they are collocated at the Gauss–Lobatto points represented as

$$\begin{aligned} \xi _j=\cos \frac{\pi j}{J}, \quad j=0,1,2,. . .,J \end{aligned}$$
(14)

where J is the number of collocations. The transformation of physical region [0, 1] results in the region \([-1, 1]\) using the mapping

$$\begin{aligned} \eta = \frac{\xi +1}{2}, \quad -1 \le \xi \le 1. \end{aligned}$$
(15)

The functions \(f_{r+1}\), \(g_{r+1}\) and \(\theta _{r+1}\) are approximated at the collocation points for \( j=0,1,2,...; J\) by

$$\begin{aligned} f_{r+1}(\xi _j)&=\sum _{k=0}^{J}f_{r+1}({\xi }_k)T_k({\xi }_j),\nonumber \\ g_{r+1}(\xi _j)&=\sum _{k=0}^{J}g_{r+1}({\xi }_k)T_k({\xi }_j),\nonumber \\ \theta _{r+1}(\xi _j)&=\sum _{k=0}^{J}\theta _{r+1}({\xi }_k)T_k({\xi }_j), \end{aligned}$$
(16)

where \(T_k\) is the \(k{{\rm th}}\) Chebyshev polynomial defined by \(T_k(\xi )=\cos [k{\cos }^{-1}{\xi }]\).

The variable derivatives \(\textit{D}\) at the collocation points \( j=0,1,2,...,J.\) satisfy the equations

$$\begin{aligned} \frac{d^n f_{r+1}}{d {\eta }^n}&=\sum _{k=0}^{J}\mathbf {D}_{jk}^{n}f_{r+1}(\xi _k),\nonumber \\ \frac{d^n g_{r+1}}{d {\eta }^n}&=\sum _{k=0}^{J}\mathbf {D}_{jk}^{n}g_{r+1}(\xi _k),\nonumber \\ \frac{d^n \theta _{r+1}}{d {\eta }^n}&=\sum _{k=0}^{J}\mathbf {D}_{jk}^{n}\theta _{r+1}(\xi _k) \end{aligned}$$
(17)

where Chebyshev spectral differentiation matrix is \(\mathbf {D} = 2 \textit{D}\) and n is the order of differentiation. Substituting Eqs. (16) and (17) into Eqs. (11)–(13) leads to the matrix equation

$$\begin{aligned} \mathbf {A}_{r}\mathbf {X}_{r+1}=\mathbf {B}_{r}; \end{aligned}$$
(18)

In Eq. (18), \(\mathbf {A}_{r}\) is a \((3J + 3) \times (3J + 3)\) square matrix and \(\mathbf {X}_{r+1}\) and \(\mathbf {B}_{r}\) are \((3J + 3)\times 1\) column vectors defined by the relations

$$\begin{aligned} \mathbf {A}_{r}=\left[ \begin{array}{lll} A_{11} &{} A_{12} &{} A_{13}\\ A_{21} &{} A_{22} &{} A_{23}\\ A_{31} &{} A_{32} &{} A_{33}\\ \end{array}\right] ,\quad \mathbf {X}_{r+1}=\left[ \begin{array}{l} \mathbf {F}_{r+1}\\ \mathbf {G}_{r+1}\\ \varTheta _{r+1}\\ \end{array}\right] ,\quad \mathbf {R}_{r}=\left[ \begin{array}{l} \mathbf {r}_{1,r}\\ \mathbf {r}_{2,r}\\ \mathbf {r}_{3,r}\\ \end{array}\right] \end{aligned}$$
(19)

where

$$\begin{aligned} {\mathbf{F}}_{r+1} &= [f_{r+1}(\xi _0),f_{r+1}(\xi _1),...,f_{r+1}(\xi _{J-1}),f_{r+1}(\xi _J)]^T,\\ {\mathbf{G}}_{r+1} &= [g_{r+1}(\xi _0),g_{r+1}(\xi _1),...,g_{r+1}(\xi _{J-1}),g_{r+1}(\xi _J)]^T,\\ \varTheta _{r+1} &= [\theta _{r+1}(\xi _0),\theta _{r+1}(\xi _1),...,\theta _{r+1}(\xi _{J-1}),\theta _{r+1}(\xi _J)]^T,\\ A_{11} &= a_{1,r}{{\mathbf{D}}^2}+a_{2,r}{\mathbf{D}},\quad A_{12} = a_{3,r}{\mathbf{D}}+N{\mathbf{I}} ,\quad A_{13} = a_{4,r}{} {\mathbf{I}} ,\\ A_{21} &= -b_{1,r}{\mathbf{D}}, \quad A_{22} = b_{2,r}{{\mathbf{D}}^2}+b_{3,r}{\mathbf{D}}-b_{4,r}{} {\mathbf{I}} , \qquad A_{23} ={\mathbf {0}},\\ A_{31} &= c_{1,r}{\mathbf{D}} , \quad A_{32} = c_{2,r}{\mathbf{D}}+c_{3,r}{}{\mathbf{I}} , \quad A_{33} = c_{4,r}{{\mathbf{D}}^2} +c_{5,r}{\mathbf{D}},\\ &\quad {\mathbf {r}}_{1,r} = a_{5,r}, {\mathbf {r}}_{2,r}={\mathbf{0}} _1, {\mathbf {r}}_{3,r} = c_{6,r}. \end{aligned}$$

Here \(\mathbf I \) and \(\mathbf 0 \) represent the \((J + 1)\times (J + 1)\) identity matrix and zero matrix, respectively.

The corresponding boundary conditions are

$$\begin{aligned} f_{r+1}(\xi _0) = 0, \quad g_{r+1}(\xi _0) &= 0, \quad \sum _{k=0}^{J}\mathbf {D}_{0k}\theta _{r+1}(\xi _k)+Bi\theta _{r+1}(\xi _0) = 0, \end{aligned}$$
(20a)
$$\begin{aligned} \sum _{k=0}^{J}\mathbf {D}_{Jk}f_{r+1}(\xi _k) &= 0, \quad g_{r+1}(\xi _J) = 0, \quad \sum _{k=0}^{J}\mathbf {D}_{Jk}\theta _{r+1}(\xi _k) = 0. \end{aligned}$$
(20b)

The boundary conditions (20) are incorporated in the matrix system (18), and thus the solution is obtained as

$$\begin{aligned} \mathbf {X}_{r+1}=\mathbf {A}_{r}^{-1}\mathbf {B}_{r}. \end{aligned}$$
(21)

The initial approximations \(f_{0}\), \(g_{0}\) and \(\theta _{0}\) are chosen to be functions that satisfy the boundary conditions (20), i.e.,

$$\begin{aligned} f_0(\eta )= \frac{\eta ^2-1}{2},\quad g_0(\eta )=0, \quad \theta _{0}(\eta ) = \frac{\eta ^2}{2}-\frac{2+Bi}{2Bi}. \end{aligned}$$
(22)

4 Entropy generation

For incompressible micropolar fluids the volumetric rate of entropy generation [29] is given by the relation

$$\begin{aligned} S_G = \frac{K_f}{T_1^2}\left( \frac{dT}{dr}\right) ^{2} + \frac{\mu + \frac{\kappa }{2}}{T_1}\left( \frac{du}{dr}\right) ^2+\frac{\kappa }{2T_1}\left[ 2\sigma +\frac{du}{dr}\right] ^2- \frac{2\beta }{T_1}\frac{\sigma }{r}\frac{d\sigma }{dr} +\frac{\gamma }{T_1}\left[ \left( \frac{d\sigma }{dr}\right) ^2+\frac{\sigma ^2}{r^2}\right] . \end{aligned}$$

According to Bejan [4], the dimensionless entropy generation number \(N_s\) is the ratio of the volumetric entropy generation rate to the characteristic entropy generation rate. Thus the entropy generation number is given by the relation

$$\begin{aligned} N_s = \theta '^2 + \frac{Br}{T_p(1-N)}\left[ \frac{2-N}{2}f'^2+\frac{N}{2}(f'+2g)^2- \frac{2B(1-N)}{\eta }gg'+\frac{N(2-N)}{m^2}\left( g'^2+\frac{1}{\eta ^2}g^2\right) \right] \end{aligned}$$
(23)

where \(T_p =\frac{T_2-T_1}{T_1}\) is the temperature difference(dimensionless), and the characteristic entropy generation rate is \(\frac{K_f (T_2-T_1)^2}{a^2T_1^2}\). Equation (23) can be expressed alternatively as follows:

$$\begin{aligned} N_s = N_h + N_v. \end{aligned}$$
(24)

The first term on the right hand side of this equation denotes the entropy generation due to heat transfer irreversibility and the second term represents the entropy generation due to viscous dissipation.

To evaluate the irreversibility distribution, the parameter Be (Bejan number), which is the ratio of heat transfer entropy generation to the overall entropy generation (24), is defined as follows:

$$\begin{aligned} Be = \frac{N_h}{N_h+N_v}. \end{aligned}$$
(25)

The Bejan number varies from 0 to 1. Subsequently, \(Be = 0\) reveals that the irreversibility due to viscous dissipation dominates, whereas \(Be=1\) indicates the dominance of heat transfer irreversibility. It is obvious that \(Be=0.5\) indicates that the heat transfer irreversibility is the same as the fluid friction irreversibility in the entropy production.

5 Results and discussion

Figures 2–6 show the variation of velocity, microrotation, temperature, entropy generation and Bejan number with \(\eta \) for different values of coupling number (N), angle of inclination (\(\alpha \)), suction parameter (R), Biot number (Bi) and Brinkman number (Br) for \(Pr=0.75\), \(g_s=0.5\), \(m=2\), \(A=-2\), \(B=0.1\) and \(T_p=1\).

In order to validate the accuracy of our method, we have compared the results of velocity and microrotation with the analytical solution of [21] in the absence of \(g_{s}\), R and \(\alpha \) as a special case by taking \(N=0.5\), \(m=2\) and \(A=-2\). The comparison in this case is found to be in good agreement, as shown in table 1.

Figure 2a–e presents the effect of coupling number (N) on non-dimensional velocity, microrotation, temperature, entropy generation and Bejan number. The coupling of linear and rotational motion arising from the micromotion of the fluid molecules is characterized by coupling number. Hence, the coupling between the Newtonian and rotational viscosities is represented by N. The microstructure effect is significant as \(N \rightarrow 1\), and for a smaller value of N the substructure individuality is limited. The fluid is non-polar as its micropolarity is lost at \(\kappa \rightarrow 0\), i.e., \(N \rightarrow 0\). Thus, as \(N \rightarrow 0\) Eqs. (7) and (8) reduce to the corresponding equations for viscous fluid. Hence it can be seen from figure 2a that the velocity in the case of micropolar fluid is less than that of viscous fluid. Furthermore, from figure 2b it is observed that for fixed N, the microrotation increases and then decreases as radial distance from the axis increases. It is observed from figure 2c–e that the temperature, entropy generation and Bejan number decrease with increase in coupling number (N).

The effects of angle of inclination (\(\alpha \)) of the circular pipe on the velocity, microrotation, temperature, entropy generation and Bejan number are shown in figure 3. Figure 3a shows that the velocity increases with increase in angle of inclination \(\alpha \), this is due to increase in forces acting upon the fluid flow. It is observed from figure 3b that the microrotation increases as angle of inclination increases. It is clear from figure 3c–e that temperature, entropy generation and Bejan number increases with increase in \(\alpha \). The peak values of temperatures are observed at the centre of the pipe. The maximum entropy generation is observed at the pipe wall due to high velocity and temperature gradients.

The variations of suction/injection parameter on veloity, microrotation, temperature, entropy generation and Bejan number are presented in figure 4a–e. Increase in the suction/injection parameter causes an increase in all the governing parameters.

Figure 5 shows the effect of Biot number on velocity, microrotation, temperature, entropy generation and Bejan number. It is observed from figure 5a and b that the velocity and microrotation decrease with an increase in Biot number. As the Biot number increases, the circular pipe thermal resistance enhances and the velocity decreases significantly. Figure 5c reveals that the temperature decreases as Biot number increases as the Biot number depends on heat transfer coefficient h, which leads to decrease in temperature. Decrease in entropy generation is observed with an increase in Biot number Bi as shown in figure 5d. This is due to the fact that both velocity and temperature gradients within the pipe decrease as Bi increases. Figure 5e shows that the Bejan number decreases as Biot number increases. This implies an increase in dominant effect of fluid friction irreversibility as Bi increases.

The effects of Brinkman number on velocity, microrotation and temperature fields are shown in figure 6a–c. Velocity, microrotation and temperature increase as Brinkman number increases. The analogous importance between viscous dissipation and fluid conduction is determined by the Brinkman number. As Br increases, more heat is generated by the viscous dissipation effect in the fluid. This generated heat by viscous dissipation effect results in higher temperature profiles. It is observed from figure 6d that the contribution of entropy is nil at the centre of the pipe since the velocity and temperature gradients are zero. As Brinkman number increases, the entropy generation increases. It is observed from figure 6e that the Bejan number increases with increase in the value of Br. It is observed that the heat transfer irreversibility dominates at the pipe wall and fluid friction irreversibility dominates at the centre of the pipe.

6 Conclusions

Entropy generation analysis of incompressible micropolar fluid flow through an inclined circular pipe with convective heating has been carried out. The velocity, microrotation and temperature distributions are achieved numerically using the SQLM, which are used to compute the entropy generation number. The effects of different parameters on velocity, microrotation and temperature are presented graphically. The influences of same parameters on entropy generation and Bejan number are also discussed.

  • The fluid velocity, microrotation and temperature decrease with increasing values of coupling number and Biot number.

  • Fluid temperature increases with increasing angle of inclination, suction parameter and Brinkman number while temperature decreases with increasing coupling number and Biot number.

  • For all the parametric values, from the Bejan number graphs it is observed that the fluid friction irreversibility dominates around the centre of the pipe and heat transfer irreversibility dominates at the pipe wall.

  • The entropy generation decreases with increasing coupling number and Biot number.

  • All the Bejan number profiles show a minimum value at the centre of the pipe and maximum value at the pipe wall.

Table 1 Comparison of SQLM solutions for the velocity and microrotation with that of analytical solution [21] for \(g_s=0\), \(R=0\) and \(\alpha = 0\).
Full size table
Figure 2
figure 2

Effect of coupling number on (a) velocity, (b) microrotation, (c) temperature, (d) entropy generation and (e) Bejan number.

Full size image
Figure 3
figure 3

Effect of angle of inclination on (a) velocity, (b) microrotation, (c) temperature, (d) entropy generation and (e) Bejan number.

Full size image
Figure 4
figure 4

Effect of suction parameter on (a) velocity, (b) microrotation, (c) temperature, (d) entropy generation and (e) Bejan number.

Full size image
Figure 5
figure 5

Effect of Biot number on (a) velocity, (b) microrotation, (c) temperature, (d) entropy generation and (e) Bejan number.

Full size image
Figure 6
figure 6

Effect of Brinkman number on (a) velocity, (b) microrotation, (c) temperature, (d) entropy generation and (e) Bejan number.

Full size image