1 Introduction

The need of generalization of traditional transportation problem to solid transportation problem arises when different kinds of conveyances are available for the transportation of goods to save time as well as money. It was first stated by Schell [1] and later on Haley [2] described its solution procedure. The multi-objective multi-item solid transportation problem (MOMISTP) is further generalization of the solid transportation problem. It deals with optimizing multiple objectives and using different types of conveyances to transport heterogeneous products from the warehouses to the consumer points. This type of transportation problem is very beneficial in many industries, where more than one kind of products are shipped. In multiple objective problems, the objectives are generally conflicting in nature, so the concept of optimal solution is replaced by optimal compromise solution also called efficient solution or pareto optimal solution or non-dominated solution.

In the conventional solid transportation problem, it is assumed that all the parameters are known exactly and many algorithms have been developed to solve these problems. But in real world situations, it is not always so. Due to uncontrollable factors like lack of information and uncertainty in judgement, the values of the transportation parameters, i.e., unit cost of transportation, availability and demand are not exact always. This impreciseness in the values of the parameters can be represented by using the fuzzy set theory given by Zadeh [3]. A systematic study of fuzzy mathematical programming has also been given by Bector and Chandra [4]. Many authors have used the fuzzy numbers to represent the uncertainty in transportation parameters and proposed methods to solve them. The MOMISTPs in which all the parameters are represented by fuzzy numbers are called fully fuzzy multi-objective multi-item solid transportation problems (FFMOMISTPs).

Fuzzy programming technique for the multi-objective transportation problems was given by Zimmermann [5]. Bit et al [6] applied the fuzzy programming technique to solve MOSTP. Li et al [7] solved the multi-objective solid transportation problem (MOSTP) using the genetic algorithm in which only objective function coefficients are taken as fuzzy numbers. Liu and Liu [8] presented the expected value model in fuzzy programming. Islam and Roy [9] studied the geometric programming approach for the multi-objective transportation problems. Ojha et al [10] proposed methods to solve fuzzy MOSTP, where all the parameters except decision variables are taken as fuzzy numbers. Gupta et al [11] proposed a method, called Mehar’s method, to find the exact fuzzy optimal solution of unbalanced fully fuzzy multi-objective transportation problems.

Uncertainty theory based expected constrained programming for the solid transportation problems in uncertain environment is studied by Cui and Sheng [12]. Recently, Kundu et al [13] have proposed a method to find the crisp optimal compromise solution of the fuzzy MOMISTP, using the fuzzy programming technique and global criterion method. Solid transportation problems are also studied by Baidya et al [14] and Kundu et al [15]. Ebrahimnejad [16] studied the transportation problem with generalized trapezoidal fuzzy numbers. To the best of our knowledge, no method has been proposed in the literature to find the fuzzy optimal compromise solution of the FFMOMISTP.

In this paper, a method is proposed to find the fuzzy optimal compromise solution of FFMOMISTP. The application of the proposed method is shown by obtaining the fuzzy optimal compromise solution of the numerical example for which Kundu et al [13] found the crisp optimal compromise solution. Since the proposed problem is the generalization of the traditional solid transportation problem, it is also applicable to solve both single and multi-objective solid transportation problems, single or multi-objective transportation problems (both for single and multi-item).

2 Preliminaries

In this section, some basic definitions and ranking approach for trapezoidal fuzzy numbers are presented.

2.1 Basic definitions [17, 18]

Definition 1

A fuzzy number \({\widetilde{A}}\) defined on the universal set of real numbers \({\mathbb {R}}\), denoted as \({\widetilde{A}} = (a, b, c, d)\), is said to be a trapezoidal fuzzy number if its membership function \(\mu _{{\widetilde{A}}}(x)\) is given by

$$\begin{aligned} \mu _{{\widetilde{A}}}(x)= {\left\{ \begin{array}{ll} \frac{(x-a)}{(b-a)}& a\le x< b\\ 1 & b\le x \le c\\ \frac{(x-d)}{(c-d)}& c < x \le d\\ 0 & \hbox {otherwise.} \end{array}\right. } \end{aligned}$$

Definition 2

A trapezoidal fuzzy number \({\widetilde{A}} = (a,b,c,d)\) is said to be zero trapezoidal fuzzy number if and only if \(a = 0, b = 0, c = 0\) and \(d = 0\).

Definition 3

A trapezoidal fuzzy number \({\widetilde{A}} = (a,b,c,d)\) is said to be non-negative trapezoidal fuzzy number if and only if \(a \ge 0\).

Definition 4

Two trapezoidal fuzzy numbers \({\widetilde{A}}_1 = (a_1, b_1, c_1, d_1)\) and \({\widetilde{A}}_2 = (a_2, b_2, c_2, d_2)\) are said to be equal if and only if \(a_1 = a_2, b_1 = b_2, c_1 = c_2 \) and \( d_1 = d_2,\) and is denoted by \({\widetilde{A}}_1 = {\widetilde{A}}_2\).

Remark 1

If for a trapezoidal fuzzy number \( {\widetilde{A}} = (a, b, c, d), b = c\), then it is called a triangular fuzzy number and is denoted by (a, b, b, d) or (a, b, d) or (a, c, d).

2.2 Arithmetic operations [17]

Let \({\widetilde{A}}_1 = (a_1, b_1, c_1, d_1)\) and \({\widetilde{A}}_2 = (a_2, b_2, c_2, d_2)\) be two trapezoidal fuzzy numbers. Then

  1. (i)

    \({\widetilde{A}}_1 \oplus {\widetilde{A}}_2 = (a_1 + a_2, b_1 + b_2, c_1 + c_2, d_1 + d_2)\)

  2. (ii)

    \({\widetilde{A}}_1 \ominus {\widetilde{A}}_2 = (a_1 - d_2, b_1 - c_2, c_1 - b_2, d_1 - a_2)\)

  3. (iii)

    \( k{{\widetilde{A}}}_1= {\left\{ \begin{array}{ll} (ka_1, kb_1, kc_1, kd_1), &{} k\ge 0\\ (kd_1, kc_1, kb_1, ka_1), &{} k\le 0 \end{array}\right. } \)

  4. (iv)

    \({\widetilde{A}}_1 \otimes {\widetilde{A}}_2 = (a,b,c,d)\), where \(a = \min (a_1a_2,a_1d_2,d_1a_2,d_1d_2)\), \(b = \min (b_1b_2,b_1c_2,c_1b_2,c_1c_2)\), \(c = \max (b_1b_2,b_1c_2,c_1b_2,c_1c_2)\), \(d =\max (a_1a_2,a_1d_2,d_1a_2,d_1d_2).\)

3 Mathematical model

A FFMOMISTP with parameters as trapezoidal fuzzy numbers can be stated as a transportation problem with R objectives in which l different items are to be transported from m sources (\(S_i, 1 \le i \le m\)) to n destinations (\(D_j, 1 \le j \le n\)) via K different conveyances. Let \({\widetilde{a}}^p_i\) denote the fuzzy availability of item p at source \(S_i, {\widetilde{b}}^p_j\) denote the fuzzy demand of item p at destination \(D_j, {\widetilde{e}}_k\) be the total fuzzy capacity of kth conveyance, \({\widetilde{c}}^{rp}_{ijk}\) be the fuzzy penalty for transporting one unit of item p from \(S_i\) to \(D_j\) via kth conveyance for rth objective \(Z_r\) and \({\widetilde{x}}^p_{ijk}\) be the fuzzy quantity of item p to be transported from \(S_i\) to \(D_j\) using kth conveyance in order to minimize R objective functions. The problem is mathematically modeled as follows:

$$\begin{aligned} (P)&\quad\,\hbox {Minimize} \quad ({\widetilde{Z}}_1, {\widetilde{Z}}_2,\ldots , {\widetilde{Z}}_R)\\&\quad\hbox {subject to}\\& \quad\sum _{j=1}^n \sum _{k=1}^K {\widetilde{x}}^p_{ijk} \le {\widetilde{a}}^p_i; 1\le i\le m, 1 \le p \le l,\\& \quad\sum _{i=1}^m \sum _{k=1}^K {\widetilde{x}}^p_{ijk} \ge {\widetilde{b}}^p_j; 1\le j\le n, 1 \le p \le l,\\& \quad\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n {\widetilde{x}}^p_{ijk} \le {\widetilde{e}}_k; 1\le k \le K, \end{aligned}$$

where \({\widetilde{x}}^p_{ijk}\) is a non-negative trapezoidal fuzzy number, \( \hbox {for all}\, i, j, k, p\) and \(\widetilde{Z_r} = \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K({\widetilde{c}}^{rp}_{ijk} \otimes {\widetilde{x}}^p_{ijk} ), 1 \le r \le R.\)

For the above problem to be balanced it should satisfy:

  1. (i)

    \( \sum _{i=1}^m {\widetilde{a}}^p_i = \sum _{j=1}^n {\widetilde{b}}^p_j , 1 \le p \le l\), i.e., for an item, its total availability at all sources should be equal to its demand at all the destinations.

  2. (ii)

    \( \sum _{p=1}^l \sum _{i=1}^m {\widetilde{a}}^p_i = \sum _{p=1}^l \sum _{j=1}^n {\widetilde{b}}^p_j = \sum _{k=1}^K {\widetilde{e}}_k \), i.e., overall availability/demand of all the items at all the sources/destinations and total conveyance capacity should be equal.

Definition 5

A fuzzy feasible solution \({\widetilde{x}} = \{{\widetilde{x}}^p_{ijk}\}\) of (P) is said to be a fuzzy optimal compromise (efficient) solution if there exists no other feasible solution \({\widetilde{y}} = \{{\widetilde{y}}^p_{ijk}\}\) such that,

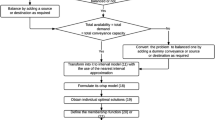
$$\begin{aligned}& \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K {\mathfrak {R}}({\widetilde{c}}^{rp}_{ijk} \otimes {\widetilde{y}}^p_{ijk} )\\ &\le \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K {\mathfrak {R}}({\widetilde{c}}^{rp}_{ijk} \otimes {\widetilde{x}}^p_{ijk}) \quad \hbox {for all} \,\textit{r}\\ \hbox {and}\\& \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K {\mathfrak {R}}({\widetilde{c}}^{rp}_{ijk} \otimes {\widetilde{y}}^p_{ijk} ) < \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K {\mathfrak {R}}({\widetilde{c}}^{rp}_{ijk} \otimes {\widetilde{x}}^p_{ijk}) \,\hbox {for atleast one} \,\textit{r}. \end{aligned}$$

4 Proposed method

In this section a method has been proposed to find the fuzzy optimal compromise solution of Problem (P).

The proposed method consists of the following steps:

Step 1: Verify whether the problem under consideration is balanced.

For all \(p, 1 \le p \le l\), find \( \sum _{i=1}^m {\widetilde{a}}^p_i\) and \( \sum _{j=1}^n {\widetilde{b}}^p_j\). Let \( \sum _{i=1}^m {\widetilde{a}}^p_i = (x_p, y_p, z_p, w_p)\) and \( \sum _{j=1}^n {\widetilde{b}}^p_j = (x_p', y_p', z_p', w_p')\).

  • Case 1: \( \sum _{i=1}^m{\widetilde{a}}^p_i = \sum _{j=1}^n {\widetilde{b}}^p_j \hbox {for all}\, p, 1 \le p \le l\). Go to Step 2.

  • Case 2: \( \sum _{i=1}^m{\widetilde{a}}^p_i \ne \sum _{j=1}^n {\widetilde{b}}^p_j\) for all or any p, \(1 \le p \le l\). To make \( \sum _{i=1}^m{\widetilde{a}}^p_i = \sum _{j=1}^n {\widetilde{b}}^p_j\), proceed according to the following subcases. One or all may apply.

  • Subcase 2a: If \(x_p \le x_p',y_p - x_p \le y_p'-x_p', z_p-y_p \le z_p'-y_p'\) and \(w_p-z_p \le w_p'-z_p' \) (for one or more values of p), then introduce a dummy source with fuzzy availability of the pth item(s) equal to \((x_p' - x_p, y_p' - y_p, z_p' - z_p, w_p' - w_p)\).

    Subcase 2b: If \(x_p \ge x_p', y_p-x_p \ge y_p'-x_p', z_p-y_p \ge z_p'-y_p'\) and \(w_p-z_p \ge w_p'-z_p' \) (for one or more values of p), then introduce a dummy destination having fuzzy demand of the pth item(s) equal to \((x_p - x_p', y_p - y_p', z_p - z_p', w_p - w_p')\).

    Subcase 2c: None of the Subcases 2a or 2b is satisfied. In such a situation add a dummy source with availability of the pth item(s) equal to \((\max \{0, (x_p' - x_p)\}, \max \{0, (x_p' - x_p)\} + \max \{0, (y_p' - x_p') - (y_p-x_p)\}, \max \{0, (x_p' - x_p)\} + \max \{0, (y_p' - x_p') - (y_p-x_p)\} + \max \{0, (z_p' - y_p') - (z_p-y_p)\}, \max \{0, (x_p' - x_p)\} + \max \{0, (y_p' - x_p') - (y_p - x_p)\} + \max \{0, (z_p' - y_p') - (z_p-y_p)\} + \max \{0, (w_p' - z_p') - (w_p - z_p)\})\) and also a dummy destination having demand of these item(s) as \((\max \{0, (x_p - x_p')\}, \max \{0, (x_p - x_p')\} + \max \{0, (y_p - x_p) - (y_p'-x_p')\}, \max \{0, (x_p - x_p')\} + \max \{0, (y_p - x_p) - (y_p'-x_p')\} + \max \{0, (z_p - y_p) - (z_p'-y_p')\}, \max \{0, (x_p - x_p')\} + \max \{0, (y_p - x_p) - (y_p' - x_p')\} + \max \{0, (z_p - y_p) - (z_p'-y_p')\} + \max \{0, (w_p - z_p) - (w_p' - z_p')\})\). Now go to Step 2.

Step 2: After Step 1, we get \( \sum _{i=1}^s{\widetilde{a}}^p_i = \sum _{j=1}^t {\widetilde{b}}^p_j \hbox {for all} \; p, 1 \le p \le l\), where \(s = m \; {\hbox{or}}\;{m+1}\) and \(t = n \; \hbox {or}\; n+1\), i.e., \( \sum _{p=1}^l\sum\nolimits _{i=1}^s{\widetilde{a}}^p_i = \sum\nolimits _{p=1}^l\sum _{j=1}^t {\widetilde{b}}^p_j = (u, v, w, \alpha )\) (say).

Now, check whether \( \sum _{p=1}^l\sum\nolimits _{i=1}^s{\widetilde{a}}^p_i = \sum _{p=1}^l\sum\nolimits _{j=1}^t {\widetilde{b}}^p_j = \sum _{k=1}^K{\widetilde{e}}_k\). Let \( \sum\nolimits _{k=1}^K{\widetilde{e}}_k = (u', v', w', \alpha ')\).

  • Case 1: If \( \sum\nolimits _{p=1}^l\sum _{i=1}^s{\widetilde{a}}^p_i = \sum\nolimits _{p=1}^l\sum _{j=1}^t {\widetilde{b}}^p_j = \sum _{k=1}^K{\widetilde{e}}_k\), i.e., the total availability of all the items, their demand and the total conveyance capacity are equal, then go to Step 3.

  • Case 2: If \( \sum\nolimits _{p=1}^l\sum _{i=1}^s{\widetilde{a}}^p_i = \sum\nolimits _{p=1}^l\sum _{j=1}^t {\widetilde{b}}^p_j \ne \sum _{k=1}^K{\widetilde{e}}_k\), then proceed according to the following subcases:

    • Subcase 2a: If \(u \le u',v - u \le v'- u', w - v \le w'-v'\) and \(\alpha - w \le \alpha ' - w' \), then check whether in Step 1 a dummy source and/or a dummy destination have been added and proceed as below:

    • Case (i): If both a dummy source and a dummy destination have been introduced, then increase their total availability and demand by the fuzzy quantity \((u' - u, v'-v, w'-w, \alpha '-\alpha )\) (The demand of only those items is to be increased whose availability has been increased at the dummy source).

    • Case (ii): If only a dummy source (destination) has been introduced, then increase its total availability (demand) by the fuzzy number \((u' - u, v'-v, w'-w, \alpha '-\alpha )\) and also introduce a dummy destination (source) having the demand (availability) of these added items as \((u' - u, v'-v, w'-w, \alpha '-\alpha )\).

    • Case (iii): If neither a dummy source nor a dummy destination has been added, then introduce a dummy source with the total availability equal to the fuzzy number \((u' - u, v'-v, w'-w, \alpha '-\alpha )\) and a dummy destination with demand of these added items equal to \((u' - u, v'-v, w'-w, \alpha '-\alpha )\).

    • Subcase 2b: If \(u \ge u',v - u \ge v'- u', w - v \ge w'-v'\) and \(\alpha - w \ge \alpha ' - w' \), then introduce a dummy conveyance having capacity \((u - u', v-v', w-w', \alpha -\alpha ')\).

    • Subcase 2c: If neither Subcase 2a nor Subcase 2b applies, then check whether in Step 1 a dummy source or a dummy destination or both have been added and proceed according to the following cases. Let \(({\bar{u}}, {\bar{v}}, {\bar{w}}, {\bar{\alpha }}) = (\max \{0, u' - u\}, \max \{0, u' - u\} + \max \{0, (v' - u') - (v - u)\}, \max \{0, u' - u\} + \max \{0, (v' - u') - (v - u)\} + \max \{0, (w' - v') - (w - v)\}, \max \{0, u' - u\} + \max \{0, (v' - u') - (v - u)\} + \max \{0, (w' - v') - (w - v)\} + \max \{0, (\alpha ' - w') - (\alpha - w)\})\) and \(({\bar{u}}', {\bar{v}}', {\bar{w}}', {\bar{\alpha }}') = (\max \{0, u - u'\}, \max \{0, u - u'\} + \max \{0, (v - u) - (v' - u')\}, \max \{0, u - u'\} + \max \{0, (v - u) - (v' - u')\} + \max \{0, (w - v) - (w' - v')\}, \max \{0, u - u'\} + \max \{0, (v - u) - (v' - u')\} + \max \{0, (w - v) - (w' - v')\}+ \max \{0, (\alpha - w) - (\alpha ' - w')\})\).

    • Case (i): If both a dummy source and a dummy destination have been introduced, then increase their total availability and demand by the fuzzy quantity \(({\bar{u}}, {\bar{v}}, {\bar{w}}, {\bar{\alpha }})\) (The demand of only those items is to be increased whose availability has been increased at the dummy source). Also, introduce a dummy conveyance with capacity \(({\bar{u}}', {\bar{v}}', {\bar{w}}', {\bar{\alpha }}')\).

    • Case (ii): If only a dummy source (destination) has been introduced, then increase its total availability (demand) by the fuzzy number \(({\bar{u}}, {\bar{v}}, {\bar{w}}, {\bar{\alpha }})\) and introduce a dummy destination (source) having the demand (availability) of these added items as \(({\bar{u}}, {\bar{v}}, {\bar{w}}, {\bar{\alpha }})\). Also, introduce a dummy conveyance with capacity \(({\bar{u}}', {\bar{v}}', {\bar{w}}', {\bar{\alpha }}')\).

    • Case (iii): If neither a dummy source nor a dummy destination has been added, then introduce both a dummy source as well as a dummy destination with the availability and demand of added items as \(({\bar{u}}, {\bar{v}}, {\bar{w}}, {\bar{\alpha }})\). Also, introduce a dummy conveyance with capacity \(({\bar{u}}', {\bar{v}}', {\bar{w}}', {\bar{\alpha }}')\).

Assume the unit transportation costs required due to the dummy source/destination/conveyance to be zero trapezoidal fuzzy number.

Now, the problem is balanced and takes the form:

$$\begin{aligned} (P') \quad&\hbox {Minimize} \quad (\widetilde{Z_1}, \widetilde{Z_2},\ldots ,\widetilde{Z_R})\\&\hbox {subject to}\\& \sum _{j=1}^t \sum _{k=1}^K (x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk}) = (a^p_i, b^p_i, c^p_i, d^p_i); 1\le i\le s, 1 \le p \le l\\& \sum _{i=1}^s \sum _{k=1}^K (x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk}) = (a'^{p}_j, b'^{p}_j, c'^{p}_j, d'^{p}_j); 1\le j\le t, 1 \le p \le l\\& \sum _{p=1}^l\sum _{i=1}^s\sum _{j=1}^t (x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk}) = (a''_k, b''_k, c''_k, d''_k); 1\le k \le K, \end{aligned}$$

where \( \widetilde{Z_r} = \sum\nolimits _{p=1}^l\sum\nolimits _{i=1}^s\sum\nolimits _{j=1}^t\sum\nolimits _{k=1}^K((a^{rp}_{ijk}, b^{rp}_{ijk}, c^{rp}_{ijk}, d^{rp}_{ijk}) \otimes (x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk})), 1 \le r \le R,(x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk})\) is a non-negative trapezoidal fuzzy number and \({\widetilde{c}}^{rp}_{ijk} = (a^{rp}_{ijk}, b^{rp}_{ijk}, c^{rp}_{ijk}, d^{rp}_{ijk}), {\widetilde{a}}^p_i = (a^p_i, b^p_i, c^p_i, d^p_i), {\widetilde{b}}^p_j = (a'^{p}_j, b'^{p}_j, c'^{p}_j, d'^{p}_j), {\widetilde{e}}_k = (a''_k, b''_k, c''_k, d''_k)\).

Step 3: Corresponding to each objective, convert the problem \((P')\) into following four crisp problems \((P'_1)-(P'_4)\):

$$\begin{aligned}&\begin{array}{ll} {\begin{array}{ll} (P'_1)\quad &{}\hbox {Minimize} \quad \sum _{p=1}^l\sum _{i=1}^s\sum _{j=1}^t\sum _{k=1}^K a^{rp}_{ijk}x^{p}_{ijk}\\ &{}\hbox {subject to}\\ &{} \sum _{j=1}^t \sum _{k=1}^K x^{p}_{ijk} = a^p_i; 1\le i\le s, 1 \le p \le l\\ &{} \sum _{i=1}^s \sum _{k=1}^K x^{p}_{ijk} = a'^{p}_j; 1\le j\le t, 1 \le p \le l\\ &{} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n x^{p}_{ijk} = a''_k; 1\le k \le K\\ &{}x^{p}_{ijk} \ge 0 \end{array}} &{} {\begin{array}{ll} (P'_2) \quad &{}\hbox {Minimize} \quad \sum _{p=1}^l\sum _{i=1}^s\sum _{j=1}^t\sum _{k=1}^K b^{rp}_{ijk}y^{p}_{ijk}\\ &{}\hbox {subject to}\\ &{} \sum _{j=1}^t \sum _{k=1}^K y^{p}_{ijk} = b^p_i; 1\le i\le s, 1 \le p \le l\\ &{} \sum _{i=1}^s \sum _{k=1}^K y^{p}_{ijk} = b'^{p}_j; 1\le j\le t, 1 \le p \le l\\ &{} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n y^{p}_{ijk} = b''_k; 1\le k \le K\\ &{}y^{p}_{ijk} \ge x^{*p}_{ijk} \end{array}} \end{array}\\&\begin{array}{ll} {\begin{array}{ll} (P'_3) \quad &{}\hbox {Minimize} \quad \sum _{p=1}^l\sum _{i=1}^s\sum _{j=1}^t\sum _{k=1}^K c^{rp}_{ijk}z^{p}_{ijk}\\ &{}\hbox {subject to}\\ &{} \sum _{j=1}^t \sum _{k=1}^K z^{p}_{ijk} = c^p_i; 1\le i\le s, 1 \le p \le l\\ &{} \sum _{i=1}^s \sum _{k=1}^K z^{p}_{ijk} = c'^{p}_j; 1\le j\le t, 1 \le p \le l\\ &{} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n z^{p}_{ijk} = c''_k; 1\le k \le K\\ &{}z^{p}_{ijk} \ge y^{*p}_{ijk} \end{array}} &{} {\begin{array}{ll} (P'_4) \quad &{}\hbox {Minimize} \quad \sum _{p=1}^l\sum _{i=1}^s\sum _{j=1}^t\sum _{k=1}^K d^{rp}_{ijk}w^{p}_{ijk}\\ &{}\hbox {subject to}\\ &{} \sum _{j=1}^t \sum _{k=1}^K w^{p}_{ijk} = d^p_i; 1\le i\le s, 1 \le p \le l\\ &{} \sum _{i=1}^s \sum _{k=1}^K w^{p}_{ijk} = d'^{p}_j; 1\le j\le t, 1 \le p \le l\\ &{} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n y^{p}_{ijk} = d''_k; 1\le k \le K\\ &{}w^{p}_{ijk} \ge z^{*p}_{ijk}\end{array}} \end{array} \end{aligned}$$

Solve the four problems sequentially using the optimal solution \(x^{*p}_{ijk}\) of \((P_1)\) in \((P_2)\); optimal solution \(y^{*p}_{ijk}\) of \((P_2)\) in \((P_3)\) and optimal solution \(z^{*p}_{ijk}\) of \((P_3)\) in \((P_4)\). Let \(w^{*p}_{ijk}\) be the optimal solution of \((P_4)\). This leads to the fuzzy optimal solution \({\widetilde{x}}^p_{ijk} = (x^{*p}_{ijk}, y^{*p}_{ijk}, z^{*p}_{ijk}, w^{*p}_{ijk})\) of \((P')\).

Step 4: Apply the fuzzy programming technique to obtain the optimal-compromise solution and calculate the value of each objective function.

5 Numerical example

Consider the multi-objective multi-item solid transportation problem solved by Kundu et al [13]. In this problem, the number of destinations is three, while that of sources, items, conveyances and objectives is two each. The authors have proposed a method to find the crisp optimal compromise solution. Since the fuzzy solution has more information than the crisp one, we solve the same problem using the method proposed by us to find the fuzzy optimal compromise solution. The data of the problem is as follows (tables 1–4):

Table 1 Unit transportation penalties for item 1 in the first objective.
Full size table
Table 2 Unit transportation penalties for item 2 in the first objective.
Full size table
Table 3 Unit transportation penalties for item 1 in the second objective.
Full size table
Table 4 Unit transportation penalties for item 2 in the second objective.
Full size table
Table 5 Availability and demand data.
Full size table

From table 5, we find that for the first item, total availability \( \sum\nolimits _{i=1}^2 {\widetilde{a}}^1_i = (21,24,26,28)\oplus (28,32,35,37) = (49,56,61,65)\) and total demand \( \sum\nolimits _{j=1}^3 {\widetilde{b}}^1_j = (14,16,19,22) \oplus (17,20,22,25) \oplus (12,15,18,21) = (43, 51, 59, 68).\) Similarly for the second item, total availability \( \sum\nolimits _{i=1}^2 {\widetilde{a}}^2_i = (57,62,67,72)\) and total demand \( \sum\nolimits _{j=1}^3 {\widetilde{b}}^2_j\)= (51,58,63,71).

Since \( \sum\nolimits _{i=1}^2 {\widetilde{a}}^1_i \ne \sum\nolimits _{j=1}^3 {\widetilde{b}}^1_j\) and \( \sum\nolimits _{i=1}^2 {\widetilde{a}}^2_i \ne \sum\nolimits _{j=1}^3 {\widetilde{b}}^2_j\), the problem is unbalanced. Now, first step is to balance the problem.

We find that neither Subcase 2a nor Subcase 2b of Step 1 holds for any of the items. So, according to Subcase 2c, we introduce a dummy source (\(S_3\)) having availabilities of the first and second items as \({\widetilde{a}}^1_3 =(0, 1, 4, 9)\) and \({\widetilde{a}}^2_3 = (0, 2, 2, 5)\), respectively. Also, we introduce a dummy destination (\(D_4\)) with demand of the first and second items as \({\widetilde{b}}^1_4 = {\widetilde{b}}^2_4 = (6, 6, 6, 6)\) so that the total availability and total demand of both the items become equal, i.e., \( \sum\nolimits _{p=1}^2\sum\nolimits _{i=1}^3{\widetilde{a}}^p_i = \sum\nolimits _{p=1}^2\sum\nolimits _{j=1}^4 {\widetilde{b}}^p_j = (106, 121, 134, 151).\)

Since, the total conveyance capacity \( \sum\nolimits _{k=1}^2{\widetilde{e}}_k = (97, 102, 107, 112)\). Clearly, \( \sum\nolimits _{p=1}^2\sum\nolimits _{i=1}^3{\widetilde{a}}^p_i = \sum\nolimits _{p=1}^2\sum\nolimits _{j=1}^4 {\widetilde{b}}^p_j \ne \sum\nolimits _{k=1}^2{\widetilde{e}}_k\). For (106, 121, 134, 151) = \((u, v, w, \alpha )\) and (97, 102, 107, 112) = \((u', v', w', \alpha ')\), the condition \(u \ge u',v - u \ge v'- u', w - v \ge w'-v'\) and \(\alpha - w \ge \alpha ' - w' \) is met and so according to Subcase 2b of Step 2, we introduce a dummy conveyance having capacity \({\widetilde{e}}_3\) = (9, 19, 27, 39). Thus the problem becomes balanced.

Since, a dummy source (\(S_3\)), a dummy destination (\(D_4\)) and a dummy conveyance are introduced so we assume \({\widetilde{c}}^{rp}_{3jk} = {\widetilde{c}}^{rp}_{i4k} = {\widetilde{c}}^{rp}_{ij3} = (0, 0,0,0) \,\hbox {for all}\, r = 1,2; p = 1, 2; i = 1, 2, 3; j= 1, 2, 3, 4\, \hbox {and} \,k =1, 2, 3\). The obtained balanced problem can be written as

Minimize \({\widetilde{Z}}_1 = (5,8,9,11)\otimes {\widetilde{x}}^{1}_{111} \oplus (9,11,13,15)\otimes {\widetilde{x}}^{1}_{112} \oplus (4,6,9,11) \otimes {\widetilde{x}}^{1}_{121} \oplus (6,8,10,12) \otimes {\widetilde{x}}^{1}_{122} \oplus (10,12,14,16)\otimes {\widetilde{x}}^{1}_{131} \oplus (7,9,12,14) \otimes {\widetilde{x}}^{1}_{132} \oplus (8,10,13,15)\otimes {\widetilde{x}}^{1}_{211} \oplus (10,11,13,15)\otimes {\widetilde{x}}^{1}_{212} \oplus (6,7,8,9) \otimes {\widetilde{x}}^{1}_{221} \oplus (6,8,10,12) \otimes {\widetilde{x}}^{1}_{222} \oplus (11,13,15,17)\otimes {\widetilde{x}}^{1}_{231} \oplus (14,16,18,20) \otimes {\widetilde{x}}^{1}_{232} \oplus (9,10,12,13)\otimes {\widetilde{x}}^{2}_{111} \oplus (11,13,14,15)\otimes {\widetilde{x}}^{2}_{112} \oplus (5,8,10,12) \otimes {\widetilde{x}}^{2}_{121} \oplus (6,7,9,11) \otimes {\widetilde{x}}^{2}_{122} \oplus (10,11,12,13)\otimes {\widetilde{x}}^{2}_{131} \oplus (8,10,11,13) \otimes {\widetilde{x}}^{2}_{132}\oplus (11,13,14,16)\otimes {\widetilde{x}}^{2}_{211} \oplus (14,16,18,20)\otimes {\widetilde{x}}^{2}_{212} \oplus (7,9,12,14) \otimes {\widetilde{x}}^{2}_{221} \oplus (9,11,3,14) \otimes {\widetilde{x}}^{2}_{222} \oplus (12,14,16,18)\otimes {\widetilde{x}}^{2}_{231} \oplus (13,14,15,16) \otimes {\widetilde{x}}^{2}_{232} \oplus (0,0,0,0) \otimes ({\widetilde{x}}^1_{113} \oplus {\widetilde{x}}^1_{123} \oplus {\widetilde{x}}^1_{133} \oplus {\widetilde{x}}^1_{141} \oplus {\widetilde{x}}^1_{142} \oplus {\widetilde{x}}^1_{143} \oplus {\widetilde{x}}^1_{213} \oplus {\widetilde{x}}^1_{223} \oplus {\widetilde{x}}^1_{233} \oplus {\widetilde{x}}^1_{241} \oplus {\widetilde{x}}^1_{242} \oplus {\widetilde{x}}^1_{243} \oplus {\widetilde{x}}^1_{311} \oplus {\widetilde{x}}^1_{312} \oplus {\widetilde{x}}^1_{313} \oplus {\widetilde{x}}^1_{321} \oplus {\widetilde{x}}^1_{322} \oplus {\widetilde{x}}^1_{323} \oplus {\widetilde{x}}^1_{331} \oplus {\widetilde{x}}^1_{332} \oplus {\widetilde{x}}^1_{333} \oplus {\widetilde{x}}^1_{341} \oplus {\widetilde{x}}^1_{342} \oplus {\widetilde{x}}^1_{343} \oplus {\widetilde{x}}^2_{113} \oplus {\widetilde{x}}^2_{123} \oplus {\widetilde{x}}^2_{133} \oplus {\widetilde{x}}^2_{141} \oplus {\widetilde{x}}^2_{142} \oplus {\widetilde{x}}^2_{143} \oplus {\widetilde{x}}^2_{213} \oplus {\widetilde{x}}^2_{223} \oplus {\widetilde{x}}^2_{233} \oplus {\widetilde{x}}^2_{241} \oplus {\widetilde{x}}^2_{242} \oplus {\widetilde{x}}^2_{243} \oplus {\widetilde{x}}^2_{311} \oplus {\widetilde{x}}^2_{312} \oplus {\widetilde{x}}^2_{313} \oplus {\widetilde{x}}^2_{321} \oplus {\widetilde{x}}^2_{322} \oplus {\widetilde{x}}^2_{323} \oplus {\widetilde{x}}^2_{331} \oplus {\widetilde{x}}^2_{332} \oplus {\widetilde{x}}^2_{333} \oplus {\widetilde{x}}^2_{341} \oplus {\widetilde{x}}^2_{342} \oplus {\widetilde{x}}^2_{343})\)

Minimize \({\widetilde{Z}}_2 = (4,5,7,8)\otimes {\widetilde{x}}^{1}_{111} \oplus (6,7,8,9)\otimes {\widetilde{x}}^{1}_{112} \oplus (3,5,6,8) \otimes {\widetilde{x}}^{1}_{121} \oplus (4,6,7,9) \otimes {\widetilde{x}}^{1}_{122} \oplus (7,9,10,12)\otimes {\widetilde{x}}^{1}_{131} \oplus (5,7,9,11) \otimes {\widetilde{x}}^{1}_{132} \oplus (6,8,9,11)\otimes {\widetilde{x}}^{1}_{211} \oplus \) (4,6,8,10)\(\otimes {\widetilde{x}}^{1}_{212}\oplus (5,6,7,8) \otimes {\widetilde{x}}^{1}_{221} \oplus (7,9,11,13) \otimes {\widetilde{x}}^{1}_{222} \oplus (6,7,9,10)\otimes {\widetilde{x}}^{1}_{231} \oplus (9,10,11,12) \otimes {\widetilde{x}}^{1}_{232} \oplus (5,7,9,10)\otimes {\widetilde{x}}^{2}_{111} \oplus (7,8,9,10)\otimes {\widetilde{x}}^{2}_{112} \oplus (4,6,7,9) \otimes {\widetilde{x}}^{2}_{121} \oplus (4,5,7,8) \otimes {\widetilde{x}}^{2}_{122} \oplus (9,11,12,13)\otimes {\widetilde{x}}^{2}_{131} \oplus (8,10,11,12) \otimes {\widetilde{x}}^{2}_{132}\oplus \) (10,11,13,14)\(\otimes \widetilde{x}_{211}^{2} \oplus (6,8,10,12)\otimes \widetilde{x}_{212}^{2} \oplus (6,7,8,9) \otimes {\widetilde{x}}^{2}_{221} \oplus (5,7,9,11) \otimes {\widetilde{x}}^{2}_{222} \oplus (7,9,11,12)\otimes {\widetilde{x}}^{2}_{231} \oplus (9,10,12,14) \otimes {\widetilde{x}}^{2}_{232} \oplus (0,0,0,0) \otimes ({\widetilde{x}}^1_{113} \oplus {\widetilde{x}}^1_{123} \oplus {\widetilde{x}}^1_{133} \oplus {\widetilde{x}}^1_{141} \oplus {\widetilde{x}}^1_{142} \oplus {\widetilde{x}}^1_{143} \oplus {\widetilde{x}}^1_{213} \oplus {\widetilde{x}}^1_{223} \oplus {\widetilde{x}}^1_{233} \oplus {\widetilde{x}}^1_{241} \oplus {\widetilde{x}}^1_{242} \oplus {\widetilde{x}}^1_{243} \oplus {\widetilde{x}}^1_{311} \oplus {\widetilde{x}}^1_{312} \oplus {\widetilde{x}}^1_{313} \oplus {\widetilde{x}}^1_{321} \oplus {\widetilde{x}}^1_{322} \oplus {\widetilde{x}}^1_{323} \oplus {\widetilde{x}}^1_{331} \oplus {\widetilde{x}}^1_{332} \oplus {\widetilde{x}}^1_{333} \oplus {\widetilde{x}}^1_{341} \oplus {\widetilde{x}}^1_{342} \oplus {\widetilde{x}}^1_{343} \oplus {\widetilde{x}}^2_{113} \oplus {\widetilde{x}}^2_{123} \oplus {\widetilde{x}}^2_{133} \oplus {\widetilde{x}}^2_{141} \oplus {\widetilde{x}}^2_{142} \oplus {\widetilde{x}}^2_{143} \oplus {\widetilde{x}}^2_{213} \oplus {\widetilde{x}}^2_{223} \oplus {\widetilde{x}}^2_{233} \oplus {\widetilde{x}}^2_{241} \oplus {\widetilde{x}}^2_{242} \oplus {\widetilde{x}}^2_{243} \oplus {\widetilde{x}}^2_{311} \oplus {\widetilde{x}}^2_{312} \oplus {\widetilde{x}}^2_{313} \oplus {\widetilde{x}}^2_{321} \oplus {\widetilde{x}}^2_{322} \oplus {\widetilde{x}}^2_{323} \oplus {\widetilde{x}}^2_{331} \oplus {\widetilde{x}}^2_{332} \oplus {\widetilde{x}}^2_{333} \oplus {\widetilde{x}}^2_{341} \oplus {\widetilde{x}}^2_{342} \oplus {\widetilde{x}}^2_{343})\)

subject to

$$\begin{aligned}& \sum _{j=1}^4 \sum _{k=1}^3 (x^{1}_{1jk}, y^{1}_{1jk}, z^{1}_{1jk}, w^{1}_{1jk}) = (21,24,26,28),\quad \sum _{j=1}^4 \sum _{k=1}^3 (x^{2}_{1jk}, y^{2}_{1jk}, z^{2}_{1jk}, w^{2}_{1jk}) = (32,34,37,39)\\& \sum _{j=1}^4 \sum _{k=1}^3 (x^{1}_{2jk}, y^{1}_{2jk}, z^{1}_{2jk}, w^{1}_{2jk}) = (28,32,35,37),\quad \sum _{j=1}^4 \sum _{k=1}^3 (x^{2}_{2jk}, y^{2}_{2jk}, z^{2}_{2jk}, w^{2}_{2jk}) = (25,28,30,33)\\& \sum _{j=1}^4 \sum _{k=1}^3 (x^{1}_{3jk}, y^{1}_{3jk}, z^{1}_{3jk}, w^{1}_{3jk}) = (0,1,4,9), \quad \quad \quad \sum _{j=1}^4 \sum _{k=1}^3 (x^{2}_{3jk}, y^{2}_{3jk}, z^{2}_{3jk}, w^{2}_{3jk}) = (0,2,2,5)\\& \sum _{i=1}^3 \sum _{k=1}^3 (x^{1}_{i1k}, y^{1}_{i1k}, z^{1}_{i1k}, w^{1}_{i1k}) = (14,16,19,22), \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 (x^{2}_{i1k}, y^{2}_{i1k}, z^{2}_{i1k}, w^{2}_{i1k}) = (20,23,25,28)\\& \sum _{i=1}^3 \sum _{k=1}^3 (x^{1}_{i2k}, y^{1}_{i2k}, z^{1}_{i2k}, w^{1}_{i2k}) = (17,20,22,25), \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 (x^{2}_{i2k}, y^{2}_{i2k}, z^{2}_{i2k}, w^{2}_{i2k}) = (16,18,19,22)\\& \sum _{i=1}^3 \sum _{k=1}^3 (x^{1}_{i3k}, y^{1}_{i3k}, z^{1}_{i3k}, w^{1}_{i3k}) = (12,15,18,21), \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 (x^{2}_{i3k}, y^{2}_{i3k}, z^{2}_{i3k}, w^{2}_{i3k}) = (15,17,19,21)\\& \sum _{i=1}^3 \sum _{k=1}^3 (x^{1}_{i4k}, y^{1}_{i4k}, z^{1}_{i4k}, w^{1}_{i4k}) = (6,6,6,6), \quad \quad \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 (x^{2}_{i4k}, y^{2}_{i4k}, z^{2}_{i4k}, w^{2}_{i4k}) = (6,6,6,6)\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 (x^{p}_{ij1}, y^{p}_{ij1}, z^{p}_{ij1}, w^{p}_{ij1}) = (46,49,51,53), \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 (x^{p}_{ij2}, y^{p}_{ij2}, z^{p}_{ij2}, w^{p}_{ij2}) = (51,53,56,59)\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 (x^{p}_{ij3}, y^{p}_{ij3}, z^{p}_{ij3}, w^{p}_{ij3}) = (9,19,27,39)\\ \end{aligned}$$

\((x^{p}_{ijk}, y^{p}_{ijk}, z^{p}_{ijk}, w^{p}_{ijk})\) for all i, j, k, p is a non-negative trapezoidal fuzzy number.

We minimize \({\widetilde{Z}}_1\) by solving the following four problems:

Minimize \(Z^1_1 = 5x^{1}_{111} + 9x^{1}_{112} + 4x^{1}_{121}+ 6x^{1}_{122}+ 10x^{1}_{131} + 7x^{1}_{132} + 8x^{1}_{211} + 10x^{1}_{212} + 6x^{1}_{221} + 6x^{1}_{222} + 11x^{1}_{231} + 14x^{1}_{232} + 9x^{2}_{111} + 11x^{2}_{112} + 5x^{2}_{121} + 6x^{2}_{122} + 10x^{2}_{131} + 8x^{2}_{132} + 11x^{2}_{211} + 14x^{2}_{212} + 7x^{2}_{221} + 9x^{2}_{222} + 12x^{2}_{231} + 13x^{2}_{232}\)

subject to

$$\begin{aligned}& \sum _{j=1}^4 \sum _{k=1}^3 x^{1}_{1jk} = 21,\quad \sum _{j=1}^4 \sum _{k=1}^3 x^{2}_{1jk} = 32, \quad \sum _{j=1}^4 \sum _{k=1}^3 x^{1}_{2jk} = 28, \quad \sum _{j=1}^4 \sum _{k=1}^3 x^{2}_{2jk} = 25, \quad \sum _{j=1}^4 \sum _{k=1}^3 x^{1}_{3jk} = 0, \\& \sum _{j=1}^4 \sum _{k=1}^3 x^{2}_{3jk} = 0, \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{1}_{i1k} = 14, \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{2}_{i1k} = 20, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{1}_{i2k} = 17, \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{2}_{i2k} = 16,\\& \sum _{i=1}^3 \sum _{k=1}^3 x^{1}_{i3k} = 12, \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{2}_{i3k} = 15, \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{1}_{i4k} = 6, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 x^{2}_{i4k}= 6,\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 x^{p}_{ij1} = 46, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 x^{p}_{ij2}=51, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 x^{p}_{ij3}= 9, \; x^p_{ijk} \ge\! 0 \; \forall \; i,j,k,p. \end{aligned}$$

Minimize \(Z^2_1 = 8y^{1}_{111} + 11y^{1}_{112} + 6y^{1}_{121}+ 8y^{1}_{122}+ 12y^{1}_{131} + 9y^{1}_{132} + 10y^{1}_{211} + 11y^{1}_{212} + 7y^{1}_{221} + 8y^{1}_{222} + 13y^{1}_{231} + 16y^{1}_{232} + 10y^{2}_{111} + 13y^{2}_{112} + 8y^{2}_{121} + 7y^{2}_{122} + 11y^{2}_{131} + 10y^{2}_{132} + 13y^{2}_{211} + 16y^{2}_{212} + 9y^{2}_{221} + 11y^{2}_{222} + 14y^{2}_{231} + 14y^{2}_{232}\)

subject to

$$\begin{aligned}& \sum _{j=1}^4 \sum _{k=1}^3 y^{1}_{1jk} = 24,\quad \sum _{j=1}^4 \sum _{k=1}^3 y^{2}_{1jk} = 34, \quad \sum _{j=1}^4 \sum _{k=1}^3 y^{1}_{2jk} = 32, \quad \sum _{j=1}^4 \sum _{k=1}^3 y^{2}_{2jk} = 28, \quad \sum _{j=1}^4 \sum _{k=1}^3 y^{1}_{3jk} = 1, \\& \sum _{j=1}^4 \sum _{k=1}^3 y^{2}_{3jk} = 2, \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{1}_{i1k} = 16, \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{2}_{i1k} = 23, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{1}_{i2k} = 20, \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{2}_{i2k} = 18,\\& \sum _{i=1}^3 \sum _{k=1}^3 y^{1}_{i3k} = 15, \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{2}_{i3k} = 17, \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{1}_{i4k} = 6, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 y^{2}_{i4k}= 6,\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 y^{p}_{ij1} = 49, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 y^{p}_{ij2}=53, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 y^{p}_{ij3}= 19, \quad y^p_{ijk} \ge x^{*p}_{ijk} \quad \forall \,i,j,k,p. \end{aligned}$$

Minimize \(Z^3_1 = 9z^{1}_{111} + 13z^{1}_{112} + 9z^{1}_{121}+ 10z^{1}_{122}+ 14z^{1}_{131} + 12z^{1}_{132} + 13z^{1}_{211} + 13z^{1}_{212} + 8z^{1}_{221} + 10z^{1}_{222} + 15z^{1}_{231} + 18z^{1}_{232} + 12z^{2}_{111} + 14z^{2}_{112} + 10z^{2}_{121} + 9z^{2}_{122} + 12z^{2}_{131} + 11z^{2}_{132} + 14z^{2}_{211} + 18z^{2}_{212} + 12z^{2}_{221} + 13z^{2}_{222} + 16z^{2}_{231} + 15z^{2}_{232}\)

subject to

$$\begin{aligned}& \sum _{j=1}^4 \sum _{k=1}^3 z^{1}_{1jk} = 26,\quad \sum _{j=1}^4 \sum _{k=1}^3 z^{2}_{1jk} = 37, \quad \sum _{j=1}^4 \sum _{k=1}^3 z^{1}_{2jk} = 35, \quad \sum _{j=1}^4 \sum _{k=1}^3 z^{2}_{2jk} = 30, \quad \sum _{j=1}^4 \sum _{k=1}^3 z^{1}_{3jk} = 4, \\& \sum _{j=1}^4 \sum _{k=1}^3 z^{2}_{3jk} = 2, \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{1}_{i1k} = 19, \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{2}_{i1k} = 25, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{1}_{i2k} = 22, \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{2}_{i2k} = 19, \sum _{i=1}^3 \sum _{k=1}^3 z^{1}_{i3k} = 18, \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{2}_{i3k} = 19, \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{1}_{i4k} = 6, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 z^{2}_{i4k}= 6,\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 z^{p}_{ij1} = 51, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 z^{p}_{ij2}=56, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 z^{p}_{ij3}= 27, \quad z^p_{ijk} \ge y^{*p}_{ijk}\quad \forall \,i,j,k,p. \end{aligned}$$

Minimize \(Z^4_1 = 11w^{1}_{111} + 15w^{1}_{112} + 11w^{1}_{121}+ 12w^{1}_{122}+ 16w^{1}_{131} + 14w^{1}_{132} + 15w^{1}_{211} + 15w^{1}_{212} + 9w^{1}_{221} + 12w^{1}_{222} + 17w^{1}_{231} + 20w^{1}_{232} + 13w^{2}_{111} + 15w^{2}_{112} + 12w^{2}_{121} + 11w^{2}_{122} + 13w^{2}_{131} + 13w^{2}_{132} + 16w^{2}_{211} + 20w^{2}_{212} + 14w^{2}_{221} + 14w^{2}_{222} + 18w^{2}_{231} + 16w^{2}_{232}\)

subject to

$$\begin{aligned}& \sum _{j=1}^4 \sum _{k=1}^3 w^{1}_{1jk} = 28,\quad \sum _{j=1}^4 \sum _{k=1}^3 w^{2}_{1jk} = 39, \quad \sum _{j=1}^4 \sum _{k=1}^3 w^{1}_{2jk} = 37, \quad \sum _{j=1}^4 \sum _{k=1}^3 w^{2}_{2jk} = 33, \quad \sum _{j=1}^4 \sum _{k=1}^3 w^{1}_{3jk} = 9, \\& \sum _{j=1}^4 \sum _{k=1}^3 w^{2}_{3jk} = 5, \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{1}_{i1k} = 22, \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{2}_{i1k} = 28, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{1}_{i2k} = 25, \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{2}_{i2k} = 22,\\& \sum _{i=1}^3 \sum _{k=1}^3 w^{1}_{i3k} = 21, \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{2}_{i3k} = 21, \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{1}_{i4k} = 6, \quad \quad \sum _{i=1}^3 \sum _{k=1}^3 w^{2}_{i4k}= 6,\\& \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 w^{p}_{ij1} = 53, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 w^{p}_{ij2}=59, \quad \sum _{p=1}^2\sum _{i=1}^3\sum _{j=1}^4 w^{p}_{ij3}= 39, \quad w^p_{ijk} \ge z^{*p}_{ijk} \quad \forall \,i,j,k,p. \end{aligned}$$

\(x^{*p}_{ijk}, \, y^{*p}_{ijk} \) and \(z^{*p}_{ijk}\) are the optimal solutions of the previous problems. On solving these problems sequentially, the obtained values of \(x_{ijk}^{p}, y_{ijk}^p, z_{ijk}^p\), and \(w_{ijk}^{p},\) for \(p = 1, 2; i = 1, 2, 3; j= 1, 2, 3, 4 \,\hbox {and} \,k =1, 2, 3\) are \({\widetilde{x}}^1_{111} = (9,9,9,9), {\widetilde{x}}^1_{113} = (0,0,2,2), {\widetilde{x}}^1_{121} = (0,2,2,2), {\widetilde{x}}^1_{132} = (12,12,12,12), {\widetilde{x}}^1_{133} = (0,1,1,3), {\widetilde{x}}^1_{211} = (5,5,5,5),\, {\widetilde{x}}^1_{213} = (0,1,2,2), {\widetilde{x}}^1_{221} = (5,5,7,7), {\widetilde{x}}^1_{222} = (12,12,12,12), {\widetilde{x}}^1_{223} = (0,1,1,3), {\widetilde{x}}^1_{233} = (0,2,2,2), {\widetilde{x}}^1_{242} = (6,6,6,6), {\widetilde{x}}^1_{312} = (0,1,1,4), {\widetilde{x}}^1_{321} = (0,0,0,1), {\widetilde{x}}^1_{332} = (0,0,3,3), {\widetilde{x}}^1_{333} = (0,0,0,1), {\widetilde{x}}^2_{111} = (1,1,1,1), {\widetilde{x}}^2_{113} = (0,2,2,4), {\widetilde{x}}^2_{121} = (16,16,16,16), {\widetilde{x}}^2_{123} = (0,0,1,1), {\widetilde{x}}^2_{132} = (15,15,15,15), {\widetilde{x}}^2_{133} = (0,0,2,2), {\widetilde{x}}^2_{211} = (10,10,10,10), {\widetilde{x}}^2_{213} = (9,9,11,11), {\widetilde{x}}^2_{223} = (0,1,1,4),{\widetilde{x}}^2_{233} = (0,2,2,2), {\widetilde{x}}^2_{242} = (6,6,6,6),{\widetilde{x}}^2_{311} = (0,1,1,2), {\widetilde{x}}^2_{322} = (0,1,1,1), {\widetilde{x}}^2_{333} = (0,0,0,2).\) The remaining variables are zero trapezoidal fuzzy numbers and \({\widetilde{Z}}_1 = (590, 791, 961, 1131).\)

Minimizing \({\widetilde{Z}}_2\) in a similar way and then applying the fuzzy programming technique, the obtained optimal-compromise solution is \({\widetilde{x}}^1_{111} = (9,9,9,9), {\widetilde{x}}^1_{121} = (0,2,2,2), {\widetilde{x}}^1_{123} = (0,1,1,3), {\widetilde{x}}^1_{132} = (12,12,12,12), {\widetilde{x}}^1_{133} = (0,0,2,2), {\widetilde{x}}^1_{212} = (5,5,5,5), {\widetilde{x}}^1_{213} = (0,1,1,1), {\widetilde{x}}^1_{221} = (17,17,19,19), {\widetilde{x}}^1_{223} = (0,3,4,6), {\widetilde{x}}^1_{242} = (6,6,6,6), {\widetilde{x}}^1_{311} = (0,1,1,1), {\widetilde{x}}^1_{312} = (0,0,3,6), {\widetilde{x}}^1_{323} = (0,0,0,1), {\widetilde{x}}^1_{333} = (0,0,0,1), {\widetilde{x}}^2_{111} = (15,15,15,16), {\widetilde{x}}^2_{113} = (0,0,2,2), {\widetilde{x}}^2_{122} = (11,11,11,11), {\widetilde{x}}^2_{123} = (0,2,3,4), {\widetilde{x}}^2_{132} = (6,6,6,6), {\widetilde{x}}^2_{212} = (5,5,5,5), {\widetilde{x}}^2_{213} = (0,1,1,2), {\widetilde{x}}^2_{221} = (5,5,5,5), {\widetilde{x}}^2_{233} = (9,11,13,15), {\widetilde{x}}^2_{242} = (6,6,6,6), {\widetilde{x}}^2_{311} = (0,0,0,1), {\widetilde{x}}^2_{312} = (0,2,2,2), {\widetilde{x}}^2_{323} = (0,0,0,2).\) All other variables are zero trapezoidal fuzzy numbers.

The values of \({\widetilde{Z}}_1\) and \({\widetilde{Z}}_2\) are found to be (635,778,955,1100) and (428,566,724,847), respectively.

6 Interpretation of results

In this section, the results of the numerical example obtained by using the proposed method are interpreted graphically.

The graph of membership functions of the obtained optimal values of \({\widetilde{Z}}_1\) and \({\widetilde{Z}}_2\) are in figures 1 and 2.

Figure 1
figure 1

Optimal value of \({\widetilde{Z}}_1\).

Full size image
Figure 2
figure 2

Optimal value of \({\widetilde{Z}}_2\).

Full size image

From figure 1, the following information about the minimum value of the objective function \(Z_1\) can be interpreted:

  1. (i)

    635\(\le \hbox {Min} Z_1 \le 1100\).

  2. (ii)

    The chances that the minimum value of \(Z_1\) will lie in the range 778–955 units are maximum.

  3. (iii)

    The overall level of satisfaction for other values of \(Z_1\) (say y) is \(\mu _{{\widetilde{Z}}_1}(y)\times \%\), where

    $$\begin{aligned} \mu _{{\widetilde{Z}}_1}(y)= {\left\{ \begin{array}{ll} \frac{(y-635)}{143}&{} 635\le y< 778\\ 1 &{} 778\le y \le 955\\ \frac{(1100-y)}{145}&{} 955 < y \le 1100\\ 0 &{} \hbox {otherwise} \end{array}\right. } \end{aligned}$$

The obtained results of the objective function \({\widetilde{Z}}_2\) can be interpreted in a similar manner.

7 Advantages of the proposed method

  1. (i)

    In the method proposed by Kundu et al [13], the multi-objective multi-item solid transportation problem with transportation parameters as trapezoidal fuzzy numbers is first converted to the equivalent crisp problem. The obtained results are thus real numbers, while the method proposed in this paper provides the fuzzy optimal compromise solution.

  2. (ii)

    Kumar and Kaur [19] pointed out the limitations of existing methods [10, 20–23, 25] and the shortcomings of the method proposed by Liu [24] to solve the single and multi-objective solid transportation problems. To overcome these limitations and resolve the shortcomings, they have proposed a method to obtain the fuzzy optimal solution of the fuzzy solid transportation problem. They have also solved two existing fuzzy solid transportation problems by their method and showed that the problems which could be solved by the existing methods can also be solved by their method.

    However, none of the method proposed in the above cited papers can be applied to a FFMOMISTP, for which a method has been proposed in the present paper. This method is also applicable to the problems considered in Gen et al [25], [10, 20–23]. We have also solved the examples in Kumar and Kaur [19] by the method proposed by us. The results obtained are same as shown in table 6.

Table 6 Results obtained by using the existing as well as proposed method.
Full size table

8 Conclusions

In this work, the fuzzy optimal compromise solution is obtained for the multi-objective multi-item solid transportation problem, where all the parameters are represented by trapezoidal fuzzy numbers. As in the real world applications, the transportation parameters are not always precise and the fuzzy numbers handle more information than the crisp ones, the obtained results are more beneficial for the decision maker.

Since the proposed method is for the FFMOMISTP, same is also applicable to the single and multi-objective solid transportation problems as well as to the single and multi-objective solid transportation problems with fuzzy parameters.