Thermally Developing Region of a Parallel Plate Channel Partially Filled with a Porous Material with the Effect of Axial Conduction and Viscous Dissipation: Uniform Wall Heat Flux

Abstract

The present investigation has been undertaken to assess the effect of axial conduction and viscous dissipation on heat transfer characteristics in the thermally developing region of a parallel plate channel with porous insert attached to both the walls of the channel. Both the walls are kept at uniform heat flux. The fully developed flow field in the porous region corresponds to Darcy–Brinkman equation and the clear fluid region to that of plane Poiseuille flow. The effect of parameters, Brinkman number, Br, Darcy number, Da, Peclet number, Pe, and a porous fraction, γ_p have been studied. The numerical solutions have been obtained for, 0.005 ≤ Da ≤ 1.0, 0 ≤ γ_p ≤ 1.0 and −1.0 ≤ Br ≤ 1.0 and Pe = 5, 25, 50, 100 and neglecting axial conduction (designated by A_c = 0) by using the numerical scheme successive accelerated replacement (SAR). There is an unbounded swing in the local Nusselt number because of viscous dissipation.

1 Introduction

Present-day applications involving flow through porous media call for including viscous dissipation effects in the conservation of energy equation. Some of them generically are described as internal flows, say, flow through a porous material partially or fully filled, pipes, channels, and in general ducts. In general, if the effective fluid viscosity is high or temperature differences are small or kinetic energy is high that warranted inclusion of Forchheimer terms, viscous dissipation can be expected to be significant. The use of porous media in the cooling of electronic equipment has been restored interest in the problem of forced convection in a channel filled with a porous medium.

Several studies (Agrawal [1], Hennecke [2], Ramjee and Satyamurty [3], and Jagadeesh Kumar [4]) have shown that the axial conduction term becomes significant in the equation of energy at the low Peclet number in the case of forced convection in the ducts. In particular, Shah and London [5] studied the problem of heat transfer in the entrance region for a viscous incompressible fluid in both two-dimensional channel and circular cylindrical tube taking into consideration axial conduction term. Ramjee and Satyamurty [3] studied local and average heat transfer in the thermally developing region of an asymmetrically heated channel.

Hooman et al. [6] have studied thermally developing forced convection in rectangular ducts subjected to uniform wall temperature. Thermally developing forced convection in a circular duct filled with a porous medium with longitudinal conduction and viscous dissipation effects subjected to uniform wall temperature studied by Kuznetsov et al. [7]. Nield et al. [8] investigated the effects of viscous dissipation, axial conduction with the uniform temperature at the walls, on thermally developing forced convection heat transfer in a parallel plate channel fully filled with a porous medium.

In the present paper, the thermally developing region of a parallel plate channel partially filled with a porous material with the effect of axial conduction and viscous dissipation with wall boundary condition uniform heat flux has been studied. Numerical solutions for the two-dimensional energy equations in both the fluid and porous regions have been obtained using numerical scheme successive accelerated replacement (Ramjee and Satyamurty [3], Satyamurty and Bhargavi [9], and Bhargavi and Sharath Kumar Reddy [10]). The effects of important parameters on the local Nusselt number have been studied.

2 Mathematical Formulation

Governing equations and the boundary conditions are non-dimensionalizing by introducing the following non-dimensional variables.

$$\left. {\begin{array}{*{20}l} {X = x/H,Y = y/H,U_{\text{f}} = u_{\text{f}} /u_{\text{ref}} ,U_{\text{i}} = u_{\text{i}} /u_{\text{ref}} ,} \hfill \\ {U_{\text{p}} = u_{\text{p}} /u_{\text{ref}} ,P = p/\rho \, u_{\text{ref}}^{2} ,\theta_{\text{f}} = (T_{\text{f}} - T_{\text{e}} )/(qH/k_{\text{f}} ),} \hfill \\ {\theta_{\text{p}} = (T_{\text{p}} - T_{\text{e}} )/(q{\kern 1pt} H/k_{\text{f}} )} \hfill \\ \end{array} } \right\}$$

(1)

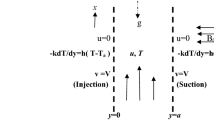
In Eq. (1), X and Y are the non-dimensional coordinates. U and P are the non-dimensional velocity and pressure. The subscripts f and p refer to fluid and porous regions. θ,{θ_f in the fluid region and θ_p in the porous region}, is the non-dimensional temperature. u_ref is the average velocity through the channel (Fig. 1).

Fig. 1

Geometry of the physical model of the problem

The non-dimensional governing equations and boundary conditions for momentum and energy equations applicable in the fluid and porous regions become [using non-dimensional variables given in Eq. (1)].

• Fluid Region:

  $$\frac{{{\text{d}}^{2} U_{\text{f}} }}{{{\text{d}}Y^{2} }} = Re \, \frac{{{\text{d}}P}}{{{\text{d}}X}}$$

  (2)
  $$U_{\text{f}} \frac{{\partial \theta_{\text{f}} }}{{\partial X^{*} }} = A_{\text{c}} \frac{1}{{Pe^{2} }}\frac{{\partial^{2} \theta_{\text{f}} }}{{\partial X^{{*{2} }} }} + \frac{{\partial^{2} \theta_{\text{f}} }}{{\partial Y^{2} }} + Br\left( {\frac{{{\text{d}}U_{\text{f}} }}{{{\text{d}}Y}}} \right)^{2}$$

  (3)

In Eq. (2), Re, the Reynolds number is defined by

$$\text{Re} = \rho u_{\text{ref}} H/\mu_{\text{f}}$$

(4)

In Eq. (3), Pe, Peclet number and Br, Brinkman number and $X^{*}$ are defined by,

$$Pe = u_{\text{ref}} H/\alpha_{\text{f}} , \, Br = \mu_{\text{f}} u_{\text{ref}}^{2} /\left( {qH} \right),\quad {\text{X}}^{*} = X/Pe$$

(5)

when Br < 0 represents the fluid is getting heated. Br > 0 represents the fluid is getting cooled.

• Porous Region:

  $$\frac{{{\text{d}}^{2} U_{p} }}{{{\text{d}}Y^{2} }} - \frac{\varepsilon }{Da}U_{\text{p}} = \varepsilon \, Re\frac{{{\text{d}}P}}{{{\text{d}}X}}$$

  (6)
  $$U_{\text{p}} \frac{{\partial \theta_{\text{p}} }}{{\partial X^{*} }} = \frac{1}{\eta }\left( {A_{\text{c}} \frac{1}{{Pe^{2} }}\frac{{\partial^{ 2} \theta_{\text{p}} }}{{\partial X^{{*^{2} }} }} + \frac{{\partial^{ 2} \theta_{\text{p}} }}{{\partial Y^{2} }}} \right) + \frac{Br}{Da}U_{\text{p}}^{2}$$

  (7)

In Eqs. (6) and (7), Da, ε, and η are defined as,

$$Da = K/H^{2} ,\quad \varepsilon = \mu_{\text{f}} /\mu_{\text{eff}} \quad {\text{and}}\quad \, \eta = k_{\text{f}} /k_{\text{eff}}$$

(8)

When $A_{\text{c}} = 1$ in Eqs. (3) and (7) means that axial conduction is included, and when $A_{\text{c}} = 0$, axial conduction is neglected. When $A_{\text{c}} = 0$, the solutions to Eqs. (3) and (7) in terms of X* do not depend on Pe.

• Non-dimensional Boundary Conditions:

  $$\frac{{{\text{d}}U_{\text{f}} }}{{{\text{d}}Y}} = 0,\quad \frac{{\partial \theta_{\text{f}} }}{\partial Y} = 0\quad {\text{at}}\;\;Y = 0$$

  (9)
  $$U_{\text{f}} = U_{\text{p}} = U_{\text{i}} ,\quad \frac{{{\text{d}}U_{\text{f}} }}{{{\text{d}}Y}} = \frac{1}{\varepsilon }\frac{{{\text{d}}U_{\text{p}} }}{{{\text{d}}Y}}\quad {\text{at}}\;\;Y = - \frac{1}{2} + \frac{{\gamma_{\text{p}} }}{2}$$

  (10)
  $$\theta_{\text{f}} = \theta_{\text{p}} = \theta_{\text{i}} ,\quad \frac{{\partial \theta_{\text{f}} }}{\partial Y} = \frac{1}{\eta }\frac{{\partial \theta_{\text{p}} }}{\partial Y}\quad {\text{at}}\;\;Y = - \frac{1}{2} + \frac{{\gamma_{\text{p}} }}{2}$$

  (11)
  $$U_{\text{p}} = 0,\quad \frac{{\partial \theta_{\text{p}} }}{\partial Y} = - \eta \quad {\text{at}}\;\;Y = - 1/2$$

  (12)

Inlet conditions

$$\theta_{\text{p}} (0,Y) = 0\quad {\text{for}}\;\; - \frac{1}{2} \le Y \le - \frac{1}{2} + \frac{{\gamma_{\text{p}} }}{2}$$

(13)

$$\theta_{\text{f}} (0,Y) = 0\quad {\text{for}}\;\; - \frac{1}{2} + \frac{{\gamma_{\text{p}} }}{2} \le Y \le 0$$

(14)

$$\begin{aligned} \frac{{\partial \theta _{{\text{b}}} }}{{\partial X^{*} }} = 0 \Rightarrow \frac{{\partial \theta _{{{\text{f}},{\text{p}}}} }}{{\partial X^{*} }} & = \frac{{\theta _{{{\text{f}},{\text{p}}}} }}{{\theta ^{*} }}\frac{{\partial \theta ^{*} }}{{\partial X^{*} }}\quad {\text{at}}\;\;X^{*} \ge X_{{{\text{fd}}}}^{*} \;{\text{for}}\; \\ & \quad - 1/2 \le Y \le 0\;\{ {\text{downstream condition}}\} \\ \end{aligned}$$

(15)

In Eq. (15), θ_b is the non-dimensional temperature based on the bulk mean temperature defined by

$$\theta_{\text{b}} = \frac{{T - T_{\text{e}} }}{{T_{\text{b}} - T_{\text{e}} }} = \frac{\theta }{{\theta^{*} }}$$

(16)

The velocity expressions in fluid and porous regions satisfying the interfacial conditions are available in Bhargavi and Sharath Kumar Reddy [10].

3 Numerical Scheme: Successive Accelerated Replacement (SAR)

Numerical solutions to non-dimensional energy Eqs. (3) and (7) along with the non-dimensional boundary conditions on θ given in Eqs. (9)–(16) have been obtained using the numerical scheme successive accelerated replacement [3, 9, 10].

3.1 Local Nusselt Number

After non-dimensionalizing (using Eq. (1)), Nu_px, the local Nusselt number at the lower plate $Y = - 1/2$, is given by

$$Nu_{\text{px}} = \frac{{h_{\text{px}} (2H)}}{{k_{\text{f}} }} = - \frac{{2\left( {\partial \theta_{\text{p}} /\partial Y} \right)|_{Y = - 1/2} }}{{\eta \left[ {\theta_{\text{w}} - \theta^{*} (X)} \right]}} = \frac{2}{{\theta_{\text{w}} - \theta^{*} (X^{*} )}}$$

(17)

4 Results and Discussion

Assumed that ε = μ_f/μ_eff = 1 and η = k_f/k_eff = 1. The channel referred to clear fluid channel when porous fraction, γ_p = 0. The channel referred to fully filled with a porous medium, when porous fraction, γ_p = 1.0. The channel referred to partially filled with a porous medium, when porous fraction, 0 ≤ γ_p ≤ 1.0.

4.1 Local Nusselt Number with the Effect of Viscous Dissipation and Without Axial Conduction

Variation of the local Nusselt number, Nu_px against X* for the Darcy number, Da = 0.005 is shown in Fig. 2a, b for Br ≤ 0 and Br ≥ 0, respectively, for porous fractions, γ_p = 0 when axial conduction is neglected ($A_{\text{c}} = 0$). Similarly, for porous fractions, γ_p = 0.2, 0.8 and 1.0 are shown in Figs. 3, 4, and 5, respectively. Clearly, Nu_px displays an unbounded swing for Br < 0 at say, $X_{\text{ee}}^{*}$ in all Figs. 2, 3, and 4. This unbounded swing $X_{\text{sw}}^{*}$ occurs for γ_p ≤ 0.8 But when Br > 0, Nu_px displays an unbounded swing $X_{\text{sw}}^{*}$ for γ_p > 0.8 see in Fig. 5. The value of $X_{\text{sw}}^{*}$ (which occurs for Br < 0) increases as γ_p increases from 0 to 0.8. The Nusselt number values, as well as the limits, differ if Da is larger. The local Nusselt number, Nu_px displays an unbounded swing for Br < 0 since the bulk mean temperature reaches wall temperature and exceeds because of viscous dissipation. Beyond $X_{\text{sw}}^{*}$, Nu_px starts decreasing to reach the limiting value.

Fig. 2

Variation of local Nusselt number against X* for a Br ≤ 0 and b Br ≥ 0 for axial conduction neglected (A_c = 0) for γ_p = 0

Fig. 3

Variation of local Nusselt number against X* for a Br ≤ 0 and b Br ≥ 0 for axial conduction neglected (A_c = 0) for γ_p = 0.2

Fig. 4

Variation of local Nusselt number against X* for a Br ≤ 0 and b Br ≥ 0 for axial conduction neglected (A_c = 0) for γ_p = 0.8

Fig. 5

Variation of local Nusselt number against X* for a Br ≤ 0 and b Br ≥ 0 for axial conduction neglected (A_c = 0) for γ_p = 1.0

4.2 Local Nusselt Number with the Effect of Viscous Dissipation and Axial Conduction

Variation of local Nusselt number, Nu_px against X* for the Darcy number, Da = 0.005 and at Brinkman numbers, (a) Br = −0.5 and (b) Br = 0.5 for different Peclet numbers, Pe = 5 and 25, respectively, are shown in Figs. 6, 7, 8, and 9 for porous fractions, γ_p = 0, 0.2, 0.8, and 1.0, respectively. In parallel plate channel partially filled with a porous medium also, Nu_px displays an unbounded swing, $X_{\text{sw}}^{*}$ for Br < 0 in all Figs. 6, 7, and 8. This unbounded swing depends on porous fractions, γ_p. At low Peclet number, the value of the $X_{\text{sw}}^{*}$ is more for all porous fractions. This unbounded swing $X_{\text{sw}}^{*}$ occurs for γ_p ≤ 0.8. But when Br > 0, Nu_px displays an unbounded swing $X_{\text{sw}}^{*}$ for γ_p > 0.8 see in Fig. 9. As Darcy number increases, there is no unbounded swing in the local Nusselt number for all porous fractions. The qualitative behavior of the present local Nusselt number values with the Jagadeesh Kumar [4] and Ramjee and Satyamurty [11] are in good agreement for the clear fluid channel (γ_p = 0).

Fig. 6

Variation of local Nusselt number against X* for different Peclet numbers, Pe for a Br = −0.5 and b Br = 0.5 for γ_p = 0

Fig. 7

Variation of local Nusselt number against X* for different Peclet numbers, Pe for a Br = −0.5 and b Br = 0.5 for γ_p = 0.2

Fig. 8

Variation of local Nusselt number against X* for different Peclet numbers, Pe for a Br = −0.5 and b Br = 0.5 for γ_p = 0.8

Fig. 9

Variation of local Nusselt number against X* for different Peclet numbers, Pe for a Br = −0.5 and b Br = 0.5 for γ_p = 1.0

5 Conclusions

Numerical solutions have been obtained for 0 ≤ γ_p ≤ 1.0, 5 ≤ Pe ≤ 100, −1.0 ≤ Br ≤ 1.0 and Da = 0.005, 0.01, and 0.1, using the SAR [3, 9, 10] numerical scheme. There is an unbounded swing in the local Nusselt number since the bulk mean temperature reaches wall temperature and exceeds because of viscous dissipation, Br < 0 for the porous fraction, γ_p ≤ 0.8. In the case of porous fraction, γ_p > 0.8, unbounded swing occurs at Br > 0. As, Darcy number increases, there is no unbounded swing in the local Nusselt number.