Series solutions and a perturbation formula for the extended Rayleigh problem of hydrodynamic stability

Abstract

We generalize Tollmien’s solutions of the Rayleigh problem of hydrodynamic stability to the case of arbitrary channel cross sections, known as the extended Rayleigh problem. We prove the existence of a neutrally stable eigensolution with wave number k _s  > 0; it is also shown that instability is possible only for 0 < k < k _s and not for k > k _s . Then we generalize the Tollmien–Lin perturbation formula for the behavior of c _i, the imaginary part of the phase velocity as the wave number k →k _s − to the extended Rayleigh problem and subsequently, we use this formula to demonstrate the instability of a particular shear flow.

1 Introduction

The stability of homogeneous and stratified shear flows of an inviscid fluid to infinitesimal normal mode disturbances has been studied extensively (see [2, 3]). These studies are restricted to rectangular cross sections. To consider flows relevant to sea straits, it is necessary to consider shear flows which are transversely uniform but are contained in straits with arbitrary cross sections. That is, the velocity and stratification are allowed to vary with the elevation z, and perhaps along with the channel direction x, but not with cross channel direction y. The stability analysis of homogeneous and stratified shear flows in sea straits of arbitrary cross section was initiated by Pratt et al [5] and a mathematical approach was adapted in Deng et al [1]. In [1], the stability equation was derived and it was found to be an extended version of the well known Taylor–Goldstein problem of hydrodynamic stability. A number of general analytical results have been obtained for this extended Taylor–Goldstein problem in [1, 4, 7].

In the special case of homogeneous shear flows, the problem reduces to the extended Rayleigh problem of hydrodynamic stability and for this problem the following results are already known:

• (i) The necessary condition for instability is that $\left(\frac{U_0^{\prime}}{b}\right)^{\prime}$ changes sign atleast once in the flow domain 0 ≤ z ≤ D, where U ₀(z) is the basic velocity profile, b(z) is the width function and a prime denotes differentiation with respect to z (cf. [1]).

• (ii) If $\left(\frac{U_{0}^{\prime}}{b}\right)^{\prime}$ equals zero at z = z _s and U _0s  = U ₀ (z _s ) then a necessary condition for insta- bility is that $\left({\frac{U_0^\prime}{b}}\right)^{\prime}\! \left({U_0 \!-\! U_{0s}}\right)\!<\!0$ atleast once in the flow domain 0 ≤ z ≤ D (cf. [1]).

• (iii) Howard’s conjecture, namely, the growth rate kc _i →0 as the wave number k → ∞ has been proved (cf. [6]).

• (iv) For a class of flows, disturbances with wave length smaller than some critical wave length are stable, that is c _i = 0 when k > k _c, where k _c is some critical value of wave number k. That is, short waves are stable (cf. [8]).

The instability of basic shear flows is demonstrated in two ways. For piecewise linear velocity profiles the stability equation is solved in each layer and then by the use of the boundary and interfacial conditions the dispersion relation between the complex wave velocity c and the wave number k is obtained. From this dispersion relation one can conclude the instability of piecewise linear profiles for a given range of k. This method has been applied to (i) the bounded vortex sheet and (ii) the bounded shear layer in Subbiah and Ramakrishnareddy [9]. For smoothly varying basic flows the instability of a particular basic flow is demonstrated by finding a neutral eigensolution and then applying the Tollmien–Lin’s perturbation formula for unstable modes adjacent to that neutral mode. Though this method has been used in many examples of basic flows in the Rayleigh problem of hydrodynamic stability (cf. [2]), this has not been done for the extended Rayleigh problem so far. So we take up this problem in this paper. First, we find sufficient conditions for the existence of neutral modes. Second, if (c _s , k _s , W _s ) is a neutral mode then we show that unstable modes adjacent to this neutral mode exists for k < k _s only. If (c, k, W) is an unstable mode such that c →c _s and W →W _s as k →k _s  − then we find an asymptotic formula for c _i, the imaginary part of c, which is the extension of the Tollmien–Lin’s perturbation formula. Then we apply this formula to a particular basic flow, namely, the flow with U ₀ = e^z sin z, T = 2 in the domain 0 ≤ z ≤ 2π.

To find the neutral solutions first we find series solutions of the extended Rayleigh problem, which are extensions of the Tollmien’s solutions of the Rayleigh problem, when the basic velocity U ₀(z) and the topography T(z) are analytic functions; that is, they can be expressed as convergent power series in (z − z _c) when z = z _c is a point such that U ₀(z _c) = c. We find that one solution of the equation is regular whereas the second linearly independent solution may have a logarithmic term. But for neutral eigensolutions the logarithmic term will disappear and both solutions are regular in that case. However, these series can not be found to converge to known special functions in many cases and so they may have to be found by numerical computation. In this case a second order equation satisfied by the regular part of the second solution is derived and it is found that the Wronskian of these two solutions is $\frac{-1}{b(z)}$ which can be used as a check on the numerical computation.

2 The extended Rayleigh problem

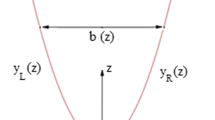
We consider the basic flow with velocity $\vec{u} =\left( {U_0 (z),0,0} \right)$ and pressure p = p ₀ (a constant). It is trivially seen that the governing equations (cf. [1]) are satisfied. Regarding the boundary conditions, we consider for example the right side wall given by y = y _R (z). Then $\check{n}=\left(0,1,\frac{-\partial y_{\rm R}}{\partial z}\right)\Big{/}{\sqrt{1 + \left({\frac{\partial y_{\rm R}}{\partial z}}\right)^2}}$ is the unit normal to the wall and it is obvious that $\vec{u} \cdot {\check{n}}=0$ on the wall. Many examples of topography have been given in Deng et al [1]. Now we shall present the sketch of the flow geometry for a flow with topography T ₀ = 2, which is the one considered in the example shown to be unstable later.

Let $y_{\rm R} (z) = \frac{{\rm e}^{2z}}{2}$ and $y_{\rm L} (z)=-\frac{{\rm e}^{2z}}{2}$ be the right and left walls respectively (see figure 1). Then b(z) = e^2z and $T_0 =\frac{b^\prime (z)}{b(z)}=2$.

Figure 1

Vertical cross section of the channel.

The extended Rayleigh problem is given by the second order ordinary differential equation

$$\label{eq1} \left[ {\frac{\left( {bW} \right)^\prime }{b}} \right]^\prime -\left[ {k^2+\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{U_0 -c}} \right]W=0, $$

(1)

with boundary conditions

$$\label{eq2} W(0)=0=W(D). $$

(2)

Here, the real part of W(z)e^{ik(x − ct)} is the vertical velocity of a normal mode disturbance, k > 0 is the wave number, c = c _r + ic _i is the complex phase velocity, U ₀(z) is the basic velocity, b(z) is the width function and $T(z)=\left[ {\ln \cdot b(z)} \right]^{'}$ is the topography.

3 Tollmien’s series solutions

The extended Rayleigh problem can also be written as

$$\label{eq3} W^{\prime\prime}+TW^{\prime} +T^{\prime} W-k^2W-\frac{U_0^{\prime\prime} -TU_0^{\prime}}{U_0 -c}W=0. $$

(3)

We consider flows for which the basic velocity U ₀(z) and the topography T(z) are analytic functions of z; that is, they can be expressed as convergent power series in (z − z _c).

Consider now the solution of the extended Rayleigh’s equation when c is not necessarily equal to c _s . A point z = z _c, where U ₀ − c = 0 and $U_{0{\rm c}}^{\prime} \ne 0$ is a regular singular point of (3) with exponents 0 and 1. Thus, in a neighbourhood of z _c there exists one solution which is analytic at z = z _c. It is convenient to write this solution in the form

$$ \label{eq4} W_1 (z)=\left( {z-z_{\rm c}}\right)P_1 (z), $$

(4)

where P ₁(z) is analytic at z _c and $P_1 (z_{\rm c})\ne 0$. For convenience, we shall choose P ₁ (z _c) = 1. The second linearly independent solution of (3), however, has a logarithmic branch point at z = z _c and it is of the form

$$ \label{eq5} W_2 =\left[ {\frac{\left( {U_0^{\prime \prime } -TU_0^\prime } \right)\left( {z_\textrm{c} } \right)}{b\left( {z_\textrm{c} } \right)U_0^\prime \left( {z_\textrm{c} } \right)}} \right]\ln (z-z_\textrm{c} )W_1 (z)+P_2 (z), $$

(5)

where P ₂(z) is also analytic at z _c with P ₂ (z _c) = 1. To make this second solution definite, it is convenient to suppose that W ₂(z) contains no multiple of W ₁(z), i.e., the coefficient of z − z _c in the power series expansion of P ₂(z) is zero. In the absence of topography i.e. when T(z) = 0, these solutions become solutions of the Rayleigh problem. The solutions of Rayleigh’s equation were first given in this form by Tollmien (cf. [3]) in connection with his discussion of the Orr–Sommerfeld equation which is the stability equation for viscous shear flows and they are often referred to as Tollmien’s inviscid solutions.

A more descriptive terminology was introduced by Drazin & Reid [3] where W ₁(z) is the regular inviscid solution, W ₂(z) the singular inviscid solution and P ₂(z) the regular part of the singular inviscid solution.

In case of neutral stability c, and hence z _c is real, it is then necessary to specify the correct branch of the multivalued solution given by (5). By letting c _i tend to zero through positive values we see that if $U_{0{\rm c}}^{\prime}>0$ and we let $\ln \left( {z-z_\textrm{c} } \right)=\ln \left| {z-z_\textrm{c} } \right|$, for z > z _c then we have $\ln \left({z-z_\textrm{c}}\right)=\ln \left| {z-z_\textrm{c} } \right|-i\pi$ for z < z _c.

In the discussion of the viscous problem the circumstances under which these solutions of Rayleigh’s equation provide approximations to the solutions of the Orr–Sommerfeld equation has been discussed in Drazin & Reid [3]. It is likely that the solutions of the extended Rayleigh problem presented above will be related to the viscous stability problem in sea straits in a similar way. The first few terms in the power series expansion of P ₁ and P ₂ are

$$ \begin{array}{rll}\label{eq6} P_1 (z) &=& 1 + \left[{\frac{U_0^{\prime\prime} (z_\textrm{c})}{2U_0^\prime (z_\textrm{c})} - T(z_\textrm{c})}\right] \left({z-z_\textrm{c}}\right)\nonumber\\[4pt] &&+\,\frac{1}{6}\left[{\frac{U_0^{\prime\prime\prime}(z_\textrm{c})}{U_0^\prime (z_\textrm{c})}+k^2-\frac{3TU_0^{\prime\prime} (z_\textrm{c})}{U_0^\prime (z_\textrm{c})}+3T^2-3T^\prime}\right]\left({z-z_\textrm{c} } \right)^2+\cdots\nonumber\\ \end{array} $$

(6)

and

$$ \begin{array}{rll} \label{eq7} P_2 (z)&=&1+\left[ \frac{U_0^{\prime \prime \prime } \left( {z_\textrm{c} } \right)}{2U_0^\prime \left( {z_\textrm{c} } \right)}+\frac{k^2}{2}-T^\prime \left( {z_\textrm{c} } \right)-\frac{TU_0^{\prime \prime } \left( {z_\textrm{c} } \right)}{2U_0^\prime \left( {z_\textrm{c} } \right)} \right. \notag\\ &&\left. -\frac{( {U_0^{\prime \prime } -TU_0^\prime} )^2\left( {z_\textrm{c} } \right)}{b\left( {z_\textrm{c} } \right)( {U_0^\prime } )^2\left( {z_\textrm{c} } \right)} \right]\left( {z-z_\textrm{c} } \right)^2+\cdots\, . \end{array} $$

(7)

For velocity profiles with a sufficiently simple analytical form, the summation of these series may be feasible. More generally, however, W ₁ and the regular singular part of W ₂ can be obtained only by direct numerical integration. When this latter method is used, W ₁ can be conveniently defined as the solution of the extended Rayleigh’s equation that satisfies the initial condition $W_1 (z_\textrm{c})=0$ and $W_1^\prime (z_\textrm{c})=1$. Similarly, P ₂ can be obtained as the solution of the inhomogeneous equation:

$$ \begin{array}{rll}\label{eq8} &&\left( {U_0 -c} \right)\big[ {P_2^{\prime \prime } +TP_2^\prime +T^\prime P_2 -k^2P_2 } \big]-( {U_0^{\prime \prime } -TU_0^\prime } )P_2\nonumber\\[6pt] &&{\kern1pc} = -\left( {U_0 -c} \right)\left[ {\frac{( {U_0^{\prime \prime } -TU_0^\prime } )\left( {z_\textrm{c} } \right)}{b\left( {z_\textrm{c} } \right)U_0^\prime \left( {z_\textrm{c} } \right)}} \right]\notag\\[6pt] &&{\kern2pc} \times\left[ {\frac{2P_1^\prime \left( {z-z_\textrm{c} } \right)+P_1 +TP_1 \left( {z-z_\textrm{c} } \right)}{\left( {z-z_\textrm{c} } \right)}} \right], \end{array} $$

(8)

that satisfies the initial condition $P_2 (z_\textrm{c})=1$. The Wronskian of the solutions W ₁ and W ₂ is ${-1}\mathord{\left/ {\vphantom {{-1} {b(z)}}} \right. \kern-\nulldelimiterspace}{b(z)}$, and this relation can provide a useful check on numerical work.

Suppose that U ₀(z) is monotone with a single point z _s where $( {U_0^{\prime\prime} -TU_0^{\prime}})=0$ in 0 < z < D. Then both solutions W ₁(z) and W ₂(z) are regular at z _s and W _s must be a linear combination of W ₁(z) and P ₂(z). Since $W_s (z_s )\ne 0$, we can write W _s (z) = AW ₁ (z) + P ₂ (z) so that W _s (z _s ) = 1 and the two boundary conditions determine the constant A and the wave number k _s of a neutral mode. Thus the two Tollmien solutions of the extended Rayleigh problem can be used to determine the neutral solution W _s .

4 Tollmien–Lin’s perturbation formula

If U ₀(z) is a monotone function with only one point where $b\left( {\frac{U_0^\prime }{b}} \right)^\prime$ changes sign then a necessary condition for instability is that $b\left( {\frac{U_0^\prime }{b}} \right)^\prime \left( {U_0 -U_{0s} } \right)\le 0$ for 0 ≤ z ≤ D with equality only at z = z _s . For the Rayleigh problem of hydrodynamic stability the standard approach for showing that a particular smooth basic flow is unstable is to find neutral eigensolutions and then use the Tollmien–Lin’s perturbation formula to show the existence of unstable eigenvalues adjacent to the neutral modes (cf. [2, 3]). Now we shall extend Tollmien–Lin’s perturbation formula to the extended Rayleigh problem. First we shall show the existence of a neutrally stable eigensolution

$$ \label{eq9} W=W_s ,\quad k=k_s >0,\quad c=c_s $$

(9)

and then, by perturbing this solution, to construct neighbouring unstable modes for k close to k _s with k < k _s .

To demonstrate the existence of a neutrally stable eigensolution with k _s  > 0, we suppose that $K(z)={-b\left( {\frac{U_0^\prime }{b}} \right)^\prime}\Big/{U_0 -U_{0s} }$ is regular at z _s , i.e., $b\left( {\frac{U_0^\prime }{b}} \right)^\prime (z_s )=0$, and let λ = − k ². If c = c _s  = U _0s , then (1) can be rewritten in the form

$$ \left[ {\frac{\left( {bW} \right)^\prime }{b}} \right]^\prime +\left[ {\lambda +K(z)} \right]W=0, $$

which, together with boundary conditions (2), is a standard Sturm–Liouville problem for which there exists an infinite sequence of eigenvalues with limit point at ∞. The least eigenvalue of this problem is given by the variational principle

$$ \label{eq10} k_s =\textrm{min}\left[ {\frac{\int {\frac{\left| {\left( {bW} \right)^\prime } \right|^2}{b}\textrm{d}z-\int {K(z)b\left| W \right|^2\textrm{d}z} } }{\int {b\left| W \right|^2\textrm{d}z} }} \right], $$

(10)

where the minimum is to be taken over functions W that satisfy the boundary conditions and have square-integrable derivatives. From the well-known Rayleigh–Ritz inequality,

$$ \label{eq11} \int {| {\left( {bW} \right)^\prime } |^2\textrm{d}z} \ge \frac{\pi^2}{D^2}\int {\left| {bW} \right|^2{\rm d}z} , $$

(11)

we see that if $K(z)\frac{b_{\min}}{b_{\max}}>\frac{\pi^2}{D^2}$ everywhere then λ _s  < 0 and hence k _s  > 0.

Multiplying (1) by bW*, integrating over [0, D] and applying (2), we get

$$ \label{eq12} \int {\left[ {\frac{| {\left( {bW} \right)^\prime } |^2}{b}+k^2b\left| W \right|^2} \right]} \,\textrm{d}z+\int {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{U_0 -c}} b\left| W \right|^2\textrm{d}z=0. $$

(12)

Now we shall prove that there is instability only for k < k _s . To show this, suppose K(z) > 0 throughout the flow and that $c_{i} \ne 0$. Then the real and imaginary parts of (12) are given by

$$ \label{eq13} \int {\left[ {\frac{| {\left( {bW} \right)^\prime } |^2}{b}+k^2b\left| W \right|^2} \right]} \,\textrm{d}z+\int {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime \left( {U_0 -c_{\rm r} } \right)}{\left| {U_0 -c} \right|^2}} b\left| W \right|^2\textrm{d}z=0 $$

(13)

and

$$ \label{eq14} c_i \int {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{\left| {U_0 -c} \right|^2}} b\left| W \right|^2\textrm{d}z=0. $$

(14)

Multiplying (14) by $\frac{\left( {U_{0s} -c_\textrm{r} } \right)}{c_\textrm{i} }$ and adding the resultant equation to (13), we get

$$ \begin{array}{rll} &\int {\left[ {\frac{| {\left( {bW} \right)^\prime } |^2}{b}+k^2b\left| W \right|^2} \right]} \,\textrm{d}z \notag\\[8pt] &{\kern1pc}-\int {\left[ {\frac{\left( {U_0 -c_\textrm{r} } \right)^2-\left( {U_{0s} -c_\textrm{r} } \right)^2}{\left| {U_0 -c} \right|^2}} \right]} K(z)b\left| W \right|^2\textrm{d}z=0; \end{array} $$

i.e.,

$$ \label{eq15} k^2\int {b\left| W \right|^2\textrm{d}z<\int {K(z)b\left| W \right|^2\textrm{d}z} } , $$

(15)

from which it immediately follows that

$$ \label{eq16} k^2<-\lambda_s =k_s^2 . $$

(16)

Hence instability is possible only when 0 < k < k _s and we have stability (c _i = 0) for k ≥ k _s .

But this argument does not show that if 0 < k < k _s then $c_{\rm i} \ne 0$, for we have not excluded the possibility of the eigensolution defined by (9) being an isolated neutral mode.

If, however, we assume the existence of unstable modes for k close to k _s with k < k _s , whose limit as c _i ↓0 is the neutrally stable eigensolution defined by (9), then they can be found by a simple perturbation procedure. For this purpose it is necessary to consider a second solution G _s (say) of (1) with k = k _s and c = U _0s  = c _s . (This solution does not of course satisfy the boundary conditions.) A standard form of this solution can be conveniently defined by

$$ \label{eq17} G_s =W_s \int\limits_{z_s }^z {\frac{\textrm{d}z}{bW_s^2 }} , $$

(17)

provided $W_s (z_s )\ne 0$ and a few of its properties may be briefly noted. The Wronskian of the two solutions is given by $W\left[ {W_s ,G_s } \right]=\frac{1}{b}$. We also have

$$ \begin{array}{rll}\label{eq18} G_s (0)&=&\frac{-1}{b\left( 0 \right)W_s^\prime (0)},\quad G_s (D)=\frac{-1}{b\left( D \right)W_s^\prime (D)}, \nonumber\\[5pt] G_s (z_s)&=&0,\;G_s^\prime (z_s )=\frac{-1}{b(z_s )W_s (z_s )}. \end{array} $$

(18)

For (k, c) near (k _s , c _s ) we now assume that W(z; k, c) can be expanded in powers of both (k − k _s ) and (c − c _s ) in the form

$$ \label{eq19} W(z)=W_s (z)+\left( {k-k_s } \right)W_1 (z)+\left( {c-c_s } \right)W_2 (z)+\cdots , $$

(19)

where W ₁ and W ₂ must satisfy the equations

$$ \label{eq20} \left( {U_0 -c_s } \right)\left[ {\left[ {\frac{\left( {bW_1 } \right)^\prime }{b}} \right]^\prime -k_s^2 W_1 } \right]-b\left( {\frac{U_0^\prime }{b}} \right)^\prime W_1 =2\left( {U_0 -c_s } \right)k_s W_s $$

(20)

and

$$ \label{eq21} \left( {U_0 -c_s } \right)\left[ {\left[ {\frac{\left( {bW_2 } \right)^\prime }{b}} \right]^\prime -k_s^2 W_2 } \right]-b\left( {\frac{U_0^\prime }{b}} \right)^\prime W_2 =\left[ {\frac{\left( {bW_s } \right)^\prime }{b}} \right]^\prime -k_s^2 W_s . $$

(21)

The solutions of these equations that vanish at z = 0 are

$$ \label{eq22} W_1 =2k_s \left[ {G_s \int\limits_0^z {bW_s^2 \textrm{d}z} -W_s \int\limits_0^z {bW_s G_s \textrm{d}z} } \right] $$

(22)

and

$$ \label{eq23} W_2 =W_s \left[ {-\int\limits_0^z {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{\left( {U_0 -c_s } \right)^2}bW_s G_s \textrm{d}z} } \right]+G_s \left[ {\int\limits_0^z {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{\left( {U_0 -c_s } \right)^2}bW_s^2 \textrm{d}z} } \right]. $$

(23)

In accordance with the requirement that c _i tend to zero through positive values, the path of integration for the first integral in (23) must lie below z _s if $U_{0s}^\prime >0$ and above z _s if $U_{0s}^\prime <0$; the integrand of the second integral, however, is regular at z _s . At z = D, W ₁ and W ₂ have the values

$$ W_1 (D)=\frac{-2k_s }{b\left( D \right)W_s^{'} (D)}\int\limits_0^D {bW_s^2 \textrm{d}z} , $$

and

$$ \label{eq24} W_2 (D)=\frac{-1}{b\left( D \right)W_s^\prime (D)}\int\limits_0^D {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{\left( {U_0 -c_s } \right)^2}bW_s^2 \textrm{d}z} , $$

(24)

and are thus independent of G _s . It may be noticed that W ₁(D) is real but W ₂(D) is complex with real and imaginary parts given by

$$ W_{2\textrm{r}} \left( D \right)=\left( {\frac{-1}{bW_s^\prime (D)}} \right){\rm P}\int\limits_0^D {\frac{b\left( {\frac{U_0^\prime }{b}} \right)^\prime }{\left( {U_0 -c_s } \right)^2}bW_s^2 \textrm{d}z} $$

and

$$ \label{eq25} W_{2\textrm{i}} \left( D \right)=\frac{-\pi }{b(D)W_s^\prime (D)}\left[ {\frac{\left( {b\left( {\frac{U_0^\prime }{b}} \right)^\prime } \right)^\prime (z_\textrm{s} )b(z_\textrm{s} )W_s^2 (z_\textrm{s} )\,\textrm{sgn}( {U_{0s}^\prime } )}{( {U_0^\prime (z_\textrm{s} )} )^2}} \right], $$

(25)

where P denotes the Cauchy principle value of the integral. With W ₁ and W ₂ determined in this manner, W in (19) automatically vanishes at z = 0; the requirement that it also vanishes at z = D shows that

$$ \label{eq26} c-c_s \sim \frac{W_1 (D)W_2^\ast (D)(k_s -k)}{\left| {W_2 (D)} \right|^2}. $$

(26)

In particular, the imaginary part of (26) is

$$ \label{eq27} c_\textrm{i} \sim \frac{-W_1 (D)W_{2\textrm{i}} (D)(k_s -k)}{\left| {W_2 (D)} \right|^2}. $$

(27)

The sign of the coefficient in this expression is determined by the sign of $\left[ {b\left( {\frac{U_0^\prime }{b}} \right)^\prime } \right]^\prime (z_\textrm{s} )\,{\rm sgn}\,U_{0s}^\prime$; alternatively if $K(z_\textrm{s} )={-\left[ {b\left( {\frac{U_0^\prime }{b}} \right)^\prime } \right]^\prime (z_\textrm{s} )} \Big/ {U_{0s}^\prime (z_\textrm{s} )}>0$ then c _i is positive for k just less than k _s .

When the width function b(z) is a constant we have T ≡ 0 and this perturbation formula reduces to the Tollmien–Lin’s perturbation formula for the Rayleigh problem of hydrodynamic stability. For the Rayleigh problem it is shown in [3] that the basic flow with velocity U ₀ = sinz, 0 ≤ z ≤ 2π is unstable by the application of this perturbation formula. For the problem with topography we modify the above flow by taking the velocity to be $U_0 =\textrm{e}^z\sin z$ and the width function $b(z)=\textrm{e}^{2z}$ in the same flow domain 0 ≤ z ≤ 2π. For this problem we have topography T = 2 and $U_0^{\prime \prime } -TU_0^\prime =-2\textrm{e}^z\sin z$. It is seen that it changes sign at z _s  = π thus satisfying the necessary condition for instability. The extended Rayleigh problem can be solved to get the neutral eigensolution c _s  = 0, $k_s ={\sqrt 3 } / 2$ and $W_s =\textrm{e}^{-z}\sin\!\left( {\frac{z}{2}} \right)$. To find c _i as k →k _s  − we have to find W ₁(z) and W ₂(z) and they are found to be $W_1 (z)=\sqrt 3 \left[ {\textrm{e}^{-z}\cos \left( {\frac{z}{2}} \right)\left[ {\sin z-z} \right]+\textrm{e}^{-z}\sin \left( {\frac{z}{2}} \right)\left[ {1-\cos z} \right]} \right]$, $W_2 (z)=-2\textrm{e}^{-z}\sin \left( {\frac{z}{2}} \right)[ {\textrm{e}^{-z}-1} ]+2\textrm{e}^{-z}\cos \left( {\frac{z}{2}} \right)\int\limits_0^z {\textrm{e}^{-z}\tan \left( {\frac{z}{2}} \right){\rm d}z}$. Substituting these in the perturbation formula (27), we get $c_\textrm{i} \sim\!\!\!-0.010548083\left( {k-\frac{\sqrt 3 }{2}} \right)$. Since c _i > 0 for $k<k_s =\frac{\sqrt 3 }{2}$, we get instability of the basic flow. So far this is the first and only example of a smoothly varying basic flow whose instability has been proved for the extended Rayleigh problem of hydrodynamic stability.

5 Concluding remarks

In this paper we have found series solutions to the extended Rayleigh equation of hydrodynamic stability. When the topography T = 0 these series solutions reduce to the Tollmien’s series solutions of the Rayleigh problem. Moreover, we have discussed the conditions under which neutral eigensolutions to the extended Rayleigh problem exist and the formula for finding unstable eigenmodes which are adjacent to these neutral modes by perturbing the neutral eigensolutions. This method is also used in demonstrating the instability of a particular basic shear flow in a channel with a particular topography, namely, the flow with velocity U ₀ = e^z sin z and the width function b(z) = e^2z in the flow domain 0 ≤ z ≤ 2π. It may be remarked here that this basic flow is an exchange flow, that is the velocity is positive in some part of the domain and is negative in some other part of the domain. As Pratt et al [5] have observed only exchange flows in the sea strait Bab al Mandab connecting the Red Sea to the Indian Ocean, the above example is likely to help in understanding of the instability of flows in sea straits.

For demonstrating the instability of smoothly varying basic flows one should first find a neutral eigensolution of the stability problem and then use the perturbation formula. For the extended Rayleigh problem we have done it only for the above example whereas for the Rayleigh problem, to which our problem reduces when T ≡ 0, many examples of unstable basic flows have been found and these examples are presented in [2]. It is hoped that the instability of many basic flows of the extended Rayleigh problem will be found in the future.