Exact solitary wave solutions for two nonlinear systems

Abstract

In this paper, we employ the powerful sine-Gordon expansion method in investigating the solitary wave solutions of the fifth-order nonlinear equation and the Date–Jimbo–Kashiwara–Miwa equation with symbolic computation. We obtain the hyperbolic, trigonometric and complex solutions and the corresponding plots of the solitary wave solutions are given out analytically and graphically.

1 Introduction

In recent years, nonlinear evolution equations (NLEEs) have attracted great interest as they play an important role in various fields such as engineering science, mathematical physics and other areas [1,2,3,4,5,6,7,8,9,10,11]. Different soliton equations consist a significant part of the NLEEs and the recent developments have shown that the scientists pay more and more attention to the exact solutions of the NLEEs [12, 13]. Many researchers have obtained the traveling wave solutions of NLEEs and presented many effective methods to find the travelling wave solutions of NLEEs. These methods include the extended direct algebraic and the extended sech-tanh methods [14], the $\left( G^{\prime }/G\right)$-expansion method [15], the inverse scattering transform method [16], the Anstatz method [17, 18], the cosine-function algorithm method [19], the tanh expand method [20], the Exp-function method [21], the first integral method [22], the simplified Hirota method and the Cole-Hopf transformation method [23], Bernoulli approach [24], the extended mapping method [25], Kudryashov method [26], the extended Jacobi elliptic function expansion method [27], and so on. Over the utmost few years, how to find more traveling wave solutions for the NLEEs has become the subject of intense investigation.

In this paper, we apply the powerful sine-Gordon expansion method (SGEM) [28] to find the complex exact travelling wave solutions of the $(1+1)$-dimensional fifth-order nonlinear integrable equation and the $(2+1)$-dimensional Date–Jimbo–Kashiwara–Miwa equation. The paper is orgnized as follows. In Sect. 2, we give a brief introduction to the powerful SGEM. The complex travelling wave solutions of the $(1+1)$-dimensional fifth-order nonlinear integrable equation and $(2+1)$-dimensional soliton equation have been obtained in Sect. 3. Finally, conclusions and discussion are given in Sects. 4 and 5 respectively.

2 Description of the sine-Gordon expansion method

In [29, 30], Baskonus and Batool proposed the sine-Gordon expansion method, which is based on a travelling wave transformation and sine-Gordon equation. Consider the following sine-Gordon equation:

$$\begin{aligned} u_{xx}-u_{tt}=m^2\sin (u), \end{aligned}$$

(1)

where $u=u(x,t)$and m is a real constant.

Applying the travelling wave transformation $u=U(\xi )$, $\xi ={\mu }(x-ct)$ to Eq. (1), we have the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} U''=\frac{m^2}{\mu ^2\left( 1-c^2\right) }\sin (U), \end{aligned}$$

(2)

where $U=U(\xi )$, $\xi$ is the amplitude of the travelling wave and c is the velocity of the travelling wave. The full simplification of Eq. (2) is given as follows:

$$\begin{aligned} \left[ \left( \frac{U'}{2}\right) \right] ^2=\frac{m^2}{\mu ^2\left( 1-c^2\right) } \sin ^2\left( \frac{U}{2}\right) +K, \end{aligned}$$

(3)

where K is an integral constant. Substituting $K=0$, $\omega (\xi )=\frac{U}{2}$ and $a^2=\frac{m^2}{\mu ^2\left( 1-c^2\right) }$ into Eq. (3), we obtain

$$\begin{aligned} \omega '=a\sin (\omega \left( {\xi }\right) ), \end{aligned}$$

(4)

putting $a=1$ into Eq. (4), we have

$$\begin{aligned} \omega '=\sin (\omega \left( {\xi }\right) ), \end{aligned}$$

(5)

then the Eq. (5) is a variables separable equation, and we obtain the following two significant equations by solving (5),

$$\begin{aligned} \sin (\omega )= \sin \left( \omega \left( \xi \right) \right) =\frac{2pe^{\xi }}{p^2e^{2\xi }+1}|_{p=1}={\mathrm{sech}}\left( \xi \right) , \end{aligned}$$

(6)

$$\begin{aligned} \cos (\omega )= \cos \left( \omega \left( \xi \right) \right) =\frac{p^2e^{2\xi }-1}{p^2e^{2\xi }+1}|_{p=1}=\tanh \left( \xi \right) , \end{aligned}$$

(7)

where p is an integral constant.

For the solution of the following nonlinear partial differential equation

$$\begin{aligned} P\left( u,u_x,u_t,u_{xx},u_{tt},u_{xt},u_{xxx},\ldots ,\right) =0, \end{aligned}$$

(8)

we consider

$$\begin{aligned} u=U\left( \xi \right) =\sum _{i=1}^{n}\tanh ^{i-1}\left( \xi \right) [B_i{\mathrm{sech}}\left( {\xi } \right) +A_i\tanh \left( {\xi }\right) ]+A_0, \end{aligned}$$

(9)

then Eq. (9) can be rewritten by using both important properties of the method like Eqs. (6) and (7) as follows:

$$\begin{aligned} U\left( \omega \left( (\xi )\right) \right) =\sum _{i=1}^{n}\cos ^{i-1}\left( \omega \left( {\xi }\right) \right) [B_i\sin \left( {\omega }\left( {\xi }\right) \right) +A_i\cos \left( {\omega }\left( {\xi }\right) \right) ]+A_0. \end{aligned}$$

(10)

We use the balance principle in determining the value of n by considering the highest power nonlinear term and the higher derivative in the obtained NODE. Letting the summation of the coefficients of $\sin ^i\left( {\omega }\left( {\xi }\right) \right) \cos ^{j}\left( {\omega }\left( {\xi }\right) \right)$$\left( i=0,1,2,\ldots ,j=0,1,2,\ldots ,\right)$ that have the same power to be all zero, one can have a system of the coefficients. After solving this system by using Maple, by substituting the values into Eq. (9), we obtain the new travelling wave solutions to Eq. (8).

3 Application of the method to two nonlinear systems

In this section, we verify the applicability of the SGEM through two nonlinear equations which have different dimension. We firstly consider the traveling wave solutions of the $(1+1)$-dimensional fifth-order nonlinear integrable equation

$$\begin{aligned} v_{ttt}-v_{txxxx}-4(v_{x}v_{t})_{xx}-4(v_{x}v_{xt})_x=0. \end{aligned}$$

(11)

In [31], Wazwaz proposed the multiple soliton solutions by using the simplified Hirota’s method established by Hereman and Nuseir [32], and the results have shown that this equation is completely integrable.

We utilize the traveling wave transformation $v=V\left( {\xi }\right)$, $\xi ={\mu }(x-kt)$, and integrating to $\xi$, taking the integral constant is zero, Eq. (11) is reduced to

$$\begin{aligned} -k^{2}V''+{\mu }^2V^{(4)}+12{\mu }V'V''=0, \end{aligned}$$

(12)

setting $U=V'$, we have

$$\begin{aligned} -k^{2}U'+{\mu }^2U'''+12{\mu }UU'=0. \end{aligned}$$

(13)

Applying the balance principle on Eq. (13) by considering the nonlinear term $UU'$ and the highest derivative $U'''$, $n+3=2n+1$, we obtain $n=2$. Taking $n=2$ in Eq. (10), we obtain

$$\begin{aligned} U\left( \omega \left( {\xi }\right) \right)= B_1\sin \left( \omega \left( {\xi }\right) \right) +A_1\cos \left( \omega \left( {\xi }\right) \right) +B_2\cos \left( \omega \left( {\xi }\right) \right) \sin \left( \omega \left( {\xi }\right) \right) +A_2\cos ^2\left( \omega \left( {\xi }\right) \right) +A_0, \end{aligned}$$

(14)

$$\begin{aligned} U'= B_1\sin \left( \omega \left( {\xi }\right) \right) \cos \left( \omega \left( {\xi }\right) \right) -A_1\sin ^2\left( \omega \left( {\xi }\right) \right) -B_2\sin ^3\left( \omega \left( {\xi }\right) \right) \nonumber \\&+B_2\sin \left( \omega \left( {\xi }\right) \right) \cos ^2\left( \omega \left( {\xi }\right) \right) -2A_2\sin ^2\left( \omega \left( {\xi }\right) \right) \cos \left( \omega \left( {\xi }\right) \right) , \end{aligned}$$

(15)

and

$$\begin{aligned} U'''&=-5B_1\sin ^3\left( \omega \left( {\xi }\right) \right) \cos \left( \omega \left( {\xi }\right) \right) +B_1\sin \left( \omega \left( {\xi }\right) \right) \cos ^3 \left( \omega \left( {\xi }\right) \right) \\&\quad -4A_1\sin ^2\left( \omega \left( {\xi }\right) \right) \cos ^2\left( \omega \left( {\xi }\right) \right) +2A_1\sin ^4\left( \omega \left( {\xi } \right) \right) -18B_2\sin ^3\left( \omega \left( {\xi }\right) \right) \cos ^2\left( \omega \left( {\xi }\right) \right) \\&\quad +5B_2\sin ^5\left( \omega \left( {\xi }\right) \right) +B_2\sin \left( \omega \left( {\xi }\right) \right) \cos ^4\left( \omega \left( {\xi }\right) \right) -8A_2\sin ^2\left( \omega \left( {\xi }\right) \right) \cos ^3\left( \omega \left( {\xi }\right) \right) \\&\quad +16A_2\sin ^4\left( \omega \left( {\xi }\right) \right) \cos \left( \omega \left( {\xi }\right) \right) . \end{aligned}$$

(16)

Substituting Eqs. (14)–(16) into Eq. (13), we obtain the summation of the coefficients of $\sin ^i\left( {\omega }\right) \cos ^{j}\left( {\omega }\right)$ with the same power. With the identity $\cos ^2\left( \omega \right) =1-\sin ^2\left( \omega \right)$, the Eq. (13) becomes

$$\begin{aligned}&\left( 12{\mu }A_1B_1+12{\mu }A_0B_2-k^2B_2+12{\mu }A_2B_2+{\mu }^2B_2\right) \sin \left( \omega \right) \\&\quad +\left( -24{\mu }A_1B_1-24{\mu }A_0B_2+2k^2B_2-60{\mu }A_2B_2-20{\mu }^2B_2\right) \sin ^3\left( \omega \right) \\&\quad +\left( -36{\mu }A_1B_2-36{\mu }A_2B_1-6{\mu }^2B_1\right) \sin ^3\left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( 12{\mu }A_1B_2+12{\mu }A_2B_1+{\mu }^2B_1+12{\mu }A_0B_1-k^2B_1\right) \sin \left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( -36{\mu }A_1A_2+24{\mu }B_1B_2-4{\mu }^2A_1-12{\mu }A_0A_1+k^2A_1\right) \sin ^2 \left( \omega \right) \\&\quad +\left( 36{\mu }A_1A_2-36{\mu }B_1B_2+6{\mu }^2A_1\right) \sin ^4\left( \omega \right) +\left( 48{\mu }A_2B_2+24{\mu }^2B_2\right) \sin ^5\left( \omega \right) \\&\quad +\left( -24{\mu }A_0A_2+2k^2A_2-12{\mu }A_1^2+12{\mu }B_1^2+12{\mu }B_2^2-24{\mu }A_2^2 -8{\mu }^2A_2\right) \sin ^2\left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( -24{\mu }B_2^2+24{\mu }^2A_2+24{\mu }A_2^2\right) \sin ^4\left( \omega \right) \cos \left( \omega \right) =0. \end{aligned}$$

We require the coefficients of $\sin ^i\left( {\omega }\right) \cos ^{j}\left( {\omega }\right)$ to be zero and solve the system of algebraic equations with symbolic computation and substitute the obtained results into Eq. (9) with $n=2$. We have four cases as follows:

Case 1:

$$\begin{aligned} A_0=\frac{8{\mu }^2+k^2}{12{\mu }},\quad A_1=0,\quad A_2=-{\mu },\quad B_1=0,\quad B_2=0, \end{aligned}$$

where ${\mu },k$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} v(x,t)=-\frac{1}{3}{\mu }^2(x-kt)+\frac{k^2}{12}(x-kt)+{\mu }\tanh \left[ {\mu }(x-kt)\right] . \end{aligned}$$

(17)

Case 2:

$$\begin{aligned} A_0=\frac{5{\mu }^2+k^2}{12{\mu }},\quad A_1=0,\quad A_2=-\frac{1}{2}{\mu },\quad B_1=0,\quad B_2 =\frac{1}{2}i{\mu }, \end{aligned}$$

where ${\mu },k$ are arbitrary constants, $i=\sqrt{-1}$, and the corresponding solution is

$$\begin{aligned} v(x,t)=-\frac{1}{12}{\mu }^2(x-kt)+\frac{k^2}{12}(x-kt)+\frac{1}{2}{\mu }\tanh \left[ {\mu } (x-kt)\right] -\frac{1}{2}i{\mu }{\mathrm{sech}}\left[ {\mu }(x-kt)\right] . \end{aligned}$$

(18)

Case 3:

$$\begin{aligned} A_0=\frac{5{\mu }^2+k^2}{12{\mu }},\quad A_1=0,\quad A_2=-\frac{1}{2}{\mu }, \quad B_1=0,\quad B_2=-\frac{1}{2}i{\mu }, \end{aligned}$$

where ${\mu },k$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} v(x,t)=-\frac{1}{12}{\mu }^2(x-kt)+\frac{k^2}{12}(x-kt)+\frac{1}{2}{\mu }\tanh \left[ {\mu } (x-kt)\right] +\frac{1}{2}i{\mu }{\mathrm{sech}}\left[ {\mu }(x-kt)\right] . \end{aligned}$$

(19)

Case 4:

$$\begin{aligned} A_1=0,\quad A_2=0,\quad B_1=0,\quad B_2=0, \end{aligned}$$

where ${A_0,\mu },k$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} v(x,t)=A_0{\mu }(x-kt). \end{aligned}$$

(20)

Obviously, Case 4 is the trivial solution of the $(1+1)$-dimensional fifth-order nonlinear equation.

We understand the sine-Gordon expansion method is very convenient for solving the $(1+1)$-dimensional fifth-order nonlinear integrable equation, and we consider the $(2+1)$-dimensional Date–Jimbo–Kashiwara–Miwa equation

$$\begin{aligned} v_{xxxxy}+4v_{xxy}v_x+2v_{xxx}v_y+6v_{xy}v_{xx}+v_{yyy}-2v_{xxt}=0. \end{aligned}$$

(21)

In [33], Yuan et al. proposed Wronskian and Grammian solutions with the help of the Hirota method and auxiliary variables, and they also obtained the bilinear Bäcklund transformation and one-soliton solution.

Using the traveling wave transformation $v=V\left( \xi \right)$, $\xi =\mu (x+ay-kt)$ and integrating to $\xi$ with the zero integral constant, Eq. (21) is reduced to

$$\begin{aligned} a{\mu }^2V^{(4)}+6a{\mu }V'V''+\left( a^3+2k\right) V''=0. \end{aligned}$$

(22)

Setting $U=V'$, we have

$$\begin{aligned} a{\mu }^2U'''+6a{\mu }UU'+\left( a^3+2k\right) U'=0. \end{aligned}$$

(23)

Applying the balance principle on Eq. (23) by considering the nonlinear term $UU'$ and the highest derivative $U'''$, $n+3=n+n+1$, we obtain $n=2$. We also obtain the $U, U', U'''$ as the Eqs. (14)–(16) by using Eq. (10) together with $n=2$.

Substituting Eqs. (14)–(16) into Eq. (23), we obtain the algebraic system of the coefficients by equating the sum of the coefficients which have the similar terms about trigonometric function. With the identity $\cos ^2\left( \omega \right) =1-\sin ^2\left( \omega \right)$, we have

$$\begin{aligned}&\left( -6a{\mu }^2B_1-18a{\mu }B_1A_2-18a{\mu }A_1B_2\right) \sin ^3\left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( a{\mu }^2B_1+6a{\mu }A_1B_2+6a{\mu }A_2B_1+6a{\mu }A_0B_1+a^3B_1+2kB_1\right) \sin \left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( -4a{\mu }^2A_1+12a{\mu }B_1B_2-18a{\mu }A_1A_2-6a{\mu }A_0A_1-a^3A_1-2kA_1\right) \sin ^2\left( \omega \right) \\&\quad +\left( 6a{\mu }^2A_1-18a{\mu }B_1B_2+18a{\mu }A_1A_2\right) \sin ^4\left( \omega \right) \\&\quad +\left( -20a{\mu }^2B_2-30a{\mu }A_2B_2-12a{\mu }A_1B_1-12a{\mu }A_0B_2-2a^3B_2-4kB_2 \right) \sin ^3\left( \omega \right) \\&\quad +\left( -8a{\mu }^2A_2-12a{\mu }A_2^2+6a{\mu }B_2^2-12a{\mu }A_0A_2-2a^3A_2-4kA_2 +6a{\mu }B_1^2\right. \\&\quad \left. -6a{\mu }A_1^2\right) \sin ^2\left( \omega \right) \cos \left( \omega \right) +\left( 24a{\mu }^2A_2+12a{\mu }A_2^2-12a{\mu }B_2^2\right) \sin ^4\left( \omega \right) \cos \left( \omega \right) \\&\quad +\left( 24a{\mu }^2B_2+24a{\mu } A_2B_2\right) \sin ^5\left( \omega \right) +\left( a{\mu }^2B_2+6a{\mu }A_2B_2+6a{\mu }A_1B_1+6a{\mu } A_0B_2\right. \\&\left. \quad +a^3B_2+2kB_2\right) \sin \left( \omega \right) =0. \end{aligned}$$

In order to obtain the new solution v(x, y, t) to Eq. (21), we solve the system of algebraic equations with symbolic computation and substitute the results of the coefficients into Eq. (9) along with $n=2$. We have four cases as follows:

Case 1:

$$\begin{aligned} A_1=0,\quad A_2=-2{\mu },\quad B_1=0,\quad B_2=0,\quad k=4a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}, \end{aligned}$$

where ${A_0,a,\mu }$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} (x,y,t)&=-2{\mu }^2\left[ x+ay-\left( 4a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t\right] \\&\quad +2{\mu }\tanh \left[ {\mu }\left( x+ay-\left( 4a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t\right) \right] \\&\quad +A_0{\mu }\left[ x+ay-\left( 4a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t\right] . \end{aligned}$$

(24)

Fig. 1

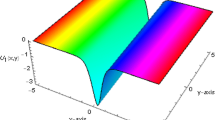
The plot of Eq. (24) with $\mu =0.5,a=1,A_0=2,t=0.002$

Fig. 2

The plot of Eq. (24) with $\mu =0.5,a=1,A_0=2,t=0.002,y=0.001$

Case 2:

$$\begin{aligned} A_1=0,\quad A_2=-{\mu },\quad B_1=0,\quad B_2=i{\mu }, \quad k=\frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}, \end{aligned}$$

where ${A_0,a,\mu }$ are arbitrary constants, $i=\sqrt{-1}$, and the corresponding solution is

$$\begin{aligned} v(x,y,t)&=-{\mu }^2\left[ x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2} \right) t\right] \\&\quad +{\mu }\tanh \left[ {\mu }\left( x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t \right) \right] \\&\quad -i{\mu }{\mathrm{sech}} \left[ {\mu }\left( x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t \right) \right] \\&\quad +A_0{\mu }\left[ x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2} \right) t\right] . \end{aligned}$$

(25)

Fig. 3

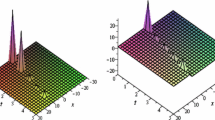
The 3D graph of the Eq. (25) with ${\mu }=1.4,a=2,A_0=2.8,t=0.007,-\,15<x<15,-\,1<y<1$

Fig. 4

The 2D graph of the Eq. (25) with ${\mu }=1.4,a=2,A_0=2.8,t=0.007,y=0.001,-\,15<x<15$

Case 3:

$$\begin{aligned} A_1=0,\quad A_2=-{\mu },\quad B_1=0,\quad B_2=-i{\mu },\quad k=\frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}, \end{aligned}$$

where ${A_0,a,\mu }$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} v(x,y,t)&=-{\mu }^2\left[ x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2} \right) t\right] \\&\quad + {\mu }\tanh \left[ {\mu }\left( x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t \right) \right] \\&\quad + i{\mu }{\mathrm{sech}}\left[ {\mu }\left( x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2}\right) t \right) \right] \\&\quad + A_0{\mu }\left[ x+ay-\left( \frac{5}{2}a{\mu }^2-3a{\mu }A_0-\frac{a^3}{2} \right) t\right] . \end{aligned}$$

(26)

Case 4:

$$\begin{aligned} A_1=0,\quad A_2=0,\quad B_1=0,\quad B_2=0, \end{aligned}$$

where ${A_0,a,\mu ,k}$ are arbitrary constants, and the corresponding solution is

$$\begin{aligned} v(x,y,t)=A_0{\mu }(x+ay-kt). \end{aligned}$$

(27)

Obviously, Case 4 is the trivial solution of the $(2+1)$-dimensional Date–Jimbo–Kashiwara–Miwa equation. The graphs of Eqs. (24) and (25) with the parametric values are shown in Figs. 1, 2, 3 and 4.

4 Results and discussion

In Sect. 3, we obtain four sets of solutions for the two integrable equations respectively. We can easily learn the structures of these solutions are similar by comparing their solutions of the two equations. The trivial solutions are the most similar solutions which have the same transformation $v=A_0{\xi }$, the form of $\xi$ depends on the dimensions of the given equation. In Eqs. (17) and (24), the solutions are the same with those structures. By analyzing Eqs. (18), (19) and (25), (26), we obtain the complex solution that the real part containing the $\tanh$ function and the imaginary part containing the ${\mathrm{sech}}$ function.

Secondly, we know a, $\mu$ are known variables in these solutions of the Date–Jimbo–Kashiwara–Miwa equation, k is expressed by $\mu$ and a. Of course, we also can use $\mu$ and k express a (or use a and k express $\mu$). Taking the Date–Jimbo–Kashiwara–Miwa equation as an example, we can obtain the solution by using the Maple

$$\begin{aligned} A_1=0,\quad A_2=-2{\mu },\quad B_1=0,\quad B_2=0, \end{aligned}$$

where $A_0,{\mu },k$ are arbitrary constants, and the constant a satisfies the equation

$$\begin{aligned} a^3+\left( -5{\mu }^2+6{\mu }A_0\right) a+2k=0. \end{aligned}$$

We select the real root as

$$a=\frac{1}{3}\left( -27k+3\sqrt{-1536{\mu }^6+3456{\mu }^5A_0-2592{\mu }^4A_0^2+648{\mu } ^3A_0^3+81k^2}\right) ^\frac{1}{3}-\frac{3\left( -\frac{8}{3}{\mu }^2+2{\mu }A_0\right) }{\left( -27k+3\sqrt{-1536{\mu }^6 +3456{\mu }^5A_0-2592{\mu }^4A_0^2+648{\mu }^3A_0^3+81k^2}\right) ^\frac{1}{3}},$$

which gives the following solution

$$\begin{aligned} v(x,y,t)&=-\,2{\mu }^2\left( x+ay-kt\right) +2{\mu }\tanh \left[ {\mu }\left( x+ay-kt \right) \right] \\&\quad +A_0{\mu }\left( x+ay-kt\right) . \end{aligned}$$

(28)

Comparing with Eq. (24), we know that different unknown variables corresponding to different solutions, and these solutions have the similar structures. But many structures of solutions are very complicated, they are very inconvenient to be used in real fields. Therefore, several simple, convenient and practical solutions are given for two integable equations in this paper. Furthermore, the powerful sine-Gordon expansion method can be used for other nonlinear systems to obtain much more exact solutions.

5 Conclusions

In this paper, we take use of the sine-Gordon expansion method to obtain four sets of exact solutions of the $(1+1)$-dimensional fifth-order nonlinear integrable equation and the $(2+1)$-dimensional Date–Jimbo–Kashiwara–Miwa equation with the help of Maple. These travelling wave solutions are given both analytically and graphically. We find the sine-Gordon expansion method is a simple, powerful and original mathematical technique to find the exact solutions of the nonlinear system, and it can be extended to solve other nonlinear evolution equations, especially higher dimension nonlinear evolution equations and the coupled nonlinear partial differential equations.