Effect of viscous dissipation and Joule heating on MHD radiative tangent hyperbolic nanofluid with convective and slip conditions

Abstract

The forthright intention of this communication is to scrutinize the effect of variable thermal conductivity and thermal radiation on the magnetohydrodynamic tangent hyperbolic fluid in the presence of nanoparticles past a stretching sheet. For heat and mass transport phenomena, the collective stimulus of slip and convective conditions with the internal heating, viscous dissipation and Joule heating have been taken into account. The boundary layer equations of two-dimensional tangent hyperbolic nanofluid have been established with the help of boundary layer approximations. With the assistance of appropriate similarity transformation, the governing set of PDEs are rendered into the coupled nonlinear ODEs. The solution of the resulting ODEs is obtained with the help of the shooting technique. Furthermore, an authentication of the computed results is obtained through benchmark with the previously reported cases. The influence of various pertinent parameters on the velocity, temperature and concentration profiles has been analyzed graphically and discussed. The physical behavior of the velocity, temperature concentration, skin friction coefficient, the Nusselt and the Sherwood numbers have been investigated diagrammatically for various pertinent parameters. It is observed that the velocity profile is declined for the growing values of the Weissenberg number and the power law index, whereas the thermal and concentration fields are observed to enhanced for the same parameters. Our analysis depicts that the temperature and the concentration profiles are enhanced for the slip parameter and the Eckert number.

1 Introduction

In recent years, the requirement of the heat transfer in efficient and small-sized electronic devices is continuously increasing. The process of cooling is one of the hard challenges faced in the industries related to automotive and electronic devices. The usual base fluids like water, ethylene glycol and mineral oils do not sufficiently meet the requirement of conducting the thermophysical properties. However, nanofluids which are the mixture of some nanometer-sized particles and the base fluids have the ability to conduct heat more effectively. Choi [1] experimentally verified that by adding the nanoparticles in the base fluid, the required thermal properties can be achieved. The nanofluids have extraordinary characteristics to improve the thermophysical properties. Due to an extensive variety of utilizations in all areas of research, these fluids have received a substantial appreciation. The effect of magnetic field-dependent viscosity (MFD) on the free convection MHD nanofluid was analyzed by Sheikholeslami et at. [2] with the concluding report that the Nusselt number increased for the growing values of the Rayleigh number. Zaimi et at. [3] used the Buongiorno’s model and studied the unsteady flow of a nanofluid past a permeable shrinking cylinder and reported that the increment in the suction parameter enhances the skin friction coefficient and the rate of heat transfer. Othman et at. [4] studied the stagnation point flow of nanofluid past a vertically stretching/shrinking sheet by considering the mixed convection. The main finding of that analysis was that the solution domain increased for the increasing values of the mixed convection parameter. Soid et at. [5] scrutinized the continuously moving needle in a nanofluid and examined that the dual solutions exist only when both the free stream and the needle move in the opposite directions. One of the recent relevant explorations may include study by Fakour et al. [6] regarding the nanofluid thin film flow past an unsteady stretching sheet. It was concluded that among different types of nanofluids, and water–alumina nanofluid has a better rate of heat transfer. By considering the activation energy and nonlinear thermal radiation, Sajid et al. [7] reported that an acclivity in the Biot number results in an enhancement in the velocity as well as the concentration profile in the Darcy–Forchheimer flow of Maxwell nanofluid. Atif et al. [8] ascertained that the stratified MHD micropolar nanofluid past a stretching sheet in the presence of the gyrotactic microorganisms and reported that the concentration profile is diminished for the enhancement in the mass stratification parameter. For further studies see articles [9,10,11].

In engineering and industrial applications, non-Newtonian fluids being ubiquitous and have been inspected extensively. Generally, these fluids have intricate constitutive relationships. These fluids have nonlinear relation between stress and strain in rheology and between heat current and temperature gradient in thermodynamics. In particular, the shear effects are significant in heat transfer of the non-Newtonian fluids. Due to flow diversity, a single mathematical model cannot incorporate all the rheological fluid properties. A few of the recent explorations may include study by Kumar et al. [12] analyzed the boundary layer flow and melting heat transfer of Prandtl fluid over a stretching surface by considering Joule heating effect and reported that the rate of heat transfer is decreased by increasing melting parameter. Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition were determined by Ishak et al. [13] and reported that gradually boosting values of the suction parameter increases the surface shear stress and as a consequence the heat transfer rate at the surface is increased. Gireesha et al. [14] scrutinized the chemical reaction effect on flow and mass transfer of Prandtl liquid over a Riga plate in the presence of solutal slip effect and observed that the solutal boundary layer thickness decreases for larger values of chemical reaction parameter and Schmidt number. Stability of MHD boundary layer flow over a Stretching/Shrinking wedge was analyzed by Awaludin et al. [15] and reported that the existence of the solution depends on the shrinking strength and the angle of the wedge, in case of shrinking parameter. Effect of thermal radiation and variable thermal conductivity on magnetohydrodynamics squeezed flow of Carreau fluid over a sensor surface was studied by Atif et al. [16] and reported that the skin friction coefficient is declined as the squeezed flow parameter is enhanced.

Tangent hyperbolic fluid is one of the non-Newtonian fluids which is capable of describing the shear thinning phenomenon. Lava, ketchup, whipped cream, blood and paints are examples of tangent hyperbolic fluid. This rheological model has certain advantages over the other non-Newtonian fluids formulations, including simplicity, ease of computation and physical robustness. Furthermore, it is deduced from kinetic theory of liquids rather than the empirical relation. From laboratory experiments, it is found that this model predicts shear thinning phenomenon very precisely. Additionally, this model describes the blood flow very accurately. By considering Biot number effects, Gaffar et al. [17] investigated the numerical solution of the heat transfer of tangent hyperbolic fluid from a sphere and reported that the fluid motion, the temperature, the skin friction coefficient and the Nusselt number is upsurged for growing values of the Biot number. With partial slip and free convection effects, Prasad et al. [18] explored the tangent hyperbolic fluid past a vertical porous sheet and reported that the slip velocity is enhanced but the Nusselt number is declined as the slip parameter is enhanced. Kumar et al. [19] studied the melting heat transfer of hyperbolic tangent fluid over a stretching sheet with fluid particles suspension and thermal radiation. They concluded that the momentum boundary layer thickness was enhanced for the growing values of the melting parameter. By using the second-order slip and convective conditions, Ibrahim [20] scrutinized the magnetohydrodynamic tangent hyperbolic fluid with nanoparticles past a stretching sheet and found that the surface drag coefficient is reduced as the value of the Weissenberg number is enhanced. By considering a permeable cylinder, Nagendramma et al. [21] deliberated the double stratified MHD tangent hyperbolic nanofluid flow and reported that the concentration field is appreciated for enhancing values of the Weissenberg number but depreciated as the Lewis number is increased. The thermal radiation phenomenon is one of the important heat transfer factors, to which the researchers have paid a serious attention. In this phenomenon, the energy spreads from a vivid surface to the absorption point in the whole region [22,23,24,25,26,27].

The non-Newtonian MHD fluids have fundamental and practical significant applications. The properties of such types of fluids play a vital role in the industrial biological and engineering applications. Few of the examples are micro-MHD pumps, micro-mixing of physiological samples, drug delivery biological transportation and petroleum production, etc [28]. MHD viscous flow past a stretching sheet was solved by the modified homotopy perturbation method by Fathizadeh et al. [29]. Das et al. [30] scrutinized the mixed convection MHD flow past an inclined plane in the presence of Joule heating and viscous dissipation and found that the velocity and the thermal fields are enhanced as the thermal buoyancy force is increased. Numerical study of MHD Casson fluid with slip boundary and Joule heating was analyzed by Kamran et al. [31] with the main finding that an increment in the Reynolds number enhances the entropy of the system. Vijayalaxmi et al. [32] observed the stagnation point flow of MHD Eyring–Powell nanofluid with convective conditions past an exponential stretching sheet. Effect of Joule heating and viscous dissipation on MHD flow and melting heat transfer over a stretching sheet was observed by Kumar et al. [33] with main finding that the fluid and the dust phase temperature was enhanced as the Eckert number is enhanced. Entropy analysis of MHD squeezing flow of nanofluid with Cattaneo–Christov model was analyzed by Naveed et al. [34]. A key observation was that an increment in the magnetic number results an increment in the temperature and the entropy of the system.

The main purpose of the present article is to study the influence of the viscous dissipation, thermal radiation and variable thermal conductivity on the magnetohydrodynamic tangent hyperbolic nanofluid past a stretching sheet. The governing equations are solved via the shooting technique. The demeanor of all the assorted physical parameters on velocity, temperature and concentration is displayed graphically and discussed.

2 Physical model and mathematical formulation

2.1 Tangent hyperbolic constitutive model

A single mathematical model cannot incorporate all the rheological fluid properties. A variety of fluid models addressing different fluid features is available in the literature. The tangent hyperbolic fluid is four-constant fluid model which has an ability of describing shear thinning effects. The apparent viscosity gradually varies between zero shear rate and infinite shear rate. The constitutive equation representing the tangent hyperbolic fluid is given by

$$\begin{aligned}&{\mathbf {\tau }}=\left[ \mu _{\infty }+\left( \mu _{0}+\mu _{\infty }\right) \tanh ({\Gamma }{\dot{\Omega }})^n\right] {\dot{\Omega }}, \end{aligned}$$

where $\Gamma$, n, ${\mathbf {\tau }}$ represents the time constant, the power law index and the extra stress tensor, respectively. $\mu _{0}$ and $\mu _{\infty }$ represents the zero shear rate viscosity and infinite shear rate viscosity. The shear rate ${\dot{\Omega }}$ is given by

$$\begin{aligned}&{\dot{\Omega }}=\sqrt{\frac{1}{2}\sum _{i}\sum _{j} {\dot{\Omega }}_{ij}{\dot{\Omega }}_{ji}}=\sqrt{\frac{1}{2}\prod }. \end{aligned}$$

Here $\prod$ is the second invariant of the strain rate tensor and is given by

$$\begin{aligned}&\prod = \frac{1}{2}\,\text {tr}\left[ (\text {grad}\;{{\mathbf {V}}})+(\text {grad}\;{\mathbf {V}})^{T}\right] ^2. \end{aligned}$$

Due to the assumption $\mu _{\infty } = 0$ and the fact, we are focusing on the shear thinning behavior of the fluid therefore for $\Gamma {{\dot{\Omega }}}<1$ the extra stress tensor $\tau$ reduces to,

$$\begin{aligned}&{\mathbf {\tau }}\,=\,\mu _{0}\left[ (\gamma {\dot{\Omega }})^n\right] {\dot{\Omega }}\,=\,\mu _{0}\left[ (1+\gamma {\dot{\Omega }}-1)^n\right] {\dot{\Omega }} =\mu _{0}\left[ 1+n(\gamma {\dot{\Omega }}-1)\right] {\dot{\Omega }} \end{aligned}$$

2.2 Problem formulation

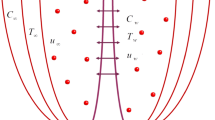
An incompressible, two-dimensional, electrically conducting tangent hyperbolic nanofluid flow past a stretching sheet with slip and convective boundary conditions has been considered for the analysis. The Cartesian coordinate system is taken in such a way that the horizontal axis is chosen in the direction of the stretching sheet with stretching velocity $u=ax$ and vertical axis is normal to the stretching surface. The flow is restricted in the region $y>0$. The surface is heated with convective temperature $T_{f}$ with $h_{f}$ as the heat transfer coefficient. The ambient temperature, concentration at the surface and ambient concentration are denoted by $T_{\infty }$, $C_{\mathrm{w}}$ and $C_{\infty }$, respectively. A uniform magnetic field of strength $B_{0}$ is applied in the positive y-axis direction. A magnetic Reynolds number is assumed to be very small such that the induced magnetic field is neglected. The physical layout of the modeled problem is illustrated in Fig. 1. Additionally, no nanoparticles flux condition and thermophoresis effect is implemented in the boundary condition. The Joule heating and viscous dissipation effects have also been incorporated.

Fig. 1

Flow configuration

Being within the above constraints, governing equations of the tangent hyperbolic nanofluid flow are formulated under the boundary layer approximation

2.2.1 Continuity equation

$$\begin{aligned} \begin{aligned} \frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}=0,\\ \end{aligned} \end{aligned}$$

(1)

2.2.2 Momentum equation

$$\begin{aligned} \begin{aligned} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \left[ (1-n)+\sqrt{2}n\Gamma \left( \frac{\partial u}{\partial y}\right) \right] \frac{\partial ^{2}u}{\partial y^{2}}-\frac{\sigma B^{2}_{0}}{\rho }u,\\ \end{aligned} \end{aligned}$$

(2)

2.2.3 Energy equation

$$\begin{aligned} \begin{aligned} u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}&= \frac{\partial }{\partial y}\left( \alpha (T)\frac{\partial T}{\partial y}\right) +\frac{\nu }{C_{p}}(1-n)\left( \frac{\partial u}{\partial y}\right) ^{2}+\frac{\nu n \Gamma }{\sqrt{2} C_{p}}\frac{\partial u}{\partial y}\left( \frac{\partial u }{\partial y}\right) ^2\\&\quad -\frac{1}{\rho C_{p}}\frac{\partial q_{\mathrm{r}}}{\partial y}+\frac{\sigma B_{0}^2}{\rho C_{p}}u^2+\Lambda \left[ D_{\mathrm{B}} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_{\mathrm{T}}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\right) ^{2}\right] , \end{aligned} \end{aligned}$$

(3)

2.2.4 Concentration equation

$$\begin{aligned} \begin{aligned} u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_{\mathrm{B}}\frac{\partial ^{2}C}{\partial y^{2}}+\frac{D_{\mathrm{T}}}{T_{\infty }}\frac{\partial ^{2}T}{\partial y^{2}}. \end{aligned} \end{aligned}$$

(4)

2.2.5 Boundary conditions

The boundary conditions are as follows

$$\begin{aligned} \left. \begin{aligned}&u=ax+L\frac{\partial u}{\partial y},\;v=0,\;-\,k \frac{\partial T}{\partial y}=h_{f}(T_{f}-T),\; D_{\mathrm{B}}\frac{\partial C}{\partial y}+ \frac{D_{\mathrm{T}}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\right) =0 \; \text {at} \; y=0,\\&\quad u\rightarrow U_{\infty }= 0, \,\,v=0,\,\, T\rightarrow T_{\infty },\,\, C \rightarrow C_{\infty } \quad \text {as} \quad y\rightarrow \infty . \end{aligned}\right\} \end{aligned}$$

(5)

In above equations, $\sigma$ represents the electrical conductivity, n the power law index, $\rho _{\mathrm{f}}$ the density of nanofluid, $\Lambda$ the ratio of the specific heat capacity of nanoparticles to the specific heat capacity of fluid, $\rho _{p}$ the density of the nanoparticles, $(C_{p})_{\mathrm{f}}$ the specific heat of fluid, L the slip parameter, $(C_{p})_{\mathrm{p}}$ the specific heat of nanoparticles and $\alpha (T)$ the temperature-dependent thermal conductivity of the tangent hyperbolic nanofluid, expressed as

$$\begin{aligned}&\alpha (T)=k_{\infty }\left( 1+\epsilon \frac{T-T_{\infty }}{\Delta T}\right) . \end{aligned}$$

Furthermore, in (3), $q_{\mathrm{r}}$ is the Rosseland radiative heat flux and is defined as [22,23,24,25,26,27]

$$\begin{aligned}&q_{\mathrm{r}}=-\frac{4\sigma ^*}{3\kappa ^*}\frac{\partial T^4}{\partial y}. \end{aligned}$$

where $\kappa ^*$ is the mean absorption coefficient and $\sigma ^*$ is the Stefan–Boltzmann constant. Using Taylor series [35] and neglecting the higher power terms, $T^{4}$ can be written as

$$\begin{aligned}&T^{4}\approx 4T^{3}_{\infty }T-3T^{4}_\infty . \end{aligned}$$

In order to make the modeled equations dimensionless, the following transformations [20] have been introduced.

$$\begin{aligned} \begin{aligned} \eta =y\sqrt{\frac{a}{\nu }},\;\;\psi =x\sqrt{a\nu }f(\eta ),\;\;\theta (\eta ) = \frac{T-T_{\infty }}{T_{f}-T_{\infty }},\;\;\phi (\eta ) = \frac{C-C_{\infty }}{C_{\mathrm{w}}-C_{\infty }}. \end{aligned} \end{aligned}$$

(6)

As a result, (1) is satisfied identically and Eqs. (2)–(4) yield the following equations:

$$\begin{aligned} \begin{aligned} \left( 1-n+nWef^{\prime \prime }\right) f^{\prime \prime \prime }+ff^{\prime \prime }-f^{\prime ^2}-Mf^{\prime }=0,\\ \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned} \begin{aligned}&\left( 1+\epsilon \theta +\frac{4}{3}Rd\right) \theta ^{\prime \prime }+Prf\theta ^{\prime }+\epsilon \theta ^{\prime ^2}+(1-n)PrEcf^{\prime \prime ^2}+\frac{nPrEcWe}{2}f^{\prime \prime ^3}\\&\quad +\, MPrEcf^{\prime ^2}+ PrNb\theta ^{\prime }\phi ^{\prime }+PrNt\theta ^{\prime ^2}=0, \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} \begin{aligned} \quad \phi ^{\prime \prime }+PrLef\phi ^{\prime }+\frac{Nt}{Nb}\theta ^{\prime \prime }=0. \end{aligned} \end{aligned}$$

(9)

The transformed boundary conditions are

$$\begin{aligned} \left. \begin{aligned} \left. \begin{aligned}&f(\eta )= 0,\quad f^{\prime }(\eta )= 1+\delta f^{\prime \prime },\\&\theta ^{\prime }(\eta )= Bi(\theta (\eta )-1),\quad Nb\phi ^{\prime }(\eta )+Nt\theta ^{\prime }(\eta )=0, \end{aligned}\right\} \quad \text {at} \quad \eta =0,\\ f^\prime (\eta )\rightarrow 0,\,\quad \theta (\eta )\rightarrow 0,\,\quad \phi (\eta )\rightarrow 0\quad \text {as} \quad \eta \rightarrow {\infty }. \end{aligned}\right\} \end{aligned}$$

(10)

In above equations, Pr denotes the Prandtl number, Nb the Brownian motion parameter, We the Weissenberg number, Le the Lewis number, Bi the Biot number, M the magnetic number, Ec the Eckert number, Nt the thermophoresis parameter, Rd the thermal radiation parameter, $Re_{x}$ the Reynolds number and $\delta$ the velocity slip parameter. These parameters are formulated as $Pr=\frac{\nu }{\alpha }$,    $Nb = \frac{\Lambda D_{\mathrm{B}}(C_{\mathrm{w}}-C_{\infty })}{\nu }$ ,    $We =\frac{\sqrt{2}a^\frac{3}{2}x\Gamma }{\sqrt{v}}$,    $Le= \frac{\alpha }{D_{\mathrm{B}}}$,   $Bi =\frac{h}{k}\sqrt{\frac{\nu }{a}}$,   $M= \frac{\sigma B^2_{0}}{a\rho }$, $Ec= \frac{a^{2}x^{2}}{(C_{p})_{\mathrm{f}}(T_{f}-T_{\infty })}$,    $Nt= \frac{\Lambda D_{\mathrm{T}}(T_{f}-T_{\infty })}{\nu T_{\infty }}$,   $Rd = \frac{4\sigma ^{*}T^3_{\infty }}{k_{\infty }\kappa ^{*}}$,    $Re_{x}=\frac{ax^{2}}{\nu }$,    $\delta =A\sqrt{\frac{a}{\nu }}$, where A is a constant.

3 Physical quantities of interest

The physical quantities of foremost interest are the local skin friction coefficient, the local Nusselt number and the local Sherwood number.

3.1 The skin friction coefficient

The skin friction coefficient is an imperative boundary layer feature and is given by

$$\begin{aligned}&C_{\mathrm{f}}=\frac{\tau _{w}}{\rho _{\mathrm{f}}u^2_{w}}, \end{aligned}$$

for the present study the wall shear stress $\tau _{w}$ is given by

$$\begin{aligned}&\tau _{w}=\mu \left[ \left( 1-n\right) \frac{\partial u}{\partial y}+\frac{n\Gamma }{\sqrt{2}}\left( \frac{\partial u}{\partial y}\right) ^2\right] _{y =_{0}}. \end{aligned}$$

In the dimensionless form, the skin friction coefficient is given by

$$\begin{aligned}&C_{\mathrm{f}}\sqrt{Re_{x}}=\left( 1-n\right) f^{\prime \prime }(0)+\frac{n}{2}We\left( f^{\prime \prime }(0)\right) ^2. \end{aligned}$$

(11)

3.2 The local Nusselt number

The Nusselt number is given by

$$\begin{aligned}&Nu=\frac{xq_{w}}{k(T_{f}-T_{\infty })}, \end{aligned}$$

for the present problem the local heat flux $q_{w}$ at the surface is given by

$$\begin{aligned}&q_{w}=-k\left[ \left( 1+\frac{16\sigma ^*T_{\infty }}{3k\kappa ^*}\right) \frac{\partial T}{\partial y}\right] _{y =_{0}}. \end{aligned}$$

In the dimensionless form, the local Nusselt number is given by

$$\begin{aligned}&Nu_{x}{Re^{-1/2}_{x}}=-\left( {1+\frac{4}{3}Rd}\right) \theta ^{\prime }(0). \end{aligned}$$

(12)

3.3 The local Sherwood number

The Sherwood number is given by

$$\begin{aligned}&Sh=\frac{xj_{w}}{D_{\mathrm{B}}(C_{\mathrm{w}}-C_{\infty })}, \end{aligned}$$

for the present study the local mass flux $j_{w}$ is given by

$$\begin{aligned}&j_{w} = -D_{\mathrm{B}}\left( \frac{\partial C}{\partial y}\right) _{y = {0}}. \end{aligned}$$

In the dimensionless form, the Sherwood number is given by

$$\begin{aligned}&Sh_{x}{Re^{-1/2}_{x}} = -\phi ^{\prime }(0), \end{aligned}$$

(13)

where $Re_{x}=\frac{ax^{2}}{\nu }$.

4 Implementation of the method

In the present article, the shooting method [35] is employed to solve the formulated ODEs  (7)–(9), subject to the boundary conditions (10).

Introducing the new variables, $y_{1}=f$, $y_{2}=f^{\prime }$, $y_{3}=f^{\prime \prime }$, $y_{4}=\theta$, $y_{5}=\theta ^{\prime }$, $y_{6}=\phi$, and $y_{7}=\phi ^{\prime }$. Equations. (7)–(9) are converted into the following system of seven first-order ODEs:

$$\begin{aligned} \left. \begin{aligned}&y_{1}^{\prime } = y_{2},\\&y_{2}^{\prime } = y_{3},\\&y_{3}^{\prime } =\frac{1}{1-n+nWey_{3}}\left[ y_{2}^2-y_{1}y_{3}+My_{2}\right] ,\\&y_{4}^{\prime } = y_{5},\\&y_{5}^{\prime } = -\frac{3}{3+3\epsilon y_{4}+4Rd} \left[ Pry_{1}y_{5}+\epsilon y_{5}^2+(1-n)PrEc y_{3}^2+\frac{n}{2}PrEcWey_{3}^3 \right. \\&\qquad \left. +PrMEcy_{2}^2+PrNb y_{5}y_{7}+PrNty_{5}^2 \right] ,\\&y_{6}^{\prime } = y_{7},\\&y_{7}^{\prime }=-PrLey_{1}y_{7}-\left( \frac{Nt}{Nb}\right) y^{\prime }_{5},\\ \end{aligned}\,\,\,\right\} \end{aligned}$$

(14)

with boundary conditions:

$$\begin{aligned} \left. \begin{aligned} \left. \begin{aligned} y_{1}(\eta )=0,\quad y_{2}(\eta )=1+\delta y_{3}(\eta ),\\ y_{5}(\eta )=Bi(y_{4}(\eta )-1),\quad \,y_{7}(\eta )=-\frac{Nt}{Nb}y_{5}(\eta )\\ \end{aligned}\right\} \,\,\text {at}\,\,\eta =0,\\ y_{2}(\infty )\rightarrow 0,\quad y_{4}(\infty )\rightarrow 0,\quad y_{6}(\infty )\rightarrow 0,\,\,\text {as}\,\,\,\eta \rightarrow \infty \end{aligned}\right\} \end{aligned}$$

(15)

To solve the above system of seven first-order ordinary differential equations (14) with the assistance of the shooting method, seven initial conditions are required. Therefore, we guess the three unknown conditions as $y_{3}(0)=s$, $y_{4}(0)=p$, and $y_{6}(0)=q$ . The suitable guesses for s, p, and q are chosen, such that the three known boundary conditions are approximately satisfied for $\eta \rightarrow \infty$. The Newton’s iterative scheme is applied to improve the accuracy of the initial guesses s, p and q until the desired approximation is met. All the computations in the rest of this article, $\lambda$ has been chosen as $10^{-6}$. The computations for different values of the emerging physical parameters have been performed over the appropriate bounded domain $\eta _{\mathrm{max}}$ instead of $[0,\infty )$. It is observed that for increasing values of $\eta _{\mathrm{max}}$, there is no significant change observed in the results. The stopping criteria for the iterative process are

$$\begin{aligned}&\text {max}{\{|y_{2}(\eta _{\mathrm{max}})-0|, |y_{4}(\eta _{\mathrm{max}})-0|, |y_{6}(\eta _{\mathrm{max}})-0|}\} < \lambda , \end{aligned}$$

where $\lambda$ is a very small positive real number.

4.1 Validation of numerical scheme

For reliability and validation of the code, we reproduce the values of the skin friction coefficient reported by Ibrahim [20] and Fathizadeh et al. [29]. Our computations have an excellent agreement with the results, which can be seen in Table 1.

Table 1 Comparison of the presently computed values of the skin friction coefficient

5 Results and discussion

5.1 The skin friction coefficient

Table 2 is presented to analyze the influence of the pertinent parameters on the skin friction coefficient $C_{\mathrm{f}}Re_{x}^{1/2}$. It is noticed that the escalating values of the magnetic number M enhance the skin friction coefficient, whereas an enhancement in the power law index n, the Weissenberg number We and the slip parameter reduces the surface drag coefficient. Figure 2a, b is prepared to present the effect of (a) slip parameter $\gamma$ and (b) the power law index n on the skin friction coefficient via magnetic number M. It is concluded that the skin friction coefficient is enhanced when magnetic number M is increased, whereas it diminished for the growing values of the slip parameter $\gamma$ and the power law index n as shown in Fig. 2a, b.

Fig. 2

Skin friction coefficient against M for different values of a $\gamma$ and b n

Table 2 Variation in the skin friction coefficient due to different values $M , We, n\,\text {and}\, \delta$ when $Bi=2, Ec=0.2, Le=5,Pr=2,Nb=0.5,Nt=0.5,Rd=0.8,\epsilon =0.1$

5.2 The heat transfer rate

Table 3 is presented to investigate the effect of assorted parameters on the heat transfer rate or the Nusselt number $Nu_{x}Re^{-\frac{1}{2}}_{x}$. It is noticed that an acclivity in each of the thermophoresis parameter Nt, the power law index n, the Weissenberg number We, small parameter $\epsilon$ and the Biot number Bi, the rate of heat transfer is reduced, whereas an increment in the Nusselt number is observed for the growing values of the thermal radiation parameter Rd and the Biot number Bi. Figure 3a, b is prepared to present the effect of (a) the Prandtl number Pr and (b) the Eckert number Ec on the Nusselt number via the magnetic number M. It is evident from Fig. 3a that the heat transfer rate is declined for the higher values of the magnetic number M. However, it is enhanced for the increasing values of the Prandtl number Pr but deprecated as the Eckert number Ec is increased. Figure 4a, b is prepared to present the effect of (a) the power law index n and (b) the Biot number Bi on the Nusselt number via the thermophoresis parameter Nt. It is evident from the figures that the heat transfer rate is declined for the growing values of the thermophoresis parameter Nt and the power law index n but increases for the larger values of the Biot number Bi.

Fig. 3

The Nusselt number against M for different values of a Pr and b Ec

Fig. 4

The Nusselt number against Nt for different values of a n and b Bi

Table 3 Variation in the Nusselt number due to different values of $Nt, n, We,Bi, Rd\,\text {and}\, \epsilon$ when $M= 0.2, Ec=0.2, Le=5,Pr=2,Nb=0.5,\delta =1$

5.3 The mass transfer rate

Table 4 is prepared to analyze the Sherwood number $Sh_{x}Re^{-\frac{1}{2}}_{x}$ for the various emerging parameters. It is observed that the local Sherwood number is enhanced for each of the gradually boosting values of the Biot number Bi and the thermophoresis parameter Nt while it is found to decrease as the values of the power law index n, the Weissenberg number We, the Brownian motion parameter Nb and the Lewis number Le. Figure 5a depicts that the Sherwood number is increased for the larger values of the Lewis number Le and the magnetic number M. Figure 5b is prepared to present the effect of the power law index n on the Sherwood number via the Lewis number Le. From this figure, it is clear that the rate of mass transfer is enhanced as the Lewis number Le and the power law index n is increased.

Fig. 5

The Sherwood number against Le for different values of a M and b n

Table 4 Variation in the Sherwood number due to different values of $n, We, Nt, Nb, Le, \text {and}\, Bi$ when $M= 0.2, Ec=0.2, \epsilon =0.1, Pr=2, Rd=0.8, \delta =1$

In order to execute the numerical simulations, the non-dimensional parameters are assigned fixed value as $Pr= 2, Rd=0.8,M= Ec=n= 0.2, Bi=2,\epsilon = 0.1, Nt= Nb= 0.5, Le= 5, We =\delta =\,1$. For the whole study, these values remain constant except the varying parameter which is presented in the respective figure.

5.4 Weissenberg number We

Fig. 6

Influence of We on a velocity, b temperature and c concentration profile

A qualitative analysis on the velocity, thermal and concentration field with the Weissenberg number We are delineated in Fig. 6a–c. Figure 6a represents the variation in the dimensionless velocity $f^\prime (\eta )$ due to the Weissenberg number We. The curves of this graph show that the velocity field is reduced as the value of the Weissenberg number We is gradually mounted. Physically, Weissenberg number is the ratio of relaxation time to the processing time. Larger value of We means an increase in relaxation time due to which the fluid motion is decreased, whereas the temperature and concentration field is enhanced as sketched in Fig. 6b, c.

5.5 Magnetic number M

Figure 7a–c portrays the impact of the magnetic number M on the velocity, temperature and concentration profile. An increment in the magnetic number means an increase in the Lorentz force which is opposing force, due to this reason the velocity and momentum boundary layer thickness is depreciated as presented in Fig. 7a. Due to an increment in the magnitude of the opposing force also leads the temperature field to enhance as shown in Fig. 7b. It also verifies the general behavior of the magnetic effect. The energy field rises because the drag force is hiked up with the gradually mounting values of the magnetic number, as a result the resistance increases. Figure 7c represents the impact of M on the concentration field. From these curves, it is evident that escalating values of M results an enhancement in the concentration profile.

Fig. 7

Influence of M on a velocity, b temperature and c concentration profile

5.6 Power law index n

Figure 8a–c is sketched to display the variations in the velocity, temperature and concentration fields due to the power law index n. Figure 8a is presented to analyze the effect of the power law index n on velocity profile. The dimensionless velocity is declined for the escalating values of the power law index n. Figure 8b, c presents the variations in the temperature and the concentration fields due to n. An enhancement in the power law index n means an increment in the viscosity of the fluid. Due to this reason, the velocity of the fluid is declined, whereas the temperature and the concentration fields are enhanced.

Fig. 8

Influence of n on a velocity, b temperature and c concentration profile

5.7 Slip parameter $\delta$

To visualize the behavior of the velocity, temperature and concentration profile due to variation in the slip parameter, Fig. 9a–c is presented. Figure 9a is presented to analyze the impact of the slip parameter $\delta$ on fluid motion. The velocity field is declined for the growing values of $\delta$. Figure 9b, c is prepared to study the influence of $\delta$ on temperature and concentration field. Both the thermal and the concentration profiles are escalated for gradually mounting values of $\delta$.

Fig. 9

Influence of $\delta$ on a velocity, b temperature and c concentration profile

5.8 Biot number Bi

The impact of Biot number Bi on temperature and concentration profile is sketched in Fig. 10a, b. The dimensionless temperature and the concentration fields both are enhanced for the growing values of Bi. Biot number represents the ratio between heat transfer resistance inside the body to the resistance at the surface of the body. Furthermore, if the Biot number is greater than 0.1 then heat convection through surface is quicker than heat conduction and the temperature gradients are significant. Increment in the Biot number means a reduction in the conductivity of the fluid due to which the temperature and the concentration profile is enhanced.

Fig. 10

Influence of Bi on a temperature and b concentration profile

5.9 Prandtl number Pr

To analyze the influence of Pr on the temperature and the concentration field, Fig. 11a, b is sketched. Figure 11a reflects the influence of the Prandtl number Pr on the thermal profile. The curves of this figure indicate that an enhancement in Pr causes a decrement in the energy profile. It is due to the reason that the thermal conductivity declines with the enhancement in Pr, due to this reason the thermal and the concentration profiles are declined. This phenomenon is evident from Fig. 11b.

Fig. 11

Influence of Pr on a temperature and b concentration profile

5.10 Small parameter $\epsilon$

To illustrate the impact of the small parameter $\epsilon$ which is associated with the variable thermal conductivity, on the temperature and the concentration, Fig. 12a, b is drawn. Figure 12a shows that an acclivity in the small parameter $\epsilon$ causes an increment in the temperature, whereas the concentration profile is declined near the surface and is enhanced away from the surface. This phenomenon is evident from Fig. 12b.

Fig. 12

Influence of $\epsilon$ on a temperature and b concentration profile

5.11 Thermal radiation parameter Rd

Figure 13a, b is prepared to establish the influence of Rd on the temperature and the concentration field. The dimensionless temperature is upsurged as the thermal radiation parameter Rd is hiked as shown in Fig. 13a. Physically, it strengthens the fact that more heat is produced due to the radiation process for which the radiation parameter is increased. Figure 13b displays the effect of Rd on concentration profile. Graphs of this figure show that the concentration profile is reduced near the surface but enhanced while moving away from the surface.

Fig. 13

Influence of Rd on a temperature and b concentration profile

5.12 Eckert number Ec

The Eckert number Ec represents the viscous dissipation effect. It is a number that represents the relation between the kinetic energy and the enthalpy. Figure 14a is drawn to visualize the impact of Ec on energy profile. It is observed that an increment in Ec causes an acclivity in the thermal profile. Physically, the thermal conductivity of the fluid improves as the dissipation is increased which helps to enhance the thermal boundary layer thickness. Figure 14b divulges the concentration distributions for the boosting values of Ec. The concentration field appears to be an increasing function of Ec. It is worth mentioning that both the Eckert number and the Weissenberg number are the functions of x; therefore, there results are locally similar.

Fig. 14

Influence of Ec on a temperature and b concentration profile

5.13 Thermophoresis parameter Nt

In the boundary layer region thermophoresis parameter Nt plays a vital role in the energy and the concentration profile. These effects are captured in Fig. 15a, b. From these figures, it is clear that for gradually increasing values of Nt both temperature and concentration profile is increased. Physically, in themophoresis the particles apply a force on the other particles due to which these particles move from the hotter region to the colder region. Therefore, an increment in the values of the thermophoresis parameter Nt means more application of the force on the other particles and as a result more fluid moves from the hotter region to the colder region. As a result, an increment in the temperature and the nanoparticles concentration is noticed.

Fig. 15

Influence of Nt on a temperature and b concentration profile

6 Final remarks

In the present article, features of the velocity, temperature and concentration profiles affected by various pertinent parameters are investigated in detail. The features findings of the investigation are enumerated below:

• The velocity distribution decreases for the large value of the velocity slip parameter $\delta$ and the power law index n.

• An increment in the temperature field is observed for the growing values of each of the velocity slip parameter $\delta$, the small parameter $\epsilon$ associated with thermal conductivity, the Eckert number Ec and the Biot number Bi.

• A increment in the concentration field is noticed for gradually mounting values of each of the power law index n, the velocity slip parameter $\delta$, the Eckert number Ec, the Biot number Bi.