1 Introduction

The dark sector of the Universe intrigues the scholars and the most recent observations [1,2,3,4,5,6,7,8,9,10] demonstrate that the dark sector contribution is roughly 95% in comparison to substratum, and the rest is radiation and 4–5% baryonic matter. The baryonic matter comprises electromagnetic radiation and can be seen directly [11]. The dark matter, which is around 25% of the matter content of the Universe, is a pressureless matter, which gives the velocity of galaxy clusters [12]. It was inferred that there was more mass in galaxies than observed by the corroboration of cold dark matter (CDM) with the rotation curves of spiral galaxies [13]. The presence of this exotic matter is affirmed by the galaxy clusters and gravitational lensing on the basis of X-ray emission. In the context of structure formation, CDM seems to play a very important role, potentialising the growth of baryonic structures after decoupling, until they reach the nonlinear regimes that is currently observed (\(\delta _{\mathrm {b}} > 1\)).

The dark energy (DE) [14, 15] is responsible for the current accelerated stage of the Universe. Under the cosmological standard description, the cosmological constant \(\Lambda \) can be used for the DE component, which is having a geometric nature in accordance with the general theory of relativity (GR). Such identification is analogous to a fluid model with a vacuum equation of state (EoS) (\(\omega = -1\)) and constant energy density [16, 17]. The description of DE is in tune with recent observational data, but it opposes the theoretical prediction for vacuum energy, which has been observed by quantum field theory [18]. This material description has a GR, the inflationary paradigm and the Big Bang nucleosynthesis (BBN), \(\Lambda \)CDM model. Instead of the vacuum description, it is also common to consider a dynamical description for the DE component through a different EoS, for example, a constant EoS parameter (\(\omega \ne - 1\)) or some time-dependent EoS parameter [19, 20]. Other proposed DE components are from the dynamical approach through a scalar field [21, 22] and modified theories of gravity [23,24,25,26].

Dynamical DE models have been constructed under general relativity and quantum gravity which help in solving the problem of cosmic expansion. Li [27] gave the holographic DE (HDE) under the umbrella of quantum mechanics and gravity, which in turn solves the problem related to quantum properties of black holes, helping the scholars to explore string theory or quantum gravity [28]. The HDE model for the expansion of the Universe [27, 29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46], taking the holographic principle [28, 47, 48] by defining the holographic energy density as \(\rho _{\mathrm {D}}= 3c^{2}M^{2}_{\mathrm {pl}}L^{-2}\), depends on the entropy–area relation of black holes [29], where c is a numerical constant.

A new development in terms of the HDE model \(S_{\delta }= \gamma A^{\delta }\), with \(\delta \) being the non-additivity parameter, \(\gamma \) an unknown constant, has been incorporated (known as Tsallis HDE (THDE)) [49], taking Tsallis generalised entropy [50], with the infrared (IR) cut-off as a Hubble horizon, in connection with the thermodynamic examinations [51, 52]. The Bekenstein entropy is obtained by taking the limit of \(\delta = 1\) and \(\gamma = 1/4G\) (where \(h = k_{\mathrm {B}} = c = 1\) in units). In this the power-law distribution of probability is useless [50]. The quantum gravity also affirms this relation [53], and opens a plethora of opportunities in terms of results in the holographic and cosmological scenario [54,55,56,57]. This forms the holographic principle as the base, which states that the degrees of freedom of a physical system should be in tune with the bounding area, not with its volume [28, 47] and to be constrained by an infrared cut-off. Cohen et al [29] formulated an accord among the system entropy (S) and the IR (L) and UV (\(\Lambda \)) cut-offs as \(L^{3} \Lambda ^{3}\le S^{{3}/{4}}\), which after combining with \(S_{\delta }= \gamma A^{\delta }\) leads to [29] \(\Lambda ^{4} \le (\gamma (4\pi )^{\delta })L^{2\delta -4}\), where \(\Lambda ^{4}\) is the vacuum energy density and \(\rho _{\mathrm {D}}\) is the energy density in the HDE formalism. By the application of this inequality, we can say the THDE as \(\rho _{\mathrm {T}} = CL^{2\delta -4}\), where C is the unknown parameter [37, 44, 51]. The above given expression gives the standard HDE, where \(C= 3c^{2}M_{p}^{2}\) and \(c^{2}\) is a dimensionless quantity. Let us consider a flat Friedmann–Robertson–Walker (FRW) Universe taking the IR cutoff as the Hubble horizon, which is a suitable candidate. In this manner \(L = H^{-1}\). Consider L as the future horizon as used in HDE, and a consistent formulation of THDE is given in [58]. The interacting and non-interacting cases have been investigated from the perspective of the dynamics of FRW [59]. THDE and its effects with Hubble horizon as IR cut-off have been checked under Brans–Dicke gravity theory and in brane cosmology [60, 61]. Tsallis agegraphic dark energy (ADE) (TADE) models have been proposed by using the age of the Universe and the conformal time as the IR cut-offs and their effects on the evolution of the Universe are studied [62]. Thermal stability of THDE in the non-flat Universe has been investigated by Zadeh et al [63]. Sharif and Saba [64] established a reconstruction scenario for THDE model in the background of f(G, T) gravity with the Hubble horizon as well as the generalised Tsallis entropy conjecture using the power-law solution of the scale factor.

The Bianchi-type models are the best and simplest anisotropic models, which completely describe the anisotropic effects. Even though Bianchi-type Universes are anisotropic, there is a cosmological view that the Universe may have been anisotropic in the early period and that over the span of its development, these characteristics may have been damped out because of a few procedures or mechanisms, bringing about a homogeneous and isotropic Universe. Many researchers have investigated different aspects of these spatially homogeneous and anisotropic Bianchi-type models in various modified theories of gravitation [65,66,67,68,69,70,71,72,73,74,75,76]. Zadeh et al [77] studied the cosmic evolution of THDE in Bianchi type-I model filled by DE and dark matter (DM) interacting with each other throughout a sign-changeable interaction with various IR cut-offs.

Motivated by the above discussion, in this paper we have investigated THDE in Bianchi-I Universe considering the IR cut-off as Hubble horizon with hybrid expansion law (HEL). The paper follows the following sequence: The field equations for Bianchi-I Universe are given in §2. In §3, we investigate the cosmological parameters, focussing on THDE EoS parameter, energy density and energy density parameter. In §4, we have plotted the statefinder evolution trajectory. In §5, the k-essence scalar field potential has been reconstructed. In §6, we conclude our results.

2 Metric and basic field equations

The metric for axially symmetric Bianchi-I space–time is described as

$$\begin{aligned} \mathrm{d}s^{2} = \mathrm{d}t^{2}- A^{2} \mathrm{d}x^{2}-B^{2} \mathrm{d}y^{2}-B^{2} \mathrm{d}z^{2}, \end{aligned}$$
(1)

with A and B, the metric coefficients, as functions of time. Here the geometric and physical parameters are taken as: average scale factor (a), the mean generalised Hubble’s parameter (H) and volume scale factor (V) and are defined as: \(a = (AB^{2})^{{1}/{3}}, H = ({1}/{3})(H_{x} + 2H_{y}), V = a^{3} = {AB}^{2}\), respectively. \( H_{x} = {\dot{A}}/{A}\) and \( H_{y} = {\dot{B}}/{B}\) are the parameters (Hubble) in the x and y directions, respectively, and the dot signifies the derivative with respect to cosmic time t. Other physical parameters, expansion scalar (\(\theta \)), average anisotropy parameter (\(A_{m}\)) and shear scalar (\(\sigma ^{2}\)), are defined as

$$\begin{aligned}&\theta = u^{i}_{;i} = \left( \frac{\dot{A}}{A} + 2 \frac{\dot{B}}{B}\right) ,\\&\sigma ^{2} = \frac{1}{2} \sigma _{ij}\sigma ^{ij} = \frac{1}{2}\left[ \frac{\dot{A}^{2}}{A^{2}} + 2 \frac{\dot{B}^{2}}{B^{2}}\right] - \frac{\theta ^{2}}{6},\\&A_{m}= \frac{1}{3}\sum _{i = 1}^{3}{\left( \frac{\triangle H_{i}}{H}\right) ^{2}}, \end{aligned}$$

where \(\triangle H_{i} = H_{i} - H \;(i = x, y, z)\).

The Einstein’s field equations in general relativity can be determined as

$$\begin{aligned} R_{ij} - \frac{1}{2} g_{ij}R =-(T_{ij} + {\bar{T}}_{ij}), \end{aligned}$$
(2)

where \(R_{ij}\) and R represent the Ricci tensor and curvature scalar, respectively. For physical interpretation, the matter energy momentum tensor and THDE can be given as \( T_{ij} = \rho _{\mathrm{m}} u_{i} u_{j}, \bar{T}_{ij} = (\rho _{\mathrm {T}} + p_{\mathrm {T}}) u_{i} u_{j} + g_{ij} p_{\mathrm {T}}\), where \(\rho _{\mathrm {T}}\) and \(\rho _{\mathrm{m}}\) illustrate the THDE density and energy density of matter and \(p_{\mathrm {T}}\) is the THDE pressure. So, the field equations for the discussed metric can be written as

$$\begin{aligned}&2\frac{\ddot{B}}{{B}} +\left( \frac{\dot{B}}{{B}}\right) ^{\!\!2} = - p_{\mathrm {T}}, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\ddot{A}}{{A}} +\frac{\ddot{B}}{B} + \frac{\dot{A} \dot{B}}{{A} {B}} = - p_{\mathrm {T}}, \end{aligned}$$
(4)
$$\begin{aligned}&\left( \frac{\dot{B}}{{B}}\right) ^{\!\!2} + 2\frac{\dot{A} \dot{B}}{{A} {B}} = \rho _{\mathrm{m}} + \rho _{\mathrm {T}}. \end{aligned}$$
(5)

Under the holographic principle, vacuum energy density (\(\Lambda ^{4}\)), also described in the introduction, thus represents the THDE density which reads [37, 44] as

$$\begin{aligned} \rho _{\mathrm {T}} = {CL}^{2\delta -4}, \end{aligned}$$
(6)

where C is an unknown parameter. The above expression gives the standard HDE, where \(C= 3c^{2}M_{p}^{2}\) and \(c^{2}\) is a dimensionless constant quantity. We mention here that the standard HDE is obtained as the subcases \(\delta =1\) and \(\delta =2\) give the standard cosmological constant. In the formulation of HDE model, one needs to identify the largest L of the theory [78]. The model proposed in [49] considers the Hubble horizon \( H^{-1}\) playing the role of L in eq. (6).

Thus, the THDE density with the identification of IR cut-off, as Hubble horizon proposed in [49], is defined as

$$\begin{aligned} \rho _{\mathrm {T}} = {CH}^{-2\delta +4}. \end{aligned}$$
(7)

The conservation law of energy \(T^{ij}_{;j} = 0\) gives \({\dot{\rho }}_{\mathrm{m}} + {\dot{\rho }}_{\mathrm {T}} + 3H (\rho _{\mathrm{m}} + \rho _{\mathrm{T}} + p_{\mathrm{T}}) = 0\). The law of energy conservation for matter and THDE are shown as \({\dot{\rho }}_{\mathrm{m}} + 3 H \rho _{\mathrm{m}} = 0\) and \( {\dot{\rho }}_{\mathrm{T}} + 3H (\rho _{\mathrm{T}} + p_{\mathrm{T}}) = 0\), respectively. The barotropic equation of state (EoS) is \( p_{\mathrm{T}} = w_{\mathrm{T}} \rho _{\mathrm{T}}\). Using eq. (7), we find \(\omega _{\mathrm {T}}\) as

$$\begin{aligned} \omega _{\mathrm {T}} = -1 - (-2\delta +4) \frac{\dot{H}}{3H^{2}}. \end{aligned}$$
(8)

3 Solution and physical properties of the THDE model

It is clear that the right-hand side of eqs (3) and (4) is the same and so we have \(2({\ddot{B}}/{{B}}) + ({\dot{B}}/{{B}})^{2} = ({\ddot{A}}/{{A}}) + ({\ddot{B}}/{B}) + ({\dot{A} \dot{B}}/{{A} {B}})\), and using \(a = (AB^{2})^{{1}/{3}}\) into this, we get \(({A}/{B})= F_{2}\exp (F_{1}\int a^{-3}\,\mathrm{d}t)\). Therefore, the metric coefficients are obtained as

$$\begin{aligned} A= & {} F_{2}^{2} a\, \mathrm{exp} \!\left( 2F_{3} \int a^{-3}\,\mathrm{d}t\right) \!,\quad \\ B= & {} F_{2}^{-1} \, a\,\mathrm{exp} (- F_{3} \int a^{-3}\,\mathrm{d}t), \end{aligned}$$

where \(F_{1}\), \(F_{2}\) and \(F_{3} \) are constants such that \(3 F_{3} = F_{1}\). As mentioned in the Introduction, the deceleration parameter (DP) must show signature flipping in accelerating the Universe of the present time. Hence, the DP is not constant but is time varying. We consider the cosmological scale factor as a hybrid expansion law (HEL) [79]:

$$\begin{aligned} a(t) = a_{0}\!\left( \frac{t}{t_{0}}\right) ^{\!\!k} \mathrm{e}^{b(({t}/{t_{0}}) - 1)}, \end{aligned}$$
(9)

where b and k are constants. Here \(t_{0}\) and \(a_{0}\) indicate the age of the Universe and scale factor at present, respectively. \(k = 0\) leads to the exponential-law cosmology and \(b = 0\) leads to the power-law cosmology. These cosmologies are special cases of the HEL cosmology. Any other values of k and b will have new directions to explore cosmology in the context of the HEL [68, 80,81,82,83]. Applying appropriate transformation in eq. (9), it has the form

$$\begin{aligned} a = (t^{k} \mathrm{e}^{bt}), \end{aligned}$$
(10)

where (\({t}/{t_{0}} )\rightarrow t\), \(k \ge 0\) and \(b \ge 0\) are constants. This is known as HEL which gives time-dependent DP. Therefore, the metric functions by putting the value of a(t) in A and B are

$$\begin{aligned} A= & {} F_2^2 t^k \mathrm{e}^{t \left( b-2 F_3 t^{-3 k} E_{3 k}(3 b t)\right) },\quad \\ B= & {} \frac{t^k \mathrm{e}^{t \left( F_3 t^{-3 k} E_{3 k}(3 b t)+b\right) }}{F_2}. \end{aligned}$$

The DP is determined by the relation \(q = -{a\ddot{a}}/{\dot{a}^2}\) and is obtained as

$$\begin{aligned} q= \frac{k}{(b t+k)^{2}}-1. \end{aligned}$$
(11)
Fig. 1
figure 1

(a) The behaviour of DP (q) with respect to time t for \(b=0.4\) and \(k = 2.15041\), \(b=0.5\) and \(k = 2.14456\), \(b=0.6\) and \(k = 2.13871\), \(b=0.7\) and \(k = 2.13287\). (b) The behaviour of DP (q) with redshift for \(b=0.4\) and \(k = 2.15041\), \(b=0.5\) and \(k = 2.14456\), \(b=0.6\) and \(k = 2.13871\), \(b=0.7\) and \(k = 2.13287\).

Full size image

From eq. (11), we see that q is time-dependent. Whether the model inflates or not, it will depend on the sign of q. The negative sign of q indicates acceleration whereas the positive sign of q corresponds to ‘standard’ decelerating model. It is exceptional to make the reference here that, however, the recent observations of cosmic microwave background (CMBR) and supernovae Ia (SNe Ia) are supportive to accelerating models (\(q < 0\)) [14, 15]. From eq. (11), we notice that \(q > 0\) for \( k(1 - k) > 2kb t + b^{2} t^{2}\) and \(q = -1\) for \(k = 0\). It is observed that for \(b = 0\), \(q =( {1}/{k} )- 1\). In this case, \(q > 0\) or \(q < 0\) according to \(k < 1\) or \(k > 1\), respectively. Figures 1a and 1b depict the variation of DP vs. cosmic time (t) and redshift (z), respectively. Moreover, it is obvious from these figures that our THDE model is in an accelerating stage. The redshift parameter (z) for our model is defined as \(z = -1 + {(a_0}/{a}) = -1 + ({a_0}/{t^{k}\mathrm{e}^{bt}})\), where \(a_0\) is the present value of the scale factor at \(z = 0\).

For this particular form of scale factor, the Hubble parameter H, shear scalar \(\sigma ^2\) and the average anisotropy parameter \(A_m\) are given as

$$\begin{aligned}&H = b + \frac{k}{t}, \nonumber \\&\sigma ^2=\frac{3}{2} F_3 \mathrm{e}^{-6 b t} t^{-6 k-1} (F_3 t-2 \mathrm{e}^{3 b t} t^{3 k} (b t+k)),\nonumber \\&A_m=\frac{2}{3} \left( \frac{F_3 \mathrm{e}^{-6 b t} t^{1-6 k} (3 F_3 t-\mathrm{e}^{3 b t} t^{3 k} (b t+k))}{(b t+k)^2}{+}1\right) \!\!. \end{aligned}$$
(12)

The scalar expansion and volume are given as \(\theta = 3 (b + {(k}/{t}))\) and \(V= {t^{3k} \mathrm{e}^{3{bt}}}\), respectively. We observe that at \(t=0\), the spatial volume is zero and the other parameters H, \(\theta \) and \(\sigma \) diverge at this stage and H, \(\theta \) and \(\sigma \) approach zero while volume becomes infinite when \(t\sim \infty \). Hence, the Universe starts with zero volume by infinite rate of expansion. The anisotropy parameter \(A_m\) is constant at \(t\sim \infty \) and the evolution of the Universe is anisotropic.

The EoS parameter for THDE is obtained as

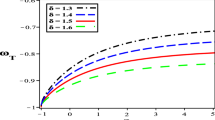
$$\begin{aligned} \omega _\mathrm {T}= -1 -\frac{2 (\delta -2) k}{3 (b t+k)^2}. \end{aligned}$$
(13)

From eq. (13), we find that the EoS parameter (\(\omega _{\mathrm{T}}\)) of THDE is a function of time and approaches \(-1\) as \(t\sim \infty \). Figure 2 shows the behaviour of THDE EoS parameter \(\omega _{\mathrm{T}}\) with redshift z. We observe from this figure that \(\omega _{\mathrm{T}}\) of the derived THDE demonstrates the changes in the k-essence locale (\(\omega _{\mathrm{T}} < - 1/3\)) all through its advancement for each of the four values of \(\delta \), e.g. \(\delta =0.05,0.15,0.25\) and 0.35. In such a case, the EoS parameter (THDE) acts as k-essence. Besides, we can see that for each of the four values of \( \delta \), the EoS parameter approaches \(\Lambda \)CDM model (\(\omega _{\mathrm{T}} = - 1)\) in future. This proposes for smaller estimations of redshift (z) and the Universe has a bigger acceleration impact.

The THDE energy density and energy density of matter are given by

$$\begin{aligned}&\rho _{\mathrm{T}} = \frac{C (b t+k)^4 (b+({k}/{t}))^{-2 \delta }}{t^4}, \end{aligned}$$
(14)
$$\begin{aligned}&\rho _\mathrm {m}(t)=C_1 \mathrm{e}^{-3 b t} t^{-3 k}, \end{aligned}$$
(15)

where \(C_{1} \) is a constant of integration. From eqs (14) and (15), it is clear that the energy density of THDE and matter decrease with time. The energy density of matter (\(\rho _{\mathrm {m}}\)) and THDE density (\(\rho _{\mathrm{T}}\)) vs. time are plotted in figures 3a and 3b. Both the graphs show a decrease in \(\rho _{\mathrm{T}}\) and \(\rho _{\mathrm{m}}\) with time. It, in turn, shows that the decrease of the energy density of THDE with time t leads to the volumetric expansion of the Universe.

Fig. 2
figure 2

Analysis of EoS parameter \(\omega _{\mathrm {T}}\) when \(k = 2.15041\), \(b = 0.4\) for different values of \(\delta \).

Full size image
Fig. 3
figure 3

(a) Variation of matter energy density with time t, for \(C_1 = 0.15\) and for \(b=0.4\) and \(k = 2.15041\), \(b=0.5\) and \(k = 2.14456\), \(b=0.6\) and \(k = 2.13871\), \(b=0.7\) and \(k = 2.13287\). (b) Graph of energy density of DE vs. time t, for \(k = 2.15041\), \(C = 7\) and \(b = 0.4\) and for different values of \(\delta \).

Full size image

Now the THDE density parameter (\( \Omega _{\mathrm{T}} \)) and the matter density parameter \((\Omega _{\mathrm{m}} )\) are defined as

$$\begin{aligned} \Omega _{\mathrm{T}} = \frac{\rho _{\mathrm{T}}}{3 H^{2}}, \quad \Omega _{\mathrm{m}} = \frac{\rho _{\mathrm{m}}}{3 H^{2}}. \end{aligned}$$
(16)

From eqs (14) and (15) we obtain

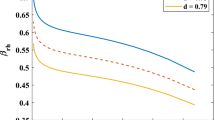
$$\begin{aligned} \Omega _{\mathrm{T}} {+} \Omega _{\mathrm{m}} {=}\frac{C_1 \mathrm{e}^{-3 b t} t^{4-3 k}{+}C (b t{+}k)^4 (b{+}({k}/{t}))^{-2 \delta }}{3 t^2 (b t+k)^2}.\nonumber \\ \end{aligned}$$
(17)

Equation (17) shows that at late times the sum of the energy density parameters tends towards one. It shows that at late times the Universe tends to be flat, which in turn predicts that the anisotropy of the Universe will end and the Universe will proceed towards the isotropic state. This outcome also affirms that the early Universe was anisotropic and it tends to isotropy as DE starts to dominate the energy density of the Universe. Figure 4 depicts the graph.

Fig. 4
figure 4

Evolution of energy density parameters with time t for \(C = 7\), \(C_1 = 0.15\), \(k = 2.15041\), \( \delta = 0.05\) and \(b = 0.4\).

Full size image

4 Statefinder diagnostic

As we know, DE [84] has properties that can be very model-dependent. In order to be able to differentiate between the very distinct and competing cosmological scenarios involving DE, a sensitive and robust diagnostic (of DE) is a must. Although the rate of acceleration / deceleration of the Universe can be described by a single parameter \(q = -{\ddot{a}}/{{aH}^{2}}\), a more sensitive discriminator of the expansion rate and hence DE can be constructed by considering the general form for the expansion factor of the Universe:

$$\begin{aligned} a(t)= & {} a(t_{0}) + \dot{a}(t_{0})(t- t_{0}) +\frac{\ddot{a}(t_{0})}{2}(t- t_{0})^{2} \nonumber \\&+ \frac{\dddot{a}(t_{0})}{6}(t- t_{0})^{3} + \cdots . \end{aligned}$$
(18)

In general, DE models such as quiessence, quintessence, k-essence, brane-world models, Chaplygin gas, etc. give rise to families of curves a(t) having vastly different properties. As we know that the acceleration of the Universe is a fairly recent phenomenon [14, 15], we can, in principle, confine our attention to small values of \(|t - t_{0}|\) in eq. (18). It has been shown by Sahni et al [85] that a new diagnostic of DE called statefinder can be constructed using both the second and third derivatives of the expansion factor. The second derivative is encoded in the DP.

The acceleration of the Universe is being shown by numerous DE models, and with the end goal of having the capacity to separate the DE models, a powerful indicator for DE models is the need of the hour. A useful diagnostic, for this purpose, that impacts the usage of parameter pair (r, s), called ‘statefinder’, was proposed by Alam et al [86]. Recently, Sharma and Pradhan [87] and Varshney et al [88] have diagnosed the geometric behaviour of non-interacting and interacting THDE in terms of statefinder parameters and \(\omega -\omega '\) pair in detail. As the models, in addition to DE, represent different evaluation trajectories in the r–s plane, the statefinder parameters can act as a panacea for DE models. For \(\Lambda \)CDM, the statefinder parameters are \({r = 1, s = 0}\). The statefinder indicative pair r, s is taken as (for the geometric idea of the models):

Fig. 5
figure 5

The statefinder evolution trajectory in the s–r plane.

Full size image
$$\begin{aligned} r= & {} \frac{\dddot{a}}{{aH}^{3}}=\frac{k (-3 b t-3 k+2)}{(b t+k)^3}+1, \end{aligned}$$
(19)
$$\begin{aligned} s= & {} \frac{r-1}{3 (q - ({1}/{2}))} =\frac{2}{3 (b t+k)}\nonumber \\&-\frac{2 b t}{3 b^2 t^2+6 b k t+k (3 k-2)}. \end{aligned}$$
(20)

We can find the difference in different DE models by statefinder analysis. The distinctive DE cosmological models tell about various subjective directions of their advancement. From eqs (19) and (20), we see different qualitative trajectories of evaluation, which ultimately give \(s = 0\) and \(r = 1\) as \(t \rightarrow \infty \). The behaviour of statefinder pair \((s-r)\) is shown in figure 5. From this figure, it has been inferred that the THDE model will occur simultaneously with the \(\Lambda \)CDM flat model.

Fig. 6
figure 6

(a) Variation of kinetic term (P) vs. time t, when \(b = 0.4\) and \(k = 2.15041\) for different values of \(\delta \). (b) The behaviour of scalar potential vs. time t, when \(k = 2.15041\), \(C = 7\), \(b = 0.4\) for different values of \(\delta \).

Full size image

5 Correspondence of THDE with k-essence

The late-time acceleration of the Universe can be explained by k-essence scalar field with negative pressure which has attractor-type dynamics. The fundamental motivation to have k-essence as one of the candidate of DE is that it does not require initial conditions fine tuning of the scalar field [89]. The classification of such models is done by kinetic energy terms (non-standard) and defined by the generalised action as the scalar field \(\phi \) function and kinetic term \(P = {{\dot{\phi }}^{2}}/{2}\) and is given as [90]

$$\begin{aligned} S = \int \mathrm {d}^{4}x\sqrt{-}{gp}(\phi ,P), \end{aligned}$$
(21)

where \(p(\phi , P)\) represents the pressure density confined normally to the Lagrangian density of the form \(p(\phi , P) = f (\phi )g(P)\) and it can be transferred to the action of string theory based on the analysis of low energy (see [90] for details):

$$\begin{aligned} p_{k} = f(\phi )(-P+P^2). \end{aligned}$$
(22)

The energy density can be expressed for this Lagrangian as (see [90])

$$\begin{aligned} \rho _{{k}} = f (\phi ) (-P+3 {P}^{2}). \end{aligned}$$
(23)

EoS parameter for k-essence using eqs (22) and (23) is given as

$$\begin{aligned} \omega _{{k}} = {\frac{-P+{P}^{2}}{-P+3 {P}^{2}}}. \end{aligned}$$
(24)

Equating this parameter with the THDE EoS parameter (13), \(\omega _{k} = \omega _{\mathrm{T}}\), we find the solution for P as

$$\begin{aligned} P = {\frac{3 b^{2} t^{2}+ 2 k (3 b t+ \delta -2)+3 k^{2}+3(bt+k)^{2}}{3(bt+k)^{2}+9 b^{2} t^{2}+ 6 k (3 b t+ \delta -2)+9 k^{2}}},\nonumber \\ \end{aligned}$$
(25)

where P is the function of time and the condition \(P < 2/3\) provides the accelerated expansion phase.

Using eq. (25), the scalar field is found to be

$$\begin{aligned} \phi {=}\sqrt{2}\int \! \!\sqrt{\!{\frac{3 b^{2} t^{2}{+} 2 k (3 b t{+} \delta {-}2){+}3 k^{2}{+}3(bt+k)^{2}}{3(bt+k)^{2}{+}9 b^{2} t^{2}{+} 6 k (3 b t{+} \delta {-}2){+}9 k^{2}}}}\,{\mathrm{d}t}.\!\!\!\!\nonumber \\ \end{aligned}$$
(26)

Now, by the correspondence between k-essence and THDE from eqs (26) and (7) (\(\rho _{\mathrm{T}} = \rho _{k}\)) and putting the value of P from eq. (25) and H by (12), we have

$$\begin{aligned} f(\phi ) = \left( \frac{C \cdot (b+ {(k}/{t}))^{(-2\delta +4)}}{P(-1+3P)}\right) \!. \end{aligned}$$
(27)

The behaviour of kinetic term P and the potential, which is given by eqs (25) and (27), are shown in figures 6a and 6b. It is clear from these figures that both are decreasing functions of time. The important point of this reconstruction for THDE model is that EoS \((\omega _{\mathrm{T}})\) is decreasing and approaches \(\omega _{\mathrm{T}}=-1\) at the present epoch.

The statefinder analysis and the correspondence between the HDE models with the quintessence DE models are established in the Bianchi types I and III Universe filled with matter and HDE [71, 82, 91]. Quintessence potential and the dynamics of the quintessence scalar field are reconstructed, which describe the accelerated expansion of the Universe. Recently, Srivastava et al [33] investigated statefinder diagnostic and the correspondence between the NHDE models with the k-essence DE models in Bianchi type-III Universe. In this work, we have shown the geometric behaviour of the THDE through statefinder and the correspondence is obtained between the THDE model with k-essence to describe the late-time accelerated expansion of the Universe.

6 Conclusion

We have investigated the THDE in the axially symmetric Bianchi-I Universe within the framework of general relativity filled with matter and THDE using HEL. We have acquired different parameters of cosmology to comprehend the accelerated evolution of the Universe in our described model. Spatially homogeneous cosmological models play important roles to understand the structure and properties of the space of all cosmological solutions of Einstein field equations. We observe that the DP of our model under certain conditions represents the accelerating phases of the Universe which is in good agreement with the current observations.

Also, in the proposed THDE model, the EoS parameter deviates in k-essence scenario and remains inside, \(\omega _{\mathrm{T}} = -1\), the phantom divide line for all four values of Tsallis parameter \(\delta \). The model shows affirmity to \(\Lambda \)CDM model for all four values of \(\delta \). So, this model shows the accelerated expansion of the Universe. From figure 4, we see that the overall density parameter (\(\Omega \)) tends to 1 as time \(t\rightarrow \infty \). Hence, for sufficiently large time, our THDE model predicts that the anisotropic nature of the model vanishes and it will become isotropic in future. This implies that our THDE model becomes isotropic at late times even though the space–time is anisotropic.

Both energy densities, matter and THDE, decrease with time. The underlying physical consequence is that the decrease of HDE and matter energy density with increase of cosmic time leads to the expanding Universe. It is also clear from the statefinder diagnosis that our proposed model of THDE would occur simultaneously with the \(\Lambda \)CDM flat model in the future [33].

The correspondence is obtained between the derived THDE model with k-essence [89, 92, 93]. It has been seen by this correspondence that our THDE model can be an answer to the question of how to describe the late-time acceleration for the expansion of the Universe. The correspondence with quintessence, phantom, tachyon and dilation field can open plenty of chances in the field of research later on to reformulate the potential and the scalar field.

In summary, the present scenario of THDE displays a richer behaviour than the standard HDE, quantified by the presence of the new parameter \(\delta \). We found, when the apparent horizon is considered as IR cut-off, that the THDE model can explain the current acceleration of the Universe expansion.