The anisotropic cosmological models in f(R, T) gravity with Λ(T)

Abstract

The general class of anisotropic Bianchi cosmological models in f(R, T) modified theories of gravity with Λ(T) has been considered. This paper deals with f(R, T) modified theories of gravity, where the gravitational Lagrangian is given by an arbitrary function of Ricci scalar R and the trace of the stress-energy tensor T has been investigated for a specific choice of f(R, T) = f ₁(R) + f ₂(T). The exact solutions to the corresponding field equations are obtained in quadrature form. We have discussed three types of solutions of the average scale factor for the general class of Bianchi cosmological models by using a special law for deceleration parameter which is linear in time with a negative slope. The solutions to the Einstein field equations are obtained for three different physical viable cosmologies. All physical parameters are calculated and discussed in each model.

1 Introduction

Despite the fact that Einstein’s general relativity is a tremendously successful theory and the basis for the description of most of the gravitational phenomena known till date, it fails to explain the recent discovery of the accelerating expansion of the Universe. Recent evidences coming from the observational data [1–6] on the late-time acceleration of the Universe and the existence of dark matter have posed a fundamental theoretical challenge to gravitational theories.The cosmic microwave background radiation (CMBR) and supernovae surveys indicate that the distribution of ordinary baryonic matter, dark matter and dark energy of our Universe is 4, 20 and 76% respectively [7–10]. One way of explaining the observations is by assuming that at large scales the Einstein gravity model of general relativity breaks down, and a more general action describes the gravitational field.

In recent years, modifications of general relativity are being used more and more to explain late acceleration and dark energy. The presence of a late-time cosmic acceleration of the Universe can indeed be explained by f(R) gravity [11,12]. A generalization of f(R) modified theories of gravity was proposed in [13]. Among the various modifications, f(R) theory of gravity is considered as the most suitable due to the cosmologically important f(R) models. It has been suggested that cosmic acceleration can be achieved by replacing the Einstein–Hilbert action of general relativity with a general function Ricci scalar, f(R). Nojiri et al [14] have studied f(R), f(G) or f(R, G) gravity in various contexts. Many researchers [15–23] have investigated f(R) gravity in different contexts. Shamir [24] has proposed a physically viable f(R) gravity model, which shows the unification of early-time inflation and late-time acceleration.

Recently, several researchers [25–27] suggested that the anisotropic Bianchi Universes have played important roles in observational cosmology. Some researchers [28–33] also suggested that the interest in such Bianchi Universes have received more attention than FRW Universe. The WMAP data [34–36] seem to require an addition to the standard cosmological model with positive cosmological constant that bears a likeness to the Bianchi morphology [37–39]. According to this, the Universe should reach a slightly anisotropic special geometry in spite of the inflation, contrary to generic inflationary models [40–44] suggesting a non-trivial isotropization history of the Universe due to the presence of an anisotropic energy source. In order to explain the homogeneity and flatness of the presently observed Universe, it is usually assumed that this has undergone a period of exponential expansion.

In a recent paper, Harko et al [45] have proposed a new generalized theory known as f(R, T) gravity. According to this theory, gravitational Lagrangian involves an arbitrary function of the scalar curvature (R) and trace of the energy–momentum tensor (T). Several researchers [46–49] have investigated f(R, T) gravity in different contexts. Recently, Reddy et al [50] have obtained a Bianchi type-III cosmological model in f(R, T) theory of gravity, Shamir et al [51] have obtained exact solutions of Bianchi types-I and V cosmological models in f(R, T) gravity and Chaubey and Shukla [52] have studied a new class of cosmological models in f(R, T) gravity. A theory whose Lagrangian density is described by an arbitrary function of R and the Lagrangian density of matter as F(R, L _m ) has been explored by Harko and Lobo [53]. Moreover, in Poplawski [54] a theory in which the cosmological constant is written by a function of the trace of the stress-energy tensor as Λ(T) has been investigated. Very recently, Ahmed et al [55] have studied Bianchi type-V cosmological model in f(R, T) gravity with Λ(T).

The present paper is organized as follows. In §1, a brief introduction is given. The field equations in metric version of f(R, T) gravity is given in §2. In this section, explicit field equations in f(R, T) = f ₁(R) + f ₂(T) are obtained by using the particular form of the functions f ₁(R) = λ ₁ R and f ₂(T) = λ ₂ T, which are used by Ahmed and Pradhan [55], with the general class of Bianchi model. Section 3 deals with cosmological solutions of the field equations using the linearly varying deceleration parameter q proposed by Akarsu and Dereli [56] and also discuss some physical properties, energy conditions and statefinder diagnostic of the constructed model in three different physical viable cosmologies. Conclusions are given in §4.

2 Model and basic equations

The f(R, T) theory of gravity is the modification of general relativity (GR). The action for the modified f(R, T) gravity is

$$ S=\frac{1}{16\pi}\int{f(R,T)\sqrt{-g} \ \mathrm{d}^{4}x}+ \int{L_{m}\sqrt{-g} \ \mathrm{d}^{4}x}, $$

(1)

where f(R, T) is an arbitrary function of Ricci scalar (R), T is the trace of stress-energy tensor (T _μν ) of matter and L _m is the matter Lagrangian density.

The f(R, T) gravity field equations are obtained by varying the action S with respect to metric tensor (g _μν ).

$$\begin{array}{@{}rcl@{}} {\kern-.2pc}f(R,T) R_{\mu\nu}{\kern-.5pc}&&-\frac{1}{2}f(R,T)g_{\mu\nu}\\ &&+\, (g_{\mu\nu}\Box - \nabla_{\mu}\nabla_{\nu}) f_{R}(R,T)\\ &&{} =8\pi T_{\mu\nu}-f_{T}(R,T)T_{\mu\nu} -f_{T}(R,T)\theta_{\mu\nu}, \end{array} $$

(2)

where

$$ \theta_{\mu\nu}=-2T_{\mu\nu}+g_{\mu\nu} L_{m}-2g^{\alpha \beta}\frac{\partial^{2}L_{m}}{\partial g^{\mu\nu}\partial g^{\alpha \beta}}. $$

(3)

Here,

$$\begin{array}{@{}rcl@{}} &&{} \Box \equiv \nabla^{\mu}\nabla_{\mu}, \quad f_{R}(R,T) = \frac{\partial f(R,T)}{\partial R},\\ &&{} f_{T}(R,T) =\frac{\partial f(R,T)}{\partial T} \end{array} $$

and ∇ _μ denotes the covariant derivative.

Taking into account the covariant divergence of eq. (2), by using the following mathematical identity [45,57]:

$$\begin{array}{@{}rcl@{}} &&{\kern-.5pc}\nabla^{\mu}\left[ f_{R}(R,T)R_{\mu\nu}-\frac{1}{2}f(R,T)g_{\mu\nu}\right.\\ &&{\kern2pc}\left.{\vphantom{\frac{1}{2}}}+(g_{\mu\nu}\Box-\nabla_{\mu}\nabla_{\nu})f_{R}(R,T)\right] =0, \end{array} $$

(4)

where f(R, T) is an arbitrary function of the Ricci scalar R and of the trace of the stress-energy tensor T, we obtain the divergence of the stress-energy tensor T _μν as

$$\begin{array}{@{}rcl@{}} \nabla^{\mu} T_{\mu \nu}\!\!&=&\!\!\frac{f_{T}(R,T)}{8\pi\,-\,f_{T}(R,T)}\\ &&\!\!\! \times\, [(T_{\mu\nu}\,+\,\theta_{\mu\nu})\nabla^{\mu} \ln f_{T}(R,T)\,+\,\nabla^{\mu}\theta_{\mu\nu}]. \end{array} $$

(5)

We know that the perfect fluid is described by energy density (ρ), pressure (p) and four-velocity (u ^μ), because there is no unique definition of the matter Lagrangian. However, in the present paper we assume that the stress-energy tensor of the matter is given by

$$ T_{\mu\nu}=(\rho +p)u_{\mu} u_{\nu}-pg_{\mu\nu}, $$

(6)

where u ^μ = ( 0 , 0 , 0 , 1 ) is the four-velocity in co-moving coordinates which satisfies the conditions u ^μ u _μ = 1 and u ^μ∇ _ν u _μ = 0 and the matter Lagrangian L _m = − p.

Then, using eq. (3), we obtain the variation of the stress-energy of a perfect fluid as follows:

$$ \theta_{\mu\nu}=-2T_{\mu\nu}-pg_{\mu\nu} . $$

(7)

From eqs (5) and (7), we can obtain the divergence of the stress-energy tensor T _μν for a perfect fluid as

$$\begin{array}{@{}rcl@{}} \nabla^{\mu} T_{\mu \nu}&=&\frac{f_{T}(R,T)}{8\pi-f_{T}(R,T)}\\ &&\times\, [-(T_{\mu\nu}+pg_{\mu\nu})\nabla^{\mu} \ln f_{T}(R,T)\\ &&-\, \nabla^{\mu}(2T_{\mu\nu}+pg_{\mu\nu})] .\end{array} $$

(8)

In this paper we take f(R, T) is as follows:

$$ f(R,T)=\lambda R+ \lambda T. $$

(9)

Here, we can see from eqs (8) and (9) that the divergence of T _μν is zero, i.e. ∇^μ T _μν = 0.

From eqs (2), (6) and (9), we get

$$ G_{\mu\nu}-\left( p+\frac{1}{2}T\right)g_{\mu\nu}=\left( \frac{8\pi +\lambda}{\lambda}\right)T_{\mu\nu}. $$

(10)

The well-known Einstein equations with cosmological constant is

$$ G_{\mu\nu}-{\Lambda} g_{\mu\nu}=-8 \pi T_{\mu\nu} . $$

(11)

The term $\big (p+\frac {1}{2}T\big )$ can now be regarded as a cosmological constant, and so we can write

$$ {\Lambda} \equiv {\Lambda} (T) = p+\frac{1}{2}T. $$

(12)

Recently, Poplawski has proposed the dependence of cosmological constant Λ on the trace of the energy– momentum tensor (T). Several researchers like Magnano [58] and Poplawski [54] have suggested that the Λ(T) gravity is more general than the Palatini f(R) and could be reduced to it if the pressure of matter is neglected. Considering the perfect fluid case, the trace T = ρ − 3p, for our model

$$ {\Lambda} = \frac{1}{2}(\rho-p). $$

(13)

The diagonal form of the metric of the general class of Bianchi cosmological model is given by

$$ \mathrm{d}s^{2}\,=\,\mathrm{d}t^{2}\,-\,{a_{1}}^{2}{\kern-.5pt}\mathrm{d}x^{2}\,-\,{a_{2}}^{2}{\kern-.5pt}\mathrm{e}^{-2x}{\kern-.5pt}\mathrm{d}{\kern-.5pt}y^{2}\,-\,{a_{3}}^{2}{\kern-.5pt}\mathrm{e}^{-2mx}{\kern-.5pt}\mathrm{d}z^{2}{\kern-.5pt}. $$

(14)

We have the additional classes of Bianchi models as follows: type-III corresponds to m = 0, type-V corresponds to m = 1, type-VI ₀ corresponds to m = −1 and all other m give VI _h , where m = h − 1.

We first define the expressions for the average scale factor and volume scale factor. Define the generalized Hubble’s parameter H in analogy with a flat FRW model.

The average scale factor (a) and spatial volume (V ) are defined as

$$ V=a^{3}=a_{1}a_{2}a_{3}. $$

(15)

We define the generalized Hubble’s parameter H as

$$ H= \frac{1}{3}\frac{\dot{V}}{V}=\frac{\dot{a}}{a}=\frac{1}{3}\left( \frac{\dot{a_{1}}}{a_{1}}+\frac{\dot{a_{2}}}{a_{2}}+\frac{\dot{a_{3}}}{a_{3}}\right), $$

(16)

where $H_{1}=\dot {a_{1}}/{a_{1}}$, $H_{2}=\dot {a_{2}}/{a_{2}}$ and $H_{3}=\dot {a_{3}}/{a_{3}}$ are the directional Hubble’s parameters. Overhead dot denotes differentiation with respect to cosmic time t.

In view of eq. (6) for the general class of Bianchi space–time eq. (14), the field eq. (10) lead to

$$ \frac{\dot{a_{1}}\dot{a_{2}}}{a_{1}a_{2}}+\frac{\dot{a_{2}}\dot{a_{3}}}{a_{2}a_{3}}+\frac{\dot{a_{3}}\dot{a_{1}}}{a_{3}a_{1}}-\frac{m^{2}+m+1}{{a_{1}}^{2}}= -\frac{(8\pi +\lambda)}{\lambda}\rho-{\Lambda} $$

(17)

$$ \frac{\ddot{a_{2}}}{a_{2}}+\frac{\ddot{a_{3}}}{a_{3}}+\frac{\dot{a_{2}}\dot{a_{3}}}{a_{2}a_{3}}-\frac{m}{{a_{1}}^{2}}=\frac{(8\pi +\lambda)}{\lambda}p-{\Lambda} $$

(18)

$$ \frac{\ddot{a_{1}}}{a_{1}}+\frac{\ddot{a_{3}}}{a_{3}}+\frac{\dot{a_{1}}\dot{a_{3}}}{a_{1}a_{3}}-\frac{m^{2}}{{a_{1}}^{2}}=\frac{(8\pi +\lambda)}{\lambda}p-{\Lambda} $$

(19)

$$ \frac{\ddot{a_{1}}}{a_{1}}+\frac{\ddot{a_{2}}}{a_{2}}+\frac{\dot{a_{1}}\dot{a_{2}}}{a_{1}a_{2}}-\frac{1}{{a_{1}}^{2}}=\frac{(8\pi +\lambda)}{\lambda}p-{\Lambda} $$

(20)

$$ (m+1)\frac{\dot{a_{1}}}{a_{1}}-\frac{\dot{a_{2}}}{a_{2}}-m\frac{\dot{a_{3}}}{a_{3}}=0. $$

(21)

We have assumed G = c = 1 in proper unit.

Let us introduce the dynamical scalars such as expansion parameter (𝜃), shear scalar (σ ²) and the mean anisotropy parameter (A) as usual.

$$ \theta=u^{\mu};_{\mu}=3H=\left( \frac{\dot{a_{1}}}{a_{1}}+\frac{\dot{a_{2}}}{a_{2}}+\frac{\dot{a_{3}}}{a_{3}}\right) $$

(22)

$$\begin{array}{@{}rcl@{}} \sigma^{2}&=&\frac{1}{2}\sigma_{\mu\nu}\sigma^{\mu\nu}\\ &=&\frac{1}{2}\left[\left( \frac{\dot{a_{1}}}{a_{1}}\right)^{2}+\left( \frac{\dot{a_{2}}}{a_{2}}\right)^{2}+\left( \frac{\dot{a_{3}}}{a_{3}}\right)^{2}\right]-\frac{\theta^{2}}{6} \end{array} $$

(23)

$$ A=\frac{1}{3}\sum\limits_{i=1}^{3}\left( \frac{\Delta H_{i}}{H}\right)^{2}, $$

(24)

where ΔH _i = H _i − H, i = 1,2,3.

Recently, a special law was proposed for the deceleration parameter which is linear in time with a negative slope. This law covers the law of Berman (where the deceleration parameter is constant) used for obtaining exact cosmological models, in the context of dark energy, to account for the current acceleration of the Universe. According to this law, only the spatially closed and flat Universes with cosmological fluid exhibiting quintom-like behaviour are allowed and the Universe ends with a big-rip. This new law gives the opportunity to generalize many of these dark energy models having better consistency with the cosmological observations. The linearly varying deceleration parameter (q) is defined as

$$\begin{array}{@{}rcl@{}} &&{} q=-\frac{a\ddot{a}}{\dot{a}^{2}}=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{H}\right)-1=- \frac{\dot{H}}{H^{2}}-1\\ &&{} =-kt+n-1, \end{array} $$

(25)

where k and n are positive constants. We see that, the deceleration parameter (q) is linear in time with negative slope. The sign of q indicates whether the model inflates or not. The positive sign of q corresponds to standard decelerating model whereas the negative sign indicates accelerated expansion.

Solving eq. (25) for the scale factor, we obtain the law of variation for average scale factor a as

$$ a=(nlt+c_{1})^{1/n}, \qquad k=0,\quad n > 0, $$

(26)

$$ a=c_{2} \mathrm{e}^{lt}, \qquad k=0, \quad n= 0, $$

(27)

$$ a=c_{3} \mathrm{e}^{\frac{2}{n}\tanh^{-1}(\frac{kt}{n}-1)}, \qquad k > 0, \quad n > 1, $$

(28)

where c ₁, c ₂ and c ₃ are constants of integration. Equation (26) implies that the condition for the expanding Universe is n(= q + 1 + kt) > 0.

3 Cosmological solutions

Here we discuss three different physically viable cosmologies k = 0, n > 0; k = 0, n = 0 and k > 0, n > 1 respectively, which have physical interests to describe the decelerating and accelerating phases of the Universe.

Case 1.

When k = 0, n > 0 and a ₃ = V ^b, where b is any constant, then from eqs (15), (21) and (26), we get

$$ a_{i}(t)=(nlt+c_{1})^{X_{i}/n},\qquad i=1,2,3, $$

(29)

where

$$\begin{array}{@{}rcl@{}} &&{\kern-.7pc}X_{1}=\frac{3+3mb-3b}{m+2},\qquad X_{2}=\frac{3+3m-3b-6mb}{m+2} \end{array} $$

and

$$\begin{array}{@{}rcl@{}} X_{3}=3b. \end{array} $$

The directional Hubble’s parameters H _i have values given by

$$ H_{i}=\frac{X_{i}l}{nlt+c_{1}}. $$

(30)

From eq. (16), the average generalized Hubble’s parameter (H) and expansion parameter (𝜃) have the value given by

$$ \theta=3H=\frac{3l}{nlt+c_{1}}. $$

(31)

From eqs (23) and (24), the shear and anisotropy parameters are given by

$$\begin{array}{@{}rcl@{}} \sigma^{2}&=&[{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ &&-2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]\\ &&\times \frac{l^{2}}{2(nlt+c_{1})^{2}} \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} A&=&\frac{1}{3}[{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ &&-2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]. \end{array} $$

(33)

The scalar curvature (R) for a general class of Bianchi cosmological model is defined as

$$\begin{array}{@{}rcl@{}} R&=&2\left[\frac{\ddot{a_{1}}}{a_{1}}+\frac{\ddot{a_{2}}}{a_{2}}+\frac{\ddot{a_{3}}}{a_{3}}+\frac{\dot{a_{1}}\dot{a_{2}}}{a_{1}a_{2}}+\frac{\dot{a_{2}}\dot{a_{3}}}{a_{2}a_{3}}+\frac{\dot{a_{3}}\dot{a_{1}}}{a_{3}a_{1}}\right.\\ &&\left.-\frac{(m^{2}+m+1)}{{a_{1}}^{2}}\right]. \end{array} $$

(34)

From eqs (29) and (34), we get

$$\begin{array}{@{}rcl@{}} R\!&=&\!\frac{2l^{2}}{(nlt\,+\,c_{1})^{2}}\{{X_{1}}^{2}\,+\,{X_{2}}^{2}\,+\,{X_{3}}^{2}\,-\,n(X_{1}\,+\,X_{2}\,+\,X_{3})\\ &&+\, (X_{1}X_{2}\,+\,X_{2}X_{3}\,+\,X_{3}X_{1})\} \\ &&-\, 2(m^{2}\,+\,m\,+\,1)(nlt\,+\,c_{1})^{-{(2X_{1}}/{n})}. \end{array} $$

(35)

Using eq. (29) in eqs (17)–(20) and solving eq. (13), we obtain the expressions for pressure (p), energy density (ρ) and cosmological constant (Λ) for the model (14) as

$$\begin{array}{@{}rcl@{}} \rho &=&-\frac{9\lambda A_{1} l^{2}}{2(4\pi+\lambda)(m+2)^{2}(nlt+c_{1})^{2}}\\ &&-\frac{\lambda^{2}}{6(4\pi{}+{}\lambda)^{2}}\left\lbrace{} \frac{3l^{2}(3{}-{}n)}{(nlt{}+{}c_{1})^{2}}{}-{}\frac{2(m^{2}{}+{}m{}+{}1)}{(nlt{}+{}c_{1})^{\frac{2(3+3mb-3b)}{n(m+2)}}}\right\rbrace\\ &&+ \frac{\lambda(m^{2}+m+1)}{2(4\pi+\lambda)(nlt+c_{1})^{\frac{2(3+3mb-3b)}{n(m+2)}}}, \end{array} $$

(36)

$$\begin{array}{@{}rcl@{}} &&{} p = -\frac{9\lambda A_{1} l^{2}}{2(4\pi+\lambda)(m+2)^{2}(nlt+c_{1})^{2}}\\ &&\quad\; +\,\frac{\lambda(16\pi+3\lambda)}{6(4\pi+\lambda)^{2}}\left\{{\vphantom{\frac{2(m^{2}+m+1)}{(nlt+c_{1})^{\frac{2(3+3mb-3b)}{n(m+2)}}}}} \frac{3l^{2}(3-n)}{(nlt+c_{1})^{2}}\right.\\ &&\quad\; \left. -\frac{2(m^{2}+m+1)}{(nlt+c_{1})^{\frac{2(3+3mb-3b)}{n(m+2)}}}\right\}\\ &&\quad\; + \frac{\lambda(m^{2}+m+1)}{2(4\pi+\lambda)(nlt+c_{1})^{\!\frac{2(3+3mb-3b)}{n(m+2)}}}, \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}} &&{} {\Lambda} =-\frac{\lambda}{6(4\pi+\lambda)}\\ &&\quad\; \times\left\lbrace \frac{3l^{2}(3-n)}{(nlt+c_{1})^{2}}-\frac{2(m^{2}+m+1)}{(nlt+c_{1})^{\frac{2(3+3mb-3b)}{n(m+2)}}}\right\rbrace, \end{array} $$

(38)

where

$$A_{1} = 1+m+2b+2mb+2m^{2}b-3mb^{2}-3m^{2}b^{2}-3b^{2}. $$

Here we observe that, the spatial volume (V ) is zero at t = t ₀ = − (c ₁/nl). The scalar curvature (R) is infinite at t = t ₀, the energy density (ρ) and pressure (p) tend to infinity at $t\!\!\rightarrow \! t_{0}$. Cosmological parameters 𝜃 and A tend to infinity as t tends to t ₀. Hence we can observe that the Universe starts evolving with zero volume at t = t ₀ and expands with cosmic time (t). From eqs (31) and (32), we observe that $\lim _{t\rightarrow \infty } {(\sigma ^{2}}/{\theta )}=0$, and so the model approaches isotropy for large cosmic time (t). The conditions of homogeneity and isotropization, formulated by Collins and Hawking [59], are satisfied in the present model.

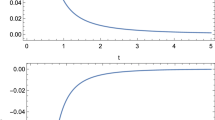
Figure 1 shows the variation of cosmological term Λ with cosmic time (t). From the figure we observe that the cosmological term (Λ) is a decreasing function of time (t). It starts from a positive value and approaches a small positive value for large t. Here, λ = −0.1, l = 5, m = −0.01, c = 1, n = 0.5, b = 0.1 in all the graphs.

Figure 1

The plot of cosmological constant (Λ) with cosmic time (t).

Figure 2 depicts the variation of pressure with time. From the figure we observe that the pressure is an increasing function of time. It starts from a negative value and approaches a small negative value near zero. From the discovery of the accelerated expansion of the Universe, it is generally assumed that this cosmic acceleration is due to some kind of energy-matter with negative pressure known as dark energy.

Figure 2

The plot of pressure (p) with cosmic time (t).

Figure 3 is the plot of energy density (ρ) vs. time. From this figure, we observe that energy density (ρ) is a decreasing function of time (t) and it approaches zero at late time (i.e. at the present epoch).

Figure 3

The plot of energy density (ρ) with cosmic time (t).

Figure 4 is the plot of Ricci scalar (R) vs. time. From this figure, we observe that the curvature is positive through the whole evolution of the Universe and $R\rightarrow 0$ as $t\rightarrow \infty$ and $R\rightarrow \infty$ as $t\rightarrow 0$ indicating the initial singularity.

Figure 4

The plot of Ricci scalar (R) with cosmic time (t).

The weak energy condition (WEC) and dominant energy conditions (DEC) are: (i) ρ ≥ 0, (ii) ρ − p ≥ 0 and (iii) ρ + p ≥ 0. The strong energy condition (SEC) is given by ρ + 3p ≥ 0.

Figures 3–7 are the plots of energy conditions (ρ) vs. time. From these figures, we observe that the WEC and DEC for our constructed model are satisfied. It is also observed that the SEC for our constructed model is not satisfied for Bianchi type-III, VI ₀ and VI _h (i.e. m ≠ 1).

Figure 5

The plot of energy condition (ρ − p) with cosmic time (t).

Figure 6

The plot of energy condition (ρ + p) with cosmic time (t).

Figure 7

The plot of energy condition (ρ + 3p) with cosmic time (t).

Sahni et al [60] proposed a cosmological diagnosticpair {r, s} called statefinder, which is defined for isotropic cosmological model as

$$ r=\frac{\dot{\ddot{a}}}{aH^{3}} \quad \text{and} \quad s=\frac{r\,-\,1}{3\big(q\,-\,\frac{1}{2}\big)}, $$

(39)

where H is the Hubble’s parameter and q is the deceleration parameter. By using eqs (25), (26), (31) and (39), the cosmological diagnostic pair $\left \{r,s\right \}$ is given by

$$ r=\frac{1}{nH^{2}}\left( nH^{2}-\frac{3n^{2}l^{2}}{(nlt+c_{1})^{2}}+\frac{2n^{3}l^{2}}{(nlt+c_{1})^{2}}\right) $$

(40)

$$ s=\frac{2}{3nH^{2}(2q-1)}\left( \frac{2n^{3}l^{2}}{(nlt+c_{1})^{2}} -\frac{3n^{2}l^{2}}{(nlt+c_{1})^{2}}\right). $$

(41)

The cosmological diagnostic pair {r, s} tends to be constant for large cosmic time (t). For n = 3/2, our model approaches to ΛCDM model (r = 1, s = 0). It has been observed that such models are compatible with present observations.

Therefore, on the basis of the above discussion and analysis, our constructed model and their corresponding solutions are physically acceptable.

Case 2.

When k = 0, n = 0 and a ₃ = V ^b, where b is any constant, then

$$ a_{i}(t)={c_{2}}^{X_{i}} \mathrm{e}^{X_{i} lt}; \qquad i=1,2,3. $$

(42)

The directional Hubble’s parameters H ₁, H ₂ and H ₂ have values given by

$$ H_{i}=X_{i} l. $$

(43)

From eq. (16), the average generalized Hubble’s parameter (H) and expansion parameter (𝜃) have the value given by

$$ \theta=3H=3l. $$

(44)

From eqs (23) and (24), the shear and anisotropy parameters are given by

$$\begin{array}{@{}rcl@{}} \sigma^{2}\!&=&\![{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ && \!-\, 2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]\frac{l^{2}}{2} \end{array} $$

(45)

$$\begin{array}{@{}rcl@{}} A&=&\frac{1}{3}[{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ &&-\, 2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]. \end{array} $$

(46)

From eqs (34) and (42), the scalar curvature (R) for the general class of Bianchi cosmological model is given by

$$\begin{array}{@{}rcl@{}} R&=&2l^{2}\{{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}-n(X_{1}+X_{2}+X_{3})\\ &&+\,(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})\}\\ &&-\,2(m^{2}+m+1){c_{2}}^{-2X_{1}}\mathrm{e}^{-2X_{1} lt}. \end{array} $$

(47)

Using eq. (42) in eqs (17)–(20) and solving eq. (13), we obtain the expressions for pressure (p), energy density (ρ) and cosmological constant (Λ) for the model (14) as

$$\begin{array}{@{}rcl@{}} \rho &=& -\frac{9\lambda A_{1} l^{2}}{(8\pi+\lambda)(m+2)^{2}}\\ &&-\frac{\lambda^{2}}{3(8\pi+\lambda)^{2}}\left\lbrace 9l^{2}-\frac{2(m^{2}+m+1)}{{c_{2}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{2(3+3mb-3b)lt}{m+2}}}\right\rbrace \\ &&+ \frac{\lambda(m^{2}+m+1)}{(8\pi+\lambda){c_{2}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{2(3+3mb-3b)lt}{m+2}}} \end{array} $$

(48)

$$\begin{array}{@{}rcl@{}} p &=& -\frac{9\lambda A_{1} l^{2}}{(8\pi+\lambda)(m+2)^{2}}\\ &&+\frac{\lambda(16\pi+\lambda)}{3(8\pi+\lambda)^{2}}\left\lbrace 9l^{2}-\frac{2(m^{2}+m+1)}{{c_{2}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{2(3+3mb-3b)lt}{m+2}}}\right\rbrace\\ &&+ \frac{\lambda(m^{2}+m+1)}{(8\pi+\lambda){c_{2}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{2(3+3mb-3b)lt}{m+2}}} \end{array} $$

(49)

$$ \begin{array}{llllllll} {\Lambda} \,=\, -\frac{\lambda}{3(8\pi\,+\,\lambda)}\left\lbrace 9l^{2}\,-\,\frac{2(m^{2}\,+\,m\,+\,1)}{{c_{2}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{2(3+3mb-3b)lt}{m+2}}}\right\rbrace\!. \end{array} $$

(50)

Figure 8 shows the variation of cosmological term Λ with cosmic time (t). From the figure we observe that the cosmological term (Λ) is a decreasing function of time (t). It starts from a large positive value and approaches a small positive value for large t.

Figure 8

The plot of cosmological constant (Λ) with cosmic time (t).

Figure 9 depicts the variation of pressure with time. From the figure we observe that the pressure is an increasing function of time. It starts from a large negative value and approaches a small negative value near zero. From the discovery of the accelerated expansion of the Universe, it is generally assumed that this cosmic acceleration is due to some kind of energy-matter with negative pressure known as dark energy.

Figure 9

The plot of pressure (p) with cosmic time (t).

Figure 10 is the plot of energy density (ρ) vs. time. From this figure, we observe that energy density (ρ) is a decreasing function of time (t) and it approaches zero at late time (i.e. at present epoch).

Figure 10

The plot of energy density (ρ) with cosmic time (t).

Figure 11 is the plot of Ricci scalar (R) vs. time. From this figure, we observe that the curvature is positive through the whole evolution of the Universe and $R\rightarrow 0$ as $t\rightarrow \infty$ and $R\rightarrow \infty$ as $t\rightarrow 0$ indicating the initial singularity.

Figure 11

The plot of Ricci scalar (R) with cosmic time (t).

Figures 10, 12, 13 and 14 are the plots of energy conditions (ρ) vs. time. From these figures, we observe that the WEC and DEC for our constructed model are satisfied. It is also observed that the SEC for our constructed model is not satisfied for Bianchi type-III, VI ₀ and VI _h (i.e. m ≠ 1).

Figure 12

The plot of energy condition (ρ − p) with cosmic time (t).

Figure 13

The plot of energy condition (ρ + p) with cosmic time (t).

Figure 14

The plot of energy condition (ρ + 3p) with cosmic time (t).

By using eqs (25), (27), (39) and (44), the cosmological diagnostic pair $\left \{r,s\right \}$ is given by r = 1 and s = 0. It is observed that this model approaches the ΛCDM model.

Therefore, on the basis of the above discussion and analysis, our constructed model and their corresponding solutions are physically acceptable.

Case 3.

When k > 0, n > 1 and a ₃ = V ^b, where b is any constant, then

$$ a_{i}(t)={c_{3}}^{X_{i}} \mathrm{e}^{{(2X_{i}}/{n})\tanh^{-1}(({kt/}{n)}-1)};\qquad i=1,2,3. $$

(51)

The directional Hubble’s parameters H ₁, H ₂ and H ₃ have values given by

$$ H_{i}=\frac{2X_{i}}{t(2n-kt)}. $$

(52)

From eq. (16), the average generalized Hubble’s parameter (H) and expansion parameter (𝜃) have the value given by

$$ \theta=3H=\frac{6}{t(2n-kt)}. $$

(53)

From eqs (23) and (24), the shear and anisotropy parameters are given by

$$\begin{array}{@{}rcl@{}} \sigma^{2}&=&[{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ &&-\,2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]\\ &&\times\,\frac{4}{t^{2}(2n-kt)^{2}} \end{array} $$

(54)

$$\begin{array}{@{}rcl@{}} A&=&\frac{1}{3}[{X_{1}}^{2}+{X_{2}}^{2}+{X_{3}}^{2}\\ &&-\,2(X_{1}X_{2}+X_{2}X_{3}+X_{3}X_{1})+3]. \end{array} $$

(55)

From eqs (34) and (51), the scalar curvature (R) for the general class of Bianchi cosmological model is given by

$$\begin{array}{@{}rcl@{}} R{}&=&{}\frac{4}{t^{2}(2n{}-{}kt)^{2}}({X_{1}}^{2}{}+{}{X_{2}}^{2}{}+{}{X_{3}}^{2}\\ &&-\,n(X_{1}{}+{}X_{2}{}+{}X_{3}){}+{}(X_{1}X_{2}{}+{}X_{2}X_{3}{}+{}X_{3}X_{1}) )\\ &&-\,\frac{2(m^{2}+m+1)}{{c_{3}}^{2X_{1}}\mathrm{e}^{(4X_{1}/{n)}\tanh^{-1}(({kt}/n){}-1)}}. \end{array} $$

(56)

Using eq. (51) in eqs (17)–(20) and solving eq. (13), we obtain the expressions for pressure (p), energy density (ρ) and cosmological constant (Λ) for the model (14) as

$$\begin{array}{@{}rcl@{}} \rho &=& -\frac{36\lambda A_{1} }{(8\pi+\lambda)(m+2)^{2}t^{2}(2n-kt)^{2}}\\ &&-\frac{\lambda^{2}}{3(8\pi+\lambda)^{2}}\left\lbrace \frac{12(3-n+kt)}{t^{2}(2n-kt)^{2}}\right.\\ &&-\frac{2(m^{2}+m+1)}{{c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}\left( \frac{kt}{n}-1\right)}}\!\!\left.\vphantom{\frac{12(3-n+kt)}{t^{2}(2n-kt)^{2}}}\right\rbrace\\ &&+ \frac{\lambda(m^{2}+m+1)}{(8\pi+\lambda){c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}\left( \frac{kt}{n}-1\right)}}\\ \end{array} $$

(57)

$$\begin{array}{@{}rcl@{}} p &=& -\frac{36\lambda A_{1} }{(8\pi+\lambda)(m+2)^{2}t^{2}(2n-kt)^{2}}\\ &&+\frac{\lambda(16\pi +\lambda)}{3(8\pi+\lambda)^{2}}\left\lbrace{\vphantom{\frac{2(m^{2}+m+1)}{{c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}\left( \frac{kt}{n}-1\right)}}}} \frac{12(3-n+kt)}{t^{2}(2n-kt)^{2}}\right.\\ &&\left.-\frac{2(m^{2}+m+1)}{{c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}\left( \frac{kt}{n}-1\right)}}\right\rbrace\\ &&+\frac{\lambda(m^{2}+m+1)}{(8\pi+\lambda){c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}(\frac{kt}{n}-1)}}\\ \end{array} $$

(58)

$$\begin{array}{@{}rcl@{}} {\Lambda} &=& \frac{-\lambda}{3(8\pi+\lambda)}\left\lbrace \frac{12(3-n+kt)}{t^{2}(2n-kt)^{2}}\right.\\ &&-\frac{2(m^{2}+m+1)}{{c_{3}}^{\frac{2(3+3mb-3b)}{m+2}} \mathrm{e}^{\frac{4(3+3mb-3b)}{n(m+2)}\tanh^{-1}(\frac{kt}{n}-1)}}\!\!\left.\vphantom{\frac{12(3-n+kt)}{t^{2}(2n-kt)^{2}}}\right\rbrace. \end{array} $$

(59)

In all the above cases, we observe that, for large cosmic time (t), the spatial volume, expansion parameter, shear scalar and mean anisotropic parameter tend to zero. The energy density and pressure also tend to zero for large cosmic time (t).

Here, from eqs (53) and (54), we observe that $\lim _{t\rightarrow \infty } {(\sigma ^{2}}/{\theta )}=0$, and so the model approaches isotropy for large cosmic time (t). The conditions of homogeneity and isotropization, formulated by Collins and Hawking [59], are satisfied in the present model.

Figure 15 is the plot of cosmological term Λ vs. time. From this figure, we observe that Λ is a decreasing function of time (t) and it approaches a small positive value at late time (i.e at the present epoch).

Figure 15

The plot of cosmological constant (Λ) with cosmic time (t).

Figure 16 depicts the variation of pressure with time. From the figure we observe that the pressure is an increasing function of time. It starts from a large negative value and approaches a small negative value near zero. From the discovery of the accelerated expansion of the Universe, it is generally assumed that this cosmic acceleration is due to some kind of energy-matter with negative pressure known as dark energy.

Figure 16

The plot of pressure (p) with cosmic time (t).

Figure 17 is the plot of energy density (ρ) vs. time. From this figure, we observe that energy density (ρ) is a decreasing function of time (t) and it approaches zero at late time (i.e. at the present epoch).

Figure 17

The plot of energy density (ρ) with cosmic time (t).

Figure 18 is the plot of Ricci scalar (R) vs. time. From this figure, we observe that the curvature is positive through the whole evolution of the Universe and $R\rightarrow 0$ as $t\rightarrow \infty$ and $R\rightarrow \infty$ as $t\rightarrow 0$ indicating the initial singularity.

Figure 18

The plot of Ricci scalar (R) with cosmic time (t).

Figures 17, 19, 20 and 21 are the plots of energy conditions (ρ) vs. time. From these figures, we observe that the WEC and DEC for our constructed model are satisfied. It is also observed that the SEC for our constructed model is not satisfied for Bianchi type-III, VI ₀ and VI _h (i.e. m ≠ 1).

Figure 19

The plot of energy condition (ρ − p) with cosmic time (t).

Figure 20

The plot of energy condition (ρ + p) with cosmic time (t).

Figure 21

The plot of energy condition (ρ + 3p) with cosmic time (t).

Therefore, on the basis of the above discussion and analysis, our constructed model and their corresponding solutions are physically acceptable.

4 Conclusions

In this paper, we have considered a general class of cosmological model in the presence of perfect fluid and variable cosmological constant in f(R, T) theory of gravity [45], where the gravitational Lagrangian is given by an arbitrary function of Ricci scalar (R) and of the trace of the stress-energy tensor (T). In this paper, the gravitational field equation has been established by taking f(R, T) = f ₁(R) + f ₂(T) [55].

We have obtained cosmological solutions of the general class of Bianchi model for different values of m. The general class of Bianchi cosmological model reduces to Bianchi type-III, V, VI ₀ and VI _h cosmological model for different values of m = 0,1,−1 and all other values of m respectively. The exact solutions to the corresponding field equations are obtained in quadrature form. The cosmological parameters have been discussed in each cases.

We have also discussed the well-known physical properties of our constructed model in three different viable cosmologies. It is shown that our constructed model represents an expanding, shearing, non-rotating and accelerated Universe. For suitable choice of constants, the anisotropic parameter tends to zero for sufficiently large time. It has been found that Λ is a decreasing function of time t and it converges to a small positive value at late time. It is also observed that $\lim _{t\rightarrow \infty } (\sigma ^{2}/{\theta })\,=\,0$, and so our constructed model approaches isotropy for large cosmic time t. We have also observed that our constructed model and our derived solutions for three different cases are physically acceptable in concordance with the fulfilment of WEC, DEC and SEC for Bianchi type-V (i.e. m = 1), whereas the WEC and DEC are satisfied but SEC is not satisfied for Bianchi type-III, VI ₀ and VI _h (i.e. m ≠ 1). For suitable values of n, this model approaches ΛCDM model. Hence, our constructed model and their solutions are physically acceptable.