1 Introduction

The mathematical modelling of physical phenomena often leads to nonlinear evolution equations. It is worth mentioning that many of these equations are integrable which implies that, from these equations, one can extract almost as much information as one can extract from the corresponding linear ones. The nonlinear equations, however, exhibit richer phenomena than the linear equation. In particular, many of them support the solitary waves or the so-called soliton solutions. Theoretically, the soliton concept was developed by Zabusky and Kruskal [1], who were experimenting with the numerical solution of the Kortweg–de Vries (KdV) equation [2].

On the other hand, electron acoustic waves (EAWs) do exhibit soliton solutions and have been investigated in detail both theoretically and experimentally by many researchers [3–5]. The evolution of small-amplitude EAWs in collisionless plasma is usually described by nonlinear evolution equations such as KdV, KdV-type, Zakharov–Kuznetsov (ZK) equation, and nonlinear Schrödinger equation [6–10]. EAWs have been observed in the laboratory when the plasma consisted of two species of electrons with different temperatures, referred to as hot and cold electrons [11,12]. Also, its propagation plays an important role not only in the laboratory but also in space plasma. For example, the EAWs have been used to describe the electrostatic component of the electrostatic noise, in the cusp of terrestrial magnetosphere, earth bow shock and the heliosphere termination shock [13–15]. It is important to note that electron acoustic waves (EAWs) are typically high-frequency dispersive plasma waves because their frequency is much larger than the ion frequency. In EAWs, the inertia is provided by the cold electrons and the restoring force comes from the presence of hot electrons [16]. The ions play the role of a neutralizing background. In this case, ion dynamics do not influence the EAWs. EAWs can only propagate in a limited region of the system parameters. This is due to the short and long wavelength of EAWs which face strong Landau damping on account of its resonance with either hot or cold electron components. Watanabe and Taniuti [17] have first showed the existence of electron acoustic waves in a plasma of two-temperature (hot and cold) electrons. The EAWs will give stable oscillations only when the hot and cold electron temperature ratio T h/T e ≤ 10 and 0.2 ≤ n e ≤ 0.8, where n e = n c + n h (the sum of cold and hot electron densities). Otherwise it will be heavily damped.

Physics of quantum plasma has attracted a lot of attention because of its significant applications in metal nanostructures [18], astrophysical systems [19], ultrasmall electronic devices [20,21], biophotonics [22], cool vibes [23], neutron stars [24], laser-produced plasmas [25], quantum wells and quantum diodes [26,27]. Thermal de Broglie wavelength can measure the quantum effects of the particle composing the plasma as \(\lambda _{\mathrm {B}}=\hbar /(mv_{\mathrm {T}})\), where \(\hbar \) is the Planck’s constant, m is the particle mass and v T is the thermal speed of the particle. When the de Broglie wavelength (λ B) is equal to or greater than the average interparticle distance n −1/3, i.e., n λ 3 ≥ 1, the quantum effect starts playing an important role. On the other hand, it is known from statistical mechanics of ordinary gases that quantum effects are significant when the temperature (T) is lower than the Fermi temperature (T Fe), i.e., \(T_{\text {Fe}}/T=\frac {1}{2}(3\pi ^{2})^{2/3}(n\lambda ^{3})\geq 1\). If we compare classical plasma with quantum plasma, we see that the electron de Broglie wavelength (λ Be) is less than the electron Debye radius (λ De) (i.e., λ Be < λ De). But in quantum plasma (i.e., λ Be > λ De) the density correction is significant because n λ 3 ≥ 1. The numerical calculations done here are for plasma parameters satisfying the above criteria. The quantum effect is incorporated in the Bohm term, introduced semiclassically in the field model by Hass et al [28].

Quantum effects are usually studied with the help of two well-known formulations, viz. the Wigner–Poisson and the Schrödinger–Poisson formulations. The Wigner–Poisson model is often used to study the quantum kinetic behaviour of plasma while the Schrödinger–Poisson model describes the hydrodynamic behaviour of plasma particles in quantum scale. The interaction of two unidirectional solitons is most frequently investigated not only in physics but also in coastal engineering.

Several researchers [29–36] have investigated head-on collision and related phase shift of different solitary waves in different plasma models. But the overtaking collisions of solitons, especially phase shifts after collision, have been studied by only a few researchers. Only recently, Sahu and his collaborators [37,38] have studied the nonplanar effect on the two-soliton interaction when one soliton overtakes the other. They used Hirota’s bilinear method to find multisoliton solution. Roy et al [39] have also studied the overtaking collision of two solitons and obtained the phase shift during such collisions. But the interaction of three solitons and their related phase shifts due to the overtaking collision have hardly been studied for quantum plasmas. The objective of the present paper is to study the interaction and phase shift during collision of two- as well as three-electron acoustic soliton interactions using Hirota’s method in nonmagnetized, collisionless, ultracold electron acoustic quantum plasma. The organization of the present paper is as follows:

Section 2 deals with the basic equations and derivation of the KdV equation by employing the reductive perturbation technique. In §3, the interactions of the two as well as three solitons and their related phase shifts have been discussed. Finally, we make some concluding remarks in §4.

2 Basic equations and derivation of KdV equation

Let us consider an unmagnetized and collisionless quantum plasma consisting of ions, and both hot and cold electrons. We consider the dynamics of cold electrons in the background of hot electrons and ions. The phase speed of EAWs lies between v Fc and v Fh, i.e. v Fc≪ω ≪ v Fh, where v Fc and v Fh are Fermi velocities of cold and hot electrons, respectively. The basic normalized equations are:

The continuity equation for cold electron is

$$\begin{array}{@{}rcl@{}} \frac{\partial n}{\partial t}+\frac{\partial(nu)}{\partial x} =0. \end{array} $$
(1)

The momentum equation for cold electron is

$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x} = \alpha \frac{\partial \phi}{\partial x}. \end{array} $$
(2)

The equation of momentum for inertialess hot electron is

$$\begin{array}{@{}rcl@{}} \frac{\partial \phi}{\partial x}-n_{\mathrm{h}}\frac{\partial n_{\mathrm{h}}}{\partial x}+\frac{H^{2}}{2}\frac{\partial}{\partial x}\left[\frac{\partial^{2}\sqrt{n_{\mathrm{h}}}/\partial x}{\sqrt{n_{\mathrm{h}}}}\right]=0. \end{array} $$
(3)

The Poission equation is

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2}\phi}{\partial x^{2}}=n_{\mathrm{h}}+\frac{1}{\alpha}n-\left( 1+\frac{1}{\alpha}\right). \end{array} $$
(4)

Integrating eq. (3) once with the boundary condition, viz. n h → 1 and ϕ → 0 at ±∞, we have

$$\begin{array}{@{}rcl@{}} \phi&=&-\frac{1}{2}+\frac{n_{\mathrm{h}}^{2}}{2}-\frac{H^{2}}{2\sqrt{n_{\mathrm{h}}}}\frac{\partial^{2}\sqrt{n_{\mathrm{h}}}}{\partial x^{2}}, \end{array} $$
(5)

where n, n h, u and m e are the electron number density normalized to n 0, hot electron number density normalized to n h0, cold electron velocity normalized to \(\sqrt {2k_{\mathrm {B}}T_{\text {Fh}}}/\alpha _{\mathrm {e}}\) and electron mass respectively. Also α = n h0/n 0>1, T Fh is the Fermi temperature of hot electron, k B is the Boltzmann constant and e is the electron charge. ϕ is the electrostatic wave potential normalized to 2k B T Fh/e, H is the nondimensional quantum parameter due to hot electron determined by \(H=\hbar \omega _{\text {ph}}/2k_{\mathrm {B}}T_{\text {Fh}},~\omega _{\text {ph}}=\sqrt {4\pi n_{\mathrm {h}0}e^{2}/m_{\mathrm {e}}}\) is the hot electron plasma frequency, \(\hbar \) is the Planck’s constant. Space variables are normalized to the Fermi wavelength of the hot electron \((\lambda _{\text {Fh}}=\sqrt {2k_{\mathrm {B}}T_{\text {Fh}}/4\pi n_{h0}e^{2}})\) and time is normalized to the inverse of the cold elctron plasma frequency \((\omega ^{-1}_{\text {pc}}=\sqrt {m_{\mathrm {e}}/4\pi n_{0}e^{2}})\). In an unperturbed state, neutrality condition gives n 0 + n h0 = n i0. The Fermi temperature of hot electrons is given by the relation \(m_{\mathrm {e}}v_{\text {Fh}}^{2}/2=k_{\mathrm {B}}T_{\text {Fh}}\). Now, we derive the KdV equation from eqs (1)–(5) by employing the reductive perturbation technique. The independent variables are stretched as ξ = 𝜖 1/2(x−λ t), τ = 𝜖 3/2 t and the dependent variables are expanded as

$$ n=1+\epsilon n^{(1)}+\epsilon^{2} n^{(2)}+\cdots, $$
(6)
$$ u=0+\epsilon u^{(1)}+\epsilon^{2} u^{(2)}+{\cdots} , $$
(7)
$$ n_{\mathrm{h}}=1+\epsilon n_{\mathrm{h}}^{(1)}+\epsilon^{2} n_{\mathrm{h}}^{(2)}+{\cdots} ,\\ $$
(8)
$$ \phi=0+\epsilon \phi^{(1)}+\epsilon^{2} \phi^{(2)}+\cdots, $$
(9)

where 𝜖 is a small nonzero parameter proportional to the amplitude of perturbation. Now, subtituting (6)–(9) into (1)–(5) and taking the terms in different powers of 𝜖, we obtain in the lowest order of 𝜖, the dispersion relation as

$$ \lambda^{2}=1. $$
(10)

In the next higher order of 𝜖, we eliminate the second-order perturbed quantities from a set of equations to obtain the required KdV equation. As this is a standard procedure, we skip the details and just write the KdV equation.

$$ \frac{\partial \phi^{(1)}}{\partial \tau}-A\phi^{(1)}\frac {\partial \phi^{(1)}}{\partial\xi}+B\frac{\partial^{3} \phi^{(1)}}{\partial \xi^{3}}=0, $$
(11)

where the nonliner coefficient A and the dispersion coefficient B are given by

$$\begin{array}{@{}rcl@{}} A&=&\frac{\lambda}{2}(3\alpha-1), \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} B&=&\frac{\lambda}{2}\left( 1-\frac{H^{2}}{4}\right). \end{array} $$
(13)

The amplitude and width of a single soliton are respectively

$$\begin{array}{@{}rcl@{}} \phi_{m}&=&-\frac{3M}{A}, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} W&=&\sqrt{\frac{4B}{M}},\ \end{array} $$
(15)

where M is the normalized constant speed of the wave frame.

Let us recall ξ by \(\bar {\xi }B^{1/3},~\phi ^{(1)}\) by \(6\bar {\phi }^{(1)}A^{-1}B^{1/3}\) and τ by \(\bar {\tau }\). Then eq. (11) will be transformed to the following standard KdV equation:

$$ \frac{\partial {\bar\phi}^{(1)}}{\partial \bar{\tau}}-6\bar{\phi}^{(1)}\frac {\partial \bar{\phi}^{(1)}}{\partial\bar{\xi}}+\frac{\partial^{3} \bar{\phi}^{(1)}}{\partial \bar{\xi}^{3}}=0. $$
(16)

The transformations (11)–(refeq1616) are valid for B > 0 which implies H < 2.

3 Results and discussion

3.1 Two-soliton solution

Now our aim is to obtain two-soliton solution of eq. (11) and to study the interaction between them. To do so, we shall employ Hirota’s billinear method and we get the Hirota bilinear form (for details, see refs [38–41])

$$ (D_{\bar{\xi}}D_{\bar{\tau}}+D_{\bar{\xi}}^{4})\{f\cdot f\}=0. $$
(17)

After some long but standard calculation, we get the two-soliton solution of the KdV equation (11) as

$$ \phi^{(1)}=-12\frac{B^{1/3}}{A}\frac{{k_{1}^{2}}\mathrm{e}^{\theta_{1}}+{k_{2}^{2}}\mathrm{e}^{\theta_{2}}+a_{12}\mathrm{e}^{\theta_{1}+\theta_{2}}({k_{2}^{2}}\mathrm{e}^{\theta_{1}}+{k_{1}^{2}}\mathrm{e}^{\theta_{2}})+2(k_{1}-k_{2})^{2}\mathrm{e}^{\theta_{1}+\theta_{2}}}{(1+\mathrm{e}^{\theta_{1}}+\mathrm{e}^{\theta_{2}}+a_{12}\mathrm{e}^{\theta_{1}+\theta_{2}})^{2}} $$
(18)

with

$$\theta_{i}=\frac{k_{i}}{B^{1/3}}\xi-{k_{i}^{3}}\tau+\alpha_{i}, \qquad a_{12}=(k_{1}-k_{2})^{2}/(k_{1}+k_{2})^{2}.$$

a 12 determines the phase shifts of the respective solitons after overtaking takes place.

When τ ≫ 1, the solution of eq. (11) asymptotically transforms into a superposition of two single-soliton solutions [41,42]

$$\begin{array}{@{}rcl@{}} \phi^{(1)}&\approx &-\frac{3B^{1/3}}{A}\left[\frac{{k_{1}^{2}}}{2}\text{sech}^{2}\left\{\frac{k_{1}}{2B^{1/3}}(\xi-B^{1/3}{k_{1}^{2}}\tau -{\Delta}_{1})\right\}\right.\\&&\left. +\frac{{k_{2}^{2}}}{2}\text{sech}^{2}\left\{\frac{k_{2}}{2B^{1/3}}(\xi-B^{1/3}{k_{2}^{2}}\tau-{\Delta}_{2})\right\}\right], \end{array} $$
(19)

where

$${\Delta}_{i}=\pm \frac{2B^{1/3}}{K_{i}}\ln|\sqrt{a_{12}}|,~i=1,2.$$

It is to be noted that the phase shifts Δ1 and Δ2 are of the same sign and both of them are proportional to B 1/3 and the amplitude, a result consistent with those obtained in the study of head-on collision [43,44] of two solitons. It is to be noted that B depends on H (see eq. (13)). The phase shifts will also depend on the parameter H.

Here, while the coefficient A is independent of H, the coefficient B depends on H. It is to be noted that dispersion coefficient B vanishes at H = 2. This critical value of H destroys the KdV equation (eq. (11)) and no soliton can occur for this critical case. No soliton solution is possible for H > 2. However, we find that when H < 2 formation of soliton structure is possible.

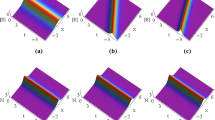
In figure 1, time evalution of the interaction of two-soliton solution ϕ (1) vs. ξ is plotted for different values of τ. At τ = −5, the larger amplitude soliton is behind the smaller amplitude solitary wave. When τ = −1, two solitons merge and become one soliton at τ = 0. But at τ = 1, they seperate from each other and then finally each appears as a seperate soliton acquiring their respective speed and shape unchanged. It can be clearly seen from the exact two-soliton solution and asymptotical solution that while the amplitude of the merged soliton is greater than the amplitude of the shorter soliton, it is less than the amplitude of the taller soliton (for example, see the solution given by Drazin et al [42] in page 76).

Figure 1
figure 1

Variation of the two-soliton profiles ϕ (1) (eq. (18)) for different values of τ with k 1 = 1, k 2 = 2, H = 1.5, α = 1.2, α 1 = 1, α 2 = 1.

Full size image

In figure 2, we have plotted the solitary potential structure ϕ (1) against ξ for different values of H. It is seen from the figure that the amplitude of the solitons decreases with the increase in H (0 < H < 2). Physically, this happens because the increase of H makes the coefficient of the nonlinear term of KdV equation to decline, as a result of which the amplitude of the soliton goes down. It is found that soliton with larger amplitude overtakes the small one eventually because a 12 is an important quantity which determines the phase shift, that is the change of position, caused by the interaction of two solitons.

Figure 2
figure 2

Two-soliton profiles ϕ (1) (eq. (18)) plotted against ξ for different values of H. Other parameters are the same as those in figure 1.

Full size image

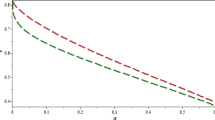
In figure 3, the variations of phase shifts are plotted against the parameter H, while the other parameters are kept the same as those in figure 2. It is seen from figure 3 that the phase shifts Δ1, Δ2 decrease with increase in H. They tend to vanish as H → 2. This behaviour can be anticipated by the relationship between Δ i (i=1,2) and H through the parametrs B (eq. (13)) and \(|{\Delta }_{i}|=\pm \frac {2B^{1/3}}{K_{i}}\ln |\sqrt {a_{12}}|,~i=1,2.\)

Figure 3
figure 3

Variation of the phase shift for two-soliton against the parameter H. Other parameters are the same as those in figure 1.

Full size image

3.2 Three-soliton solution

To construct three-soliton solution we use the Hirota perturbation and finally we get the three-soliton solution of the KdV equation (11) as

$$\begin{array}{@{}rcl@{}} \phi^{(1)}=-12\frac{B^{1/3}}{A}\frac{L_{1}}{M_{1}}, \end{array} $$
(20)

where

$$\begin{array}{@{}rcl@{}} L_{1}&=&\mathrm{e}^{\theta_{1}+\theta_{2}}\left[2(k_{1}-k_{2})^{2}+2(k_{1}-k_{2})^{2}a_{13}a_{23}\mathrm{e}^{2\theta_{3}} +a_{12}{k_{1}^{2}}\mathrm{e}^{\theta_{2}}+a_{12}{k_{2}^{2}}\mathrm{e}^{\theta_{1}}\right]\\ &&+\mathrm{e}^{\theta_{1}+\theta_{3}}\left[2(k_{1}-k_{3})^{2}+2(k_{1}-k_{3})^{2}a_{12}a_{23}\mathrm{e}^{2\theta_{2}} +a_{13}{k_{1}^{2}}\mathrm{e}^{\theta_{3}}+a_{13}{k_{3}^{2}}\mathrm{e}^{\theta_{1}}\right]\\ &&+\mathrm{e}^{\theta_{2}+\theta_{3}}\left[2(k_{2}-k_{3})^{2}+2(k_{2}-k_{3})^{2}a_{12}a_{13}\mathrm{e}^{2\theta_{1}} +a_{23}{k_{2}^{2}}\mathrm{e}^{\theta_{3}}+a_{23}{k_{3}^{2}}\mathrm{e}^{\theta_{2}}\right]\\ &&+{k_{1}^{2}}\mathrm{e}^{\theta_{1}}+{k_{2}^{2}}\mathrm{e}^{\theta_{2}}+{k_{3}^{2}}\mathrm{e}^{\theta_{3}}\\ &&+B_{1}\mathrm{e}^{\theta_{1}+\theta_{2}+\theta_{3}}\left[a_{12}{k_{3}^{2}}\mathrm{e}^{\theta_{1}+\theta_{2}} +a_{13}{k_{2}^{2}}\mathrm{e}^{\theta_{1}+\theta_{3}}+a_{23}{k_{1}^{2}}\mathrm{e}^{\theta_{2}+\theta_{3}}\right] \end{array} $$
$$\begin{array}{@{}rcl@{}} &&+\mathrm{e}^{\theta_{1}+\theta_{2}+\theta_{3}}[a_{12}({k_{1}^{2}}+{k_{2}^{2}}+{k_{3}^{2}}+2k_{1}k_{2}-2k_{1}k_{3} -2k_{2}k_{3})\\ &&+a_{13}({k_{1}^{2}}+{k_{2}^{2}}+{k_{3}^{2}}+2k_{1}k_{3}-2k_{1}k_{2}-2k_{2}k_{3})\\ &&+a_{23}({k_{1}^{2}}+{k_{2}^{2}}+{k_{3}^{2}}+2k_{2}k_{3}-2k_{1}k_{2}-2k_{1}k_{3})\\ &&+B_{1}({k_{1}^{2}}+{k_{2}^{2}}+{k_{3}^{2}}+2k_{1}k_{2}+2k_{1}k_{3}+2k_{2}k_{3})],\\ M_{1}&=&[1+\mathrm{e}^{\theta_{1}}+\mathrm{e}^{\theta_{2}}+\mathrm{e}^{\theta_{3}}+a_{12}\mathrm{e}^{\theta_{1} +\theta_{2}}+a_{13}\mathrm{e}^{\theta_{1}+\theta_{3}}+a_{23}\mathrm{e}^{\theta_{2}+\theta_{3}}\\ &&+B_{1}\mathrm{e}^{\theta_{1}+\theta_{2}+\theta_{3}}]^{2},\\ B_{1}&=&a_{12}a_{13}a_{23},\\ \theta_{i}&=&\frac{k_{i}}{B^{1/3}}\xi-{k_{i}^{3}}\tau+\alpha_{i},\qquad i=1,2,3. \end{array} $$

For τ≫1, the above solution is asymptotically transformed into a superposition of three single-soliton solution as [41]

$$\begin{array}{@{}rcl@{}} \phi^{(1)}\approx -{{\sum}_{i}^{3}}A_{i}\,\text{sech}^{2}\left[\frac{k_{i}}{2B^{1/3}}(\xi-{k_{i}^{2}}B^{1/3}\tau-{\Delta}_{i}^{\prime})\right], \end{array} $$
(21)

where

$$A_{i}=3B^{1/3}{k_{i}^{2}}/2A,\quad i=1,2,3$$

are the amplitudes and

$${\Delta}_{1}^{\prime}=\pm\frac{2B^{1/3}}{k_{1}}\ln\left|\frac{B_{1}}{a_{23}}\right|,\quad {\Delta}_{2}^{\prime}=\pm\frac{2B^{1/3}}{k_{2}}\ln\left|\frac{B_{1}}{a_{13}}\right|,$$
$${\Delta}_{3}^{\prime}=\pm\frac{2B^{1/3}}{k_{3}}\ln\left|\frac{B_{1}}{a_{12}}\right|$$

are the phase shifts of the solitons.

In figure 4, time evalution of the interaction of three-soliton solution ϕ (1) vs. ξ is plotted for different values of τ. At τ = −10, the larger-amplitude soliton is behind the smaller amplitude solitary wave. When τ = −5, two solitons merge and become one soliton at τ = 0. But at τ = 1, they seperate from each other and then finally each appears as a seperate soliton acquiring its original speed and shape.

Figure 4
figure 4

Variation of the three-soliton profiles ϕ (1) (eq. (20)) for different values of τ.

Full size image

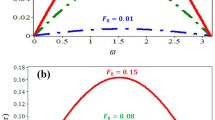
Figure 5 shows the variation of phase shift for respective solitons against H when the values of the other parameters are kept fixed. As before, the phase shifts decrease with increase in H as the value of B decreases with an increase of H.

Figure 5
figure 5

Variation of the phase shift for three-soliton against the parameter H.

Full size image

4 Conclusion

In this paper, we have investigated the nature of nonlinear propagation of two- and three-electron acoustic soliton solutions in an unmagnetized quantum plasma consisting of ions, and both cold and hot electrons. The KdV equation is derived by RPT. Standard KdV equation is obtained by suitable transformation. Using the Hirota’s direct method, we have obtained two-soliton solution of the KdV equation. Propagation of two-soliton and three-soliton has been discussed. We have observed that the larger soliton moves faster, approches the smaller one and after the overtaking collision both resume their orginal shape and speed. The effects of parameters involved in the nonlinear and dispersion coefficients of the KdV equation on the amplitude of two-solitons have been investigated. Although head-on collision and overtaking collision are different phenomena, qualitatively they are consistent with each other. In two-soliton solutions, it is found that k i Δ i , i=1,2 have the same values. However, in three-soliton case, k i Δ i is not the same for i=1,2,3. Each of them is different from the others. Results obtained here could be of interest in space and laboratory plasmas.