1 Introduction

Geodesy was defined by Helmert (1880) as the science devoted to measuring and mapping the Earth’s surface. Further to this effectual definition, the scope of geodesy has been extended, especially due to space-based techniques allowing geodesy to determine the parameters of Earth system with high accuracy. Today, geodesy is the science of determining the geometry, gravity field, and rotation of the Earth and their evolution in time. This understanding of modern geodesy is based on the definition of the three pillars of geodesy: (1) geokinematics, (2) Earth rotation and (3) gravity field (Plag et al. 2009). Geokinematics (geometry and kinematics) refers to determine and monitor with utmost precision the geometric shape of the Earth (land, ice and ocean surface) as well as its variations with time. This pillar of geodesy addresses the problems of the determination of precise three-dimensional object positions from global to local spatial scale and their changes in time. In recent decades, comprehensive efforts have been made to determine these time variations which have become possible owing to the accuracy of new space-geodetic methods, and also owing to a truly global reference system that only space geodesy can realise (Altamimi et al. 2002). Defining a suitable reference system and its realisation as a reference frame is a demanding endeavour to consider the time variation in geokinematics. The geodetic reference frames are the basis for providing means to assign three-dimensional coordinates to points as a function of time in global, regional and national geodetic reference networks. One of the major functions of geodesy is the establishment and maintenance of geodetic reference networks for the presentation of geospatial positioning. Geodetic reference networks are comprised of a set of properly-defined and constructed points distributed on the surface of the Earth to materialise the reference systems to support sub-millimetre global change measurements over space, time and evolving technologies (Pearlman et al. 2006).

According to the theory of plate tectonics, the Earth’s surface is in constant motion. As such, the points in the geodetic networks are not static entities. The crustal motion of the Earth’s surface emanated from tectonic plate movements and displacements associated with earthquakes can cause the geodetic points to move at predictable rates from year to year. These kinematic effects on the geodetic points can be defined by a phenomenon called point velocity (Mathews and Biediger2012). The most demanding scientific and non-scientific requirements concerning positioning are not only the increase in accuracy and temporal stability, but also high spatial and temporal resolution and low latency (Gross et al. 2007). In order to meet these demands, it is vital to determine velocities for all geodetic points on the Earth’s surface. The widespread availability of GPS equipment provides accurate velocity information which results in the determination of precise three-dimensional point coordinates in geodetic networks by considering the time evolution. The spatial positions of geodetic points on the Earth’s surface change over time due to the plate tectonics, and therefore, they are dependent on the epoch of their determination. All these spatial changes have paramount importance in geodetic applications. If we have GPS measurements at least in two epochs, it is possible to compute the change of geodetic point coordinates. Otherwise, a continuous contemporary velocity field of geodetic network is essential. The velocity field of geodetic network is determined from the periodic GPS measurements. The velocities of the new structured geodetic points (e.g., densification points) within the geodetic network are estimated from the velocity field of geodetic network or from the velocities of the existing geodetic points determined by campaign type repeated GPS sessions (static GPS surveying for 8–24 h) by the interpolation methods. The geodetic point velocities derived from measured time series of positions are used as the basic parameter in geodetic and geophysical applications including velocity field determination of geodetic networks, kinematic modelling of crustal movements, understanding plate boundary dynamics, and monitoring global sea level change (Yilmaz 2012). The estimation of an accurate geodetic point velocity has, therefore, great importance in geosciences.

The velocity field determination has been investigated by several researchers (e.g., Demir and Acikgoz 2000; Nocquet and Calais 2003; Perez et al. 2003; D’Anastasio et al. 2006; Hefty 2008; Novotny and Kostelecky 2008; Aktug et al. 2011). The velocity information has been used by several researchers in crustal movements, plate boundary dynamics, seismic site characterization and deformation kinematics (e.g., McClusky et al. 2000; Delacou et al. 2008; Hackl et al. 2009; Kanli 2009; Perez-Pena et al. 2010; Foti et al. 2011; Pinna et al. 2011).

Artificial neural network (ANN) can be viewed as a computational method that is a highly simplified model of learning, interpretation and decision-making processes presented in human biological nerve systems, and it is formed by layers of interconnected artificial neurons which transform the input data into associated output data. ANNs have been applied in diverse fields of science and engineering for several types of functions such as estimation, modelling, classification, prediction, filtering, and optimisation because of their major advantages (i.e., non-parametric nature, tolerance to noisy data, applicability to complex data, arbitrary decision making capabilities and incorporation of different types of data) (Yilmaz 2012). Many geophysical phenomena are described as self-affine fractals characterized by coefficients that can be calculated by various methods such as wavelet transform, power spectrum and rescaled range analysis, etc. In practice, the geophysical data are of limited duration with gaps or noises and non-stationary, and the calculation of coefficient is not reliable for short or noisy time series (Chamoli et al. 2007). ANNs gave a new dimension for solving complex geophysical problems. Neural-based methods are well equipped to deal with the real world problem of non-stationarity and non-linearity (Dimri and Chamoli 2008). ANNs have been found to be effective in identifying the complex behaviour of most geophysical data which, by their very nature, exhibits extreme variability (Shahin et al. 2008) and have the ability to analyse non-stationary geophysical data like wavelet transforms. In geophysical and geodetic applications, the data are assumed to have a normal distribution, but in real life problems this assumption is not always realistic as dataset might show abnormal and highly skewed distribution. ANNs provide linear and non-linear mapping between input and output spatial data by its non-parametric nature which assumes no a priori knowledge (as in traditional regression models), particularly of the frequency distribution of the data. This provides ANN a unique advantage over other statistical and conventional prediction techniques such as regression and interpolation methods (i.e., Pariente 1994; Kumar 2005; Singh et al. 2005; Karabork et al. 2008; Erol and Erol 2013).

ANN applications in geophysical and geodetic velocity modelling problems have increased in the last decade. Calderon-Macias et al. (2000) have used ANN in order to obtain 1D velocity models from seismic waveform data. Eskandari et al. (2004) compared multiple regression and ANN to predict shear wave velocity in the seismic exploration. Baronian et al. (2007) described an ANN approach for seismic velocity analysis. Peak ground velocities are used as input data in ANN application in the seismic design of deep tunnels by Ornthammarath et al. (2008). Moghtased-Azar and Zaletnyik (2009) have compared the ability of ANNs and polynomials for modelling the crustal velocity field. Gullu et al. (2011) have applied ANN for the velocity estimation of the points in a local geodetic network.

The main objective of this study is to evaluate the utility of ANN in order to estimate the velocities of the points as an alternative tool for the conventional methods in a regional geodetic network. The development and optimisation of ANN are searched to obtain the best model configuration for the geodetic velocity estimation prediction. There are numerous kinds of neural networks. However, two different types of ANN that have been more widely applied among all other ANN applications are back propagation artificial neural networks (BPANN) and radial basis function neural networks (RBFNN), which are used to estimate the geodetic point velocities in this study. In order to evaluate the performance of BPANN and RBFNN, the point velocities are also estimated by Kriging (KRIG) interpolation method, and the results are compared in terms of the root mean square error (RMSE) over five different geodetic networks in the study area. The general scheme of this paper is organised as follows: In section 2, the theoretical aspects of BPANN, RBFNN, and KRIG are described. Section 3 outlines the study area, the structured geodetic networks, the point velocity data used and the evaluation methodology. The detailed information about the design and the optimisation of ANN is given in section 4. Section 5 is concerned with the case study. The results and conclusions of ANN’s utility for geodetic point velocity estimation are presented in section 6 to motivate further studies.

2 Theoretical aspects

Two supervised and feed-forward ANN types, BPANN and RBFNN were used in artificial neural approach of this study. A commonly applied method for spatial data, KRIG, was used in interpolation approach. The detailed theoretical information about these methods is given below.

2.1 Back propagation artificial neural network

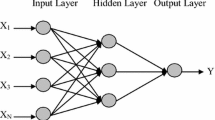
BPANN (Werbos 1974; Rumelhart et al. 1986) is a widely used and effective multilayer perceptron (MLP) model due to their simple implementation and 'exibility for a wide spectrum of problems in many application areas varying from military purposes to finance, medicine, engineering and space sciences. BPANN consists of (i) an input layer with neurons representing input variables to the problem, (ii) one or more hidden layers containing neurons to help capture the nonlinearity in the data and (iii) an output layer with neurons representing the dependent variables. The architecture of a simple BPANN is shown in figure 1. All inter-neuron connections have been associated by means of synaptic weights that are adjusted by an iterative back propagation algorithm known as training process. The introduction of back propagation algorithm has overcome the drawback of previous ANN algorithm of 1970s where the single layer perceptron failed to solve a simple XOR (Exclusive OR) problem. After the training procedure, an activation function is applied to all neurons to generate the output information (Leandro and Santos 2007) within a permissible amplitude range.

Figure 1
figure 1

The BPANN architecture.

Full size image

The output of BPANN with a single output neuron (output layer represented by only one neuron, i.e., n = 1) can be expressed according to Nørgaard (1997) by:

$$ y=f\left( {\sum\limits_{j=1}^{q} {W_{j} f\left( {\sum\limits_{l=1}^{N} {w_{j,l} x_{l} +w_{j,0} } } \right)+W_{0} } } \right), $$
(1)

where N is the number of inputs, q is the number of hidden neurons, W j is the weight between the jth hidden neuron and the output neuron, w j,l is the weight between the lth input neuron and the jth hidden neuron, x l is the lth input parameter, w j,0 is the weight between a fixed input equal to 1 and jth hidden neuron, and W 0 is the weight between a fixed input equal to 1 and the output neuron (Valach et al. 2007). The sigmoid function is the most commonly used activation function satisfying the approximation conditions of BPANN (Haykin 1999; Beale et al. 2010) and is represented by:

$$ f(z)=\frac{1}{(1+e^{-z})}, $$
(2)

where z is the input information of the neuron and f(z) 𝜖 [0, 1]. The input and output values of BPANN have to be scaled in this range.

The back propagation algorithm based on squared error minimization corresponds to an adjustment of the weights between the hidden layer and the output layer. This iterative process updates the weights in order to decrease the residuals of the predicted output of the neural network. It requires the estimation of the network parameters that lead to the global minimum of a cost function E. Typically, this cost function is chosen to be the sum of the squared discrepancies between computed and target output over all samples N and all output units K:

$$ E=\frac{1}{N}\sum\limits_{i=1}^{N} {\left[ {\frac{1}{2}\sum\limits_{k=1}^{K} {\left( {y_{i}^{\prime} ( k )-y_{i} ( k )} \right)^{2}} } \right],} $$
(3)

where \(y^{\prime }_{i}\)(k) is the BPANN output and y i (k) is the target response of each output neuron k.

The new weights are estimated by modifying them in the opposite direction of the gradient of the cost function in the point of actual estimation. The weight-update at iteration ‘t’ is given by:

$$ \Delta w_{j,l} (t)=-\eta \frac{\partial E}{\partial w_{j,l} }+\alpha \cdot \Delta w_{j,l} ({t-1}), $$
(4)

where the parameter η denotes learning rate and α is the momentum term.

2.2 Radial basis function neural network

RBFNN (Powell 1987) is known from the approximation theory as it is applied to the real multivariate interpolation problem. RBFNN is popularized by Moody and Darken (1989), and many researchers suggested it as an alternative ANN structure to MLP. RBFNN is very useful for function approximation and classification problems because of its more compact topology and faster learning speed. RBFNN is conFigured with three layers (figure 2). An input layer consists of source neurons (sensory units) and distributes input vectors to each of the neurons in the hidden layer without any multiplicative factors. The single hidden layer has receptive field units (hidden neurons) each of which represents a nonlinear transfer function called a basis function. The output layer produces a linear weighted sum of hidden neuron outputs and supplies the response of RBFNN.

Figure 2
figure 2

The RBFNN architecture.

Full size image

The output of ith output neuron can be described in a general expression as follows:

$$ y_{i} =\sum\limits_{j=1}^{q} {w_{ij} \phi_{j} (x)+w_{0}}, $$
(5)

where q is the number of hidden neurons, w ij is the weight between the jth hidden neuron and the ith output neuron, and w 0 is the bias value. The basic function ϕ(⋅) is a nonlinear transformation from the input layer to hidden layer of high dimensionality, and it plays the role of the activation function in MLPs. The most common form of basic function in RBFNN is the Gaussian function (Bishop 2005; Yeung et al. 2010) and it is defined by:

$$ \phi_{j} (x)=\exp \left({-\frac{\| {x-u_{j} }\|^{2}}{2{\sigma_{j}^{2}}}}\right), $$
(6)

where x𝜖R d is the input vector and u j 𝜖 R d and σ j are the centre value and the width parameter of the basic function, respectively, associated with the jth hidden neuron. ||⋅|| denotes the Euclidean distance. The hidden neuron is activated whenever x is close enough to its corresponding uin RBFNN. The location of neurons, the weight coefficients, and the bias are defined during the training process of RBFNN. The training of RBFNN requires a set of data samples for which the corresponding network outputs are known. Mathematically, the training can be considered as an optimization problem where the network parameters are to be solved while the error of the neural network must be minimal.

2.3 Kriging interpolation method

KRIG (Krige 1951) is a geostatistical and 'exible interpolation method which has been extensively used in diverse fields of mathematics, earth sciences, geography and engineering and has proved to be powerful and accurate in its fields of use. According to KRIG, both the distance and the degree of variation between reference points are taken into account for optimal spatial prediction (Joseph 2006). KRIG assigns a mathematical function to a certain number of points or all the points located within a certain area of effect in order to determine the output values for each location (Chaplot et al. 2006). KRIG uses the semivariogram which measures the average degree of dissimilarity between unsampled values and nearby values to define the weights that determine the contribution of each data point to the prediction of new values at unsampled locations (Krivoruchko and Gotway 2004). KRIG is based on a constant mean μ for the data and random errors ε with spatial dependence as follows:

$$ Z( {x_{0} })=\mu ( {x_{0} } )+\varepsilon ( {x_{0} } ), $$
(7)

where Z( x 0) is the variable of interest, μ(x 0) is the deterministic trend, and ε( x 0) is the correlated error (Erdogan 2010). In the ordinary algorithm of KRIG, equation (7) can be given as follows:

$$ Z( {x_{0} } )=\mu ( {x_{0} } )+\sum\limits_{i=1}^{n} {\lambda_{i} [ {z( {x_{i} } )-\mu ( {x_{0} } )} ]} , $$
(8)

where n is the number of sampled points used for the estimation, λ i is the weight assigned to the sampled point ( x i ), and \(\sum \limits _{i=1}^{n} {\lambda _{i} =1}\) is forced (Li and Heap 2008). KRIG is the most appropriate interpolation method when a spatially correlated distance or directional bias in the data is known.

3 Data acquisition and evaluation methodology

The estimation of the geodetic point velocities is performed over a study area located in central and western Anatolian parts of Turkey. The study area is limited by 36.95°–40.50°N in latitude and, 27.10°–32.75°E in longitude, and it defines a total area of ∼182,500 km 2. Its span is approximately 380 km in the north–south direction and 480 km in the east–west direction.

The evaluating procedure of the geodetic points’ velocity refers to a source dataset in the study area that comprises 125 control points belonging to Turkish National Fundamental GPS Network (TNFGN) (Ayhan et al. 2002). The positional accuracies of the TNFGN stations are about 1–3 cm whereas the relative accuracies are within the range of 0.01–0.1 ppm. For each TNFGN station, time-dependent 3D coordinates and their associated velocities were computed in ITRF2000 (reference epoch 2005.00) with repeated GPS observations (Caglar 2006). Velocity solution of TNFGN over the interval 1992–2004 was obtained by the procession of campaign type GPS measurements of 366 TNFGN points. TNFGN velocities with 1 σ standard deviations used in this study are given in table 1.

Table 1 Standard deviations (1 σ) of TNFGN velocities (units in mm/year).
Full size table

The source dataset (125 TNFGN points) is classified into two groups as a reference dataset for the training (modelling) process and a test dataset for the controlling process. In ANN approach, the reference points are used to train BPANN and RBFNN, and the test points are used to evaluate the performance of ANNs. In KRIG approach, the reference points are used to generate a surface model of the study area, and the test points are used to check the estimation accuracy of KRIG. Five different geodetic networks are generated to assess the impact of the point density on the velocity estimation results. The reference points are selected to cover the study area from outside, and the test points are selected as densification points of the geodetic network formed by the reference points. The point classification and density information about the geodetic networks are summarized in table 2, and the spatial distribution of the reference and test points in geodetic networks within the study area is plotted in figure 3.

Figure 3
figure 3

Geodetic networks ( → reference; ● → test).

Full size image
Table 2 Point classification and density of geodetic networks.
Full size table

The evaluation of the geodetic point velocity estimation by BPANN, RBFNN, and KRIG is focused on the differences between the known and estimated point velocities using the equation below:

$$\begin{array}{@{}rcl@{}} \Delta V_{X,Y,Z} &=&V_{X,Y,Z} ( {\text{TNFGN}} )\notag\\ &&-V_{X,Y,Z} ( {\text{BPANN}, \text{RBFNN}, \text{KRIG}}),\notag\\ \end{array} $$
(9)

where ΔV X,Y,Z is the geodetic point velocity residual, V X,Y,Z (TNFGN) is the point velocity known through repeated GPS measurements within TNFGN, and V X,Y,Z (BPANN, RBFNN, KRIG) is the point velocity based on BPANN, RBFNN, and KRIG.

For the statistical analysis of geodetic point velocity residuals ( ΔV X,Y,Z ) minimum, maximum, and mean values were determined and investigated by RMSE value because RMSEs are sensitive to even small errors to measure the deviations between known and estimated discharges on models (Gullu et al. 2011), RMSEs are global measures for comparing interpolation techniques (Erdogan 2010), and are effective tools for evaluating the results of ANN applications (Schroederet al. 2009). RMSE is always positive and it is defined by:

$$ \text{RMSE}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n} {( {\Delta V_{X,Y,Z} } )^{2},} } $$
(10)

where n is the number of test points used in the geodetic network.

4 ANN design and optimisation

The main goal of ANNs is to find a solution to generalize the multidimensional input–output mapping problems. In other words, ANNs perform well when they do not extrapolate beyond the range of the (training) data used for the estimation of their parameters. In order to do so, ANNs have to capture the functional relationship that leads to the mapping of the input data into the output data. ANN structure that is chosen to be too complex in relation to the functional relationship that has to be captured also memorises its free coefficients, the noise contained in the data. This occurrence is called overfitting. Such a model will perform well in approximating the data used in order to estimate its parameters (ANN has memorised the training data) but it will be extremely poor on new data (ANN has not learnt to generalize). To allow proper generalization capabilities, ANN overfitting of the training data must be avoided (i.e., model should be fitted only to the signal present in the training sample, not to the noise). A number of techniques have been developed to further improve ANN generalization capabilities including different variants of cross-validation (Haykin 1999), noise injection (Holmstrom and Koistinen 1992), error regularization, weight decay (Poggio and Girosi 1990; Haykin 1999), and the optimized approximation algorithm (Liu et al. 2008). A number of cross-validation variants exist, and some of them are of special attention when data are very scarce, i.e., multifold cross-validation or leave-one-out (Haykin 1999). But probably the most popular in practical applications (Liu et al. 2008) is the so-called early stopping (Piotrowski and Napiorkowski 2013). To use the early stopping approach in this study, the available dataset is divided into two subsets: (i) training (reference) data used during ANN optimization and (ii) the test data (not presented to ANN during optimization) used to define stopping criteria to prevent overfitting thus ensuring a generalised solution. The division is done keeping in mind that training dataset should be extensive and comprehensive (representative of all possible variations of the data on which ANN will be tested). The mean square error (MSE) (Graupe 2007; Hsieh 2009) is used as the model evaluation indicator. For a given set of N inputs, MSE is defined by:

$$ \text{MSE}={\sum\limits_{1}^{N}} ({y_{\text{act}}-y_{\text{pred}}})^{2}/{N}, $$
(11)

where y act denotes the given actual output value, and y pred denotes the ANN (predicted) output. The performance of ANN during the training and testing process is monitored in the form of MSE. The testing error normally decreased during the initial phase of training, as did the training error. However, when overfitting occurred, the testing error typically began to rise. When the testing error increased, the training process was stopped, and it is assumed that optimal ANN parameters were reached. In table 3, the MSEs of ANNs obtained by early stopping to avoid overfitting are shown for training and test dataset on Geodetic Network (1).

Table 3 MSEs of the datasets (units in mm/year).
Full size table

Once the available data have been divided into training (reference) and testing subsets, ANN training can be made more efficient by pre-processing the data in a suitable form before they are applied to ANN. Data pre-processing is necessary to ensure that all inputs receive equal attention during the training process and to give numerical stability to ANN. Moreover, pre-processing usually speeds up the learning procedure and minimizes the prediction error (Boukhrissa et al. 2013). Pre-processing can be in the form of data scaling, normalization and transformation (Shahin et al. 2008). In this study, the minimum–maximum normalization (a linear transformation that preserves exactly all relationships of the original data) is used for scaling the inputs and outputs to commensurate within the specified range of the activation function used for ANN. The associated normalization is expressed by:

$$ P_{n} ( \mathrm{i} )=\frac{( {P_{i} - P_{\text{min}} } )}{( {P_{\text{max}} - P_{\text{min}} } )} $$
(12)

where P n (i) is the normalized parameter, P is either input or output parameter, P min and P max refers to the minimum and maximum values of the parameters, respectively.

The architecture of ANN determines the number of parameters to be calibrated. This architecture should always be adapted to the problem in question (Zhang et al. 1998), as it depends on the number of input and output variables. Generally, the number of neurons in the input layer depends on the number of possible inputs (independent variables) that we used in ANN. However, the number of neurons in the output layer depends on the number of desired (target) outputs. For this study, ANNs are proposed with two neurons in the input layer and one neuron in the output layer. The geographical coordinates (latitude and longitude) of the geodetic point are selected as input quantities, and the velocity component of the point ( V X,Y,Z ) is used as output quantity for training and testing procedure of BPANN and RBFNN.

In ANN approach, there are two major challenges regarding the hidden layers: the number of hidden layers and how many neurons will be in each of these hidden layers. Two hidden layers are required for modelling data with discontinuities such as a sawtooth wave pattern. Actually, one hidden layer is suffcient for nearly all problems (Panchal et al. 2011). In the present study, the proposed BPANN and RBFNN are composed of one hidden layer. ANN with one hidden layer can approximate any continuous function given a suffcient number of hidden neurons (Cybenko 1989; Funahashi 1989; Hornik et al. 1989; Bishop 2005). Essentially, the number of neurons in the hidden layer defines the complexity and power of ANN to delineate the underlying relationships and structures inherent in a dataset. The number of hidden layer neurons has a considerable effect on both classification accuracy and training time requirements. The accuracy that can be produced by ANN relates to the generalisation capabilities. Basically, the number of neurons in the hidden layer should be large enough for the correct representation of the problem, but at the same time low enough to have adequate generalisation capabilities (Kavzogluand Mather 2003). Several strategies and heuristics (destructive, constructive, and hybrid methods) have been suggested to estimate the optimum number of hidden layer nodes (i.e., Hecht-Nielsen 1987; Ripley 1993: Kaastra and Boyd 1996; Kanellopoulos and Wilkinson 1997; Witten and Frank 2005). Another way of determining the optimal number of hidden neurons that can result in good generalization and avoid overfitting is to relate the number of hidden neurons to the number of training samples (i.e., Masters 1993; Rogers and Dowla 1994; Amari et al. 1997). A number of systematic approaches have also been proposed to obtain the optimal ANN architecture (i.e., Ghaboussi and Sidarta 1998; Chakraverty et al. 2006; Chakraverty 2007; Kingston et al. 2008). However, none of these suggestions has been universally accepted or used. There is no direct and precise way of determining the best number of nodes in each hidden layer. In most of the reported applications, the number of hidden neurons is determined from the experience of individuals using trial-and-error strategies. Hence, a trial-and-error strategy with 30 neurons in the hidden layer of ANN is applied in this study, and ANN is pruned by gradually decreasing the hidden neurons. Consequently, the optimal number of neurons in the hidden layer was selected as 20 for BPANN and 17 for RBFNN which produced the smallest MSE. Thus, the optimum structure of BPANN [2:20:1] and of RBFNN [2:17:1] was determined by MATLAB ANN module that allows changing the learning algorithm parameters dynamically, monitoring error values, and generating digital data about suffcient learning rates. The significance of pruning away hidden neurons in ANN architecture on Geodetic Network (5) is represented in figure 4.

Figure 4
figure 4

The significance of pruning away hidden neurons in ANN architecture.

Full size image

The main disadvantage of ANNs that use back propagation algorithm is its slow convergence to the global minimum. It is also likely to become trapped into a local minimum. The learning rate ( η), also referred to as the step size, is used to control the degree of the change in the weights in response to errors in the output during each training cycle. The learning rate determines the size of the steps taken towards the global minimum error throughout the training process. It can be considered as the key parameter for a successful ANN application because it controls the learning process (Kavzoglu and Saka 2005). If the learning rate is set too high, then large changes are allowed in the weight and no learning occurs. Conversely, if the learning rate is set too low, only small changes are allowed, which can increase the learning time. The momentum term ( α) dampens the amount of weight change by adding in a portion of the weight change from the previous iteration. The momentum term is credited with smoothing out large changes in the weights and with helping the network converge faster when the error is changing in the correct direction (Neyamadpour et al. 2010). In this study, the estimation is started with a learning rate of 0.3 according to the guidelines suggested by Neuner (2010). Due to the fact that only an adaptive learning rate ensures the convergence (Bishop 2005), the learning rate is decreased by a factor of 0.5 if the cost function decreases and it is increased by a factor of 1.05 when the cost function increases during the training procedure. Also, the momentum term is fixed to 0.6 for weight update process. According to the general guidelines from ANN literature (i.e., Gallagher and Downs 1997; Graupe 2007), the initial values of the inter-neuron weights were set to a range [−0.25, 0.25] (suitable for the activation function) at the beginning of the training process for converging to global minimum quickly without getting stuck in a local minimum. The design and optimization parameters of ANNs of this study are summarized in table 4.

Table 4 Design and optimization parameters of ANNs.
Full size table

5 Case study

BPANN and RBFNN are trained in Geodetic Network (5) (maximum reference points), and the velocities of the test points are estimated via the trained ANNs for the controlling process. The ANN parameters obtained in the training procedure in Geodetic Network (5) are fixed and used as constants in the training process of ANNs for the other geodetic networks.

In KRIG approach, the reference velocity field vectors of the study area are generated from the reference dataset by Surfer 11 surface modelling program that is used widely for contour mapping, terrain modelling, and 3D surface mapping. These vector maps are overlaid on the velocity field contour maps (figure 5) to describe the directional dependence. Figure 5 reveals that the reference velocity fields used in this study are consistent with the horizontal and vertical velocity fields of Turkey computed by Aktug et al. (2011). The KRIG defaults of the software were accepted for modelling the velocity fields which were point Kriging type, non-drift type (ordinary Kriging), and linear variogram model. The reference velocity fields were checked by cross-validation technique and the velocity residuals of the test points were computed from these fields.

Figure 5
figure 5

Reference velocity fields of geodetic networks: V X (left), V Y (middle), and V Z (right).

Full size image

The results of the test dataset are significant in the evaluation procedure of BPANN, RBFNN and KRIG. Therefore, velocity residual maps are produced with regard to the velocity differences of the test points computed by equation (9) in the geodetic networks. The velocity residual maps of the test points associated with ΔV X,Y,Z are given in figures 6–8, respectively. The contour lines are drawn at 2 mm intervals on the velocity residual maps.

Figure 6
figure 6

ΔV X velocity residual maps: BPANN (left), RBFNN (middle), and KRIG (right).

Full size image
Figure 7
figure 7

ΔV Y velocity residual maps: BPANN (left), RBFNN (middle), and KRIG (right).

Full size image
Figure 8
figure 8

ΔV Z velocity residual maps: BPANN (left), RBFNN (middle), and KRIG (right).

Full size image

6 Results and conclusions

The analysis of the velocity residuals plotted in figures 6–8 shows that the point velocity residuals are getting smaller depending on the increase in the number of the reference points in geodetic networks. BPANN’s point velocity estimation is better than RBFNN’s estimations in all geodetic networks for ANN approach.

The statistical values of the test dataset’s velocity residuals are presented in table 5, and the velocity residual RMSEs of the test points based on BPANN, RBFNN and KRIG are shown in figure 9.

Figure 9
figure 9

RMSEs of velocity residuals of the test dataset.

Full size image
Table 5 Statistics of test dataset’s velocity residuals over the geodetic networks (units in mm/year).
Full size table

When the results summarized in table 5 are evaluated, it can be seen from figure 9 that BPANN estimated the point velocities more accurately in Geodetic Networks (1), (2), and (3), with respect to KRIG, in terms of RMSE as compared to the others. In Geodetic Networks (4) and (5), KRIG is more useful than BPANN for the point velocity estimation. RBFNN’s estimation accuracy is approximately at the same level with KRIG’s estimation only in Geodetic Network (1). On the other geodetic networks, KRIG’s results are better than RBFNN’s results.

Based on the experimental results of evaluating the utility of ANN for the velocity estimation in regional geodetic networks, the following conclusions can be drawn from this study:

  • The employment of BPANN is an alternative tool to KRIG for the geodetic point velocity estimation, in practice.

  • BPANN can be used effectively with a small reference point density in geodetic networks. A rough guideline of point density can be introduced as ≤∼3000 km2/point with respect to the accuracy of the result. When the number of the points that will be estimated (test) is smaller than the number of the points known (reference), the estimation of geodetic point velocity with the use of KRIG is evaluated as more powerful than using BPANN.

  • The main advantage of BPANN considered as a velocity estimator is model-free estimation of its 'exible structure. The properly trained BPANN can be used in the geodetic velocity estimation for additional points, whereas KRIG is re-determining weights for each additional point in geodetic network.

  • The combination of ANN models (with diverse architecture; e.g., different training algorithms and activation functions, additional hidden layers and neurons) with interpolation methods would be an appealing tool in geodetic velocity field applications where one has little or incomplete point velocity data, because of ANN’s adaptive feature that ‘learning by example’ replaces ‘programming’ and extrapolation ability in estimation problems (for boundary or outside of the geodetic networks).

ANN is a data-driven approach in which the model can be trained by input–output data to determine the structure (parameters) of the model. For ANN, there is no need to either simplify the physical complexity of the problem or incorporate any assumptions about the frequency distribution of the data. Besides, ANN can always be updated with new training data to obtain better results. In this regard, ANN outperforms the conventional methods and can be used as a powerful modelling tool in geodetic and geophysical problems. The results of this study re'ect that the application of ANN has the ability to estimate the point velocity estimation for regional geodetic networks. The diverse ANN architectures can be applied to other datasets for determining the velocity field of geodetic GPS networks which is an open research problem. Despite the feasibility of ANN in velocity field determination, future research should give further attention to ensuring robust models, improving extrapolation ability, and dealing with uncertainty.