Introduction

Branching structures are frequently observed in nature. Compared to their volume, the surface of such structures is relatively big. This allows for a large interface to the environment and increases the possibility of interaction. Prominent examples are the lung and blood vessels or the neuronal cells, which will be the main topic of this document. The branching structure of neuronal cells is determined partly by inherent genetic factors, such as place of origin, and partly by modifications resulting from environmental factors, such as interaction with surrounding cells. Although there are no two neurons with the same morphology, there exist characteristic branching patterns. In studies concerning morphological classification, function-structure relationship or morphological correlates of diseases problems arise, where the branching pattern has to be described precisely to detect significant differences, which distinguish different cell types (Hillmann 1979; da Costa et al. 2002). As a next step, algorithms for the generation of realistic cells can be developed on the basis of these cell descriptions. These algorithms generate arbitrarily many non-identical neurons (Ascoli and Krichmar 2000; Eberhard et al. 2006) and enable scientists to make simulations with a high number of cells or to study the impact of even minute changes in morphology on the function-form relationship (Schäfer et al. 2003).

In order to get a complete description which captures characteristic shape variability, well-defined morphological measures are needed. Following Uylings and van Pelt (2002) these measures can be divided into two classes: The first sort of measures describe a feature of the whole tree, like the number of branching points. A second sort of measures describe features of a part of the tree, like the number of branching points subject to the distance from the soma or degree of the branching point. This principle can be further extended in defining the partitioning of the tree not only by one but by two or more variables. Schäfer et al. (2003) for example defines the two-dimensional branching density as the number of branching points subject to the distance to the soma and to the terminal tips. The popular Scholl analysis (Scholl 1953) can also be viewed in this framework. In this measure the orientation of the tree is taken into account, by counting the number of intersections with equidistant consecutive spheres centered at the soma.

It is obvious that unimaginably many topological and metrical measures can be defined in this way (Rocchi et al. 2007). Due to the high complexity of neuronal systems it is desirable to isolate a few measures which capture the whole variability. An analysis of the correlation of different measures and the definition of generation algorithms on subsets of all measures can point out redundant measures.

If, on the other hand, we are just interested in detecting significant dissimilarities between different cell species, it is quite a challenging work to limit the search on a promising subset of all measures. But since, in most cases, even with modern microscopy and computer-based reconstruction methods, less cells than measures are available, this task is important to establish a conclusion at all. The values of these measures give then a representation of each neuron in an abstract feature space. In the case of single-valued measures this is just the vector space \(\mathbb R^n\), if n is the number of measures. The dissimilarities between two cells is then given by a distance metric, e.g. Euclidean metric, of the vector space. If one can now detect different agglomerations of feature representations, called clusters, one can conclude, that the shape of the associated neurons is more similar to neurons of the same cluster than to neurons of another cluster. While for one-dimensional and two-dimensional feature spaces these agglomerations can be detected visually, this is a non-trivial problem for higher dimensions. The various methods for detecting such clusters are subsumed under the term of cluster analysis. If we incorporate measures that describe properties of different parts of the dendritic tree, the feature space is a more abstract vector space. But the concept of dissimilarity between different cells can be extended using norm functions to define dissimilarity between these components of the feature space.

Another approach to detect groups of cells with characteristic shape avoids the definition of explicit measures and determines directly a kind of distance or dissimilarity between neurons. This approach defines an abstract distance metric d on the set of all neurons. We then say that two neurons cell 1 and cell 2 are similar if their distance d(cell 1,cell 2) is small. One recently presented adaption of this approach uses the so called Hausdorff distance metric, a metric on abstract sets. Mizrahi et al. (2000) represent the three-dimensional shape of a neuron as discrete points, called dendritic clouds, and define the distance between two cells by the Hausdorff distance.

A disadvantage of the representations of neurons that have been described so far is that they strongly abstract from the real tree-like shape. The representation in the feature space resembles the tree shape only with regard to more or less sophisticated measures like the tree-asymmetry (Uylings and van Pelt 2002) or the measures based on Scholl analysis and its variations. The representation as dendritic clouds completely neglects the difference between connected and disconnected parts of the dendritic tree.

In this paper we introduce a new method to quantify morphological variability that incorporates the tree-like shape automatically. This method is based on a distance between unordered labeled tree-graphs, called tree-edit-distance, which is known from theoretical computer science (Wagner and Fischer 1974; Zhang 1996). While many other classification methods reported so far have been formulated and evaluated on two-dimensional projections of cell shape our method is for the full three-dimensional morphology and applied directly to it. By taking into account the full three-dimensional shape of the neuron, our novel approach, satisfies the condition of a mathematical distance, unlike other methods based on 2d projections. This property is basic to reliably separate different cells without the arbitrariness of additional projections.

Methods

Representation of neurons as labeled trees

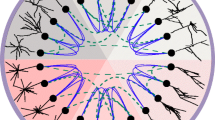
The proposed measure is based on the representation of neurons as node labeled trees. If we consider the dendritic entities between two branching points as units, called sections, the topological organization of these sections is determined by the tree shape and can be presented as a graph. A graph G = (V,E) is a set V of vertices and a set of edges E beginning and ending in a vertex. More precisely, this graph is even a rooted tree in the sense of graph theory with a root vertex representing the soma. As the child vertices do not have any special order imposed by the dendritic tree, this tree representation is an unordered tree. We can now assign to each vertex one or more attributes or labels, which describe the geometry of the underlying section. Finally we conclude, that every neuron can be represented as a node labeled unordered tree. Figure 1 illustrates these ideas. Extracting such a representation from experimental data is obviously a non-trivial task and a challenging research area in digital image processing. Although there are a few reconstruction programs available, e.g. NEURA,Footnote 1 there is a demand in improving important steps such as filtering (Broser et al. 2004), segmentation or skeletonization (da Costa 2000; Lam et al. 1992).

Fig. 1
figure 1

CA1 pyramidal cell (n412) from Duke-Southampton archive, a clipping and the schematic picture of the representation as a labeled tree. The dendritic entities between two branching points or between a branching point and a terminal tip, called sections, are represented as a vertex t[i k ], where i k is the index of an arbitrary numeration. The geometric properties of these sections are encoded as labels \({\rm label}(t[i_k])=({\rm length, surface, volume,} ...)^T\) of the vertices. The triangles are placeholders for binary trees. The contour of the whole cell representation is sketched by dotted triangles and lines

Full size image

Tree-edit-distance

Wagner and Fischer (1974) proposed in the seventies a distance function between strings, which is the minimal cost of a sequence of edit-operations, atomic operation which modify a string slightly by deleting, inserting or substituting characters. This was a generalization of the ideas of Levenshtein (1966) and Hamming (1950). The algorithm for computing this distance function is the starting-point for many problems that can be modeled as strings. One famous example is DNA-sequencing in molecular biology. Later on the idea of finding minimum cost sequences was transferred to trees (Tai 1979; Selkow 1977). But while there exist algorithms for computing the edit-distance between ordered labeled trees, Zhang et al. (1992) and Kilpelläinen and Mannila (1991) proved that the computation of this distance is a NP-complete problem in the case of unordered trees. That means that it is quite improbable to find an algorithm with polynomial running time solving this optimization problem. Nevertheless, there exists a slightly modified definition of the edit-distance, called constrained tree-edit-distance, which was proposed by Zhang (1996). This distance can be computed in polynomial time. In what follows, we present the principal ideas concerning the edit-distance between trees.

Adapting the edit-operations on strings substitution, deletion and insertion operations on trees can now be defined. The substitution operation changes the label of a vertex, the insertion operation adds a vertex to the tree and the deletion operation makes the father of a vertex v become the father of the children of v and removes v. Figure 2 illustrates these transformations. Introducing a symbol λ for denoting the label of the empty vertex the notation label \(_1 \longrightarrow\) label 2 (short: s = (label 1, label 2)) can be used consistently for the edit-operations, e.g. (λ, label) and (label, λ) for insertion and deletion operation. Then we examine sequences S = (s i )1 ≤ i ≤ n of those atomic edit-operations that transform one labeled tree T 1 into a tree T 2. By assigning a weight γ(s) to each operation s i , the weight γ(S) of each of these sequences S is just defined as the sum of its elements \(\gamma(S)=\sum_{i=1}^n \gamma(s_i)\). The distance between the trees T 1 and T 2 is the minimal weight of a feasible sequence. Wagner and Fischer (1974) have proven that in the case of strings this distance is indeed a metric distance, that means it satisfies non-negativity, identity of indiscernibles, symmetry and the triangle inequality, if the weight γ of the edit-operations is a metric distance on the space of the labels joined with {λ}. This assertion and the proof can be carried over directly to the case of trees.

Fig. 2
figure 2

Example of a sequence of edit-operations. If the local weight function γ, is the discrete metric, e.g. γ(a,b) = 1 if a ≠ b and 0 else, the weight of this sequence is 3. Obviously we can replace the first two operations with (b,λ) and get a sequence of weight 2

Full size image

As already mentioned, it is unlikely to find a polynomial-time algorithm for computing the edit-distance between unordered trees. In order to clarify the modification of Zhang (1996), yielding the computable constrained tree-edit-distance, the concept of matching between trees is important. Equivalent to Fischer’s and Wagner’s (1974) trace between strings this matching is a kind of structure preserving bijective mapping from some vertices of the first tree to vertices of the second one. A trace on two strings preserves the positions of letters. A matching between trees, preserves the partial order imposed by the predecessor-successor-relationship of the vertices. The link between the two concepts, sequence of edit-operations and matching, is the fact that given two trees T 1 and T 2 and a matching there exists always a sequence of edit-operations which transforms T 1 into T 2. On the other hand every sequence induces a matching. The weight of a matching is defined by the weight of its associated sequence of edit-operations. Therefore, the distance between two trees can either be defined as the minimum weight of a feasible sequence or, equivalently, as the minimum weight of a matching between the vertices. Vertices touched by that mapping are weighted as substitutions, all others are weighted as insertion or deletion operations (Fig. 3). It is possible to show that in the case of strings the problem of finding the minimum weight of a feasible sequence is equivalent to a shortest path problem on a grid-like, edge-weighted graph, called edit graph, and can therefore be solved by dynamic programming. To obtain a computable distance function for unordered trees Zhang (1996) extended the principle of structure preserving mappings and imposed another constraint to characterize valid mappings, called constrained matching. The intuitive idea behind this additional constraint is, that different subtrees of one tree should be mapped on different subtrees of the second one. This can be formalized by introducing the term least common ancestor lca(node 1,node 2). If we consider the two paths from the vertices node 1 and node 2 to the root vertex of the tree the lca(node 1,node 2) is the first vertex that is included in both paths. In Fig. 3, for example, lca(t 2[2],t 2[4]) is the vertex t 2[1]. We can now reformulate the definition of Zhang’s (1996) constrained mapping:

Fig. 3
figure 3

Example of a matching M between the trees T 1 and T 2. Formally a matching M is a set of pairs of vertex indices: M = {(1,1),(2,3),(4,4)}. The set M ∪ {(3,2)} is not a matching, because t 1[2] is predecessor of t 1[3] which is not true for the image vertices t 2[3] and t 2[2]. M corresponds to the edit sequence ((c,λ), (b,f), (λ,c)). Using the discrete metric as local weight function γ the weight of this matching is 3

Full size image

Definition 1

(Constrained matching) Given two labeled unordered trees T 1 and T 2 with vertices V 1 = {t 1[1], ...t 1[n 1]} and V 2 = {t 2[1], ...t 2[n 2]}, a constrained matching M is a set of ordered pairs of vertex indices:

$$M \subset \{1,\dots n_1\}\times\{1,\dots n_2\} $$
(1)

such that, for (i 1,i 2), (j 1,j 2) and (k 1,k 2) ∈ M:

  • \(i_1=j_1 \Leftrightarrow i_2=j_2\);

  • t 1[i 1] is predecessor of t 1[j 1] \(\Leftrightarrow\) t 2[i 2] is predecessor of t 2[j 2];

  • lca(t 1[i 1],t 1[j 1]) is predecessor of t 1[k 1] \(\Leftrightarrow\) lca(t 2[i 2], t 2[j 2]) is predecessor of t 2[k 2].

Given a weight function on edit-operations the weight γ(M) of a matching M is defined as:

$$\label{eq:def_matchweight}\begin{array}{lll} \gamma(M)&=&\sum\limits_{(i,j)\in M}\gamma(t_1[i],t_2[j])+\sum\limits_{(\cdot,j)\notin M}\gamma(\lambda,t_2[j])\\&&+\sum\limits_{(i,\cdot)\notin M}\gamma(t_1[i],\lambda) \end{array} $$
(2)

The last requirement in this definition is Zhang’s extension and formalizes the idea that separate subtrees of the first tree should be mapped on different subtrees in the second tree (see Fig. 4). The constrained tree-edit-distance between two trees, then, is the minimum weight of a constrained matching which is indeed a metric distance function on the set of all labeled unordered trees.

Fig. 4
figure 4

Example for matching M = {(3,2),(4,3),(5,4)} which is not a constrained matching. Different subtrees of T 1 marked with dotted boxes are mapped on just one subtree of T 2. More precisely the observation that lca(t 2[2],t 2[3]) is the predecessor of t 2[4] but lca(t 1[3],t 1[4]) is not that of t 1[5] shows that Zhang’s constraint is violated

Full size image

Theorem 1

(Constrained tree-edit-distance) Given two labeled unordered trees T 1 and T 2 , the constrained tree-edit-distance

$$d_{edit}(T_1,T_2)=\textnormal{min}_{\{M | M {\textnormal{ constrained matching}}\}}\gamma(M) $$
(3)

is a metric on the set of all labeled unordered trees.

Zhang (1996) proves this theorem and gives a recursive formulation for the computation of this algorithm which leads to a dynamic program that computes the distance between two trees in polynomial time. For each pair of vertices t 1[i] and t 2[j] a MinCostMaxMatching problem must be solved to determine first the distance between the two forests F 1[i] and F 2[j], where the forests are the sets of trees rooted at children of t 1[i] and t 2[j]:

$$ \label{forestdist}\begin{array}{l} D(F_1[i],F_2[j])\\=\textnormal{min}\left\{ \begin{array}{l} D(\Theta ,F_2[j])+\underset{1\leq t \leq n_j}{\min} \{D(F_1[i],F_2[j_t])\\{\kern15pt} - D(\Theta, F_2[j_t])\} , \\ D(F_1[i], \Theta)\!+\!\underset{1\leq s \leq n_i}{\min} \{D(F_1[i_s],F_2[j])\\{\kern15pt} -D(F_1[i_s], \Theta )\} , \\ \underset{M_{lim}(i,j)}{\min}\Gamma(M_{lim}) \; MinCostMaxMatching. \end{array}\right. \end{array} $$
(4)

To determine the minimal cost of a constraint matching between forests we need to know the cost of matchings of substructures. The matching then either assigns subtrees of the first forest to subtrees of the second (MinCostMaxMatching in line 3), or it assigns one forest, say F 1(i), to a subforest F 2(j t ) of the second one. The cost is then the sum of the matching cost D(F 1[i],F 2[j t ]) and the cost of deleting F 2[j] expect for its subforest F 2[j t ]. These cases are covered by the first and second line in Eq. 4, where Θ is placeholder for the empty forest. Knowing D(F 1(i),F 2(j)) we can determine the distance between the trees T 1[i] and T 2[j] rooted at t 1[i] and t 2[j]:

$$\label{equ5}\begin{array}{l} \nonumber D(T_1[i],T_2[j])\\=\textnormal{min} \left\{\begin{array}{l} D(\Theta ,T_2[j])\!+\!\underset{1\leq t \leq n_j}{\min} \{D(T_1[i],T_2[j_t])\\{\kern15pt} -D(\Theta, T_2[j_t])\} , \\ D(T_1[i], \Theta)\!+\!\underset{1\leq s \leq n_i}{\min} \{D(T_1[i_s],T_2[j])\\{\kern15pt} -D(T_1[i_s], \Theta )\} ,\\ D(F_1[i],F_2[j])+\gamma(i,j). \end{array}\right.\end{array} $$
(5)

Here a constraint matching is either a matching between the forests and the assignment of the roots (3rd line in Eq. 5), or the assignment of one tree to a subtree of the second one (1st and 2nd lines in Eq. 5). Hence the distance between trees T 1(i) and T 2(j) is the minimal cost of all these cases. If the number of direct children is bounded the complexity of the whole algorithm is O(|T 1||T 2|), where |T k | is the number of vertices in T k . We refer to Zhang (1996) for further details on the complexity and the algorithm.

Cluster analysis

Given a set of neurons P = {cell 1, ... cell 2} and using the constrained tree-edit-distance for the tree representation or another arbitrary distance function, the dissimilarity between these cells can be summarized in a distance matrix (D ij )1 ≤ i,j,n , where the element D ij is the distance between cell i and cell j . Due to the properties of a metric distance, D is symmetric and D ii  = 0. With the concepts of multidimensional scaling (Härdle and Simar 2003) these distances can be viewed as the Euclidean distances between vector representations in a high dimensional vector space ℝn. There exist a huge number of methods to explore the distribution of data represented as vectors or described by dissimilarity measures. While some methods use training sets to build class predictors others estimate a distribution of classes solely on the available data. Statistical discriminant analysis is a proxy for the former (Lachlan 1992), hierarchical cluster analysis for the latter. We will focus here on cluster analysis, since class prediction without a priori knowledge of classes is still a demanding problem. The aim of cluster methods is the identification of groups or clusters which embrace similar and separate dissimilar objects. Agglomerative hierarchical cluster algorithms arrange the elements hierarchically in merging iteratively more and more elements. In our analysis, we use the agglomerative hierarchical approach of Ward (1963), which yielded good results in a similar setting (da Costa and Velte 1999). The second method applied there, k-means, is not applicable for distance matrices. Other clustering approaches could include model and density based clustering methods (Fraley and Raftery 2002).

Local weight functions

As already mentioned geometrical properties of each section are coded as labels of the representing vertex. These labels could include length, volume or surface properties of the section, the path from the section to the soma or the tree rooted at that section. From a statistical point of view a standardization of labels would be desirable. But if we standardize just each pair of cells, the triangle inequality could be violated, while the standardization of the whole set would lead to high computational efforts if we add just one more cell. As local weight function γ the metric induced by a l p − norm was chosen.

Definition 2

(Local weight function) Given node labeled trees T 1, T 2, ..., with node labels label ∈ ℝl ∪ {λ}, p ∈ ℕ +  we define the local weight function γ p for two labels label 1 and label 2 as follows:

$$ \begin{array}{lll} &&{\kern-6pt}\gamma^p({\bf label}^1,{\bf label}^2)\\&&{\kern1pt}= \begin{cases} \left(\sum_{k=1}^{l}|{{\rm label}^1_k}|^p\right)^{1/p} \quad if \quad {\bf label}^2=\lambda ; \\ \left(\sum_{k=1}^{l}|{{\rm label}_k^2}|^p\right)^{1/p} \quad if \quad {\bf label}^1=\lambda ;\\ \left(\sum_{k=1}^{l}|{{\rm label}_k^1-{\rm label}_k^2}|^p\right)^{1/p} \qquad else. \end{cases} \end{array} $$
(6)

For l = 1 the weight functions γ p are identical for all p.

Local and non-local labels

In the case of constant labels, e.g. all vertices v have the label \(label_{top_1}(v):=1\), the choice of γ p leads to a distance that counts the minimal number of vertices that must be deleted and inserted in a tree T 1 to obtain tree T 2. This is the direct extension of Levenshtein (1966) definition of distance between strings. Ferraro and Godin (2000) has shown empirically that the value of this distance is strongly correlated with the difference in number of vertices. Denoting by |T i | the number of vertices of tree T i and by |D i | ≤ |T i | the number of vertices that are deleted from tree T i , we can state the following two equations for the edit-distance \(d_{\rm edit}^{{\rm top}_1}\) using only \({\rm label}_{{\rm top}_1}\):

$$ d^{\rm top_{1}}_{\rm edit}(T_1,T_2)\stackrel{\text{Def.\, 2}}{=}|D_1|+|D_2|,$$
(7)
$$ |T_1|-|D_1|=|T_2|-|D_2|. \label{eqn:relat} $$
(8)

Combining these two equations this gives:

$$ d^{{\rm top}_1}_{\rm edit}(T_1,T_2)=2|D_2|+|T_1|-|T_2|. $$
(9)

We assume without loss of generality that |T 1| ≥ |T 2| and get a lower and an upper bound for this distance

$$ 0\leq|T_1|-|T_2|\leq d^{\rm top_1}_{\rm edit}(T_1,T_2)\leq |T_1|+|T_2| $$
(10)

which is consistent with Ferraros observation.

As it is much easier to examine the topological structure of neurons than to examine exact geometrical properties like the radius, we define another label which considers just the topology of a tree T i :

$$ {\rm label}_{{\rm top}_2}(v):=\frac{1}{|T_i|}, \qquad \text{$v$ vertex of tree $T_i$}. $$
(11)

Using this label, we model the fact that vertices in small trees are more important than vertices in bigger trees. The deletion of a vertex in a small tree is more likely to destroy the structure than a deletion in a bigger tree. Recalling that the number of substitutions is equal to |T 1| − |D 1|, we can rewrite the value of the constrained tree-edit-distance \(d_{\rm edit}^{{\rm top}_2}\) using only \({\rm label}_{{\rm top}_2}\) as follows (|T 1| > |T 2|):

$$\begin{array}{lll} d^{{\rm top}_2}_{\rm edit}(T_1,T_2)&\stackrel{\text{Def.\; 2}}{=} &(|T_1|-|D_1|)\left(\frac{1}{|T_2|}-\frac{1}{|T_1|}\right) \\&&+\; \frac{|D_1|}{|T_1|}+ \frac{|D_2|}{|T_2|}, \end{array}$$
(12)
$$ \qquad\qquad\qquad\;\;=\frac{|T_1|\!-\!|D_1|\!+\!|D_2|}{|T_2|}\!+\!\frac{2 |D_1|\!-\!|T_1|}{|T_1|} $$
(13)
$$ \qquad\qquad\qquad\;\;\stackrel{\text{Equ. }{8}}{=} 2\frac{|D_1|}{|T_1|}. $$
(14)

We can see that the value of this distance is determined by the minimal number of vertices that must be deleted from the bigger tree relative to the number of its vertices. The substitutions and the deletions from the smaller tree influence this value just implicitly.

Along the lines of this second topological label, we define geometrical labels which can be interpreted as normalized. This is done by dividing the value of a geometrical property of a section by the summed values of the whole tree, e.g.

$$ {\rm label}_{L_{\rm sec}}(v)=\frac{{\rm length}(v)}{\sum_{v\in T}{\rm length}(v)}=\frac{{\rm length}(v)}{{\rm length}(T)}. $$
(15)

In Table 1 we summarize 22 different labels. Besides the two topological labels, we use length, volume and surface properties in both local and non-local settings. A pure local setting is e.g. \({\rm label}_{l_{\rm sec}}(v)={\rm length}(v)\) which is the length of the underlying section v of the dendrite. \({\rm label}_{l_{\rm soma}}(v)\) and \({\rm label}_{l_{\rm tree}}(v)\) in contrast encode the length of the dendrite between the soma and section v and the total length of that part of the dendritic tree rooted at section v. With this we take into account the global position of section v within the tree. The definition of labels depending on global properties is justified by the constrained matching view point. Another label that should emphasise the spatial orientation is \({\rm label}_{a_{\rm sec}}(v)\). This label is the angle between the subsequent sections of v.

Table 1 Local and non-local labels
Full size table

Apart from these topological and geometrical labels, it is possible to attach labels describing channel distributions or other electrophysiological properties.

Results

To test whether the constrained edit distance is an adequate method to capture neuronal morphology we implemented Zhang’s algorithm for computing the constrained tree-edit-distance in C++. Our program needs two or more cells encoded in the hoc-format (Hines and Carneval 2002) as input and calculates the distance between each pair of cells. By choosing the labels that are incorporated during the computation we can model various ideas of similarity of neuronal shape. The output is a simple text file containing the distance matrix. The text file, in turn can be used as an input file for various tools which compute for a given distance matrix a partitioning of cells. In our studies we used cluster tools of the statistic package R Development Core Team (2008).

We first evaluated the constrained tree-edit-distance on hippocampal neurons published in the Duke-Southampton archive (Cannon et al. 1999). This archive contains several CA1 pyramidal cells, CA3 pyramidal cells, dentate granule cells and interneurons. For the subsequent analysis we removed the axons and pooled basal and apical dendrites together. Cannon et al. (1999) used some of these cells to analyze the distribution of 32 parameters. They concluded that pyramidal cells, dentate granule cells and interneurons form groups which differ significantly in some of these parameters. Another source for morphologies is the cell generation tool NeuGen (Eberhard et al. 2006). This tool generates from distributions of several parameters non-identical neurons of morphological classes of the cortex. In Table 2 we summarize the employed data.

Table 2 Overview over the employed morphologies
Full size table

Partitioning error

First we concentrate on the discrimination between two different cell classes, say class A and B, for which a and b representative cells are available in the hoc-format. As already mentioned we use cluster analysis to show that the constrained tree-edit-distance discriminates between different cell classes. We calculate the distance of every pair of two cells and obtain the distance matrix D. Then the clustering methods generate a clustering C 1, C 2 ⊂ A ∪ B, C 1 ∩ C 2 = ∅ of the cells based on their pairwise distances. The absolute error Δabs of a partitioning is the number of wrongly clustered cells:

$$ \Delta_{\rm abs}\!=\!min\{|A\!\cap\! C_1|\!+\!|B\!\cap\! C_2|,|A\!\cap\! C_2|\!+\!|B\!\cap\! C_1|\}. $$
(16)

As \(\Delta_{\rm abs}\leq \frac{|A|+|B|}{2}\) we define the relative error Δ as following:

$$ \Delta=\frac{2 \Delta_{abs}}{|A|+|B|}.$$
(17)

Note that a relative partitioning error Δ = er means that \(\frac{\rm er}{2}(|A|+|B|)\) cells were assigned to the wrong cluster.

Pyramidal and non-pyramidal hippocampal cells

Table 3 summarizes the comparison of pyramidal cells and non-pyramidal cells from hippocampus. As expected the error for the predicted clustering depends on the choice of the labels. We observe that the corresponding labels v sec, v soma, v tree, s soma and s tree do not capture the characteristic dissimilarities and we will exclude them in subsequent discussion. Furthermore, we can say that distances which describe length and surface properties lead to better result than those describing volume properties and for normalized labels the error is smaller. Nevertheless we can conclude that the constrained tree-edit-distance reflects the dissimilarity between pyramidal and non-pyramidal cells, as for some labels the partitioning error is very small or even zero. An interesting result is the good prediction property of both topological labels top1 and top2, where our improved label top2 is slightly better.

Table 3 Clustering for distances based on single-valued labels
Full size table

Hippocampal cell groupings

As a next step we want to examine if the constrained tree-edit-distance reproduces the classical hippocampal cell groupings as CA1 pyramidal cells, CA3 pyramidal cells, interneurons and dentate granule cells. We are restricting our data, following the work of Cannon et al. (1999), to cells that have been reconstructed with comparable experimental background. In Fig. 5 we illustrate the ranges of the partitioning error if we compare each pair of cell groups. If we just want to discriminate between pyramidal and non-pyramidal classes good results are obtained with labels top2, l soma, S sec and S soma. The distance using label top1 fails to discriminate between CA1 pyramidal and dentate granule cells and between CA1 pyramidal cells and interneurons. The most interesting observation in this figure is probably the fact that some labels lead to a distance that can differentiate quite well between CA1 and CA3 pyramidal cells. This extends the result of Cannon et al. (1999) and supports Scorcioni’s (2004) observation that CA1 and CA3 pyramidals differ morphologically. In the case of label V tree this is shown in a more detailed way in Fig. 6.

Fig. 5
figure 5

Pairwise clustering of 4 different hippocampal cell groups. The gray scale of each square shows the range of the particular partitioning error

Full size image
Fig. 6
figure 6

CA1 and CA3 pyramidal cells can be discriminated quite well using the label V tree for the calculation of the constrained tree-edit-distance. Only one cell is in the wrong class

Full size image

The only unsatisfactory aspect here seems to be the poor result for the classification of interneurons and dentate granule cells. A closer look on the absolute number of misclassified cells, e.g. label V sec in Fig. 7, shows that for some labels the number is small and the relative error is just slightly larger than the chosen threshold of 0.2. One could try to combine several labels and distance matrices to improve this result. A systematic discussion of such derived dissimilarity measures goes beyond the scope of this work.

Fig. 7
figure 7

Number of misclassified cells using the constrained tree-edit-distance for label V sec. The number in brackets is the total sum of cells. For interneurons and dentate granule cells the relative error is Δ = 0.26, slightly larger than the chosen threshold

Full size image

Synthetic cortical cells

Due to the statistical components of our and most other approaches analyzing neuronal morphology we need a huge amount of data to generalize observations. We therefore tested the constrained tree-edit-distance on a set of synthetic cells of 5 different cortical cell groups. Using the generation tool NeuGen (Eberhard et al. 2006), we are able to generate arbitrary many non-identical L2/3 pyramidal cells, L4 stellate cells, L4 star pyramidal cells, L5a pyramidal cells and L5b pyramidal cells. This algorithm, based on a set of descriptive and iterative rules, generates dendritic morphology in stochastically sampling parameters from experimental distributions.

In Fig. 8 we summarize the discriminative power for every edit-distance and for each pair of cortical cell groups. Here again we can conclude that the edit-distance and the cluster method can stress characteristic differences in the morphological shape of neurons. While so far the presented results were restricted to the discrimination between two classes, it is also possible to calculate the distances between cells from three or more classes and compare the outcome of a cluster analysis with the known cell groupings. In Fig. 9 this is illustrated for the edit-distance using label S sec. All cells of each cell group are integrated to one cluster. An ongoing interpretation might observe that L5b pyramidal cells together with L2/3 pyramidal cells and L5a pyramidal cells together with L4 stellate cells form two general groups.

Fig. 8
figure 8

Pairwise clustering of 5 different cortical cell groups. The gray scale of each square shows the range of the particular partitioning error

Full size image
Fig. 9
figure 9

The edit-distance using label S sec seems to discriminate quite well between different cortical cell groups

Full size image

Discussion

In this work we reviewed the constrained tree-edit-distance introduced by Zhang (1996) and showed how this distance measure can be used to obtain a dissimilarity measure for dendritic arborization. The comparison of several hippocampal and cortical cell classes has shown that the constrained tree-edit-distance together with cluster analysis can indeed discriminate different classes.

The disadvantage of single-valued measures like the number of branching points or the total length is the loss of characteristics by the averaging process. Vector valued measures like the Scholl (1953) analysis try to overcome this problem by defining different regions and reducing the comparison of different cells to the comparison of similar regions. We think that it is quite an artificial step to decide a priori which parts of two cells represent regions, that are in some sense equivalent. In cases where the examined cells are well-studied, knowledge about characteristic differences will lead to good measures. But in the general case we are interested in measures which stress characteristic dissimilarities, which are yet unknown. So we need to observe a huge amount of measures, measures which are both general and complete. Completeness is an outstanding problem which could be investigated by generation algorithms (Ascoli and Krichmar 2000) and correlation analysis.

The constrained tree-edit-distance intrinsically follows the principle of comparing only equivalent parts of the dentritic tree. Unlike other measures, the equivalent parts are determined dynamically during the computation of the distance value. Equivalent parts are those sections which are touched by the constrained matching with minimum costs. With the definition of this constrained matching it is clear that these sections have topological equivalent positions in the dentritic arborization. On the other hand the constrained tree-edit-distance can be regarded as the weight of a sequence of some simple transformation operations which simulate a kind of evolutionary process. This interpretation shows again that the constrained tree-edit-distance automatically takes into account the tree-like shape. We gain this methodical superiority by the use of digital reconstructed data. But these reconstructions are just an approximation to the real morphologies and functional relevance should be interpreted carefully. It is important to single out artifacts due to preprocessing steps. But this does not disqualify the tree-edit distance, since any morphological measure is based on derived data.

The use of non-local labels such as the distance to the soma or the tree size above a section takes into account the spatial distribution of neuronal shape. The results show that the edit-distances based on such labels can discriminate quite well between shapes of different three-dimensional distribution. There are other recently reported methodologies including the excluded volume (da Costa et al. 2005), the Minkowski functionals (Barbosa et al. 2004) or the percolation critical density (da Costa and Manoel 2003), that put special emphasis on the spatial distribution. They have been found to be effective means for expressing different aspects of spatial distribution in the case of two-dimensional representation of cells. It seems to be obvious that this generalizes to three-dimensional representations. If this is indeed the case it would be interesting to study the correlation of these measures with the constrained tree-edit-distance. A further topic would be the combination of e.g. percolation and tree-edit-distance. The time consuming percolation measures could be evaluated for just a few cells and the results may then be applied for all cells that are close in the sense of some tree-edit-distance. The recently released data base NeuroMorpho.OrgFootnote 2 (Ascoli et al. 2007) is a source of data for such intensive studies.

We used the distance matrices and cluster analysis to predict classes and compared these with a priori known partitioning. Provided we have enough data the next step is then the search for certain new subclasses. In this we just have to examine the hierarchy produced by the cluster methods. Alternatively we could use the constrained tree-edit-distance to determine whether some new cell is closer to one or the other known class of cells. This amounts in calculating the distance to each cell and checking for some minimal distance. A further application is the validation of virtual neurons (Eberhard et al. 2006) which was already sketched here. It should be even possible to use the constrained tree-edit-distance to tune the parameters of generation algorithms by an iterative procedure. Given an initial choice of parameters for a given class, we generate artificial cells, calculate their distances to a set of real cells and check whether a slight change in the parameters could decrease the distances. The new parameter values are then the initial choice for the next iteration.

By the definition of labels and the local weight function γ it is possible to model various ideas of similarity. Apart from the metrical labels examined in this work, it is for example possible to use channel distributions as labels. We showed that even topological versions of the constrained tree-edit-distance yielded considerable results. Furthermore we extended Cannons (Cannon et al. 1999) results and showed that CA1 and CA3 pyramidal cells can be discriminated by their morphological shape.

The limited number of cells is the weakest part in this and most other classification approaches. We hope that further research can benefit from increasing willingness to share reconstruction data (Ascoli 2007; Liu and Ascoli 2007).

Information Sharing Statement

Specific requests regarding the implementation of the constrained tree-edit-distance and the cluster analysis should be addressed to the corresponding author. We will make our implementation available on request. The code, however, was not written for a general public. Using it will need some proficiency in dealing with advanced and experimental computer codes.