Introduction

The white rot fungus Phanerochaete chrysosporium is well-known for its ability to degrade a variety of hazardous pollutants owing to its lignin-degrading enzyme system [1]. It is a basidiomycete and grows with the formation of basidiospores when cultured in liquid medium [2]. Reactor as well as batch shake flask studies with the fungus confirms that the production of the enzymes is dependent on physico-chemical parameters [3, 4] of the system such as media composition, temperature, pH, agitation, etc. Among the enzymes produced by this fungus, lignin peroxidase (LiP) has been shown to be important. Secretion of this enzyme is understood to be mainly dependent on nutrient-limiting conditions and biomass growth and other physico-chemical factors such as agitation [5] and temperature [6], which are also responsible for the biomass growth. However, there is no clear study undertaken to elucidate variability in biomass growth and enzyme secretion kinetics of this environmentally important fungus in relation with these physico-chemical factors, which may form the basis for improved performance of the fungus for specific applications. Therefore, the aim of the present study was to understand and model the biomass growth and LiP secretion kinetics as a function of certain important physico-chemical variables such as glucose concentration, nitrogen concentration, agitation, etc.

In literature, there are very few models for describing growth of fungus. For instance, the growth model described by Peilin et al. [7] is based on the Monod–Jacob operon model and takes into account the production of repressors and mRNA for the estimation of secondary metabolites. However, the substrate depletion and growth rate were estimated using first- and second- order differential relationships with biomass itself. It does not describe the change in the biomass growth behavior caused by physico-chemical parameters. The model provided by Sugden et al. [8] details on the mycelial growth of filamentous fungi and it mainly depends on the accumulation of microtubule-transported vesicles containing nutrition as well as their distribution near the hyphae in Neurospora crassa. Dynamics of growth as well as substrate depletion was studied by Osorio et al. [9] with an unstructured Monod and Leudeking–Piret model on Aspergillus flavipes, which is however restricted to the determination of kinetic parameters of the system. In order to study the time evolution of a system with many different time scales for its sub-processes, stochastic approach can be more useful over the deterministic models considered mostly in the literature. In the present work, a Monte Carlo method was developed to model three different processes such as glucose consumption, cell division, and enzyme secretion by a non-specific fungus. The results obtained from the model were compared with that of the experiments and a good qualitative agreement was observed.

Experimental Methods

P. chrysosporium MTCC 787, purchased from IMTECH Chandigarh, India, was maintained at 25 °C on malt agar slants; for spore production, slants were maintained at 39 °C for 2–5 days in medium containing (grams per liter): 10 glucose, 10 malt extract, 2 peptone, 2 yeast extract, 1 asparagine, 2 KH2PO4, 1 MgSO4·7H2O, 0.001 thiamin-HCl, and 20 agar.

Medium optimized by Kirk et al. [10] was initially used to subculture the fungus from spores and later modified to include only glucose as the sole carbon source along with other nutrients in the medium in order to study the effect of glucose and other parameters on the fungal growth and LiP secretion kinetics. Thus the medium used was composed of Basal III Medium (100 ml), glucose (10 g L−1), 0.1 M 2,2-dimethyl succinate (1.46 g L−1), thiamin (0.001 g L−1), ammonium chloride (4.68 g L−1), 1 % Tween 80 (50 ml) and trace elements, where the basal III medium contains KH2PO4 (20 g L−1), MgSO4 (5 g L−1), CaCl2 (1 g L−1) and trace elements. Initial pH of the medium was set to 4.5.

During the experiments, the fungal samples were collected at 6-h intervals from the medium and centrifuged to remove fungal spores. Fungal growth was measured by counting the spores using a hemocytometer [11]. Biomass-free supernatants were divided into two portions. While one portion was analyzed for LiP activity by the fungus, the other portion was analyzed for glucose concentration. For glucose analysis, dinitrosalicylate method was adopted by taking the absorbance of the color developed at 540 nm [12]. LiP activity was determined spectrophotometrically by the oxidation of veratryl alcohol to veratraldehyde [10, 13, 14].

To determine the effect of initial glucose concentration, its level was varied in the range 5–25 g L−1 keeping the other media constituents at fixed level. All batch shake flasks experiments in the study were carried out by incubating the flasks in an orbital incubator shaker set at 30 °C and 150 rpm.

Results

It can be seen from Fig. 1 that the rate of consumption of glucose increased with initial glucose concentration in the medium. In Fig. 2, the spore count is plotted against time for the same initial glucose concentrations, which shows that the whole growth process has three distinct phases with an initial lag phase during which the growth is slow and the corresponding rate of glucose consumption is also less. It may be because of time taken to adapt to the new environment due to introduction of the mature spores to another medium. It can also be noticed that the duration of lag phase shortens as the initial glucose concentration in the medium is high, because low glucose concentration corresponds to less availability of glucose to a spore to consume. During the intermediate phase and the end of the lag phase, a fast growth is observed corresponding to higher rate of glucose consumption due to the more number of mature spores available for cell division to occur, besides the availability of glucose in the medium. During the last phase or the saturation phase, the spore count reaches a maximum value and remains almost constant over a longer period of time. By this time, the glucose supplied to the medium is completely consumed by the spores, with no further cell division possible. It is also observed that the maximum spore count is directly proportional to the initial glucose concentration.

Fig. 1
figure 1

Residual glucose remained, C G % (as percentage of initial concentration) for different initial glucose concentration [5 % (circle), 10 % (square), 15 % (diamond, 20 % (triangle), 25 % (asterisk)]

Full size image
Fig. 2
figure 2

Growth in terms of generations of initial inoculums (G N ) for different initial glucose concentration as in Fig. 1, with same symbols

Full size image

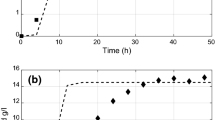
The LiP activity by the fungal culture is plotted against time in Fig. 3, where three distinct phases can be observed. The first phase is of very low enzyme activity, which may be because spores take time to adapt to the new environment it was inoculated and also they sense presence of glucose. Hence, the production of enzymes was initially low. This phase is short in the case of high initial glucose concentration in the medium that may be because of faster consumption of glucose, Fig. 1 (inset), which causes spores to secrete enzymes at a higher rate as scarcity of glucose reaches faster at higher initial concentration. At the end of this phase, enzyme activity increases rapidly denoting that most of the spores are producing enzymes. At the last phase, the activity saturates as there was no more glucose as well as the spore number is also not increasing.

Fig. 3
figure 3

LiP activity (A C) at different initial glucose concentration as in Figs. 1 and 2, with same symbols

Full size image

Though growth mechanism and LiP activity of P. chrysosporium is characterized from the results obtained in the controlled experiments, it is not clear what empirical laws governed the growth and enzyme activity of this fungus. In order to have some idea about these empirical laws behind the growth and enzyme activity, one needs to develop a model assuming certain growth law and check that the model results reproduce qualitatively the experimental results obtained.

Model

Based on the experimental findings, glucose seemed to influence both biomass growth and LiP secretion by the fungus. A stochastic model of fungal growth and activity of the enzyme secreted by the fungus was developed in order to understand the experimental results obtained. The model was developed taking into account that glucose is the sole source of carbon. The growth process contains three major steps: (a) consumption of glucose, (b) cell division, and (c) secretion of enzyme. A self-stabilized Monte Carlo algorithm [15, 16] has been developed in order to study the time evolution of these processes. Initially, Ns(0) number of cells and NG(0) number of glucose molecules were taken in a constant arbitrary volume V as the initial parameters of the model. Glucose molecules are consumed by the cells during the growth. As a consequence, the glucose concentration in the medium decreases with time t. The instantaneous glucose concentration in the medium at any time t is then given by:

$$ {G_t} = {G_0}\left( {1 - \frac{{{n_{\text{G}}}(t)}}{{{N_{\text{G}}}(0)}}} \right) $$
(1)

where \( {G_0} = {N_{\text{G}}}(0)/V \) is the initial glucose concentration and \( {n_{\text{G}}}(t) = \sum\limits_{{i = 1}}^t {{n_{\text{G}}}(i)} \) is the number of glucose molecules consumed upto time t. Two main criteria for glucose consumption are: (1) availability of a glucose molecule to a cell which is directly proportional to the instantaneous glucose concentration Gt of the medium and (2) intake probability Pintake of a glucose molecule by a cell which depends on the size of the cell. The size of a cell is defined as the number of glucose molecules present inside the cell at a given time. A matured cell contains gc amount of glucose and has all active primary functions. A cell of size less than a mature cell is less probable to intake a glucose molecule than a cell of size more than that of a mature cell. The probability that a cell will intake a glucose molecule is assumed to be a Poisson's distribution and is given by

$$ {p_{\text{intake}}} \propto {g_r}\exp \left( { - {g_r}} \right) $$
(2)

where, \( {g_r} = g/{g_c} \) is the relative cell size. The probability of glucose consumption is then given by

$$ {p_{\text{GC}}} = \Gamma {G_t}{p_{{{\text int} ake}}} $$
(3)

where Г is the molar ability of attachment of a glucose to a cell. In order to make glucose consume exactly with probability PGC, a Monte Carlo technique is adopted. In this method, a random number r, uniformly distributed between 0 and 1, is called corresponding to that cell and if r ≤ PGC, the glucose molecule is consumed by the cell otherwise it is left out. The number of glucose molecules to be taken up by the cell is determined by the number glucose molecules present in the system per cell. All the cells present in the medium at that time were called for consumption of glucose.

Cell division is the process of release of daughter cells by the matured cells. It is assumed in the model that the division of a cell solely depends on the size of a cell. The probability of cell division is modeled by a sigmoidal growth probability distribution and is given as

$$ {p_{\text{div}}} = \frac{1}{{1 + {e^{{ - \left( {g - {g_c}} \right)/{\sigma_{\text{d}}}}}}}} $$
(4)

where σd is the capability of cell division of a matured cell. Again, a Monte Carlo technique is adopted to perform cell division exactly with the probability P div. A random number r was called and if r < P div the cell was allowed to divide, otherwise no cell division occurred. All mother cells (cells of the previous time step) were called for cell division. It is known that P. chrysosporium, is a basidiomycete and grows by forming basidiospores (multiple spores released at a single ejaculation). This phenomenon was incorporated in the model by the release of a number of daughter cells at a time by the mother cell. The number of daughter cells to be produced depends on its glucose content g. The glucose content of a cell is utilized as one glucose molecule for the release of every daughter cell, cell division cost and one glucose molecule for every new born daughter cell as initial glucose content.

It had already been established that P. chrysosporium produces LiP as secondary metabolite when glucose concentration in the medium is less [4]. It is also known that the activity depends on the size of a cell for an underdeveloped cell [17]. In order to model the enzyme activity, the cells are classified as developed and underdeveloped cells. A cell is considered as a developed cell if it undergoes a cell division. The probability of an underdeveloped cell to produce enzyme is given by

$$ {p_E} = \left( {1 - {G_t}/{G_0}} \right)\exp \left( { - \Delta g_i^2} \right) $$
(5)

where \( \left( {1 - {G_t}/{G_0}} \right) \), is the fractional glucose consumed from the medium, \( \Delta g_i^2 = {\left[ {\left( {{g_C} - g} \right)/\sqrt {2} {\sigma_E}} \right]^2} \), is the measure of deviation of size of a cell from the maturity and σE is the ability of enzyme production by a cell. For a developed cell, the probability to produce enzyme depends only on the scarcity of glucose in the medium and it is given by,

$$ {p_E} = \left( {1 - {G_t}/{G_0}} \right) $$
(6)

The enzyme secretion is also modeled stochastically by adopting a MC technique. A random number r, uniformly distributed between 0 and 1, is called corresponding to a cell and if r ≤ P E certain amount of enzyme is released by the cell otherwise no enzyme is released. Certain unit of glucose is reduced from the glucose content g of the cell as enzyme production cost on the release of one unit enzyme. All the cells were called for the production of enzyme. The three sub-processes, glucose consumption, cell division, and release of enzyme constitute a single MC time step. The process stops on its own when either there is no glucose to consume or no further cell division occurs.

In order to measure the enzyme activity, a simplified enzyme kinetic reaction is considered here as\( E + S \to E + P \), where E stands for enzyme, S stands for substrate, and P stands for product. The enzyme–substrate reaction rate should be proportional to the concentrations of enzyme and substrate in the medium. Thus,

$$ {\text{Rate}} = A{C_E}{C_S} $$
(7)

where A is a constant based on activation energy of the enzyme–substrate complex. As per the collision theory [18], the value of A is given by,

$$ A = {d^2}\pi {\left( {\frac{{8{k_B}T}}{{\pi \mu }}} \right)^{{ \frac{1}{2} }}}\exp \left( {\frac{\varepsilon }{{RT}}} \right) $$
(8)

where ε〉Ε α , Ε α is the activation energy for the current reaction, k B is the Boltzmann constant, R is universal gas constant, T is the temperature, d is the average diameter of the two reacting species called as collision distance, and μ is the reduced mass of the enzyme–substrate complex. As the enzyme concentration C E is known from the MC process, the rate could be calculated for a given substrate concentration C S . The substrate concentration C S is usually kept much larger than C E in the enzyme assay and hence, C S in the medium remains almost constant during the assay period. The same condition is also maintained here to calculate the enzyme production rate.

Model Results and Comparison with Experiment

The model of biomass growth and enzyme activity is now studied for the parameters listed in Table 1. Results obtained from the model are presented in Figs. 4, 5, and 6. The results are shown to 5,000 MC steps to display the actual behavior, though the process stops at more than 12,700 MC steps. The drop in glucose concentration C G in the medium is shown in Fig. 4 against the MC time steps. The model result has depicted more or less the same nature of the experimental data. It shows three different regimes in the consumption of glucose, slow, rapid, and saturation. Initially, glucose consumption is found slow followed by a rapid consumption. As time passes, more and more cells are produced and consumption is increased. Finally, glucose concentration goes to a very low value. Glucose consumption rate is also found higher for the higher initial glucose concentration in the medium as in the experiment.

Table 1 Values of the parameters taken initially in the simulation
Full size table
Fig. 4
figure 4

Plot of instantaneous glucose concentration (C G ) in the medium against MC time steps for different initial glucose [10 % (circle), 20 % (square), 30 % (diamond), 40 % (triangle), 50 % (asterisk)] concentrations

Full size image
Fig. 5
figure 5

Plot of number of cells per single initial spore (G N ) against MC time steps for different initial glucose concentrations as in Fig. 4 with same symbols

Full size image
Fig. 6
figure 6

Enzyme concentration (C E ) obtained from the simulation is plotted against MC time step for different initial glucose concentrations as in Figs. 4 and 5 with same symbols

Full size image

The growth of the cells at any time t is monitored by counting the number of cells per single initial spore G N . It is plotted in Fig. 5 against the MC time steps. The growth of the cells is also found similar to that of the experimental observations. However, it may be noticed that the growth form observed in the model has a better agreement to the experimental results at lower initial glucose concentration than that of higher initial glucose concentration. The growth process has an initial lag phase followed by the rapid growth and finally it saturates. Initial slow growth is due to less number of spores and saturation in growth is due to non-availability of glucose in the medium. The saturation values are also found directly proportional to the initial glucose concentration in the medium as in the experiment (see inset of Fig. 5). The results then confirm that the sigmoidal growth adopted here in a self-stabilized glucose medium is a suitable growth model for this fungus. One may notice that the saturation growth regime is achieved by nearly 5,000 MC time steps for the given parameter values whereas such a regime is achieved in the experiment by about 96 h. One MC step is then approximately 1 min of experimental time.

In the experimental situation, enzyme activity is measured by performing enzyme assay. However, enzyme activity here can be measured directly from the enzyme concentration of the medium applying the rate Eq. (7). The enzyme concentration C E in the medium is plotted in Fig. 6 against the MC time steps. Since at room temperature, the product conversion rate per unit volume is directly proportional to the enzyme concentrationC E for a given substrate concentrationC S , Fig. 6 can represent the rate versus time plot if multiplied by an appropriate pre-factor. If the enzyme activity of 150 U L−1 obtained in the experiment correspond to enzyme concentration 0.4 per unit volume in the simulation, the pre-factor in the rate equation will be10−4. It may be noticed that enzyme concentration represents a similar behavior to that obtained in the experiment with three different phases of activity. Since the enzyme activity is qualitatively reproduced in this simulation, it may be concluded that the enzyme secretion is appropriately modeled for this fungus.

Summary and Conclusion

The experiments performed varying the physico-chemical parameters has shown the behavior of the fungus P. chrysosporium, in the controlled medium. The experiments suggest that the biomass growth and LiP activity, both are dependent on the initial glucose concentration of the medium. However, higher concentrations (>20 g L−1) of glucose may show different effects. This can be attributed to the change in the cellular membrane capabilities of the cell [17]. The maximum biomass growth varies almost linearly with the initial glucose concentration of the medium, Fig. 2 (inset). LiP activity varies similarly with the initial glucose concentration, Fig. 3, as the other parameters are kept constant. By the model developed, one can observe qualitatively similar behavior as that observed in the experiments conducted within the controlled medium for varying initial glucose concentrations. The constants should be adjusted according to the experimental condition to obtain quantitative agreement with the experimental data. Though the model produces results that qualitatively agree with the experiments, the model should be improved incorporating other details such as cell death, loss of enzyme, etc. The model can also be used for studying the behavior of similar kind of fungal system by readjusting different parameters of the model.