On the formulation of optimization problems under uncertainty in mechanical design

Abstract

This paper proposes a guide to help designer to formulate the optimization under uncertainty in mechanical design problem. An efficient tool based on the necessary conditions for each optimization under uncertainty type is introduced here. This tool is capable to guide the designer to choose between different types of optimization under uncertainty, the suitable method for a given problem. The problematic of the antagonism between the performance and its stability is studied. We also identify the importance of the evaluation of this antagonism before solving the design problem in robustness formulation. An efficient general method is developed for this evaluation. This method is very useful to save computational time and to give to the designer an early information about the stability of performance under uncertainties of his design.

1 Introduction

In engineering design, the designer have to take decision in order to meet the customers and manufactures requirements. The best decision is achieved using design optimization methods. Design optimization is widely used in mechanical engineering, khoury et al. [26] develop an optimization methodology of a rough forged part. In [29] multi-objective structure dynamic optimization is studied. Optimization of composite structure is treated in [18, 22]. In [34] an optimization method is used to find the best “belleville” spring for the designer requirement. The hybrid reconfigurable system design and optimization for a top class car aluminum chassis is studied in [2].

Deterministic optimization (DO) is the most frequently used in engineering design. However, in recent years, design optimization under uncertainty or optimization under uncertainty (OU) has widely evolved in mechanical engineering. OU is highly demanded due to the irreducible sources of uncertainties in mechanics, like tolerances, material densities, environmental temperature, etc. OU is employed, when DO fails to product high reliable and (or) robust design. In [49], the reliability is defined by the likelihood that a component (or a system) will perform its intended function without failure for a specified period of time under stated operating conditions. And the robustness is defined by The degree of tolerance of the system to be insensitive to variations in both the system itself and the environment. In most practical design problems, we cannot ensure a fully reliable or robust design. However we can obtain a high reliable design when it performs its intended function with a very low probability of failure. And we can obtain a robust one, when it is less sensible to the inputs uncertainties. OU is highly expensive, especially when costly numerical simulations are used to evaluate the response of the design. In reliability case, the cost is related to the evaluation of the constraints violation probability, which demands the estimation of design response not only on its deterministic configurations but also in their neighbors. In robust case, the cost is related to the multi-objective problem formulation, by taking both the performance and its stability as objective functions. These costs added to the cost of numerical simulations and the cost of optimization algorithm is the major challenge of OU in mechanical design [10]. Whereas, this cost can be reduced by the designer when he chooses well the suitable OU formulation for his design problem. In some problems, design performance and its stability are not conflicted, in this case, robust formulation is not needed. The choice of suitable OU formulation is related to the necessary conditions for each one, and how theses conditions are respected in a design problem.

In the literature, no tools is developed to help designer to choose which OU formulation is required to his problem. In addition, none of the authors has approached the question of the antagonism between the performance and its stability.

In this work, we propose a new methodology to help the designer to test the influence of the uncertainties to the performance and the robustness of his design. This interactive method implements the numerical optimization tools like (R,Scilab,ACTrESS or Matlab,$\ldots$) in order to guide the designer in the formulation of OU problems and to help him to find the solution for the suitable formulation.

In addition, we highlights the necessary conditions for each OU formulation and we classify OU based on these conditions, we study the existence of performance-stability antagonism and we propose a new method to help designer to choose the suitable formulation for a given design problem, with a minor computational cost. Several case study are presented to illustrate our proposal: a two bars design problem [20], a Bracket structure design [44] and the design of a welded beam [37].

This paper is divided into five sections. Firstly, in Sect. 2, a state of the art of multi-objective optimization and OU is presented. Section 3 discusses the different types and formulations of OU and their necessary conditions. The general method is described in Sect. 4. The mechanical applications are treated in Sect. 5. Finally, the conclusions of this paper and some perspectives are outlined in Sect. 6.

2 State of the art

In this section, we treat the state of the art of OU and the conception of antagonism in multi-objective optimization.

2.1 State of the art of OU

As mentioned in the introduction, OU has widely used in mechanical engineering. For example, OU of automobile structures for crash-worthiness is studied in [1, 31]. Reliability modeling and optimization of die-casting existing epistemic uncertainty is studied in [50]. In [36], the variabilities in functioning, manufacturing and modeling phases are taken into account in multi-objective optimization. Baudoui et al. [5, 6], propose a method for robust design optimization and apply it to aircraft design system. Composite panels are optimized under uncertainties in [4, 12]. In [42], reliability based optimization in aeroelastic stability problems is studied.

In some works, unsuitable problems are studied with robustness OU formulation. Such as, in [35], the two-bars problem is used as an example of robustness OU formulation. Similarly, Lelievre et al. [28], treat the bracket structure problem in robust OU formulation. In Sect. 5, we demonstrate the absence of the antagonism between the performance and its stability in these works.

2.2 Antagonism in multi-objective problems

Multi-objective optimization design involves simultaneous optimization of several conflicting objectives, all objective functions are to be optimized. Conflicted objective functions means that neither solution can be found where every objective function attains its optimum [30].

Multi-objective optimization is often used in engineering design, to take into consideration several design criteria or objective functions simultaneously. For example, khodaygan et al. [25], use multi-objective optimization to find the best part orientation that ensure higher quality at the lower time in additive manufacturing. In [40], multi-objective optimization is used to maximize both the efficiency and the recovered heat rate of the transparent transpired collectors. In [32], multi-objective optimization algorithm has been used to optimize a wood plastic composite for decking application.

In multi-objective problems, a necessary condition to obtain Pareto front is the presence of antagonism between the objective functions in their optimum zones included in the domain of definition. If the antagonism exists outside these zones, Pareto front is reduced to one point. In this case, the problem could be studied in mono-objective optimization. To illustrate this situation, we consider the Schaffer’s bi-objective optimization problem [39]. In this problem, the two objective functions to be minimized are $f_1(x)=x^2+2$ and $f_2(x)=(x-2)^2$, where $x\in \mathbb {R}$. These functions are studied in the domain of definition D where $x\in [-2,4]$ as shown in Fig. 1a. For $x\in \mathcal {D}$, this bi-objective problem has a Pareto front which is plotted in blue in Fig. 1b and the two functions $f_1(x)$ and $f_2(x)$ are minimized in two distinct points at $x=0$ and $x=2$ respectively. In this case, the Pareto front exists because these functions are antagonistic in their optimum zones (between their minimums in the corresponding domain of definition). If we change the domain of definition to $x\in [2,4]$ or $x\in [-2,0]$, the Pareto front disappears and the optimum of this problem is obtained at $x=2$ and $x=0$ respectively. The absence of the Pareto front is due to the fact that the functions are not antagonistic in these two domains of definition. The condition of Pareto front existence is used to determine the necessary conditions to define RDO and RBRDO problems in the next section.

Fig. 1

Antagonism existence between $f_1(x)$ and $f_2(x)$ of the Schaffer’s bi-objective optimization problem a Schaffer’s functions $f_1(x)$ and $f_2(x)$. b Pareto front $f_1(x)$ versus $f_2(x)$

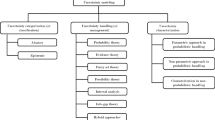
3 Types of optimization under uncertainty

Optimization problems can be divided into two main categories: deterministic optimization and optimization under uncertainty.

3.1 Deterministic optimization

DO is the classical optimization category, its minimization formulation for mono-objective function is presented in Eq. 1. The objective function is represented by $f( \mathbf {x} )$, $\mathbf {x}$ is a vector of n variables bounded by the lower and upper vectors $\mathbf {x} _l$ and $\mathbf {x} _u$ respectively, $\mathbf {h} ( \mathbf {x} )$ and $\mathbf {g} ( \mathbf {x} )$ are the vectors of l equality constraints and s inequality constraints respectively. DO produces optimums without taking environmental uncertainties into consideration. Ignoring these uncertainties risks obtaining results that are sensitive to variables and parameters uncertainties and have low reliability degree.

$$\begin{aligned} \begin{aligned} \text {Minimize:}&\quad f( \mathbf {x} )\\ \text {Subject to:}&\quad \mathbf {h} ( \mathbf {x} ) = 0\\&\quad \mathbf {g} ( \mathbf {x} ) \le 0\\&\quad \mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\\ \text {Where: }&\quad x=\{x_1,x_2,\ldots ,x_{n}\} \\&\quad \mathbf {h} ( \mathbf {x} )=\{h_1( \mathbf {x} ),h_2( \mathbf {x} ),\ldots ,h_{l}( \mathbf {x} )\}\\&\quad \mathbf {g} ( \mathbf {x} )=\{g_1( \mathbf {x} ),g_2( \mathbf {x} ),\ldots ,g_{s}( \mathbf {x} )\} \end{aligned} \end{aligned}$$

(1)

3.2 Optimization under uncertainty

Optimization under uncertainty is used to overcome DO risks. In OU, uncertainties in input variables and parameters are considered in the process. From the literature[28], we can identify three main types of OU.

• Reliability based design optimization (RBDO).

• Robust design optimization (RDO).

• Reliability-based robust design optimization (RBRDO).

3.2.1 Reliability based design optimization

RBDO is the optimization type that produces high-reliable results, due to the evaluation of the problem constraints under uncertainty. Many papers have studied RBDO like [3, 19, 23, 45]. RBDO formulation for mono-objective problem is presented in Eq. 2, where $\mathbb {E}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ is the expected value of f. In order to model uncertainties, $\tilde{ \mathbf {x} }$ and $\tilde{ \mathbf {p} }$ are the vectors of the random variables and the random environmental parameters respectively. The vector of deterministic parameters is represented by $\mathbf {p}$ which contains m components. The uncertainties associated to the variables and the parameters of the problem are $\tilde{\varvec{\chi }}_x$ and $\tilde{\varvec{\chi }}_p$ respectively, the deterministic constraints $\mathbf {h}$ and $\mathbf {g}$ are replaced by their quantiles $Q_\alpha [ \mathbf {h} ]$ and $Q_\alpha [ \mathbf {g} ]$, where $\alpha$ is the desired reliability degree. It is sufficient to convert only one deterministic constraint into probabilistic to define RBDO problem. The objective function can be replaced by its mean or evaluated deterministically.

$$\begin{aligned} \begin{aligned} \text {Minimize: }&\quad \mathbb {E}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\\ \text {Subject to: }&\quad Q_\alpha [ \mathbf {h} ( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]= 0\\&\quad Q_\alpha [ \mathbf {g} ( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]\le 0\\&\quad \mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\\ \text {Where: }&\quad \tilde{ \mathbf {x} }= \mathbf {x} + \tilde{\varvec{\chi }}_x\\&\quad \tilde{ \mathbf {p} }= \mathbf {p} + \tilde{\varvec{\chi }}_p\\&\quad \mathbf {x} =\{x_1,x_2,\ldots ,x_{n}\} \\&\quad \mathbf {p} =\{p_1,p_2,\ldots ,p_{m}\} \\&\quad \mathbf {h} ( \mathbf {x} )=\{h_1( \mathbf {x} ),h_2( \mathbf {x} ),\ldots ,h_{l}( \mathbf {x} )\}\\&\quad \mathbf {g} ( \mathbf {x} )=\{g_1( \mathbf {x} ),g_2( \mathbf {x} ),\ldots ,g_{s}( \mathbf {x} )\} \end{aligned} \end{aligned}$$

(2)

They exists other formulations for RBDO, such as worth case formulation which is a special formulation of 2 and is obtained by taking $\alpha =100\%$. In this paper we use this general formulation based on the probability theory. Other RBDO formulations are referred to [49].

3.2.2 Robust design optimization

The robust design concept is introduced by the Japanese engineer Genichi Taguchi, who develops a Taguchi method to improve the quality of the product and make it insensitive to the variables variations [33, 43]. RDO is discussed in [7,8,9, 14, 17]. RDO targets to produce results which are less sensitive to inputs uncertainties. Severals metrics are used in the literature to measure the robustness of a design, Gohler et al. [21] identify 38 different metrics. In this paper we used the classical formulation for RDO by implementing a dispersion or stability measure of the function f to the objectives of the problem, whereas the constraint functions remain deterministic. This implantation can be realized by adding a second objective function to the problem or by a simple aggregation with the performance measure (e.g.[28, 49]). Variance, standard deviation or difference of quantile could be used as stability measure. RDO formulation based on the mean and variance quantity is used in this paper, and presented in Eq. 3, where $\mathbb {V}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ is the variance of f. Notice that an aggregation formulation lead to a single point on the performance-stability Pareto front. Whereas this formulation is capable to obtain the entire Pareto front which gives the designer multiple options and choices.

$$\begin{aligned} \begin{aligned} \text {Minimize: }&\mathbb {E}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]; \mathbb {V}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\\ \text {Subject to: }&\mathbf {h} ( \mathbf {x} )= 0\\&\mathbf {g} ( \mathbf {x} )\le 0\\&\mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\\ \text {Where: }&\tilde{ \mathbf {x} }= \mathbf {x} + \tilde{\varvec{\chi }}_x\\&\tilde{ \mathbf {p} }= \mathbf {p} + \tilde{\varvec{\chi }}_p\\&\mathbf {x} =\{x_1,x_2,\ldots ,x_{n}\} \\&\mathbf {p} =\{p_1,p_2,\ldots ,p_{m}\} \\&\mathbf {h} ( \mathbf {x} )=\{h_1( \mathbf {x} ),h_2( \mathbf {x} ),\ldots ,h_{l}( \mathbf {x} )\}\\&\mathbf {g} ( \mathbf {x} )=\{g_1( \mathbf {x} ),g_2( \mathbf {x} ),\ldots ,g_{s}( \mathbf {x} )\} \end{aligned} \end{aligned}$$

(3)

3.2.3 Reliability-based robust design optimization

RBRDO is the OU type that combines RDO and RBDO. It has been studied in [27, 38, 41, 47]. This type is used when stable results with high reliability degree are demanded. The function f is represented by its two measures performance and stability, while the problem constraints are replaced by their quantiles. Despite the capability of RBRDO to produce results that contain all design requirements, it stills the more complex type and requires a huge computational cost. This cost is very significant in mechanical problems especially when numerical simulations are demanded to evaluate problem objectives and constraints. The formulation of RBRDO is shown in Eq. 4.

$$\begin{aligned} \begin{aligned} \text {Minimize: }&\mathbb {E}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]; \mathbb {V}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\\ \text {Subject to: }&Q_\alpha [ \mathbf {h} ( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]= 0\\&Q_\alpha [ \mathbf {g} ( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]\le 0\\&\mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\\ \text {Where: }&\tilde{ \mathbf {x} }= \mathbf {x} + \tilde{\varvec{\chi }}_x\\&\tilde{ \mathbf {p} }= \mathbf {p} + \tilde{\varvec{\chi }}_p\\&\mathbf {x} =\{x_1,x_2,\ldots ,x_{n}\} \\&\mathbf {p} =\{p_1,p_2,\ldots ,p_{m}\} \\&\mathbf {h} ( \mathbf {x} )=\{h_1( \mathbf {x} ),h_2( \mathbf {x} ),\ldots ,h_{l}( \mathbf {x} )\}\\&\mathbf {g} ( \mathbf {x} )=\{g_1( \mathbf {x} ),g_2( \mathbf {x} ),\ldots ,g_{s}( \mathbf {x} )\} \end{aligned} \end{aligned}$$

(4)

3.3 Necessary conditions for OU types

The challenge for the designer is to choose what OU type is required to make a design decision. let us identify the necessary condition for each type of OU.

Firstly, RBDO problem cannot be defined without the existence of problem constraint, this necessary condition for RBDO can be checked explicitly. However for RDO which is a bi-objective problem, the necessary condition is the antagonism between the performance and its stability in the optimum zones. In a mean-variance problem, $\mathbb {E}\left[f( \tilde{x}, \tilde{p})\right]$ and $\mathbb {V}\left[f( \tilde{x}, \tilde{p})\right]$ should be antagonist at their Pareto front. But this condition is more difficult to test than that of RBDO. By the way, we can define the necessary condition for RBRDO problem by the existence of the two above conditions for RDO and RBDO. Many questions can be arise here.

• Does this performance-stability antagonism exist systematically?

• If no, can this antagonism be detected explicitly?

• How can this antagonism be detected before the construction of the entire Pareto front?

Performance-stability antagonism does not exist systematically. None of the previous works has treated the problematic of the performance-stability antagonism. Usually, an aggregation of the performance and stability is used to solve RBRDO problem due to the huge computational time of multi-objective (performance-stability) RBRDO formulation [49]. This aggregation hides the non-existence of this antagonism, and the authors believe that exists systematically. However we will demonstrate the non-existence of this antagonism in several design problems in Sect. 5.

The evaluation of the antagonism condition explicitly or before construction of the entire Pareto front reduces the computational time significantly. If performance-stability problem does not have any antagonism, RDO and RBRDO can be replaced by mono-objective problems, RBRDO can be replaced by RBDO and RDO can be replaced by the minimization of the performance. For that we propose a forth type for OU called performance design optimization under uncertainty (PDOU), which aims to optimize only the performance measure. Notice that when the performance measure is very close to the deterministic measure, RDO can be replaced by DO. The formulation of PDOU is given in Eq. 5, problems in PDOU are treated without constraints or with only deterministic constraints. Based on these conditions, we identify in Table 1, the suitable OU type for each design case.

$$\begin{aligned} \begin{aligned} \text {Minimize: }&\mathbb {E}\left[f( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\\ \text {Subject to: }&\mathbf {h} ( \mathbf {x} )= 0\\&\mathbf {g} ( \mathbf {x} )\le 0\\&\mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\\ \text {Where: }&\tilde{ \mathbf {x} }= \mathbf {x} + \tilde{\varvec{\chi }}_x\\&\tilde{ \mathbf {p} }= \mathbf {p} + \tilde{\varvec{\chi }}_p\\&\mathbf {x} =\{x_1,x_2,\ldots ,x_{n}\} \\&\mathbf {p} =\{p_1,p_2,\ldots ,p_{m}\} \\&\mathbf {h} ( \mathbf {x} )=\{h_1( \mathbf {x} ),h_2( \mathbf {x} ),\ldots ,h_{l}( \mathbf {x} )\}\\&\mathbf {g} ( \mathbf {x} )=\{g_1( \mathbf {x} ),g_2( \mathbf {x} ),\ldots ,g_{s}( \mathbf {x} )\} \end{aligned} \end{aligned}$$

(5)

Table 1 The suitable OU type for each design case

The existence of performance-stability antagonism can be checked explicitly in some instance. Such as in two bars problem, which is treated in Sect. 5.1, or with our proposed general method in other instances. The general method is detailed in the following section.

4 General method

The performance-stability antagonism cannot be evaluated explicitly in all mechanical design problems. In addition, exploring solutions domain by sampling method is not efficient for high dimensional problems, especially when the uncertainty propagation is performed using Monte-Carlo simulation (MCs) (see [13]) . In Sect. 5.1, this sampling method is employed in the two-bars problem which has only two design variables and uncertainty propagation is calculated analytically. But, when the number of variables increases, the number of sampling points needed to maintain the same density of points increases exponentially. The total evaluated points is the product of the number of sampling points by the number of MCs sampling points, which entails an enormous computational cost.

To overcome these difficulties, a new general method is introduced here to evaluate this antagonism without losing time by constructing the entire Pareto front. Besides evaluation of the antagonism, the proposed method evaluates the amelioration in the results stability if the problem is treated in RDO or RBRDO instead of PDOU or RBDO. These pieces of information help the designer to decide which OU type is required to its design problem. To describe the method we use the mean and variance as measures of performance and stability respectively. Note that this method can be employed for any two other measures. The method measures the lengths of Pareto front of mean-variance problem in objectives and variables spaces. At first, the anchor points of the problem are calculated, these points are obtained by minimizing $\mathbb {E}\left[f\right]$ and $\mathbb {V}\left[f\right]$ separately under the same problem constraints and variables domain of the bi-objective problem. The obtained points are named $A_E(E_E,V_E)$ and $A_V(E_V,V_V)$ respectively, where $E\text { and }V$ are their coordinates in the objectives space. Likewise, they are represented in the variables space by their coordinates $\tilde{ \mathbf {x} }_E$ and $\tilde{ \mathbf {x} }_V$ respectively. If $A_E$ and $A_V$ are the same point, the obtained minimum is the best design. While, if one of these points dominates the other, this dominant point is the optimum design. In these two situations, no additional calculation is required. If these two points are different, and no point is dominated by the other, the antagonism exists. But it is important to evaluate the lengths of the Pareto front and know if the calculation of anchor points is sufficient, or the construction of the entire Pareto front is needed. At second, the distances $D_E$ and $D_V$ between these points in mean-variance space along each axes are evaluated. After that, two dispersion measures $\delta _E$ and $\delta _V$ are calculated by Eq. 6. Finally, $\delta _E$ and $\delta _V$ should be compared respectively to the basic measures $\varDelta _E$, $\varDelta _V$, which are predetermined by the designer. If at least one of $\delta _E$ and $\delta _V$ is bigger than its corresponding basic measure, the bi-objective problem should be solved, and more points of Pareto front must be generated to find a trade-off design. If both $\delta _E$ and $\delta _V$ are less than their basic measures, the Pareto length in variables space must be evaluated to taking design decision. For it, the euclidean distance $D_x$ between $A_E$ and $A_V$ in variables spaces is calculated. Thereby, a dispersion measure $\delta _x$ which is obtained by Eq. 7 must be compared to a basic measure $\varDelta _x$. If $\delta _x$ is less than $\varDelta _x$, there is no need for RDO or RBRDO, the designer can choose one of the anchor points as optimum design. If $\delta _x$ is greater than $\varDelta _x$, the bi-objective problem should be run to discover more design configurations. This method is summarized in Algorithm 1.

$$\begin{aligned} D_E= & {} E_V-E_E\nonumber \\ D_V= & {} V_E-E_V\nonumber \\ \delta _E= & {} \frac{D_E}{max\{|E_E|,|E_V|\}}\nonumber \\ \delta _V= & {} \frac{D_E}{V_E} \end{aligned}$$

(6)

$$\begin{aligned} \delta _x= & {} \frac{|| \tilde{ \mathbf {x} }_E- \tilde{ \mathbf {x} }_V||}{max\{|| \tilde{ \mathbf {x} }_E||,|| \tilde{ \mathbf {x} }_V||\}} \end{aligned}$$

(7)

5 Applications

In this section, we study three applications that are treated in the literature. The first is the two-bars problem which is introduced by [20] and is studied in [24, 35]. In this problem the existence of performance-stability antagonism is evaluated analytically without any optimization run. The second application is the bracket structure, it is introduced by [44] and used an example for robust design optimization in [28]. The third application is the welded beam problem that is introduced by [37] and studied in [16]. In the last two problems, the general method is applied to evaluate the performance-stability antagonism. In all optimization problems, the Matlab function “fmincon”, with multi-start option, is used to perform optimization, this function is a gradient based algorithm. The Pareto fronts are constructed using the Normal boundary intersection (NBI) method [15]. Uncertainty propagation is performed analytically in the two-bars problem using Eq. 13 [46]. However, in the other problems, it is performed using Monte-Carlo simulation, with a sampling number $n_s=1 \times 10^{6}$. MCs method is performed using common random number (CRN) technique [48], which allow us to use gradient based algorithm for optimization.

Fig. 2

Two-bars structure

Table 2 Variable bounds in the two-bars problem

Table 3 Distributions of variables and parameters in the two-bars problem

5.1 Two-bars problem

The two-bars structure is a design problem that aims to minimize the volume $f_v$ of the structure shown in Fig. 2. In this problem, the design variables are d and l, an accepted design should respect that its normal stress s should be less than normal stress limit $s_{max}$ and the buckling stress $s_{crit}$. Deterministic formulation of the problem is given in Eq. 11, the upper and lower bounds of d and l are presented in Table 2. This problem is studied in two cases, which differ by the modeling of uncertainties associated to the design variables $\tilde{d}$ and $\tilde{l}$, as described in Table 3. While, uncertainties associated to environmental parameters do not change between these cases. The distribution types and their parameters used for design variables and environmental parameters for both cases are given in Table 3, where the mean value of each parameter and variable is used in the deterministic case. To evaluate the necessary condition for RBRDO formulation, the mean-variance antagonism for this problem is tested analytically by calculating the relation between $\mathbb {E}\left[f_v\right]$ and $\mathbb {V}\left[f_v\right]$ in both cases based on the Eq. 8. For the first case, where the standard deviations of the variables are constant, if we consider that $\mathbb {V}\left[ \tilde{d}\right]=c_1^2$ and $\mathbb {V}\left[ \tilde{l}\right]=c_2^2$, where $c_1,c_2 \in \mathbb {R}^{2*+}$, we obtain the Eq. 9, which is a family of parabolic curves, in this case the antagonism can be exist and it depends on the domain of definition. For the second case, we consider that $\mathbb {V}\left[ \tilde{d}\right]=\beta _1^2 \mathbb {E}\left[ \tilde{d}\right]^2$ and $\mathbb {V}\left[ \tilde{l}\right]=\beta _2^2 \mathbb {E}\left[ \tilde{l}\right]^2$, where $\beta _1,\beta _2 \in \mathbb {R}^{2*+}$. We obtain Eq. 10, which is the equation of a single parabolic curve, which means that the antagonism does not exist

$$\begin{aligned} \mathbb {E}\left[f_v( \tilde{d}, \tilde{l})\right]&=2\pi \mathbb {E}\left[ \tilde{T}\right] \mathbb {E}\left[ \tilde{d}\right] \mathbb {E}\left[ \tilde{l}\right]\nonumber \\ \mathbb {V}\left[f_v( \tilde{d}, \tilde{l})\right]&=4\pi ^2 \mathbb {E}\left[f_v( \tilde{d}, \tilde{l})\right]^2\Psi ( \tilde{d}, \tilde{l})\nonumber \\ \Psi ( \tilde{d}, \tilde{l})&=\frac{ \mathbb {V}\left[ \tilde{d}\right]}{ \mathbb {E}\left[ \tilde{d}\right]^2}+\frac{ \mathbb {V}\left[ \tilde{l}\right]}{ \mathbb {E}\left[ \tilde{l}\right]^2}+\frac{ \mathbb {V}\left[ \tilde{T}\right]}{ \mathbb {E}\left[ \tilde{T}\right]^2}+\frac{ \mathbb {V}\left[ \tilde{d}\right] \mathbb {V}\left[ \tilde{l}\right]}{ \mathbb {E}\left[ \tilde{d}\right]^2 \mathbb {E}\left[ \tilde{l}\right]^2}\nonumber \\&+\frac{ \mathbb {V}\left[ \tilde{d}\right] \mathbb {V}\left[ \tilde{T}\right]}{ \mathbb {E}\left[ \tilde{d}\right]^2 \mathbb {E}\left[ \tilde{T}\right]^2}+\frac{ \mathbb {V}\left[ \tilde{T}\right] \mathbb {V}\left[ \tilde{l}\right]}{ \mathbb {E}\left[ \tilde{T}\right]^2 \mathbb {E}\left[ \tilde{l}\right]^2}\nonumber \\&+\frac{ \mathbb {V}\left[ \tilde{d}\right] \mathbb {V}\left[ \tilde{l}\right] \mathbb {V}\left[ \tilde{T}\right]}{ \mathbb {E}\left[ \tilde{d}\right]^2 \mathbb {E}\left[ \tilde{l}\right]^2 \mathbb {E}\left[ \tilde{T}\right]^2} \end{aligned}$$

(8)

$$\begin{aligned} \mathbb {V}\left[f_v( \tilde{d}, \tilde{l})\right]&=4\pi ^2 \mathbb {E}\left[f_v\right]^2\Psi (d,l)\nonumber \\ \Psi (d,l)&=1.6 \times 10^{-3}\left\{ 1+\frac{c_1^2}{d^2}+\frac{c_2^2}{l^2}+\frac{c_1^2c_2^2}{d^2l^2}\right\} \nonumber \\&+\frac{c_1^2}{d^2}+\frac{c_2^2}{l^2}+\frac{c_1^2c_2^2}{d^2l^2} \end{aligned}$$

(9)

$$\begin{aligned} \mathbb {V}\left[f_v( \tilde{d}, \tilde{l})\right]&=4\pi ^2 \mathbb {E}\left[f_v\right]^2\Psi (d,l)\nonumber \\ \Psi (d,l)=&1.6 \times 10^{-3}\left\{ 1+\beta _1^2+\beta _2^2+\beta _1^2\beta _2^2\right\} \nonumber \\&+\beta _1^2+\beta _2^2+\beta _1^2\beta _2^2 = \text {constant}>0. \end{aligned}$$

(10)

Secondly, the solution domains for both cases are explored in the objectives space, $\mathbb {E}\left[f_v\right]$ and $\mathbb {V}\left[f_v\right]$ are calculated in 400 points which are equally distributed along the entire domain. The calculations are performed using Eq. 13 and the obtained results for both cases are shown in Figs. 3 and 4. The results corresponding to case 2 illustrate the analytic demonstration presented in Eq. 10, a parabolic form is obtained in Fig. 4, which confirms the absence of antagonism in all points. On the other side, the results shown in Fig. 3 form a family of curves. In this case, the existence of antagonism depends on problem constraints which can affect the domain of definition. This situation is like that one identified in the Schaffer example treated in Sect. 2.2 where the Pareto front is affected by the domain of definition.

Fig. 3

$\mathbb {E}\left[f_v\right]$ versus $\mathbb {V}\left[f_v\right]$ for two-bars problem treated in case 1 which corresponds to constant variance. The points A and B are the anchor points of the RBRDO problem

Fig. 4

$\mathbb {E}\left[f_v\right]$ versus $\mathbb {V}\left[f_v\right]$ for two-bars problem treated in case 2 which corresponds to proportional variance. The point O is the optimum point for the RBRDO problem

The RBRDO problem is formulated in Eq. 12, and is solved in both cases. For the first one, the corresponding anchor points are shown in Table 4, the value of the corresponding dispersions measures are shown in Table 5. These values reflect the short distance between the anchor points in the objectives and variables spaces. The necessity of constructing the entire Pareto front is depended on the choice of the basic measures, we consider that the basic measures are equal $1\%$. Therefore, the corresponding Pareto front is shown in Fig. 5. In the case 2 no Pareto front is found, the two anchor points are coincident, the obtained optimum point is presented in Table 6. These results show the influence of uncertainties modeling on the existence of Pareto front. This influence is studied in [11]. The deterministic optimum is calculated, and the values of the objectives functions in this point are estimated for the first case of uncertainties modeling. The results are given in Table 7. The results show that this point dominate all Pareto front points, whereas it is not a feasible point due the low degree of reliability which are 0.5 for both constraints. This reveals the importance of RBRDO formulation and the failure of DO to produce reliable and robust design.

$$\begin{aligned} \text {Minimize: }&f_v( \mathbf {x} )=2\pi Tdl\nonumber \\ \text {Subject to: }&g_1( \mathbf {x} )=s( \mathbf {x} )-s_{max} \le 0\nonumber \\&g_2( \mathbf {x} )=s( \mathbf {x} )-s_{crit} \le 0\nonumber \\ \text {Where: }&\mathbf {x} =\{d,l\}\nonumber \\&s( \mathbf {x} )=\frac{Fl}{2\pi Td\sqrt{l^2-B^2}}\nonumber \\&s_{crit}( \mathbf {x} )=\frac{\pi ^2E(T^2+d^2)}{8l^2} \end{aligned}$$

(11)

$$\begin{aligned} \text {Minimize: }&\mathbb {E}\left[f_v( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]; \mathbb {V}\left[f_v( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\nonumber \\ \text {Subject to: }&Q_\alpha [g_j( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]\le 0 \qquad j=1,2\nonumber \\&\mathbf {x} _l\le \mathbf {x} \le \mathbf {x} _u\nonumber \\ \text {Where: }&\tilde{ \mathbf {x} }=\{ \tilde{d}, \tilde{l}\}\nonumber \\&\tilde{ \mathbf {p} }=\{ \tilde{B}, \tilde{E}, \tilde{F}, \tilde{T}\} \nonumber \\&\alpha =0.95\end{aligned}$$

(12)

$$\begin{aligned} f( \tilde{ \mathbf {x} })&=K\prod _{i=1}^{n} \tilde{x}_i^{a_i}\text { where } K,a_i\in \mathbb {R}^2\nonumber \\ \mathbb {E}\left[f( \tilde{\mathbf {x}})\right]&=K\prod _{i=1}^{n} \mathbb {E}\left[ \tilde{x}_i^{a_i}\right]\nonumber \\ \mathbb {V}\left[f( \tilde{\mathbf {x}})\right]&=K^2\left\{ \prod _{i=1}^{n} \mathbb {E}\left[ \tilde{x}_i^{2a_i}\right]-\prod _{i=1}^{n} \mathbb {E}\left[ \tilde{x}_i^{a_i}\right]^2\right\} \end{aligned}$$

(13)

Table 4 Optimum points for RBRDO two-bars problem (case 1)

Table 5 Dispersion measures for two-bars problem (case 1)

Fig. 5

Pareto front for RBRDO two-bars problem treated in case 1 which corresponds to constant variance

Table 6 Optimum point for RBRDO two-bars problem (case 2)

Table 7 The deterministic optimum for the two bars problem

Fig. 6

Bracket structure

Table 8 Variable bounds in the bracket problem

Table 9 Distributions of variables and parameters in the bracket problem

Table 10 Anchor points for RBRDO bracket problem

5.2 Bracket structure

The bracket structure is used in the literature as an application of optimization under uncertainty and robust design optimization, it is illustrated in Fig. 6. The problem aims to design the lightest structure that respects the mechanical constraints, the deterministic problem is formulated in Eq. 14. Let consider that, $f_w$ is the weight of the structure, $\sigma _y$ and $\sigma _B$ are the yield strength and the maximum bending stress in the CD beam respectively. As well, $F_{AB}$ and $F_{Bk}$ are the maximum axial load in the bar AB and Euler critical buckling load respectively. Variables bounds are shown in Table 8, and the problem is formulated in RBRDO in Eq. 15. In RBRDO, the deterministic variables and parameters are converted into random variables, the type of distributions and their parameters are shown in Table 9, where the deterministic values are used as mean values for all random variables. The general method is applied to this problem to evaluate the necessary condition for RBRDO, the corresponding anchor points $A_E$ and $A_V$ are presented in Table 10. They are two different points , and no point dominates the other. The, the dispersion measures are calculated, their values are presented in Table 11. They are very small and less than ${1}{\%}$ which is taken as a value for the basic measures. This problem does not require a RBRDO optimization. Both obtained anchor points can be considered as best design. The problem is also resolved in DO and the optimum point and the corresponding estimated $\mathbb {E}\left[f_w( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ and $\mathbb {V}\left[f_w( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ are given in Table 12. Similarly to the two bars problem, the deterministic optimum point has better values for the objective functions than that for the RBRDO optimums, however its corresponding reliability degree are 0.52 for $g_1$ and 0.47 for $g_2$.

$$\begin{aligned} \text {Minimize: }&f_w ( \mathbf {x} )=2\rho tL\left( \frac{2w_{AB}}{3\sin (\theta )}+W_{CD}\right) \nonumber \\ \text {Subject to: }&g_1(x)=\sigma _B( \mathbf {x} )-\sigma _y \le 0\nonumber \\&g_2(x)=F_{AB}( \mathbf {x} )-F_{Bk}( \mathbf {x} ) \le 0\nonumber \\ \text {Where: }&\mathbf {x} =\{w_{AB},w_{CD},t,\theta \}\nonumber \\&\sigma _B( \mathbf {x} )=\frac{6M_B}{w_{CD}t^2}\nonumber \\&M_B( \mathbf {x} )=\frac{PL}{3}\frac{\rho gw_{CD}tL^2}{18}\nonumber \\&F_{Bk}( \mathbf {x} )=\frac{9\pi ^2Etw^3_{AB} \sin ^2\theta }{48L^2}\nonumber \\&F_{AB}( \mathbf {x} )=\frac{1}{\cos \theta }\left( \frac{3P}{2}+ \frac{3\rho gw_{CD}tL}{4}\right) \end{aligned}$$

(14)

$$\begin{aligned} \text {Minimize: }&\mathbb {E}\left[f_w( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]; \mathbb {V}\left[f_w( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\nonumber \\ \text {Subject to: }&Q_\alpha [g_j( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]\le 0 \qquad j=1,2\nonumber \\ \text {Where: }&\tilde{ \mathbf {x} }=\{ \tilde{w}_{AB}, \tilde{w}_{CD}, \tilde{t}, \tilde{\theta }\}\nonumber \\&\tilde{ \mathbf {p} }=\{ \tilde{P}, \tilde{E}, \tilde{\sigma }_y, \tilde{\rho }, \tilde{L}\} \nonumber \\&\alpha =0.977 \end{aligned}$$

(15)

Table 11 Dispersion measures for the bracket problem

Table 12 Deterministic optimum for the bracket problem

Fig. 7

welded beam

Table 13 Variable bounds in welded beam problem

5.3 Welded beam

Welded beam problem which is shown in Fig. 7 is introduced by Phillips et al. in [37] and used in [16] as an application to introduce robustness in multi-objective optimization. In this problem, the cost of the welded beam is to be minimized, this cost depends on the geometric variables of the bar and its weld joint. Deterministic and RBRDO problems are formulated in Eqs. 16 and 17 respectively, where.

Table 14 Distributions of variables and parameters in the welded beam problem

Table 15 Anchor points for RBRDO welded beam problem

• (1) $f_c$: total cost including set up, welding labor costs and material cost.

• (2) $\tau _d$: design shear stress of weld.

• (3) $\tau ( \mathbf {x} )$: maximum shear stress in weld.

• (4) $\sigma _d$: design normal stress for beam material.

• (5) $\sigma ( \mathbf {x} )$: maximum normal stress in beam.

• (6) $P_c( \mathbf {x} )$: bar buckling load.

• (7) $\lambda ( \mathbf {x} )$: bar end deflection.

• (8) E: Young’s modulus for beam material.

• (9) G: Shearing modulus for beam material.

Upper and lower bounds of each variable are shown in Table 13, and the distribution types and their parameters associated to each random variables are presented in Table 14. In this problem we apply the general method, the obtained anchor points are presented in Table 15. As in the bracket problem, we obtain two different and non dominated anchor points. We calculate the dispersion measures, and we compare these measures to their corresponding basic measures which are considered equal to $1\%$. It is clear in Table 16 that all dispersion measures have high values. This RBRDO problem has an antagonism between their objective functions, and the corresponding Pareto front is drawn in Fig. 8. The deterministic optimum obtained by solving the problem 16 and its corresponding estimated $\mathbb {E}\left[f_c( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ and $\mathbb {V}\left[f_c( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]$ are given in Table 17. As above, the deterministic optimum is not an admissible point due to its low reliability degrees, which equal to 0.499, 0.0, 0.4175 and 0.5 for the first four constraints respectively, however for the last constraint the probability degree is equal to 1. This RBRDO problem can be converted into problem without antagonism between its objective functions by changing the uncertainties modeling in design variables. To demonstrate that, we resolve the problem after doing this change, in the new uncertainties modeling, each variable has a standard deviation proportional to its mean as shown in Table 18, and the optimum point found is presented in Table 19.

$$\begin{aligned} \text {Minimize: }&f_c ( \mathbf {x} )=c_1h^2l+c_2tb(L+l)\nonumber \\ \text {Subject to: }&g_1( \mathbf {x} )=\tau ( \mathbf {x} )-\tau _d \le 0\nonumber \\&g_2( \mathbf {x} )=\sigma ( \mathbf {x} )-\sigma _d \le 0\nonumber \\&g_3( \mathbf {x} )=F-P_c( \mathbf {x} ) \le 0\nonumber \\&g_4( \mathbf {x} )=h-b \le 0\nonumber \\&g_5( \mathbf {x} )=\lambda ( \mathbf {x} )-\lambda _{max} \le 0\nonumber \\ \text {Where: }&\mathbf {x} =\{h,l,t,b\}\nonumber \\&c_1={6.74}\times 10^{4}\,\$/\hbox {m}^{3}\nonumber \\&c_2={2.94e3}\times 10^{3}\,\$/\hbox {m}^{3}\nonumber \\&\tau _1=\frac{F}{\sqrt{2}hl}\nonumber \\&\tau _2=\frac{MR}{J}\nonumber \\&M=F[L+0.5l]\nonumber \\&R=\sqrt{0.25[l^2+(t+h)^2]}\nonumber \\&J=2\left\{ 0.707hl\left[ \frac{l^2}{12}+0.25(t+h)^2\right] \right\} \nonumber \\&\tau =\sqrt{\tau _1^2+2\tau _1\tau _2\frac{l}{2R}+\tau _2^2}\nonumber \\&\sigma ( \mathbf {x} )=\frac{6FL}{bt^2}\nonumber \\&P_c( \mathbf {x} )=\frac{4.013\sqrt{EI\alpha }}{L^2}\left[ 1-\frac{t}{2L}\sqrt{\frac{EI}{\alpha }}\right] \nonumber \\&I( \mathbf {x} )=\frac{1}{12}tb^3\nonumber \\&\alpha ( \mathbf {x} )=\frac{1}{3}Gtb^3\nonumber \\&\lambda ( \mathbf {x} )=\frac{4FL^3}{Et^3b}\nonumber \\&\lambda _{max}={6.35}\,{\hbox {mm}} \text { (maximum deflection)} \end{aligned}$$

(16)

$$\begin{aligned} \text {Minimize: }&\mathbb {E}\left[f_c( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]; \mathbb {V}\left[f_c( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })\right]\nonumber \\ \text {Subject to: }&Q_\alpha [g_j( \tilde{ \mathbf {x} }, \tilde{ \mathbf {p} })]\le 0 \qquad j=1,\ldots ,5\nonumber \\ \text {Where: }&\tilde{ \mathbf {x} }=\{ \tilde{h}, \tilde{l}, \tilde{t}, \tilde{b}\}\nonumber \\&\tilde{ \mathbf {p} }=\{ \tilde{G}, \tilde{E}, \tilde{F}, \tilde{\sigma }_d, \tilde{\tau _d}, \tilde{L}\} \nonumber \\&\alpha =0.95 \end{aligned}$$

(17)

Table 16 Dispersion measures for welded beam problem

Fig. 8

Pareto front for RBRDO welded beam problem and deterministic optimum

6 Conclusion and perspective

Table 17 Deterministic optimum for the welded beam problem

Table 18 New uncertainties modeling of design variables in welded beam problem

Table 19 Optimum point for RBRDO welded beam problem with the new uncertainties modeling

This paper identifies the necessary conditions for different OU types. In addition, the subject of performance-stability antagonism in mechanical design engineering is studied. A new general method is proposed to evaluate the existence of this antagonism in OU problems. this method is very efficient in helping the designer to choose what OU types is required to his problem. The performance-stability Pareto front does not exist systematically in RDO and RBRDO problem. When the Pareto front is absent, RDO and RBRDO formulations should be replaced by PDOU and RBDO formulations respectively, to save computational time and simplify the problem. In some instance, absence of the Pareto front can be detected explicitly before optimization run. In other instance, this absence is very difficult or impossible to detect explicitly. The proposed method is efficient to identify the situation before calculation of the entire Pareto front. The effectiveness of this method is illustrated after its application on the bracket structure and welded beam problems. This method is applied to problem with one objective function. It is possible to extend it to cover multi objective problems by simply testing each function individually and reformulate the multi-objective problem under uncertainty, whereas the difficulty here is in the dimension of objective space and the presentation of hyper surface Pareto fronts. The problem situation is affected by the objective functions, the problem constraints and the uncertainties modeling, this influence is not sufficiently treated in the literature and in this work. Further works are needed to study this influence, these works may lead to identify special cases problem where the mean-variance antagonism could be evaluated explicitly.