1 Introduction

In today’s society, an abundance of information is available through media and technology. To be effective in such an environment in the twenty-first century, citizens need to be prepared for utilizing information, media and technology effectively (see framework for twenty-first century learning, http://www.p21.org). Hence twenty-first century learning skills emphasize the importance of equipping young people with competencies for working collaboratively and for thinking critically and creatively about real-world problems and using data to deal with them. A significant source of such activity is the use of models in statistics, since it bridges the real world where the problems reside and the theoretical world in which analyses are done of the data emerging from the problem context. Our aim in this study is to engage students in a data-rich task which will necessitate critical and creative thinking while we research the nature of the models constructed and how the students evaluate them.

2 Models and modelling in mathematics and statistics

Mathematical models have been a key element in the historical development of both the disciplines of mathematics and statistics. Lesh and Doerr (2003) describe models as follows:

conceptual systems (consisting of elements, relations, operations, and rules governing interactions) that are expressed using external notation systems, and that are used to construct, describe, or explain the behaviours of other system(s)–perhaps so that the other system can be manipulated or predicted intelligently. (p. 10)

So, modelling refers to this process of designing, describing or explaining another system for a particular purpose.

In statistics, modelling and reasoning with models are considered as essential components of statistical thinking when analysing data (Wild and Pfannkuch 1999). Moore (1990) describes the role of statistical models in “moving from particular observations to an idealized description of all observations” (p. 109). For example, the normal or uniform distributions are such models for describing the overall pattern in data. According to Garfield and Ben-Zvi (2008), one of the main uses of models in statistics is fitting a statistical model, such as normal distribution, to data that already exist or are collected through survey or experiment in order to explain and describe the variation in the data. The role of statistical graphs is also important in statistical modelling since they enable us “to look for the shape, center, and spread of the displayed distribution, to weigh the five-number summary against \(\bar{x}\) and s as a description of center and spread, and to consider standard density curves as possible compact models” (Moore 1999, p. 251). In other words, data representations can be seen as models for describing the overall pattern in sample data to make predictions about a population or phenomenon with a degree of uncertainty.

3 Models and modelling in pedagogy

Given the importance of models in mathematics and statistics, it is not surprising that school curricula over many decades have been peppered with the requirement that students are able to make use of given models such as Newton’s laws of motion in applied mathematics and the normal distribution in statistics. Such models have played a key role in transmission models of teaching and learning where the models appear as representations. The challenge for the student experiencing the transmission model of teaching is one of recognising the nature of the set problem and translating (a term coined in this context by Gravemeijer 2002) the problem into one of the various models that would have been previously introduced in the curriculum. These models/representations in themselves contain no intrinsic meaning and students often struggle to make sense of them.

More recently, the Common Core Standards Writing Team (2013) pointed out that, although there was no single definition of mathematical modelling that was agreed upon, its various descriptions tended to have the following common features:

mathematical modeling authentically connects to the real world; it is used to explain phenomena in the real world and/or make predictions about future behavior of a system in the real world; it requires creativity and making choices, assumptions, and decisions; it is an iterative process; and there can be multiple approaches and answers. (p. 8)

It seems then that it is not enough to simply manipulate and calculate with given statistical representations. A more holistic approach to teaching statistical concepts, ideas and tools within a broader context of data enquiry with emphasis on reasoning and inference is needed. One way of doing this is to adapt a teaching perspective that focusses on informal statistical inference (ISI) (Bakker and Derry 2011). This increasingly recognized approach entails the following essential components: (1) making a generalization beyond the data; (2) using the data as evidence for the generalization; and (3) acknowledging uncertainty in describing the generalization (Makar and Rubin 2009). A generalization beyond the data might, for example, involve identifying a signal in the data, that is to say a feature or trend in the data that might be explained by an associated or causal factor. Acknowledging uncertainty requires recognising the noise in the system which cannot be explained but could be regarded as random error. As more attention has been paid to innovative ways of connecting chance and data and to reasoning about uncertainty in the context of ISI, the role of statistical models and modelling has come into prominence in developing students’ statistical understanding and reasoning at different levels of statistics teaching (e.g. Fielding-Wells and Makar 2015; Noll and Kirin 2017).

Yet, mathematical or statistical modelling within ISI contrasts with the transmission model of teaching and learning. Students do not translate problems into a given model. On the contrary, in ISI the expectation is that students impose a structure upon the real world problem. Gravemeijer (2002) calls this process ‘organising’. The students select or generate data which might inform their investigation and then they seek to make sense of the data by representing it in many different forms, typically supported by the use of technology. Gravemeijer (2002) describes a process of emergent modelling in which students move from making a specific ‘model-of’ a situation to seeing the model as an entity in itself, a ‘model for’ more formal mathematical reasoning.

To assist understanding of Gravemeijer’s ideas, let us point to similarities with notions of reification developed by Sfard (1991) and others (Tall and Gray 1991), insofar as the movement towards model-for as an entity in itself parallels the learner’s facility to recognise a concept such as function as an object with its own attributes and properties, rather than being only a part of a process. Returning to statistics education, Pratt and Noss (2010) proposed a pedagogic tool in which learners would edit the configuration of a random generator, such as that of a digital version of a die, to control its behaviour until the configuration becomes so familiar it is recognised as a model for the concept of distribution with predictive power even without the need to run the process. In Gravemeijer’s terminology, Sfard’s students and those of Pratt and Noss progress from a model-of a situation to a model-for function or distribution.

The notions of emergent modelling and ISI are relatively recent developments in statistics education research. Even so, there has been some recognition of the importance of modelling in standard curricula. For example, in the USA Common Core State Standards for Mathematics at high school, there is a tendency to include statistics when describing mathematical modelling in school mathematics as “using mathematics or statistics to describe (i.e. model) a real world situation and deduce additional information about the situation by mathematical or statistical computation and analysis” (Common Core Standards Writing Team 2013, p. 5). Focussing on statistical models and modelling in school mathematics can provide opportunities to connect data, chance and context, but the use of modelling in these curriculum statements might be interpreted according to the traditional transmission model or in terms of emergent modelling. In this study, we sought to explore the challenges that students might find when working within the emergent modelling paradigm.

4 Research on the teaching and learning of modelling and distribution

4.1 Models and modelling

In mathematics education, Lesh and Doerr’s (2003) perspective on models and modelling focuses on designing instruction that promotes mathematical problem solving, learning and teaching of mathematics. In alignment with the ISI approach, they typically present students with data-rich situations that might be elaborated by the construction of models.

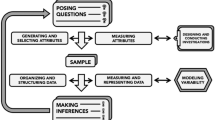
Lehrer and Romberg (1996) refer to this approach as data modelling: the construction (i.e. collecting certain types of information based on research questions) and use of data to solve a problem, a process closely linked to the development of mathematical models. They argue that “data require construction of a structure to represent the world; different structures entail different conceptions of the world” and thus “thinking about data involves modeling practices” (p. 70). Data modelling is a cyclic activity in which one begins with posing questions to solve a problem using a statistical investigation and identifying variables and their measures; moves to an analysis phase in which decisions are made for structuring and representing data; then makes inferences in relation to knowledge about the world (Lehrer and Schauble 2004).

Using their data-modelling approach, Lehrer and Schauble (2004) conducted a design study in a fifth grade classroom and focused on the development of students’ modelling variation through their understanding about distributions in a context. Students investigated questions about the nature of plant growth over time, such as height change and the effects of fertilizer and light. Through student-invented displays of data in small groups, changes in the distributions of plant height measures were discussed and interpreted in relation to the overall shape of data in whole class discussions. Students also compared distributions of heights of the plants grown under different conditions. In addition, posing a question such as “what if we grow the plants again?” provided opportunities to make inferences and reason about uncertainty which were not usually part of the curriculum at elementary grades. Researchers argued that generating, evaluating and revising models of data collected helped students to reason about natural variability. They emphasised the value of student-generated data representations in this data modelling process. After Gravemeijer, it would be reasonable to say that these students developed a ‘model-for’ natural variability, insofar as the students were able to recognise natural variability as a phenomenon evident across different situations.

English and Watson (2017) developed a framework of four components to examine sixth grade (age 11) students’ modelling with data as students were required to construct a model for selecting a national swimming team for the 2016 Olympics using the data sets of swimmers’ previous performances. The first component was called ‘working in shared problem spaces between mathematics and statistics’. There is clearly a resonance here with our interest in the potential for emergent modelling to connect statistics and probability. The following three components were closely aligned to ISI: ‘interpreting and re-interpreting problem contexts and questions’; ‘interpreting, organising and operating on data in model construction’; and ‘drawing informal inferences’.

During the task, students were able to use both statistical and mathematical reasoning/procedures in solving the problem as they were constructing their models based on given data. They also showed acknowledgement of key statistical ideas, such as calculating means (as a variable) as a way to account for variability in data, the limitation of using only one performance variable, and referring to uncertainty in team selections. In fact, English and Watson’s students, while being engaged in data modelling in the sense of Lehrer and Schauble, were developing models-for the mean (after Gravemeijer). That is to say, the students began not only to calculate means as part of the model-of the swimmers’ performance, they also began to appreciate how they could calculate the mean to find which data set of swimming times contained smaller numbers overall, imbuing mean with a certain utility in its own right. Moreover, students tended to consider both problem context and data variation in connection with selecting variables when constructing models. A consideration of problem context along with purpose of selecting a swimming team with the highest chance of winning in the Olympics also appeared in student responses. This framework clearly has potential to inform our first research focus on the nature of the student-generated models. However, we needed to look elsewhere in order to elaborate our second focus on how students evaluate their models.

With recent developments in technology, such as TinkerPlots 2.0 (Konold and Miller 2011), research on data modelling has begun to focus on combining exploratory data analysis with probability through computer simulations. Konold et al. (2007) reported on how middle school students built models of real-world objects using the random data generator devices in TinkerPlots to produce data, called data factories, and how they tested and refined their models through simulations and looking at graphs of their data. Building on this idea of a data factory, Ainley and Pratt (2017) developed a pedagogic approach, called purposeful computational modelling, which enabled 11-year-old students to build models for generating data that were represented in tables and graphs, and to revise them using modelling and simulation features of TinkerPlots. Their research findings suggested some possible issues about how children might judge the success of a model: (1) evaluating whether the model was working as they expected by comparing the outcomes to the structure of the model built in TinkerPlots; (2) comparing the simulation results with the original data to see if the model was generating data resembling the original data; (3) evaluating whether the model worked in terms of generating realistic data.

4.2 Distribution

Our research will focus on the emergence of a model-for the notion of model through data modelling by challenging the students to make sense of a distribution of data about the distances jumped by paper frogs. Konold and Kazak (2008) see distribution as the emergent, aggregate properties of data. This perspective on distribution fits well with the notion of emergent modelling since we wish to view statistical modelling as developing a model of data to move from individual cases or observations to describe a global pattern in data and then moving from data to context in which one makes sense of the data. We believe that reasoning about distributions to make inferences and predictions is a key aspect in this modelling process, as argued by English and Watson (2017). Reasoning about distributions on the other hand requires an aggregate thinking about data, which is beyond simply reasoning about a form of visual representations of data (Konold et al. 2015). According to Konold et al., aggregate is defined as “the way in which that form is perceived, as indicated by the sorts of questions it is used to address” (p. 307). Although students can intuitively generate data representations to organize data to answer certain statistical questions (Lehrer and Schauble 2002), previous research highlights young students’ difficulty in perceiving data as an aggregate (e.g. Cobb 2009; Hancock et al. 1992). In these studies, students tended to see data as individual cases rather than to focus on the global features of distribution, such as what the distribution of data looks like (shape), where the data values cluster and how spread-out they are. However, Konold et al. (2002) reported on how seventh and nineth grade students used a central range of values to refer to what was typical, called a modal clump, when describing distributions. In addition, these modal clumps can in some ways indicate how the data are distributed. Thus, it was suggested that “the idea of modal clump may provide a more useful beginning point for learning to summarize variable data” (p. 6).

According to the previous studies described above, the idea of data modelling has a potential to connect data, chance and context through emergent modelling. The practices of data modelling could also provide a means of developing students’ understanding of key statistical ideas and tools, such as distribution, measures of central tendency and variability, data representations and inference. Even so, our research focus is to investigate young students’ emergent ideas about models and modelling as they engage in reasoning about distributions during a data-modelling task. We have two research questions, both of which relate to how a ‘model-for’ model might emerge as the students engage in data modelling: As students identify what and how to measure, decide how to structure and represent data, and make inferences and predictions based on data: (1) what is the nature of the student-generated models? and (2) how do students evaluate their models?

5 Methodology

5.1 Research setting

Our study took place in Turkey, where the National School Mathematics Curriculum (MEB 2018a, b) includes data topics from the first to nineth grades and probability topics from eigth to 12th grades. The data topics do include the statistical investigation cycle (formulating research questions, data collection, data structuring and representation, data analysis and interpretation) at grades 5–8 (ages 11–14). This aspect of the curriculum offers a gateway for ISI; in our study we sought to engage the students in ISI through data modelling. At the same time, the Turkish curriculum places great emphasis on calculations and graphing and almost none on making inferences based on data at all grade levels. Moreover, probability topics are treated as completely separate from data. We intended that our approach in this study would construct a learning path that bridges data, chance and context in order to help learners develop competencies for using data to solve real-world problems. In this respect we see ourselves as aligned with English (2010) who argues that modelling can be used as a vehicle to provide an authentic problem situation for students to develop an understanding of important statistical ideas and tools. In fact, one such key idea is that of ‘model’ itself. In effect, we invite students to develop a ‘model-for’ model by evaluating their models that begin to emerge through their data modelling activity. That is to say, we intend that the student begin to gain a sense of ‘model’ as an entity in its own right which has power to allow prediction of outcomes from the situation being modelled, even prior to data collection or the running of a simulation.

In this report we describe a possible learning trajectory for developing young students’ emergent ideas about statistical models and modelling. This learning trajectory was tested in two different sixth grade classrooms where students (ages 11–12) working in small groups, engaged in a data-modelling task in the context of selecting one of the origami frog designs for the Olympics jumping race.

5.2 Research design and participants

In order to address the research questions stated above, we used a design study method (Cobb et al. 2003) as we had an iterative process to design, test and revise a learning trajectory about developing and supporting young students’ ideas about models and modelling through data-modelling activities. The retrospective analysis of the first cycle provided the basis for the new design phase in the second cycle.

We conducted teaching experiments in two different sixth grade classrooms in a large urban middle school (with approximate enrolment of 1600 students from fifth to eighth grades) in Denizli, Turkey. While 30 students (13 boys, 17 girls) of ages 11–12 participated in the first teaching experiment in April–May 2017, 16 students took part in the second teaching experiment in June 2017. Participants were familiar with formulating research questions, collecting data, making frequency tables and bar graphs to structure and represent data, computing and interpreting the mean and the range of a data set and using them to compare two data sets, but had no experience with using computer simulation tools, such as TinkerPlots, and were usually required to work with small data sets. They were familiar with conducting experiments in science where they take measurements and record data.

5.3 Task description and procedure

The data modelling task, called the Frog Olympics, is designed to engage young students in experiences of data modelling that involves what and how to measure, deciding how to structure and represent data, and making inferences and predictions based on data. The purpose of the task was to determine which of the given two different frog designs made by origami (Fig. 1) to choose for a 100-m ‘jumping’ race in the Frog Olympics.

Fig. 1
figure 1

Two different frog designs used in the Frog Olympics task (the smaller one is referred to as “pink frog” and the bigger one as “orange frog” throughout the paper)

Full size image

We designed and tested a learning trajectory (Table 1) to support young students’ data modelling. This learning trajectory addressed reasoning with key statistical ideas, such as distributions, central tendency, variability and predictions with uncertainty, and developing ideas about statistical models and modelling. Students worked in small groups (4–5 students). The teacher and researcher acted as facilitators as students worked together on the task. Each small group discussion was followed by a whole-class discussion. Due to the nature of design study, as the classroom implementation of the task proceeded, the research team negotiated revisions to reshape the next teaching session throughout the study.

Table 1 Learning trajectory for the Frog Olympics task (one class period = 40 min)
Full size table

To introduce the context of the task, the teacher initiated a class discussion about Olympics in real life and then explained the 100-m ‘jumping’ race rules in the Frog Olympics: “One of the games in the Frog Olympics is a 100-m jumping race. In this race, each frog begins to jump at the start line and keeps jumping to finish the race. The frog arriving at the finish line first wins the game. When any part of the frog crosses the finish line, it wins the race”. After each group discussed how they could decide which frog design to choose for the Frog Olympics, a mutual decision for collecting repeated measures of a single jump distance was made as a whole class. Each group was asked to discuss and write down how they would collect data after playing with the two origami frogs. After a whole class discussion of various ways of collecting data, each group marked a start line and fixed the measuring tape perpendicularly (starting from 0) on their desk to measure how far the frog jumped and repeated this 15 times for each frog design. In the next class, students were asked to make a graphical representation of the jump distances of each frog design on the given graph papers in a way to help them decide which frog to choose for the Olympics. Using their representations, students were encouraged to make informal inferences. During the first iteration of the task, Group E spontaneously created a physical dot plot using stickers even though this had not been taught. So we encouraged the other groups to make dot plots of their data and interpret them.

In order to foster students’ ideas about models and modelling, we combined the experimental data from all groups in the dot plots for each frog design in TinkerPlots that were displayed on the classroom interactive board and asked students to predict what the two frogs might do in many repeated jumps in the future. The following scenario was introduced:

A mobile game developer wants to make a digital version of each frog design for a game. Your task is to help the developer, using the data you collected from flipping paper frogs. By looking at the dot plots of jump distances of pink and orange frogs, what might the distribution of jump distances for each frog design look like if we were to collect more data?

We did not raise issues about sample size as we wanted to know whether the students would decide if this was relevant, and how. We introduced sketching as a way to generate a model of expected results. When instructing students on how to sketch a distribution shape using a curve, we demonstrated quick sketching and emphasised paying attention only to the overall shape. Then each group sketched their prediction on the worksheet, including a horizontal axis for the jump distances scaled from 0 to 100 for each frog design, and explained how they made the prediction.

Building and testing the groups’ models (the sketches) using TinkerPlots did not work in the class as we planned due to technical difficulties using the software on the interactive board. Then the research team decided to conduct interviews with specific groups to examine their ideas about evaluating models more closely after the last class. As seen in Table 2, five groups were asked to evaluate 3–4 sketches, including their own, where their model sketch has the same nomenclature as their group. Note Group D was not interviewed but their model sketch was used in the student evaluation.

Table 2 Groups interviewed for evaluating models
Full size table

After the evaluations, the interviewer showed the students the TinkerPlots model created based on their sketch. Since they did not have a prior experience of using the software, the interviewer explained how the TinkerPlots model was created and how the simulation worked. Then to make sure they understood the process, the interviewer asked them to describe what would happen when they ran the simulation. When everyone was happy with this model, the interviewer ran the model and asked the group whether the results turned out the way they expected and how so. After a few more runs, the interviewer asked whether they wanted to change anything in the model and why. By simulating the agreed model for distances jumped by each frog design using a moderate sample size, such as n = 500, we intended to reveal different behaviours between models with a hump and models that were wavy with spikes in places where there were comparatively large frequencies of distances jumped. In the case of a model with a hump, the outcomes when running the model would show a similar hump, suggesting an invariant feature. In contrast, in the case of the wavy models, there would be no such invariance unless the model was run for a very large sample. Then the students were shown the given models again to evaluate to see if they changed their ideas about their initial evaluations after testing their model. In the end, groups were asked again which frog design they would choose for the Olympics.

5.4 Data collection and analysis

Teaching sessions and interviews were co-conducted by the first author as the teacher–researcher, and the third author who was the classroom teacher. The interviews with selected groups were 20–30 min long to discuss how they produced their model and evaluated the given models generated in the last class by sketching. The data consisted of written artefacts, including responses on the worksheets and representations generated by group work, audio-recordings of interviews and field notes. Since the second teaching experiment was conducted towards the end of spring semester, there was a high absenteeism among the participants in the last teaching sessions. Therefore, in this article we focus mainly on the data from the first teaching experiment and mention the results from the second teaching experiment only in passing.

Documents including written artefacts from each group work and transcripts of audio recordings of group interviews were analysed qualitatively. In our analysis we used progressive focussing (Parlett and Hamilton 1972) to describe and interpret the data throughout the teaching sessions by concentrating on the emerging features of the practices of data modelling in the classroom. In progressive focussing, the researcher commits to multiple stages of analysis during which insights can gradually emerge allowing the data to be compacted around those insights. For our progressive focussing, in the first stage, the data captured by audio of the interactions was transcribed into Turkish. In the second stage, the students’ written responses along with the pictures of student-generated representations and models and the researchers’ field notes about each session were translated from Turkish into English. In addition, the following two foci were used to select excerpts of the transcribed data, which were also translated: (1) how students explained construction of their own model; and (2) how they evaluated the given models and their interpretation of simulation data. In the third stage, the authors independently analysed the content of these documents and transcripts using the following six foci: (1) What the student-generated sketches tell us about their ideas about models of real data distributions; (2) what were the distinguishing features in the students’ models; (3) what made some students pay attention to the overall trend in the data while others were influenced by the ups and downs in the data; (4) how students judged what was a good model; (5) what sorts of criteria they used when evaluating the models; and (6) how simulating the models in TinkerPlots affected their model evaluations. In the fourth stage, the first and second authors compared and discussed their analyses, through which process themes began to emerge. In the fifth stage, further detailed discussion between these two authors focussed on interpreting and re-interpreting these foci.

6 Results

The presentation of findings is divided into two subsections corresponding to the research questions addressed in the study: (1) what was the nature of the student-generated models? (2) How did students evaluate their models?

6.1 Students’ models

Students’ emergent models of actual data distributions for predictions arose from several actions in which they constructed a graphical representation of empirical results in the earlier stages of the task (3–5 in Table 1). Similar to the anticipated path described in Gravemeijer (2002), students spontaneously began to make sense of their empirical data with their choice of representation consisting of value bars each of which corresponded to a single measure of distance jumped on the vertical axis (Fig. 2). This representation led students to talk about the regularity and consistency of the jump distances when comparing each frog design, in order to make a decision. Then the dot plot representation, introduced to the students as part of our learning trajectory, played a key role in transitioning from “the magnitude-value-bar graph” (Gravemeijer 2002, p. 4) to a graph of a density function that is the sketched model constructed by the students to make predictions within the scenario described in Sect. 5.3. For example, when interpreting dot plots of their actual data, students used various ways: groups B and C tended to compare modal clumps and group F compared the piling-up in each distribution.

Fig. 2
figure 2

Value-bar graphs (showing the order of trials on the horizontal axis, i.e. trial 1, trial 2 etc., and jump distances on the vertical axis) made for pink frog (on the left) and orange frog (on the right) by group G

Full size image

Since the height of the stacked dots at a given range could be considered as a measure of the density in that interval, the perceived shape of the dot plot through sketching could be seen as a qualitative precursor to the visual density function as argued by Gravemeijer (2002). Our data support this argument. For instance, when group B constructed their emergent model (Fig. 3b) which was based on a modal clump around a broad range of jump distances, as seen in the excerpt below, students primarily focussed on a range of data where the most frequent values were clustered and how the data were distributed in the combined experimental results (Fig. 3a):

Fig. 3
figure 3

a Dot plots of combined data showing the distance jumped on the horizontal axis for orange frog (at the top) and pink frog (at the bottom); b, c models based on a modal clump around a broad range of jump distances (by groups B and C respectively); d–g models based on several small ranges of jump distances (by groups D, E, F and G respectively)

Full size image

Taha: We tried to make the curve higher where the most of the jumps are in the class data.

Berk: We determined the range of values where the most are.

Taha: For example between 10 and 65 for the orange frog.

Mina: Here (the orange frog) jumped mostly around this area. Here (the pink frog) scattered but jumped still more around a certain area. We paid attention to that.

Similarly, in their written explanation, group G stated, “Based on the data of the orange and pink frogs (Fig. 3a), we decided that if we made them jump more, they could jump to the same places (the same distances) more”. During the interviews they also commented on the several smaller humps for the pink frog in their emergent model, which was based on several small ranges of jump distances (Fig. 3g). They argued that those were because of the “waviness” in the actual data and they made some of them taller since there were more dots stacked up. In addition to the overall shape, the emergent models took the minimum and maximum value of distances jumped into account. For example, one of the students, Seda, in group G, expressed a concern that, although they paid attention to the start point (the minimum distance jumped) in sketching their model, they made a “mistake” in the end point (the maximum distance jumped) which was extended to 100. Sevil, in reply to that, suggested, “Actually if we were to flip the frog more times, it could have these jump distances”, which indicated an acknowledgment of uncertainty in the long run for their emergent model.

As a result, we found the following tendencies to generate models of real data distributions as seen in Fig. 3b–g:

  • Matching ‘ups and downs’ in the actual data but not the jump distance values on the horizontal axis;

  • Matching the minimum and maximum values or only the minimum values of the model and actual distributions;

  • Going a bit lower/higher than the actual range of data;

  • Drawing the curve higher than the maximum height of the actual clusters.

Then two categories of models were identified from these analyses. In the first category, students tended to use their idea of a modal clump around a broad range of jump distances (Fig. 3b, c). Two groups (groups B and C) created a model of this nature. In the second category, students chose to have several small ranges of jump distances, which led to a series of ‘ups and downs’ (Fig. 3d–g). The other four groups (groups D, E, F and G) created such a model.

6.2 Students’ model evaluation criteria

Above we presented how the features of emergent models across the groups differed. In evaluating these models, although all groups (note Group D was not interviewed) believed that the model distribution should look like the real distribution, their ideas about what made a good resemblance varied too. Table 3 gives a summary of the criteria the students used to evaluate their and others’ models. We now present examples of how each group evaluated the various models, including how they tended to use the same criteria for evaluating the models of others as they used for creating their own.

Table 3 Summary of criteria used to evaluate emergent models
Full size table

6.2.1 Examples of groups’ evaluation of emergent models

Group B This group created a more holistic model and examined the models B, D, F and G in Fig. 3. They agreed that the model G was “good” because it was “well thought out” and looked like the actual results. They thought their model (B) was “OK” since it showed which jump distances were the most common (criterion a in Table 3) but was a “rough sketch” compared to the model G. They rated the models D and F as “bad” using the shape criteria c and d in Table 3. However, students switched their ratings for model G to “OK” and theirs (B) to “good” after seeing the simulation results of these models (Figs. 4, 5) for a large number of trials. They reasoned that the simulated results for the orange frog in Fig. 5 did not look like the actual data because there were ‘ups and downs’ where there was a cluster of most jump distances in the actual distribution. For this group, a ‘good model’ seems to have a general shape based on where the cluster of data is located in the actual distribution.

Fig. 4
figure 4

On the left the Sampler built for group B’s model in TinkerPlots using the curve device, and on the right simulation results from a large number of trials that show the distance jumped on the horizontal axis for orange frog (at the top) and pink frog (at the bottom)

Full size image
Fig. 5
figure 5

Group G’s model in TinkerPlots using the curve device and simulation results from a large number of trials that show the distance jumped on the horizontal axis for orange frog (at the top) and pink frog (at the bottom)

Full size image

Group E Since this group tended to show details in their model, they were given the other two more holistic models, which were constructed based on a modal clump around a broad range of jump distances (b and c in Fig. 3) to evaluate. While the students rated the model B as “good”, they considered the model C to be in between “OK” and “bad”. The main criterion used in their evaluation was the shape of the distribution (criterion b in Table 3). They rated their model (E) as “OK” since they thought that the rises and falls were good but there was too much detail. After watching the simulation results of their model created in TinkerPlots several times, the students tried to test the match between their model and the actual distribution by superimposing the sheet with their model onto the sheet with the actual distributions as seen in Fig. 6. After repeating this test for the other models, they changed their initial ratings based on the match they observed: “good” for Model E, “OK” for model B and “bad” for model C. For this group, a ‘good model’ is the one that has a shape with ‘ups and downs’ similar to the ones seen in the actual distribution.

Fig. 6
figure 6

Members of group E comparing the match between models and actual data

Full size image

Group F For the evaluation, this group was given the other two models which were more holistic (b and c in Fig. 3) and another model (E) similar to theirs (F). Initially they considered models B and C as “sloppy” because “the students did not try hard” while they thought that the models E and F were more thorough. Similarly to the group E, their attempt to superimpose the models on the actual data distributions to see the match was a clear indication of their attention to the details of rises and falls in the data (criterion b in Table 3). Therefore, they rated the models B and C as “bad” and the models E and F as “good”. After seeing the simulation results of their model created in TinkerPlots several times, they thought that the results were as good as they expected and did not need to re-evaluate the models. Similarly to group E, this group seems to consider that a ‘good model’ needs to have a shape matching the ‘ups and downs’ in the actual distribution.

Group C This group created a more holistic model and evaluated the models C, D, F and G in Fig. 3. The group rated the model F as “good”. Nadide reasoned “because they made the increases and decreases well” and Yaman added “they made them proportional, very similar to [the experimental results]”. They considered model G and their model (C) were “OK” using the shape criterion c (Table 3). Similarly, they rated model D as “bad” because according to Meltem “the zigzags are too high, they could be lower”. After running the group’s model created in TinkerPlots several times, the group members re-evaluated each model but their ratings did not change. According to this group a ‘good model’ seems to show the waviness of the actual distribution to some degree, with a proportional curve height.

Group G The students evaluated the two models which were more holistic (b and c in Fig. 3) and their model (G). They rated the model C as “good”, the model G as “OK” and the model B as “bad”. The main criterion in their decision seemed to be the match between the start and end points of the model and the actual data (criterion d in Table 3). Furthermore, in model B the students were concerned about the curve starting at 0 for the orange frog because they thought that would not be possible. After seeing the simulated results in TinkerPlots, students switched their rating for the model C to “OK” and theirs (G) to “good” because they thought, “The jump distance of 100 could occur with 500 or 1000 jumps”. However, they insisted that the jump distance of 0, as seen in model B, could not occur. This group seems to value where the curve starts and ends and thinks that a ‘good model’ needs to start and end at a ‘reasonable’ value in the data context.

In summary, the students tended to pay more attention to the shape than the start and end points when evaluating the models. The inclination to match the ‘ups and downs’ in the actual distribution with a proportional curve height appeared to be strong in these evaluations.

7 Discussion and conclusion

In this paper, we presented a possible learning trajectory for developing sixth grade students’ ideas about models and modelling as they engaged in reasoning about distributions during a data-modelling task. We focussed on the following research questions: (1) What was the nature of the student-generated models? and (2) How did they evaluate the models?

7.1 Emergent modelling

As we reflect on the findings of our study in relation to our two research questions, we turn to Gravemeijer’s (2002) emergent modelling view (as opposed to modelling as translation) in which we observe students’ ideas about models as a result of an organising activity during a data-modelling task.

Initially students structured the empirical data collected as part of the problem situation in order to make a decision. Using their value-bar graphs and dot plot representations, they began to see patterns in the distributions (where the data were clustered and how they were spread out) and in turn they made a decision about selecting one of the frog designs for the Olympics. Introduced to a new scenario in which they were required to predict the future distributions of jump distances of each frog design if more data were collected, students then proceeded to create a model based on empirical distributions through a sketching activity (as seen in Fig. 3). In Gravemeijer’s terms, we can describe these sketched distributions as a ‘model-of’ a set of measures (jump distances in the given problem context) since they tended to represent rather too literally the data themselves without expressing a sense of how random effects might be a model-for variation and signal a model-for invariant features of the system. At this stage, students were primarily concerned with the ‘ups and down’ and the minimum and maximum values in the real data when constructing their models.

Our findings suggest that there is an ongoing process in developing a ‘model-for’ the notion of a statistical model, incorporating a signal (explained variation) in the presence of noise (unexplained variation). We do see the beginning of the shift from ‘model of’ to ‘model for’ when we examine the change in how some students applied criteria for evaluating other students’ models. Thus, in the first instance, one group (B) argued that the other group (G) had a better model because it looked like the actual data, whereas they had a different criterion when judging their own model earlier—“it shows which jump distances were most common (between 10 and 65)”. Yet, after seeing the simulated data in TinkerPlots for both models, the same group decided their own model was in fact better. They appeared to have a sense of how further data (as the sample size increased) would not necessarily match the ‘ups and downs’ in the original small set of data whereas the overall trend would continue to match. In this example we see how the model this group of students constructed becomes part of their thinking about models in general as they evaluated the other group’s model. Their evaluation involves insights into properties of models, such as the unchanging aspects of the population or process (i.e. signal), when they expected a modal clump within the range of 65 and 100 in 500 flips.

7.2 The role of data-modelling activity

The data modelling activity presented in this paper was designed on the premise of reasoning about distributions. As seen in previous studies (e.g. Cobb 2009; Konold et al. 2015; Lehrer and Schauble 2002; English and Watson 2017), focussing on the idea of distribution and reasoning about distributions to make inferences and predictions helped our students make sense of key statistical ideas and procedures (e.g. mean, range, variability, data representations, etc.) that are usually treated in isolation and without context in school mathematics. Throughout the task students engaged in interpreting value-bar graphs and dot plots each of which was a representation of the distribution (Gravemeijer 2002) while using the notions of centre, spread, consistency and variability to talk about the patterns in the data. Then through the sketching activity students eventually constructed models of empirical distributions to make predictions. While students in previous studies developed a ‘model for’ natural variability (Lehrer and Schauble 2002) and a ‘model for’ the mean (English and Watson 2017) through reasoning about distributions, our study particularly focussed on development of the key idea of ‘model’ itself through students evaluations of models that began to emerge from comparing the models and real distributions.

However, we observed some challenges that students might encounter when working within the emergent modelling paradigm. When sketching a model of jump distances of pink and orange frogs to predict a future distribution, most groups were strongly influenced by the ups and downs from one cluster to another in the original combined data of jump distances. In this tendency of matching the generated distribution to the original distribution, several small ranges of jump lengths in the model look almost similar to the more naive focus on individual cases (Cobb 2009; Hancock et al. 1992). Only two groups (B and C) seemed better able to look through the data and see a more general trend as seen in statistical models (Moore 1990). These were the two groups that used modal clumps (Konold et al. 2015) when comparing their dot plots earlier in the task. Their models seemed to have a sense of ‘signal’ as describing a range of values repeated most often.

Although the tendency to draw the curve higher where there is a pile of data and to go a bit higher/lower than the actual range of data in sketching models appeared to be a common intuition to acknowledge the likelihood and variability under uncertainty, one group (G) particularly was concerned about the ‘reasonableness’ of a model starting from 0 rather than 5 or 10 as in the actual data during their evaluation. This finding suggests a tendency to evaluate whether the model is the realistic representation of the actual situation (Ainley and Pratt 2017). In general, use of different criteria for judging what is a good model (Ainley and Pratt 2017) was evident in groups’ evaluations of models. For instance, some groups seemed to compare the model with the original dot plot of data to match start and end points of the distributions. While most groups paid a lot of attention to the several ‘ups and downs’ in their model evaluations, they did not worry about the actual lengths of the jumps, except the match between the start points and endpoints.

7.3 Implications

This study extends previous research on modelling with young students as it examines the emergence of a ‘model-for’ the notion of model through data modelling, in which the students are required to compare and reason about distributions of their experimental data. The learning trajectory we described here provided the students with an opportunity to experience the practice of data modelling in an engaging context. This data-modelling process also fostered making sense of key ideas, tools and procedures in statistics that are usually treated in isolation in school mathematics. Sketching models of distances jumped by origami frogs enabled students to make predictions beyond the data. Evaluating different models offered insights into different criteria that might be used by students for judging what a good model is. It was through this process of emergent modelling that students began to develop a ‘model-for’ a notion of model in statistics. However, findings would have been enhanced by further exploration of this process with more support from the use of computational modelling (Ainley and Pratt 2017). Although we attempted to use the simulation features of TinkerPlots in testing and evaluating models during the interviews, its use was limited in this study. The students could benefit more if they had an experience of building ‘data factories’ (Konold et al. 2007) prior to this task, and were then allowed to create their own models and test them in TinkerPlots. Moreover, the learning trajectory component of this study has the potential to suggest a learning environment that broadens data analysis activities in schools through modelling.