1 Introduction

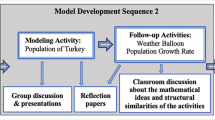
The purpose of this article is to provide an account of how a model development sequence (Lesh et al., 2003) can support the development of students’ interpretations and reasoning about phenomena with negative average rates of change in different contexts. The difficulties students encounter in learning to reason about and interpret rates of change are well known in the research literature (Carlson et al., 2002; Monk, 1992; Oehrtman, Carlson, & Thompson, 2008; Thompson, 1994), and recent research highlights that reasoning about and interpreting phenomena involving negative rates of change are especially challenging (Ärlebäck, Doerr & O'Neil, 2013). Yet, it is important that students of science, engineering and mathematics are able to interpret and reason about changing phenomena with negative rates of change in various contexts (Beichner, 1994; Carlson, 1998; Hestenes, 2010; McDermott, Rosenquist, & van Zee, 1987). Following the suggestion by Carlson and colleagues (2002) to give students opportunities to work with more extensively with lines of inquiry focusing on change in real-world contexts, we designed a model development sequence (Lesh et al., 2003) to support the development of students’ capabilities to interpret and reason about phenomena with negative rates of change in a range of contexts. In this article, we report our analysis of how students’ interpreted and reasoned about negative rates of change in three contexts (motion along a straight path, light intensity at a distance from a point source, and the discharge of a capacitor in a simple circuit) with different underlying mathematical structures as they engaged with these contexts in a model development sequence.

2 Interpreting and reasoning about rates of change

Much research over the last 20 years has documented the difficulties that students at different educational levels encounter when interpreting and reasoning about rates of change (Carlson et al., 2002; Monk, 1992; Oehrtman et al., 2008; Thompson, 1994). For example, in the context of linear functions, a study by Nagle et al. (2013) of 65 introductory calculus students found little evidence of covariational reasoning in the students’ conceptualizations of rate of change. The complexity of interpreting and reasoning about rates of change has proven difficult for high achieving undergraduate mathematics students and students studying physics (Beichner, 1994; Carlson, 1998; Hestenes, 2010; McDermott et al., 1987). In a 2 year longitudinal study of ten students ages 16 to 18, Roorda, Vos and Goedhart (2015) found that even after learning about rate of change in mathematics and physics, students had “a narrow and disconnected repertoire of rate of change procedures” (p. 881) and a poor understanding of the concept. To reason about rates of change, students must simultaneously attend to and distinguish among three related quantities: the value of the output of a function, the change in the values of the function’s output over a subinterval, and the change in values of the input to the function (Carlson et al., 2002; Johnson, 2012; Monk, 1992; Oehrtman et al., 2008; Thompson, 1994). When reasoning about changing phenomena, students often confuse these three quantities (Carlson et al., 2002; Carlson, 1998; Lobato, Hohensee, Rhodehamel, & Diamond, 2012; McDermott et al., 1987). Reasoning about the latter two quantities is a foundational understanding for average rates of change in pre-calculus and instantaneous rates of change in calculus. Reasoning involving phenomena with negative average rates of change has proven to be even more complex and especially challenging (Ärlebäck et al., 2013).

Science, engineering and mathematics students will encounter many contexts where they will need to interpret and reason about physical phenomena with changing rates of change and with negative rates of change. Indeed, Carlson and colleagues (2002) stress the importance and potential of using real-world dynamic events to provide students with opportunities to develop their reasoning about changing quantities. Roorda, Vos and Goedhart (2015) suggest a teaching approach centered around “a curriculum in which students repeatedly work with the same concepts and procedures, but in different contexts, at a level of increasing difficulties, with new perspectives and with possibilities for the weaker students to catch up” (p. 886). However, this is potentially problematic since researchers have found that students’ understandings of rate in one context (such as kinematics or work) or in one representation (such as a table or graph) do not necessarily translate to other contexts or representations (Herbert & Pierce, 2011; Ibrahim & Rebello, 2012; Johnson, 2012; Oehrtman et al., 2008). Little research has attended to the design of instruction for addressing the challenges students encounter when interpreting and reasoning about changing physical phenomena across different contexts in general, and about physical phenomena with negative rates of change in particular.

In this study, we aim to further our understanding of how a modeling-based approach to teaching and learning can support students’ learning over multiple contexts, by examining the use of a model development sequence (Lesh et al., 2003) to support students in interpreting and reasoning about changing phenomena with negative average rates of change. The question we investigated in this research study was: How can the design of a model development sequence support the development of students’ interpretations and reasoning about negative rates of change across differing contexts of physical phenomena?

We begin this paper by describing the theoretical perspective that informed the design of the sequence of model development activities. We elaborate the specific activities in the model development sequence, followed by a description of the research setting and the participants, the data sources and our methods of analysis. We report our findings on students’ interpretations and reasoning about phenomena with negative rates of change across three contexts: motion along a straight path, light intensity at a distance from a point source, and the discharge of a capacitor in a simple circuit. We conclude with a discussion of the results, their implications, and directions for future research.

3 Theoretical perspectives on models and modeling

Within the field of mathematics education, models and modeling have been given a prominent role in national curriculum documents and in research over the last 30 years (Blum et al., 2007; Blum, 2015). There are many different approaches to and perspectives on modeling in the research literature; Julie and Mudaly (2007) broadly conceptualized the multitude of perspectives on modeling as modeling as self standing content or as modeling as vehicle for learning other curricula objectives. Some perspectives on modeling tend to bring these two objectives together. For example, the instructional theory of Realistic Mathematics Education (Freudenthal, 1983) emphasizes the context of the problems used in learning in terms of horizontal- and vertical mathematization (Treffers, 1987).

In the models and modeling perspective (Lesh & Doerr, 2003), modeling is conceptualized both as a means of learning mathematics and other curricular content and of learning to do modeling per se. Students develop, modify, and use models to make sense of particular contexts and problems by interacting with other learners in multiple cycles of conjecturing, interpreting, describing and explaining some problem situation. A model is defined as a system consisting of elements, relationships, rules and operations that can be used to make sense of, explain, predict or describe some other system. A mathematical model is a model that focuses on the structural characteristics of the system in question. Thus, learning mathematical content occurs while students develop a useful and generalized mathematical model that can be used and re-used in a range of structurally similar contexts. In this paper, we examine the models of average rate of change that students develop and use to interpret and reason about physical phenomena with negative average rates of change.

3.1 Model development sequences

The models and modeling perspective offers a systematic way to think about the design and implementation of tasks and instruction to further students’ learning in terms of how their models develop across instructional tasks. A model development sequence is a carefully designed instructional sequence of modeling tasks that aims to support the development of students’ models (or conceptual systems) that can be applied in a range of contexts (Doerr & English, 2003; Lesh et al., 2003; Ärlebäck et al., 2013; Hjalmarson, Diefes-Dux, & Moore, 2008).

A model development sequence always starts with a model eliciting activity (MEA) and is followed by model exploration activities and model application activities. The MEA is designed to elicit the students’ initial ideas about a meaningful and realistic problem situation, in such a way that students engage in an iterative process to express, test and revise their ways of thinking about the quantities and relationships involved. Principles for designing MEAs (Lesh, Hoover, Hole, Kelly & Post, 2000) have been extensively used in research on students’ modeling a wide range of contexts from primary to post-secondary schools (English, 2006; Koellner-Clark & Lesh, 2003; Yoon, Dreyfus & Thomas, 2010). MEAs confront students with the need to develop a model that they can use to describe, explain, predict or control the behavior of meaningful problem situation. Students’ initial models (or conceptual systems) are often not very sophisticated or useful, but these initially elicited models are evaluated, revised and refined as students discuss their approaches with other students and share their interpretations and representations with the whole class. While the model elicited through the MEA captures the underlying structure of the problem situation and holds the potential for applicability to range of structurally similar situations, these two aspects of the initial model are further developed through model exploration activities (MXAs) and model application activities (MAAs).

The focus of model exploration activities is for students to explicitly think about the underlying mathematical structure of their elicited model by attending to different representations and how to interpret and use those representations purposefully and productively. The focus of the model application activities is for students to think with their model by applying their models in new contexts, resulting in further adaptations of their model, and thereby extending their use of representations, refining their language for describing phenomena, and deepening their understandings of the phenomena and its underlying mathematical structure (Ärlebäck et al., 2013). Through their interactions with other students and their teachers, students simultaneously learn mathematics and develop their proficiencies in modeling problem situations.

4 Research design and methodology

This case study took place in a 6-week summer mathematics course for students who were preparing to study engineering at a mid-sized university in the United States. The course was designed around a model development sequence aimed at supporting students in developing their models (conceptual systems) of average rates of change. The sequence began with an MEA eliciting students’ ideas about positive, negative, and changing velocity by creating position graphs with a motion detector and their bodily motion. The students then explored positive and negative velocity for motion along a straight path in a computer simulation environment where velocity graphs created motion of a simulated character. This was followed by an investigation of how light intensity changes with respect to the distance from a light source. In this context, the phenomenon has distance as the independent variable rather than time. In the final context, time was reintroduced as the independent variable as the students studied how voltage changes across a discharging capacitor, an exponentially decreasing phenomenon. Across all three contexts, students had to simultaneously attend to, coordinate and distinguish among the values of the output of the context specific functions, the change in the values of the functions’ output over different subintervals, and the changes in values of the input to the functions. To support students in this endeavor, the tasks engaged students in making scatter plots, calculating values of the average rates of change and creating rate graphs of the different physical phenomena. In all contexts, the values and graphs not only had to be created but also interpreted in terms of the context and students had to reason about the relationships among various quantities. The students worked in small groups to complete the activities in the model development sequence. Class discussion following the modeling activities focused on the relationships among different representations of negative rates of change and students’ interpretations of change in different contexts.

The sequence was designed collaboratively by the authors and the teacher of the summer course, and subsequently implemented, evaluated and re-designed, over three consecutive years. In the following section, we present in detail the design of the tasks and the choice of contexts that were used over the 3 years of the teaching experiment. As we implemented and evaluated the model development sequence, we became increasingly aware of the difficulties students encountered in interpreting and reasoning about negative rates of change in contexts other than motion. In the third year of implementation, we provided the students with more opportunities to communicate their interpretations and reasoning in both written work and classroom discussions. Hence, the data for the analysis in this paper consisted of student’s written work on in-class modeling activities, student assessments, and pre- and posttest results from the third year of implementation.

4.1 The design and implementation of the model development sequence

4.1.1 Motion along a straight path model eliciting and exploration activities

The model development sequence began with an MEA to elicit the notion of negative velocity by using motion detectors to generate position graphs of the students’ bodily motion along a straight path. We selected this context for two reasons. First, students’ difficulties in reasoning about negative velocity are well-known in the research literature and are an important learning goal in both calculus and physics (Beichner, 1994; Thornton & Sokoloff, 1998). Second, this context provided the students with a meaningful and familiar situation to reason about negative rates in terms of their own enacted bodily motion. The context of motion provided students with the opportunity to develop their interpretations and reasoning about negative rates of change by sorting out the meanings and differences between the formal language of velocity and the everyday language of speed.

We followed the MEA with a model exploration activity using SimCalc MathWorlds, a computer simulation of motion along a straight path (Kaput & Roschelle, 1996). The simulation environment reversed the representational space of the MEA, where bodily motion created a position graph. In the simulation environment, students created piecewise linear velocity graphs to generate the motion of simulated characters. In this environment, the students explored the linked relationship between piecewise linear velocity graphs and their associated position graphs. This was intended to continue to support the students in interpreting and reasoning about velocity when given a position graph and interpreting and reasoning about position when given a velocity graph. Particular attention was paid to graphs where the velocity was negative and where the velocity was linearly increasing or decreasing.

4.1.2 The light intensity model application activity

The light intensity task was designed to provide the students with an opportunity to apply their understandings of average rate of change, initially elicited in the context of linear motion, in a new context and one in which the independent variable was distance rather than time, and where the decrease in the dependent variable was non-linear (an inverse square). The activity consisted of three parts. The first part aimed at making explicit the students’ intuitive and initial models about the relationship between light intensity and the distance from a point source. The students considered the scenario of an approaching car and sketched a qualitative graph of how the intensity of the car’s headlights changed with the distance from the car. The students wrote descriptions of the light intensity with respect to the distance from the car and the rate at which the light intensity changes with the distance from the car. Writing such a description required the students to simultaneously reason about the quantity of the light intensity and the rate at which this quantity changes. This was precisely the reasoning that the students had previously explored graphically between the quantities of position and velocity in the simulation environment. However, despite having had a year of physics in high school, there was significant disagreement among the students as to how the light intensity changed with respect to distance from the light source, including confusion over the role of time as a variable.

The disagreement about the behavior of light intensity with respect to distance, was resolved by engaging students in collecting and analyzing light intensity data with a point source of light, a meter stick, and a light sensor. The students interpreted the scatter plot of their data and wrote descriptions of the intensity of the light and the rate at which the intensity changed with respect to distance from the light source. The students calculated the average rates of change of the light intensity data over 1 cm intervals. They described the average rates of change of the data over subsequent subintervals as the distance from the light source increased, and created a graph showing the calculated average rates of change over the 1 cm intervals.

In the third part of the activity, the students found a function fitting their collected data and analyzed the average rates of change of their function over 1 cm intervals. Due to the physical limitations of the light sensor, students needed to construct a piecewise function, consisting of a horizontal linear piece for the first two or three data points and an inverse squared piece for the remainder of the data set. Working with a partner, students wrote a report that described the values of the light intensity in terms of a piecewise linear and inverse squared function; computed and interpreted average rates of change over 1 cm intervals of distance; graphically represented these average rates of change; and described how the values of the average rates of change of the function, over 1 cm intervals, changed as the distance from the light source increased.

4.1.3 The discharging capacitor model application activity

The second model application activity was an investigation of the rate at which a fully charged capacitor in a simple resistor–capacitor circuit discharged with respect to time, a phenomenon which is governed by an exponential decay function. The students built the circuits, charged a capacitor, and measured the voltage drop across the capacitor as it discharged. Students were asked to develop a model they could use to compare the rates at which the capacitor is discharging at the beginning, middle and end of a total time interval and to interpret how the average rates of change of the function change as time increased.

As with the light intensity model application activity, the students engaged in several iterations of applying and interpreting their model of average rates of change as they reasoned about three quantities: (1) the values of the exponential decay function that represented the voltage drop across the discharging capacitor; (2) the values of the average rates of change of the voltage drop computed over 5 s intervals; and (3) how the function values and the sequence of average rates of change values were changing as the capacitor discharged.

4.2 Setting, participants, data sources and analysis

A total of 35 students (11 female and 24 male) preparing to study engineering at a mid-sized university participated in the study; 23 students had studied calculus in high school and 12 had not studied any calculus. All students had taken a high school course in physics. During the 6 weeks of the course, the students and the teacher meet for 1 h and 45 min four times a week. The students worked in small groups on the modeling activities and engaged in a whole class discussion focused on the relationships among different representations of negative rates of change and students’ interpretations of change in different contexts. All students had graphing calculators that were used in the three different contexts together with a motion detector, a light sensor and voltage probe to collect, graph and analyze data, and transfer data between their calculators and a computer.

To address the research question about how the model development sequence supported the development of students’ interpretations and reasoning about negative rates of change across differing contexts of physical phenomena, we report on our analysis of data from three contexts of change: motion along a straight path, light intensity, and the discharge of a capacitor in a simple circuit. These different physical phenomena are modeled with different underlying mathematical structures: piecewise linear, inverse square, and exponential decay. Our analysis focused on those data sources where negative rates were explicitly addressed in order to examine how the students’ reasoned across different contexts and about different underlying mathematical structures.

We examined how students related the value of the output of a function, the change in the values of the function’s output over a subinterval, and the change in values of the input to the function in terms of how the students expressed these quantities numerically, graphically and in written language. In each of the three contexts, the analysis focused on how and to what extent students used these forms of representations to correctly or incorrectly describe the behaviour of the function and the average rates of change in terms of the phenomena.

For the context of motion along a straight path (piecewise linear), we analyzed three data sources: (1) students’ responses to three items from a pretest that was completed at the beginning of the course; this provided baseline data on the students’ reasoning with positive and negative rates in this context; (2) students’ written work on three assessment items given at the end of the model exploration activity; and (3) the students’ responses to the same three items as in (1) above from a posttest at the end of the course.

For the context of light intensity (inverse square), we analyzed two data sources: (1) the students’ graphs of how the intensity of the car’s headlights changed with respect to the distance from the car, and their written descriptions of how the intensity changes with respect to the distance from the car; and (2) the students’ written reports completed at the end of the light intensity activity. For the first data source, the analysis focused on capturing the students’ initial models of how the light intensity varies with distance from the light source and students’ abilities to interpret and distinguish between two quantities: the intensity at a given distance and the rate at which the intensity is changing at two given distances. The analysis of the students’ written reports (n = 18) focused on interpretations and reasoning about how the intensity varied with the distance from the light source and how the average rates of change over 1 cm subintervals varied, the graphs the students produced, and how students attended to the context in their written interpretations.

For the context of the discharging circuit (exponential decay), we report on the analysis of the data on a written assessment item after the model application activity. The students were given (via their graphing calculator) a numerical table of data of the voltage drop across a discharging capacitor for 50 s. The calculator graph of this data set is shown in Fig. 1a. Students were asked to find an equation of the form that could be used to describe the data. The students were also asked to (a) compute the average rate of change over the three subintervals from t = 5 to t = 10 s, t = 20 to t = 25 s, and t = 35 to t = 40 s respectively, and (b) write two or three sentences that describe how the voltage across the capacitor changes over time and how the sequence of average rates of change of the voltage data in (a) changed over time. Figure 1b shows the calculations of the average rates of change over the three intervals asked for in part (a) of the test item.

Fig. 1
figure 1

A plot of the voltage data and calculations of three average rates of change

Full size image

Since a discharging capacitor is modeled by an exponential decay function, the average rate of change over any subinterval of the domain is negative. The sequence of average rates of change over the 5 s subintervals is getting less negative and closer to zero and, hence, the sequence of average rates of change is increasing. In terms of the phenomena, a negative average rate of change means that the voltage across the capacitor is decreasing for that subinterval; but, as we will show in the results below, interpreting the meaning of the sequence of increasing average rates of change in terms of the voltage is considerably more difficult.

5 Results

We found that after completing the model development sequence nearly all students became proficient at constructing graphical representations of changing phenomena and their associated rates of change graphs in all three contexts and across all three underlying mathematical structures: motion along a straight path (piecewise linear functions), light intensity (inverse square) and discharging capacitor (exponential decay). We found that nearly all students were able to interpret and clearly distinguish between the function values and the values of both positive and negative rates of change in the context of motion along a straight path. However, the student difficulties that were initially resolved in the context of motion arose again when interpreting decreasing non-linear functions and sequences of negative average rates of change in the contexts of the light intensity and the discharging capacitor. We elaborate and provide evidence for these findings in the following sections.

5.1 Motion along a straight path

Our results show that most students were able to develop and maintain the distinctions between the velocity graph and the position graph and between velocity as a signed quantity and speed as the magnitude of velocity. As we had anticipated from the research literature, the students initially had difficulties in reasoning about velocity and changes in velocity when given a position graph. Through the computer simulation environment in the model exploration activity, the students gained proficiency in reasoning about and interpreting the graphical representations of velocity and position when both quantities were positive. However, student difficulties in carefully distinguishing among position, velocity and speed re-surfaced when the rate of change of position (velocity) was negative or linearly decreasing.

The students’ difficulties in distinguishing among position, velocity and speed can be seen in the students’ responses to creating and interpreting a velocity graph when given the position graph shown in Fig. 2a. Nearly all of the students correctly constructed the corresponding velocity graph shown in Fig. 2b. When asked to interpret the velocity graph with its negative values, 44% of the students correctly identified the greatest velocity occurring in the interval between t = 2 and t = 4 s. However, 38% of the students identified the greatest velocity as occurring between t = 0 and t = 2 s. These students were attending to the magnitude of the velocity since this is the interval where the magnitude of the velocity (speed) is the greatest. One of the students argued that the first interval showed the greatest velocity because the sign of the number only provided direction of the movement, not how fast the object was moving. This student was reasoning about the velocity as if it were two separate quantities: a sign that indicated direction and a numerical value that indicated how fast the object was moving. It would appear that the student did not see the value of the velocity as a single negative quantity that could be compared to other negative quantities. The 18% of the students who identified the interval between t = 4 and t = 6 s as having the greatest velocity were correctly comparing the relative velocities of the first and third intervals, but not regarding a value of zero as greater than both of the negative quantities.

Fig. 2
figure 2

Creating and interpreting a velocity graph from a position graph

Full size image

Students’ difficulties in the context of linearly decreasing velocity were evidenced by their low scores (29% correct) on the pre-test item shown in Fig. 4 below. However, at the conclusion of the model exploration activity, we found that most students were able to successfully interpret velocity information from a position graph and position information from a velocity graph for both positive and negative velocities and for constant and non-constant velocities. On the midterm exam, 66% of the students could correctly construct the velocity graph given a position graph and 71% could correctly construct the position graph given a velocity graph. This success was also evidenced in the substantial improvement on three of the pre- and posttest items, given at the beginning and the end of the course. These three items address determining the velocity and average velocity given a piecewise linear position graph (shown in Fig. 3), interpreting a linearly decreasing velocity graph that takes on negative values (shown in Fig. 4), and interpreting an object’s motion when given a position graph (shown in Fig. 5).

Fig. 3
figure 3

Interpreting instantaneous and average velocity from a position graph

Full size image
Fig. 4
figure 4

Interpreting position from a velocity graph

Full size image
Fig. 5
figure 5

Interpreting an object’s motion when given a position graph

Full size image

In the first item, the students were asked to determine the speed (at time t = 7 s) of a person running along a straight path as represented by the position graph in Fig. 3. On the pretest, only 26% of the students gave the correct answer (1.25 m/s). Rather than finding the velocity as the slope of the second linear piece of the function between t = 3 s and t = 15 s, 34% of the students divided the y-value of 35 meters by t = 7 s resulting in 5 m/s; 31% of the students gave the y value with an attached velocity unit, 35 m/s, as the answer. On the posttest, however, 69% of the students correctly answered this question.

On the pretest, the students were also asked to determine the average speed of the runner throughout the 15 s race; only 40% of the students correctly answered 2 m/s. Instead, 23% of the students averaged the two velocities between t = 0 s and t = 3 s (5 m/s), and between t = 3 s and t = 15 s (1.25 m/s), resulting in an average velocity of 3.125 m/s. Another 20% of the students failed to recognize that the runner not did not start at the origin, and thus incorrectly concluded the average velocity to be 3 m/s. On the posttest, 77% of the students correctly answered this question.

The second item asked students to identify which of a set of position versus time graphs would best represent an object’s motion as shown in the velocity graph in Fig. 4. This item requires an understanding of how to reason about position when given a velocity graph. On the pretest, only 29% of the students were able to correctly identify the correct position graph (alternative B). On the posttest, 71% of the students correctly identified the position graph.

The third item asked the students to choose a written description of the motion of an object whose position is shown in Fig. 5, taken from Beichner (1994).

On the pretest, 34% of the students selected a correct interpretation (alternative d); the posttest results showed that 80% of the students were able to select a correct interpretation. Results reported by Beichner (1994) on this item showed that only 37% of the students interpreted the motion correctly after kinematics instruction. Taken together, these three items indicate that at the end of the model development sequence the students were able to successfully interpret velocity (rate) information from position graphs and to interpret position information from velocity graphs for both positive and negative velocities and for changing velocities.

5.2 Light intensity

We found that the students’ initial difficulties in distinguishing between the values of the function and the values of the average rates of change of the function over subintervals of the domain, that were overcome in the context of motion, resurfaced as students applied their developing models of average rate of change in the new context of the light intensity with respect to distance. The students’ initial interpretations of the relationship between light intensity and the distance from the light source are summarized in Fig. 6. Although all of the students had taken a course in high school physics, nearly all of the students (83%) drew a linear relationship (C, D and F shown in Fig. 6) between the intensity of light and the distance from the source. All but one student correctly described how the intensity at 1000 yards compared to the intensity at 2000 yards based on the graph they drew.

Fig. 6
figure 6

Students’ initial models of intensity vs. distance from light source

Full size image

However, when asked to “Compare the rate at which the intensity is changing at 1000 yards and 2000 yards”, only half of the students (n = 17 of the 34 students) correctly interpreted or calculated the rate of change based on their graphical representation. For example, one student correctly concluded from his incorrect C graph that: “The rate at which the intensity is changing at 1000 yards and 2000 yards is the same.” However, nearly half of the students (n = 16 out of the 34 students) did not compare the rate at which the intensity was changing, but rather compared the values of the function at the two distances. The remaining one of the 34 students simply gave an equation of a linear function that did not correspond to his graph. Thus, for about half of the students, their earlier distinctions, in the context of motion, between the value of the output of the function value (e.g., position) and the value of its rate of change (e.g., velocity) were not readily applied in the new context of light intensity.

In our analysis of the students’ written reports completed at the end of the model application activity on light intensity, we found that nearly all of the students’ reports (89%) included correct interpretations of correct graphs of the values of the light intensity as a function of the distance from the light source (such as that shown in Fig. 7a). Nearly all reports (89%) also included a correct graph of the average rates of change over 1 cm intervals (similar to that in Fig. 7b). Almost half of the students (44%) described the average rates of change (shown in Fig. 7b) as the slopes of the line segment connecting two consecutive points.

Fig. 7
figure 7

A typical scatter plot of the light intensity data (a) and its corresponding average rate of change graph (b)

Full size image

Over half (56%) of the students correctly interpreted a correct graph of the average rates of change of the light intensity over 1 cm subintervals. Some students were able to correctly interpret the values of the sequence of average rates of change and to refer to the magnitude of those values when describing the changing light intensity. For example, one pair of students wrote:

Although the majority of the average rates of change are increasing, the absolute value of average rates of change are decreasing which tells us that as the distance from the light source increases, the intensity of the light decreases quickly at first and then decreases more slowly.

In this statement, the students reasoned from the graph of the average rates of change values (shown in Fig. 7b), and correctly articulated that the “majority” of these values are increasing, seemingly focusing on the average rate of change values when the distance from the light source is greater than 3 cm. This pair of students used the absolute values of the negative average rates of change to give a qualitative interpretation of the function values (“intensity of the light”) that is “decreasing quickly at first and then decreases more slowly.” This pair of students maintained the distinction between the function values (the light intensity) and the average rates of change values in their reasoning about the light intensity. By shifting to the language of the absolute value of the average rates of change, this pair of students correctly interpreted how the light intensity changed: “quickly” and then “slowly.”

Many students encountered difficulty in maintaining these distinctions and correctly expressing them in terms of the phenomena. In some cases, this led to contradictions within the students’ description. For example, one pair of students wrote:

The intensity of the light decreases at a decreasing rate with respect to the distance from the light source, as predicted earlier. The average rates of change increase at a decreasing rate as distance from the light source increases.

Within this description, the students first referred to the rate as a “decreasing rate” and then in the second sentence claimed that the “average rates of change increase.” Many students who displayed this difficulty used phrases such as “decreasing at a decreasing rate” rather than writing two separate statements: one about the function and one about its rate of change. Examples such as this point to the complexity of expressing the ideas involved with negative rates of change and their representations in an applied context.

5.3 Discharging capacitor

In the context of the discharging capacitor we found that 83% of the students (n = 29) explicitly showed and used one or more representations to support their written descriptions of the behavior of the voltage and its average rates of change. Eighteen students (51%) drew function graphs of the voltage over the discharging capacitor; 15 students (43%) drew rate graphs; and 11 students (31%) made tables. Only three students (9%) did not supply any representations to support their descriptions.

A significant number of students had difficulty maintaining the distinction between the behavior of the function and the behavior of average rates of in the context of the discharging capacitor. Only 56% of the students (n = 19) could correctly describe both behaviors within this context. One example of a correct student description is: “The voltage is decreasing. The average rate of change is increasing because it’s negative and moving towards zero. Therefore, the voltage is decreasing at an increasing rate.” For the other 44% of the students, the most common difficulty was to make an incorrect assertion about the negative average rates of change, such as “The average rate of change of the voltage decreases over time.” However, the students drew on a number of different graphical representations to support their claims about the rates at which the voltage is changing.

One student made the graph shown in Fig. 8 of the voltage over the discharging capacitor that included segments of slope-lines over three intervals, illustrating how the calculated average rate of change changed as time progressed. The student’s description accompanying the graph drew on language of speed and velocity:

Fig. 8
figure 8

Function graph with segments of slope-lines drawn

Full size image

In the first 25 s. the voltage across the capacitor decreases quickly at a high speed but in a negative velocity. As more and more of the voltage in the capacitor is discharged, the graph begins to plateau. This shows that as the voltage gets closer to 0 the average rate of change becomes closer to 0 and is discharging very slowly until the capacitor is fully discharged.

This student drew on the context of motion to describe the voltage over the discharging capacitor, choosing to use the language of speed, velocity, slowly, and quickly. The language of speed as the magnitude of velocity seemed to help this student to correctly interpret the rate of discharge and to shift to the language of a “very slow” discharge to interpret the long run behavior of the changing phenomenon.

Another student used a similar representation with slope-triangles draw in the function graph (see Fig. 9) to illustrate and support his description of the changing voltage across the discharging capacitor:

Fig. 9
figure 9

Function graph with slope-triangles drawn

Full size image

Over time, the voltage across the capacitor drops and approaches, but never reaches, zero. At first, the voltage across the capacitor drops drastically, reaching 1.34 in the first 14 s, but then begins to slow down as time goes on. This decrease in the charge of voltage explains why the average rate of change of voltage decreases as time passes. As shown above, the average rate of change @ t = 5 to t = 10 is −0.392 v/s, compared to the −0.006 v/s @ t = 35 to t = 40.

This student used more colloquial language such as “drops drastically” and “begin to slow down” describing the voltage discharge. The incorrect statement that “the average rate of change of voltage decreases as time passes” might be due to the student focusing on the wrong aspects of his representation; perhaps the student was seeing the heights of the slope-triangles as positive and successively decreasing, despite having explicitly and correctly calculated negative values for the slopes.

Although many of the students struggled in expressing the behavior of the average rates of change of the voltage across the capacitor, 56% of the students were able to carefully and correctly interpret the rates, supported by their data and references to graphical representations. For example, one student correctly drew a function plot and the corresponding rate graph, and wrote: “As time increases, the voltage across the capacitor is decreasing. The average rate of change of the voltage increases (getting less negative and closer to zero). The magnitude of the average rate of change of the voltage decreases (0.392, 0.048, 0.0062) meaning over 5 s intervals, the capacitor loses less and less voltage.” However, some students, even when drawing a correct corresponding rate graph, encountered difficulty in giving a correct interpretation of their graph. For example, the student whose graphs are shown in Fig. 10 gave the following interpretation:

Fig. 10
figure 10

Supporting graphs

Full size image

The voltage across the capacitor decreases over time at a decreasing rate. Although the [average rates of change] are increasing from [0,40], the absolute value is decreasing which tells us that the rate at which the voltage across the capacitor is decreasing at a decreasing rate.

The student’s first assertion that the voltage is “decreasing at a decreasing rate” is an incorrect interpretation of the data. The student then correctly stated that the values of the sequence of average rates of change are increasing (as shown in the graph) and that the magnitudes of those values are decreasing. However, the student’s meaning is then obscured by the final assertion of “decreasing at a decreasing rate.”

Some of the students used their work in finding an equation to fit the data to describe the rate at which the voltage was changing, by interpreting the cstant 0.87 in their derived expression \(y=7.99{(.87)^t}\). Shifting their focus to the value of the base of the exponential function allowed these students to interpret the change in the voltage as a percentage change. Comparing the amount of voltage across the capacitor over consecutive seconds, one student wrote “over each 1 s interval, the capacitor’s voltage decreases to 87% of the previous voltage.” Another student correctly interpreted the constant 0.87 to mean “that at each second the voltage is 13% less than the voltage it was the previous second” and provided the graphical representation shown in Fig. 11.

Fig. 11
figure 11

Graphical representation of the percentage rate of change

Full size image

This representation makes it clear that this student understood that the amount of voltage over the capacitor decreases by 13% each second. However, we do not know if these students have coordinated their models of percentage change and with their models of average rate of change.

6 Discussion and conclusions

An underlying assumption of this study has been the importance for science, engineering and mathematics students to create, interpret and reason about models of changing phenomena (Beichner, 1994; Carlson, 1998; Hestenes, 2010). However, reasoning about rates of change in general is difficult for students (Carlson et al., 2002; Herbert & Pierce, 2011; Johnson, 2012; Oehrtman et al., 2008), and especially complex and challenging when the phenomena at hand involves an average rate of change that is negative (Ärlebäck et al., 2013). The account of the model development sequence and its implementation illustrates how the activities in the sequence supported the students in interpreting and reasoning about phenomena with negative rates of change in different contexts. Our results provide empirical support for the recommendations for instruction by Carlson and colleagues (2002) and Roorda et al. (2015).

The model development sequence began with the familiar context of motion along a straight path. This context (unlike the contexts of light intensity and discharging capacitors) has distinct words for the rate of change (velocity) and the absolute value of the rate of change (speed). While working through a set of model exploration activities in a computer simulation environment, the students came to recognize velocity as a signed quantity (distinct from speed) and distinguished between the values of the output of a position function and the values of the average rates of change of that function. Nearly all students were successful in interpreting and distinguishing between velocity graphs and position graphs. However, when we shifted from the phenomenon of motion to the phenomena of light intensity and voltage drop across a capacitor, and in line with other researcher’s results (Herbert & Pierce, 2011; Ibrahim & Rebello, 2012), student difficulties in interpreting and distinguishing between the function and its average rates of change re-surfaced for many of the students.

The conceptual challenges in interpreting rates of change reside, in part, in attending simultaneously to the global features of the behavior of the function and in coordinating one’s understanding of three quantities: the change in function values, the rate of that change over various subintervals, and changes in sequences of average rates of change (e.g., Carlson et al., 2002; Lobato et al., 2012). Our study shows that the difficulty of such comparisons becomes more complex when the rates are negative and increasing. In the case of the light intensity and the discharging capacitor contexts, the magnitude of the average rates of change over a sequence of subintervals decreased, while the sequence of signed average rates of change increased as they became less negative. For many students, the language for describing this change in terms of the context of light intensity and capacitance appeared in conflict with formal mathematical language for describing that change.

The language of magnitude (or absolute value) appeared to be helpful to some students in using clear language to interpret changing phenomena with negative rates of change. Unlike in the case of motion, where there are different words for describing the signed quantity (velocity) and its magnitude (speed), for other phenomena, such as light intensity and the voltage drop across a capacitor, there are no such distinct and familiar words. This suggests that greater attention needs to be paid to the use of the language of magnitude (or absolute value) to help students in interpreting and reasoning about these phenomena. Expressions like “increasing at a decreasing rate” and “decreasing at an increasing rate” appeared to be especially problematic for many students. It would appear that separating such a statement about a function into two statements (one about the function increasing and the other about the rate of change decreasing) would help students to articulate precise mathematical formulations about changing phenomena and to avoid the easy slip into conflating the function and its rate of change.

In the context of the discharging capacitor (an exponential decay phenomena), the notion of percentage change provided some students with language for dealing with this difficulty. Referring to the constant percentage change, students were able to express the amount of change using everyday language of decreasing with a comparison to a previous value. Just as importantly, the constant percentage change provides an opportunity to express an explanatory model of the phenomena based on fact that the amount of discharge is directly proportional to the amount of charge in the capacitor. Future research needs to investigate how students can connect and coordinate this explanatory model to the descriptive exponential decay model with its negative and non-constant sequences of average rates of change.

This study suggests that explicit attention needs to be paid to helping students learn to communicate about the context of changing phenomena, not simply to calculate numerical relationships and construct the graphical representation of the phenomena. Although nearly all students became proficient at calculating average rates of change and constructing graphical representations of the changing phenomena and their associated rate of change graphs in all three contexts, some students continued to have difficulties in interpreting such numerical results and graphs in terms of the phenomena using precise, careful mathematical language. This suggests the need for closer attention to interpreting and reasoning about the concept of rate of change in a range of contexts, which is in line with the suggestion by English, Ärlebäck and Mousoulides (2016) to rethink and broaden the perspectives of model and modeling within a multidisciplinary context. Based on our results, we also concur with Roorda et al. (2015), that since motion is a familiar experience for students, this would appear to be a useful and productive context for introducing negative rates and distinguishing between the magnitude of the average rate of change (speed) and the average rate of change as a signed quantity (velocity). However, when shifting to other contexts, students will likely need support to interpret and reason about new contexts This paper has illustrated that model development sequences provide a structure to organize and plan learning and instruction through eliciting, exploring and applying mathematical concepts.