1 Introduction

Mathematical diagrams at primary school are often used as visual aids to enhance children’s learning of mathematical concepts. As described by many mathematics educators, those diagrams are not at all self-evident. Rather, they are ambiguous and have to be interpreted actively by the students (Steinbring 2005; Söbbeke 2005; Jahnke 1984; Lorenz 1993; Voigt 1990). As often observed in mathematics classrooms at primary school, children find their own way to make sense of mathematical representations—and not seldom they ignore implicit structures (Söbbeke 2005). Usually, a variety of different interpretations among students—even within the same classroom—indicate the complexity of the interpreting processes.

Sonja, an eight-year-old pupil of a primary school for instance, interprets the unlabelled number line in a very unexpected way (Fig. 1). During an interview, conducted in this study, she was asked to think of a number sentence that fits exceptionally well to the number line (see Sect. 3.2 for further explanation).

Fig. 1
figure 1

Sonja interprets the number line in the pre-interview

Full size image

Sonja says “12 + 7” fits, and one could think that she interprets the arc as a representation of an addition “+7”. The interviewer asks her to draw the addition task into the scheme and the result is surprising (Fig. 1).Footnote 1

From a didactic point of view, Sonja’s individual construction in Fig. 1 is not intended: she ignores important structural elements of the diagram—such as the arc for instance. Thus, spontaneously her interpretation seems to be less sophisticated and not at all structure-oriented. But what is the background of her interpretation? Which factors control her reading of the diagram?

To better understand children’s use of visual aids, this project aims at looking under the surface of what can be seen directly in the children’s interpreting processes by means of clinical interviews. Therefore interviews with 20 eight-year-old children were videotaped before and after a series of ten intervention lessons in which these young students jointly used and interpreted visual diagrams (see Sect. 4). To characterize the children’s specific interpretations, the construct “frame-based interpreting competence” (fric) is developed.

Based on the view of mathematics as science of patterns and structures (Devlin 2002), learning mathematics can be conceived as a process of interpreting visual diagrams in a more-and-more complex way (Steinbring 2005). Furthermore, regarding mathematics learning as an activity (Freudenthal 1973), there is no predetermined, objective or inherent meaning of mathematical diagrams. In fact the meaning of those representations is constituted through social interaction processes and negotiated conventions (Steinbring 2005; Dörfler 2006). To put it briefly, according to Wittgenstein, one could say that the meaning of a diagram is its use. From this perspective, subjective individual employments of visual representations get a crucial role: generally speaking, the question “what influences children’s meaning-making?” becomes important.

Basically, weFootnote 2 regard this problem from two sides: on the one side there is the given object, which is the mathematical diagram itself; and on the other side there is the interpreting subject, the young student. Both sides are considered to have an impact on the interpreting process, or as Otte writes: “All knowledge is under a double influence: the epistemic learning subject and the epistemic object of knowledge” (Otte 1994, p. 281, translated from German by the authors).

Concerning the given object we argue that it can be perceived and interpreted in multiple ways. What could be a representation of a complex mathematical system for the mathematician (Fig. 1) could be a concrete, material horizontal stroke with smaller vertical strokes on it for a young child. That is, the seemingly “given object” gets its meaning by an interpreting subject: it could be a theoretical object for one person and an empirical, material object (Söbbeke 2005) for another. Furthermore we focus on the special epistemological conditions of learning processes with visual mathematical diagrams. Sonja is confronted with a complex symbolic mathematical system (Jahnke 1984; Dörfler 2006) that cannot be grasped immediately through visual perception. According to Duval, Sonja has to “visualize” and to recognize the diagram’s implicit structures, which means that she has to be aware of the representation’s epistemological function (Duval 1999, p. 13).

Concerning the interpreting subject, we argue that individual interpreting processes are embedded in and influenced by a cultural social context (Steinbring 2005; Radford 2010). Together with Voigt (1990, p. 360) we claim that children might establish habitual interpreting schemes (frames), or even interpreting rules, in mathematics classroom culture. We consider this interpreting scheme as a necessary “interpretation foil” to make sense of the diagram. To investigate this social-cultural component of learning with visual aids we apply the “frame concept” of the American sociologist Goffman (1974); Krummheuer (1984). In Sonja’s case we are trying to understand more precisely: Which frame does she adopt to interpret the number line? In which way does this frame effect a structure-based interpretation of the diagram?

In the following, the two analysis dimensions “epistemological conditions of the given visual representation” and “subjective interpreting schemes—frames” will be explained in more detail.

2 Theoretical background

2.1 Epistemological conditions of learning processes with mathematical diagrams

As outlined before, mathematical visual representations are symbolic, ambiguous elements. They do not convey a mathematical concept directly into the students’ heads, but they have to be actively interpreted, embedded in a social-cultural milieu. Furthermore, the handling of mathematical representations is even more demanding for students—and for teachers as well. There is no fixed “instruction manual” that could be given to the children. On the contrary: a flexible use is indispensable for exploring the diagram’s implicit structures. Thus, children should not be restricted by predetermined, maybe implicitly learned, interpretation rules such as, for instance, “the number line always starts with zero” (which could be observed in the interviews). Then again, there exist historically developed conventions (Steinbring 1998, p. 161; Dörfler 2006, p. 210), for instance the reading direction from left to right, that regulate the number line’s use. Thus, in the mathematics classroom the teacher (and the student) has to handle a “delicate blending of instruction and construction that is a fine-tuning of the teacher’s craft” (Presmeg 2012, p. 2ff). Presmeg describes this subtlety of dynamic teaching and learning processes between instruction and construction with the metaphor of a “dance”:

Within the set moves of a particular dance there is freedom, creativity, and vigor. Certainly a dancer can decide to construct a different set of movements and they may be harmonious and beautiful, but if they are too far from the set moves, that dancer cannot be considered to be doing that particular dance. (Presmeg 2012, p. 3)

To stay with this metaphor, this “dance” concerning the handling of mathematical representations becomes even more “swirling” and challenging: from an epistemological point of view, mathematics is seen rather as process than as a given product, thus its diversity becomes central:

In the process of developing mathematical knowledge, cultural contexts, subjective influences, and situative dependencies are both effective and inevitable, and are the reasons for an observable diversity and a non-uniformity of the emerging knowledge. (Steinbring 2005, p. 15)

In this regard, visual diagrams serve as an epistemological learning tool to explore manifold mathematical structures and in the same way serve as a communicative tool to communicate about these invisible structures (Steinbring 2005; Söbbeke 2005).

Regarding the epistemological learning conditions and constraints for the representation in Fig. 1, we highlight that it is not the concrete materially given representation itself which conveys meaning, but the relation between the single elements of the diagram. Here, the “paradoxical character” (Duval 1999, p. 3) of visual representations emerges: on the one hand, invisible mathematical concepts need (semiotic and other forms of) representation to become communicable; on the other hand the representation must not be confused with the mathematical object itself (Duval 1999, p. 3). Looking at the number line in Fig. 1, an obstacle for children which is often observed is the representation of numbers: a number is not represented through the visible single scaling bars at hand, but through the relation between (two) neighbouring scaling bars (Söbbeke 2005; Lorenz 1993).

In an empirical case study Söbbeke (2005) examined the ability to built abstract structures and relations into a given diagram. Derived from careful analyses of clinical interviews at primary school, she elaborated four levels that characterize children’s interpretations in a range between concrete material and complex relational interpretations (Söbbeke 2005). She even could demonstrate that visual aids are by no means a familiar reference context to young students. Rather, the individual interpreting processes appear as productive interplay between the diagram’s well-known elements and its new and symbolic aspects (Söbbeke 2005; S. 370). Concerning Sonja’s production (Fig. 1), the “arc” as one element of the number line appears to be unfamiliar—in any case Sonja doesn’t label it, so it seems as if she doesn’t make sense of this element. The next subsection will explain the expression symbolic context element as one of the keywords in this study.

2.1.1 Symbolic context elements

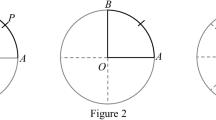
From a mathematics educational perspective, the diagram’s single elements have to be correlated with each other and they have to be interpreted as parts of a complex symbol system to become meaningful. In this study those elements are named symbolic context elements. The term “context” is taken from cognitive psychology, which argues that seeing is not merely a simple stimulus–response mechanism, but a complex and active construction (Hoffman 2000; von Glasersfeld 1987). This process of construction is influenced by the spatial context (Fig. 2) of an illustration (once there is actively identified a B and once a 13).

Fig. 2
figure 2

The spatial context of an illustration effects its interpretation

Full size image

In this study, young students do not cope with an everyday illustration, but with mathematical diagrams (number line and hundred board), which have to be interpreted in a specific, mathematical manner. In this regard, the term symbolic context elements describes the diagram’s given symbolic elements, which—solely in their mutual relation—build a complex mathematical symbol system. Even though there is no complete and objective valid catalogue, there seem to be prominent context elements in the number line (Fig. 3), which are relevant for its interpretation. The following—by no means exhaustive—list shows those salient context elements (Fig. 3). Its predefinition is based on an a priori mathematical analysis as well as on results from the pilot study, in which noticeable specific features concerning children’s handling with visual aids could be observed.

Fig. 3
figure 3

Symbolic context elements of the number line

Full size image

The first long bar (1) seems to be an important starting point from which several children generate their interpretations more or less spontaneously. It is striking that for many of them the number line apparently “naturally” starts with zero. Other important context elements are the single scaling bars (SB) (2) that can be seen materially in their cardinality as concrete objects to count, as ordinal number, or—for instance—relationally as a marker point for a measurement with flexible units (Söbbeke 2005). The different lengths of the scaling bars (3) could be used in a structuring way, so that the middle ones represent for example multiples of five and the long ones multiples of ten. Likewise, the different lengths could stand for fixed predetermined numbers. The arc (4), in textbooks at primary school often demonstrated with an arrowhead at the left or at the right, usually indicates an operation such as a subtraction or an addition. Interviews with primary school children revealed that the arc could be interpreted as a kind of “stroke container” as well. In this case the number of bars under the arc becomes important (Söbbeke 2005, p. 185). As already mentioned, the basic unit (5) seems to form a special obstacle for primary school children, not only in our interviews. To most children a number is represented through the discrete material single scaling bars, not through the relational distance between two scaling bars (Söbbeke 2005, p. 91; Lorenz 1998, p. 151ff). Furthermore, the unit can be seen flexibly as a unit of “one”, “five”, “ten” or whatever.

To sum up: from an epistemological point of view it is apparent that the context elements in their mutual relation (Fig. 3) can and should be interpreted in many different ways. Because of this theoretical ambiguity (Steinbring 1994) it becomes obvious that mathematical visual diagrams can serve as an epistemological learning tool for exploring mathematical relations.

2.2 The frame concept

First results in this study reveal that the frame within which a young student interprets a mathematical diagram decisively influences his or her use and interpretation of the context elements. Goffman (1974) elaborated the frame concept to describe and examine people’s organization of everyday experiences. As a sociologist, who partially shared positions of Symbolic Interactionism (Blumer 1973), he describes frames as socially learned interpreting schemes that people adopt to give meaning to a situation:

I assume that definitions of a situation are built up in accordance with principles of organization which govern events […] and our subjective involvement in it; frame is the word I use to refer to such of these basic elements as I am able to identify. (Goffman 1974, p. 10)

Thus, for each agent, frames are an indispensable reference for interpreting a situation and coordinating his or her actions.

To analyse subjective interpreting processes in the mathematics classroom (see for example Krummheuer 1983, 1984, 1992), the frame concept is particularly interesting, because it provides a bridge between structural necessities and the interpretive paradigm of an agent, who actively arranges and builds his or her situation (Goffman 1974; Lübcke 2011, p. 107). For this reason, both perspectives, individual and cultural, are considered. Frames are cultural elements—each person is endued with a broad set of cultural interpreting schemes—learned in a cultural milieu through socialization. But these frames can be modified during their application (Goffman 1974). Goffman speaks of “framing” as the situational application of a frame (frame-in-use) and of “frame” as a generally learned interpreting scheme (frame-as-structure). Frame and framing represent “two sides of one coin” (Willems 1997, p. 46ff). Whereas the “frame” is independent of a situation and in this respect quite stable, “framing” is highly unstable and fragile (Willems 1997, p. 46). Krummheuer claims that in mathematics classrooms this fragility of framing processes is a prerequisite for the interactive construction of new meaning: he describes differences between teachers’ and students’ frames as constitutive for subjective learning processes (Krummheuer 1992, p. 169). Accordingly, academic classes can be characterized as “interface between frames of two different interaction habits” (Krummheuer 1992, p. 168, translated by the authors). Whereas the teacher commonly adopts a specialized didactic frame, the student often prefers extracurricular everyday frames (Krummheuer 1992, p. 168). Concerning visual diagrams, it is the teacher who recognizes implicit structures by means of advanced mathematical frames. The student who does not come with these advanced frames has to construct those structures anew (Krummheuer 1992, p. 191).

In spite of these discrepancies between frames, teacher and students try to create a common ground for communication by modulating their frames and thereby easing differences. Those modulation processes (Goffman 1974; Krummheuer 1983) offer the potential for subjective learning. Through expanding and verifying their interpreting schemes, students gain new references for meaning-making and are able to interpret a mathematical task, situation or diagram against another (more sophisticated) background.

Further, Krummheuer stresses that modulations are based on conventions; hence students can learn them in social interaction. As examples he names processes in the classroom such as “simplifying”, “concretizing”, “composing analogies” or “visualizing” (Krummheuer 1983, p. 109).

Transferring the frame concept to interpretation processes of mathematical visual diagrams at primary school, it means that children are endued with a socially learned catalogue of frames. They adopt these frames—unconsciously in most cases—to give meaning to a visual diagram. On the one hand pupils’ frames are an indispensable background that enables them to make sense of a visual representation. On the other hand those frames constrain possibilities of interpretation. It is the modulation of frames that might enable children to interpret diagrams in a more complex and structure-oriented way.

To give an example, in a particular classroom culture a child could learn the interpreting scheme “the number line always starts with zero”. In this way the diagram would be seen as a line segment or half line with a fixed starting-point “zero”. Within this frame, the context element first long scaling bar gets a crucial and distinct role as “zero”. Such a perspective enables a meaningful interpretation, but on the other hand it predetermines the interpretation. From this point of view, the subjective frame fixes in advance the objective structure between the given context elements. A given object like a mathematical diagram does not have an ontological status per se, but solely gains it within a particular frame. As a kind of “sense-making machine” (Willems 1997) it is the frame that defines the meaning and structure of a given diagram for an interpreting subject. Consequently, modulating their frames is an indispensable prerequisite for students to build “new” structures into a mathematical visual diagram.

Lorenz stresses that it is the handling with the number line that might open up new perspectives:

First of all the number line is merely a stroke (of limited length). It gains its function through pupils’ actions that control a new perspective on the number line, such as comparing it with other objects and their relations and discovering common structure elements. (Lorenz 1993, p. 130, translated by the authors)

Until now, from a theoretical background, we have considered the interpretation of diagrams to be influenced by two dimensions. The first is the “objectively” given diagram itself with its symbolic context elements. We have stressed that from an epistemological point of view, those elements could be interpreted in manifold different ways, for instance as more empirical or more theoretical objects. Furthermore, we have highlighted that it is not the material context element itself that conveys meaning, but the relation between those elements. Moreover, we have assumed that the students’ subjective and individual frames effect the interpretation of a diagram.

Returning to Sonja’s interpretation at the beginning, the questions remain: Which frame does she adopt to interpret the number line? And: In which way does this frame effect an interpretation of the diagram? In the next section we will try to examine Sonja’s interpretation more deeply.

3 The case of Sonja in the pre-interview—extract from an interpretive context and frame analysis

3.1 Analysis steps

In Sect. 2.2 we argued that an adopted frame predetermines the structure between the context elements of visual diagrams. Of course, a child seldom expatiates on his or her frame—especially because it is taken up unconsciously in most cases. Because of the dialectic relationship between frame and context, we draw conclusions from the structure the child construes between the context elements about his or her underlying interpreting scheme. Thus, in a first analysis step we examine the questions: Which context elements does Sonja use to interpret the diagram? Which elements are relevant to her? And: Does she use the elements in an object-oriented Footnote 3 way as if they were concrete empirical objects or in a relational way as if they were theoretical objects and part of a web of structural relationships?

Sfard (1991) describes objectification as follows: “Seeing a mathematical entity as an object means being capable of referring to it as if it was a real thing—a static structure, existing somewhere in space and time (Sfard 1991, p. 4). From our point of view, those objectifications can take place on different qualitative mathematical epistemological levels. That means a child who copes with a mathematical diagram as if it was a concrete object is not necessarily unable to see its implicit structures.

We differentiate between two approaches to using the context elements as objects.

In a relational way a child might correlate or compare these objects as theoretical objects with others to see them in a new light and to reinterpret them. Jonny for instance interprets the first long bar (Fig. 1) as object “500”. He does not see the context element as a discrete, isolated object with a fixed meaning, but he uses it in a relational, hypothetical way to explore mathematical relations: “Here (points at the first long bar) could be 500 then, then this could be steps of ten, and then this (points at the second long bar) would be 600, then this (points at the next two short bars) would be six hundred and ten, twenty” (Jonny to the number line with arc in the post-interview). In an object-oriented way, a child uses the context elements as if they were concrete empirical objects with an inherent meaning. We will see later that one can describe Sonja’s approach as object-oriented.

The analysis with the grid depicted in Fig. 8 gives information about the structure between the context elements a child construes. Based on this information, in a second step we draw conclusions about the child’s underlaying interpreting scheme, his or her framing. Our approach will be illustrated in the next section by means of short interview sequences with Sonja in pre- and post-interview.

3.2 The interview-guideline

The interviews took place before and after a series of ten mathematics lessons in which visual structuring competence (Söbbeke 2005) was fostered. During the semi-structured clinical interview, twenty children of grade three worked on tasks with the commonly used visual aids hundred board and number line. In Fig. 4 one of the interview tasks is depicted. Each number sentence on the task cards fits in a way to the number line, but they offer a differing reference to the diagram’s structure. The first task card (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1/7 + 1) could lead to an empirical interpretation that focuses on the number of strokes under the arc. In contrast to the other three task cards its conception does not follow common conventions as “linearity” or “interpreting the arc as a representation of an arithmetical operation”. Here, other operations such as “22 − 9” or “13 + 7 + 2” are possible, too.

Fig. 4
figure 4

Unlabelled number line with task cards

Full size image

By contrast, the number sentences “99 − 7” and “620 + 70” need complex, relational interpretations and re-interpretations of the diagram. The arc is interpreted as an addition or as a subtraction, the number line is seen as a section from a number line, thus the first long line could be “500” or “70”. The single units (or the single strokes) are to be seen flexibly as steps of one or steps of ten. The task cards were designed for a quantitative study and for methodological reasons it was therefore necessary to put two number sentences on one task card. However, they are used for qualitative analyses within this study. The different number sentences serve as an offer for the children to think about the unlabelled number line according to their individual mathematical competences.

Concerning the unlabelled number line in Fig. 4, the pupils were first of all asked to choose one card that fits exceptionally well to the number line. Thereafter they justified their choice and had to draw both number sentences into the scheme. In a next step the children were asked to explain why they did not choose the other task cards, so that during the interview they commented on each number sentence.

3.3 Description of the situation

The following episode stems from the pre-interviews. These interviews took place before a series of ten mathematics lessons in which visual structuring competence was fostered.

Sonja is a third grade student. According to her mathematics teacher, her effort in mathematics is moderate to weak. Before the intervention took place, she worked with different labelled number lines (with the units “one” and “ten”). The complete interview episode on the number line with arc takes 12 min. At the beginning, the interviewer asks Sonja to choose one of the problem cards that fits exceptionally well to the number line (Fig. 4). Sonja looks from the problem cards to the number line and back for about twenty seconds before she chooses “12 + 7” and “7 + 12”. Then, the interviewer asks her to draw the addition tasks into the scheme. We have already mentioned that the result is quite amazing (Fig. 1). During the interview, Sonja’s interpretation isn’t immediately clear. Several times the interviewer asks cautiously for information, so that the complete conversation concerning the drawing (Fig. 1) takes 4 min. Because of space constraints, here we will only depict two short extracts from the interview episode and try to present the results of our interpretation as transparently as possible. One of Sonja’s explanations is the following:

1 S: Well, this here (points at the first middle scaling bar) and the two little ones (points at the little scaling bars next to the middle one) this is twelve (Fig. 5).

Fig. 5
figure 5

Sonja points at twelve

Full size image

2 S: And this is four (points at the circled area around the scaling bars at the left) then these are six (moves in circles with the end of a pen around scaling bar 8 and 9) (Fig. 6).

Fig. 6
figure 6

Sonja points at six

Full size image

3 S: Then I just have to add the small one here (points at scaling bar 11) then these are seven, too (points roughly from scaling bar 1 to scaling bar 11). Then these are seven, too (Sonja in the pre-interview to the number line with arc) (Fig. 7).

Fig. 7
figure 7

Sonja points at seven

Full size image

By her gestures, Sonja locally focuses on discrete, single scaling bars (line 1; 2; 3). Firstly she taps on the first middle bar and the two proximate scaling bars and names them with “this is twelve” (line 1). Then she points at the circled area left of “twelve” and circuits around the two small scaling bars right of “twelve” (line 2). Again, she zooms in on single bars and “collects” them to six (Fig. 6) (line 2). Finally, Sonja taps on the short scaling bar next to the second long one (Fig. 7) and summarizes the encircled small bars to seven (line 3).

Another utterance in the same interview—approximately 3 min later—spotlights on Sonja’s underlying “interpretation foil” for her interpretation. The interviewer asks the question whether the small bars can be tens as well and Sonja answers:

4 S: No, that doesn’t work, because we learned it at school that the small bars are always ones, the middle ones fives or tens and the long bars are hundreds.

3.4 First interpretation

Sonja sums a middle bar (ten) and two short bars (two) to “twelve”. Then she adds four small bars left of “twelve”, together with three small bars to the right of it to “seven” (Fig. 1) (line 1; 2; 3). In this way, she identifies both summands on the problem card concretely on the number line. Further, she explains that small bars are “always” ones, the middle bars fives or tens and the long ones are hundreds (line 4). Here, Sonja expresses an individually generalized “interpretation rule” that one “always” has to follow. Hence, our interpretation is that to Sonja the single scaling bars have, according to their length, predetermined values—similar to Cuisenaire rods. Those “rods” can be collected and summed to several numbers.

3.5 Results of context and frame analysis

In this case we can see from Sonja’s utterances and her drawing that she focuses on the single scaling bars and the different length of the scaling bars. She seems to ignore the arc and she doesn’t comment on the first long scaling bar or the basic unit (Fig. 8).

Fig. 8
figure 8

Analysis grid for the pre-interview

Full size image

How does she use these elements? Sonja’s oral and gestural statements indicate that she interprets both in an object-oriented way: The single scaling bars seem to be concrete, material (Söbbeke 2005) strokes or “calculating bars” with fixed, inherent and unambiguous properties: the short bars mean “one”, the middle ones “five” or “ten” and the long ones “hundred” (line 4). Also, Sonja does not use the different length of the scaling bars to structure the diagram, but for her it yields explicit information about the bar’s value so that even this context element is interpreted in an object-oriented way (Fig. 8) (line 4). Even her gestures refer directly to discrete scaling bars or to a “bunch” of scaling bars, not to relations between those elements (line 1; 2; 3). In the same way she seems to count the strokes and not the distances between two strokes, which means the single units.

Which frame does Sonja adopt for interpreting the number line? First of all, the context analysis shows that, in this situation, Sonja does not interpret the number line diagram as a complex system of symbols. Rather, she reads it as a concrete material, empirical object with predetermined, unambiguous properties. Obviously, the young student does not focus on the relations between single context elements, but on the discrete context elements themselves. To her the number line seems to be a horizontal line with vertical lines of different lengths that can be collected and summed, like empirical objects in a “world of things”. We characterize Sonja’s individual situational framing with the term calculating-bar framing. Furthermore we classify it as an unambiguous object-oriented frame type.

During the ongoing interview, our interpretation is confirmed: Sonja is asked to comment on the other problem cards that she did not choose. She rejects the problem card “620 + 70” and “99 − 7” and argues:

Six hundred and twenty add seventy? That cannot fit, because therefore you need six long bars, because here it means six hundred. You don’t have so many big long bars here (Sonja touches all long scaling bars of the number line). (Sonja in the pre-interview to the number line with arc)

We see here that Sonja adopts an interpreting scheme that frames the structure on the diagram. Her interpretation is bound to the concrete empirical objects of the number line. Within this “calculating-bar framing”, Sonja cannot construe more complex structures into the number line. At this time, her frame avoids a structure-oriented and flexible interpretation. Modulating and expanding her interpreting scheme is an indispensable first step to developing a flexible, structure-based use with respect to the diagram’s epistemological nature.

The intervention in this study will enhance and initiate those modulation processes.

4 The intervention lessons

4.1 Background and implications

The intervention lessons were planned together with teachers from the primary school. In ten mathematics lessons of 45 min each, students of year three employed the hundred board and number line, commonly used visual aids. The aim was to introduce children into a special culture (Söbbeke 2005) of handling and speaking with visual diagrams, thereby enhancing visual structuring competence (Söbbeke 2005). As Söbbeke revealed in her study, young children do not learn to build abstract structures into visual diagrams merely by coping with them. In fact visual diagrams should be a topic on its own in the mathematics classroom (Söbbeke 2005, p. 23ff). Additionally, teachers have to be aware that the discursive context is crucial for the “effectiveness” of visual aids. Söbbeke writes:

Visual aids do not transmit “their message” by themselves, but they are a cultural occurrence, that unfolds its meaning only in interaction processes between teacher and learner. In this connection, a new “culture” of symbol use is established. This culture is not limited to looking at the media and fixing unique meanings, but stresses the symbolic use of visual aids in interaction. (Söbbeke 2005, p. 29, translated by the authors)

We emphasize clearly—based on an epistemological understanding of the theoretical ambiguity (Steinbring 1994) of visual aids (Sect. 2.1)—that we do not understand the intervention lessons as a kind of “training program” in which students simply learn how to use those visual representations “correctly”. We further do not think that teachers can directly show students how to use a diagram in a flexible way—there is no recipe teachers could resort to. Söbbeke’s results illustrate that such a simplistic view clearly ignores the complexity of learning processes with mathematical diagrams. Rather, teacher and students have to establish a common classroom culture in which young students like Sonja stand a chance of gaining a first understanding of the epistemological nature of visual aids (Söbbeke 2005, p. 373ff).

Moreover—based on the frame concept (Sect. 2.2)—we argue with Krummheuer (1984, 1992) that children can modulate or expand their frames through social interaction, thereby developing more and more differentiated interpreting schemes. Hence, during the lessons the teacher exploits the diagram’s theoretical ambiguity productively to provoke verbalization and exchange of different frames among the children. We think that the debates about different perspectives could initiate modulating processes that help children such as Sonja to develop rich and multilayered patterns of interpretation.

This approach aims at enriching children’s interpreting possibilities; however, it should not be misunderstood as “fostering arbitrariness”. Of course, there are conventions that have to be defined among students and teachers. But in the same way teachers should make clear that those determinations are temporally limited and not applied in the media itself (Söbbeke 2005, p. 375).

4.2 Example: an intervention lesson on the unlabelled number line

Over a period of 5 weeks a mathematics primary school teacher (Mrs. S.) with 6 years of teaching experience conducted twice a week two mathematics intervention lessons of 45 min each. Two third grade classes from two different German primary schools with a heterogeneous social status participated in the intervention. According to the mathematics teacher, both classes had worked with a labelled number line and with a hundred board before. The completely unlabelled number line was unfamiliar to all students in both classes.

The whole teaching unit included in the following order:

  • Three lessons on the topic “hundred board”

  • Two lessons on the topic “unlabelled number line without arc”

  • Two lessons on the topic “unlabelled number line with arc”

  • Three lessons with mixed tasks on both visual representations and a closing reflection about the learning progress

To provide an insight into the intervention tasks, a short example is given in Fig. 9. The example originates from the first lesson on the topic “unlabelled number line with arc”.

Fig. 9
figure 9

Task for the intervention lesson

Full size image

Similar to the interview, first of all Mrs. S. encouraged the students to think on their own of problems that fit well to the number line.

Additionally, Mrs. S. asked the children to explain their answers and to draw the problems into the scheme. In a next step, the teacher invited the students to compare their interpretations with their neighbours and to decide on one common number sentence that fits well.

The students presented the results of their work in a common discussion with the whole class. To the unlabelled number line in Fig. 9, there were numerous different number sentences: many children counted the number of strokes under the arc (“1 × 10 = 10”); some counted each single stroke from the beginning and interpreted the arc as an addition (“8 + 9 = 17”); several pupils wrote a subtraction (“15 − 9”); one pupil interpreted the single units as steps of hundred and wrote the number sentence “600 + 900 = 1,500”.

Mrs. S. started a discussion about the presented work:

  • What did your classmate mean by this number sentence?

  • Which problem fits exceptionally well from your point of view. Why?

  • Which problem doesn’t fit from your point of view? Why not?

The reflection was not about “right or wrong”, but picked up the different quality of the number sentences, concerning the varied references to the diagram’s structure. We want to stress once again that this approach was not planned as an “anything-goes” approach, but as a common development of reasonable agreements. Furthermore, the intervention aimed at enabling the experience of different interpretations being requested and allowed:

  • The arc can represent an addition or a subtraction.

  • The single units could be steps of one, steps of ten, steps of hundred or whatever.

  • The first long scaling bar does not have to be zero.

  • The different length of the scaling bars can be used to structure the diagram, so that one does not have to count each single line.

4.2.1 Sonja’s work during the lesson

The drawing in Fig. 10 shows Sonja’s product in this lesson. She worked together with her neighbour Julia and wrote the number sentence “23 − 10 = 13”. The two girls explained their interpretation, writing: “Because it just fits and we had sentences like that on the blackboard”.

Fig. 10
figure 10

Sonja’s work

Full size image

What did Sonja and Julia do here? The pupils wrote “23 − 10 = 13” on the work sheet, additionally “−10” above the arc, and encircled the strokes that are not under the arc. They also wrote “23” under the number line, left and right of the arc. Our interpretation is that the girls counted each single scaling bar (twenty-three total) and subtracted ten (the number of strokes under the arc). Although all intervention lessons were videotaped, we do not have information about how the two girls discussed and worked together. Hence, this production could illustrate the interpretation of just one girl, or it could show the result of a common consideration. Nevertheless, it is interesting to observe that some specifics of Sonja’s interpretation in the pre-interview seem to recur. First of all, the students count strokes rather than units. Also, they use the single scaling bars in an object-oriented way, because they count and collect the strokes as if they were empirical concrete objects in a “world of things”. Similar to the pre-interview, the two girls sort the strokes and encircle different groups.

However, compared with Sonja’s drawing in the pre-interview there are differences as well: now, each single scaling bar refers to “1”; their differing lengths are not relevant here. The arc is not ignored, but is a starting point for their interpretation. It seems as if it is used as some kind of “stroke-container”, which contains 10 scaling bars. Furthermore, the girls consider the whole diagram and not only a part of it as Sonja did in the pre-interview. All in all, the drawing in Fig. 10 indicates that Sonja seems to have developed new perspectives on the number line, based on her prior understanding.

5 The case of Sonja in the post-interview—extract from an interpretive context and frame analysis

5.1 Description of the situation

The following episode is taken from the post-interview after the intervention lessons took place. Sonja works on exactly the same task as in the pre-interview, but comes to a different solution and chooses “99 − 7/620 + 70” (Fig. 11). This is how she explains her drawing:

Fig. 11
figure 11

Sonja interprets the number line in the post-interview

Full size image

  • 1 S: Here is ninety-nine (writes 99 above the first short scaling bar) and here (points above the middle of the arc and shortly on the scaling bars under the arc) are the seven.

  • 2 I: Yes. And how do you know that here (points with the pen at the first short bar) it is ninety-nine?

  • 3 S: Because here could be the hundred (points imprecisely at the first long bar (…) and then this is ninety-nine (circuits the pen several times around the first short bar)

  • 4 I: Well, then there is just the other problem. Six hundred and twenty add seventy.

  • 5 S: Mmh. Here (moves the pen in circles around the first long bar) could be six hundred and twenty and (…) (moves the pen slowly along the number line towards the arc) here (forms an arc with the end of her pen under the scaling bars under the arc, shortly moves her pen across the bars under the arc) if these were steps of ten then seventy.

In the post-interview Sonja chooses two completely different problems. First she calls the first short bar “ninety-nine” and the bars under the arc “seven”. Being asked why, she explains her designation of “99” (line 1) by referring to the neighbouring next long bar that “could be the hundred” (line 3). Further, she localizes six hundred and twenty on the first long scaling bar and seventy under the arc “if these were steps of ten” (line 5).

5.2 First interpretation

In the post-interview, Sonja gives different names to the number line’s scaling bars. The first long bar for instance could be “a hundred” (line 3) or “six hundred and twenty” (line 5). Sonja uses the subjunctive (“could be hundred”, “could be six hundred and twenty”, “if these were steps of ten”) taking into account the diagram’s ambiguity. Her gestures—Sonja often points at or circuits around the beginning of the number line (line 1; 3; 5)—indicate that she focuses on the “beginning” of the number line as the diagram’s “starting point”. Further, she localizes the first summands “99” and “620” at the diagram’s left end (the beginning) and the second summand “7” or “seventy” under the arc (line 1; 5). Presumably, she refers here to seven strokes under the arc, because she briefly points to them and forms an arc under them (line 5). Her concept of “steps of ten” (line 5) remains unclear. Again, Sonja isolates the depicted numbers on the problem card and locates them concretely on the number line, thereby ignoring the additive or subtractive relationship between both summands. We interpret that to Sonja the number line is an ambiguous line with scaling bars one can “label” with different “ordinal numeral names”.

5.3 Results of context and frame analysis

Which context elements does Sonja use during this post-interview episode? As we can see from her statements, gestures and drawing, she uses the arc to “find” the second summands, besides the single scaling bars and the first long scaling bar to “find” the first summands. Sonja does not comment on the basic unit or on the different length of the scaling bars in this sequence (Fig. 12).

Fig. 12
figure 12

Analysis grid for the post-interview

Full size image

Moreover, again she interprets these context elements in an object-oriented way: Her statements indicate that she still uses the bars as if they were isolated empirical objects, which can be labelled with different “names”. Even the arc is not seen in relation to the problem, for instance as an addition or subtraction, but it is a kind of “stroke-container” which contains seven or seventy. Sonja’s use and interpretation of the context elements during this post-interview episode is illustrated in Fig. 12.

What can we say about Sonja’s adopted framing in this sequence? First of all, we reconstructed that Sonja modulated her “calculating-bar framing” during the intervention. The scaling bars are no longer similar to Cuisenaire rods with fixed values, but now they can be labelled with different names (line 1; 3; 5). Moreover, her use of the subjunctive (line 3; 5) shows that she takes into account the ambiguity of the scaling bars. Nevertheless, Sonja again interprets the scaling bars as isolated single material objects and takes them completely out of the system. Furthermore, she isolates the single numbers (99, 7, 620 and 70) from the problem card, ignoring the additive respectively subtractive relation and allocates these numbers in a direct way to concrete material context elements. Accordingly, these context elements (the first long or short scaling bar and the arc) are not related to each other at all. We call Sonja’s situational framing number-allocating framing. This framing can be classified as object-oriented type as well, but this time Sonja adopts an ambiguous object-oriented frame type.

6 Conclusion

Comparing the pre- and post-interview, we see that Sonja modulated her individual and situational “calculating-bar framing” to a “number-allocating framing”, hence we notice some individual progress. Nevertheless, compared with most of the other nineteen students she was not as successful and the improvement of her interpretation competence was marginal. Anyway, particularly the openness towards students’ individual, maybe “incorrect”, handling of mathematical diagrams revealed some extraordinary interpretations like Sonja’s.Footnote 4 Our hitherto existing analyses reveal that the case study of Sonja is a notable clear case disclosing the difference between an object-oriented and a relational interpretation. Therefore it is a valuable case study for developing the theoretical construct “frame-based interpreting competence”.

What did we learn from Sonja’s interpretations? Firstly, we observe that an underlying “interpretation foil”, learned in a common classroom culture, controls her visual structuring ability (Söbbeke 2005).

As said above, in both interviews the number line to Sonja is some kind of concrete empirical object with predetermined properties. Whereas during the pre-interview the single scaling bars had fixed unambiguous properties, during the post-interview Sonja takes their ambiguity into account. However, in both cases she interprets the context elements as concrete single objects, isolated from the other context elements. Here, we have to differentiate between an ambiguous object-oriented frame type in the post-interview and an unambiguous object-oriented frame type in the pre-interview.

Moreover, the qualitative comparison underlines the complexity of learning processes with visual diagrams: Sonja modulated her interpretations based on a pre-existing frame. Once again it is stressed that the “effect” of the intervention depends not only on the intervention tasks themselves. Rather, Sonja’s learning process arises from an individual sense-making interpretation background, too. As a matter of course the intervention does not “function” unequivocally as a kind of input/output mechanism. First results in this study show that different types of tasks, which challenge the students to re-interpretations, can initiate productive modulation processes during the intervention, as well as during the interview.

We further argue that in the mathematics classroom those “mechanisms” of meaning-making usually operate implicitly under the surface of what can be seen directly. The approaches of context and frame analysis presented in this paper serve as first elements of the analysis grid “fric” (frame-based interpreting competence) to lay open those individual interpreting processes under the surface.

Previous analyses revealed that each of the twenty students interprets the visual diagrams within a specific individual framing. Thus, all framings that are reconstructed until now differ in some detailed aspects. In a first approach, these specific individual framings can be categorized as object-oriented frame types and system-oriented frame types. Within the former frame, children use the context elements as if they were concrete empirical objects (as Sonja did in both interviews); within the latter, the child focuses on the relations between the context elements and interprets the diagram as a symbol system. The single context elements in this symbol system do not have a predetermined meaning on their own, but they gain their meaning solely through their relation to other elements in the diagram, as part of a system. To improve the construct “fric”, these frame types will be complemented and elaborated more explicitly by further detailed analyses.