Minimum Halloysite Length for Efficient Load Transfer Through the Interphase of Polymer Nanocomposites in Biomedical Applications

Abstract

“L_c” as a compulsory length of halloysite nanotubes (HNTs) that leads to efficient load transfer through the interphase zone is correlated to the interphase characteristics according to the predictions made by linking the Pukanszky model and the proposed model for determining the strength of nanocomposites. The proposed model assumes effective levels of interphase depth and filler concentration. The predictabilities of the model are demonstrated by comparing the prediction results to experimental data, and it is found that the effects of all factors on “L_c” and nanocomposite strength are justified. The maximum value of “L_c” is 1504 nm in the absence of the interphase zone, but “L_c” decreases to 1378 nm when the interphase depth is 20 nm. Similarly, the maximum value of “L_c” is 1520 nm when the interphase strength is 100 MPa, but it decreases to 1405 nm when the interphase strength is 1000 MPa. Hence, the interphase depth and strength adversely affect the value of “L_c.” The interphase depth of 20 nm substantially increases the system strength by 40%. Moreover, the composite strength improves by 21% when the interphase strength is 1000 MPa. Therefore, the interphase depth and strength directly govern the strength of nanocomposites.

Introduction

Polymer nanocomposites comprising various types of inorganic nanofillers have attracted considerable attention from researchers in recent decades owing to their excellent performance.^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30} As inorganic nanoparticles, nano-tubular halloysite nanotubes (HNTs) are natural fillers.^31,32 HNTs do not require exfoliation because of their hydrophobic nature and the presence of few inter-tubular contacts.^33,34 They offer high strength, considerable ductility, and low weight, and they can be used as catalysts, bioreactors, capsules, and reinforcements.^{32,35,36,37,38} The siloxane and a few hydroxyl groups on the surface of HNTs ease their dispersion in polymer media.³⁹ These attractive features have persuaded researchers to improve the characteristics of polymer media by using HNTs.^40,41,42 Prashantha et al.⁴¹ combined modified and neat HNTs with polypropylene. They found that the samples containing modified HNTs had superior properties compared to those of the samples containing neat HNTs. Moreover, HNTs can enhance the crystallinity of polyamide-11 system, thereby improving its mechanical properties.⁴² Generally, the studies in the literature have largely focused on experimental characterizations of HNT-modified polymer media samples, and modeling-related views have been overlooked.

An interphase is commonly formed in polymer nanocomposites,^43,44,45,46 but it is mostly imperfect in nanocomposites because of defects in interfacial contacts between the polymer matrix and the nanofillers.^47,48 The defective interphase partially transmits tension from the polymer medium to the nanofillers, which diminishes performance. Therefore, an incomplete interphase is inadequate for bearing the stress. Stress transmission through the interphase has a significant effect on the rigidity of nanocomposites. A weak interphase induces debonding, whereas a hard interphase serves as a strong reinforcement. The studies published thus far have seldom described the effects of a defective interphase on the mechanics of the tested samples. “L_c” is considered as the compulsory nanofiller length for the efficient load shifting in nanocomposites.^48,49,50 When the filler length exceeds “L_c,” stress transfer is efficient, and the samples are reinforced. By contrast, when “L_c” is greater than the filler length, the stress transfer is poor, and the sample is not strengthened adequately. Therefore, “L_c” has a significant effect on the operative aspects of the nanoparticles and interphase section in a system. The existing models have usually ignored the effects of an imperfect interphase and “L_c” on the stiffness of nanocomposites.

Pukanszky model⁵¹ reflects the effects of filler volume fraction and interfacial bonding on the tensile/yield strength of various types of samples.^49,50,52 Because Pukanszky model is applicable and easy-handling, it can be used to analyze a multitude of samples. This model considers “B” as an interfacial factor to demonstrate the stress-shifting capability of the interphase zone. “B” is defined by the properties of the interphase zone in a given system. As mentioned, in terms of efficient stress transfer, “L_c” is related to the interphase potential. Both “L_c” and “B” represent the magnitudes of interfacial interaction and stress transfer in nanocomposites. However, “L_c” is correlated to filler properties and interfacial shear strength,⁵⁰ but the effects of the depth and strength of the interphase zone on “L_c” were neglected in previous studies. An equation for “L_c” that links it to interphase properties can help researchers to find the effective factors for realizing the maximum stress transfer through the interphase zone.

In this work, “L_c” is correlated to the interphase characteristics by combining the developed Pukanszky and novel approaches for modeling the strength of HNT-filled systems. Both the advanced Pukanszky model and the novel approaches assume an incomplete interphase based on the effective levels of interphase depth and filler concentration. “L_c” is linked to HNT size, interphase depth, and interphase strength. The predictabilities of both models are confirmed by using the tentative strength data obtained from numerous examples. Furthermore, the effects of all issues on “L_c” and strength are explained. The equations suggested in this study are useful for identifying the efficient factors for handling the stress transfer through the interphase zone and improving the strength of HNT-based nanocomposites.

Equations

Pukanszky model assumes an interfacial parameter including the thickness and strength of interphase in nanocomposites. Pukanszky⁵¹ formulated the following equation for determining the tensile strength of nanocomposites:

$$ \sigma_{{\text{R}}} = \left( {\frac{{1 - \phi_{{\text{f}}} }}{{1 + 2.5\phi_{{\text{f}}} }}} \right)\exp (B\phi_{{\text{f}}} ) $$

(1)

where “σ_R” is the ratio of system strength to polymer strength. “$\phi_{{\text{f}}}$” is filler volume fraction, and “B” represents the stress-transfer capability of the interphase.

“B” is associated with the depth and strength of the interphase as:

$$ B = (1 + A_{{\text{c}}} d_{{\text{f}}} t)\ln \left( {\frac{{\sigma_{{\text{i}}} }}{{\sigma_{{\text{m}}} }}} \right) $$

(2)

where “A_c” and “d_f” denote the specific surface zone of particles and filler density, respectively. “σ_m” is the strength of polymer matrix, and “t” and “σ_i” denote the depth and strength of the interphase section, respectively. Therefore, “B” assumes the properties of filler and interphase section.

The value of “A_c” for nanocomposites comprising well-dispersed HNTs is expressed as follows:

$$ A_{{\text{c}}} = \frac{A}{m} = \frac{2\pi Rl}{{d_{{\text{f}}} \pi R^{2} l}} = \frac{2}{{d_{{\text{f}}} R}} $$

(3)

where “m” and “A” denote the mass and surface area of HNTs, respectively. Similarly, “R” and “l” denote the radius and length of nanotubes, respectively. By replacing “A_c” from Eq. 3 into Eq. 2, “B” is expressed as follows:

$$ B = \left( {1 + \frac{2t}{R}} \right)\ln \left( {\frac{{\sigma_{{\text{i}}} }}{{\sigma_{{\text{m}}} }}} \right) $$

(4)

which is a simple equation to analyze the extent of interfacial bonding in nanocomposites.

In Refs. 48 and 50 “L_c” as the compulsory length of nanofillers for actual tension transfer through the interphase zone was defined as:

$$ L_{{\text{c}}} = \frac{{\sigma_{{\text{f}}} R}}{\tau } $$

(5)

where “σ_f” denotes filler strength, and “τ” is interfacial shear strength.

The stress-transfer capability of the interphase is related to “L_c,” which handles the operative interphase depth as follows:

$$ t_{{{\text{eff1}}}} = t\left( {\frac{{L_{{\text{c}}} }}{l}} \right)\,\,\,l < \, L_{{\text{c}}} $$

(6)

$$ t_{{{\text{eff2}}}} = t\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\,\,\,l > \, L_{{\text{c}}} $$

(7)

The total operative interphase depth obtained using Eqs. 6 and 7 is:

$$ t_{{{\text{eff}}}} = \left( {\frac{{L_{{\text{c}}} }}{l}} \right)t\left( {\frac{{L_{{\text{c}}} }}{l}} \right) + \left( {\frac{{l - L_{{\text{c}}} }}{l}} \right)t\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right) $$

(8)

The complete share of interphase volume in a sample composed of cylindrical particles is expressed as:⁵³

$$ \phi_{{\text{i}}} = \left[ {\left( {1 + \frac{t}{R}} \right)^{2} - 1} \right]\phi_{{\text{f}}} $$

(9)

Both the nanoparticles and the adjoining interphase section simultaneously reinforce the system. The operative filler concentration accounts for the HNTs and the interphase zone as follows:

$$ \phi_{{{\text{eff}}}} = \phi_{{\text{i}}} + \phi_{{\text{f}}} = \left( {1 + \frac{t}{R}} \right)^{2} \phi_{{\text{f}}} $$

(10)

When “t_eff” from Eq. 8 is substituted in Eq. 10, the operative volume portion of HNTs is calculated as follows:

$$ \phi_{{{\text{eff}}}} = \left( {1 + \frac{{\left( {\frac{{L_{{\text{c}}} }}{l}} \right)t\left( {\frac{{L_{{\text{c}}} }}{l}} \right) + \left( {\frac{{l - L_{{\text{c}}} }}{l}} \right)t\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)}}{R}} \right)^{2} \phi_{{\text{f}}} $$

(11)

which indicates the important influence of “L_c” on the operative filler concentration.

The assumption of “$\phi_{{{\text{eff}}}}$” (Eq. 11) expands the Pukanszky model as follows (Eq. 1):

$$ \sigma_{{\text{R}}} = \left( {\frac{{1 - \phi_{{{\text{eff}}}} }}{{1 + 2.5\phi_{{{\text{eff}}}} }}} \right)\exp (B\phi_{{{\text{eff}}}} ) $$

(12)

considering the effect of “L_c” on strength. The applicability of this model to determine the strength of polymer HNT samples is explained in the following section.

Several models have considered the interphase in determining the strength of a nanocomposite,^54,55 but they ignored “L_c.” In this study, the authors attempt to recommend a valid model for determining the strength of a system by assuming an incomplete interphase and “L_c.”

The strength of a system is linked to “L_c”,⁵⁰ “α”,⁴⁹ and “$\phi_{{\text{f}}}$”⁵⁶ as follows:

$$ \sigma_{{\text{R}}} \approx 1 + \left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{\text{f}}} $$

(13)

where “α” is filler aspect ratio (l/2R). In the absence of nanofillers ($\phi_{{\text{f}}}$ = 0), the relative strength of 1 can rationally be predicted as the polymer strength.

“$\phi_{{{\text{eff}}}}$” (Eq. 11) assumes that the interphase section is operative on the strength of nanocomposites. Therefore, Eq. 13 is expressed as follows:

$$ \sigma_{{\text{R}}} = 1 + 4\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{{\text{eff}}}} $$

(14)

which reflects the effects of HNT features, interphase depth, and “L_c” on the strength of the system. The predictability of this model for the strength of HNT samples is described in the following section.

Now, the models in Eqs. 12 and 14 are combined to correlate “L_c” to the interphase characteristics by assuming an inadequate interphase in nanocomposites.

The developed Pukanszky model (Eq. 12) is rearranged as follows:

$$ \ln \left( {\sigma_{{\text{R}}} \frac{{1 + 2.5\phi_{{{\text{eff}}}} }}{{1 - \phi_{{{\text{eff}}}} }}} \right) = B\phi_{{{\text{eff}}}} $$

(15)

which is rewritten as:

$$ \ln (\sigma_{{\text{R}}} ) + \ln \left( {\frac{{1 + 2.5\phi_{{{\text{eff}}}} }}{{1 - \phi_{{{\text{eff}}}} }}} \right) = B\phi_{{{\text{eff}}}} $$

(16)

Substituting “σ_R” from Eq. 14 into Eq. 16 yields the following expression:

$$ \ln \left[ {1 + 4\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{{\text{eff}}}} } \right] + \ln \left( {\frac{{1 + 2.5\phi_{{{\text{eff}}}} }}{{1 - \phi_{{{\text{eff}}}} }}} \right) = B\phi_{{{\text{eff}}}} $$

(17)

When “$\phi_{{{\text{eff}}}}$” is extremely small ($\phi_{{{\text{eff}}}} \ll 1$), it is estimated that

$$ \ln \left[ {1 + 4\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{{\text{eff}}}} } \right] \cong 2\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{{\text{eff}}}} $$

(18)

$$ \ln \left( {\frac{{1 + 2.5\phi_{{{\text{eff}}}} }}{{1 - \phi_{{{\text{eff}}}} }}} \right) \cong 3.4\phi_{{{\text{eff}}}} $$

(19)

which simplifies Eq. 17 as follows:

$$ 2\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha \phi_{{{\text{eff}}}} + 3.4\phi_{{{\text{eff}}}} = B\phi_{{{\text{eff}}}} $$

(20)

When “B” is expressed as

$$ B = 2\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha + 3.4 $$

(21)

which correlates “B” to “L_c” through a simple equation.

By substituting “B” from Eq. 4 into Eq. 21, one obtains the following:

$$ \left( {1 + \frac{2t}{R}} \right)\ln \left( {\frac{{\sigma_{{\text{i}}} }}{{\sigma_{{\text{m}}} }}} \right) = 2\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)\alpha + 3.4 $$

(22)

which can be reorganized to define “L_c” as follows:

$$ L_{{\text{c}}} = l - R\left( {1 + \frac{2t}{R}} \right)\ln \left( {\frac{{\sigma_{{\text{i}}} }}{{\sigma_{{\text{m}}} }}} \right) + 3.4R $$

(23)

which correlates “L_c” to filler features and interphase characteristics. Actually, Eq. 23 provides a simple association between “L_c” and meaningful aspects of HNTs, and the interphase zone.

“L_c” from Eq. 23 is used to calculate the operative interphase depth (Eq. 8) and operative filler concentration (Eq. 11).

Both “$\phi_{{{\text{eff}}}}$” (Eq. 11) and “L_c” (Eq. 23) progress the advanced model (Eq. 14) for the strength of nanocomposites as:

$$ \sigma_{{\text{R}}} = 1 + 4\left[ {1 - \frac{{l - R\left( {1 + \frac{2t}{R}} \right)\ln \left( {\frac{{\sigma_{{\text{i}}} }}{{\sigma_{{\text{m}}} }}} \right) + 3.4R}}{l}} \right]\alpha \phi_{{\text{f}}} \left[ {1 + \frac{{\left( {\frac{{L_{{\text{c}}} }}{l}} \right)t\left( {\frac{{L_{{\text{c}}} }}{l}} \right) + \left( {\frac{{l - L_{{\text{c}}} }}{l}} \right)t\left( {1 - \frac{{L_{{\text{c}}} }}{l}} \right)}}{R}} \right]^{2} $$

(24)

when “L_c” (Eq. 23) is substituted in the last equation, the proposed model uses the extent and concentration of HNTs and depth and strength of the interphase to approximate system strength. All the equations presented in this paper were developed for nanocomposites containing cylindrical nanofillers such as HNTs and CNTs. These equations cannot be applied to other types of nanocomposites.

Results and Discussion

Validation of Models by Measured Details

The measured levels of several HNT-based composites were used to validate the ca L_c ulations of the proposed models (Eqs. 12 and 24). Table I displays the samples comprising several types of matrixes and HNTs. The matrix and filler extent data were approximated from their sources. They were used in the advanced Pukanszky model (Eq. 12) to guesstimate “σ_R.” Fig. 1 shows the tentative and forecasted data of “σ_R” obtained using the developed Pukanszky model for the systems considered in this study. All predictions correctly fit the experimental data. This reveals the exactness of the proposed Pukanszky model for determining the strength of a system by supposing the efficient aspects of an imperfect interphase. The values of “B” were obtained using Eq. 12 as 5.4, 8.5, 22, and 9.5 for PA12, cellulose, poly (l-lactic acid) (PLLA), and starch samples, respectively. These data express the dissimilar levels of interfacial communications among the polymer media and HNT in these samples, which yield various extents of stress transfer and reinforcement.

Table I Studied HNT samples and their features

Fig. 1

Tentative and predicted facts of “σ_R” by using the modified Pukanszky model (Eq. 12) for (a) PA12,⁵⁷ (b) cellulose,⁵⁸ (c) PLLA,⁵⁹ and (d) starch⁶⁰ specimens containing HNTs.

Figure 2 depicts the tentative facts and outputs of “σ_R” obtained using the proposed model (Eq. 24). All estimates are consistent with the experimental values at various levels of filler content. This indicates that the proposed model accurately calculates the strength of the samples by assuming the creation of an imperfect interphase. Therefore, the tentative facts of many samples confirm the predictabilities of both the proposed equations that account for the efficient interphase characteristics. By properly fitting the model-calculated values to the measured data, the models can be used to determine the properties of the interphase section and the value of “L_c.”

Fig. 2

Experimental values of relative strength and model productions (Eq. 24) for (a) PA12,⁵⁷ (b) cellulose,⁵⁸ (c) PLLA,⁵⁹ and (d) starch⁶⁰ HNT nanocomposites.

Table I summarizes the interfacial data estimated using the proposed models. The calculated values of “σ_i” ranged from 600 MPa to 750 MPa, which were judicious, because they alter among the strengths of HNT and polymer medium. The interphase depth (t) values ranged from 12 nm to 19 nm for these samples. The deepest and slimmest interphases were detected in the starch and PA12 samples, respectively. These results, too, are logical because they are at the nanoscale.

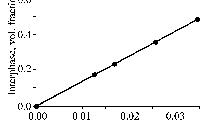
“L_c” is calculated as 860.8 nm–1920 nm by using Eq. 23. The smallest and the largest values of “L_c” were obtained for the PLLA and cellulose samples, respectively. All values of “L_c” were smaller than the HNT length, indicating an efficient interphase and operative stress transfer leading to strengthening. In addition, the effective interphase depth was calculated as 10.7–15.5 nm. These values are lower than the interphase depth, thus revealing the major influence of “L_c” on the efficiency of the interphase section. The reasonable interfacial/interphase properties of the samples demonstrate the correctness of the proposed models.

Analyses of Factors

The impacts of all factors on “L_c” (Eq. 23) and relative strength (Eq. 24) were justified to support the proposed equations. The plots linking “L_c” and relative strength to a factor in the typical ranges of the other parameters as R = 30 nm, σ_m = 20 MPa,$\phi_{{\text{f}}}$ = 0.02, l = 1500 nm, t = 10 nm, and σ_i = 500 MPa. These schemes indicate the trends between the outputs and the factors determining the desirable magnitudes of stress transfer and strengthening in the nanocomposites.

Figure 3a shows the influence of “R” on “L_c” according to Eq. 23. R = 20 nm minimizes “L_c” to 1439.2 nm, but “L_c” increases with the addition of HNT radius and reaches 1446.5 nm at R = 60 nm. Hence, filler radius directly governs “L_c,” and denser HNT lead to a higher “L_c.” These results indicate that thinner HNTs can optimize “L_c.” This connection is linear; thus, denser HNTs usually cause “L_c” to increase. The link between “L_c” and HNT radius is reasonable because denser HNTs limit the interphase section and interfacial communication. The interphase area is shortened when thicker HNTs are used (Eq. 9), and thicker HNT cannot produce strong connections with polymer matrixes. Consequently, one can expect to observe poor stress transfer and weak interfacial interaction when using thick HNTs that increase “L_c.” By contrast, narrow HNTs expand the interphase section and intensify interfacial linking with polymer chains. It was reported that tiny nanoparticles create the nano-effect in polymer nanocomposites.⁶¹ Accordingly, narrow HNTs are desirable for strengthening the interphase section to ensure efficient stress transfer because they reduce “L_c.” Based on this explanation, HNT radius directly affects “L_c,” thus validating the proposed equation.

Fig. 3

Correlations of (a) “L_c” and (b) relative strength to HNT radius using the advanced equations.

Figure 3b shows the dissimilarity of “σ_R” for various HNT radii, as determined using Eq. 24. The maximum “σ_R” of 1.26 was obtained for the HNT radius of 20 nm, but “σ_R” decreased when the HNT radius was increased, and its minimum value was 1.05 nm for the HNT radius of 60 nm. Narrow HNTs led to massive strengthening in the samples, whereas thick HNTs led to a poor reinforcing effect. This relation was nonlinear, and the strength of the samples was constant at extremely high HNT radii (R > 50 nm). Nevertheless, the nanocomposite strength decreased quickly as the HNT radius increased from 20 to 50 nm. The optimized strength level was obtained when using narrow HNTs.

Slim HNTs enlarge the interphase section in nanocomposites and promote strengthening because a thick interphase translates into massive strength gains owing to the strong reinforcing effect of the interphase section.^62,63,64,65 Indeed, slim HNTs enhance the stress transfer capability of the interphase because they decrease “L_c” and increase the operative interphase depth (Eq. 8). Accordingly, one can expect to obtain a sturdier sample by using thinner HNTs. Conversely, dense HNTs lead to the formation of a small interphase zone, which diminishes the stress transfer capability and the reinforcement efficacy of the interphase. Thick HNTs increase “L_c,” which decreases the efficient magnitudes of interphase depth and filler concentration. Owing to the undesirable effects of thick HNTs on stress transfer capability and strengthening of the interphase, dense HNT diminish the system strength. This observation confirms the predictableness of the proposed model.

Figure 4a depicts the calculation of “L_c” for a range of interphase depths by using Eq. 23. The maximum “L_c” is 1504 nm in the absence of the interphase zone, but “L_c” decreases to 1378 nm when the interphase depth is 20 nm. “L_c” is shortened by a deeper interphase, and the interphase depth adversely manipulates the value of “L_c.” This correlation is linear, and a deeper interphase typically causes “L_c” to decrease. It is essential to increase the interphase depth to limit “L_c” to a small value. A shorter interphase depth implies poor interfacial bonding in the samples, which reduces their stress transfer capability. In this context, a higher “L_c” expectedly implies a weak interphase in the system. Nevertheless, a deeper interphase reveals the formation of a robust interphase and strong interfacial connections, which improve the stress transfer capability. Because “L_c” is inversely correlated to the stress transfer capability of the interphase, a denser interphase yields a shorter “L_c.” Consequently, “L_c” is adversely related to the interphase depth, verifying the estimates obtained using the proposed equations.

Fig. 4

Data of (a) “L_c” (Eq. 23) and (b) “σ_R” (Eq. 24) for several interphase depths.

Figure 4b depicts the predictions obtained using the proposed model (Eq. 24) for several interphase depths. The relative strength is 1 in the absence of the interphase, while it increases to 1.4 when t = 20 nm. Accordingly, the interphase depth directly affects the system strength, and a thicker interphase leads to greater strengthening. The strength of the samples recovers slowly when the interphase depth is low (< 10 nm), but the relative strength increases considerably when the interphase depth exceeds 10 nm. The nanocomposite strength improves by 40% at the interphase depth of 20 nm, demonstrating the key effect of interphase depth on strengthening.

A thin interphase marginally strengthens the nanocomposites because it cannot generate a large reinforcing phase in the system. Moreover, a narrow interphase weakens the efficacy of the interphase for strengthening. A narrow interphase leads to a large “L_c,” which is indicative of an interphase with poor stress-bearing capability. By contrast, a deep interphase enhances the reinforcing effect because it expands the interphase section, which is responsible for strengthening. Moreover, a deep interphase reduces “L_c” and provides a desirable condition for stress transfer, which increases strengthening. A deep interphase has a beneficial role in terms of reinforcing nanocomposites.^66,67,68 Notably, a thick interphase increases the reinforcement efficacy. Thus, the proposed model correctly relates relative strength to interphase depth.

Figure 5a plots the effect of interphase strength on “L_c” according to Eq. 23. The maximum value of “L_c” was 1520 nm at the interphase strength of 100 MPa, but as the interphase strength increased to 1000 MPa, “L_c” decreased to 1405 nm. These results indicate an inverse relationship between “L_c” and interphase strength, where a tougher interphase yields a lower “L_c” value. The low “L_c” values sharply changed the “L_c,” but the high interphase strength values led to a gradual change in “L_c.” Extremely high values of interphase strength led to a constant “L_c.” It is necessary to create a strong interphase for reducing “L_c.” A poor interphase is indicative of weak interfacial links between the polymer medium and the nanofiller, which degrades stress transfer. Moreover, a deprived interphase diminishes the stress-bearing capability of the interfacial region. Therefore, a weak interphase increases “L_c,” which represents inefficient stress transfer. By contrast, a tough interphase can tolerate and transfer a large amount of stress owing to robust interfacial bonding. A stronger interphase leads to a smaller “L_c” because of its enhanced stress transfer efficiency. Therefore, there is an inverse correlation between “L_c” and interphase strength, which validates the proposed equation.

Fig. 5

Dependencies of (a) “L_c” and (b) “σ_R” on the interphase strength according to the proposed equations.

Figure 5b depicts the effect of interphase strength on “σ_R” according to the proposed model. “σ_R” is 0.95 at the interphase strength of 100 MPa, while “σ_R” increases to 1.21 at the interphase strength of 1000 MPa. These records reveal the positive role of interphase strength on the strength of materials. A tougher interphase leads to a stronger system, while a weaker interphase deteriorates the strength of nanocomposites. Relative strength increases considerably as the interphase strength develops from 100 to 600 MPa, but any further increase in the interphase strength only marginally increases the system strength, and the relative strength becomes constant at extremely high values of interphase strength.

A weak interphase negatively affects the strength of nanocomposites because it cannot endure stress and weakens the system. Moreover, a weak interphase reduces the reinforcement efficiency because it cannot facilitate efficient stress transfer. Generally, the system strength is directly correlated to the interphase strength.^69,70,71 Therefore, one can expect that a nanocomposite with a weak interphase will be weak overall. By contrast, a tough interphase increases the system strength considerably because it is adequately sturdy to bear and transfer tension from the polymer host to the nanoparticles. A robust interphase improves the system strength because the interphase is a component of the entire nanocomposite, and its strength directly governs the strength of the entire nanocomposite system. Accordingly, the strength of the samples is directly associated with the interphase strength, which is consistent with the model ca L_c ulations.

Figure 6a shows the relationship between “L_c” and HNT length according to the proposed equation. The smallest HNT length of 1000 nm led to the smallest “L_c” of 1000 nm. Moreover, “L_c” increased as the HNT length increased, and its value reached 3000 nm when the HNT length was 3000 nm. There was a direct relationship between “L_c” and HNT length, and a higher HNT length led to an increase in “L_c.” This link was linear, and the longer HNTs permanently increased “L_c.” According to Eq. 23, “L_c” is directly correlated to HNT length, and larger HNT yielded higher “L_c” values. This relationship is logical because “L_c” is a component of HNT length, and it increases with HNT length. Consequently, “L_c” increased as the HNT length increased, which is consistent with the calculation results obtained using the proposed equation. By contrast, “L_c” clearly decreased when the HNT length decreased because “L_c” represents the compulsory HNT length required for facilitating operative stress transfer. This description confirmed the predictability of the proposed equation for “L_c.”

Fig. 6

Influences of HNT length on (a) “L_c” and (b) relative strength according to the proposed equations.

Figure 6b depicts the disparity in “σ_R” by HNT length according to the proposed model. When the HNT length is 1000 nm, the relative strength is 1.132, but “σ_R” improves as the HNT length increases and reaches 1.137 for the HNT length of 3000 nm. This plot establishes a direct link between sample strength and HNT length, but HNT length has a minor effect on system strength. The longer HNTs (l > 2500 nm) change the relative strength only marginally, and excessively long HNTs have no effect on nanocomposite strength.

Long HNTs have a high aspect ratio, which increases the relative strength (Eq. 24). However, long HNTs increase “L_c” (Fig. 6a), which has detrimental effects on the efficiencies of the interphase section (Eq. 8) and nanoparticles (Eq. 11) in the samples. A high “L_c” resulting from long HNTs deteriorates the interphase efficacy in terms of stress bearing/transfer. Therefore, long HNTs prevent strengthening in nanocomposites, although they increase the aspect ratio. Conversely, short HNTs lead to a small “L_c,” which increases the effectiveness of the interphase zone and nanoparticles in terms of reinforcement. However, the low aspect ratio due to short HNTs weakens the strengthening efficiency of the system according to Eq. 24. Accordingly, the relationship between strength and HNT length is acceptable, which validates the predictions made using the proposed model.

Figure 7a shows the predictions of the proposed model (Eq. 24) for several levels of “L_c.” The relative strength is 1.93 when L_c is 1000 nm, whereas the relative strength is at the minimum value of 1 when L_c 1500 nm. These results suggest an inverse relationship between nanocomposite strength and “L_c,” indicating that a low “L_c” is desirable for enhancing the system strength. This relationship is relatively linear, and a higher “L_c” commonly leads to a poorer sample. The system strength can be improved by 93% at the “L_c” value of 1000 nm, which indicates the significant effect of a small “L_c” on system strength. Therefore, the optimum nanocomposite strength is achieved in the minimum “L_c” range.

Fig. 7

Relative strength predicted using Eq. 24 as a function of (a) “L_c” and (b) HNT volume fraction.

A short “L_c” increases the effectiveness of the interphase section according to Eq. 8. An efficient interphase leads to a high effective filler concentration (Eq. 11), which increases the sample strength. Generally, a short “L_c” is indicative of the formation of a strong interphase in the system, which is desirable for stress transfer.^49,50 Therefore, a small “L_c” improves the strengthening capability of the interphase zone. Nevertheless, a large “L_c” degrades the reinforcement ability of the interphase section and the HNTs because the efficient interphase depth and operative filler concentration decrease when the “L_c” value is large. Normally, the stress handling of the interphase section decreases when “L_c” increases because poor interfacial communication reduces the system strength. This reveals that the proposed model accurately connects system strength to “L_c.”

Figure 7b depicts the effect of HNT concentration on “σ_R” according to the proposed model. “σ_R” is 1 in the absence of HNTs, which is correct, because this value represents the strength of the polymer medium. However, the system strength increases to 1.27 when the filler volume fraction is 0.04. A higher number of particles leads to a stronger sample, but a small number of HNTs improves the system strength only marginally. This relationship is linear, and a higher amount of filler permanently increases the relative system strength. These results indicate that the sample strength is at its optimum level when the HNT content is higher.

HNTs offer excellent levels of strength and stiffness,⁷² and their strength is more significant than those of polymer media. The excellent strength of HNTs strengthens the polymer matrixes in nanocomposites because the stiff HNTs bear stress and withstand deformation. Notably, a higher amount of HNTs enhances the stiff phase in the samples, thus providing better strengthening, while a low amount of fillers weakens the reinforcement phase, thus deteriorating the strengthening efficiency. A higher HNT concentration can enlarge the interphase section according to Eq. 9. Consequently, HNT content manipulates the strengthening efficiencies of nanoparticles and the surrounding interphase in nanocomposites. A higher HNT content increases the magnitudes of reinforcement provided by nanoparticles and the interphase zone, while a low HNT content weakens the strengthening efficiencies of these phases in a sample. Consequently, HNT concentration directly influences the reinforcement efficiency, which validates the prediction power of the proposed model.

Conclusion

“L_c” was linked to interphase characteristics by using the Pukanszky model and a novel model for the strength of HNT systems that assumes an incomplete interphase section. The predictions of both models fit acceptably to the experimentally determined strengths of various samples. Denser HNTs led to a higher “L_c” value, but HNT radius had a minor effect on “L_c.” The maximum “σ_R” of 1.26 was obtained when the HNT radius was 20 nm, although “σ_R” decreased to 1.05 as the HNT radius increased to 60 nm. Accordingly, narrow HNTs led to massive strengthening in the samples. “L_c” was shortened by a deeper interphase, but the deeper interphase yielded a tougher sample (maximum increase of 40% was obtained with the interphase depth of 20 nm). The tougher interphase decreased “L_c” and produced a stronger nanocomposite, and “σ_R” increased to 1.21 when the interphase strength was 1000 MPa. There was a direct relationship between “L_c” and HNT length, and larger nanotubes led to harder samples. Nonetheless, HNT length had a negligible effect on the strength of the nanocomposites. “σ_R” was 1.93 when L_c was 1000 nm, whereas the relative strength was at the minimum value of 1 when L_c was 1500 nm. These results demonstrate that a low “L_c” is desirable for increasing the system strength. Among the parameters, extremely high levels of interphase strength did not lead to any change in “L_c,” but nanocomposite strength was found to be relatively constant at extremely high magnitudes of HNT radius, interphase strength, and HNT length.