Laser Additive Melting and Solidification of Inconel 718: Finite Element Simulation and Experiment

Abstract

The field of powdered metal additive manufacturing is experiencing a surge in public interest finding uses in aerospace, defense, and biomedical industries. The relative youth of the technology coupled with public interest makes the field a vibrant research topic. The authors have expanded upon previously published finite element models used to analyze the processing of novel engineering materials through the use of laser- and electron beam-based additive manufacturing. In this work, the authors present a model for simulating fabrication of Inconel 718 using laser melting processes. Thermal transport phenomena and melt pool geometries are discussed and validation against experimental findings is presented. After comparing experimental and simulation results, the authors present two correction correlations to transform the modeling results into meaningful predictions of actual laser melting melt pool geometries in Inconel 718.

Introduction

The field of additive manufacturing and rapid prototyping is a relatively young technology first explored in the 1970s using fused deposition in plastic.1 The technology is significantly beneficial to the design process because it allows for single stream three dimensional (3D) model to prototype conversion, taking hours instead of days to create a physical realization of the design. It has further opened the mechanical design space by allowing developers to create complex geometries and internal features not feasible or cost effective through traditional, subtractive, manufacturing methods. From the potential seen in plastic additive techniques, methods were developed to fabricate metallic parts additively. Extrusion and deposition methodologies are presented in the literature,2–4 but in macro-scale manufacturing environments, opposed to micro- and nano-manufacturing environments, the focus has been on powder bed technologies. These technologies are most simply broken into two categories: laser-based and electron beam-based. The laser-based category includes such technology as selective laser sintering (SLS) and melting (SLM) and direct metal laser sintering (DMLS), while electron beam melting (EBM) is the major player in the electron beam-based category. A distinguishing factor in this characterization is the heating source melting the metallic powders within the powder bed. Another important factor to consider is heating of the base plate. Both laser and EBM methods can make use of a heated base plate, but the technology is generally seen in EBM and is absent in SLS and SLM. The scope of the work presented here will include only the laser-based process without a heated base plate.

Discounting subtleties in the interaction between different source beams and the metallic powder, the powder bed process can be considered using a common physical model, regardless of heating source. Figure 1 portrays the heat transfer model that is used to develop the finite element model presented in this work. Heat is generated within the powder bed under the beam spot of the source beam. The amount of heat delivered to the powder is governed by the optical properties of the beam and the absorbance properties of the individual powder particles within the bed. After heat is delivered to the powder bed, various heat transfer modes work to neutralize the thermal gradients created by the heat generation and bring the model into thermal equilibrium. It is important to consider the transport, not only through the powder layer but also through previously built layers and into the build base plate to consider the effects of thermal cycling within previously built layers and the effectiveness of the base plate as a heat sink for the process.

Fig. 1

Thermal transport phenomena within model

In developing a physically consistent and accurate model of the powder bed additive manufacturing process, thermal transport phenomena at both the bulk scale and the individual powder particle scale must be considered. On the bulk scale, in laser-based processes, radiative and convective cooling of the powder bed surface are possible but have negligible effects compared to conduction into the solid and build plate structures below the powder layer.5,6 Due to the random size distribution and packing structure of the particles in the powder bed, evaluation of thermal transport at the independent particle scale is difficult. Due to the voids existing between individual particles, and the much higher conductivity of the metal compared to voids media (e.g., N or Ar), the conductive effect within the powder bed is diminished compared to the bulk scale effect. Due to the complexities associated with evaluating the particle scale transport properties, an effective thermal conductivity has been devised that allows the interactions within the powder bed to be modeled as a bulk scale phenomenon.7

A variety of experiments and modeling works exist within the literature discussing the use of Inconel alloys as additively manufactured materials. Studies such as those by Zhao et al.,8 Jia et al.,9 and Baufeld10 discuss the mechanical properties and microstructural composition of Inconel 718 parts built additively. Zhao et al. determined experimentally that, due to internal voids existing in the gas atomized (GA) powders they were using, a high void fraction existed within the finished part resulting in low ductility and low stress rupture properties regardless of the inclusion of post-process heat treatment. The addition of heat treatment was able to increase the ultimate tensile strength (UTS) of the part to 1.5 times that of the baseline part and comparable to that of wrought Inconel 718. Jia et al. studied densification, microstructure, microhardness and wear performance in Inconel 718 parts produced by SLM. The authors developed relationships between the energy input of the SLM process and the physical properties aforementioned. A positive correlation was observed between energy density and part density and microhardness. An inverse correlation was seen between energy density and part coefficient of sliding friction and wear rate. Baufeld studied the tensile strength and strain rate dependence of Inconel 718 parts produced by shaped metal deposition (SMD). SMD is a metallic process in which a continuously extruded wire of metal is melted and solidified to form a part. While this technique does not belong to the powder bed family, the results seen in Baufeld shed some insight into how additively manufactured parts may differ from parts created by subtractive means. He concluded that SMD produces parts very close to full density, no strain rate dependence exists for the ultimate tensile strength and such produced parts and tensile strengths from SMD produced parts are consistent with parts produced by other additive methods, EBM and SLM. Anam et al.11 produced a model and experimental validation assessing the use of Inconel 625 in SLM. The authors focused on modeling phase transformation during the build. Through the melting, solidification, and cyclic reheating of the powder bed from the addition of layers, a variety of phase transformations occur. An understanding of the phase field within the part is important to predict the mechanical properties exhibited by the finished part. Prabhakar et al.12 developed a model for residual stresses formed in Inconel manufactured by EBM. In this work, the authors both fabricated and simulated the fabrication of test coupons. The simulation makes use of a layer-by-layer model and looks at thermal transport and stress analyses after the addition of each layer of material. In the model, after each layer is added, the entire model is subjected to a cyclic temperature profile to simulate beam traversal across the powder bed, building up the layer. Deformations and Von Mises stresses are qualitatively compared between the modeling effort and the fabricated test coupons to provide meaningful model validation.

Various studies exist in the literature that model thermal transport in powder bed processes.5,6,13–16 Due to the transient nature of the manufacturing process, the developed model must consider many physical phenomena to include: phase change, a variety of heat and mass transport phenomena, and moving heat sources. The Roberts model5 simulates heat flow in laser-based processes to investigate the relative importance of powder transport properties on heat flow. In this study, the laser is modeled as a moving source heat generation with a Gaussian distributed decay in the build plane and a linear decay into the part. Roberts also makes use of element “birth and death” to simulate new layers being added to the powder bed. Due to the way finite element codes are constructed, all elements in the analysis must be initialized before calculations begin. In the use of birth and death, the user may set some group of elements as inactive for a portion of the analysis. Roberts concluded that the time required for the powder bed to dissipate heat is much smaller than the recoat time of the system, or the time required for the system to add a new layer of powder. He also found that the maximum temperature under the beam increased marginally with each additional powder layer and beam pass. Shen and Chou6 developed a model to investigate the effects of changing various process parameters on part quality in the EBM process. They found a direct relationship between powder bed porosity and melt pool diameter and temperature: as porosity was increased or decreased a similar trend was seen in the melt pool diameter and temperature.

Zeng et al.17 provides a quite thorough review of thermal modeling efforts in SLS and SLM processes. Many of the models reviewed in this work make use of a Gaussian distributed heat generation function, as discussed in the work of Roberts and Shen and Chou. Courtney and Steen18 have measured the diameter and intensity distribution of a laser beam and have confirmed that the Gaussian model approach is valid. They have additionally determined the effective beam radius term that is part of the Gaussian model, as seen below. Zeng also discusses the derivation and use of effective powder conductivity values within thermal modeling efforts. This phenomenon is also discussed in the work of Sih and Barlow.19 Regardless of the source, the objective of deriving an effective powder bed conductivity is to encapsulate the micro-scale thermal transport modes into a macro-scale transport property to ease computational requirements.

The Beuth group at Carnegie Mellon has carried out a plethora of experimental and simulation work in additive manufacturing processes for Inconel 62520 and Ti6Al4V.21,22 In these models, finite element models produced in ABAQUS are used to predict melt pool geometries in laser melting,20 electron beam melting21 and wire feed E-beam22 processes. In the simulation efforts, an axis of symmetry is imposed so reduce computational resources. Additionally, an adaptive meshing scheme is utilized with very fine meshing at the heat source application area and progressively coarser mesh away from the heated area. These works assume constant volume and density throughout the simulation to conserve mass and model density variation effects through scaling conductivity. The bulk of the Beuth group work, however, is in experimental measurement and optimization through the use of a process mapping technique.20,22,23 In this technique, scan speed, beam power, feed rates, thermal history of the part and part geometry are varied and the effects on transient melt pool size are determined.

Model Setup

The model presented here includes the melting, solidification, and conductive heat transfer through the powder bed.24,25 However, it neglects fluid flow within the melt pool, automatically satisfying continuity. Due to the existence of only thermal loading conditions in this model, a momentum balance does not provide any meaningful information and is therefore absent from the analysis. The thermal analysis is completed by solving the energy equation (Eq. 1) at each location and time step within the computational domain.26

$$ \varvec{\rho}\frac{\varvec{D}}{{\varvec{Dt}}}\left( {\varvec{e} + \frac{{\varvec{v}^{2} }}{2}} \right) = - \nabla \cdot \varvec{q}^{{\prime \prime }} + \varvec{q}^{{{\prime \prime \prime }}} + \nabla \cdot \left( {\varvec{\tau}\cdot \varvec{v}} \right) + \sum {(\varvec{\rho X}) \cdot \varvec{v}} $$

(1)

Equation 1 uses the following parameters; ρ: density, e: specific internal energy, v: velocity vector, q″: heat flux vector, q′″: heat generation, τ: total stress tensor including hydrostatic and deviatoric stresses, and X: specific body force acting on the element. Also note that $\frac{D}{Dt}$ represents a material derivative, or total derivative, and is expanded as seen in Eq. 2 where φ is some parameter being differentiated

$$ \frac{{\varvec{D\varphi }}}{{\varvec{Dt}}} = \frac{{\partial \varvec{\varphi }}}{{\partial \varvec{t}}} + \varvec{v} \cdot \nabla \varvec{\varphi } $$

(2)

X can be any body force resulting from conservative potential fields acting on the finite element. This model neglects both gravity effects and magnetic interactions; therefore the body force term is neglected. Additionally, the kinetic energy term within the material derivative and the stress term are assumed negligible since there is no motion considered within the model. The no motion assumption also drives the convective term to zero, leaving only the differentiation with respect to time. Using the fundamental thermodynamic coupling of internal energy and temperature through the specific heat, outlined in Eq. 3, the familiar Heat Equation is derived as seen in Eq. 4.

$$ \varvec{de} = \varvec{cdT} $$

(3)

$$ \varvec{\rho c}\frac{{\partial \varvec{T}}}{{\partial \varvec{t}}} = - \nabla \cdot \varvec{q}^{{\prime \prime }} + \varvec{q}^{{{\prime \prime \prime }}} $$

(4)

In Eqs. 3 and 4, c represents the specific heat and T represents the temperature of the particular node. Fourier’s law (Eq. 5) shows the constitutive model for the heat flux in the system resulting from conduction. Equation 6 is added into the heat flux term at the top surface where radiative cooling is allowed to occur.

$$ \varvec{q}^{{\prime \prime }} = - \varvec{k}\nabla \varvec{T} $$

(5)

$$ \varvec{q}^{{\prime \prime }} = \varvec{\varepsilon \sigma T}^{4} $$

(6)

In Eq. 5, k represents the thermal conductivity. In Eq. 6, ε denotes the emissivity of the material and σ is the Stefan–Boltzmann constant relating black body radiation to temperature.

The heat function is presented here as Eq. 7 where the following parameters apply; α: thermal absorptivity, $\dot{W}$: beam power, Φ: effective beam diameter, and h: beam penetration depth. x _c and y _c describe the center of the beam.

$$ \varvec{q}^{{{\prime \prime \prime }}} \left( {\varvec{x},\varvec{y},\varvec{z}} \right) = \varvec{f}\left( \varvec{z} \right)\frac{{8\varvec{\alpha \dot{W}}}}{{\varvec{\pi \varPhi }^{2} }}\varvec{e}^{{\frac{{ - 8\left[ {\left( {\varvec{x} - \varvec{x}_{\varvec{c}} } \right)^{2} + \left( {\varvec{y} - \varvec{y}_{\varvec{c}} } \right)^{2} } \right]}}{{\varvec{\varPhi}^{2} }}}} $$

(7)

with $\varvec{f}\left( \varvec{z} \right) = \frac{2}{\varvec{h}}\left( {1 - \frac{\varvec{z}}{\varvec{h}}} \right)$

In the same fashion as in other works in the literature,5,6,27 the heat generation model presented in this work varies radially, conformant to a Gaussian distribution and decays linearly in depth into the powder bed. The effective radius, or half the effective beam diameter in Eq. 7 is defined as the radial distance at which the energy density is reduced to 1/e ² 28 The heat generation function can be visualized as a conical heat distribution where the effective radius and the maximum energy density decay linearly with depth.

A major difference between EBM and laser melting (LM) processes is the penetration depth of the beam into the powder bed. Research29 has shown that laser sources penetrate several particle diameters into the powder bed, less penetration than seen in EBM. Average powder particle sizes in the laser melting process range from 20 μm to 80 μm in diameter. A penetration depth of 100 μm was assumed in this work. To be sure to model the full effect of beam speed and the transient nature of the problem, a longer model length than in previous studies24,25 is considered. The elongation further ensures that there is adequate free powder surrounding the beam line of action to accurately represent a laser scan occurring within a larger powder bed. The problem is considered transient in nature due to phase change phenomena changing the thermophysical description of the elements during simulation. Additionally, heat input at the beginning of a particular scan may result in different thermal reactions than later in the scan since there is no molten region at the beginning of the scan while one exists later in the scan. The powder and molten regions have different thermophysical property descriptions, and therefore different thermal effects are seen with and without the existence of a molten region.

Figure 2 illustrates the model geometry and model dimensions listed in Table I. This model contains three layers of material: a top layer of powder material, a middle layer of previously solidified material, and a steel baseplate. To reduce computational resources required, the powder layer and top 10% of the solid layer are meshed at a much finer rate, 22,500 elements per mm³, than the rest of the solid layer and the base plate, 100 elements per mm³. The baseplate acts as a structural support for the part during building as well as a heat sink to facilitate rapid solidification of the molten powder. The model is subjected to a radiative cooling boundary condition, radiating to atmospheric temperature of the build chamber, discussed in the results section of this work. No other cooling phenomena are allowed at the top surface of the powder bed. The bottom of the build plate layer is given an adiabatic constraint since there should be no meaningful heat transfer out of the heat sink. The other four sides are held constant at the initial powder bed temperature and the beam starts and ends 3 mm from the left and right sides of the block, respectively, to simulate scanning within a larger powder bed.

Fig. 2

Block orientation, beam direction and direction of motion. h ₁ , h ₂ and h ₃ denote the thickness of powder, solid and build plate layers, respectively

Table I Model dimensions

A mesh sensitivity analysis was performed on a previous iteration of the model working in Ti6Al4V, as seen in Ref. 25. While the material used has changed and some thermophysical property models have been updated since the previous version of the model, the authors believe the mesh sensitivity is still valid. In the sensitivity study, four cases are considered with varying mesh densities. The maximum temperatures after a simulation time of 0.675 ms are plotted against the mesh density for the four cases considered as seen in Fig. 3, in which there is a constant temperature region for element densities 10,000–30,000 elements/mm³. Since the mesh rate used in this modeling study produces a fine mesh density of 22,500 elements/mm³, the authors can say that the fine mesh scheme yields a convergent temperature profile. A sensitivity analysis for the coarse meshing scheme does not provide meaningful information since the thermal gradients within the model have dissipated before entering the coarsely meshed region and temperature distribution is not critical in this area.

Fig. 3

Fine mesh sensitivity analysis

Material Properties

Previous works5,13,19 have shown that thermal conductivity and emissivity properties differ greatly between a powdered metal and the same metal in a wrought state. These differences are a function of the porosity of the powder bed, the medium filling said voids, and the level of sintering exhibited within the powder bed.30,31 Table II shows the material properties for Inconel 718 used in this analysis. All properties, with the exception of emissivity and absorptivity, were from Mills.32 The emissivity and absorptivity data were taken from data published by Touloukian for nickel-chromium alloys.33 The powder conductivity comes from a well-accepted correlation for unsintered powder beds proposed by Hadley22 labeled Eq. 8. The unsintered correlation was chosen for this study because laser-based processes typically include no initial preheating and sintering of the powder bed, as is characteristic of the EBM process.

Table II Thermo-physical properties of Inconel 718

The solid property values in Table II above the liquidus temperature, in bold in the table, present the properties assigned to the molten material. These liquid properties are also tabulated by Mills,32 with the exception of emissivity which is from Touloukian.33 A modification was made to the liquid thermal conductivity data to account for the added heat transfer effects occurring within the real process due to fluid flow that are absent from the model definition used here. Elevated conductivity values of 15 times the original conductivity values. A study was conducted in which the liquid conductivity was systematically increased and the resulting maximum temperatures compared. The conductivity was considered to be saturated when the maximum model temperature reached an asymptotic value and no longer decreased with increasing conductivity. This analysis showed that conductivity is saturated at a ×15 increased conductivity value.

$$ \frac{{\varvec{k}_{\varvec{e}} }}{{\varvec{k}_{\varvec{g}} }} = \left( {1 - \varvec{a}} \right)\frac{{\varvec{pf}_{0} + \frac{{\varvec{k}_{\varvec{s}} }}{{\varvec{k}_{\varvec{g}} }}\left( {1 - \varvec{\varepsilon f}_{0} } \right)}}{{1 - \varvec{p}\left( {1 - \varvec{f}_{0} } \right) + \frac{{\varvec{k}_{\varvec{s}} }}{{\varvec{k}_{\varvec{p}} }}\varvec{p}\left( {1 - \varvec{f}_{0} } \right)}} + \varvec{a}\frac{{2\left( {\frac{{\varvec{k}_{\varvec{s}} }}{{\varvec{k}_{\varvec{g}} }}} \right)^{2} \left( {1 - \varvec{p}} \right) + \left( {1 + 2\varvec{p}} \right)\frac{{\varvec{k}_{\varvec{s}} }}{{\varvec{k}_{\varvec{g}} }}}}{{\left( {2 + \varvec{p}} \right)\frac{{\varvec{k}_{\varvec{s}} }}{{\varvec{k}_{\varvec{g}} }} + 1 - \varvec{p}}}\varvec{ } $$

(8)

where:

$$ f_{0} = 0.8 + 0.1p $$

and

$$ \log \left( a \right) = \left\{ {\begin{array}{*{20}c} { - 4.898p} & {0 \le p \le 0.0827} \\ { - 0.405 - 3.154(p - 0.0827)} & {0.0827 \le p \le 0.298} \\ { - 1.084 - 6.778(p - 0.298)} & {0.298 \le p \le 0.580} \\ \end{array} } \right. $$

In Eq. 8, the following parameters are used: k _e : effective thermal conductivity of powder; k _g : Thermal conductivity of gas filling voids between powder particles; k _s : thermal conductivity of the solid material; a: some scaling factor based on powder bed porosity p: powder bed porosity; f ₀ : function of powder bed porosity. In this analysis, only the powder bed porosity is a constant throughout the simulation, while the conductivity values are functions of temperature as seen in Table II.

Results

The model is conducted with actual parameters taken from the experiment to have direct comparison with experimental values. It is repeated at different values in order to understand and validate the model results and verify the effect of factors such as power. Table III presents the parameter sets used in the trial cases considered. A variety of power values are compared against the experimental findings to ensure proper model agreement with experiments across the entire operating range of the laser melting process.

Table III Simulation process parameters

The simulation trials were evaluated by measuring the melt pool width at the end of the simulation and comparing to experimental readings after fabrication. Samples considered were built in house using an EOSIN M 280 machine at the scan speed and beam power outline in Table III. The scan lines are each built upon a base block with dimensions 25.4 mm × 25.4 mm × 4.0 mm. The bases are built using a beam power of 285 W and a scan speed of 960 mm/s. The melt pool geometry readings presented here were measured by analyzing cross-sectional images of the single scan solidified region taken with an optical microscope at ×200 magnification. For each parameter set, 10 scan lines were analyzed and the results averaged to ensure proper characterization in melt pool geometry while varying process parameters. Using Matlab processing tools, the melt pool width, depth, and bead height were measured in pixel count, as seen in Fig. 4, in which the horizontal measurement denotes the melt pool width; the measurement from the horizontal upward denotes the bead height; and the measurement from the horizontal downward denotes the melt pool depth. By measuring the pixel count across the scale provided by the optical microscope images, the physical dimension is calculated.

Fig. 4

Cross-sectional optical microscope measurement method

As a second measurement technique, a Matlab code was written that senses solidified region by sensing pixel color within the image, measuring the number of pixels within the solidified region, and converting this pixel count to physical dimensions in accordance with the scale stamp from the optical microscope software. This technique is seen in Fig. 5, in which the red and green lines show the locations at which the program senses the top and bottom of the melt pool respectively. The blue lines at top and bottom show the average top and bottom locations. The experimental results listed in Table IV represent averaged measurements from the two techniques.

Fig. 5

Average melt pool width measurement method

Table IV Comparison of simulation and experimental melt pool geometries

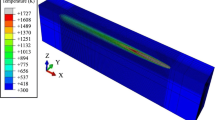
The size of the solidified region in the simulation trials was determined by counting the number of elements along a single line perpendicular to the laser line of action, originally powder that ended the simulation as a solid material. Since each element within the powder bed is of uniform size, the overall size of the solidified region is easily determined by multiplying the number of solid elements by the side length of each element. Figure 6 shows the simulation results with the corresponding experimental trials looking at the scan line from above. The purple region denotes the areas within the model that ended the simulation as a powdered material. The cyan region denotes elements that were part of the solid layer and were not melted at any point within the simulation. The red region is the molten region at the end of the simulation and the dark blue region is the build plate region. The orange region acts as a history of the molten area—it denotes elements that melted and subsequently resolidified through the course of the simulation. Figure 7 shows the corresponding experimental trials for comparison. In both the experimental and the simulation cases there is some degree of fluctuation in the melt pool width particularly in the high power trial.

Fig. 6

Final element definitions in model; power as labeled

Fig. 7

Top view of experimental trials power as labeled

As a second method of determining melt pool width, as well as determining the melt pool length and depth, a similar technique as seen in previous works by the author24 was adopted. For this analysis of the results, the melt pool geometry was determined by considering the temperature map existing in the model at a simulation time of 9 ms and determining at what elements the temperature transitioned from above the liquidus temperature of Inconel 718 to below the liquidus temperature. The distance between these transition elements were measured in the x direction: the melt pool length; the y direction: the melt pool width; and the z direction: the melt pool depth. The temperature data used in this analysis are seen in Fig. 8 with reference lines denoting the solidus and liquidus lines so that the molten region, mushy zone, and solidified regions can all be identified. The melt pool depth is recorded as the distance at which the temperature profile in the depth-wise direction crosses the liquidus line. The melt pool length and width are measured as the distance between the two points where the temperature profiles intersects the liquidus line. From right to left, the temperature profiles represent the depth, width, and length. Note that the length and width data locations have been transcribed across the graph so that each profile can be seen clearly without interfering with other profiles. The measurements taken from this analysis, along with measurements from the cross-sectional experimental method and the element-wise simulation measurement, are shown in Table IV.

Fig. 8

Melt pool geometry and temperature data

Table IV shows the simulation measurements compared with the experimental measurements. The third column in the table shows a correction factor calculated by dividing the simulation measurement by its corresponding experimental measurement. These correction factors were then plotted against beam power, and a regression analysis was performed. This analysis yielded two correction equations, one for width and one for depth, to be used to correct the simulation data. Equation 9 shows the correction equation for the melt pool width and Eq. 10 shows the correction for melt pool depth.

$$ F_{\text{width}} = - 1 \times 10^{ - 5} P^{2} + 0.0083P + 0.4056 $$

(9)

$$ F_{\text{depth}} = - 6 \times 10^{ - 6} P^{2} + 0.0002P + 1.3669 $$

(10)

In these two equations, F denotes the correction factor to be applied to the simulation results and P denotes the beam power for the simulation trial. The width regression had an R ² value of 0.988 and the depth regression had an R ² value of 0.8682. The trends between calculated correction factor and beam power for both melt pool width and depth are seen in Fig. 9. These trends show that at low power the agreement between simulation and experimental width measurements is closest, the calculated correction factor is closest to 1, and at high power the agreement between depth measurements is closest. The divergent width measurements with increasing power can be explained by the balling phenomenon present in the experimental trails that is not considered in the simulation. Due to metallic bonding forces, the molten pool creates a non-wetting interface with its solid counterpart. This means that the molten pool is consolidated into a droplet shape above the surface instead of spreading out across the solid surface. Since our model does not consider the fluid dynamics of the melt pool, this non-wetting effect is not considered and the simulated melt pool does not take into account contraction in the width and length directions to create the molten droplet. No correction analysis was available for melt pool length since no experimental data could be used to determine the instantaneous melt pool length during the process, just the final length of the entire scan line created. If the simulation measurements are divided by the correction factors from the regression analysis, the simulation values fall within a 16% error of the experimental values. The same correction scheme was applied to the simulation measurements taken from counting elements and errors on the order of 20–25% were seen. The authors believe that thermal mapping is a more accurate way of determining melt pool geometry, since it is independent of element size within the model. Counting elements, on the other hand, is constrained by the element size within the model as elements only change material id if all nodes within the element have reached the solidus, or liquidus, temperature depending on the applicable phase transformation. As seen in Table IV, the calculated correction factor increases with increasing beam power. The melt pool depth in the high power cases may have been artificially inflated due to the small model width. A model width of 3 mm was chosen to allow for faster run times, but the constant temperature boundary condition may have caused more energy to be dissipated into the depth of the model since the elements at the boundary could not be elevated in temperature and therefore saw no heat transfer. Future works will be completed using a larger model width. The erroneous melt pool geometries can be attributed to ambiguity correlating the actual beam diameter used within the experimental process and the effective diameter needed for the simulation. Another source for inconsistent simulation results is a discrepancy between the solid layer thickness used in the simulation and that fabricated in the experiment. In the experiment, a 1-in-thick solid base was built below the scan lines analyzed; however, only a 1-mm-thick solid layer was included. The smaller solid layer was chosen to relieve computational resources and since thermal gradients seemed to have dissipated before reaching the entire depth of the 1-mm solid layer. It is possible, however, that the solid layer thickness could adversely affect the validity of the simulation compared to the experiment. The authors are, however, confident that by employing these correction factors the model may be used to provide an accurate starting point for assessing changes in process parameter sets and their effect on melt pool geometry.

Fig. 9

Correction factor; beam power regression analysis

Conclusion

By comparing the results from the finite element model presented in this work to experimental work being conducted within the authors’ research group, two correction correlations between simulation melt pool geometry and beam power were developed, one for melt pool width and the other for melt pool depth. When comparing the experimental data against simulation measurements taken via analyzing the thermal history of the model, these correction correlations allowed simulation results to fall within a 16% error range from the experimental findings. Correction factors, as presented in this work, are a mere beginning to tuning the described model for determining melt pool geometry and temperature distribution in SLS built Inconel 718 parts. Causes for the discrepancy between the simulation and experimental measures are discussed and improvements proposed. By exploring the phenomenological causes for discrepancy between simulation and experimental measurements that led to the creation of correction factors in this work, and by including these phenomena into later works, the authors will be able to more fully understand the physical phenomena occurring during part production using powder bed-based additive manufacturing techniques. With the corrected model, the work presented here can be further improved and later used as a stepping stone to better predicting melt pool geometries while assessing variations in process parameters across a broad range of novel engineering materials.