Pressure–Impulse (P–I) Diagrams for Reinforced Concrete (RC) Structures: A Review

Abstract

In recent years, many studies have been conducted by governmental and nongovernmental organizations across the world attempt to better understand the effect of blast loads on structures in order to better design against specific threats. Pressure–Impulse (P–I) diagram is an easiest method for describing a structure’s response to blast load. Therefore, this paper presents a comprehensive overview of P–I diagrams in RC structures under blast loads. The effects of different parameters on P–I diagram is performed. Three major methods to develop P–I diagram for various damage criterions are discussed in this research. Analytical methods are easy and simple to use but have limitations on the kinds of failure modes and unsuitable for complex geometries and irregular shape of pulse loads that they can capture. Experimental method is a good way to study the structure response to blast loads; however, it is require special and expensive instrumentation and also not possible in many cases due to the safety and environmental consideration. Despite numerical methods are capable of incorporating complex features of the material behaviour, geometry and boundary conditions. Hence, numerical method is suggested for developing P–I diagrams for new structural elements.

1 Introduction

Reinforced concrete (RC) is one of the most widely used construction materials in the buildings. In the past, they were generally not designed to sustain large lateral dynamic loads such as blast loading and, for that reason, are very susceptible to terrorist attacks. RC structures may undergo large deformations when subjected to blast load. For this reason, the need of better understanding on the structural behavior quickly has become essential and significant in the field of progressive collapse. Publications such as Unified Facilities Criteria 3-340-02 [1], ASCE Blast Protection of Buildings [2], and TM5-1300 Guideline for Structures to resist the effects of the accidental explosions [3] are few example of publications produced in light of the development accomplishments in this field and are available to engineers to better design both military and civilian structures. In spite of these guidelines, much more work still remains to be done to better understand structural behaviour of a variety of different structures, structural components and structural materials when subjected to blast loads.

The performance of RC structures during blast detonation has been investigated by a number of researchers over the past five decades [4,5,6,7,8,9,10,11]. For real analysis of any structural element or personnel safety, the design codes suggest the preparation of the P–I curves. P–I diagrams is a commonly used simplified methods for describing a structure’s response to an applied explosive load [12, 13]. The P–I diagrams are developed to determine levels of damage on a structure and have also been used in the past to evaluate human response to shock wave generated by an explosion. This approach is typically used for each blast resistant element such as columns, beams, slabs and etc. After World War II, they became widely used in the field of protective structure engineering [13]. Single graph is a straightforward way to relate simplified damage level and combination of blast and impulse values. Based on many real life or numerical tests the different damage scenarios are presented in the diagram. Various researchers have performed research to the Pressure–Impulse (P–I) diagram for structural component under blast loading [14,15,16,17,18,19]. Development of P–I diagrams in reinforced concrete (RC) structures subjected to explosive loads was overviewed in this research study. This research also illustrated blast load parameters, definition of P–I diagram, assessment of the failure modes, damage criterion for different RC structure members and various methods to develop P–I diagrams. Conclusions and future work recommendations are presented to develop of reinforced concrete structures under blast loads.

2 Blast Loads

The safety of reinforced concrete structures subjected to blast and impact loads has been one of the primary concerns for designers in recent years. Many research works on the effects of blast loading on reinforced concrete elements have been published [20,21,22,23,24]. In order to provide an accurate prediction of the dynamic response of RC structures when subjected to blast loads, the first step is to correctly estimate the blast loads likely to be applied on the structure. The formulations of incident blast overpressure P_so, reflected pressure P_r, and other parameters of blast loads obtained from TM5-855-1 code [25], Conwep [26, 27], and empirical analysis proposed by a number of researchers [28,29,30,31]. TM5-855-1 code provides a useful estimation for assessing blast loads especially when many combinations of explosives and locations are considered. Several graphs to obtain the incident overpressure P_SO, reflected pressure P_r, incident impulse I_S, reflected impulse I_r, as well as the positive phase duration t_D of a spherical blast were given in TM5-855-1 code as a function of scaled distance Z and charge weight W [25, 32, 33].

A number of finite element codes are available to numerically predict blast pressure. Some of them are commercialized (e.g. AUTODYN [34], LS DYNA [35], ANSYS/LS-DYNA [36] and ABAQUS [37]). For simulating structures subjected to blast loads different methods of analysis are available in LS-DYNA. First, a purely lagrangian approach using the Load-Blast-Enhanced (LBE) feature of LS-DYNA, defining the blast parameters, and allowing the program to apply the blast pressure on the surfaces of the structure. Second method is Multi-Material Arbitary Lagrangian–Eulerian (MM-ALE) and the third method is LBE and MM-ALE coupling [35, 38, 39]. Another method is calculating the pressure–time history of a blast event and then, applying the blast pressure directly on the surfaces of the structure [40,41,42,43]. Classifications on the basis of ratio of the blast wave duration to time period of the Structure are as:

• (I) Impulsive loading

• (II) Dynamic loading

• (III) Quasi-static loading

The load is quasi-static if the period of vibration is less with reference to the load duration. The load is impulsive if the period of vibration is long. The load is dynamic when the time vibration is about the same as loading duration [44,45,46]. The amplitudes and distributions of blast loads on a structure’s surface are governed by factors including explosive charge characteristics (e.g. weight and type), standoff distance between explosive and structure and the pressure enhancement due to interaction either with ground or structure itself or the combination of the two. A building structure might be fully engulfed by the blast wave as it impinges on the targeted structure depending on the structure size and standoff distance between the explosive and structure.

The parameters influence in blast are depends on the value of energy released by a detonation in the form of a blast wave and the distance from the explosion [47, 48]. All these factors need to be accounted as they have strong influences on the structural response [49]. The most widely used form of blast scaling is the Hopkinson–Cranz or cube root method presented in the following relationship [49, 50];

$$Z = \frac{R}{{W^{1/3} }}$$

(1)

where R is the actual effective distance from the explosion and W is the charge weight as an equivalent mass of TNT [49, 51]. When the scaled distance increases, the peak blast load decreases but the duration of the positive phase blast wave increases resulting in lower amplitude, longer-duration shock pulse [52]. The P–I curves divide into several regions and corresponding to a specific level of damage. To identify blast loading conditions that fall in each regime, Smith et al. [53] used the scaled distance Z, which is defined as the ratio of the standoff distance to the cubic root of the charge weight. The response regime is shown in Table 1 [53]:

Table 1 Categorized of the response regime in the Smith et al. [53] study

The close-in regime is associated with the type of loading where the explosive is very close to the structure [54]. In this case, the duration of loading is much lower than the natural period of the structure. Hence, the loading is impulsive and it generates points in the impulsive-control region (region I) of the P–I diagram. The far field regime includes the loading cases in which the standoff distance is very high. In the near field regime, the standoff distance is high enough to generate the blast wave with duration close to the natural period of the structure. In this type of loading, both the pressure and impulse affect the response of the structure. Thus, the points associated with the region II of the P–I diagram are generated.

3 Definition of P–I Diagrams

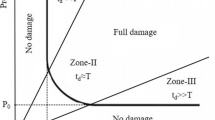
Pressure and impulse, as the two normalized parameters of a blast load, can be used to represent any blast condition [55]. P–I diagrams provide a reliable method for evaluation of the response of a structural member under different types of explosive loading. In fact P–I diagrams is a suitable method to correlate the duration of blast pressure along with its amplitude to reaching a different level of damage in structures and that is used to assessment of RC structures damages. A P–I diagram is a design tool that allows of evaluating the damage level of structural components induced by blast loads [31]. Recently, a great deal of progress has been made on the development of P–I diagrams for structural members. In each P–I curve three domains can be identified: an impulsive, a dynamic, and a quasi-static loading regime [56]. Adopting this assortment, the maximum response may depend only on the applied impulse (impulsive region), the pressure only (quasi-static region), or on both the impulse and pressure (dynamic region) [57]. The impulsive regime is characterized by short load duration where the maximal structural response is not reached before the load duration is over. The dynamic regime is characterized by the maximum response being reached close to the end of the loading regime. Lastly, the quasi-static regime is characterized by a structure having reached its maximum response before the applied load is removed. The primary features of P–I curves represent in Fig. 1.

Fig. 1

A typical pressure–impulse diagram [57]

According to Fig. 1, the P–I diagram contains impulsive asymptote and pressure asymptote that the impulsive asymptote is associated with the loads with very short duration relative to the structure’s natural frequency whereas the pressure asymptote is associated with the loading that its duration is longer than the natural frequency of the structure, thus, subjects the structure to quasi-static loading. The impulsive asymptote represents the minimum impulse required to reach a particular level of damage and in the impulsive region, the structure response is sensitive only to the associated impulse and not to the peak pressure. In the quasi-static region, the response of the structures becomes insensitive to impulse and sensitive to peak pressure. Therefore, the horizontal asymptote represents the minimum level of peak pressure required to reach that particular damage level [41].

According to Abrahamson and Lindberg study [58], P–I diagrams can be used to assess the structural dynamic response. It illustrates that the combination of pressure and impulse produces an equal structure response. P–I diagrams can be divided into three categories—impulse sensitive range, dynamic range and pressure sensitive range—as shown in Fig. 2.

Fig. 2

Description of the P–I damage curve [58]

Typical set of P–I diagrams is presented in Fig. 3, in which each curve is associated with a different response limit. These curves can be calculated to represent the P–I combinations associated with the levels of protection specified in CSA S850-12 and ASCE 59-11, as shown for primary structural elements [2, 59].

Fig. 3

Typical pressure impulse diagram [59]

Cormie et al. [60] presented three regimes of blast loading to generate P–I diagram based on the positive phase duration of blast loads, t_D and the natural period of the structure T, that shown in Table 2.

Table 2 Three regimes of blast loading in the Cormie [60] study

The aforementioned three regimes are plotted into an exponential curve with respect to the logarithmic values of impulse, I and pressure, P as represent in Fig. 4.

Fig. 4

Three regimes of loading [60]

Soh and Krauthammer [61] performed a methodology that would produce numerically stable P–I diagrams. They estimate the locations of the asymptotes by using the energy balance method. The numerical procedures presented by Soh and Krauthammer [61] produced reasonably accurate P–I diagrams; however, there are a few disadvantages to their algorithms.

Development of P–I diagram by utilizing multiple analytical techniques observed in the Rhijnsburger et al. [62] study. They assessment the impulsive and quasi-static asymptotes by using energy balance method while a numerical analysis procedure generates the dynamic regime using a branch-tracing algorithm.

In the other study Li and Meng [63] define P–I diagrams as isodamage curves which include three regimes of structural loading and response: impulse-controlled, peak load and impulse-controlled, and peak load-controlled regimes. These regimes are illustrated in Fig. 4 as regimes I, II, and III respectively [63]. Li and Meng [63] conducted a fundamental study of the P–I diagram for various descending pulse loads based on dimensional analysis and a SDOF model. They observed three different pulse loading shapes: rectangular, linear decaying (triangular), and exponential decaying. In the dynamic regime, they showed that the P–I curves are sensitive to the pulse shape. Empirical equations were also proposed to generate the P–I curves taking into account the pulse shape and inverse ductility ratios. Mays and Smith [64] proposed a set of limits on the product wt_d defining the impulsive, dynamic and quasi-static response regimes that shown in Table 3.

Table 3 Proposed method on the product wt_d by Mays and Smith [64] study

A P–I diagram is simply an iso-damage or iso-response contour plot consisting of a series of P–I combinations which generate the same level of structural response. Structural response may be observed qualitatively (i.e. high, medium, low blast damage) or measured quantitatively (displacement, ductility ratio, support rotation, etc.). Figure 5 represents P–I diagram based on the maximum displacement, u_max. P–I combinations which lie to the left and below the contour indicate response levels less than maximum displacement, while those which lie above and to the right will result in response levels greater than the defined limit. The performance of the structure may be evaluated graphically by generating a P–I diagram for a given structural element, and plotting P–I combinations corresponding to different explosive threats.

Fig. 5

Typical iso-damage counter plot/pressure–impulse diagram

P–I diagrams can re-plotted in the form of range-to-effect curves. Figure 6 shows an example of a range-to-effect chart that indicates the stand-off to which a given bomb will produce a given effect [65]. Therefore, P–I space diagrams are developed with the aim to describe the level of damage suffered for level of protection (LOP) by a structural member when exposed to different combinations of pressure and impulse created by explosives [19, 66, 67].

Fig. 6

Explosive environments—blast range to effects [65]

4 Mode of Failure

Blast loading effects on structural members may produce both local and global responses associated with different failure modes [68]. Global failure results in the collapse of the entire structure, localised failure occurs on only some reinforced concrete members such as beams, slabs and columns. Global failure usually occurs under static and quasi-static loading [69]. The general failure modes associated with blast loading can be flexure, direct shear or punching shear. Krauthammer et al. [70] concluded that the flexural failure modes and direct shear failure modes are always independent to each other. In general, the response and failure for most structures can occur in more than one mode. Although flexure is usually the predominant mode, but under certain circumstances, failure may occur in other mode (e.g. direct shear). According to a Fig. 7, there is two failure modes that in the P–I diagram consists of two threshold curves, each representing a failure mode that the true threshold curve shown by the dotted line [71].

Fig. 7

P–I diagram with two failure modes [71]

According to Ngo [68], the essential characteristics of loading and building response for transient loads produced by explosions depend primarily on the relationship between the effective duration of the loading and the fundamental period of the structure on which the loading acts. T. Ngo done a field blasting test of a RC wall subjected to a close-in explosion of 6000 kg TNT equivalent, the wall suffered direct shear failure as shown in Fig. 8. Direct shear failure occurs in high velocity impact and in the case of explosions close to the surface of structural members.

Fig. 8

Breaching failure due to a close-in explosion [68]

Mutalib and Hao [42] observed three main damage modes of RC columns in their numerical simulation as shown in Fig. 9. They observed that when the column is subjected to impulsive load the failure is inclined to be damaged by shear and in the dynamic loading region failure of the column is a combination of shear and flexural damage and finally in the quasi-static region, the column is likely damaged by flexural failure mode.

Fig. 9

Damage modes of the non-retrofitted RC column [42]

Fujikura and Bruneau [72] performed Blast testing on 1/4 scale ductile RC columns, and nonductile RC columns retrofitted with steel jacketing. Figure 10 show the shear failure at the base and top of the RC column in the Fujikura and Bruneau [72] study.

Fig. 10

Shear failure at the base and top of the RC column [72]

In the Shi study, two damage modes have been observed during the numerical simulation of RC column damage to blast loads [41]. One is shear damage, and the other is flexural damage. Sometimes the failure of the column could be a combination of the above two modes. The typical results of these three damage modes derived from numerical simulation are shown in Fig. 11.

Fig. 11

Damage modes of RC column under blast loads. a Shear damage; b Flexural damage; c Combined shear and flexural damage [41]

Ngo performed a blast test on one-way panels with the average reflected impulse and average reflected pressure of 2876 kPa ms and 735 kPa, respectively [73]. The one-way panel failed due to concrete breach and mid-span crack formed vertically at the front and rear surface. Figure 12 shows the failure mode of the RC panel [73]. The similar damage mode is observed in [74] in a shock tube test of a 0.62 m × 1.75 m × 0.12 m panel as shown in Fig. 13. The panel failed in the flexural mode at the tested value of 208 kPa peak pressure and 3038 kPa ms impulse.

Fig. 12

After the blast in Ngo [73] field test

Fig. 13

Result from a shock tube test of a RC panel in [74]

Weerheijim et al. [75] tested square RC panels simply supported at four sides by a blast simulator at different pressure levels. Figure 14a show the extensive cracks after a blast load of 160 kPa peak pressure. The crack pattern is consistent with that observed in field blasting test carried out by Muszynski and Purcell [76] shown in Fig. 14b, where the tested wall failed due to tension failure resulted from an explosive charge of 830 kg detonated at 14.6 m standoff distance from the structure.

Fig. 14

Crack patterns in a Weerheijim et al. [75] field test and b Muszynski and Purcell [76] test

The failure mode categories for simply supported beams and fully clamped beams are evaluated in Ma et al. [77] study. They assessment bending failure and shear failure in their research and the responses of the beams are analysed based on five transverse velocity profiles. The failure mode for simply supported beams and fully clamped beams are show in Fig. 15. Failure modes of simply supported and fully clamped beams are shown in Table 4.

Fig. 15

Distribution of Failure modes for simply supported and fully clamped beams [77]

Table 4 Failure modes of simply supported and fully clamped beams [77]

In 1973, Menkes and Opat [78] were the first to report the three possible failure modes on fully clamped plates and beams loaded impulsively. Three clearly different damage modes are shown schematically in Fig. 16. They are described as: Mode I: large inelastic deformation; Mode II: tearing (tensile failure) in outer fibres, at or over the support; and Mode III: transverse shear failure.

Fig. 16

Failure modes for explosively loaded plates and beams

The same failure modes are also observed in blast load experiments on circular [79] and square steel plates [80, 81]. When the explosion centre is very close to the structure, RC panel might suffer localized crushing and spalling damage. Otherwise, damage modes of RC panels are similar to those of steel plate as observed in various field blasting tests reviewed above. The RC panel damage mode not only depends on the amplitude and duration of the blast loads but also depends on the boundary conditions and panel material properties. Ma et al. [82] observed three failure modes in their study. Mode 1 contains the shear failure only. Mode 2 indicates the bending failure which has a plastic hinge at the centre of the element. Mode 3 can be considered as the combination of mode 1 and mode 2.

5 Damage Criterion

In order to define damage, the damage criteria used should be suitable for evaluation of RC structures related to the member global and material damage, easy to use in assessing the element conditions and easily obtained from numerical or experimental test [41]. The P–I diagram is generally used to numerically describe an exact damage level to joint blast pressures and impulses applied on a specific structural member [83]. A damage index numerically indicates the level of damage of a particular structure or a component [84, 85]. This is a valuable tool in evaluating the damage and design to resist disasters such as an earthquake or blast [86, 87]. Each P–I curve represents a damage level that a structure experiences due to the various blast loading conditions. Damage assessment plays an important role in the evaluation of the stability and strength of structures. In an extreme condition, such as a blast load scenario that is normally not considered in the original structural design of civilian structures, structural elements may experience damage in different degrees. An effective damage assessment method of a structure is essential in order to apply protective measures when there exist potential blast load risks. For a RC structural element, the analysis becomes more complicated because the reinforced concrete always deforms in a nonlinear way, especially in the post-failure stage.

Biggs and Mendis et al. observed an example of a P–I diagram to illustrate levels of damage of a structural element that is shown in Fig. 17 [68, 88]. Region (I) describes significant structural damage and region (II) displays no or minor damage. Three categories of blast-induced injury concern with human response to blast for develop P–I diagram, namely: primary, secondary, and tertiary injury [70, 89].

Fig. 17

Typical pressure–impulse (P–I) diagram

To generate the P–I diagram, previous researcher studies on the simplified single degree of freedom (SDOF) model. Fallah and Louca [90] evaluated a damage criterion based on the mid-height deflection of the column for the SDOF system. The y_C values and the corresponding damage degrees are given in Table 5. In their study damage criterion is based on flexural failure of the column that it may not give reliable prediction of column capacity with other failure modes. Fallah and Louca [90] neglects the axial load effects on column load carrying capacity. Since columns are primarily designed to carry the axial load, the residual axial load carrying capacity should be a better damage criterion of a column.

Table 5 Damage criterion based on Fallah and Louca [90] study

Shi et al. [41] and Mutalib and Hao [3] proposed a new method to estimate the damage index in RC columns that shown in Fig. 18. According to Fig. 18, the axial load applied to the column in stage one and after that blast load is applied to the column after the time for stress equilibrium is attained along the length of the column in the stage two and in the third stage Post-blast analysis is carried out to evaluate the residual axial load carrying capacity of the column. This simulates a displacement controlled load testing.

Fig. 18

Loading procedures to determine the damage index [41, 42]

Shi et al. [41] and Mutalib and Hao [42] for assessment the RC column damage determined damage index based on the residual axial load carrying capacity. It is defined as

$$D = 1 - \frac{Presidual }{ Pdesign }$$

(2)

where P_residual = The residual axial load-carrying capacity of the damaged RC column [91], P_design = The maximum axial load carrying capacity of RC column.

The advantages of the damage index proposed by Shi et al. [41] are that it has direct physical meanings that are independent of the failure modes and also it is easy to use in evaluating column conditions because the primary function of columns is to carry axial load. In addition, it is easy to use in numerical simulation or experiment tests. Damage Index classification shown in Table 6 and Fig. 19 respectively.

Table 6 Damage index classification in the Shi et al. [41] study

Fig. 19

Damage Index classification [41]

Cui et al. [92] proposed new formulae to analysis and damage assessment of RC columns under close-in explosions. They show that the maximum residual plastic deflection of the RC column often occurs at the height of the centre of the blast loaded area. The residual deflection along the RC column is a combination of the overall deflection and the local deflection directly induced by the concentrated blast load. Based on the numerical results, the blast load concentrated area is defined, which is shown in Fig. 20a. And the damage index λ is defined as the ratio of the relative residual deflection and the column depth;

$$\uplambda = \frac{\delta }{h}$$

(3)

where δ is relative residual deflection of the blast load concentrated area, which is calculated as the difference between the maximum residual deflection and the residual deflection at the edge of the blast load concentrated area as shown in Fig. 20b; h is the column depth.

Fig. 20

a Area of concentrated blast load and b relative residual deflection, in the Jian Cui study [92]

Cui et al. [92] evaluated the relationship between damage index λ and axial load carrying capacity degradation-based damage index D (based on the Shi et al. [41] study) that it is independent of column depth. The damage D can be derived as a function of λ;

$$D = 1.9 + 0.25ln\uplambda\quad \left( {\uplambda \le 0.015} \right)$$

(4)

Shi and Stewart [93] conducted the damage and risk assessment for RC wall panels subjected to explosive blast loading. They used the maximum support rotation (θ) obtained from the LS-DYNA analysis to estimate the degree of damage of RC wall panels. Three damage limit states based on test data and UFC 3-340-02 [1] are used that shown in Table 7 [88]:

Table 7 Damage criterion based on test data and UFC 3-340-02 [1, 88]

Support rotation $\frac{1}{4}$ Arctan (mid height deflection/mid-wall height). Repairable damage means that the component has some permanent deflection. It is generally repairable, if necessary, although replacement may be more economical and aesthetic. Heavy damage defines that the component has not failed, but it has significant permanent deflections causing it to be unrepairable. Hazardous failure means the component has failed, and debris velocities range from insignificant to very significant.

Wang et al. [94] established the damage criteria for different levels of damage in the square reinforced concrete slab under close-in explosion that show in the Table 8. They proposed empirical damage criterion by the support rotation angle and the support rotation is defined by the ratio of the calculated peak deflection to half a span length for one-way slabs:

$$\tan \theta = \frac{{x_{m} }}{L/2}$$

(5)

where $x_{m}$ = the centre maximum deflection, L = length of the slab.

Table 8 Damage criterion of the slab in the Wang et al. [94] study

Syed et al. [95] utilized the UFC-3-340-02 [1] damage criteria for damage assessment of RC panel and beam in equivalent SDOF analysis. The damages are defined based on the support rotation of the members and are classified into low, moderate and severe. When support rotation is 2°, yielding of the reinforcement is first initiated and the compression concrete crushes, the damage of the wall is termed as low (LD). When the support rotation is 4°, the element loses its structural integrity, and moderate damage (MD) occurs. At 12° support rotation, tension failure of the reinforcement occurs. This is defined as the severe damage (SD). Zhou et al. [96] used a dynamic plastic damage model to estimate responses of both an ordinary reinforced concrete slab and a high strength steel fibre concrete slab for concrete material under to explosive loading. Shope [97] used the maximum deflection, δ corresponds to the specific support rotation, θ defined in UFC-3-340-02 and illustrated in Fig. 21 to define the damage level. The respective δ value for each damage level is calculated by

$$\delta = \frac{b}{2}\tan \theta$$

(6)

where b is the shortest span of the wall. The critical values of δ are set to be the numerical maximum mid-height deflection of the RC panel. These damage criteria are used in this study to define damage levels of P–I diagrams.

Fig. 21

Resistance-deflection curve for flexural response of concrete elements [1]

6 Development of Pressure–Impulse Diagrams for RC Structures

This section describes the research conducted to develop P–I diagrams for reinforced concrete structures under blast loads. A lot of studies have been carried out to derive the P–I diagrams in the literature. Different methods have been typically used to develop PI diagrams for various RC structural elements under explosive loads. The various method used to develop P–I diagram are

• a. Analytical method

  • i. Single Degree of Freedom (SDOF) method

  • ii. Energy balance method

• b. Numerical method

• c. Experimental method

6.1 Analytical Method

Analytical and Theoretical methods for deriving P–I diagrams for structural elements subjected blast loads are described in this section. Single degree of freedom (SDOF) system and energy balance method are commonly used to derive P–I diagram for structural elements. A summary of analytical method studies are listed at Table 9.

Table 9 Summary of analytical method studies

6.1.1 Single Degree of Freedom (SDOF) Method

During preliminary dynamic loading resistant design, structures are normally reduced to a single-degree-of-freedom (SDOF) model using equivalent mass, damping parameter and resistance function for simplicity. The single degree of freedom (SDOF) model is the most widely used method for predicting dynamic response of structures under blast and impact loading [105, 125, 126]. Traditionally, P–I diagrams for structural components are developed using SDOF systems. The structure is visualized as a single degree of freedom (SDOF) system and the relation between the natural period of vibration and the positive duration of the blast load of the structure is created to analyse comprehensively.

A simple approach using the single degree of freedom (SDOF) method to analyse structural elements subjected to blast loads has been performed by Mays and Smith [64]. The simplest vibratory system can be illustrated by a single mass connected to a spring. The mass is allowed to travel only along the spring elongation direction. Such systems are called Single Degree-of-Freedom (SDOF) systems and are shown in the Fig. 22. The equation of motion that describes the behaviour of the equivalent SDOF system is written in Eq. 7.

Fig. 22

Single degree of freedom system (SDOF)

$$m\ddot{x} + c\dot{x} + kx = f\left( t \right)$$

(7)

The equivalent SDOF method is widely used to generate P–I diagram in the structural components. An idealized resistance deflection curve using SDOF method is illustrated in Fig. 23a. As the graph goes from the elastic to the inelastic stages the equation of motion governing its behaviour changes according to the resistance function in Fig. 23a KL1 and KL2 represent equivalent stiffness for elastic and elastic–plastic regions. The pressure vs. impulse curve generated for the system model is illustrated in Fig. 23b. These curves were created by solving the equation of motion of different stages in the resistance deflection curve [88].

Fig. 23

SDOF method to generate a Resistance deflection curve and b P–I diagram

SBEDS is an Excel-based tool used to perform Single-Degree-of-Freedom (SDOF) dynamic analyses of structural components subjected to blast loads [111]. It was developed for the U.S. Army Corps of Engineers Protective Design Centre to meet Department of Defense Antiterrorism standards [127]. SBEDS follows guidance contained in Army TM 5-1300 [3] and Unified Facilities Criteria (UFC) 4-010-01 [127] as applicable.

Xu et al. [101] developed P–I diagram of flexural and direct shear failure modes for an RC slab under external blast loading. In their study, dynamic response equations of a structural member experiencing direct shear failure are derived for elastic, plastic and elasto-plastic shear resistance-slip models. With these equations the P–I curves of both flexural and direct shear failure modes are generated for an RC slab. In addition they evaluate the effect of different parameters of RC slabs on the P–I diagrams based on the elasto-plastic model.

The typical P–I curves of the RC slab with two failure modes are generated using the SDOF system as shown in Fig. 24. Regions A, B, C and D represent a particular situation of the slab under explosion blast load. In the region labelled C, the slab remains safe without shear and bending failure under the impact loads. In region D, the slab is merely influenced by bending failure without direct shear failure. The area of B presents direct shear failure occurring without flexural failure. The position located in the region of a fails in both direct shear and bending modes. These typical outcomes demonstrate that when a large loading is applied at a rapid rate to the members, the slab is damaged by direct shear force.

Fig. 24

P–I relationships of flexural and direct shear failure modes [101]

As shown in the impulsive loading region, the failure area of direct shear mode is much greater than the region of flexural failure. As the failure region is difficult to compare within the dynamic region of the P–I diagram, the failure of the slab could either be the shear failure or bending failure or both failures reinforcing one another. As peak reflected overpressure drops, the failure trends to flexural failure mode in the quasi-static region, which is the safety region in the flexural failure mode, and is smaller than the safety region under the curve in the direct shear failure mode. Also influences of structural behaviour on P–I diagrams were investigated by comparing the P–I curves in both flexural and direct shear failure modes in elastic, plastic and elasto-plastic models. The failure regions varied significantly with different resistance deflection/slip responses (Fig. 25). As shown in Fig. 25, the plastic model has the largest “safe” region unaffected by shear and bending failure under different impact loads. Conversely, the elastic model can sustain relatively less loading in both failure modes due to having the largest failure region [101].

Fig. 25

P–I relationships of direct shear and flexure failure modes with different structural resistances [101]

Xu et al. [101] generated analytical formulae for predicting the pressure asymptote and impulsive asymptote for the elasto-plastic model. The formulae of the pressure asymptote and impulsive asymptote of the elasto-plastic model under direct shear failure mode are

$$\begin{aligned} P_{0} & = 10000 \times [0.0055 \times \exp \left( {\frac{{f_{c}^{'} }}{30}} \right) + 0.012 \times \exp \left( {\frac{{f_{y} }}{300}} \right) + 0.048 \times \exp \left( {\frac{\rho }{0.03}} \right) + 0.017\left( {\frac{L}{1000}} \right)^{2} \\ & - 0.18\left( {\frac{L}{1000}} \right) - 1.03\left( {\frac{h}{2000}} \right)^{3} + 3.11\left( {\frac{h}{200}} \right)^{2} - 2.45\left( {\frac{h}{200}} \right) + 0.8 \\ \end{aligned}$$

(8)

$$\begin{aligned} I_{0} & = 0.026 \times \exp \left( {\frac{{f_{c}^{'} }}{30}} \right) + 0.039 \times \exp \left( {\frac{{f_{y} }}{300}} \right) + 0.22 \times \ln \left( {\frac{\rho }{0.03}} \right) + 0.054\left( {\frac{L}{1000}} \right)^{2} - 0.56\left( {\frac{L}{1000}} \right) \\ & + 0.058\left( {\frac{h}{200}} \right)^{2} + 1.59\left( {\frac{h}{200}} \right) + 0.72 \\ \end{aligned}$$

(9)

By using Eqs. (8) and (9), it is very easy to generate the values of the pressure asymptote and impulsive asymptote based on the parameters of the RC slab [101].

Dragos and Wu [105] presented a new general approach to generate P–I diagrams. They used SDOF model to evaluate P–I diagram for elastic, rigid plastic and elastic plastic hardening structural members, the effective pulse load is a new approach to present P–I curves. They also determined three parameters which describe the shape of the effective pulse load and these parameters are then applied to generate a method for specify a point on the P–I diagram for elastic, mentioned structural members. They present that the new approach can be used to structural members subjected to any arbitrary pulse loads.

Dragos and Wu [102] studied Interaction between direct shear and flexural responses for blast loaded one-way reinforced concrete slabs using a finite element model. In their research both the moment–curvature flexural behaviour and the direct shear behaviour are incorporated into a numerically efficient one dimensional finite element model, utilizing Timoshenko Beam Theory, to determine the member and direct shear response of one-way reinforced concrete slabs subjected to blasts. The model is used to undertake a case study to demonstrate the flexural member response behaviour during the direct shear response and is then used to carry out a parametric study to better understand the interaction of the flexural member response and the direct shear response. This is done by comparing P–I curves corresponding to direct shear failure for one-way reinforced concrete slabs with varying depth, span and support conditions. The results aim to provide insight to facilitate the development of more accurate simplified methods for determining the direct shear response of blast loaded reinforced concrete members, such as the single degree of freedom method.

Huang et al. [108] presented damage assessment of reinforced concrete structural elements subjected to blast Load. They derived P–I diagrams with respect to combined bending and shear failure. They define dimensionless pressure P and impulse I for the blast load as:

$$P = \frac{{P_{0} L}}{{Q_{e} }} = \frac{{P_{0} L^{2} }}{{2\upsilon M_{e} }}$$

(10)

$$I = \frac{{P_{0} t_{d} }}{{\sqrt {2mQ_{e} } }} = \frac{{P_{0} t_{d} }}{{\sqrt {4mM_{e} .\upsilon /L} }}$$

(11)

From the equations for the final displacements induced by the shear and bending failure, the P–I diagrams can be represented in unified forms as:

$$S\left( {P,I} \right) = \delta h\gamma_{\upsilon } = y_{s}$$

(12)

$$B\left( {P,I} \right) = L.\beta = y_{m}$$

(13)

where $y_{s}$ = maximum displacement due to shear, $y_{m}$ = maximum displacement due to bending.

S(P, I) and B(P, I) are implicit expressions with respect to the normalized pressure and impulse for shear and bending deformation modes according to the failure criteria. They suggested the P–I diagrams for the rigid-plastic model, the elastic-rigid-plastic model, and multi-linear model with respect to the three failure modes that shown in Fig. 26.

Fig. 26

P–I diagrams of failure modes [108]

El-Dakhani et al. [109] used a SDOF model based on the guidelines of UFC 3-340-02 to generate P–I diagrams and compared to the results of experimentally validated nonlinear explicit FE analysis of two way slabs. It was concluded that the deficiencies in the SDOF resistance functions included strength underestimation resulting from neglecting multiple yield line patterns and corner effects. P–I curves are characteristic to the material and sectional properties of the structural element and also dependent upon damage level of the structural element.

P–I diagrams for combined failure modes of rigid plastic beams was proposed by Ma et al. [77]. In their study, closed-form solutions for P–I diagrams of simply supported and fully clamped rigid-plastic beams subjected to a rectangular pulse were developed. They assessment bending failure and shear failure in their research and the responses of the beams are analysed based on five transverse velocity profiles. Also they evaluated the effects of shear-to-bending strength ratio and the boundary conditions on the P–I diagrams and compared the results with SDOF model. The results of their study shown the proposed P–I diagrams can be applied to determine beam damage and the proposed P–I diagrams have reliable agreement with those based on an elastic, perfectly plastic model.

P.H. Ng generated P–I curve independently of the asymptotes. In their study the RC slabs were idealized as two loosely coupled SDOF systems and present flexural and direct shear behaviours [118]. The proposed algorithm in their study is based on the threshold curve and Threshold points are found by keeping the pressure constant and checking whether the P–I combination is either safe or damaged. When it is safe, the impulse is increased until the point results in damaged and also conversely, reducing the impulse for a damage point will eventually find a safe point and finally the threshold point is found between these two boundaries. These results of Ng [118] study demonstrate reliable accurate P–I diagrams; however, there are a few disadvantages to their algorithms.

Hamra et al. [16] developed P–I diagram of a frame beam subjected to blast loading. They obtained analytical formulae to generate the asymptotes in the P–I diagram and also they provided parametric study on the P–I diagram. A dimensional analysis of the problem reveals that, under the considered assumptions, four dimensionless parameters mainly required ductility of the beam. Two of them are related to the behaviour of the indirectly affected part and another one is related to the mechanical properties of the investigated beam.

Fallah and Louca [90] studied the effect of material hardening and softening on P–I diagrams. They proposed quasi-static and impulsive asymptote equations as follows:Quasi-static asymptote

$$\frac{{F_{m} }}{{Ky_{m} }} = \alpha \left( {1 - \theta \psi^{2} } \right) + \frac{\theta }{2}\left( {\psi^{2} - \theta \alpha^{2} + \alpha^{2} \psi^{2} } \right)$$

(14)

Impulsive asymptote

$$\frac{1}{{y_{m} \sqrt {KM} }} = \sqrt {2\alpha \left( {1 - \theta \psi^{2} } \right) + \theta \left( {\psi^{2} - \theta \alpha^{2} + \alpha^{2} \psi^{2} } \right)}$$

(15)

where I = total impulse, $y_{m}$ = maximum structural deflection, K = elastic stiffness, M = lump mass of the SDOF system, $F_{m}$ = maximum force on the system, α, ψ and θ are dimensionless parameters, defined as

• $\alpha = \frac{{y_{el} }}{{y_{c} }}$

• $\psi^{2} = \frac{K\beta }{K}$

• θ = + 1 for elastic plastic hardening and − 1 for elastic–plastic softening

Li and Meng [63] derived P–I diagram from dimensionless parameters that shown in the Eqs. 16 and 17.

$$i = \frac{I}{{y_{m} \sqrt {KM} }}$$

(16)

$$p = \frac{{F_{m} }}{{Ky_{m} }}$$

(17)

where i = scaled impulse, p = scaled pressure, I = total impulse, $y_{m}$ = maximum structural deflection, K = elastic stiffness, M = lump mass of the SDOF system, $F_{m}$ = maximum force on the system.

They defined three damage regimes on a P–I diagram as shown in Table 10 and the general representative of a p–i diagram is demonstrated in Fig. 27.

Table 10 Three regimes of P–I diagram in the Li and Meng [63] study

Fig. 27

Normalized p–i diagram in the Li and Meng study [63]

Where p₁ and i₁ are the threshold values to distinguish Regimes I, II, and III on a p–i diagram. Also a unique effective P–I diagram, which is independent of pulse loading shape, is obtained in their study as shown in Fig. 28.

Fig. 28

Unique effective P–I diagram in the Li and Meng study [63]

Syed used bilinear and nonlinear resistance functions in SDOF analysis to obtain the P–I diagrams to correlate the blast pressure and the corresponding concrete flexural damage [95]. Syed et al. [95] utilized the UFC-3-340-02 [1] damage criteria for damage assessment of RC panel and beam in equivalent SDOF analysis. They obtained P–I diagrams of the panel with 1% reinforcement for different damage levels by using Nonlinear and Bilinear resistance functions as shown in Fig. 29.

Fig. 29

P–I diagrams of the panel with 1% reinforcement for different damage levels using a nonlinear, b bilinear resistance functions

Li and Meng [120] observed pulse loading shape effects on P–I diagram of an elastic–plastic, single-degree-of-freedom structural model. A general descending pulse load is described by Li and Meng [120]:

$$f\left( \tau \right) = \left( {1 - \lambda \frac{\tau }{{\tau_{d} }}} \right)\exp ( - \gamma \frac{\tau }{{\tau_{d} }}) for 0 < \tau < \tau_{d}$$

(18)

$$f\left( \tau \right) = 0\quad for\quad \tau > \tau_{d}$$

(19)

$\alpha$ and loading pulse shape are the parameters which influence the P–I diagram defined by Eq. (20). The influence of $\alpha$ on the P–I diagram can be separated, i.e.

$$g\left( {p,i} \right) = 1$$

(20)

$$g\left( {\frac{p}{{h_{1} \left( \alpha \right)}},\frac{i}{{h_{2(} \alpha )}}} \right) = 1$$

(21)

$$h_{1} \left( \alpha \right) = 0.2993 + 1.6065\alpha - 0.9448\alpha^{2}$$

(22)

$$h_{2} \left( \alpha \right) = 0.0204 + 2.015\alpha - 1.0216\alpha^{2}$$

(23)

Figure 30a–c shows the non-dimensional P–I diagrams for rectangular, triangle and exponential loading shapes and Fig. 30d demonstrates the normalized non-dimensional P–I diagram for three pulse shapes with various α values from 0.1 to 1.0.

Fig. 30

Non-dimensional P–I diagrams for a rectangular loading shape, b triangle loading shape, c exponential loading shape and d Normalized non-dimensional P–I diagrams for three pulse loading shapes with various α values from 0.1 to 1.0. Source: [120]

6.1.2 Energy Balance Method

Energy balance approach is mostly used to generate P–I curves. In this approach two distinct energy formulations exists that include impulsive and quasi-static loading regime. To obtain the impulsive asymptote, it can be assumed that due to inertia effects the initial total energy imparted to the system is in the form of kinetic energy only. Equating this to the total strain energy stored in the system at its final state (i.e. maximum response), one obtains an expression for the impulsive asymptote. For the quasi-static loading regime, the load can be assumed to be constant before the maximum deformation is achieved. By equating the work done by load to the total strain energy gained by the system, the expression for the quasi-static asymptotes is obtained. Expressing these approaches mathematically, one obtains

$$K.E = S.E\quad Impulsive\;asymptote$$

(24)

$$W.E = S.E\quad Quasi - static\;asymptote$$

(25)

where $K.E$ = kinetic energy, $S.E$ = strain energy, $W.E$ = maximum work.

The energy expressions for elastic system are

$$K.E = \frac{{I^{2} }}{2M}$$

(26)

$$W.E = P_{0} x_{max}$$

(27)

$$S.E = \frac{1}{2}Kx_{max}^{2}$$

(28)

Energy balance method greatly reduces computation and its formulation is enforceable to the impulsive and quasi-static regimes. The dynamic regime of the P–I diagram approximated using analytical functions. For this purpose, Baker et al. [31] introduced a correlation as follows:

$$S.E. = W.D.tanh^{2} \sqrt {(K.E./W.E.)}$$

(29)

Soh and Krauthammer [61] represent the energy balance method for an undamped, perfectly elastic SDOF system that shown in Fig. 31a. According to Fig. 31a:

Fig. 31

Typical response spectra and P–I diagram [61], a shock spectrum, b P–I diagram

• Xmax = The maximum displacement

• M = lumped mass

• K = spring stiffness

• P₀ = peak load

• t_d = load duration

• T = natural period

Figure 31b is shown the same response spectrum transformed into a P–I diagram. The response spectrum focuses the influence of scaled time on the system response, while the P–I diagram shows the combination of peak load and impulse for a given damage level [61].

The P–I curve indicates the combination of pressure and impulse values that will cause the specified damage that the curve divides into two regions which indicate either failure or non-failure cases. The right and above of the diagram shown the threshold curve indicates failure in excess of the specified damage level criterion and the left and below of the diagram shown the curve indicates no failure.

In structural dynamics is a correlation between the structural response and the ratio of the load duration to the natural period of the structure [35, 40]. This relationship can be categorized into the impulsive, dynamic and quasi-static regimes. As seen in Fig. 33, the P–I diagram better differentiates the impulsive and quasi-static regimes, in the form of vertical and horizontal asymptotes.

Oswald and Skerhut [121] recommend the simple hyperbolic function, shown in Eq. (30) to curve-fit the transition region, where A and B are the values of the impulsive asymptote and quasi-static asymptote, respectively. This equation is based on limited comparisons to response curves developed with dynamic SDOF analyses, where blast loading has been idealized as a triangular pressure history with the same impulse as the positive phase of the blast wave. Modifications of this approach can be obtained by shifting the curves to fit test data [121]:

$$\left( {\bar{P} - A} \right)(\bar{I} - B) = 0.4\left( {\frac{A}{2} + \frac{B}{2}} \right)^{1.5}$$

(30)

Blasko et al. [112] developed a more efficient search algorithm. The procedure uses a single radial search direction, originating from a pivot point (I_p, P_p) which is located in the failure zone of the P–I diagram (see Fig. 32). Iterations using Bisection method are carried to generate the threshold curve. This approach can be applied effectively to any structural system for which a resistance function can be defined.

Fig. 32

Search algorithm for P–I diagram. a Establish pivot point. b Data pivot search [112]

Qasrawi et al. [98] evaluated P–I diagrams for concrete-filled FRP tubes under field close-in blast loading based on the analytical and experimental work. They used the following formulae to approximate the impulsive, dynamic and quasi-static region.

$$I = \sqrt {2M_{eq} \int_{0}^{{y_{max} }} {R\left( y \right)dy} }$$

(31)

$$F = \frac{{\mathop \smallint \nolimits_{0}^{{y_{max} }} R\left( y \right)dy}}{{y_{max} }}$$

(32)

$$\int_{0}^{{y_{max} }} {R\left( y \right)dy} = Fy_{max} tanh^{2} \sqrt {\frac{{I^{2} }}{{2M_{eq} Fy_{max} }}}$$

(33)

where F = force, I = impulse, M_eq = SDOF equivalent mass, y_max = SDOF displacement of interest, R(y) = SDOF resistance function, y_max = SDOF displacement of interest, R(y) = SDOF resistance function.

Rhijnsburger et al. [62] presented a procedure to generate P–I diagrams by utilizing multiple analytical techniques. The energy balance method estimates the impulsive and quasi-static asymptotes, while a numerical analysis procedure generates the dynamic regime using a branch-tracing algorithm. This process, as shown in Fig. 33, extrapolates the slope on the curve from two previously known points and a prediction point is made. A response calculation follows with the predicted P–I combination, and the ductility of the system is obtained.

Fig. 33

Branch-tracing technique [62]

Krauthammer et al. [66] observed P–I diagrams for the behaviour assessment of structural elements under transient loads. In their research for deriving P–I diagrams three different search algorithms developed. The P–I diagrams of a linear elastic system under rectangular and triangular load pulses are derived and also they illustrated these approaches to assessment of tested structural elements. They also observed the Influence of load and structural properties on the P–I diagrams. They evaluated the influence of pulse shape, rise time, damping and ductility on the P–I diagram that shown in Fig. 34.

Fig. 34

Influence of pulse shape, rise time, damping and ductility on the P–I diagram. Source: [66]

6.2 Numerical Modelling

This section is the basis to derive P–I diagram by using the numerical method for the reinforced concrete structures subjected to explosive loadings. The use of finite element modeling has many advantages over using SDOF modeling. First, it allows using different elastic–plastic material models for concrete. The sophisticated concrete material models that have been developed for different applications provide more accurate representation of the actual response of concrete. Second, finite element modeling allows that steel reinforcements be modeled as discrete elements using separate material models while coupled with concrete elements. This type of modelling improves the accuracy of the results. In addition, it provides a means for modelling several arrangements of reinforcement and studying the effect of change in the ratio and form of reinforcement as well as the effect of confinement provided by various types and spacing of transverse reinforcement. Third, finite element modeling by using LS-DYNA allows that the blast loads are applied to the structure in two methods. One method is calculating the pressure–time history of a blast event and then, applying the blast pressure directly on the surfaces of the structure. Another method is using the Load_Blast feature of LS-DYNA, defining the blast parameters, and allowing the program to apply the blast pressure on the surfaces of the structure. Table 11 represent the brief of numerical study to evaluate the P–I diagram under blast and impact loads in different structures such as slabs, columns, frame etc.

Table 11 Brief of numerical works

Astarlioglu and Krauthammer [132] presented response of normal-strength and ultra-high-performance fiber-reinforced concrete columns to idealized blast loads. In their research a numerical study was used to study the response of a normal-strength concrete (NSC) column that was not design for blast resistance subjected to four levels of idealized blast loads. Then, to compare the behaviour of the NSC column with a column made with ultra-high performance fiber reinforced concrete (UHPFRC) that had the same dimensions and reinforcing details as the NSC column and subjected to the same loading conditions. The boundary conditions and the level of compressive axial load due to gravity were also considered in the analyses. The behavioural comparisons were made both in the time-history domain, as well as in the load–impulse (P–I) domain. They generated P–I diagram for simply supported and fixed of NSC and UHPFRC columns as shown in Fig. 35.

Fig. 35

P–I diagram for simply supported (a, b) and fixed (c, d) of NSC and UHPFRC columns [132]

Numerical study on the dynamic response of RC columns under axial and blast-induced transverse loads performed in the Astarlioglu et al. [136] research. They observed two parameters in their study that is longitudinal reinforcement ratio and level of axial force. The influence of diagonal shear, flexural, and tension behaviours were included in the RC column response and blast loads were idealized as triangular load. They use ABAQUS to validation of the results from the SDOF analyses. In their research the parametric study demonstrated that the level of axial compressive load has a significant effect on the behaviour of RC columns.

Shi et al. [41] developed P–I diagrams for reinforced concrete columns by using numerical analysis performed using LS-DYNA. The residual axial load carrying capacity of columns was selected as the damage criterion for development of P–I diagrams. Effect of different parameters including column depth, height, and width, concrete strength, transverse reinforcement ratio, and longitudinal reinforcement ratio was evaluated by comparing the P–I diagrams developed for each case. Figure 36 shows the P–I diagram of RC column derived from (a) Numerical data and fitted curves; (b) fitted curves according to Eq. 34 and (c) comparison of the curves in (a) and (b).

Fig. 36

P–I diagram for RC column. a Numerical data and fitted curves; b fitted curves according to Eq. 34; c comparison of the curves in (a) and (b) [41]

Also they expressed analytically formula to generate P–I diagram that defined as

$$\left( {P - P_{0} } \right)\left( {I - I_{0} } \right) = 12\left( {\frac{{P_{0} }}{2} + \frac{{I_{0} }}{2}} \right)^{1.5}$$

(34)

where P₀ = the pressure asymptote, I₀ = the impulsive asymptote.

Shi et al. [41] derived analytical formulae based on the numerical results to predict the pressure asymptotes and impulsive asymptotes for the P–I curves when the degree of damage equals 0.2, 0.5 and 0.8. They are

$$\begin{aligned} P_{0} \left( {0.2} \right) & = 1000\left[ {0.007exp\left( {\frac{{\rho_{s} }}{0.01}} \right) + 0.069\left( {\frac{\rho }{0.01}} \right) + 0.034exp\left( {\frac{{f_{c}^{{\prime }} }}{30}} \right) - 0.835ln\left( {\frac{H}{4}} \right)} \right. \\ & + \left. {\left( {\frac{h}{0.6}} \right)^{1.804} +\, 0.067ln\left( {\frac{b}{0.6}} \right) - 0.168} \right] \\ \end{aligned}$$

(35)

$$\begin{aligned} I_{0} \left( {0.2} \right) & = 1000\left[ {0.053exp\left( {\frac{{\rho_{s} }}{0.01}} \right) + 0.107\left( {\frac{\rho }{0.01}} \right) + 0.021exp\left( {\frac{{f_{c}^{{\prime }} }}{30}} \right)} \right. \\ & + \left. {\left( {\frac{H}{4}} \right)^{ - 0.207} + 1.203exp\left( {\frac{h}{0.6}} \right) - 0.943ln\left( {\frac{b}{0.6}} \right) - 2.686} \right] \\ \end{aligned}$$

(36)

$$\begin{aligned} P_{0} \left( {0.5} \right) & = 1000\left[ {0.143ln\left( {\frac{{\rho_{s} }}{0.01}} \right) + 0.32ln\left( {\frac{\rho }{0.01}} \right) + 0.063exp\left( {\frac{{f_{c}^{{\prime }} }}{30}} \right)} \right. \\ & + \left. {\left( {\frac{H}{4}} \right)^{ - 1.39} + \,2.639\left( {\frac{h}{0.6}} \right) + 0.318ln\left( {\frac{b}{0.6}} \right) - 2.271} \right] \\ \end{aligned}$$

(37)

$$\begin{aligned} I_{0} \left( {0.5} \right) & = 1000\left[ {0.837\left( {\frac{{\rho_{s} }}{0.01}} \right) + 0.036\left( {\frac{\rho }{0.01}} \right) + 0.235exp\left( {\frac{{f_{c}^{{\prime }} }}{30}} \right)} \right. \\ & \left. { - \left( {\frac{H}{4}} \right)^{ - 0.274} +\, 2.271exp\left( {\frac{h}{0.6}} \right) - 0.998ln\left( {\frac{b}{0.6}} \right) - 5.286} \right] \\ \end{aligned}$$

(38)

$$\begin{aligned} P_{0} \left( {0.8} \right) & = 1000\left[ {0.062ln\left( {\frac{{\rho_{s} }}{0.01}} \right) + 0.238\left( {\frac{\rho }{0.01}} \right) + 0.291ln\left( {\frac{{f_{c}^{{\prime }} }}{30}} \right)} \right. \\ & \left. { - 1.676ln\left( {\frac{H}{4}} \right) + 2.439ln\left( {\frac{h}{0.6}} \right) + 0.21ln\left( {\frac{b}{0.6}} \right) + 1.563} \right] \\ \end{aligned}$$

(39)

$$I_{0} \left( {0.8} \right) = 1000\left[ {3.448\left( {\frac{{\rho_{s} }}{0.01}} \right) - 0.254\left( {\frac{\rho }{0.01}} \right) + 1.2\left( {\frac{{f_{c}^{'} }}{30}} \right) - 0.521\left( {\frac{H}{4}} \right) + 6.993\left( {\frac{h}{0.6}} \right) - 2.759ln\left( {\frac{b}{0.6}} \right) - 2.035} \right]$$

(40)

A correlations between the damage levels of FRP strengthened RC columns and blast loadings for FRP strengthened RC columns numerically performed in the Mutalib and Hao [42] study. They developed Numerical model of RC columns without and with FRP strengthening using LS-DYNA. In their study the residual axial-load carrying capacity is utilized to quantify the damage level. They also observed Dynamic response and damage of RC columns with different FRP strengthening measures using the developed numerical model and compare with the Eq. 34 as shown in Fig. 37.

Fig. 37

Comparison of P–I curves of strengthened RC column with FRP wrap and strips from Eq. (34) and the fitted numerical data [42]

They performed parametric studies on the P–I curves and generate empirical formulae to predict the impulse and pressure asymptote of P–I curves. These empirical formulae can be used to construct P–I curves for assessment of blast loading resistance capacities of RC columns with different FRP strengthening measures.

$$P_{O} \left( {0.2} \right) = 7.25f_{cu} + 2.37d - 0.147H - 0.414b + 7342.47\rho + 10073.44\rho_{s} + \alpha_{1}$$

(41)

$$I_{O} \left( {0.2} \right) = 25f_{cu} + 7.289d - 0.158H - 0.168b + 19261.3\rho + 44864.881\rho_{s} - 2398.62 + \alpha_{2}$$

(42)

$$P_{O} \left( {0.5} \right) = 2f_{cu} + 3.174d - 0.217H - 0.445b + 15786.72\rho + 18137.95\rho_{s} + 210 + \alpha_{3}$$

(43)

$$I_{O} \left( {0.5} \right) = 27.5f_{cu} + 9.75d - 0.168H - 1.776b + 13121.77\rho + 29433.94\rho_{s} - 1848.178 + \alpha_{4}$$

(44)

$$P_{O} \left( {0.8} \right) = 11f_{cu} + 3.456d - 0.268H - 1.552b + 14753.44\rho + 8924.068\rho_{s} + 851.90 + \alpha_{5}$$

(45)

$$I_{O} \left( {0.8} \right) = 59f_{cu} + 13.16d - 0.43H - 0.26b + 1091.78\rho + 489.97\rho_{s} - 3302.33 + \alpha_{6}$$

(46)

where $\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,\alpha_{4} ,\alpha_{5} ,\alpha_{6} = 0$ for non-retrofitted RC columns, while for FRP strengthened RC columns,

$$\alpha_{1} = \exp \left( {0.000169f_{strip} + 0.000423f_{wrap} + 0.252t_{wrap} + 3.114} \right)$$

(47)

$$\alpha_{2} = \exp \left( {0.000163f_{strip} - 0.000132f_{wrap} + 0.307t_{wrap} + 5.09} \right)$$

(48)

$$\alpha_{3} = 0.0539f_{strip} - 0.00909f_{wrap} + 54.53t_{wrap} + 32.302$$

(49)

$$\alpha_{4} = \exp \left( { - 0.00000295f_{strip} + 0.00124f_{wrap} + 0.382t_{wrap} + 2.524} \right)$$

(50)

$$\alpha_{5} = \exp \left( {0.000189f_{strip} + 0.0000795f_{wrap} 0.16t_{wrap} + 4.286} \right)$$

(51)

$$\alpha_{6} = \exp \left( {0.0000868f_{strip} + 0.0012f_{wrap} + 0.549t_{wrap} + 2.068} \right)$$

(52)

Bao and Li [142] performed numerical simulation using LS-DYNA to evaluate the influence of longitudinal reinforcement ratio, transverse reinforcement ratio, axial load and column aspect ratio on the damage level of RC columns under blast loading. They did not construct P–I curves, they used impulse to study and compare the effect of each parameter on the residual lateral displacement and residual axial capacity of columns [142].

6.3 Experimental Study

This section describes the experimental works to develop P–I diagrams for reinforced concrete structures under blast loads. To evaluate the P–I diagram under extreme loading some experimental study are available in the literature that shown in the Table 12.

Table 12 Summary of experimental works

Parlin et al. [148] performed experimentally and numerically assess the dynamic blast response of lightweight wood-based flexible wall panels and development of P–I diagrams based on a maximum deflection damage criterion. In their study laboratory pseudo-static bending tests were performed to determine the panel’s load-deformation properties. They developed P–I diagrams using both linear and nonlinear dynamic analysis. They indicate that the blast response of the wall panels can be reasonably represented with a nonlinear SDOF dynamic model and also they indicate that P–I diagrams are a potentially valuable tool for assessing damage under a variety of blast loads.

Wang et al. [94] presented a method to generate P–I diagram with multiple failure modes of one-way reinforced concrete slab subject to blast loads by utilizing two loosely coupled single degree of freedom model. In their study the results of blast test show SDOF system are better predicting the failure mode of the slab by incorporating the influence of the strain rate effect caused by rapid load application. They proposed analytical formulae to generate P–I diagrams as follows:

$$\left( {P - P_{0} } \right)\left( {I - I_{0} } \right)^{n} = 0.33\left( {\frac{{P_{0} }}{2} + \frac{{I_{0} }}{2}} \right)^{1.5}$$

(53)

They observed P–I diagram for two failure modes with different damage criteria and they evaluated various parameters like concrete strength reinforcement ratio and span length of the slab on the P–I diagram. These results demonstrate when a slab is of a smaller span length, slab tends to fail in direct shear mode and when it is of a larger span length. Slab tends to fail in flexure mode. Also the presented that flexure and shear capacity increased when concrete strength or reinforced ratio are increased. According on the results a simplified method and an analytical equation for the P–I diagram for RC slabs are proposed for different failure modes and damage levels.

Shope [67] observed comparisons of an alternative P–I formulation with experimental and finite element results. The failure criterion used in then Shope [67] study is based on the assumption of FACEDAP that yielding occurs in the centre of the slab first, and then propagates out to the corners. The P–I curve for test data were obtained from tests conducted by the Defense Threat Reduction Agency over a period of several years shown in Fig. 39. A 10 degree support rotation failure criterion was used to determine the impulse asymptote in the Fig. 38. The red points in Fig. 38 represent specimens that failed during the test as a result of the blast load. The blue points represent specimens that survived. Ideally, all red points should be above the line, which would indicate failure by the P–I model, and all blue points should plot below the line. Point C on Fig. 38 is labelled severe damage. For this case, the floor slab was not destroyed but major cracking, exposed rebar, and permanent deformation was observed after the test. The P–I model predicts failure, but the point is only slightly above the failure line, indicating that this case is near the threshold for surviving.

Fig. 38

Test data plotted on P–I curve in Shope [67] study

The Facility and Component Explosive Damage Assessment Program (FACEDAP) uses P–I curves that relate air blast environment and structural element properties to damage level (or survivability for 100% level) [156]. FACEDAP specifies that the damage of the structural components can be determined in terms of qualitative and quantitative damage levels. Their qualitative damage criterion depends on the reusable and repairable of the structural component which is not straightforward to be objectively determined in numerical simulations. Whereas its quantitative damage criteria are based on the member’s ductility ratio defined as the ratio of the maximum deflection to the yield deflection at mid span or the ratio of the maximum deflection to the span length. Actually FACEDAP provides damage response curves for a variety of building components in a dimensionless P–I space. Figure 39 shows an example P–I curve for two-way reinforced concrete slabs. The curve shown in Fig. 39 can be used to quickly estimate the level of damage or survivability of a reinforced concrete slab. First, the values of P_bar and I_bar are calculated for a given element and load. Next, the point is plotted on the curve. Based on the P–I curve estimate, the slab will experience the given level of damage if the point falls above the corresponding curve.

Fig. 39

P–I diagram of two-way reinforced concrete [156] $Ibar = \sqrt {\frac{Eg}{\gamma }\left( {\frac{{I_{eff} }}{{\emptyset_{i} M_{p} ch}}} \right)i} ,\quad Pbar = \frac{{px^{2} I_{eff} }}{{4\emptyset_{p} M_{p} ch^{2} }}$

Wesevich and Oswald [152] generate P–I diagrams for varying Degrees of Damage in concrete masonry unit (CMU) walls subjected to blast loads. A general pictorial representation of each damage level is provided in Fig. 40. They used Eqs. 54 and 55 to compute the non-dimensionalized P–I data points for common and retrofitted wall configurations.

Fig. 40

Wall damage classifications in the Wesevich and Oswald study [152]

$$P_{bar} = \frac{{PL^{2} }}{{K_{p} M}}$$

(54)

$$I_{bar} = i\sqrt {\frac{{L_{g} }}{{K_{LM} K_{r} wM}}}$$

(55)

Figure 41 show the non-dimensionalized P–I diagrams masonry wall test data for Unreinforced, reinforced, E-Glass retrofitted and comparison of blast capacities between a typical retrofitted and un-retrofitted reinforced masonry wall.

Fig. 41

P–I diagrams for a unreinforced wall, b reinforced wall, c E-Glass retrofitted wall and d potential blast capacity enhancement of typical reinforced CMU Wall [152]

7 Recommendation of Future Studies

Based on the research study conducted, the following recommendations are made for future research work on the P–I diagrams.

• P–I diagrams for strengthening structures

• Development damage for different structural elements and different boundary condition

• Derivation of formulae for different structural elements and different boundary condition

• Development of P–I diagram using different finite element modeling software

• Through experimental works since it is very limited

• P–I diagrams for other materials and the combination of a few materials to enhance a structural blast resistance capacity

• Development of P–I diagram for complex geometry and boundary conditions

8 Conclusion

The structural response evaluation of reinforced concrete structures has been carried out through the generation of P–I diagram. This research is an attempt to a review of P–I diagrams for RC structures under blast loading. P–I diagrams is found to be greatly influenced by shape of pulse load, geometry of the structure and material properties. An explanation of the blast loads and the modes of failure under explosive loads are given. This paper introduces analytical, numerical and experimental methods to develop P–I diagrams in reinforced concrete (RC) structures. Experimental testing of blast load is expensive and requires much preparation. On the other hand, design guidelines may be expedient to design against specific threats but also come with a cost as they should not be applied to all cases and may not yield the most cost efficient design as conservative measures may be built into them. Numerical simulation of blast experiments is the most widely used approach to verify a design for a specific threat as it offers great capabilities. The data collected from this research are being used to improve the knowledge of how structures will respond to a blast event.